基于热-流-固耦合的齿轮箱稳态热性能研究

doi:10.16183/j.cnki.jsjtu.2023.225

基于热-流-固耦合的齿轮箱稳态热性能研究

刘逸, 张开林^,, 邵帅, 向泓旭

西南交通大学轨道交通运载系统全国重点实验室,成都 610031

Investigation on Steady-State Thermal Performance of Gear Box Based on Thermal-Fluid-Solid Coupling

LIU Yi, ZHANG Kailin^,, SHAO Shuai, XIANG Hongxu

State Key Laboratory of Rail Transit Vehicle System, Southwest Jiaotong University, Chengdu 610031, China

通讯作者: 张开林,研究员;E-mail:zhangkailin@swjtu.cn.

责任编辑: 王一凡

收稿日期: 2023-06-2 修回日期: 2023-07-24 接受日期: 2023-08-28

基金资助:

国家自然科学基金(U2268211)
大功率交流传动电力机车系统集成国家重点实验室开放课题(R111720H01385)

Received: 2023-06-2 Revised: 2023-07-24 Accepted: 2023-08-28

作者简介 About authors

刘逸(1999—),硕士生,从事计算流体动力学研究.

摘要

为准确预测轨道交通传动系统齿轮箱的温度分布,采用一种基于计算流体动力学(CFD)的混合时间尺度耦合法对齿轮箱进行仿真分析.对齿轮箱的内部流场与温度场同时进行数值模拟,通过数据传输实现齿轮箱流场与温度场的实时双向耦合,最后根据内部温度场计算结果,通过有限元方法得到箱体温度分布情况.另外,分析转速、浸油深度、喷油润滑等因素对齿轮箱稳态热性能的影响.研究结果表明:该数值模型在温度预测方面具有良好的性能,仿真结果与实验测量值之间的最大相对误差为7.4%.随着转速的增加,齿轮箱温度随之上升;而随着浸油深度的增加,除下箱体底部温度逐渐上升外,其余区域温度均下降.相同转速时,喷油润滑下的箱体最高温度对比飞溅润滑,降低幅度可达14%;且转速越高,冷却效果越明显.

关键词： 热-流-固耦合; 箱体温度场; 混合时间尺度; 润滑方式; 计算流体动力学

Abstract

In order to accurately predict the temperature distribution of the gearbox of the rail transit transmission system, a mixed timescale coupling method based on computational fluid dynamics (CFD) was adopted to simulate the gearbox. The internal flow field and temperature field of the gearbox were simultaneously simulated, and the real-time two-way coupling between the flow field and temperature field was realized through data transmission. Finally, based on the calculation results of the internal temperature field, the temperature distribution of the gearbox was obtained by using the finite element method. In addition, the effects of rotational speed, immersion depth, injection lubrication, and other factors on the steady-state thermal performance of the gearbox were analyzed. The results show that the numerical model has a good performance in temperature prediction. Moreover, the maximum relative error between the simulation results and the experimental values is 7.4%. With the increase of rotational speed, the temperature of gear box rises accordingly. With the increase of oil immersion depth, except the fact that the bottom temperature of the lower box gradually increases, the temperature of other areas decreases. At the same speed, the maximum temperature of the box under oil injection lubrication can be reduced by up to 14% compared with splash lubrication. In addition, the rotational speed increases, the cooling effect becomes more apparent.

Keywords： thermal-fluid-solid coupling; box temperature field; mixed timescale; lubrication mode; computational fluid dynamics (CFD)

PDF (16774KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘逸, 张开林, 邵帅, 向泓旭. 基于热-流-固耦合的齿轮箱稳态热性能研究[J]. 上海交通大学学报, 2025, 59(5): 666-674 doi:10.16183/j.cnki.jsjtu.2023.225

LIU Yi, ZHANG Kailin, SHAO Shuai, XIANG Hongxu. Investigation on Steady-State Thermal Performance of Gear Box Based on Thermal-Fluid-Solid Coupling[J]. Journal of Shanghai Jiaotong University, 2025, 59(5): 666-674 doi:10.16183/j.cnki.jsjtu.2023.225

齿轮箱作为轨道交通车辆传动系统的关键部件,其可靠性直接影响列车的安全与动力性能.齿轮箱通常采用飞溅润滑,齿轮等零部件的旋转会产生一定的功率损失,引起油温升高.油温的升高会降低润滑油的黏度,进一步增加各零部件产热量,最终会导致齿面点蚀、胶合、轴承磨损甚至烧伤等故障.同时,高温会造成各零部件之间的配合间隙减小甚至消失,产生较大的热应力以及接触应力,从而导致零部件损伤或失效,降低齿轮箱的使用可靠性.因此,准确的预测齿轮箱内部以及箱体的温度分布对列车的正常运行和提升齿轮箱使用寿命等方面都具有重大意义.

关于齿轮箱稳态温度场的研究,主要分为3种方法:实验法、热网络法和有限元法.实验法只可获得某一固定测点温度或零件的平均温度,且周期长、费用高、可重复性差^[1];热网络法尽管简单易行,但计算精度不高^[2];有限元方法可以弥补上述缺点,能够高效预测齿轮箱稳态温度场.陈晓玲等^[3]建立齿轮箱三维模型,以功率损失作为热源项附加在相应位置,并计算不同部件的对流换热系数,对箱体温度场进行仿真分析,但是该研究忽略了箱体内部油气混合物流动对温度场的影响.相比于瞬态温度,研究者们更加关注齿轮箱正常工作时的稳态温度分布.薛浩^[4]和徐宏海等^[5]基于齿轮箱内流场仿真分析结果,计算发热功率与对流换热系数,运用有限元软件分析运行工况参数对齿轮箱稳态温度场分布的影响,但后者在计算发热功率时未考虑风阻的功率损失.鲍和云等^[6]基于Fluent平台,先后对浸油润滑齿轮箱瞬态流场和稳态温度场进行分析.尽管上述研究对齿轮箱稳态温度场进行了详细的分析,但是将稳态热性能的分析,割裂为先后对齿轮箱流场和稳态温度场数值分析的方法与实际情况不符合.Lu等^[7]提出一种双向热流耦合方法对直升机中间齿轮箱进行数值模拟,并使用多参考系(multiple reference frame,MRF)法计算得到中间齿轮箱内的润滑及温度特性.该方法预测的监测点温度与试验结果吻合较好,可以推广到其他齿轮传动系统的温度场仿真计算之中.林腾蛟等^[8]基于计算流体动力学(computational fluid dynamics,CFD)仿真和混合弹流润滑分析,利用有限元法预测星形人字齿轮系统稳态温度场.Deshpande等^[9]提出一种双向耦合方法,预测采用喷油润滑变速器的齿轮温度,预测结果与测量结果具有良好的相关性.

在既往研究中,对于齿轮箱热性能的研究多集中于内部温度场,而对于箱体温度场的研究亟待完善.本文采用一种基于CFD的混合时间尺度耦合法(mixed timescale coupling)来预测飞溅润滑齿轮箱的稳态温度分布.该方法以传热学理论和齿轮摩擦学为基础,建立齿轮箱的热-流-固耦合模型,对齿轮箱的内流场与温度场同时进行数值分析.通过数据传输实现齿轮箱内部流场与温度场的实时双向反馈,最后利用有限元方法得到箱体稳态温度场.此外,还考虑了转速、浸油深度等因素的影响,并对比飞溅润滑与喷油润滑齿轮箱稳态温度分布,分析了齿轮箱稳态温度场在各因素影响下的变化规律.

1 数值分析理论

1.1 控制方程

应用CFD方法计算齿轮箱的耦合模型时需要满足3个基本方程:质量守恒方程、动量守恒方程与能量守恒方程^[10].在求解基本方程的过程中,其温度场需要较长时间才能达到稳态,对仿真计算资源的消耗巨大.MRF模型将流动运动方程转换到旋转坐标系中,在相对静止的旋转坐标系中得出数值解.MRF模型属于稳态模型,能够得出可信的计算结果^[6].

1.2 多相流模型与湍流模型

齿轮箱飞溅润滑只存在油-气两相,为了准确分析油液分布,选用流体体积法^[11] (volume of fluid,VOF)两相流模型分析齿轮箱内部流场.相比于VOF模型,Mixture模型更适用于流动过程中存在相混合或分离的情形,常用于模拟耦合关系较强的两相流体.该模型计算稳定、容易收敛,故在齿轮箱内部温度场分析中,选用Mixture模型求解油气混合物的连续性方程、动量守恒方程与能量守恒方程.

为保证计算精度的同时减少计算时长,引入湍流模型,因不需要对每个单独的漩涡求解,从而提高了计算效率.考虑齿轮箱飞溅润滑的内流场具有高应变率和流线弯曲程度大等特点,选择重整化群(renormalization group,RNG) k-ε湍流模型^[12-13]:

(1)

\frac{\partial (ρ k)}{\partial t} + \frac{\partial (ρ k u_{i})}{\partial x_{i}} = \frac{\partial}{\partial x_{j}} [(α_{k} μ_{e f f}) \frac{\partial k}{\partial x_{j}}] + G_{k} + G_{b} - ρ ε - Y_{M} + S_{k}

(2)

\frac{\partial (ρ ε)}{\partial t} + \frac{\partial (ρ ε u_{i})}{\partial x_{i}} = \frac{\partial}{\partial x_{j}} [(α_{ε} μ_{e f f}) \frac{\partial ε}{\partial x_{j}}] + C_{1 ε} \frac{ε}{k} (G_{k} + C_{3 ε} G_{b}) - C_{2 ε} ρ \frac{ε^{2}}{k} + S_{ε}

式中: ρ为流体密度;t为时间;u_i为流体速度沿坐标轴分量;k为湍动能;ε为湍流耗散率;G_k为平均速度梯度引起的湍动能;G_b为浮力引起的湍动能;Y_M为可压缩流体的脉动扩张;α_k、α_ε分别为k、ε的有效普朗特数的倒数;C_1ε、C_2ε、C_3ε为常数;S_k、S_ε为源相;μ_eff为有效黏度,μ_eff=μ_t+μ,其中μ为流体动力黏性系数,μ_t 为湍动黏度.

1.3 混合时间尺度耦合法

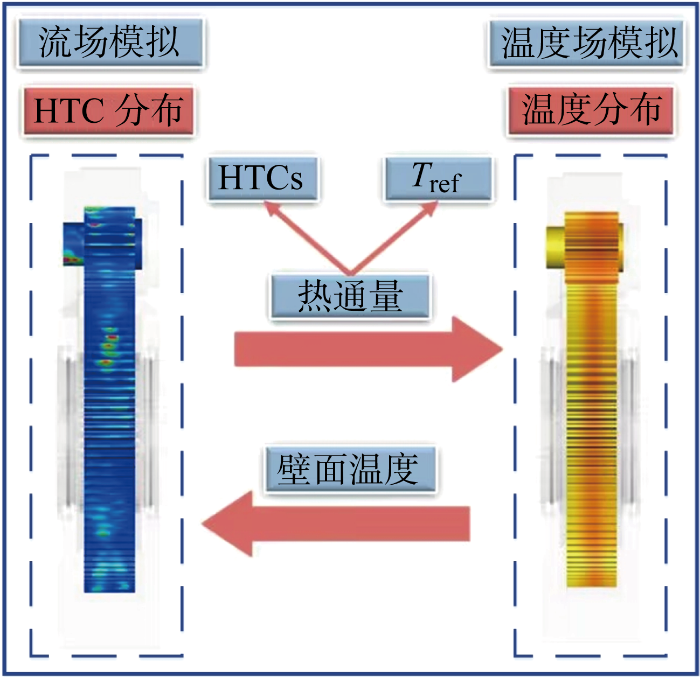
在对齿轮箱的温度场进行数值分析的过程中,固体与流体的传热方式不同,传热能力差异显著,导致流固耦合传热时间尺度跨度较大.固体部分热惯性大,温度达到稳态的时间在分钟级;液体部分热惯性小,温度达到稳态的时间在秒级.若直接进行耦合计算,时间尺度不一致,计算量巨大.因此,采用混合时间尺度耦合法解决齿轮箱共轭传热时长的问题.

该耦合方法如图1所示.流体部分模拟采用瞬态方法计算,利用实时获得的齿轮箱内部油气混合物的分布场、速度场和压力场求解对流换热.对于和固体接触的流体表面,将其热通量以对流换热系数(heat transfer coefficient,HTC)和参考温度(reference temperature,T_ref)的形式映射到固体域的数值模拟中.固体部分传热模拟采用稳态方法计算,以发热部件为热源,并利用由流体表面传递的边界条件进行热分析,收敛后将温度场结果映射回流体模拟.耦合分析重复上述步骤,直至所有流固接触面的热通量达到平衡,且固体域温度稳定为止.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 齿轮箱热-流-固耦合关系

Fig.1 Thermal-fluid-solid coupling of gear box

2 齿轮箱仿真模型

2.1 几何模型与网格划分

所研究的轨道交通传动齿轮箱主要结构包括:上箱体、下箱体、齿轮副、轴承等.图2展示了齿轮箱的三维模型.图2(a)为齿轮箱结构爆炸视图,本文主要分析齿轮箱的内部温度场和箱体温度场,因此忽略输出轴端盖、输出轴衬套、轴承止挡、输出轴密封圈、齿轮轴等部件.简化后提取的流体域模型如图2(b),为了分析齿轮箱关键位置的温度,在相应位置设置监测点进行记录.另外,为对比两种润滑方式的温度分布,在啮合区上方设置喷油孔.

图2

新窗口打开| 下载原图ZIP| 生成PPT

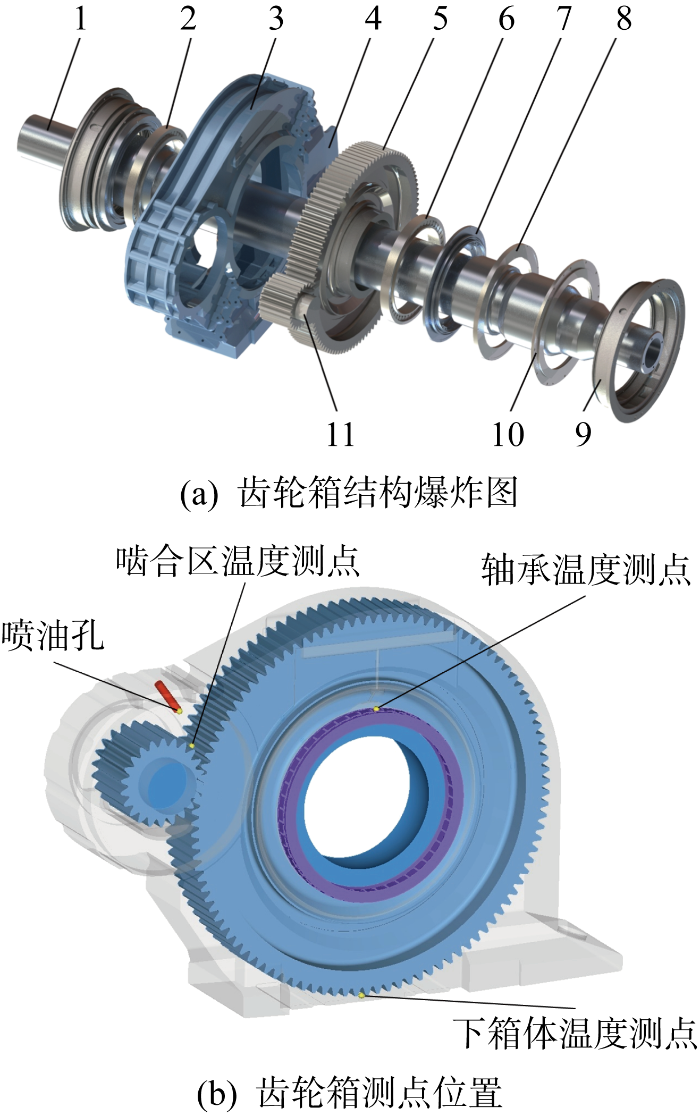
图2 齿轮箱三维模型

1—输出轴,2—输出轴车轮侧圆柱滚子轴承(GW),3—齿轮箱上箱体,4—齿轮箱下箱体,5—从动齿轮,6—电动机侧输出轴圆柱滚子轴承(GM),7—输出轴密封圈,8—轴承止挡,9—输出轴端盖,10—输出轴衬套,11—主动齿轮

Fig.2 3D model decomposition of gear box

齿轮啮合区域狭小的间隙给流体域网格划分以及仿真分析带来极大困难,为在保留齿轮真实结构的前提下解决这个问题,将齿轮副缩放至原始尺寸的99%^[6].齿轮副参数如表1所示.

表1 齿轮结构参数

Tab.1 Parameters of gear structure

参数	取值
压力角,α/(°)	22.5
传动比,i	103/22
齿轮导热系数,k_gear/[W·(m·K)^-1]	40
齿轮模数,m/mm	9
齿轮齿宽,b/mm	150
比热容,c/[J·(kg·K)^-1]	9
齿轮中心距,a/mm	567
齿高,h/mm	20

新窗口打开| 下载CSV

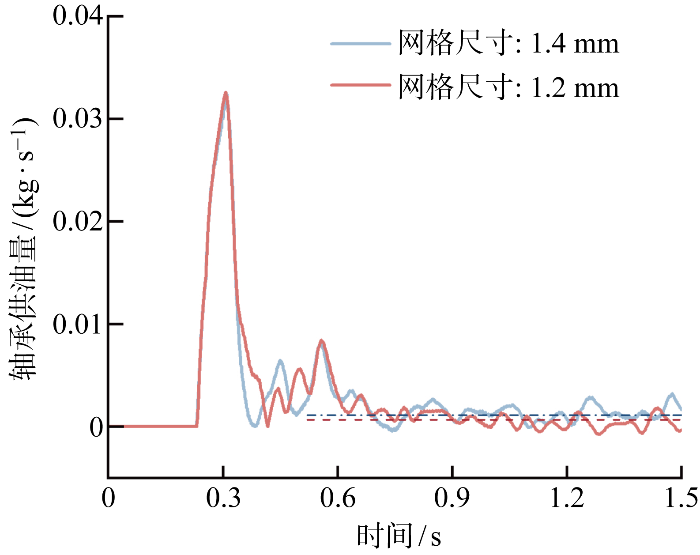
由于齿轮箱内部结构复杂,且流体域中齿轮啮合区流体变形大,为使网格更好适应几何形状,旋转啮合区域划分为结构化网格,非旋转区选用几何等角自适应二叉树网格,提高计算精度和效率.若要使有限元模型中细小流道更好地与实际模型中对应结构吻合,整体网格尺寸需要小于2 mm.因此,分别采用1.4和1.2 mm两种不同整体网格尺寸的数值模型计算轴承供油量,结果如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 不同网格模型下轴承供油量

Fig.3 Oil supply for the bearings of different grid quality models

由图3可知,初始时刻,两种网格模型下的实时轴承供油量数值相近,变化趋势相同.0.6 s后稳定,两种网格模型下的轴承供油量平均值相近.计算资源方面,采用12核(Intel Core i7-8700K CPU 3.70 GHz)处理器.网格尺寸为1.4 mm时,仿真总耗时约86 h,而当网格尺寸为1.2 mm时,仿真总耗时约152 h.显然,1.4 mm网格尺寸可在保证精度的同时,还拥有远高于1.2 mm网格尺寸的计算效率.因此,本文仿真模型采用整体尺寸为1.4 mm的网格进行模拟.最终流体域网格数为 1 388 859,网格节点数为 1 722 228.对于固体域,将箱体模型划分为四面体非结构化网格,为了避免网格过疏降低精确度与网格过密增加计算时长,对箱体网格进行局部细化,最终箱体固体域网格数为 3 216 711,网格节点数为 704 710.

2.2 物性参数

齿轮箱采用牌号为80W-140的润滑油,在本研究中,密度和黏度是润滑油的重要指标,考虑到温度对润滑油物理性质的影响,参照40与100 ℃下润滑油的相关物理参数,依据标准AGMA 925 A03给出的表达式,计算得出不同油温下对应的密度与黏度:

(3)lg[lg(ν+0.7)]=A-Blg T

$B = \frac{l g [l g (ν_{40} + 0.7)] - l g [l g (ν_{100} + 0.7)]}{l g 373.15 - l g 313.15}$

A=lg[lg(ν₄₀+0.7)]+Blg 313.5

式中: T为绝对温度; A和B是常数;ν₄₀和ν₁₀₀ 分别是油温在40和100 ℃时的运动黏度.

2.3 边界条件

使用有限元方法分析齿轮箱内部热性能时,准确计算各部件的发热功率与对流换热系数非常重要.齿轮箱内热源包括齿轮啮合功率损失、齿轮搅油功率损失、齿轮风阻功率损失和轴承摩擦功率损失;外热源主要为电动机运行中产生的热辐射,可忽略不计.齿轮副在啮合过程中由于相对滑动和滚动造成的功率损失,采用Coy等^[14]提出的公式计算.齿轮箱飞溅润滑中,搅油功率损失占比较大,相比于Luke等^[15]的方法,Changenet等^[16]提出的计算公式在不同影响因素下对搅油功率损失的计算更加准确,故采用Changenet提出的方法计算搅油功率损失.依据Anderson等^[17]的方法计算齿轮风阻功率损失,轴承功率损失采用ISO/TR 14179^[18]中提出的方法求解.在以上对齿轮箱内各部件发热功率的计算中,所用润滑油的浓度由内部流场的仿真结果提取得到,所用油气混合物的物性参数根据文献[19]中的方法求解得到.齿轮箱散热包括箱体散热和齿轮散热两部分,其散热能力与各流固接触面的对流换热系数有重要的联系,而对流换热系数由流体模拟获得的实时油气混合物分布场、压力场和速度场共同求解得到.

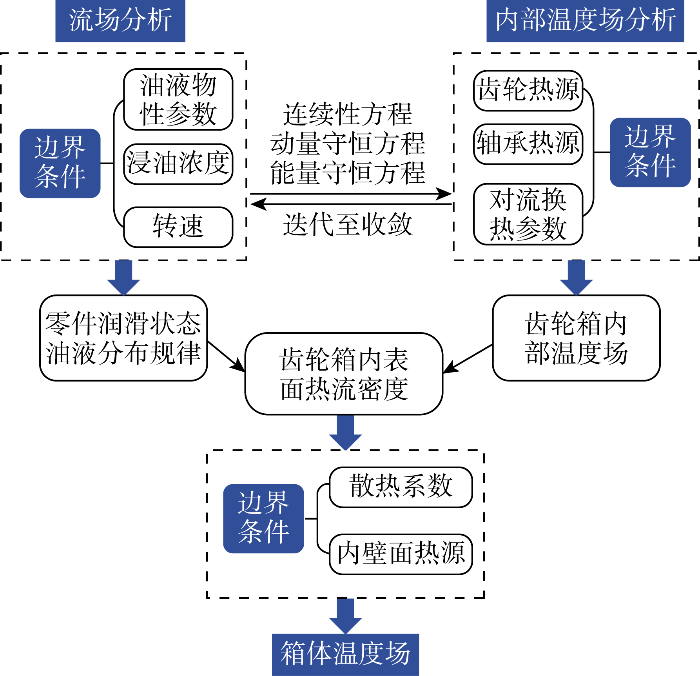
热-流-固耦合方法的关键在于流体与固体的热量传递,本文研究方法如图4所示.由图4可知,在齿轮箱内部的流场分析中,将微分方程离散化为有限差分方程并求解,得到油气混合物分布场、压力场和速度场,进而求得齿轮箱内部对流换热情况.在齿轮箱内部的热分析中,齿轮和轴承为体热源,并通过热传导、热对流和各流固接触面的对流换热进行热传递.求解流体和固体的能量方程,得到两相流体和固体部件的温度.上述迭代过程的同时,热通量在流体与固体之间传递,直至流体传递至固体的参考温度与固体传递给流体的温度场平衡,并且固体部分的温度达到稳态.在箱体的热分析中,将箱内热平衡后流体域外表面的热流密度作为热源施加在箱体内壁面,通过热传导与对流换热进行热传递.求解固体能量方程,最终得到箱体温度场.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 热-流-固耦合方法流程图

Fig.4 Flow chart of heat-fluid-structure coupling method

3 齿轮箱稳态仿真结果与分析

3.1 齿轮箱内流场分析

本文选用从动齿轮转动7周后的内流场^[20],如图5所示.图5(a)显示了飞溅润滑齿轮箱内油液体积分数高于4.0%的油气混合物分布规律,由图5(a)可知,准稳态时齿轮箱内部润滑油主要分为4部分,分别为箱底积油、啮合区润滑油、轴承集油槽内润滑油和内部近似均匀分布的油气混合物中润滑油.图5(b)为喷油润滑齿轮箱内油液分布与喷射油液的速度迹线图.由图5(b)可知,与飞溅润滑相比,喷油润滑齿轮箱啮合区油液分布明显增加,其他区域油液流动无明显变化.

图5

新窗口打开| 下载原图ZIP| 生成PPT

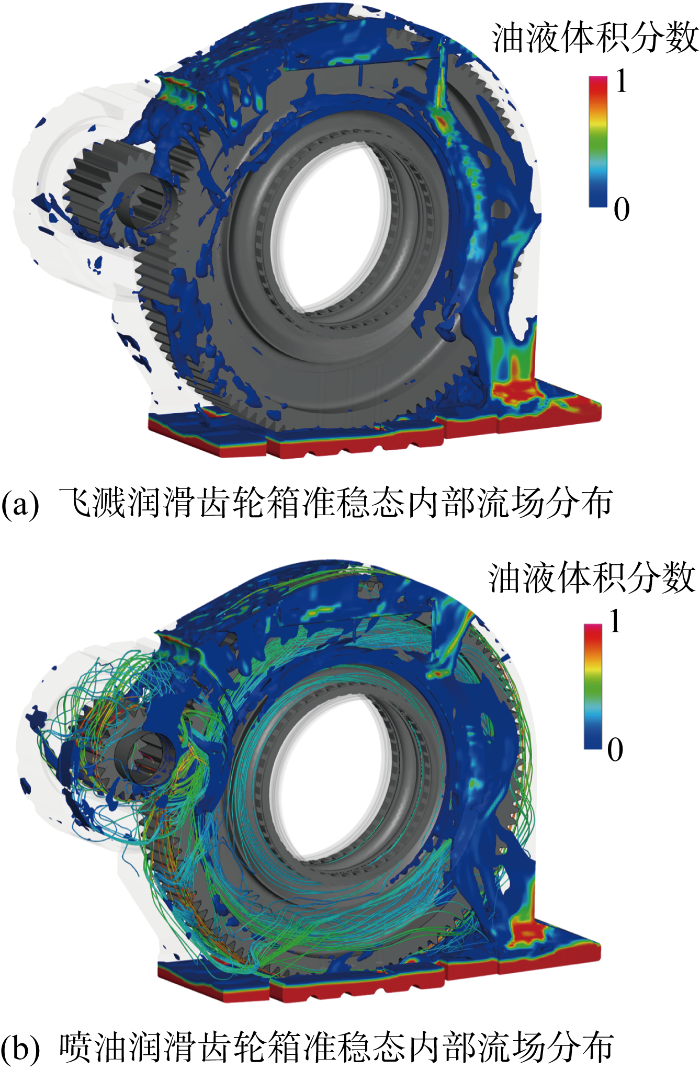
图5 齿轮箱内部润滑油分布与流线

Fig.5 Distribution and streamline of lubricating oil in gearbox

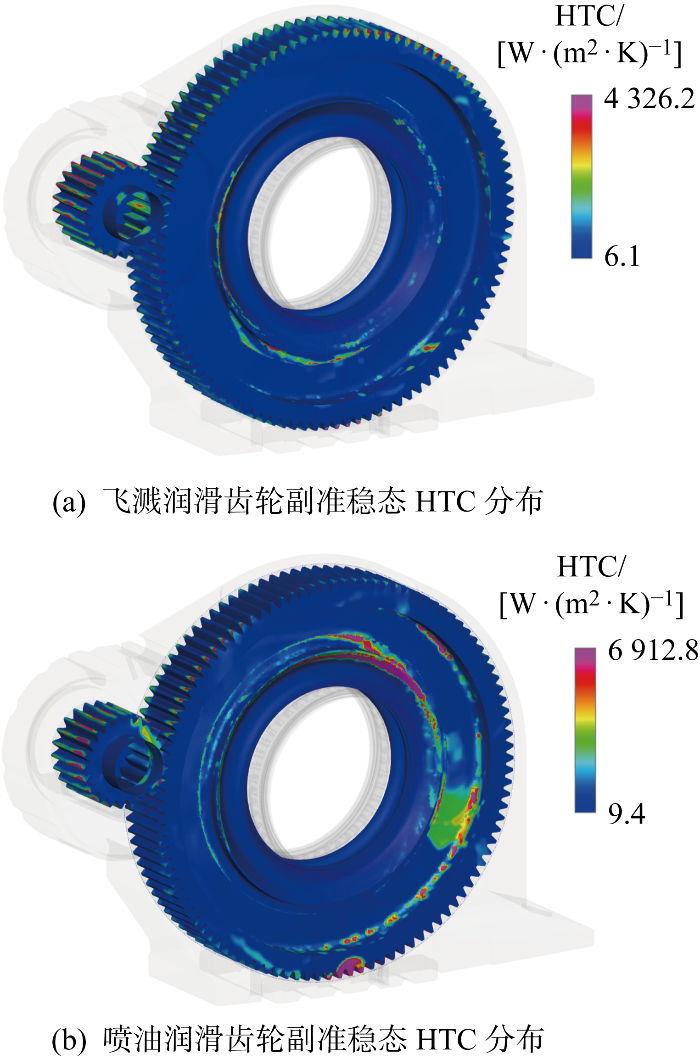
齿轮副的对流换热系数分布如图6所示.由图6(a)可知,相比于其他位置,啮合区和齿轮底部具有更高的对流换热系数,分别为 4 326.2 和3 766.5 W/(m²·K).这是因为啮合区油气混合物中油相体积占比高,齿面被油膜覆盖,而且啮合区挤压强烈,相对速度高,故对流换热系数最大.而齿轮底部浸入在润滑油中,直接与油液发生热量交换,故对流换热系数较高.由图6(b)可知,与飞溅润滑相比,喷油润滑极大程度提高了啮合区和齿轮表面对流换热能力.啮合区最大对流换热系数达 6 912.8 W/(m²·K),与飞溅润滑相比增长59.8%.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 齿轮副对流换热系数分布

Fig.6 Distribution of HTC of gear pair

3.2 齿轮箱稳态热性能分析

图7显示了齿轮箱内部油气混合物的稳态温度分布.由图7(a)可知,轴承区域的温度最高,最高温度为119.9 ℃,其次是齿轮啮合区,主动齿轮齿面温度高于从动齿轮,远离齿轮的区域温度略低,轴承外侧的密封区域和箱底积油区域温度相对其他区域较低,最低温度为28.5 ℃,位于箱底波浪型凹槽的边缘处.由图7(b)可知,与飞溅润滑相比,喷油润滑齿轮箱的啮合区温度显著降低,其余区域略有降低.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 齿轮箱内部稳态温度场

Fig.7 Steady state temperature field inside gear box

齿轮副高速啮合时,轴承与从动齿轮保持相同转速,齿轮副和轴承的摩擦产生大量的热.结合图5中油液的分布情况,可知啮合区油气混合物浓度高,油液的流动可以带走较多热量.而轴承区域外侧是复杂的迷宫密封结构,不利与热量传递.因此,轴承区域散热性能较弱,造成了轴承区域温度高于啮合区温度的现象.另外,从动齿轮搅起的油液进入啮合区、轴承区域等关键区域,带走各部件产生的部分热量并最终回到箱底,此循环过程中箱底积油温度逐渐上升,直至内部温度场达到动态平衡.

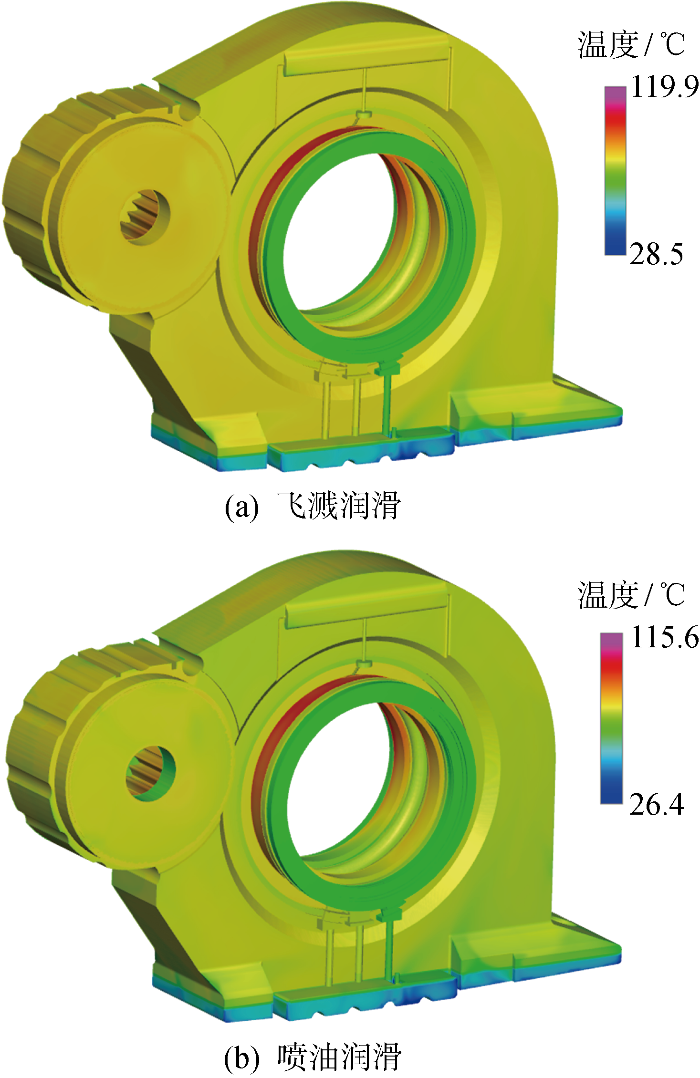
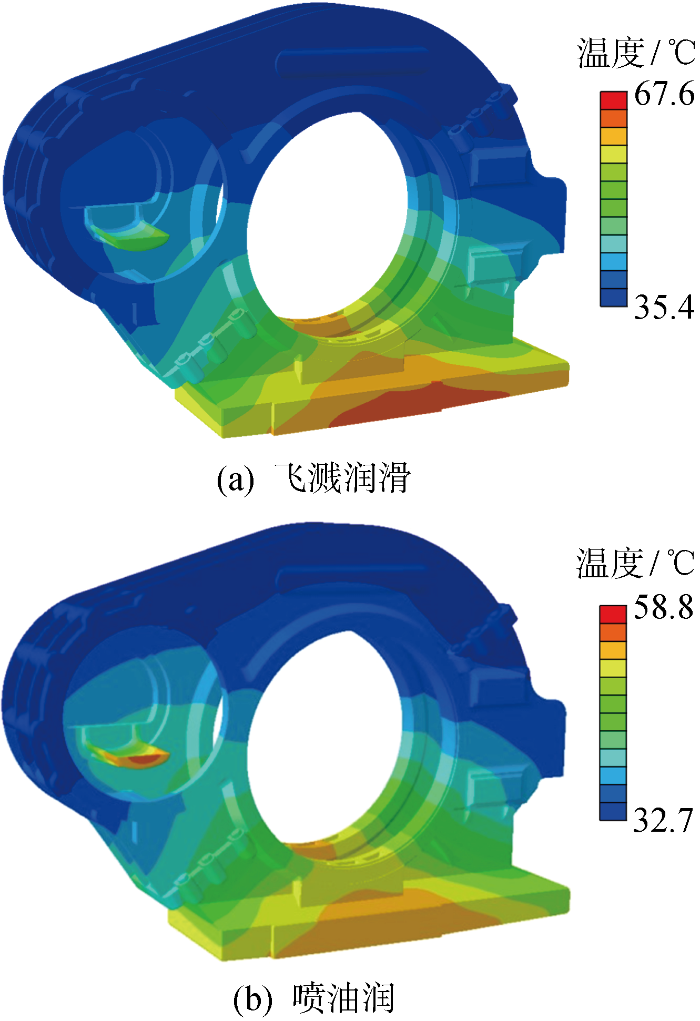
图8显示了箱体的稳态温度特性.由图8(a)可知,上箱体温度较低,其顶部表面温度分布均匀,约36 ℃.下箱体温度较高,尤其是箱体底部与润滑油接触的区域,最高温度为67.6 ℃.齿轮箱工作时,高温润滑油飞溅并黏附在箱体内壁上,将热量传递给箱体,因此,箱体的温度分布与润滑油的覆盖率^[21]相关.结合内流场油气混合物的分布,上箱体油液分布较少,故温度较低,箱底主要积存高温润滑油,故下箱体底部温度高.另外,箱体内部气相传热能力弱,而液相传热能力强.齿轮副上方油气混合物中油液浓度低,虽然该区域温度高,但是难以通过空气将热量传递至上箱体.箱底积油温度在齿轮箱内部温度场中相对较低,然而热量很容易通过油液与箱体的直接接触传导,故下箱体底部温度高.这解释了齿轮箱内部温度场与箱体温度场分布规律的差异.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 箱体稳态温度场

Fig.8 Steady state temperature field of box

由图8(b)可知,与飞溅润滑相比,箱体温度整体更低且更均匀.主动齿轮下方的集油槽温度较高,最高温度为50.5 ℃,这是由于吸收了啮合区热量的油液积累于此处造成的.

3.3 运行参数对稳态热性能的影响

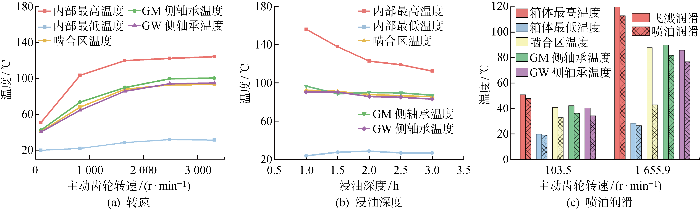
为准确分析运行参数对齿轮箱稳态热性能的影响,在不同速度、浸油深度的工况下进行数值模拟,并对比分析喷油润滑对于齿轮箱温度场的影响.

在同一影响因素的不同工况下,内部温度分布变化差异不大.不同运行参数下内部温度场仿真结果如图9所示.由图9(a)可知,随着转速的增大,内部各区域温度均呈增大趋势.其中内部最高温度、啮合区温度与轴承区域温度变化趋势相同,最低温度增大趋势缓慢.主动齿轮转速越高,各部件的功率损失越多,内部温度越高.而在 1 655 r/min后内部温度增加缓慢,这主要是由于各区域对流换热系数的骤增.由图9(b)可知,随着从动齿轮浸油深度的增加,内部各区域稳态温度呈下降趋势,最低温度变化差异不大.浸油深度的增加对内部最高温度影响最大,内部最高温度出现在轴承区域.由3.2节可知轴承区域散热能力较弱,而低油量工况意味着轴承散热能力更弱,造成局部高温.当从动齿轮浸油深度从1倍齿高(1.0h)增加至2.0h,齿轮、轴承等关键区域供油量显著增加,散热能力大幅增加,故温度大幅下降.而当浸油深度从2.0h增加至3.0h,散热能力趋近于饱和,故温度下降幅度不大.由图9(c)可知,与飞溅润滑相比,喷油润滑使啮合区温度显著降低,其余位置温度略有下降.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同运行参数下内部温度场变化规律

Fig.9 Variation law of internal temperature field at different operating parameters

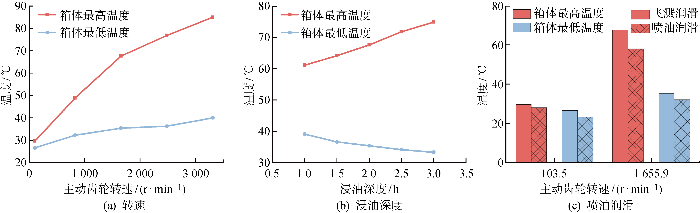
在同一影响因素的不同工况下,箱体温度分布变化差异不大.不同运行参数下箱体温度场的仿真结果中,下箱体温度高于上箱体,高温区均位于下箱体底部;上箱体温度分布均匀,顶部温度最低.

箱体最高与最低温度随运行参数的变化规律如图10所示.由图10(a)、图10(b)可知,箱体温度随转速增大而升高,这与内部流场和温度场的仿真结果一致.随着浸油深度的增加,下箱体底部温度增加,而上箱体顶部温度逐渐降低.通过图9(b)可知箱底积油温度在浸油深度的影响下变化小,可近似认为不同浸油深度下箱底积油保持同一温度.则相同温度下初始油量越多,所含热能也越多,热平衡下与其直接发生热量传递的下箱体底部温度也越高.浸油深度的增加使温度场各区域油液温度降低,因此上箱体顶部温度也随之降低.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同影响因素下箱体温度变化规律

Fig.10 Variation law of case temperature at different influencing factors

由图10(c)知,与飞溅润滑相比,采用喷油润滑的整个齿轮箱体温度由67.6 ℃下降至58.0 ℃,下降14%.且在一定速度范围内,转速越高,降温效果越明显.

4 数值方法验证

为评估本数值方法预测流场的适用性和准确性,参考德国慕尼黑工业大学齿轮与传动研究中心(FZG)试验台齿轮箱模型,建立内部尺寸为280 mm×60 mm×180 mm的箱体,齿轮副参数和润滑油物理参数与文献[22]中一致.为与试验结果进行比较,采用相同的工况条件对齿轮箱中的润滑油分布进行数值模拟,得到主动齿轮旋转50° 与100° 后的油液分布情况,如图11所示.仿真结果表明:主动齿轮旋转50° 后,油液黏附在齿顶形成清晰的油迹,旋转100° 后,油液在齿顶处形成油螺纹.这与高速摄像机的记录结果吻合较好.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 仿真结果与试验结果对比

Fig.11 Comparison of simulation results and test results

为验证本数值方法预测温度的能力,在浸油深度2.0h、主动齿轮转速 1 655 r/min的飞溅润滑条件下进行试验.在齿轮箱稳定运行30 min后结束,立刻使用红外测温仪对齿轮箱外表面进行温度测量,并通过测温孔测量内部各部件的温度^[23].得到各测点的温度,并与相应的仿真结果进行对比,如图12所示.

图12

新窗口打开| 下载原图ZIP| 生成PPT

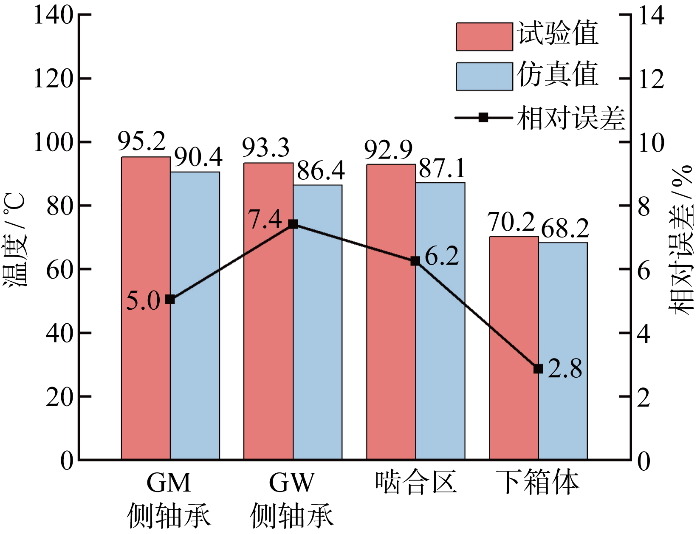
图12 齿轮箱关键区域温度试验与仿真结果对比

Fig.12 Comparison of temperature test and simulation results in key areas of gear box

从上述对比可知,仿真结果与试验测量值之间的最大相对误差为7.4%,最小相对误差为2.8%.表明该数值模型在预测温度方面具有良好的性能,也从侧面验证了在各部件发热功率的计算中,相关发热系数经验值选取的准确性.综上所述,可认为本文所用的数值分析方法对齿轮箱流场与温度场的预测效果较好.

5 结论

本文采用一种基于热-流-固耦合理论的CFD方法,系统地研究了齿轮箱内部流场与温度场.并通过实验验证数值模拟方法的可行性和准确性.另外,讨论了不同因素对温度场的影响,得出以下结论.

(1) 齿轮箱内部热分析中轴承区域的温度最高,其次是齿轮啮合区,箱底波浪型凹槽的边缘处温度最低;箱体热分析中下箱体温度高于上箱体温度,靠近主动齿轮一侧的合口面温度高于远离主动齿轮一侧的合口面,下箱体温度受箱底积油影响从中心向周围逐渐降低,上箱体温度分布比较均匀.

(2) 随着转速的增大,内部各区域与箱体各区域温度大多随之上升.而随着浸油深度的增加,内部各区域温度与上箱体温度逐渐下降,下箱体底部温度逐渐上升.

(3) 喷油润滑齿轮箱的温度对比飞溅润滑有所降低,且降幅随着转速的增大而增大.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

高超

. 基于热流耦合高速列车齿轮箱温度场的数值研究[D]. 成都: 西南交通大学, 2019: 2-10.