交/直流混合配网多逆变器分布式协同抗扰控制

doi:10.16183/j.cnki.jsjtu.2023.492

交/直流混合配网多逆变器分布式协同抗扰控制

全少理¹, 于昊正¹, 马杰¹, 王炜宇^,², 郭勇¹, 陈春²

1.国网河南省电力公司经济技术研究院,郑州 450052

2.长沙理工大学电气与信息工程学院,长沙 410114

Distributed Cooperative Disturbance-Rejection Control of Hybrid Alternating Current/Direct Current Distribution Grids with Multiple Inverters

QUAN Shaoli¹, YU Haozheng¹, MA Jie¹, WANG Weiyu^,², GUO Yong¹, CHEN Chun²

1. Economic and Technological Research Institute, State Grid Henan Electric Power Company, Zhengzhou 450052, China

2. College of Electrical and Information Engineering, Changsha University of Science and Technology, Changsha 410114, China

通讯作者: 王炜宇,讲师;E-mail:WYWang@csust.edu.cn.

责任编辑: 王历历

收稿日期: 2023-09-25 修回日期: 2023-11-12 接受日期: 2023-11-17

基金资助:

国网河南省电力公司科技项目(5217L0220013)

Received: 2023-09-25 Revised: 2023-11-12 Accepted: 2023-11-17

作者简介 About authors

全少理(1981—),高级工程师,从事配电网规划技术研究.

摘要

电力电子设备的强非线性、模型误差以及外部系统扰动给配电网的电压稳定控制带来巨大挑战.多逆变器分布式协同抗扰控制是提升配电网电压稳定性的一种新思路.首先,将复杂的逆变器高维模型转换为输入-输出等效模型,利用高增益扩展状态观测器对系统中多种扰动影响进行估计;同时,根据一致性协同控制理论设计多逆变器的分布式协同控制策略,结合扰动估计结果,实现逆变器网络的电压协同控制和主动扰动抑制.为确保协同控制的动态性能,从图论和网络控制的角度提出通信拓扑优选方法.在PowerFactory软件中搭建由4个逆变器构成的配电网测试系统,仿真结果表明:所提控制策略和通信拓扑优选方法能够实现多逆变器的电压协同跟踪调控以及扰动抑制.

关键词： 配电网; 高增益观测; 分布式控制; 一致性理论; 抗扰控制

Abstract

Voltage stability control in distribution grids faces challenges due to strong nonlinearity, modeling error of power electronic devices, and external disturbances. Distributed cooperative disturbance-rejection control of multiple inverters is a novel and promising approach to improve voltage stability in distribution grids. First, the high-dimension model of inverters is simplified into an equivalent input-output model. An extended state high-gain observer is utilized to estimate the effects of multiple disturbances in the equivalent model. Then, a distributed cooperative control strategy for multiple converters is designed based on the consensus theory, achieving coordinated voltage control and active disturbance suppression by integrating the disturbance estimation results. To ensure the dynamic performance of the distributed controller, an optimal topology selection method is proposed based on the graph theory and network control system. A test system consisting of four inverters is built in PowerFactory to verify the proposed control strategy. The simulation results show that the proposed control strategy effectively realizes coordinated voltage tracking control and suppress external disturbances.

Keywords： distribution grid; high gain observer; distributed control; consensus theory; disturbance rejection control

PDF (2881KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

全少理, 于昊正, 马杰, 王炜宇, 郭勇, 陈春. 交/直流混合配网多逆变器分布式协同抗扰控制[J]. 上海交通大学学报, 2025, 59(5): 605-616 doi:10.16183/j.cnki.jsjtu.2023.492

QUAN Shaoli, YU Haozheng, MA Jie, WANG Weiyu, GUO Yong, CHEN Chun. Distributed Cooperative Disturbance-Rejection Control of Hybrid Alternating Current/Direct Current Distribution Grids with Multiple Inverters[J]. Journal of Shanghai Jiaotong University, 2025, 59(5): 605-616 doi:10.16183/j.cnki.jsjtu.2023.492

为应对全球气候变化和能源短缺问题,我国提出“双碳”新型能源发展战略目标,清洁能源的大规模利用对“双碳”目标的实现至关重要^[1-2].然而,风电、光伏、储能等新型能源设备大多通过电力电子逆变器接入电网,整个电力系统将呈现更为复杂的非线性动态特性,稳定控制难度剧增.配电网功率平衡能力较弱,分布式新能源设备、储能设备和电动汽车充电桩等设备接入后,系统呈现强非线性、不确定性,电压稳定性受到系统中多样扰动的影响,面临巨大挑战^[3-4].

为提升配电网的电压稳定性,众多学者从不同角度设计控制方法,主要可划分为设备级控制和系统级控制两个层面.在设备级控制层面,最为常用的是逆变器无功功率-电压(Q-V)下垂控制^[5-6],通过给具有电压调节能力的并网逆变器设计合适的Q-V下垂曲线,即可实现多逆变器之间的无功比例控制,确保电网在负荷波动、新能源出力波动等扰动下电压在较小范围内变化.然而,这种电压控制方法属于有差调节,无法消除母线电压偏差.为消除电压偏差,文献[7]中提出一种模型参考自适应比例积分微分控制方法,该方法通过设定参考模型,利用自适应环节对参数进行在线调整,从而使系统电压达到期望输出值,可有效抑制负载非线性动态和波动对电网电压的影响.为了对配电网中扰动对电压的影响进行直接补偿抑制,文献[8-9]中提出一种逆变器自抗扰控制方法,该控制器可实现 dq 轴电流解耦控制,提高逆变器在各谐波频率处的跟踪精度和抗扰性能,确保设备级电压有效控制.

在配网的系统级控制策略方面,通过多逆变器之间的协同动作可实现电网电压优化控制,其中分布式协同控制技术近年来得到较为广泛的研究^[10-12].分布式协同控制策略无需控制中心统一调度,各设备与邻居之间通过稀疏通信网络进行信息交换,并根据特定的协同控制算法产生控制指令.由于通信网络具有稀疏特性,所以这种控制方式具有良好的即插即用特性^[13-14].文献[6]中较早研究了配网中的电压协同控制问题,利用反馈线性化技术将逆变器高维模型转换为等效二阶线性模型,进而基于一致性理论设计电压协同控制策略;然而,该方法需要量测逆变器所有状态变量,控制效果极易受系统模型误差影响.文献[14 -16]中设计了网络平均电压观测器,通过相邻逆变器之间的信息交换使各逆变器能够估计全网的平局电压水平,进而实现配网平均母线电压控制.文献[17]中进一步考虑逆变器后储能电源的荷电状态,提出一种基于主从结构的荷电均衡控制策略,在调控系统电压同时,确保各储能单元荷电状态的一致性.文献[18]中提出一种基于多智能体技术的区域自治-协同控制方法,有效降低高渗透分布式能源并网下的配电网电压并提高新能源的消纳率.文献[19]中则考虑交、直流微网群的组网形式,提出一种基于离散一致性算法的智能多级控制策略,实现配电网电压和频率的多目标协同调控.文献[20]中进一步将优化控制的思想融入,构建包含微型燃气轮机、分布式电源、飞轮储能等多设备随机功率增量约束的优化控制模型,通过子控制器之间的联络关系和模块化 Q 函数改进多智能体深度确定性策略梯度(MA-DDPG)算法,设计了多智能体控制器的状态、动作空间与奖励函数,实现了多个子网的协同控制.文献[21]中设计了基于预定时间一致性的分布式协同控制策略,该策略能够在预先设定的时间内调控分布式电源功率和电压,系统故障后能够将电压快速恢复至额定值附近.然而,以上控制方法通常以精确的变换器模型为基础,未考虑模型误差、参数不确定性等因素对协同控制的影响,同时缺乏考虑通信拓扑结构对协同控制器收敛速度的影响,这些因素可能造成以下问题:①模型误差等因素会造成电压动态跟踪性能降低,电压调控过程可能出现超调甚至引发失稳等问题;②不合适的通信拓扑结构会导致多个逆变器的电压一致收敛速度降低.

为提高配电网多逆变器系统的电压稳定性,本文提出一种分布式协同抗扰控制策略,该策略的创新点主要包括:①基于反馈线性化技术将逆变器的高维复杂模型转换为等效模型,进而将模型不确定性、参数误差以及外部扰动等因素等效为集总扰动项,并通过高增益扩展状态观测器进行估计,降低了对模型精确性的要求;②根据一致性协同控制理论设计多逆变器的分布式协同抗扰控制策略,每个逆变器通过与邻居逆变器交换量测数据和观测器估计结果,实现全网电压协同控制和主动扰动抑制;③从图论和网络动态特性的角度提出通信拓扑优选方法,兼顾协同控制器网络的动态特性和通信系统成本.仿真结果表明,所提控制策略在系统参数存在误差的情况下,依旧能够实现多逆变器的电压协同跟踪调控.

1 逆变器非线性模型

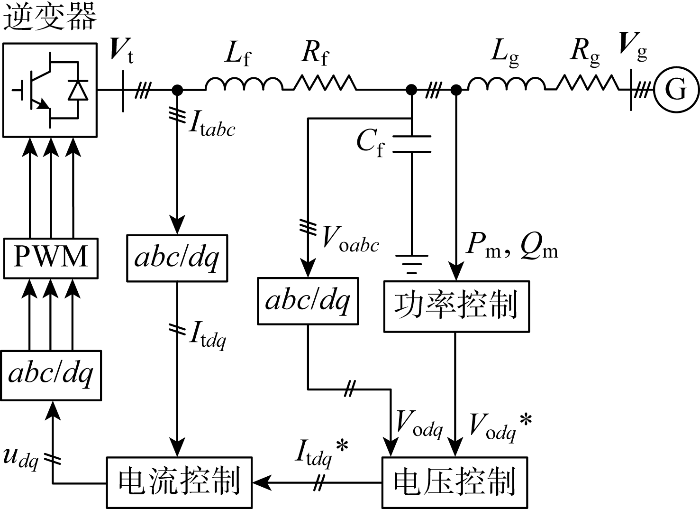
逆变器模型包括电路模型和控制器模型两部分,如图1所示.图中:R_f、L_f、C_f分别为逆变器交流侧LC滤波器的电阻、电感和电容;R_g、L_g分别为逆变器等效并网电阻和电感;V_g、V_o、V_t分别为电网母线电压向量、逆变器并网点(point of common coupling, PCC)电压向量和逆变器交流侧母线电压向量;I_t为滤波器电流;P_m、Q_m分别为变流器输出有功功率和无功功率的量测值; u_dq为电流控制环输出的d轴和q 轴控制信号;PWM代表最终所生成的脉宽调制波;G代表等值电网;上标*代表控制信号参考值,下标 dq分别代表d轴分量和q轴分量,abc 代表变量的三相正弦量.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 逆变器基本控制结构

Fig.1 Classical control blocks of inverters in distribution grids

1.1 逆变器本体模型

逆变器的详细电磁模型具有较好仿真精度,但是该模型十分复杂,电网级仿真效率较低.本文采用平均值模型(averaged-value model,AVM),如图2所示.图中:I_o为并网等效阻抗电流.该模型聚焦逆变器外部动态特性,能够确保较高的仿真精度,同时有效减少计算负担,可用于两电平、三电平和模块化多电平换流器的机电暂态仿真计算^[22-23].

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 逆变器等效均值模型

Fig.2 AVM of inverters

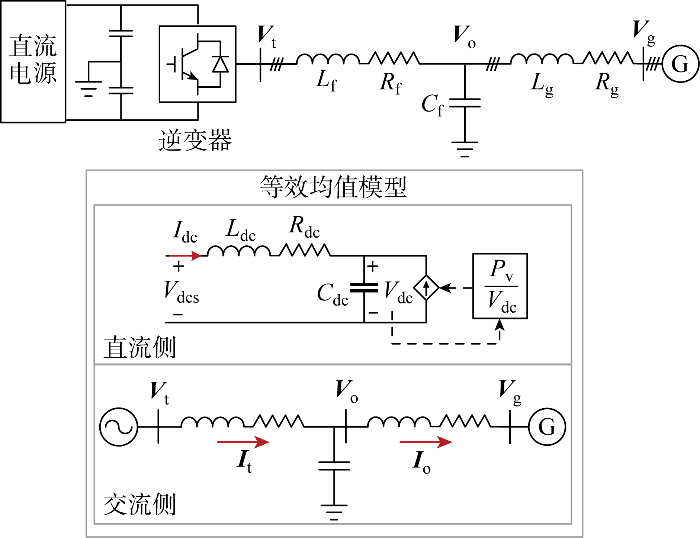
AVM模型由两部分构成,在直流侧,换流器等效为受控电流源:

$\begin{array}{l} {\overset{\cdot}{V}}_{d c} = \frac{1}{C_{d c}} (I_{d c} - \frac{P_{v}}{V_{d c}}) \\ {\overset{\cdot}{I}}_{d c} = \frac{1}{L_{d c}} (V_{d c s} - V_{d c} - R_{d c} I_{d c}) \end{array}\}$

(1)

式中:P_v为逆变器端口输出的有功功率;R_dc、L_dc分别为逆变器等效电阻和电感,可由桥臂电阻R_arm和桥臂电感L_arm计算得到,即R_dc=2/3R_arm,L_dc=2/3L_arm;C_dc为逆变器等效电容,可由子模块电容C_arm计算得到,即C_dc=6C_arm/N,N为子模块数量;I_dc为直流电流;V_dcs、V_dc分别为直流电源电压和逆变器直流母线电压.

逆变器交流侧等效为受控电压源,其模型构建在dq同步旋转坐标系下,具体可写为

$\begin{array}{l} {\overset{\cdot}{I}}_{t d} = - \frac{R_{f}}{L_{f}} I_{t d} + ω I_{t q} + \frac{1}{L_{f}} V_{t d} - \frac{1}{L_{f}} V_{o d} \\ {\overset{\cdot}{I}}_{t q} = - \frac{R_{f}}{L_{f}} I_{t q} - ω I_{t d} + \frac{1}{L_{f}} V_{t q} - \frac{1}{L_{f}} V_{o q} \\ {\overset{\cdot}{V}}_{o d} = ω V_{o q} + \frac{1}{C_{f}} I_{t d} - \frac{1}{C_{f}} I_{o d} \\ {\overset{\cdot}{V}}_{o q} = - ω V_{o d} + \frac{1}{C_{f}} I_{t q} - \frac{1}{C_{f}} I_{o q} \\ {\overset{\cdot}{I}}_{o d} = - \frac{R_{g}}{L_{g}} I_{o d} + ω I_{o q} + \frac{1}{L_{g}} V_{o d} - \frac{1}{L_{g}} V_{g d} \\ {\overset{\cdot}{I}}_{o q} = - \frac{R_{g}}{L_{g}} I_{o q} - ω I_{o d} + \frac{1}{L_{g}} V_{o q} - \frac{1}{L_{g}} V_{g q} \end{array}\}$

(2)

式中:ω为逆变器交流侧母线电压频率.

1.2 基本控制模型

逆变器的基本控制系统包括下垂模块、电压/电流双环控制模块^[24],具体如图3所示.图中:ω_n为系统额定频率;s为微分算子;V_n为电压参考值;PI代表比例积分控制.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 逆变器基本控制器

Fig.3 Conventional controller of inverters

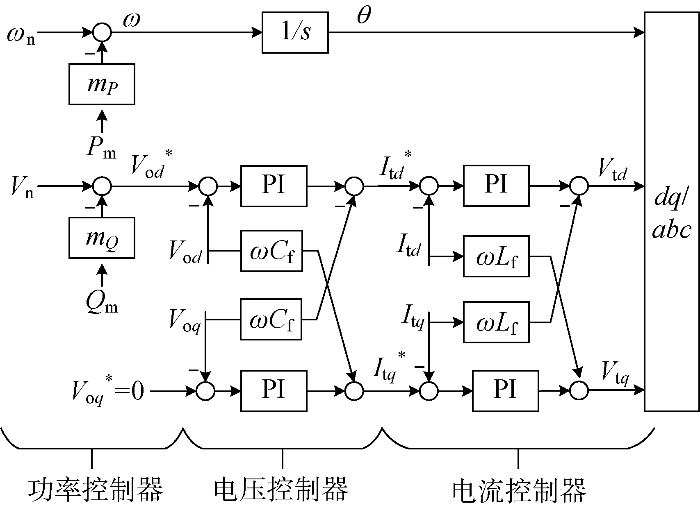
动态模型可表达为

$\begin{array}{l} ω = ω_{n} - m_{P} P_{m} \\ \overset{\cdot}{θ} = ω \\ V_{o d}^{*} = V_{n} - m_{Q} Q_{m} \\ V_{o q}^{*} = 0 \\ {\overset{\cdot}{P}}_{m} = - ω_{c} P_{m} + ω_{c} (V_{o d} I_{o d} + V_{o q} I_{o q}) \\ {\overset{\cdot}{Q}}_{m} = - ω_{c} Q_{m} + ω_{c} (V_{o q} I_{o d} - V_{o d} I_{o q}) \\ {\overset{\cdot}{ϕ}}_{d} = V_{o d}^{*} - V_{o d} \\ {\overset{\cdot}{ϕ}}_{q} = V_{o q}^{*} - V_{o q} \\ I_{t d}^{*} = - ω_{n} C_{f} V_{o q} + K_{p v} (V_{o d}^{*} - V_{o d}) + \\ K_{i v} ϕ_{d} + I_{o d} \\ I_{t q}^{*} = ω_{n} C_{f} V_{o d} + K_{p v} (V_{o q}^{*} - V_{o q}) + K_{i v} ϕ_{q} + I_{o q} \\ {\overset{\cdot}{γ}}_{d} = I_{t d}^{*} - I_{t d} \\ {\overset{\cdot}{γ}}_{q} = I_{t q}^{*} - I_{t q} \\ V_{t d} = - ω_{n} L_{f} I_{t q} + K_{p c} (V_{o d}^{*} - V_{o d}) + \\ K_{i c} γ_{d} + V_{o d} \\ V_{t q} = ω_{n} L_{f} I_{t d} + K_{p c} (V_{o q}^{*} - V_{o q}) + K_{i c} γ_{q} + V_{o q} \end{array}\}$

(3)

式中:m_P、m_Q分别为有功、无功功率下垂系数;ω_c为功率环滤波常数;θ为逆变器交流侧母线电压相位;ϕ、γ分别为电压和电流控制器内部状态变量;K_pc、K_ic分别为电流控制器比例和积分系数;K_pv、K_iv分别为电压控制器比例和积分系数.

1.3 完整非线性模型

根据式(1)~(3),逆变器的完整非线性模型为

$\begin{array}{l} \overset{\cdot}{x} = f (x) + k (x) D + g (x) u \\ y = h (x) \end{array}\}$

(4)

式中: x=[V_dcI_dcI_t_d I_t_q V_o_d V_o_q I_o_d I_o_q θ P_mQ_mϕ_d ϕ_q γ_d γ_q]^T为状态向量;D=[V_g_d V_g_q]^T为网络扰动;f(x)、k(x)、g(x)分别为状态函数、网络扰动输入函数和控制输入函数;h(x) 为输出函数.

由于逆变器在锁相环作用下使交流测母线电压向量V_o与 d轴对齐,所以有V_o_d=V_o,V_o_q = 0.以逆变器并网点电压幅值为控制输出量,功率下垂控制器的输入V_n为控制输入信号,则模型式(4)中的输出量为y=V_o_d,控制输入信号为u=V_n. 由式(4)可知,逆变器的动态特性受到网络扰动D的影响,同时也受到逆变器模型本身误差影响,这些因素可能导致电压控制误差,在系统复杂扰动作用下引发振荡、失稳等问题.

2 分布式协同抗扰控制策略设计

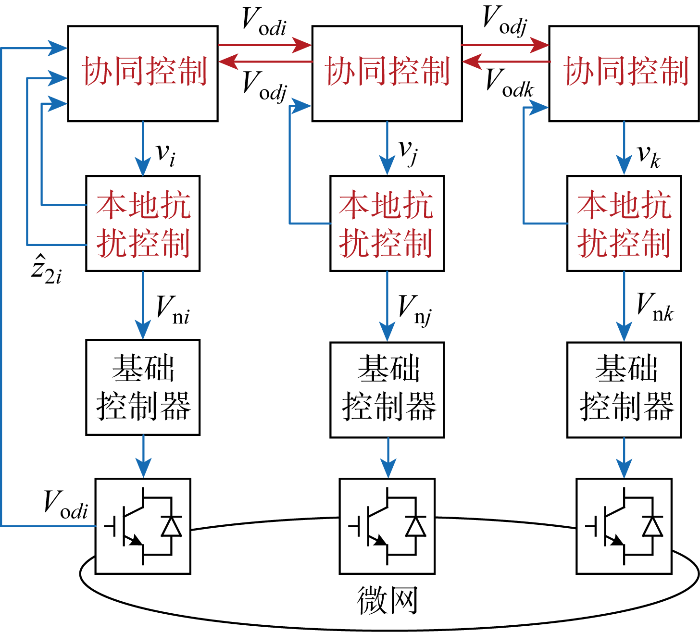
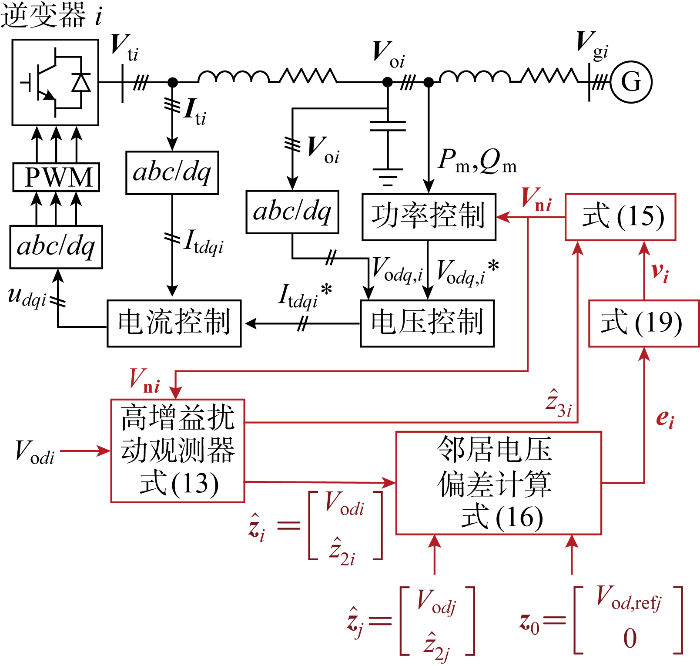
分布式协同抗扰控制方法主要包括两部分,分别为本地抗扰控制器和分布式协同控制,总体框架如图4所示.图中: v为协同控制器输出控制信号; ${\hat{z}}_{2 i}$ 为状态量估计值;下标i、j和k 表示逆变器编号.首先,以反馈线性化技术和扰动观测器技术为基础,设计逆变器的本地扰动观测器,在此基础上根据一致性理论设计协同控制器,各逆变器通过与邻居之间的数据交换,实现各逆变器电压收敛至额定值.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 分布式协同抗扰控制整体框架

Fig.4 Framework of distributed cooperative disturbance rejection control

2.1 本地抗扰控制器设计

为消除外部扰动和模型不确定性对逆变器控制性能的影响,利用反馈线性化技术得到逆变器控制输入V_n和逆变器并网点电压 V_o_d 之间的微分关系.根据式(4)所示的逆变器模型,利用Lie导数可求得该相对关系为

${\ddot{V}}_{o d} = ω {\dot{V}}_{o q} + \frac{1}{C_{f}} {\overset{\cdot}{I}}_{t d} - \frac{1}{C_{f}} {\overset{\cdot}{I}}_{o d} = L_{F (x)}^{2} h (x) + L_{g (x)} L_{F (x)} h (x) V_{n}$

(5)

式中: F(x)=f(x)+k(x)D,L_F₍_x₎h(x)为F(x)对于h(x)的Lie导数,即

L_F₍_x₎h(x)=Δh(x)F(x)= (∂h(x)/∂x)F(x)

$L_{F (x)}^{2} h (x) = L_{F (x)} (L_{F (x)} h (x)) = (\partial (L_{F (x)} h (x)) / \partial x) F (x)$

L_g₍_x₎L_F₍_x₎h(x)=(∂(L_F₍_x₎h(x))/∂x)g(x)

由式(5)可知,逆变器并网点电压 V_o_d与控制信号V_n之间呈现二阶非线性微分关系.为消除式(5)中的非线性项 $L_{F (x)}^{2}$ h(x)和L_g₍_x₎L_F₍_x₎h(x), 引入附加控制信号:

$v = L_{F (x)}^{2} h (x) + L_{g (x)} L_{F (x)} h (x) V_{n}$

(6)

则控制输入信号可设计为

$V_{n} = \frac{v - L_{F (x)}^{2} h (x)}{L_{g (x)} L_{F (x)} h (x)}$

(7)

将式(7)代入式(5)中,则 V_o_d和附加控制信号v 之间呈现出二阶线性关系,即

${\ddot{V}}_{o d} = v$

(8)

由式(8)可知,在附加控制信号 v作用下,V_o_d 的二阶非线性动态式(5)简化为简单的线性动态,将式(8)整理为状态空间形式,有

$[\begin{array}{l} {\overset{\cdot}{z}}_{1} \\ {\overset{\cdot}{z}}_{2} \end{array}] = [\begin{array}{l} 0 & 1 \\ 0 & 0 \end{array}] [\begin{array}{l} z_{1} & z_{2} \end{array}] + [\begin{array}{l} 0 \\ 1 \end{array}] v$

(9)

式中: z₁、z₂为等效状态变量,z₁=V_o_d,z₂= ${\overset{\cdot}{V}}_{o d}$ .令z=[z₁z₂]^T, A=[0 1; 0 0],B=[0; 1].

式(7)中 $L_{F (x)}^{2}$ h(x)和L_g₍_x₎L_F₍_x₎h(x)组成十分复杂,需要逆变器的精确模型参数和大量的量测信号支持.然而,模型结构和参数误差在实际中普遍存在,并且逆变器很多内部状态变量无法直接量测得到,因此式(7)难以直接使用.结合高增益观测器技术,可对 $L_{F (x)}^{2}$ h(x)和L_g₍_x₎L_F₍_x₎h(x)进行综合估计.记α= $L_{F^{2} (x)}$ h(x),β=L_g₍_x₎L_F₍_x₎h(x),集总扰动项为p, 可定义为

p=α+(β-β₀)V_n

(10)

式中: $β_{0} = \frac{K_{p v} K_{p c}}{C_{f} L_{f}}$ .α和β 中包含逆变器控制器参数、电气参数、并网点电网电压、电流等电气参量,因此实际电网中故障扰动所引发的电网电压、电流和频率波动都可以纳入集总扰动,此外,集中扰动还包括了模型整体的不确定性、控制器/电气参数误差的影响.式(5)可改写为

${\ddot{V}}_{o d} = p + β_{0} V_{n}$

(11)

在式(11)的基础上,扩展一个新的状态变量 z₃来表征集总扰动p, 扩展状态模型可写为

$\begin{array}{l} {\overset{\cdot}{z}}_{1} = z_{2} \\ {\overset{\cdot}{z}}_{2} = z_{3} + β_{0} V_{n} \\ {\overset{\cdot}{z}}_{3} = \overset{\cdot}{p} \end{array}\}$

(12)

为估计集总扰动项p,基于高增益观测器设计扰动观测器为

$\begin{array}{l} {\overset{\cdot}{\hat{z}}}_{1} = {\hat{z}}_{2} + \frac{h_{1}}{ε} (z_{1} - {\hat{z}}_{1}) \\ {\overset{\cdot}{\hat{z}}}_{2} = {\hat{z}}_{3} + β_{0} V_{n} + \frac{h_{2}}{ε^{2}} (z_{1} - {\hat{z}}_{1}) \\ {\overset{\cdot}{\hat{z}}}_{3} = \frac{h_{3}}{ε^{3}} (z_{1} - {\hat{z}}_{1}) \end{array}\}$

(13)

式中:上标^代表各状态量的估计值; ε为一个较小的正实数,且0<ε≪1;h₁~h₃ 为观测器增益.

观测器性能主要由观测器增益 h₁~h₃ 决定,由于逆变器的输入-输出扩展状态模型式(13)为串联积分器形式,所以 h₁~h₃的选择应确保多项式s³+h₁s²+h₂s+h₃=0 满足劳斯-赫尔维茨稳定判据,利用带宽整定法可计算合适的观测器增益:确定好观测器带宽 ω_o,令s³+h₁s²+h₂s+h₃=(s+ω_o)²,即可求解得到h₁~h₃.

式(13)的状态量 ${\hat{z}}_{3}$ 即为集总扰动p 的估计值,式(11)可重写为

${\ddot{V}}_{o d} = {\hat{z}}_{3} + β_{0} V_{n}$

(14)

因此,控制输入信号V_n可重新设计为

$V_{n} = \frac{v - {\hat{z}}_{3}}{β_{0}}$

(15)

对比式(7)可以发现,式(15)所示的控制器无需系统精确模型和参数,利用集总扰动的估计值 ${\hat{z}}_{3}$ 进行补偿,后续协同控制器仅需要生成附加控制输入信号v.

需要说明的是,虽然利用反馈线性化技术所得到的输入-输出模型式(5)难以直接利用,但是该模型表明了逆变器控制输入和输出之间的相对阶,这是设计本地抗扰控制器的基础,因此利用反馈线性化技术对原始非线性模型式(4)进行处理十分有必要.然后,在模型式(5)的基础上才能进一步设计扰动观测器的结构,因此反馈线性化是扰动观测器设计的前置步骤,不可或缺.所提扰动观测器设计方法以电压外环-电流内环控制为基础,如果底层控制器为其他类型,虽然所设计的扰动观测器阶数可能会发生变化,但是所提出控制器设计方法和思路依然适用.

2.2 分布式协同控制器设计

分布式协同控制依赖于通信网络,通常用有向图对通信网络进行描述,各逆变器节点等效为图的节点,逆变器之间的通信链路可等效为节点之间的边 a_ij.当逆变器i与逆变器j之间存在通信链路时,a_ij=1,否则a_ij=0.整个通信网络拓扑由邻接矩阵A_dj表示,即A_dj=[a_ij]∈R^m^×^m,其中m为逆变器数量.单个逆变器所能访问的所有邻居总数为节点的入度,用矩阵D_in表示,即D_in=diag(d_i),其中d_i= $\sum_{j \in N_{i}}$ a_ij,N_i代表第i个逆变器的邻居数量;邻接矩阵A和入度矩阵D_in 进一步构成Laplacian矩阵,即 L=D_in-A, Laplacian矩阵对协同控制器动态特性有重要影响.

在本地抗扰控制器的基础上,进一步构建分布式协同控制器.选定一个逆变器作为主导逆变器,接受来自调度中心下发的电压控制参考指令 $V_{o d}^{*}$ ,其余逆变器则跟踪主导逆变器的电压状态.各逆变器之间通过稀疏通信网络进行信息交换,交换信息包括并网点母线电压V_o_d和电压变化率估计量 ${\hat{z}}_{2}$ .

分布式协同控制的目标是设计式(15)中附加控制信号v,使所有逆变器交流母线电压收敛一致.为此,定义各逆变器与邻居之间的电压误差为

$e_{i} = \sum_{j \in N_{i}} a_{i j} (z_{i} - z_{j}) + g_{i} (z_{i} - z_{0})$

(16)

式中: z_i为逆变器交换信息向量,z_i=[V_o_di ${\hat{z}}_{i 2}$ ]^T;z₀为参考指令,z₀=[V_o_d_,ref 0]^T;g_i为逆变器的参考值增益,当逆变器i为主导逆变器时,g_i=1,否则g_i=0.

对于含有m个逆变器的配网而言,逆变器网络的全局跟踪误差向量为

e=[(L+G)⊗I₂](Z-Z₀)≡[(L+G)⊗I₂]δ

(17)

式中: Z=[ $z_{1}^{T}$ $z_{2}^{T}$ … $z_{m}^{T}$ ]^T,e=[ $e_{1}^{T}$ $e_{2}^{T}$ … $e_{m}^{T}$ ]^T,Z₀=1_mz₀,1_m为长度为是m的1向量;G为参考值增益矩阵,即G=diag(g_i);I₂为2阶单位矩阵;δ为电压偏差向量,即δ=Z-Z₀; ⊗为Kronecker积.

根据逆变器等效二阶模型式(9),全局开环系统模型为

$\overset{\cdot}{Z} = (I_{m} \otimes A) Z + (I_{m} \otimes B) v$

(18)

式中: I_m为m阶单位矩阵;v=[v₁v₂ … v_m]^T 为全局附加控制向量.

为消除逆变器间的电压误差,根据一致性理论,式(15)中附加反馈控制信号v设计为

v_i=-cKe_i

(19)

式中: K为反馈增益矩阵;c 为耦合系数,用来控制逆变器附加控制信号与控制网络之间的耦合程度.

将式(17)和式(19)代入式(18)可得系统的闭环模型为

$\overset{\cdot}{Z} = [I_{m} \otimes A - c (L + G) \otimes B K] Z + [c (L + G) \otimes B K] Z_{0}$

(20)

由式(20)可知,闭环系统的稳定性由矩阵 A_c=I_m⊗A-c(L+G)⊗BK决定.令λ_r为(L+G)的第r个特征值,反馈增益矩阵K应使(A-λ_rBK)的所有特征值都具有负实部,则系统闭环模型A_c稳定.为了求解反馈增益矩阵K, 采用线性二次型最优控制方法.定义各逆变器的优化指标为

$J_{i} = \int_{0}^{\infty} (δ_{i}^{T} Q δ_{i} + u_{i}^{T} R u_{i}) d t$

(21)

式中: Q、R为半正定实对称矩阵,矩阵Q决定逆变器电压状态与参考值之间的偏离程度,R决定控制成本;δ_i 为第i个逆变器的等效状态偏差,即δ_i=z_i-z₀;u_i为根据式(15)计算出的逆变器电压参考值V_n_i的矢量形式;t为时间.

当 J_i越小时,表明逆变器的电压偏差越小,为使性能指标函数J_i最小化,K 计算如下:

K=R^-1B^TP

(22)

式中:P为Riccati方程的正定解,即

A^TP+PA-PBR^-1B^TP+Q=0

(23)

此外,为保证系统的稳定性,耦合系数 c的选择应满足c≥1/λ_min,其中λ_min 为系统式(9)最小特征值^[6].由此,在分布式协同控制式(19)和本地抗扰控制式(15)的作用下,多逆变器网络可实现复杂扰动下的电压协同控制目标,完整控制框图如图5所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 分布式协同抗扰控制完整控制结构

Fig.5 Control block of distributed cooperative disturbance rejection control

2.3 通信拓扑选择

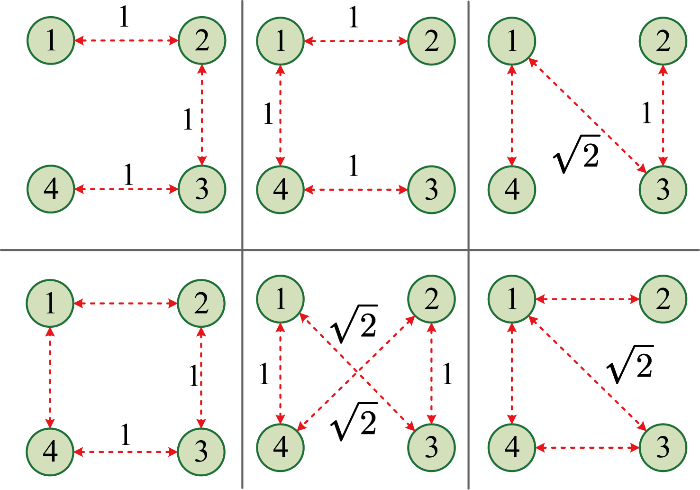
通信拓扑对分布式协同控制的动态性能影响较大,为使各逆变器能够快速收敛至额定值,应在成本限制的情况下选择动态性能最佳的通信拓扑.设计3个评估指标:①通信线路长度;②节点介数指标 B_t,网络介数中心性可以衡量网络中各节点重要性^[25],对于逆变器网络中的主导逆变器节点,其节点介数B_t越大,说明该主导逆变器对其他逆变器节点的影响越强;③第二小特征值指标λ₂,由分布式控制理论可知,对于网络动力学系统,可根据邻接矩阵A的第二小特征值λ₂评估协同控制的收敛速度^[26].λ₂ 越大意味着网络动力系统的收敛速度越快.例如由4个逆变器组成的网络系统,若逆变器1号为主导逆变器,对比通信线路总长度、 B_t和λ₂, 通信拓扑方案如图6所示,分析结果如表1所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 通信拓扑示例

Fig.6 Examples of communication topology

表1 拓扑性能评估

Tab.1 Performance of communication topology

方案	通信线路长度	B_t	λ₂
A	3.000	1.0	0.5857
B	3.000	2.0	0.5857
C	3.414	2.0	1.0000
D	4.000	0.5	2.0000
E	4.828	0.5	2.0000
F	4.414	2.0	1.0000

新窗口打开| 下载CSV

如图6和表1所示,当通信拓扑较为简单时,通信线路总长度较短,成本较低,如A、B方案,但是λ₂较小,分布式控制网络的动态性能较弱;当通信拓扑较为复杂时,虽然通信成本上升,但是分布式控制的收敛速度也会更快,如方案C.虽然方案D、E的λ₂较大,但是主导逆变器节点的节点介数B_t较小,因此综合性能也较差.方案F的性能指标虽然与方案C一样,但是通信线路过长,成本太高.综上,方案C可选做通信拓扑,其动态性能将在后续仿真分析中进行验证.

2.4 主导逆变器选择

分布式协同抗扰控制中需要一个主导逆变器接受调度中心的参考值控制指令,理论上任何逆变器都可以作为主导逆变器,考虑到实际的配电网结构和通信拓扑结构,应优先选择容量较大或者具有较大节点介数B_t的逆变器作为主导逆变器.

3 仿真测试

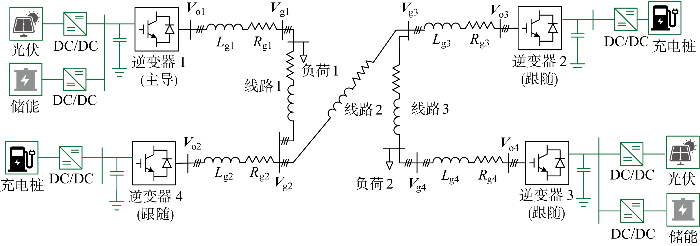
3.1 测试系统介绍

为验证分布式协同抗扰控制策略的有效性,在PowerFactory软件中构建由4个逆变器组成的孤岛配电网,拓扑结构如图7所示.其中,DG1的逆变器为主导逆变器,其余DG通过分布式控制跟随DG1的母线电压,系统参数如表2所示.表中:P_load、Q_load分别为负荷的有功功率和无功功率;p.u.表示标幺值.使用PowerFactory的电磁暂态(EMT)仿真进行测试,仿真步长设置为10 μs.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 测试系统拓扑结构

Fig.7 Topology of test system

表2 测试系统参数

Tab.2 Parameters of test system

参数种类	参数	数值	参数	数值
逆变器参数	额定容量/(MV·A)	1	交流额定电压/kV	10
	直流额定电压/kV	30	R_dc/Ω	2
	L_dc/mH	0.1273	C_dc/μF	750
	R_f/Ω	0.1	L_f/mH	1
	C_f/μF	50	R_g/Ω	0.1
	L_g/mH	0.5	$m_{P}^{p . u .}$	0.01
	$m_{Q}^{p . u .}$	0.01	ω_c/(rad·s^-1)	10
	$K_{p v}^{p . u .}$	1	$K_{i v}^{p . u .}$	20
	$K_{p c}^{p . u .}$	1	$K_{i c}^{p . u .}$	1000
线路参数	线路电阻/(Ω·km^-1)	0.5	线路电感/(mH·km^-1)	100
负荷参数	P_load1/kW	200	Q_load1/kvar	100
	P_load2/kW	300	Q_load2/kvar	200
	P_load3/kW	150	Q_load3/kvar	100

新窗口打开| 下载CSV

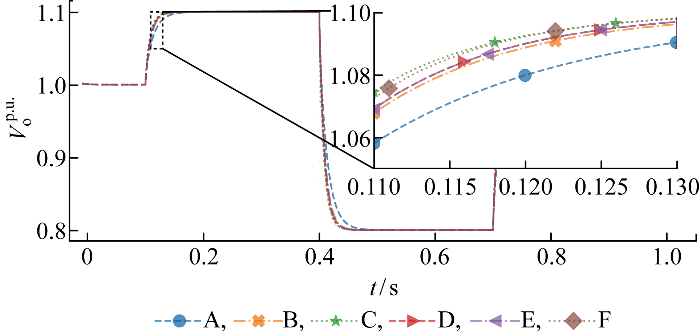
3.2 不同通信拓扑下的电压跟踪能力测试

为测试不同通信拓扑下的协同控制性能,设置3个电压参考值调整事件,即t=0.1 s时,主导逆变器的参考值标幺值从1变化到1.1;t=0.4 s时,参考值标幺值从1.1变化到0.8;最后t=0.7 s时,参考值标幺值从0.8恢复到1,对图6所示的6种通信拓扑进行测试.为方便比较,仅对比不同拓扑下逆变器并网点电压均值的响应情况,如图8所示.由图可知,当采用拓扑方案C和F时,系统逆变器网络的电压跟踪速度最好,由于方案F的通信线路比方案C长,所以方案C为最佳通信拓扑.

图8

新窗口打开| 下载原图ZIP| 生成PPT

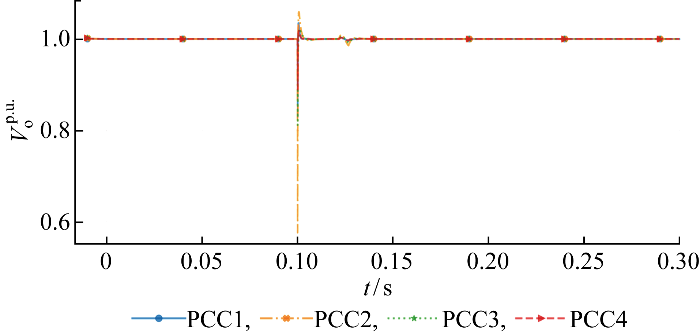
图8 不同通信拓扑下分布式协同抗扰控制的电压跟踪能力

Fig.8 Voltage tracking performance of distributed cooperative disturbance rejection control with different communication topologies

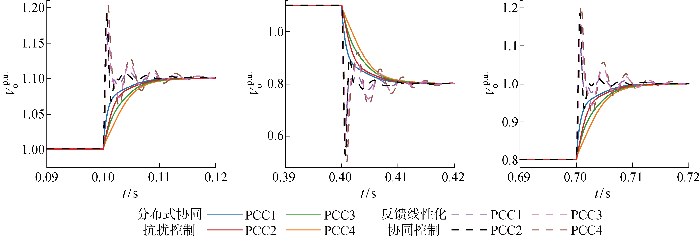
3.3 模型参数存在误差时的电压跟踪能力测试

令逆变器的滤波器参数存在1 mH误差,设置和3.1节相同的3个电压参考值调整事件,测试控制器的电压跟踪能力.以基于反馈线性化的协同控制^[6]作为对照,仿真结果如图9所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

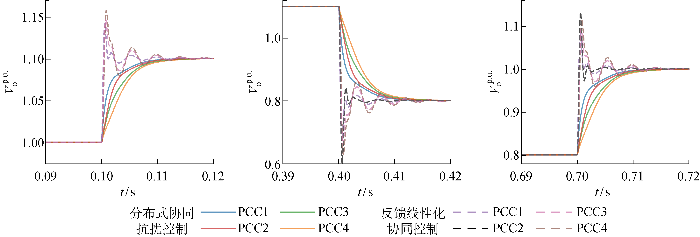
图9 不同控制器下各逆变器电压跟踪能力测试

Fig.9 Voltage tracking performance of different control strategies

由图9中实线可见,所提分布式协同抗扰控制器即使在系统参数存在误差时,也能够保持良好的电压跟踪效果,所有逆变器都在0.2 s内实现电压跟踪,并且没有电压超调现象.然而,反馈线性化协同控制器无法处理系统参数的误差,如图9中虚线所示,虽然最终也能够实现电压跟踪,但是在电压跟踪过程中会出现较大超调.

为进一步说明分布式协同抗扰控制器的有效性,可对比并网点电压变化率估计值的准确性,以逆变器1的并网点电压V_o1为例,如图10和图11所示.由图可见,即使在系统参数存在误差的情况下,分布式协同抗扰控制器依旧能够准确估计主导逆变器并网点电压的一阶和二阶导数, 从而确保扰动补偿的准确性和协同控制的精确度,整个系统的鲁棒性因此得到提升.

图10

新窗口打开| 下载原图ZIP| 生成PPT

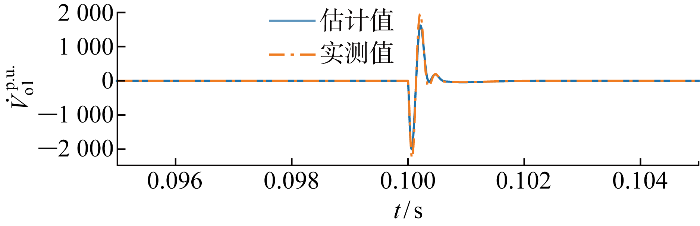
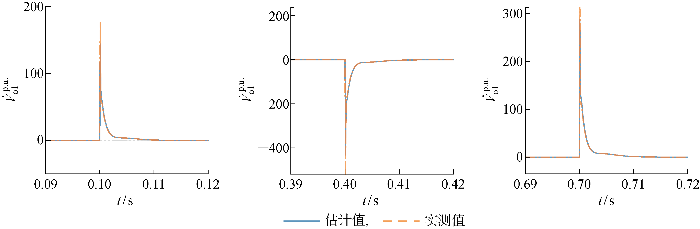
图10 电压跟踪过程中主导逆变器并网点电压一阶导数估计结果

Fig.10 Estimation results of first derivative of PCC voltage of dominant inverter by distributed cooperative disturbance rejection control in voltage tracking process

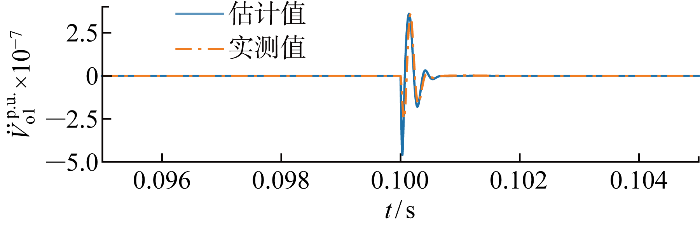
图11

新窗口打开| 下载原图ZIP| 生成PPT

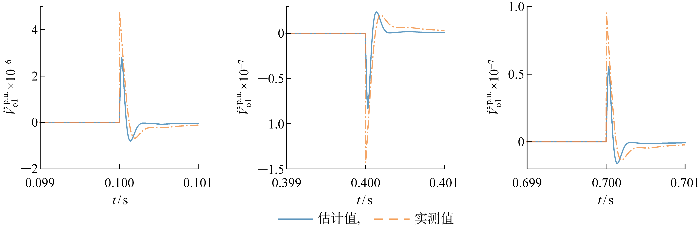
图11 电压跟踪过程中主导逆变器并网点电压二阶导数估计结果

Fig.11 Estimation results of second derivative of PCC voltage of dominant inverter by distributed cooperative disturbance rejection control in voltage tracking process

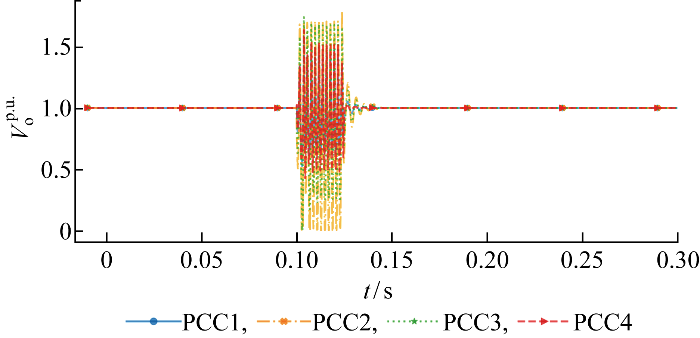
3.4 模型参数存在误差时的故障响应特性

令逆变器滤波电容参数存在50 μF误差,t=0.1 s时,逆变器2的并网母线发生三相短路故障,故障接地电阻为5 Ω,t=0.12 s时,该故障消失,仿真结果如图12和13所示.由图12可见,即使系统参数存在误差时, 分布式协同抗扰控制器作用下各逆变器交流母线电压受影响较小.然而,反馈线性化协同控制器难以处理参数误差的影响(见图13),在母线短路故障期间,系统存在剧烈的电压振荡,故障消失后,母线电压经历振荡才会恢复到故障前状态.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 分布式协同抗扰控制器的电压稳定控制能力测试

Fig.12 Voltage stability control performance of distrib~uted cooperative disturbance rejection control

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 反馈线性化协同控制器的电压稳定控制能力测试

Fig.13 Voltage stability control performance of distributed feedback linearization control

分布式协同抗扰控制器对并网点电压变化率的估计值如图14和图15所示.由图可见,即使在系统参数存在误差且发生较为严重的短路故障冲击时,分布式协同抗扰控制器能够对电压快速变化情况进行准确估计,从而尽可能减小故障对系统的冲击,并在故障消失后,使电压快速恢复至额定值.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 电网短路故障状态下主导逆变器并网点电压一阶导数估计结果

Fig.14 Estimation results of first derivative of PCC voltage of dominant inverter by distributed cooperative disturbance rejection control under grid fault condition

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 电网短路故障状态下主导逆变器并网点电压二阶导数估计结果

Fig.15 Estimation results of second derivative of PCC voltage of dominant inverter by distributed cooperative disturbance rejection control under grid fault condition

3.5 通信系统存在时滞时的电压协同跟踪性能

为测试通信时滞对控制器性能,令逆变器之间的信号传输存在500 ms延迟,电压控制指令与3.3节保持一致,仿真结果如图16所示.由图中实线可见,通信时滞对分布式抗扰协同控制器的电压跟踪性能影响较小,各逆变器能够迅速收敛至目标电压水平,并且没有电压超调现象.然而,通信时滞对反馈线性化协同控制器影响较大,如图中虚线所示,电压跟踪过程中的超调量较大,不利于系统稳定性.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 通信时滞下不同控制策略的电压跟踪能力测试

Fig.16 Voltage tracking performance of different control strategies under communication delay

4 结论

含有高比例逆变器电源的配电网中存在多种扰动复杂,包括逆变器模型不确定性、参数误差以及电网短路故障等扰动,给配电网的电压稳定控制带来巨大挑战.本文提出一种配电网的分布式协同抗扰控制策略,具体结论如下:

(1) 逆变器的高维复杂非线性模型可等效为二阶输入-输出等效模型,所设计的高增益扩展状态观测器能够准确估计等效模型中的集总扰动,从而在控制环路中精准补偿系统多种扰动,有效提升了逆变器的抗扰能力.

(2) 根据一致性协同控制理论设计了多逆变器的分布式协同抗扰控制策略,每个逆变器仅需要本地的量测信号、观测器估计结果以及邻居逆变器的量测热和估计结果,即可实现全网电压协同抗扰控制.

(3) 基于图论和网络控制理论提出的通信拓扑优选方法,能够有效筛选出兼顾建造成本和分布式协同控制器收敛速度的最佳拓扑.

通过算例测试发现,所提控制策略在参数误差下能够实现多逆变器的电压协同跟踪调控以及扰动抑制,具有一定的工程实用价值.本文虽然在仿真部分测试了通信时滞对所提控制策略动态性能的影响,但是未在理论部分进行严格理论分析.未来将进一步从机理角度研究通信时滞对多逆变器分布式协同控制系统稳定性的影响,并在控制器设计中增加时滞补偿环节.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

张子扬, 张宁, 杜尔顺, 等.

双高电力系统频率安全问题评述及其应对措施

[J]. 中国电机工程学报, 2022, 42(1): 1-25.