基于超螺旋扩张状态观测器的耦合单电感双输出Buck变换器串级滑模解耦控制

doi:10.16183/j.cnki.jsjtu.2023.349

基于超螺旋扩张状态观测器的耦合单电感双输出Buck变换器串级滑模解耦控制

皇金锋^,, 章乾

陕西理工大学电气工程学院,陕西汉中 723001

Cascade Sliding Mode Decoupling Control of Coupled Inductor Single-Input Dual-Output Buck Converter Based on Super-Twisting Extend State Observer

HUANG JinFeng^,, ZHANG Qian

School of Electrical Engineering, Shaanxi University of Technology, Hanzhong 723001, Shaanxi, China

责任编辑: 王历历

收稿日期: 2023-07-28 修回日期: 2023-10-5 接受日期: 2023-10-19

基金资助:

陕西省自然科学研究资助项目(2023-JC-YB-442)

Received: 2023-07-28 Revised: 2023-10-5 Accepted: 2023-10-19

作者简介 About authors

皇金锋(1978—),教授,从事新能源发电及电力电子变换器控制策略研究;E-mail:jfhuang2000@163.com.

摘要

针对耦合单电感双输出(CI-SIDO)降压式(Buck)变换器输出支路间的耦合效应导致交叉影响进而影响系统动态性能的问题,提出基于超螺旋扩张状态观测器(ST-ESO)的串级滑模解耦控制策略.首先,建立CI-SIDO Buck变换器的状态空间平均模型,再通过具有快速收敛性质的ST-ESO 观测估计变换器内外环中的耦合项、内部扰动和未建模部分,并将其视为内外环中的总扰动.其次,结合超螺旋滑模控制器对内外环中总扰动进行补偿,实现系统的解耦,保证系统的鲁棒性和输出电压的稳定.然后,根据Lyapunov理论对ST-ESO和超螺旋滑模控制器进行稳定性分析,理论验证了控制策略的可行性.最后,利用实验平台对所提控制策略进行验证.结果表明所提控制策略实现了系统解耦,抑制了交叉影响并提高了系统的动态性能.

关键词： 耦合单电感双输出; Buck变换器; 超螺旋扩张状态观测器; 超螺旋滑模控制器; 解耦控制

Abstract

To address the coupling effect between the output branches of the coupled inductor single-input dual-output (CI-SIDO) Buck converter, which leads to the cross-influence and thus affects the dynamic performance of the system, a cascaded sliding mode decoupling control strategy based on the super-twisting extend state observer (ST-ESO) is proposed. First, a state-space averaging model of the CI-SIDO Buck converter is established. Then, the coupling terms, internal perturbations, and unmodeled parts in the inner and outer loops of the converter are estimated by using the ST-ESO with a fast-convergence property, which are regarded as the total perturbations in the inner and outer loops. Next, the total perturbation in the inner and outer loops is compensated by using a super-twisting sliding mode controller to achieve the decoupling of the system and ensure the robustness of the system and the stability of the output voltage. Furthermore, the stability of the super-twisting extend state observer and super-twisting sliding mode controller is analyzed using the Lyapunov theory, providing theoretical verification of the feasibility of the control strategy. Finally, the proposed control strategy is experimentally validated on the experimental platform. The results show that the proposed control strategy realizes the decoupling of the system, suppresses the cross-influence and improves the dynamic performance of the system.

Keywords： coupled inductor single-input dual-output (SIDO); Buck converter; super-twisting extend state observer (ST-ESO); super-twisting sliding mode control; decoupling control

PDF (4220KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

皇金锋, 章乾. 基于超螺旋扩张状态观测器的耦合单电感双输出Buck变换器串级滑模解耦控制[J]. 上海交通大学学报, 2025, 59(5): 592-604 doi:10.16183/j.cnki.jsjtu.2023.349

HUANG JinFeng, ZHANG Qian. Cascade Sliding Mode Decoupling Control of Coupled Inductor Single-Input Dual-Output Buck Converter Based on Super-Twisting Extend State Observer[J]. Journal of Shanghai Jiaotong University, 2025, 59(5): 592-604 doi:10.16183/j.cnki.jsjtu.2023.349

随着便携式设备更新迭代,电动汽车领域快速发展,与之相应的集成模块也在不断增加;而不同模块之间通常需要等级不同的供电电压,因此具有高功率密度、低成本、小体积、多输出电压等级的供电方式得到越来越多的应用.当系统需要多输出电压等级时,传统方法是采用多个降压式(Buck)变换器并联,这无疑增大了设备的体积,增加了成本^[1-4].而单电感双输出(single-input dual-output,SIDO)Buck变换器采用一个电感就可以实现两路不同输出电压等级,具有功率密度高、无电磁干扰、低成本等优点,在便携式设备、电动汽车等领域中具有广泛的应用前景.

SIDO Buck变换器输入端采用一个功率开关管控制变换器的输入能量,同时,输出两支路采用两个开关管对输入能量进行分配,且两支路占空比为互补导通,因此该系统为一个强耦合系统.SIDO Buck变换器暂态和稳态均存在交叉影响,会导致变换器的控制器设计困难^[5-9].文献[10]中提出一种耦合单电感双输出(couple inductor single-input dual-output, CI-SIDO)Buck变换器拓扑,该拓扑采用一个反向耦合电感为两路输出支路传递能量,减小了磁芯的数量和大小;支路采用两个功率开关管对输出支路分别进行控制,输出支路占空比不受另一输出支路占空比影响.与此同时,变换器工作为连续导电模式(continuous conduction mode, CCM)时,交叉影响只存在暂态过渡过程^[11].CI-SIDO的交叉影响与SIDO相比较小,控制相对容易,因此CI-SIDO具有更加广泛的应用前景.

有学者针对CI-SIDO变换器相关特性以及工作模式进行分析^[12-14].然而,耦合电感使两输出支路存在耦合效应,造成输出支路间的交叉影响,具体表现为当一条支路的电感电流发生变化时,耦合电感的存在使得另一输出支路的能量发生变化,影响系统的动态性能.因此,实现CI-SIDO开关变换器的解耦,抑制输出支路间的交叉影响成为国内外研究的热点.文献[15]中采用对角化解耦,设计电压型解耦控制,实现CI-SIDO Buck变换器输出支路间的解耦,抑制了交叉影响,但未解决耦合效应对动态性能的影响.文献[16]中采用平均电流解耦控制,设计电流控制器实现CI-SIDO Buck变换器输出支路间的解耦,有效地抑制了输出支路间的交叉影响,提升了系统的动态性能.文献[17]中采用峰值电流解耦控制,抑制CI-SIDO Buck变换器和CI-SIDO Boost变换器的交叉影响的同时也提高了系统的动态性能.文献[18]中通过逆动力精确线性化解耦,将CI-SIDO Buck变换器分解为两个伪线性子系统,从模型上实现系统的解耦,并采用自适应滑模控制提高了系统动态性能.以上研究对提高CI-SIDO变换器的动态性能及抑制交叉影响有较好的作用,但这些控制以小信号数学模型为基础,采用对角化和逆动力学进行解耦,解耦整体设计过程复杂,过于依赖变换器精确模型,并未对未建模部分进行处理.

在电机以及无人机等具有强耦合系统的领域中,常用方法之一是采用扩张状态观测器(extended state observer, ESO)对系统中的耦合项以及其他外界扰动和内扰进行实时观测,并设计反馈控制律进行补偿,以此实现系统的解耦,同时也提高系统的抗干扰能力^[19-23].其中,文献[24]中利用滑模自抗扰控制实现SIDO Buck解耦,抑制了SIDO Buck变换器输出支路间的交叉影响,提高了系统的动态性能.文献[25]中基于自适应扩张状态观测器结合终端滑模实现永磁同步电动机d-q轴电流完全解耦,提高了电流动态性能和鲁棒性.文献[26]中采用增益连续扩张状态观测器对电流环中的耦合项以及其他不确定性扰动进行观测,并对扰动进行补偿实现永磁同步电动机的完全解耦.

上述扩张状态观测器以及改进型扩张状态观测器大多是渐进收敛的,相较于有限时间收敛观测器收敛速度较慢,且抗干扰能力较差^[27].其中,文献[28]中应用高阶超螺旋扩张状态观测器观测有限时间,估计各通道的误差信息并结合快速非奇异终端滑模实现四旋翼无人机三通道解耦.文献[29]中采用超螺旋扩张状态观测器结合分数阶滑模控制器对感应电机进行解耦,提高了感应电机的磁链和速度跟踪精度以及系统的鲁棒性.上述文献采用超螺旋扩张状态观测器结合滑模等控制方法在耦合系统解耦中取得显著的效果,并且提高了系统的鲁棒性以及动态性能.

针对目前CI-SIDO变换器强耦合系统实现解耦,用以解决交叉影响所提出的控制方案需要变换器的精确数学模型,以及对未建模部分未进行处理的问题,结合其他具有强耦合效应领域的解耦控制方法和文献[27]的启发,进一步提高系统的动态性能,提出不依赖系统精确数学模型的串级滑模解耦控制策略.该策略由超螺旋扩张状态观测器(super-twisting extend state observer, ST-ESO)观测系统耦合项,由未建模部分以及内外扰动构成总扰动,并结合超螺旋滑模控制对总扰动进行补偿.首先,对CI-SIDO Buck变换器进行状态空间平均建模,再分别设计变换器电压和电流控制环节;其次,将电流内环内的耦合项、内环干扰以及未建模部分视为内环总扰动,利用超螺旋扩张状态观测器进行观测估计,并利用超螺旋滑模控制器进行补偿,实现系统的解耦控制.然后,将电压环中未建模部分和外界干扰视为外环总扰动,应用超螺旋扩张状态观测器和超螺旋滑模控制器进行估计和补偿,提高系统的鲁棒性,保证输出电压的稳定,并为电流环提供参考值.最后,利用仿真以及实验平台验证所提控制策略.

1 CI-SIDO Buck变换器建模

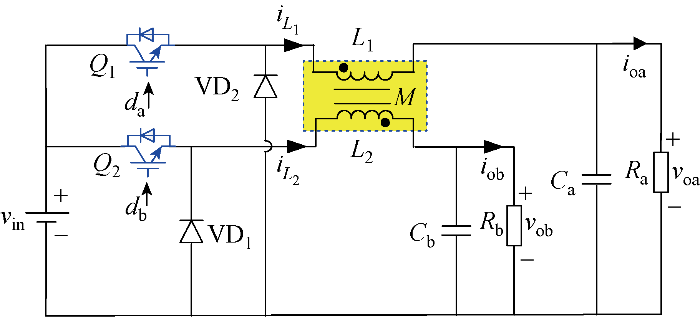
CI-SIDO Buck变换器的电路拓扑如图1所示.图中:v_in为输入电压; Q₁、Q₂为支路开关管;L₁、L₂为自感电感;M 为互感电感;VD₁、VD₂为支路续流二极管;C_a、C_b分别为a、b支路输出滤波电容; $i_{L_{1}}$ 、 $i_{L_{2}}$ 为支路电感电流;i_oa、i_ob为支路a、b输出电流;d_a、d_b为支路a、b占空比;R_a、R_b分别为a、b支路负载;v_oa、v_ob分别为a、b支路输出电压.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 CI-SIDO Buck变换器

Fig.1 CI-SIDO Buck converter

根据图1可推导出CI-SIDO Buck变换器工作在CCM模式下状态空间平均模型为

(1)

\begin{matrix} \frac{d i_{L_{1}}}{d t} = \frac{- L_{2} v_{o a}}{L_{1} L_{2} - M^{2}} + \frac{- M v_{o b}}{L_{1} L_{2} - M^{2}} + \frac{(L_{2} d_{a} + M d_{b}) v_{i n}}{L_{1} L_{2} - M^{2}} \\ \begin{matrix} \frac{d i_{L_{2}}}{d t} = \frac{- M v_{o a}}{L_{1} L_{2} - M^{2}} + \frac{- L_{1} v_{o b}}{L_{1} L_{2} - M^{2}} + \frac{(M d_{a} + L_{1} d_{b}) v_{i n}}{L_{1} L_{2} - M^{2}} \\ \frac{d v_{o a}}{d t} = \frac{1}{C_{a}} i_{L_{1}} - \frac{1}{R_{a} C_{a}} v_{o a} \\ \frac{d v_{o b}}{d t} = \frac{1}{C_{b}} i_{L_{2}} - \frac{1}{R_{b} C_{b}} v_{o b} \end{matrix} \end{matrix}\}

式中:t为时刻.

利用伏秒平衡可求得CI-SIDO Buck变换器工作在CCM模式下的稳态增益为

(2)

\begin{array}{l} v_{o a} = d_{a} v_{i n} \\ v_{o b} = d_{b} v_{i n} \end{array}\}

分析式(1)和式(2)可知,当CI-SIDO Buck变换器工作在CCM时,输出支路间的耦合效应只存在暂态,与a、b各支路输出电压、占空比和输入电压存在耦合关系;稳态时各支路间输出电压仅与该支路的占空比有关.

2 CI-SIDO Buck变换器控制器设计

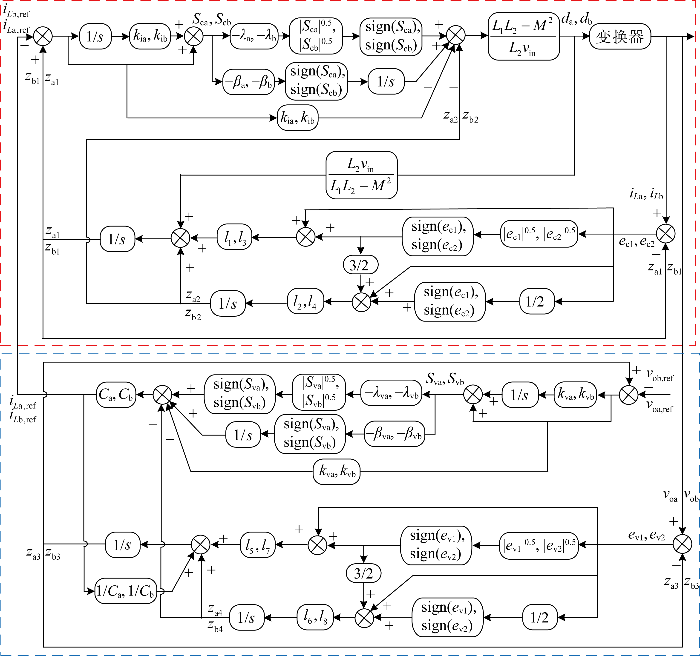
采用电压电流双环控制可以提高系统的响应速度和抗干扰能力,通过有限时间收敛的ST-ESO对电流内环中的耦合项、内部扰动以及未建模部分被视为的内环总扰动进行实时观测,并利用同样具有有限时间收敛性质和抑制系统抖振的超螺旋滑模控制器对内环总扰动进行补偿,实现系统解耦的同时提高系统抗干扰能力.同时,电压外环采用ST-ESO观测外环总扰动,并结合超螺旋滑模控制;超螺旋滑模为有限时间收敛,收敛速度相较传统滑模的收敛速度快,可以实现对电压跟随的快速响应,提高系统的鲁棒性和输出电压的稳定性.所提控制策略控制框图如图2所示.图中:1/s为积分.下面分别进行超螺旋扩张状态观测器及电流内环和电压外环的控制器设计,图2中的其他变量在设计过程中说明含义.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 CI-SIDO Buck变换器控制框图

Fig.2 Control block of CI-SIDO Buck converter

2.1 内环控制设计

2.1.1 内环超螺旋扩张状态观测器设计

将电流内环未建模部分以及内环的其他扰动视为内环的内部扰动,并用f_ca和f_cb表示,结合式(1)可将a、b支路电感电流状态方程重新表述为

(3)

\begin{array}{l} {\overset{\cdot}{x}}_{c 1} = \frac{- L_{2} v_{o a}}{L_{1} L_{2} - M^{2}} + \frac{- M v_{o b}}{L_{1} L_{2} - M^{2}} + \\ \frac{(L_{2} d_{a} + M d_{b}) v_{i n}}{L_{1} L_{2} - M^{2}} + f_{c a} \\ {\overset{\cdot}{x}}_{c 2} = \frac{- M v_{o a}}{L_{1} L_{2} - M^{2}} + \frac{- L_{1} v_{o b}}{L_{1} L_{2} - M^{2}} + \\ \frac{(M d_{a} + L_{1} d_{b}) v_{i n}}{L_{1} L_{2} - M^{2}} + f_{c b} \end{array}\}

式中:x_c1、x_c2分别为a、b支路电感电流的状态量.

将电流内环的耦合项以及电流内环的内部扰动视为内环总扰动,并用f_c1、f_c2表示,则式(3)表示为

(4)

\begin{array}{l} {\overset{\cdot}{x}}_{c 1} = \frac{L_{2} v_{i n} d_{a}}{L_{1} L_{2} - M^{2}} + f_{c 1} \\ {\overset{\cdot}{x}}_{c 2} = \frac{L_{1} v_{i n} d_{b}}{L_{1} L_{2} - M^{2}} + f_{c 2} \end{array}\}

f_{c 1} = \frac{- L_{2} v_{o a} - M v_{o b} + M v_{i n} d_{b}}{L_{1} L_{2} - M^{2}} + f_{c a}

f_{c 2} = \frac{- M v_{a} - L_{1} v_{b} + M v_{i n} d_{a}}{L_{1} L_{2} - M^{2}} + f_{c b}

将f_c1、f_c2扩张为新的状态变量x_c3、x_c4,式(4)可重新表示为

(5)

\begin{array}{l} {\overset{\cdot}{x}}_{c 1} = \frac{L_{2} v_{i n} d_{a}}{L_{1} L_{2} - M^{2}} + x_{c 3}, {\overset{\cdot}{x}}_{c 3} = {\overset{\cdot}{f}}_{c 1} \\ {\overset{\cdot}{x}}_{c 2} = \frac{L_{1} v_{i n} d_{b}}{L_{1} L_{2} - M^{2}} + x_{c 4}, {\overset{\cdot}{x}}_{c 4} = {\overset{\cdot}{f}}_{c 2} \end{array}\}

针对式(5)设计超螺旋扩张状态观测器为

(6)

\begin{array}{l} e_{c 1} = z_{a 1} - x_{c 1} \\ {\overset{\cdot}{z}}_{a 1} = \frac{L_{2} v_{i n} d_{a}}{L_{1} L_{2} - M^{2}} + z_{a 2} - \\ l_{1} ({|e_{c 1}|}^{\frac{1}{2}} s i g n (e_{c 1}) + e_{c 1}) \\ {\overset{\cdot}{z}}_{a 2} = - l_{2} (\frac{1}{2} s i g n (e_{c 1}) + \\ \frac{3}{2} {|e_{c 1}|}^{\frac{1}{2}} s i g n (e_{c 1}) + e_{c 1}) \\ e_{c 2} = z_{b 1} - x_{c 2} \\ {\overset{\cdot}{z}}_{b 1} = \frac{L_{1} v_{i n} d_{b}}{L_{1} L_{2} - M^{2}} + z_{b 2} - \\ l_{3} ({|e_{c 2}|}^{\frac{1}{2}} s i g n (e_{c 2}) + e_{c 2}) \\ {\overset{\cdot}{z}}_{b 2} = - l_{4} (\frac{1}{2} s i g n (e_{c 2}) + \\ \frac{3}{2} {|e_{c 2}|}^{\frac{1}{2}} s i g n (e_{c 2}) + e_{c 2}) \end{array}\}

式中:z_a1、z_b1分别为x_c1、x_c2的估计值;e_c1、e_c2分别为z_a1、z_b1与x_c1、x_c2的观测误差;z_a2、z_b2为a、b输出支路的耦合项,内部扰动以及未建模部分等的总扰动估计值;l₁~l₄为观测器增益,并采用带宽法进行整定^[30], l₁=l₃=2w_o,l₂=l₄= $w_{o}^{2}$ ,w_o 为观测器带宽.

2.1.2 内环超螺旋滑模控制器设计

定义a、b输出支路电流环电感电流跟踪误差分别为

(7)

\begin{array}{l} e_{a 1} = z_{a 1} - i_{L a, r e f} \\ e_{b 1} = z_{b 1} - i_{L b, r e f} \end{array}\}

式中:i_L_a_,_ref、i_L_b_,_ref分别为支路a、b电流内环的参考值.

构建a、b输出支路电流环滑模面分别为

(8)

\begin{array}{l} S_{c a} = e_{a 1} + k_{i a} \int e_{a 1} d t \\ S_{c b} = e_{b 1} + k_{i b} \int e_{b 1} d t \end{array}\}

式中:k_ia、k_ib分别为a、b支路电流内环滑模面参数,k_ia >0,k_ib>0.

对式(8)求导数可得:

(9)

\begin{array}{l} \frac{d S_{c a}}{d t} = \frac{L_{2} d_{a} v_{i n}}{L_{1} L_{2} - M^{2}} + z_{a 2} + k_{i a} e_{a 1} \\ \frac{d S_{c b}}{d t} = \frac{L_{1} v_{i n} d_{b}}{L_{1} L_{2} - M^{2}} + z_{b 2} + k_{i b} e_{b 1} \end{array}\}

设计电流内环超螺旋滑模控制律u_ca、u_cb分别为

(10)

\begin{array}{l} \frac{d S_{c a}}{d t} = u_{c a} \\ u_{c a} = - λ_{a} {|S_{c a}|}^{\frac{1}{2}} s i g n (S_{c a}) + w_{c a} \\ {\overset{\cdot}{w}}_{c a} = - β_{a} s i g n (S_{c a}) \\ \frac{d S_{c b}}{d t} = u_{c b} \\ u_{c b} = - λ_{b} {|S_{c b}|}^{\frac{1}{2}} s i g n (S_{c b}) + w_{c b} \\ {\overset{\cdot}{w}}_{c b} = - β_{b} s i g n (S_{c b}) \end{array}\}

式中:λ_a、λ_b、β_a、β_b为电流内环控制器参数;w_ca、w_cb为切换项的积分.

由式(9)和式(10)可得a、b支路电流内环控制律为

(11)

\begin{array}{l} d_{a} = \frac{(L_{1} L_{2} - M^{2}) (u_{c a} - k_{i a} e_{a 1} - z_{a 2})}{L_{2} v_{i n}} \\ d_{b} = \frac{(L_{1} L_{2} - M^{2}) (u_{c b} - k_{i b} e_{b 1} - z_{b 2})}{L_{1} v_{i n}} \end{array}\}

2.2 外环控制设计

2.2.1 外环超螺旋扩张状态观测器设计

将外环未建模部分以及外环内外干扰视为外环扰动,并用f_va、f_vb表示,结合式(1)可将电压外环重新表示为

(12)

\begin{array}{l} {\overset{\cdot}{x}}_{v 1} = \frac{1}{C_{a}} i_{L_{1}} - \frac{1}{R_{a} C_{a}} v_{o a} + f_{v a} \\ {\overset{\cdot}{x}}_{v 2} = \frac{1}{C_{b}} i_{L_{2}} - \frac{1}{R_{b} C_{b}} v_{o b} + f_{v b} \end{array}\}

式中:x_v1、x_v2分别为a、b支路电压外环的状态量.

为了提高系统的扰动,将a、b支路中易受外界扰动的输出电流i_oa和i_ob以及外环扰动视为外界总扰动,并用f_v1和f_v2进行表示,则式(12)可重新表述为

(13)

\begin{array}{l} {\overset{\cdot}{x}}_{v 1} = {\overset{\cdot}{v}}_{o a} = \frac{1}{C_{a}} i_{L_{1}} + f_{v 1} \\ {\overset{\cdot}{x}}_{v 2} = {\overset{\cdot}{v}}_{o b} = \frac{1}{C_{b}} i_{L_{2}} + f_{v 2} \end{array}\}

f_{v 1} = \frac{i_{o a}}{C_{a}} + f_{v a}, f_{v 2} = \frac{i_{o b}}{C_{b}} + f_{v b}

i_{o a} = \frac{v_{o a}}{R_{a}}, i_{o b} = \frac{v_{o b}}{R_{b}}

将f_v1、f_v2扩张为新的状态变量x_v3、x_v4,式(13)可重新表示为

(14)

\begin{array}{l} {\overset{\cdot}{x}}_{v 1} = {\overset{\cdot}{v}}_{o a} = \frac{1}{C_{a}} i_{L_{1}} + x_{v 3} \\ {\overset{\cdot}{x}}_{v 3} = {\overset{\cdot}{f}}_{v a} \\ {\overset{\cdot}{x}}_{v 2} = {\overset{\cdot}{v}}_{o b} = \frac{1}{C_{b}} i_{L_{2}} + x_{v 4} \\ {\overset{\cdot}{x}}_{v 4} = {\overset{\cdot}{f}}_{v b} \end{array}\}

针对式(14)设计超螺旋扩张状态观测器为

(15)

\begin{array}{l} e_{v 1} = z_{a 3} - x_{v 1} \\ {\overset{\cdot}{z}}_{a 3} = \frac{1}{C_{a}} i_{L_{1}} + z_{a 4} - \\ l_{5} ({|e_{v 1}|}^{\frac{1}{2}} s i g n (e_{v 1}) + e_{v 1}) \\ {\overset{\cdot}{z}}_{a 4} = - l_{6} (\frac{1}{2} s i g n (e_{v 1}) + \\ \frac{3}{2} {|e_{v 1}|}^{\frac{1}{2}} s i g n (e_{v 1}) + e_{v 1}) \\ e_{v 2} = z_{b 3} - x_{v 2} \\ {\overset{\cdot}{z}}_{b 3} = \frac{1}{C_{b}} i_{L_{2}} + z_{b 4} - \\ l_{7} ({|e_{v 2}|}^{\frac{1}{2}} s i g n (e_{v 2}) + e_{v 2}) \\ {\overset{\cdot}{z}}_{b 4} = - l_{8} (\frac{1}{2} s i g n (e_{v 2}) + \\ \frac{3}{2} {|e_{v 2}|}^{\frac{1}{2}} s i g n (e_{v 2}) + e_{v 2}) \end{array}\}

式中: z_a₃、z_b₃分别为x_v₁、x_v₂的估计值;z_a₄、z_b₄ 分别为a、b输出支路扰动项估计值;e_v1、e_v2为观测误差;l₅~l₈为观测器增益,并采用带宽法进行整定^[30], l₅=l₇=2w_o,l₆=l₈= $w_{o}^{2}$ .

2.2.2 外环超螺旋滑模控制器设计

定义变换器电压外环跟踪误差为

(16)

\begin{array}{l} e_{a 2} = z_{a 3} - v_{o a, r e f} \\ e_{b 2} = z_{b 3} - v_{o b, r e f} \end{array}\}

式中:v_oa,ref、v_ob,ref分别为电压外环输出电压的参考值.

构建a、b输出支路电流环滑模面分别为

(17)

\begin{array}{l} S_{v a} = e_{a 2} + k_{v a} \int e_{a 2} d t \\ S_{v b} = e_{b 2} + k_{v b} \int e_{b 2} d t \end{array}\}

式中:k_va、k_vb为电压外环滑模面参数,均大于0.

对式(17)求导数可得:

(18)

\begin{array}{l} \frac{d S_{v a}}{d t} = \frac{1}{C_{a}} i_{L_{1}} + z_{a 4} + k_{v a} e_{a 2} \\ \frac{d S_{v b}}{d t} = \frac{1}{C_{b}} i_{L_{2}} + z_{b 4} + k_{v b} e_{b 2} \end{array}\}

设计电压外环超螺旋滑模控制律u_va、u_vb分别为

(19)

\begin{array}{l} \frac{d S_{v a}}{d t} = u_{v a} \\ u_{v a} = - λ_{v a} {|S_{v a}|}^{\frac{1}{2}} s i g n (S_{v a}) + w_{v a} \\ {\overset{\cdot}{w}}_{v a} = - β_{v a} s i g n (S_{v a}) \\ \frac{d S_{v b}}{d t} = u_{v b} \\ u_{v b} = - λ_{v b} {|S_{v b}|}^{\frac{1}{2}} s i g n (S_{v b}) + w_{v b} \\ {\overset{\cdot}{w}}_{v b} = - β_{v b} s i g n (S_{v b}) \end{array}\}

式中:λ_va、λ_vb、β_va、β_vb为电压外环控制器参数;w_va、w_vb为切换项的积分.

由式(18)和式(19)可得a、b输出支路电压外环控制律分别为

(20)

\begin{array}{l} i_{L_{1}} = C_{a} (u_{v a} - z_{a 4} - k_{v a} e_{a 2}) = i_{L a, r e f} \\ i_{L_{2}} = C_{b} (u_{v b} - z_{b 4} - k_{v b} e_{b 2}) = i_{L b, r e f} \end{array}\}

2.3 稳定性分析

CI-SIDO Buck变换器内外环超螺旋扩张状态观测器与控制器设计过程相似,表达形式基本一致.下面仅以a支路电流环为例对观测器和控制器进行稳定性分析.

2.3.1 超螺旋扩张状态观测器稳定分析

令a支路超螺旋扩张状态观测器的观测误差 e₁=z_a₁-x_c₁和e₂=z_a₂-x_c₂, 由式(5)和式(6)可得超螺旋扩张状态观测器的观测误差为

(21)

\begin{array}{l} {\overset{\cdot}{e}}_{1} = e_{2} - l_{1} ϕ_{1} (e_{1}) \\ {\overset{\cdot}{e}}_{2} = - l_{2} ϕ_{2} (e_{1}) - f_{R} \end{array}\}

式中: ϕ₁(e₁)= ${|e_{c 1}|}^{\frac{1}{2}}$ sign(e₁)+e_c₁,ϕ₂(e₁)= $\frac{1}{2}$ sign(e_c₁)+ $\frac{3}{2} {|e_{c 1}|}^{\frac{1}{2}}$ sign(e_c₁)+e_c₁;f_R 为有界扰动.

定义Lyapunov函数为

(22)

V_{1} (e) = ς^{T} P ζ

式中: P为正定矩阵;ζ^T= $[\begin{array}{l} ϕ_{1} (e_{1}) & e_{2} \end{array}]$ ,为 $ς$ 的转置矩阵.

对式(22)中 $ς$ 求导可得:

(23)

\dot{ς} = Φ (e_{1}) [\begin{array}{l} - l_{1} ϕ_{1} (e_{1}) + e_{2} \\ - l_{2} ϕ_{1} (e_{1}) - \frac{{\dot{f}}_{R}}{Φ (e_{1})} \end{array}] = Φ (e_{1}) (A ς - B ρ)

Φ (e_{1}) = \frac{1}{2} {|e_{1}|}^{- \frac{1}{2}} + 1, ρ = \frac{f_{R}}{Φ (e_{1})}

A = [\begin{array}{l} - l_{1} & 1 \\ - l_{2} & 0 \end{array}], B = [\begin{array}{l} 0 \\ 1 \end{array}]

实际系统中,扰动f_R是有界的,且满足 $|{\dot{f}}_{R}|$ ≤D,因此可知总扰动f_R≤D,其中D 为一个已知常数,可定义:

(24)

ψ (ρ, ς) = - ρ^{2} + D^{2} = [\begin{matrix} ς \\ ρ \end{matrix}] [\begin{matrix} D^{2} & 0 \\ 0 & - 1 \end{matrix}] [\begin{matrix} ς \\ ρ \end{matrix}] \geq 0

引理^[31]假设存在一个正常数κ,且有一个对称正定矩阵P满足以下矩阵不等式:

(25)

[\begin{array}{l} A^{T} P + P A + κ P + D^{2} & P B \\ B^{T} P & - 1 \end{array}] \leq 0

则超螺旋扩张状态观测器将在有限时间 $\bar{t}$ 收敛至原点,收敛时间为

(26)

\bar{t} \leq \frac{2}{κ} l n (\frac{2 V_{1}^{\frac{1}{2}} (e_{0})}{λ_{m i n}^{\frac{1}{2}} {P}} + 1)

式中: e₀为系统0时刻初始状态状态; $λ_{m i n}^{\frac{1}{2}} {P}$ 为矩阵P 的最小特征值的平方根.

由式(25)和式(26)结合定理可得Lyapunov函数的一阶导数为

(27)

\begin{array}{l} {\dot{V}}_{0} = Φ (e_{1}) [ς^{T} (Α^{T} P + P A) ς + ρ B^{T} P ς + ς^{T} P B ρ] = \\ Φ (e_{1}) [\begin{matrix} ς \\ ρ \end{matrix}] [\begin{matrix} Α^{T} P + P A & P B \\ B^{T} P & 0 \end{matrix}] [\begin{matrix} ς \\ ρ \end{matrix}] \end{array}

V₀为二次正定函数,结合式(24)和式(27)可得:

(28)

λ_{\min} {P} {‖ς‖}_{2}^{2} \leq ς^{T} P ς \leq λ_{\min} {P} {‖ς‖}_{2}^{2}

式中: ${‖ς‖}_{2}^{2}$ 为 $ς$ 的二范数,表达式为

(29)

{‖ς‖}_{2}^{2} = {|ϕ_{1} (e_{1})|}^{2} + {|e_{2}|}^{2} = |e_{1}| + 2 {|e_{1}|}^{\frac{3}{2}} + e_{1}^{2} + e_{2}^{2}

由式(29)可得:

(30)

{|e_{1}|}^{\frac{1}{2}} \leq {‖ς‖}_{2} \leq \frac{V_{0}^{\frac{1}{2}}}{λ_{min}^{\frac{1}{2}} \{P\}}

联立式(21)、式(26)~(30)可得:

(31)

\begin{array}{l} {\dot{V}}_{0} (e) \leq Φ (e_{1}) {[\begin{matrix} ς \\ ρ \end{matrix}]}^{T} [\begin{array}{l} A^{T} P + P A & P B \\ B^{T} P & 0 \end{array}] \leq \\ Φ (e_{1}) |{[\begin{matrix} ς \\ ρ \end{matrix}]}^{T} [\begin{array}{l} A^{T} P + P A & P B \\ B^{T} P & 0 \end{array}] [\begin{matrix} ς \\ ρ \end{matrix}] + ψ (ρ, ς)| \leq \\ Φ (e_{1}) {[\begin{matrix} ς \\ ρ \end{matrix}]}^{T} [\begin{array}{l} - κ P & 0 \\ 0 & 0 \end{array}] [\begin{matrix} ς \\ ρ \end{matrix}] = \\ Φ (e_{1}) (- κ ς^{T} P ς) = - Φ (e_{1}) κ V_{0} = \\ - \frac{κ V_{0}}{2 {|e_{1}|}^{\frac{1}{2}}} - κ V_{0} \end{array}

根据Lyapunov稳定性理论可知,式(31)满足引理的有限时间稳定性判据,因此估计误差可以在有限时间收敛到0.

2.3.2 超螺旋滑模控制器稳定分析

根据式(10)所示a支路电流内环超螺旋滑模控制律可得控制器闭环等式为

(32)

\begin{array}{l} {\overset{\cdot}{S}}_{c a} = - λ_{a} {|S_{c a}|}^{\frac{1}{2}} s i g n (S_{c a}) + w_{c a} \\ {\overset{\cdot}{w}}_{c a} = - β_{a} s i g n (S_{c a}) + {\overset{\cdot}{z}}_{a 2} \end{array}\}

定义Lyapunov函数为

(33)V₂=χ^TP_mχ

式中: $χ^{T} = [\begin{array}{l} χ_{1} & χ_{2} \end{array}] = [\begin{array}{l} {|S_{c a}|}^{\frac{1}{2}} s i g n (S_{c a}) & w_{c a} \end{array}]$ ; $P_{m} = \frac{1}{2} [\begin{array}{l} 4 β_{a} + λ_{a}^{2} & - λ_{a} \\ - λ_{a} & 2 \end{array}]$ 为正定矩阵.

对式(33)中χ求导可得:

(34)

\overset{\cdot}{χ} = [\begin{array}{l} \frac{1}{2} {|S_{c a}|}^{- \frac{1}{2}} (- λ_{a} {|S_{c a}|}^{\frac{1}{2}} s i g n (S_{c a}) + {\overset{\cdot}{w}}_{c a}) \\ - β_{a} s i g n (S_{c a}) + {\overset{\cdot}{z}}_{a 2} \end{array}] = \frac{1}{|χ_{1}|} (A_{1} χ + B_{1} z_{a 2})

A_{1} = [\begin{array}{l} - \frac{λ_{a}}{2} & \frac{1}{2} \\ - β_{a} & 0 \end{array}]

B_{1} = [\begin{array}{l} 0 \\ 1 \end{array}]

对式(33)求导并联立式(34)可得:

(35)

\begin{matrix} {\overset{\cdot}{V}}_{2} = \frac{1}{|χ_{1}|} {[\begin{array}{l} χ \\ z_{a 2} \end{array}]}^{T} [\begin{array}{l} A_{1}^{T} P_{m} + P_{m} A_{1} & P_{m} B_{1} \\ B_{1}^{T} P_{m} & 0 \end{array}] [\begin{array}{l} χ \\ z_{a 2} \end{array}] \leq \\ \begin{matrix} \frac{1}{|χ_{1}|}| {[\begin{array}{l} χ \\ z_{a 2} \end{array}]}^{T} [\begin{array}{l} A_{1}^{T} P_{m} + P_{m} A_{1} & P_{m} B_{1} \\ B_{1}^{T} P_{m} & 0 \end{array}] [\begin{array}{l} χ \\ z_{a 2} \end{array}] + \\ \begin{matrix} D^{2} χ_{1}^{2} - z_{a 2}^{2}| \leq \frac{1}{|χ_{1}|} χ^{T} (A_{1}^{T} P_{m} + P_{m} A_{1} + \\ D C^{T} + P_{m} B_{1} B_{1}^{T} P_{m}) χ \end{matrix} \end{matrix} \end{matrix}

式中: $C = [\begin{array}{l} 1 & 0 \end{array}]$ .

令 $A_{1}^{T}$ P_m+P_mA₁+DC^T+P_mB₁ $B_{1}^{T}$ P_m=- ${\bar{Q}}_{m}$ <0,则式(35)化简可得:

(36)

{\overset{\cdot}{V}}_{2} \leq - \frac{1}{|χ_{1}|} χ^{T} {\bar{Q}}_{m} χ

{\bar{Q}}_{m} = [\begin{array}{l} \frac{λ_{a}}{2} (2 β_{a} + λ_{a}^{2}) - D^{2} - \frac{λ_{a}^{2}}{4} & \frac{λ_{a}}{2} - \frac{λ_{a}^{2}}{2} \\ \frac{λ_{a}}{2} - \frac{λ_{a}^{2}}{2} & \frac{λ_{a}}{2} - 1 \end{array}]

要使系统在有限时间收敛,保证 ${\bar{Q}}_{m}$ 正定, ${\overset{\cdot}{V}}_{2}$ 负定,即λ_a>2, $β_{a} > \frac{λ_{a}^{2}}{4 (λ_{a} - 2)} + \frac{D^{2}}{λ_{a}}$ .

3 仿真与实验验证

3.1 仿真分析

为了对比超螺旋扩张状态观测器与线性扩张状态观测器的观测效果,采用表1所示电路参数和表2所示控制参数,基于MATLAB/Simulink搭建仿真平台,并均采用超螺旋滑模作为控制器,再分别采用超螺旋扩张状态观测器与线性扩张状态观测器进行仿真对比,控制器参数、观测器带宽参数均一致.

表1 CI-SIDO Buck变换器电路参数

Tab.1 Circuit parameters of CI-SIDO Buck converter

参数	数值
v_in/V	15~30
开关频率,f/kHz	20
v_oa/V	10
v_ob/V	5
L₁/μH	100
L₂/μH	100
M/μH	80
C_a/μF	470
C_b/μF	470
R_a/Ω	5.0~10
R_b/Ω	2.5~5

新窗口打开| 下载CSV

表2 CI-SIDO Buck变换器控制参数

Tab.2 Control parameters of CI-SIDO Buck converter

参数	数值
k_ia, k_ib	100
k_va, k_vb	80
λ_a, λ_b	1000
β_a, β_b	100
λ_va, λ_vb	800
β_va, β_vb	80
w_o	12.56×10³

新窗口打开| 下载CSV

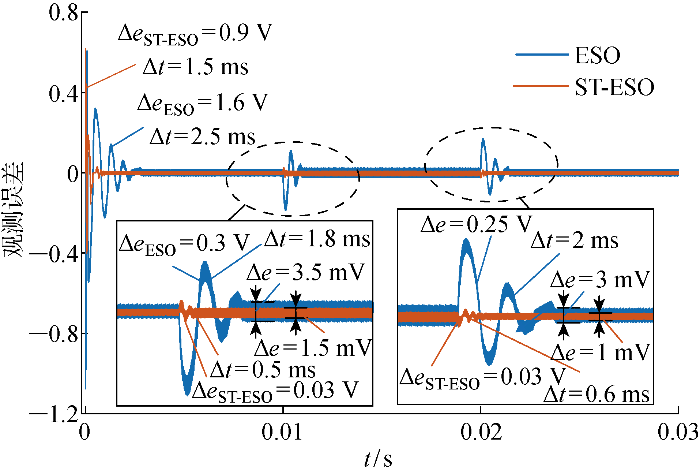
图3为ESO与ST-ESO的性能对比仿真图.分析图3可知,系统启动阶段,ST-ESO的收敛超调Δe_ST-ESO为0.9 V,收敛时间Δt为1.5 ms,观测误差Δe为1 mV;ESO的收敛超调Δe_ESO为1.6 V,收敛时间Δt为2.5 ms,观测误差Δe为3 mV.在0.01 s受到扰动时,ST-ESO的收敛超调Δe_ST-ESO为0.03 V,收敛时间Δt为0.5 ms,观测误差Δe为1.5 mV,ESO的收敛超调Δe_ESO为0.3 V,收敛时间Δt为1.8 ms,观测误差Δe为3.5 mV.在0.02 s系统受到扰动时,ST-ESO收敛超调Δe_ST-ESO为0.03 V,收敛时间Δt为0.6 ms,观测误差Δe为1 mV,ESO的收敛超调Δe_ESO为0.25 V,收敛时间Δt为2 ms,观测误差Δe为3 mV.对比系统启动阶段和受到扰动时的收敛超调、收敛速度以及观测误差可知,ST-ESO 的整体性能优越于ESO.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 观测器性能仿真对比

Fig.3 Performance comparison of observer simulation

3.2 实验验证

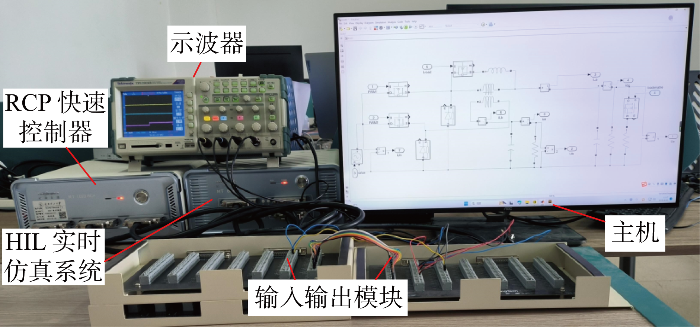
为了验证理论分析的正确性,采用硬件在环实验平台进行实验验证,分别将文献[16]中所采用的平均电流控制和ESO结合传统滑模控制与所提控制进行实验对比.变换器电路参数和控制参数同表1和表2,硬件在环(HIL)实验平台如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 硬件在环实验平台

Fig.4 Hardware-in-the-loop platform

传统滑模控制器的滑模面与所提控制滑模面一致,趋近律表达形式为 $\overset{\cdot}{S}$ =-λS-βsign(S),其中S为滑模面,λ、β 分别为趋近律的控制器参数,ESO设计过程和观测器带宽与所提控制一致.

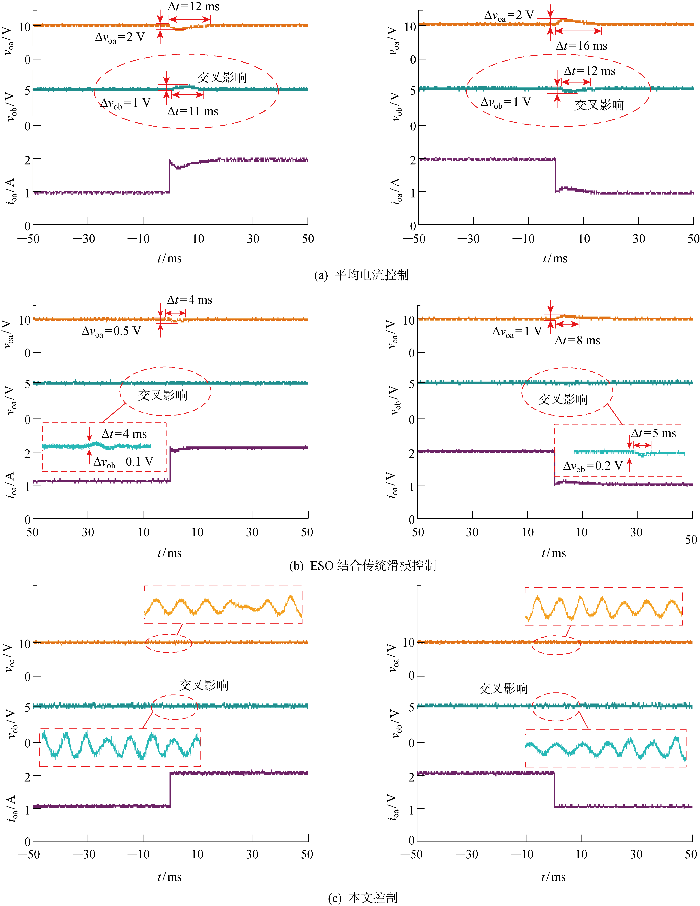
图5为支路a负载跳变的实验结果.分析图5可知,a支路负载由1 A突变为2 A时,平均电流控制下变换器a支路的超调电压为2 V,a支路输出电压经过12 ms恢复稳态;b支路受到a支路的交叉影响引起的超调电压为1 V,b支路输出电压经过11 ms恢复稳态;a支路负载电流由2 A突变为1 A时,a支路超调电压为2 V,a支路输出电压经过16 ms 恢复稳态,b支路受到a支路的交叉影响引起的超调电压为1 V,b支路输出电压经过12 ms恢复稳态.ESO结合传统滑模控制下的变换器a支路的超调电压为0.5 V,a支路输出电压经过4 ms恢复稳态;b支路受到a支路的交叉影响超调电压为0.1 V,经过4 ms恢复稳态;a支路负载电流由2 A变为1 A时,a支路超调电压为1 V,a支路输出电压经过8 ms恢复稳态,b支路受到a支路的交叉影响引起的超调电压为0.2 V,b支路输出电压经过5 ms 恢复稳态.实验结果表明,所提控制策略很好地抑制了a支路对b支路造成的交叉影响,并提高了a支路的抗负载扰动能力.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 i_oa突变的实验结果

Fig.5 Experimental results of i_oa mutation

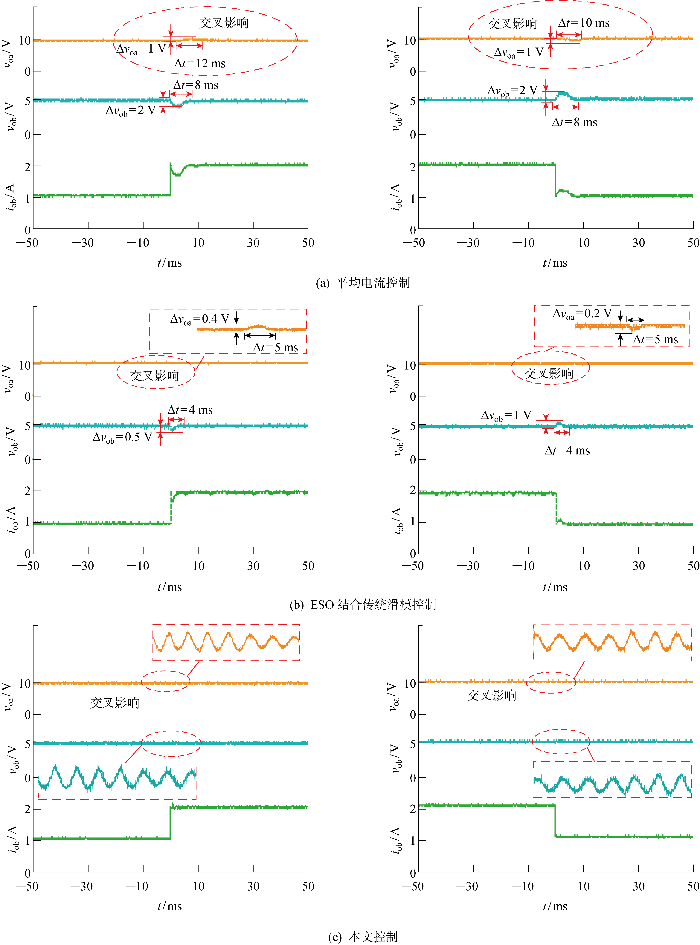
图6为b支路负载跳变的实验结果.分析图6可知,在b支路负载由1 A突变为2 A时,平均电流控制策略下的变换器b支路的超调电压为2 V,b支路输出电压经过8 ms恢复稳态;a支路受到b支路的交叉影响引起的超调电压为1 V,a支路输出电压经过12 ms恢复稳态;b支路负载电流由2 A突变为1 A时,b支路超调电压为2 V,b支路输出电压经过8 ms恢复稳态,a支路受到b支路的交叉影响引起的超调电压为1 V,b支路输出电压经过10 ms 恢复稳态.ESO结合传统滑模控制下变换器b支路的超调电压为0.5 V,b支路输出电压经过4 ms 恢复稳态;a支路受到b支路的交叉影响引起的超调电压为0.4 V,a支路输出电压经过5 ms恢复稳态;b支路负载电流由2 A变为1 A时,b支路超调电压为1 V,b支路输出电压经过4 ms恢复稳态,a支路受到b支路的交叉影响引起的超调电压为0.2 V,a支路输出电压经过5 ms恢复稳态.实验结果表明,所提控制策略很好地抑制了b支路对a支路的交叉影响,并提高了b支路的抗负载扰动能力.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 i_ob突变的实验结果

Fig.6 Experimental results of i_ob mutation

以上结果表明,所提控制策略可实现 CI-SIDO Buck变换器输出支路间的解耦,抑制交叉影响的同时也提高了系统的鲁棒性和抗负载扰动能力以及系统的动态性能.

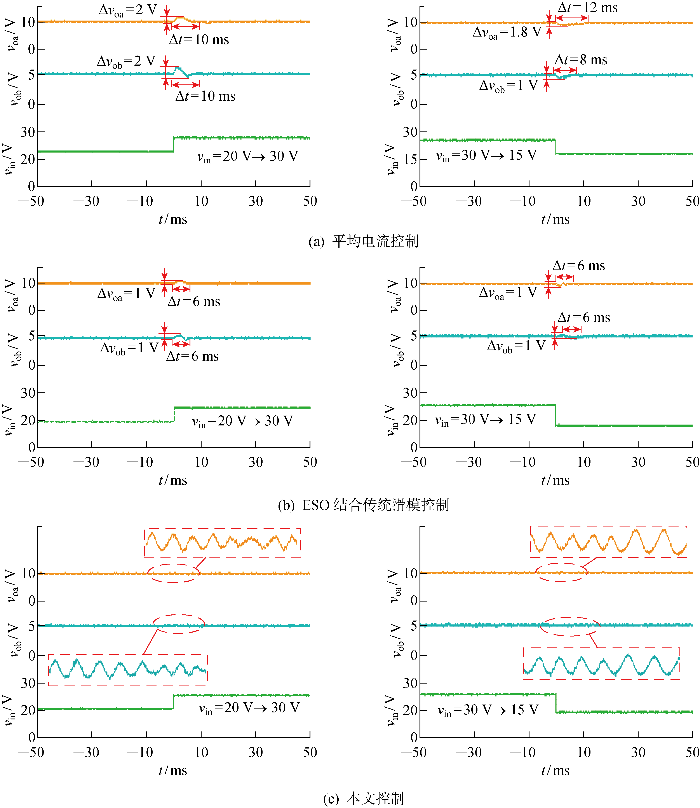
图7为输入电压突变的实验结果,分析图7知,输入电压由20 V突变为30 V时,平均电流控制下的变换器a支路输出超调电压为2 V,经过10 ms系统恢复稳态,b支路输出超调电压为2 V,经过 10 ms 恢复稳态;输入电压由30 V突变为15 V时,a支路输出超调电压为1.8 V,经过12 ms恢复稳态,b支路输出超调电压为1 V,经过8 ms恢复稳态.ESO结合传统滑模控制下变换器 a、b支路输出超调电压为1 V,a、b输出电压经过6 ms恢复稳态,输入电压从30 V突变为15 V时,a支路输出超调电压为1 V,经过6 ms恢复稳态,b支路输出超调电压为0.5 V,经过6 ms恢复稳态.而所提控制策略下输入电压突变时,超调电压以及调节时间均较小.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 v_in突变的实验结果

Fig.7 Experimental results of v_in mutation

以上实验结果表明,所提控制策略具有良好的抗输入电压扰动能力,提高了系统的鲁棒性和动态性能.

4 结论

为了抑制CI-SIDO Buck变换器输出支路间的交叉影响,提高系统动态性能,提出基于 ST-ESO 的串级滑模解耦控制策略.通过理论分析和实验验证了控制策略的有效性以及优越性,得出以下结论:

(1) 通过ST-ESO对变换器内外环中的耦合项和内部扰动以及未建模部分视为的总扰动进行观测,采用超螺旋滑模控制器对内外环中总扰动进行补偿,实现了系统的解耦.

(2) 通过对比平均电流控制相比,分析在负载扰动和输入电压扰动下的超调量和超调时间,可知控制策略抑制了系统的交叉影响,提高了系统的动态性能和抗扰能力,保证了输出电压的稳定.

(3) 所提控制策略不依赖变换器精确数学模型,控制器过程设计简单,易于实现,也可应用于其他耦合单电感双输出变换器.

未来可将所提控制策略应用在CI-SIDO Buck变换器DCM工作模式下,使得CI-SIDO Buck变换器可工作在宽输入及宽负载范围,进一步体现 CI-SIDO Buck变换器采用该控制方法下在电动汽车和便携式设备等领域的应用价值.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

MARKKASSERY

, SARADAGI

, MAHINDRAKAR

A D

, et al.

Modeling, design and control of non-isolated single-input multi-output zeta-buck-boost converter

[J]. IEEE Transactions on Industry Applications, 2020, 56(4): 3904-3918.