黏弹性围岩纵向变形曲线及其释放系数演化规律

doi:10.16183/j.cnki.jsjtu.2023.350

黏弹性围岩纵向变形曲线及其释放系数演化规律

王嘉琛¹, 孟令赞¹^,², 张顶立^,¹, 卢松¹, 文明³

1.北京交通大学城市地下工程教育部重点实验室,北京 100044

2.北京城建设计发展集团股份有限公司北京市轨道结构工程技术研究中心,北京 100037

3.北京市应急管理科学技术研究院城市运行安全研究中心,北京 101101

Evolution Law of Longitudinal Deformation Curve and Release Coefficient of Viscoelastic Rock

WANG Jiachen¹, MENG Lingzan¹^,², ZHANG Dingli^,¹, LU Song¹, WEN Ming³

1. Key Laboratory for Urban Underground Engineering of the Ministry of Education, Beijing Jiaotong University, Beijing 100044, China

2. Beijing Engineering Research Center of Track Structure, Beijing Urban Construction Design and Development Group Co., Ltd., Beijing 100037, China

3. Urban Operation Safety Research Center, Beijing Academy of Emergency Management Science and Technology, Beijing 101101, China

通讯作者: 张顶立,教授,博士生导师,电话(Tel.):010-51688114;E-mail:zhang_dingli@263.net.

责任编辑: 王一凡

收稿日期: 2023-07-28 修回日期: 2024-02-20 接受日期: 2024-03-27

基金资助:

中央高校基本科研业务费专项资金(2023YJS049)

Received: 2023-07-28 Revised: 2024-02-20 Accepted: 2024-03-27

作者简介 About authors

王嘉琛(1998—),博士生,从事隧道与地下工程研究.

摘要

常规的弹性解无法对具有强蠕变特性的软岩隧道变形规律提出合理解释.因此,针对软岩隧道施工的时间-空间效应,引入Burgers模型揭示其时空演化规律,并通过数值计算探究不同因素对黏弹性围岩纵向变形规律的影响.同时基于响应面法得到位移释放系数的经验公式,与现场监测和其他理论比较验证了本文方法的可行性.研究结果表明地应力对位移释放系数影响可忽略,Kelvin切变模量、Kelvin黏滞系数、Maxwell切变模量和开挖速度显著影响位移释放系数,而根据延滞时间的不同可分为低延滞系数、中延滞系数和高延滞系数3类;针对时间效应影响型、空间效应影响型和时空效应影响型3种黏弹性围岩纵向变形曲线类型拟合得到相应的经验公式.研究结论可为软岩隧道变形预测提供更简便的方法.

关键词： 黏弹性; 纵向变形曲线; 软岩隧道; 时空效应; 位移释放系数

Abstract

Conventional elastic solutions cannot explain the deformation characteristics of soft rock tunnels exhibiting creep behavior. Therefore, a Burgers model is introduced to demonstrate the space-time effects in the construction period of soft rock tunnel. The influences of different factors on the longitudinal deformation behavior of viscoelastic rock as well as the spatiotemporal evolution patterns have been revealed through numerical simulations. An empirical formula for the displacement release coefficient is derived using the response surface method. The feasibility of the proposed method is validated by comparing the results with on-site monitoring data and other theoretical values. The findings indicate that geostress has a negligible effect on the displacement release coefficient. In constrast, the Kelvin shear modulus, viscosity coefficient, Maxwell shear modulus, and excavation speed significantly affect the displacement release coefficient. According to viscosity time, the hysteresis coefficient can be divided into three categories: low, medium, and high. Empirical formulas are fitted for the longitudinal deformation curve, including time, spatial, and spatiotemporal factors. The research conclusion can provide a more convenient method for predicting the deformation of soft rock tunnels.

Keywords： viscoelasticity; longitudinal deformation profile; soft rock tunnel; time-space effect; displacement release coefficient

PDF (8387KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王嘉琛, 孟令赞, 张顶立, 卢松, 文明. 黏弹性围岩纵向变形曲线及其释放系数演化规律[J]. 上海交通大学学报, 2025, 59(4): 513-524 doi:10.16183/j.cnki.jsjtu.2023.350

WANG Jiachen, MENG Lingzan, ZHANG Dingli, LU Song, WEN Ming. Evolution Law of Longitudinal Deformation Curve and Release Coefficient of Viscoelastic Rock[J]. Journal of Shanghai Jiaotong University, 2025, 59(4): 513-524 doi:10.16183/j.cnki.jsjtu.2023.350

随着西南地区快速发展,高地应力软弱围岩(简称软岩)成为隧道建设的主要难题之一.高地应力软岩在隧道建设时,常表现出大变形和较强的蠕变特性,给隧道支护设计带来极大的挑战.收敛约束法因理论清晰且经过长期实践的验证,而仍被广泛使用^[1].隧道围岩全过程纵向变形曲线(LDP曲线)作为收敛约束法的核心,如何确定具有蠕变特性的围岩全过程纵向变形曲线是解决高地应力软岩隧道设计的关键^[2].

由于软岩具有较强的蠕变特性,所以在软岩隧道施工过程中,围岩会同时受到时间效应与空间效应的影响.相关学者分别采用理论解析、数值模拟和现场实测对两种效应展开研究.文献[3 -6]中基于三维黏弹性力学解析方法得到了围岩黏弹性本构模型,该模型仅考虑隧道开挖的空间效应;Wang等^[7]和Zeng等^[8]基于复变函数、保角映射及Laplace变换的方法,探究了考虑隧道开挖顺序的围岩应力变化情况.文献[9-10]中在Burgers模型条件下,探究了围岩压力和应力释放率、地应力、支护方案的关系;苏永华等^[11]根据Hoek-Brown强度准则,总结了围岩临界软化参数的求解方法,并引入LDP曲线中进行计算.谭代明等^[12]、霍晓龙等^[13]、Liu等^[14-17]利用不同的数值模拟软件探究不同施工方法、施工顺序、黏弹性围岩参数对隧道安全性的影响,并提出相应的优化方案.卢伟^[18]、左清军等^[19]、王建等^[20]和杨成忠等^[21]分别以将军岭隧道、姚家隧道、道吾山特长隧道、长城岭隧道为背景,探究围岩变形的时空效应.总体而言,以往针对黏弹性围岩的研究较少考虑时间效应,更多只针对于空间效应.实际上,软岩隧道在支护施作后仍会产生持续的变形,这是时间效应和空间效应叠加的效果,因此仅考虑空间效应进行支护设计有较大的缺陷.

综上,本文针对软岩隧道施工的时间-空间效应,引入Burgers模型,基于有限元软件对不同的Burgers参数展开模拟,并引入洞周位移释放系数对围岩蠕变特性进行分析,探究不同典型因素对围岩纵向变形曲线和位移释放系数的影响.最终通过响应面法分别得到空间效应、时间效应和时空效应控制的纵向变形经验公式,并与现场监测结果和既有公式进行比较验证本文方法的可行性.本文基于不同黏弹性围岩参数推导出的黏弹性纵向变形经验公式,相较于以往理论公式更为简化,方便工程师对具有较强蠕变特性的软岩进行变形预测,为后续软岩隧道支护设计工作提供支持.

1 黏弹性围岩纵向变形曲线模型

1.1 基本假设与问题描述

随着隧道围岩条件变得越来越复杂,常规的弹性解答已无法准确描述具有较强蠕变特性的软弱围岩支护关系,需要引入考虑围岩时空效应的黏弹性理论进行研究.围岩纵向变形曲线是收敛约束法解决三维变形问题的关键曲线,同时为探究围岩变形沿纵向分布规律,引入隧道洞周位移释放系数,表达式为

(1)

\begin{matrix} u^{*} (x) = u (x) / u_{m a x} \end{matrix}

式中: x表示距离掌子面的距离(正值为掌子面后方;负值为掌子面前方); $u_{m a x}$ 表示围岩变形最大值; $u^{*} (x)$ 和 $u (x)$ 表示距离掌子面x的位移释放系数和变形量, $u (x)$ 可简写为u.

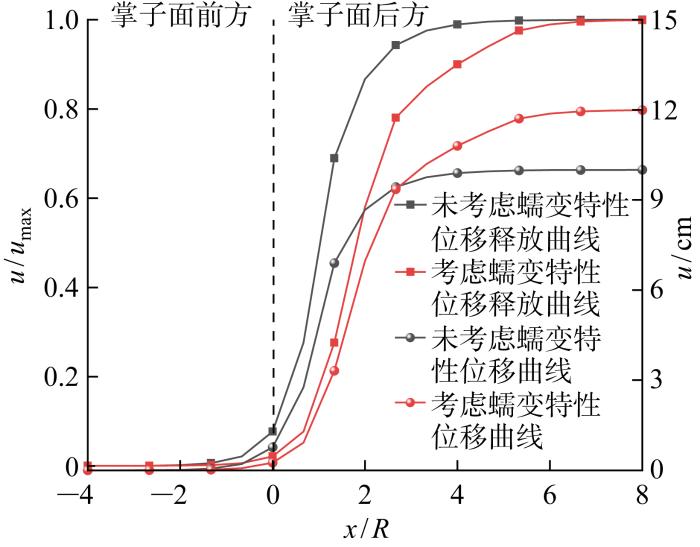
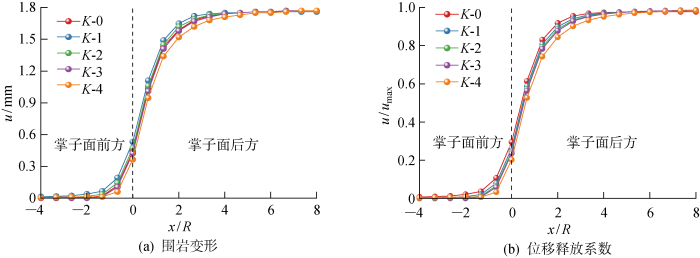
将考虑与未考虑蠕变特性的位移曲线和位移释放系数曲线绘制于图1.图中:R表示隧道开挖半径.在纵向变形曲线中,考虑蠕变特性的黏弹性解答达到最大变形的位置晚于未考虑蠕变特性的弹性解答;而考虑蠕变特性的最大变形大于未考虑蠕变特性,因此在针对软岩隧道设计时必须考虑蠕变特性的作用.而本文将由于蠕变特性导致围岩变形收敛时间显著增长的情况称为围岩的时间效应;将不同位置围岩变形不同的情况则称为围岩的空间效应.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 围岩纵向变形曲线

Fig.1 Longitudinal deformation profile

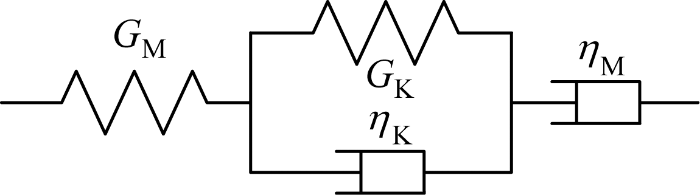
为通过数值模拟归纳总结得到考虑时空效应的围岩释放系数的经验公式,本文采用Burgers本构模型展开研究,如图2所示,并做出以下假定:① 围岩各向同性且具有稳定蠕变特性;② 隧道为深埋圆形隧道,且模型不考虑重力作用;③ 围岩为均质黏弹性材料,变形满足小变形假设.图中:G_K表示Kelvin切变模量;η_K表示Kelvin黏滞系数;G_M表示Maxwell切变模量;η_M表示Maxwell黏滞系数.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 Burgers模型

Fig.2 Burgers model

目前没有Burgers模型取值范围和建议值,因此为建立黏弹性围岩纵向变形曲线数据库,本文选取14个不同的Burgers参数反演结果作为计算参数,具体如表1所示.表中:K表示体积模量.

表1 14种实际Burgers参数

Tab.1 Fourteen actual Burgers parameters

系列	G_K/GPa	η_K/(GPa·h)	G_M/GPa	K/MPa	系列	G_K/GPa	η_K/(GPa·h)	G_M/GPa	K/MPa
1	3.72	0.13	8.90	95.14	8	3.23	16.7	0.410	160.32
2	2.38	0.11	5.16	65.79	9	0.94	9.7	0.088	74.36
3	0.23	0.03	0.68	47.44	10	4.21	155.2	9.770	58.33
4	9.75	0.23	16.66	60.42	11	2.27	185.3	1.660	168.00
5	3.65	0.13	8.42	70.83	12	2.27	182.4	2.020	178.79
6	2.38	0.11	4.85	48.48	13	0.28	91.1	0.160	50.79
7	12.61	286.20	22.54	186.31	14	0.07	44.6	0.058	111.73

新窗口打开| 下载CSV

1.2 模型建立

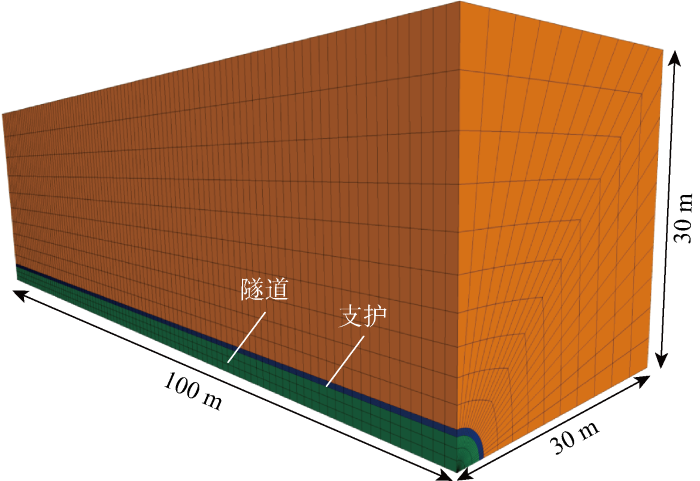
由于不考虑重力作用,模型(见图3)可以选取1/4进行模拟分析.现有理论认为空间效应只存在于10倍隧道半径以内^[15],因此选择隧道的开挖半径为3 m,模型的水平和和竖直方向均为10倍洞径(30 m),纵向长度为100 m.根据隧道的实际情况,模型上方以外的边界均设置为固定边界,地应力可按照相应的梯度施加在模型节点上.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 数值模型示意图

Fig.3 Model diagram

在以往的研究中,因只考虑空间效应,纵向变形曲线的提取采用一次开挖再提取的方法.本文同时研究空间效应和时间效应的影响,因此只能采用分步开挖并记录的方法,具体方法为:每次开挖一定长度,软件内部的记录功能(history)对所研究位置的变形进行记录.随着隧道不断开挖,所得到的围岩变形与隧道纵向位置的关系曲线即是具有时空效应的纵向变形曲线.

2 典型因素影响规律

2.1 地应力影响分析

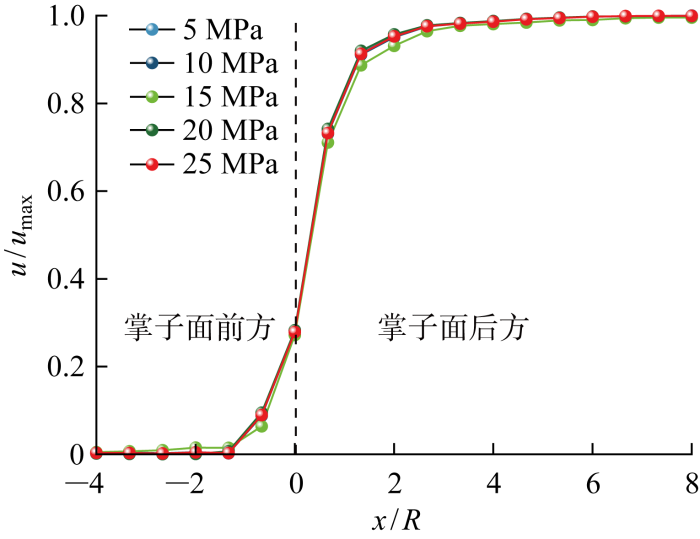
为探究地应力对围岩纵向变形曲线的影响,选取5个地应力梯度5、10、15、20、25 MPa 开展研究,将各组拟合结果绘制于图4.在各系列中,不同初始地应力的位移释放系数曲线基本相同,因此地应力对位移释放系数的影响基本可忽略不计.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 各地应力对应的位移释放系数

Fig.4 Displacement release coefficient of each stress

在既有研究中,Burgers模型二维平面应变条件下围岩特性曲线只与时间有关,相应表达式为

(2)$u_{r}(t)=\frac{\sigma^{0} R}{2}\left[\frac{1}{G_{M}}+\frac{1}{G_{K}}\left(1-e^{-\frac{G_{K}}{\eta_{K}} t}\right)\right]$

式中:σ⁰为原岩应力.

当t→∞时:

(3)

\begin{matrix} \frac{u_{m a x}}{σ^{0}} = \frac{R}{2} (\frac{1}{G_{M}} + \frac{1}{G_{K}}) = \frac{R}{2} (\frac{G_{M} + G_{K}}{G_{M} G_{K}}) \end{matrix}

在黏弹性围岩不考虑时空效应的条件下, $u_{m a x} / σ^{0}$ 只与 $R 、 G_{M} 、 G_{K}$ 有关.将数值模拟的斜率k与解析公式获得的 $u_{m a x} / σ^{0}$ 汇总于表2进行比较,两者数值差异均小于4×10^-4,因此数值模拟的结果符合既有理论研究,该数值模拟结果可信.

表2 最大位移解析解与数值模拟结果对比

Tab.2 Comparison of maximum displacement theoretical results and numerical simulation results

系列	k×10⁴	u_max/σ⁰×10⁴	系列	k×10⁴	u_max/σ⁰×10⁴
1	5.23	5.49	8	37.72	39.40
2	8.45	8.86	9	170.05	176.79
3	79.90	83.40	10	4.67	4.88
4	2.19	2.29	11	14.44	15.09
5	5.32	5.59	12	12.83	13.33
6	8.56	8.97	13	141.55	146.02
7	1.69	1.76	14	428.45	445.90

新窗口打开| 下载CSV

2.2 Burgers参数影响分析

为了进一步探究Burgers参数对围岩变形和位移释放系数的影响,以系列7为基础,基于控制变量法设计试验工况.将系列7的Burgers参数均额外设计4个水平进行计算,其中0、1、2、3和4水平分别对应系列7中该参数原值,原值的10%、50%、150%和 1 000%,如表3所示.

表3 系列7位移释放系数计算参数

Tab.3 Calculation parameters of displacement release rate in Series 7

工况	G_K/GPa	η_K/(GPa·h)	G_M/GPa	K/MPa	工况	G_K/GPa	η_K/(GPa·h)	G_M/GPa	K/MPa
K-1	12.61	286.20	22.54	18.63	η_K-1	12.61	28.62	22.54	186.31
K-2	12.61	286.20	22.54	93.16	η_K-2	12.61	143.10	22.54	186.31
K-3	12.61	286.20	22.54	279.47	η_K-3	12.61	429.30	22.54	186.31
K-4	12.61	286.20	22.54	1 863.10	η_K-4	12.61	28620	22.54	186.31
G_K-1	1.261	286.20	22.54	186.31	G_M-1	12.61	286.20	2.254	186.31
G_K-2	6.31	286.20	22.54	186.31	G_M-2	12.61	286.20	11.27	186.31
G_K-3	18.92	286.20	22.54	186.31	G_M-3	12.61	286.20	33.81	186.31
G_K-4	126.10	286.20	22.54	186.31	G_M-4	12.61	286.20	225.40	186.31

新窗口打开| 下载CSV

2.2.1 K的影响

如图5所示, K的变化对围岩纵向变形曲线、位移释放系数曲线影响不显著,两者变化趋势相同.研究断面位移变形范围从掌子面前2倍隧道半径开始,到掌子面后6倍隧道半径抵达最大值.K是岩石的固有性质,当K增大,相同应力条件下其变形将越小,但是支护状态并未发生改变,因此整体围岩-支护受力未改变,最大变形不变,K增大将导致围岩变形曲线和位移释放曲线收敛缓慢.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 体积模量K的影响

Fig.5 Effect of bulk modulus (K)

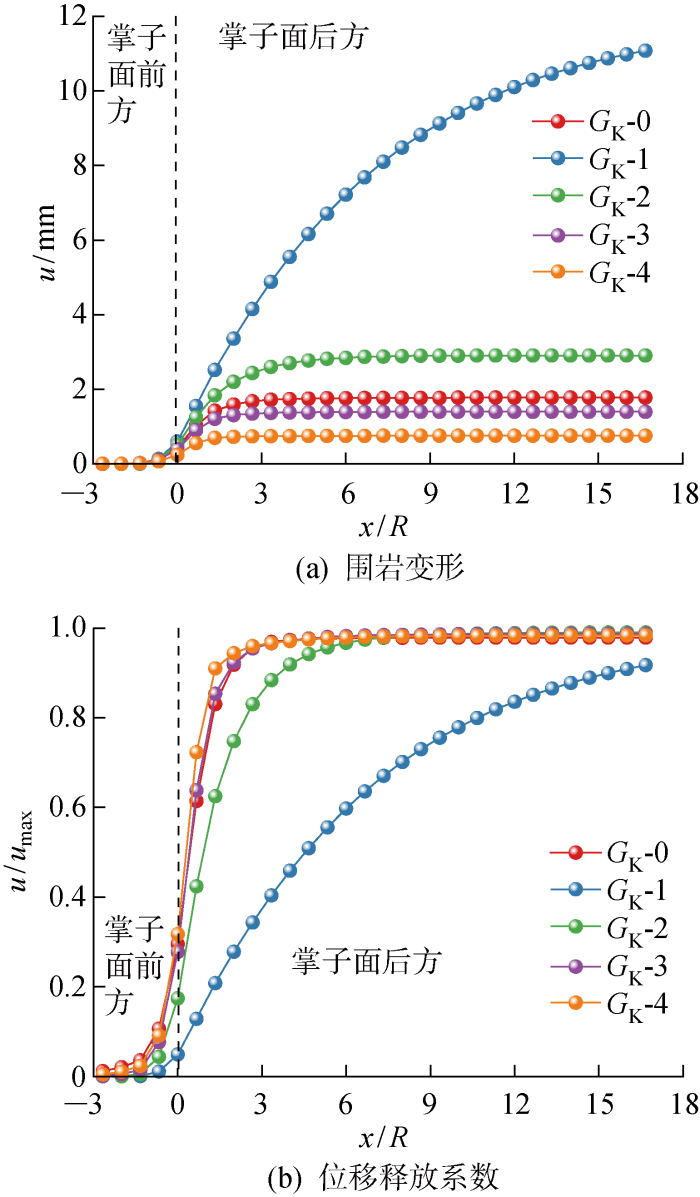
2.2.2 G_K的影响

如图6所示,G_K减小导致围岩变形增加的同时会出现在模型计算范围内无法达到最大变形的情况.而在位移释放系数方面,模型范围内无法达到最大收敛位移的工况(G_K-1)对应的位移释放系数同样低于其他组.位移释放系数随着G_K的增加而增加,工况G_K-1、G_K-2的增长幅度较大,而工况G_K-3和G_K-4的变化不显著.G_K是与黏壶元件并联的弹簧元件的切变模量,相同受力条件下随着G_K不断减小,围岩变形将不断增大.当G_K相对较大时,其对变形的影响相对较小,而当G_K足够小时,围岩变形将快速增大.由于工况G_K-1未达到最大变形,所以该工况对应的位移释放系数曲线未形成完整的S形曲线,其余工况均形成了完整的S形曲线,因此相应的位移释放系数曲线基本保持一致.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 Kelvin切变模量G_K的影响

Fig.6 Effect of Kelvin shear modulus (G_K)

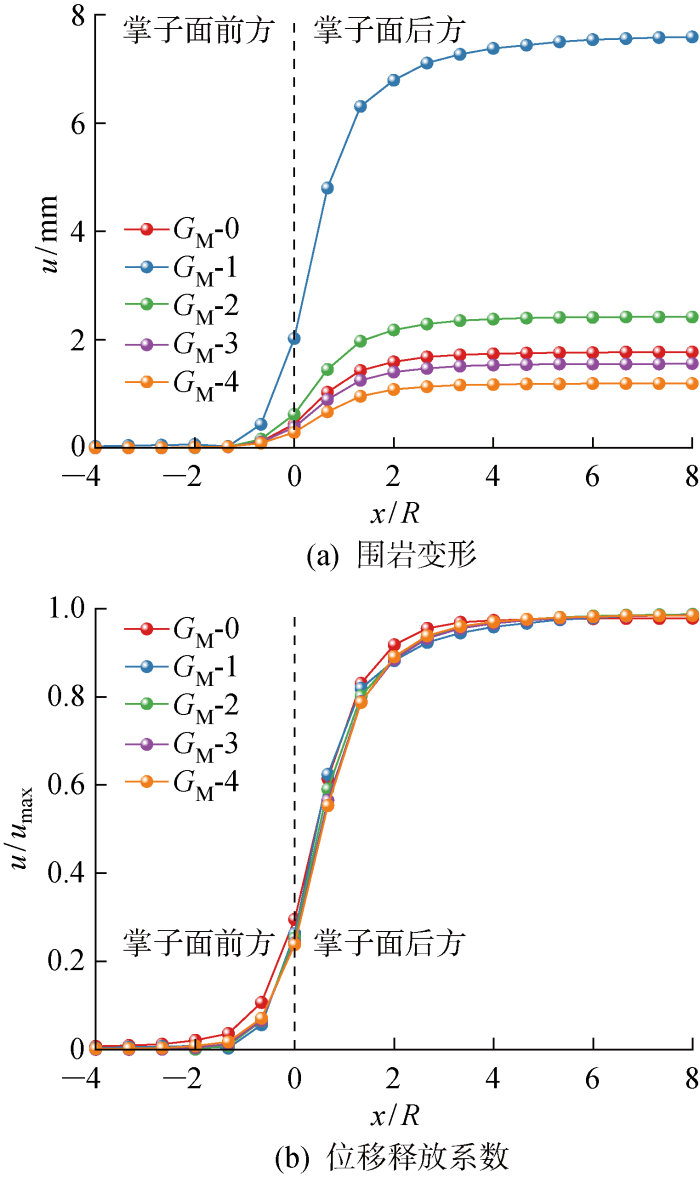
2.2.3 G_M对位移、位移释放系数的影响

如图7所示,G_M的减小会导致围岩变形的增加,其中工况G_M-1围岩变形远大于其他工况;而位移释放系数随G_M的变化不显著.变形影响范围同样为掌子面前2倍隧道半径至掌子面后6倍隧道半径.G_M是与黏壶元件串联的弹簧元件的切变模量,可表示瞬时形态.相同受力条件下随着G_M的不断减小,围岩变形将不断增大.当G_M相对较大时,其对变形的影响相对较小,而当G_M足够小时,围岩变形将快速增大.由于不同G_M均形成了完整的S形曲线,所以相应的位移释放系数曲线基本保持一致.与G_K相比,G_M不同水平下各曲线间差异较小且围岩变形更小,因此参数G_M相较于参数G_K对围岩变形影响较小.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 Maxwell切变模量G_M的影响

Fig.7 Effect of Maxwell shear modulus (G_M)

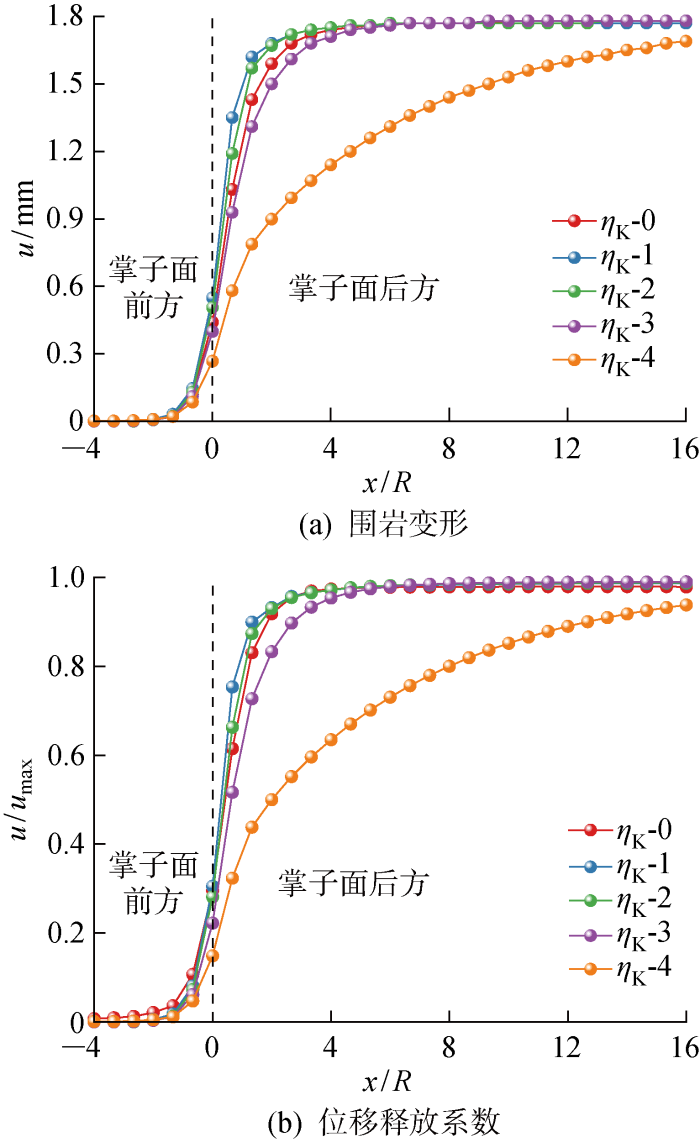
2.2.4 η_K对位移、位移释放系数的影响

如图8所示,η_K的增加会导致出现无法达到最大变形(η_K-4)的情形,但是η_K的改变不会影响最大变形.围岩变形在η_K-4至η_K-3变化较大,而在η_K-3、η_K-2、η_K-1的变化过程中差距较小.位移释放系数变化规律与围岩变形趋势基本一致.黏壶是控制围岩蠕变特性的核心元件,但其不是强度控制的元件,因此其只能控制围岩变形曲线的形态.当黏滞系数较小时,其蠕变差异并不明显,各曲线差别较小;当黏滞系数较大时,其蠕变特性较为明显,因此前期变形速率较慢,达到平衡的时间也更长.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 Kelvin黏滞系数η_K的影响

Fig.8 Effect of Kelvin viscosity coefficient (η_K)

2.3 开挖速度影响分析

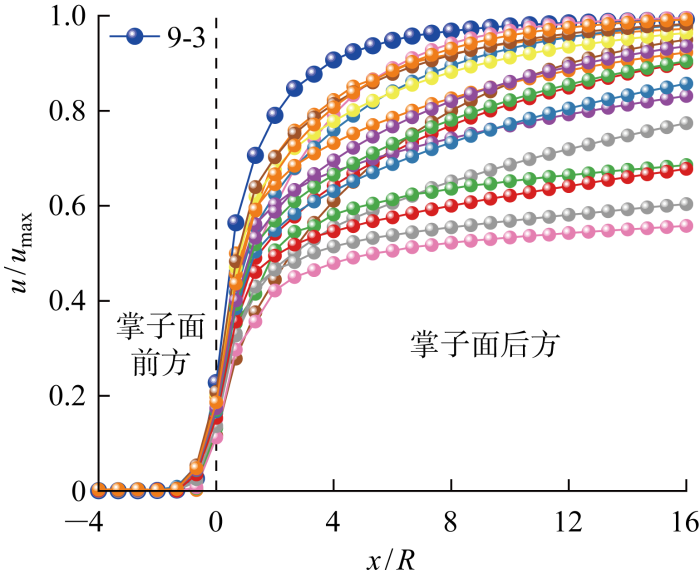
由式(1)可知,三维条件下Burgers模型中时间相关的围岩特性与延滞时间t_d(t_d=η_K/G_K)密切相关.在对单一变量Burgers参数的影响研究中,随着η_K增大,时间效应的作用更明显,模型计算收敛时间也更长.因此,本文为进一步研究开挖速度的影响,共设置9组工况,工况1~9分别代表施工速度为16、8、4、2、1.3、1、0.8、0.4、0.2 m/d.后续研究中工况标号将按照系列号+开挖速度工况,如9-1表示系列9开挖速度为16 m/d.计算结果表明,不同延滞时间所对应的位移释放系数曲线可根据其能否形成完整的S形曲线和围岩开始变形的位置,划分为3类:低延滞系数、中延滞系数和高延滞系数.

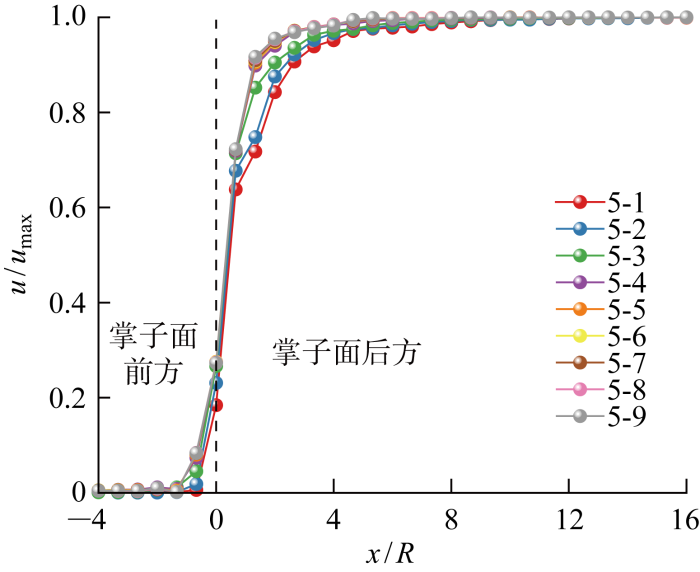
当延滞时间较小时(系列1~6最大延滞时间为470 s),在掌子面前方即x/R<0,位移释放的时空效应均从2倍隧道半径内才开始出现.以系列5为例,不同速度对应的位移释放系数曲线绘制于图9.当速度为16和8 m/d时,位移释放系数随着开挖速度的减小而增大;当开挖速度小于或等于2 m/d时,开挖速度对位移释放系数变化基本没有影响;开挖速度为4 m/d的工况介于上述情况之间.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 系列5位移释放系数

Fig.9 Displacement release coefficient of Series 5

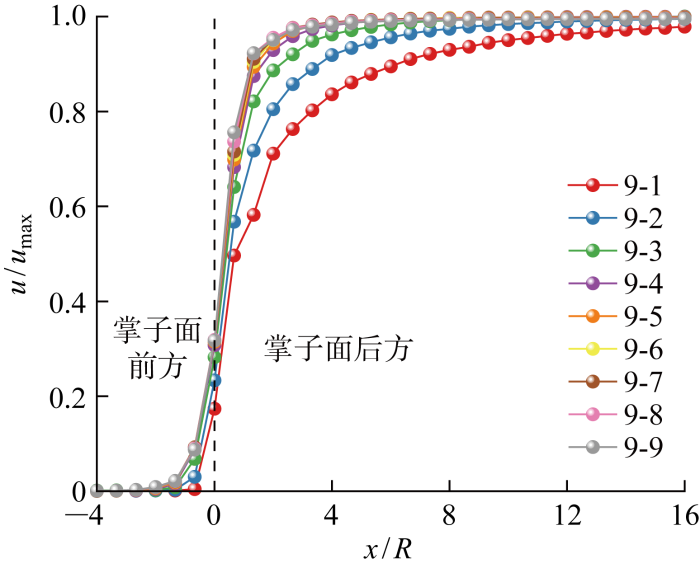
系列7、8、9的延滞时间大于470 s,将其归纳为中延滞系数,以系列9为例,相应工况的位移释放系数曲线如图10所示.掌子面前方位移释放系数曲线的起始点相较于低延滞系数提前至掌子面前方3倍隧道半径处.掌子面后方,当开挖速度大于2 m/d时,时间效应在隧道开挖循环内无法释放完全,且开挖速度在16、8、4 m/d时位移释放率差异更大.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 系列9位移释放系数

Fig.10 Displacement release coefficient of Series 9

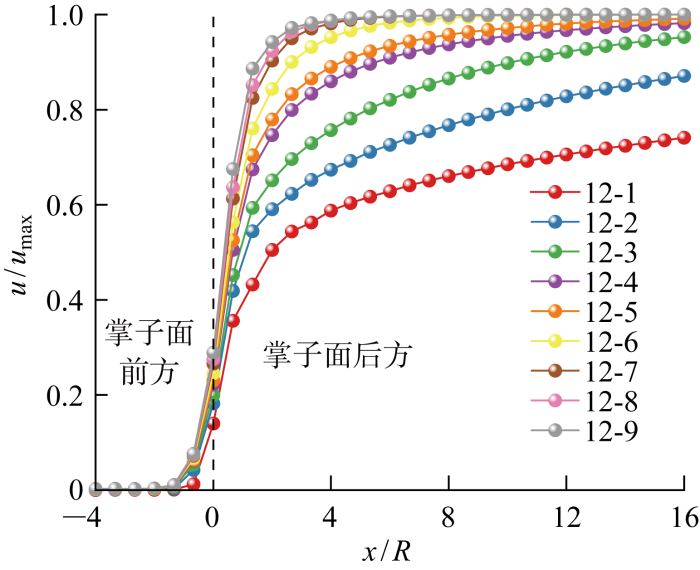
高延滞时间工况(系列10~14,以系列12为例)的位移释放系数曲线如图11所示,曲线在掌子面前方的起点相较于低延滞时间系列距离掌子面更远.而在掌子面后方,围岩变形的持续时间将随着延滞时间的增加而逐渐增加,因此在数值模拟的模型范围内越来越难以达到最大收敛位移.因而在系列12中,12-1、12-2和12-3这3条曲线在16倍隧道半径的范围内无法形成完整的S形曲线.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 系列12位移释放系数

Fig.11 Displacement release coefficient of Series 12

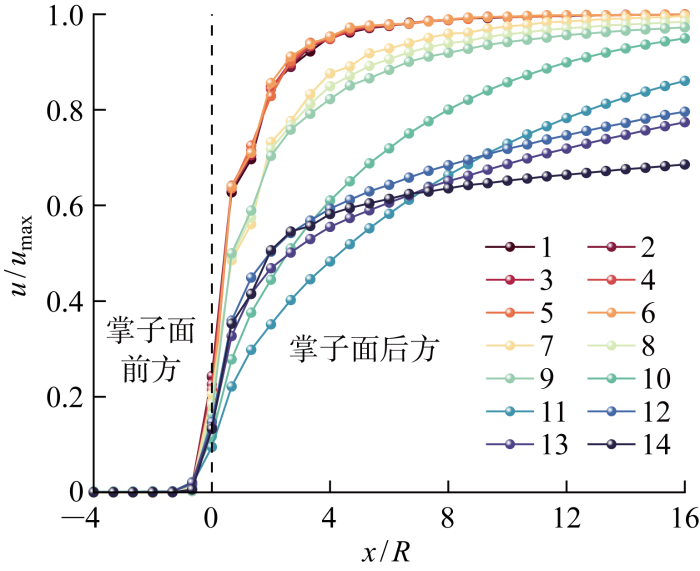
为探究不同延滞时间下位移释放系数曲线的差异,将开挖速度为16 m/d的各系列位移释放系数曲线绘制于图12.系列1~6均形成了完整的S形曲线,且各曲线差别较小;系列7~9逐渐开始无法形成完整的S形曲线,但仍在逐渐接近于1,因此基本可认为形成了完整的S形曲线;系列10~14在16倍隧道半径的范围内均无法形成完整的S形曲线,且随着延滞时间的增加,位移释放系数增长越缓慢,围岩更难达到平衡.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 开挖速度16 m/d下各系列位移释放系数

Fig.12 Displacement release coefficient of each series at excavation speed of 16 m/d

3 位移释放系数经验公式

3.1 掌子面前方拟合公式

根据前文参数讨论的结果可以发现掌子面前后的位移释放系数有所不同.掌子面前方围岩位移释放系数在不同施工速度的工况中整体保持一致,因此可认为掌子面前方围岩位移释放系数只受空间效应的影响,可直接对计算结果进行拟合,得到掌子面前方位移释放系数经验表达式:

(4)

\begin{matrix} \frac{u (x)}{u_{m a x}} = 0.231 e x p (1.94 \frac{x}{R}) \end{matrix}

在掌子面的后方,隧道10倍开挖半径内的围岩同时受到时间和空间效应的影响^[15],因此为准确分析围岩变形特征,本文将原曲线分为3类展开分析.

3.2 掌子面后方空间效应控制型

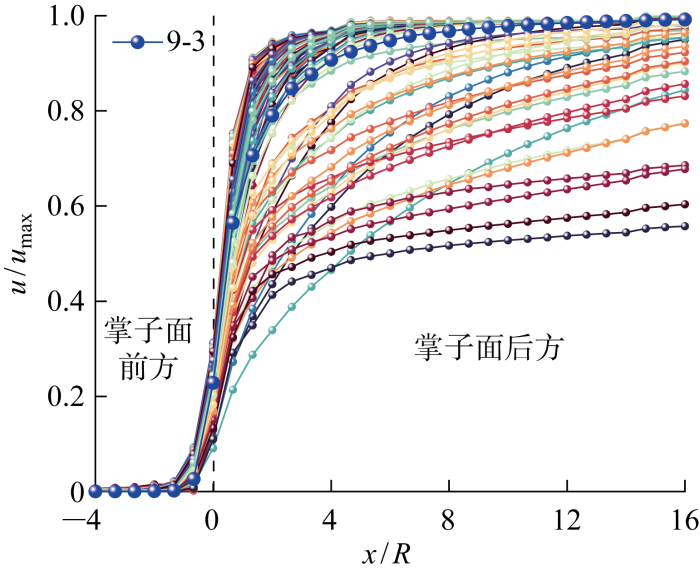
将2.3节中计算得到的所有位移释放系数曲线绘制于图13,从图中可以清晰地发现以工况9-3为分界线,工况9-3计算结果以上的位移释放系数曲线密集,以下的较为“发散”.工况9-3以上密集区域内的位移释放系数曲线最大值均为1.0,形成了完整的S形曲线,其他曲线最大值虽未达到1.0,但其形状仍为S形,因此本文选取函数 $f (x) = a e^{b x} + c$ 进行拟合.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 各工况位移释放系数汇总

Fig.13 Summary of displacement release coefficient of each item

由第2章的研究结果可知,开挖速度对各工况的位移释放系数的影响均是明显的,随着黏滞系数的增大,越来越多的曲线无法形成完整的S形曲线.因此将16倍隧道半径内可形成完整S形曲线的工况归纳为空间效应控制型曲线,而其对应的临界开挖速度如表4所示.以临界速度为判断基础,拟合函数作为判断位移释放系数是否为主要受空间效应控制的依据,该判别方法同样适用于弹性围岩判别:

(5)$v＜16 \mathrm{e}^{-t_{\mathrm{d}}}$

式中:v为隧道开挖速度.

表4 临界开挖速度

Tab.4 Critical excavation speed

系列	t_d/d	v/(m·d^-1)	系列	t_d/d	v/(m·d^-1)	系列	t_d/d	v/(m·d^-1)
1	1.47×10^-3	16	6	1.93×10^-3	16	11	3.40	0.8
2	1.93×10^-3	16	7	0.946	4	12	3.35	0.8
3	5.44×10^-3	16	8	0.215	8	13	13.56	0.4
4	9.83×10^-4	16	9	0.431	4	14	26.55	0.2
5	1.48×10^-3	16	10	1.54	2

新窗口打开| 下载CSV

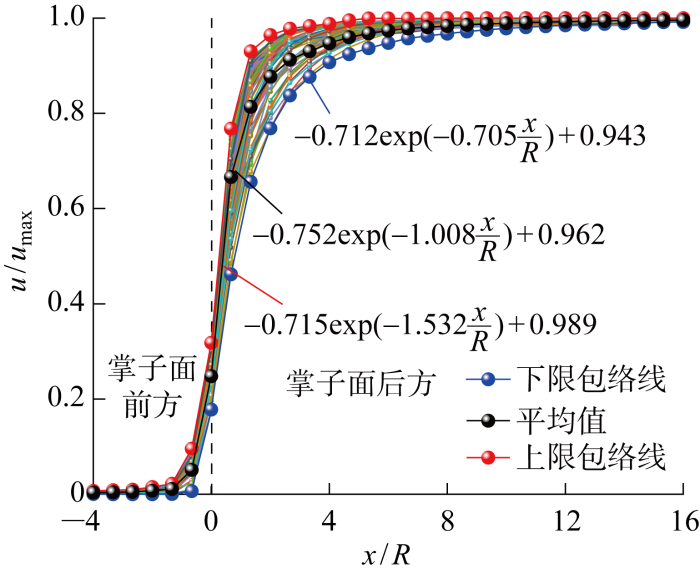
开挖速度小于判别速度则对应的位移释放系数受空间效应影响显著,同时相应的曲线均在工况9-3曲线的上方,各曲线的集中度较高,因此可直接借助包络线以及对应的平均值进行预测,如图14所示.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 空间效应控制型位移释放系数曲线与包络线

Fig.14 Envelope lines and curves of displacement release coefficient affected by spatial effect

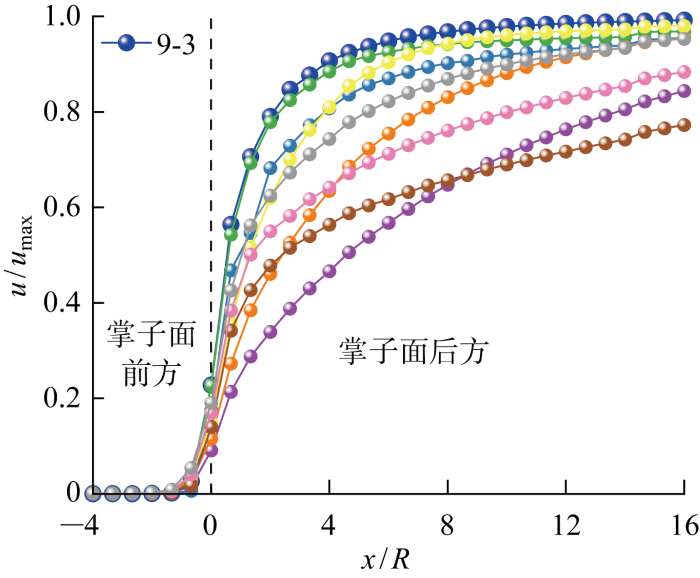
3.3 掌子面后方时空效应控制型

由时空效应的影响因素研究结论可知,空间效应与距掌子面的距离相关,距离掌子面越近则越显著;时间效应则与开挖速度、延滞时间的相对关系有关,开挖速度越快、延滞时间越大则时间效应越显著.两者不同点在于空间效应存在最大影响效果,即本文求解位移释放系数曲线的上限包络线;而时间效应不存在最大影响效果,其会直接改变围岩的基本性质,进而影响围岩持续变形的时间.

时空效应综合控制型围岩在实际中将表现为极为复杂的状态.当时间效应足够大则时间效应影响占主要因素;而若时间效应较小时,随着隧道的开挖空间效应逐渐衰减,隧道受时间-空间效应的共同影响显著.总结可知,时空效应控制型围岩同时受到时间和空间效应的作用,两个效应影响的程度不同,该类曲线存在快速增加区间不统一的情况,进而导致曲线有较多交叉.

时空效应控制型同时受到时间和空间效应的影响,因此需同时考虑临界速度和延滞时间.由图15可知,时空效应控制型曲线均在9-3工况之下,因此取系列9(延滞时间为0.431 d)中空间效应影响型的临界速度为4 m/d.而当延滞时间过大时,时间效应的影响程度将超过空间效应.图中主要时空效应控制型曲线集中在系列10和11,因此选择系列11对应的延滞时间3.40 d作为上限.改进后的判别公式如下:

(6)

\begin{matrix} \begin{array}{l} v 16 e^{- t_{d}} \\ 0.431 d t_{d} 3.40 d \end{array}\} \end{matrix}

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 时空效应控制型位移释放系数

Fig.15 Displacement release coefficient affected by space-time effect

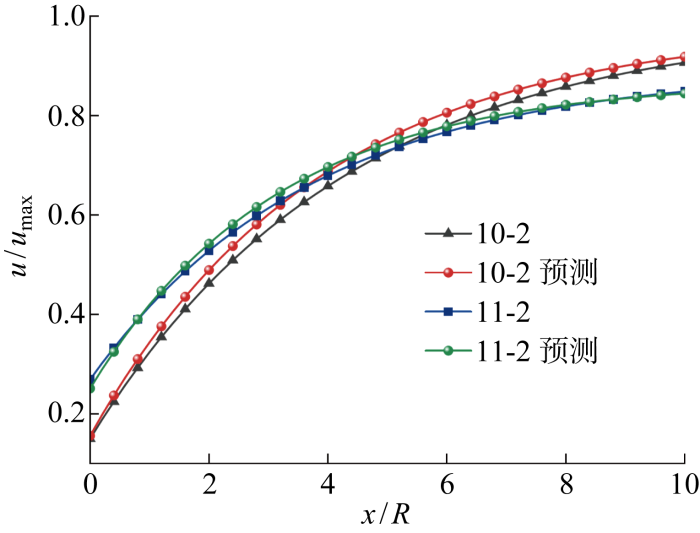
基于拟合公式 $f (x) = a e^{b x} + c$ 对各条曲线进行拟合,拟合结果如表5所示.不同于空间影响型,时空效应控制型曲线集中度不高,但对应的延滞时间在0.431~3.40 d范围内,因此可考虑基于插值法对不同类型曲线进行预测.

表5 时空效应控制型工况位移释放曲线拟合结果

Tab.5 Fitting results of the displacement release curve affected by time-space effect

工况	a	b	c
7-1	-0.814	-0.203	0.974
7-2	-0.823	-0.358	0.993
10-1	-0.801	-0.136	0.943
10-2	-0.838	-0.233	0.988
10-3	-0.835	-0.321	0.998
11-1	-0.539	-0.276	0.771
11-3	-0.698	-0.359	0.963

新窗口打开| 下载CSV

根据上述假设,将原工况10-2和11-2作为标准组,并取两工况的相邻组10-1、10-3和11-1、11-3进行插值处理,确定10-2和11-2预测曲线的对应系数分别为a=-0.824,b=-0.259,c=0.98;a=-0.619,b=-0.318,c=0.87.将预测结果和数值模拟结果绘制于图16,两组曲线的拟合度分别为 R²=0.988,R²=0.989,因此插值法可用于时空效应控制性曲线的预测.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 工况10-2和11-2预测结果与实际值对比

Fig.16 Comparison of predicted results with actual values in Items 10-2 and 11-2

3.4 掌子面后方时间效应控制型

当时间效应占据主要影响因素时,相应的位移释放系数曲线将表现出与时间的强相关性.由“时空效应控制型”的分析结果可知,时间效应控制型曲线应具备变形时间长、开挖速度快的特点.因此取延滞时间3.40 d为分界线,修改后的判别公式为

(7)

\begin{matrix} \begin{array}{l} v 16 e^{- t_{d}} \\ t_{d} 3.40 d \end{array}\} \end{matrix}

将符合上述条件的曲线绘制于图17中,各曲线均在16倍隧道半径内无法形成完整的S形曲线,且无任何交叉现象,表现出与时间效应的强相关性.因此在确定各个参数的过程中需要考虑开挖速度与延滞时间.在后续拟合过程中发现b与开挖速度的关系较弱,因此b与延滞时间的函数关系如下:

(8)

\begin{matrix} b = - 0.412 e^{- 0.134 t_{d}} + 0.715 \end{matrix}

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 时间效应控制型位移释放系数曲线

Fig.17 Curves of displacement release coefficient affected by time effect

拟合优度为0.96.而a、c与开挖速度和延滞时间具有较强的关系,因此基于响应面法对a、c拟合,拟合结果如下:

(9)

a = - 0.812 + 0.009 t_{d} + 0.04 v - 0.000 23 v t_{d} - 0.001 9 v^{2}

(10)

\begin{array}{l} c = 1.315 - 0.011 t_{d} - 0.042 v + \\ 0.000 37 v t_{d} + 0.001 61 v^{2} \end{array}

其拟合度分别为0.93和0.97.

通过式(8)~(10)可以求解“时间效应控制型”位移释放系数.值得注意的是,本文计算中最大延滞时间为26.55 d,实际围岩如果遇到更大的延滞时间仍需数值模拟手段计算围岩纵向变形结果.

综上所述,掌子面前方的位移释放系数曲线差异较小,可取统一的经验公式进行表示;掌子面后方的位移释放系数可按照空间效应控制型、时间-空间效应控制型和时间效应控制型3种模型分别确定相应的经验公式.各类型经验公式的系数取值如表6所示.

表6 位移释放系数经验公式取值

Tab.6 Values of empirical formula for displacement release coefficients

位置	模型	a	b	c
掌子面前方		0.231	1.94	0
掌子面后方	空间效应控制型	基于图14进行上下限求解
	时空效应控制型	基于表5进行插值求解
	时间效应控制型	式(9)	式(8)	式(10)

新窗口打开| 下载CSV

4 位移释放系数经验公式验证与分析

4.1 与实测结果比较

甜水堡煤矿位于庆阳市环县甜水镇境内,矿井设计生产能力2.4×10⁶ t/a,服务年限51 a.矿井井田面积 26.628 5 km²,地质储量为 2.910 95×10⁸ t,设计可采储量1.652×10⁸ t,可采煤层8层.1304巷道回风巷位于采区南翼,3#煤层赋存较稳定.

从1304巷道回风巷钻芯取样并进行三轴蠕变试验,试验采用岩石力学实验室的微机岩石综合控制系统(见图18),该系统由轴向系统、围压系统、孔隙水加载系统和计算机系统组成.该试验设备具有高精度测量岩石三轴全过程力学性质,满足本次试验的要求.根据试验结果可以得到相应的Burgers参数为:G_M=93.5 MPa,G_K=16.7 MPa,η_K=684 MPa·h,可以确定该围岩对应的延滞时间为t_d=1.71 d,引用判据式得到临界速度为v=2.89 m/d,而该煤矿单日掘进距离大于10 m,同时0.431 d<1.71 d<3.40 d,因此该巷道围岩属于时空效应控制型.可基于表5进行内插得到相应的位移释放系数表达式:

(11)

\begin{matrix} f (x) = - 0.809 e^{- 0.214 x} + 0.967 \end{matrix}

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 试验仪器

Fig.18 Test instruments

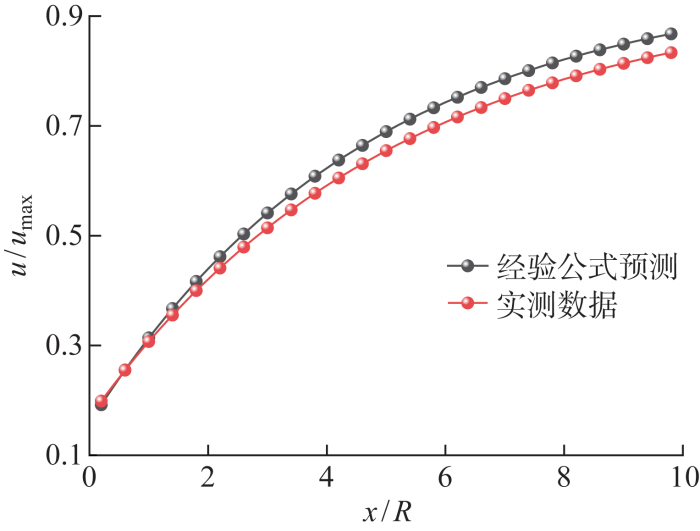
将预测值与现场监测结果对比如图19所示,两条曲线基本吻合,预测公式拟合度为R²=0.973,因此该方法可以较好地描述隧道开挖过程中位移释放系数随掌子面推进的关系.

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19 预测结果与实际值对比

Fig.19 Comparison of predicted results and actual values

4.2 与既有公式对比

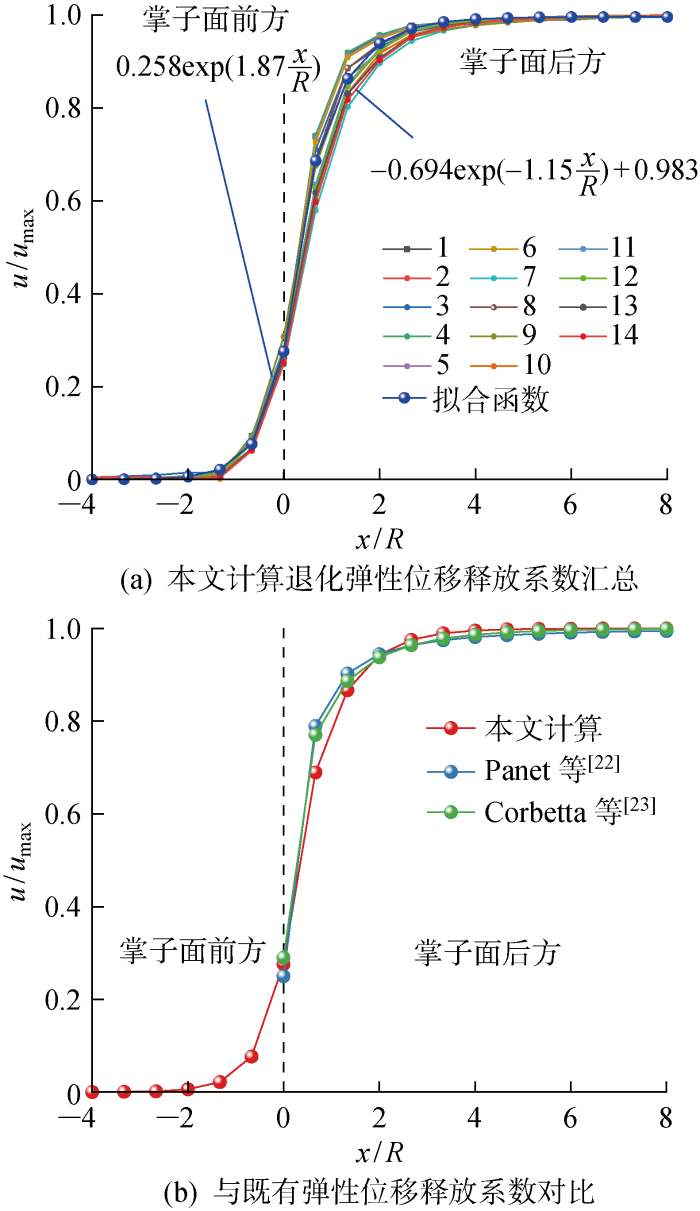
在传统的弹性力学中,围岩变形仅需考虑其空间特征.当开挖速度较小时,时间效应可被忽略,本文中的黏弹性围岩位移释放系数解答可退化为弹性解,如图20所示.取开挖速度为0.2 m/d,将本文计算结果绘制于图20(a),不同围岩参数具有一致的空间效应,可用统一的函数分别对掌子面前方和后方的位移释放曲线进行拟合.将计算结果与其他学者^[22-23]所提出的位移释放系数计算方法进行对比,对比情况如图20(b)所示.本文中黏弹性围岩位移释放系数解答退化后的弹性解与其他学者所提出的弹性结果重合度较高,表明了本文拟合函数的可靠性.然而既有公式均未考虑时间效应,与黏弹性洞周位移规律有较大偏差.因此,本文所确定的位移释放系数可更好地反映黏弹性洞周位移规律,保证隧道支护设计的安全性和科学性.

图20

新窗口打开| 下载原图ZIP| 生成PPT

图20 退化弹性解与既有弹性解对比

Fig.20 Comparison of degenerate elastic solutions and existing elastic solutions

5 结论

本文针对黏弹性围岩建立相应围岩纵向变形和位移释放系数曲线数据库,探究地应力、Burgers参数和开挖速度对围岩释放系数的影响及其演化过程,同时根据主要影响因素将各曲线进行划分并得到不同类型围岩释放系数的经验公式,并得到如下结论:

(1) 以Burgers模型和参数为基础,通过大量数值模拟计算,构建黏弹性围岩纵向变形曲线数据库,并引入位移释放系数探究了黏弹性围岩纵向变形的时间-空间演化规律.

(2) 地应力对位移释放系数没有影响;K对位移释放系数影响较小;G_K、η_K、G_M在极端取值时将导致围岩变形发生突变;根据能否形成完整的S形曲线和围岩开始变形的位置,可将曲线划分为低延滞系数、中延滞系数和高延滞系数3类.

(3) 基于数值模拟结果对掌子面后方围岩的时空变形特征进行分析,将其分为空间效应控制型、时空效应控制型、时间效应控制型3种类型.所提出的判断依据以及经验公式与甜水堡煤矿试验结果和现有公式比较,表明本经验公式可有效预测围岩变形时空分布.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[16]

LIU

, ZHANG

et al.

Model tests on progressive collapse mechanism of a shallow subway tunnel in soft upper and hard lower composite strata

[J]. Tunnelling and Underground Space Technology, 2023, 131: 104824.

[17]

王嘉琛, 张顶立, 孙振宇,

等.

水平互层围岩隧道破坏机理及其范围预测模型

[J]. 力学学报, 2022, 54(10): 2835-2849.