基于响应面法-遗传算法的船舶推进轴系多目标优化设计

doi:10.16183/j.cnki.jsjtu.2023.318

基于响应面法-遗传算法的船舶推进轴系多目标优化设计

张聪¹^,²^,³, 疏炳南¹^,²^,³, 张江涛¹^,²^,³, 金勇^,¹^,²

1.武汉理工大学交通与物流工程学院,武汉 430063

2.水路交通控制全国重点实验室,武汉 430063

3.武汉理工大学国家水运安全工程技术研究中心,武汉 430063

Multi-Objective Optimization Design of Ship Propulsion Shafting Based on Response Surface Methodology and Genetic Algorithm

ZHANG Cong¹^,²^,³, SHU Bingnan¹^,²^,³, ZHANG Jiangtao¹^,²^,³, JIN Yong^,¹^,²

1. School of Transportation and Logistics Engineering, Wuhan University of Technology, Wuhan 430063, China

2. State Key Laboratory of Maritime Technology and Safety, Wuhan 430063, China

3. National Engineering Research Center for Water Transport Safety, Wuhan University of Technology, Wuhan 430063, China

通讯作者: 金勇,副教授;E-mail:jy761121@whut.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-07-14 修回日期: 2023-10-9 接受日期: 2023-12-15

基金资助:

国家自然科学基金资助项目(51839005)

Received: 2023-07-14 Revised: 2023-10-9 Accepted: 2023-12-15

作者简介 About authors

张聪(1986—),副教授,从事船舶推进轴系动力学特性及优化设计方向的研究.

摘要

为降低船舶在航行过程中传动设备的功率损失,提高推进轴系的传递效率,并改善轴系振动性能,基于响应面模型与遗传算法(GA)对某船舶轴系实验台进行了多目标优化设计.采用星点设计(CCD)方法,在优化设计空间中选取合理实验点,拟合构建最小总功耗和振动响应幅值的响应面模型.基于GA,利用MATLAB软件求解响应面模型回归函数的Pareto最优解.对比分析各组优化结果,获得最佳优化设计方案,研究结果表明采用这种联合方法后,轴系功耗损失降低了约7.10%,轴系振动幅值降低了2.30%,能有效提高轴系传递效率和抑制推进轴系振动问题,从而验证了船舶推进轴系多目标优化方法的正确性和可行性.

关键词： 推进轴系; 传递效率; 响应面法; 遗传算法

Abstract

In order to reduce the power loss of the transmission equipment, enhance the transmission efficiency of the propulsion shafting, and improve the vibration performance of the shafting, a multi-objective optimization design of a ship shafting experimental platform is performed based on the response surface model and genetic algorithm. The central composite design (CCD) method is used to select appropriate experimental points in the optimized design space, and the response surface model is developed with minimum total power consumption and vibration response amplitude. Based on the genetic algorithm, the Pareto optimal solution of response surface model regression function is solved through MATLAB software. The optimal design scheme is obtained by comparing and analyzing several groups of optimization results. The results show that the combined method can reduce the power loss of shafting by approximate 7.10% and reduce the vibration amplitude of shafting by 2.30%, while significantly improving the shafting transmission efficiency and effectively suppressing the vibration problem of propulsion shafting. The fiudings validate the feasibility of the multi-objective optimization method for the ship propulsion shafting.

Keywords： propulsion shafting; transfer efficiency; response surface methodology; genetic algorithm

PDF (9630KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张聪, 疏炳南, 张江涛, 金勇. 基于响应面法-遗传算法的船舶推进轴系多目标优化设计[J]. 上海交通大学学报, 2025, 59(4): 466-475 doi:10.16183/j.cnki.jsjtu.2023.318

ZHANG Cong, SHU Bingnan, ZHANG Jiangtao, JIN Yong. Multi-Objective Optimization Design of Ship Propulsion Shafting Based on Response Surface Methodology and Genetic Algorithm[J]. Journal of Shanghai Jiaotong University, 2025, 59(4): 466-475 doi:10.16183/j.cnki.jsjtu.2023.318

船舶在航行过程中,推进轴系扮演了“动力中枢”的重要角色,其运转的可靠性和稳定性直接影响到船舶的运行.船舶推进轴系运转过程中,推进轴系会受到轴承摩擦、螺旋桨水动力、船体变形等各种动态因素的影响,从而导致轴系功率损耗和轴系振动的产生.功率损耗以及振动幅值过大的推进轴系会造成轴系振动噪声的增加、轴承的磨损加剧和能源的浪费,严重时,甚至还会造成轴承摩擦副烧结、轴系停转以及船体变形等故障.降低推进轴系的功率损耗以及振动幅值不仅可以节能降碳,而且对提高舰船的隐身性能、稳定性具有重大的意义.因此,推进轴系传递效率以及振动幅值的多目标优化设计是船舶结构优化设计的重要研究方向之一.

近年来,许多学者对船舶结构性能及数值优化方法开展了大量研究.龙周等^[1]提出了基于过采样技术(synthetic minority oversampling technique,SMOTE)算法的船舶结构可靠性优化设计方法,为大型工程结构的可靠性优化设计提供了思路;夏国清等^[2]利用改进的非支配排序遗传算法对推进器能耗、磨损以及推力误差进行多目标优化;陆金铭等^[3]通过计算反力影响数矩阵,确定最佳轴向位置和偏移量以达到优化逼近.王建午等^[4]计算传递矩阵和雷诺方程,以减轻轴系振动,并达到振动和校中双目标优化的优化目标.肖能齐等^[5]采用单纯形法结合层次分析法的优化方法,研究分析轴系校中关键优化设计问题.而关于数值优化方法,如运用目标规划法、极大值极小值法、序列二次规划梯度法、约束变尺度法等传统算法,其求解强非线性、多变量模型时并不能保证获取全局最优解^[6-8].随着计算机的发展,多目标优化及智能算法如今得到广泛应用,杨观赐等^[9]提出了基于Pareto最优原理的混合动力汽车多目标优化进化算法,能够较好地解决混合动力汽车多目标优化问题;何小二等^[10]利用MATLAB调用有限元软件,将粒子群优化(PSO)算法引入复杂船舶结构的优化中,实现了PSO对复杂船舶结构的优化;曾漾等^[11]利用遗传算法(genetic algorithm,GA)和响应面法(response surface methodology,RSM)对复合材料舱壁进行了多目标优化设计.卢熹等^[12]通过在多维空间中求得船舶轴系合理校中可行解集,并进行网格划分,结合挠度曲线和解在解集空间中的位置等因素,完成轴系多目标优化设计;周瑞^[13]通过一种多目标优化计算方法,以各轴承的径向变位值为变量,获得了相邻轴承负荷更均衡、后艉轴承负荷最小的优化结果.上述研究中对于船舶推进轴系传递效率和振动性能优化方向的研究相对较少,且部分模型存在不具备通用性、单目标优化、计算成本过高以及计算精度较低等问题.

本文在已有文献的基础上,采用RSM中的星点设计(central composite design,CCD)法,结合GA,对多目标优化模型中的设计变量、目标函数以及约束条件进行定义,同时对功耗和振动幅值进行方差分析,并利用MATLAB软件求解响应面模型回归函数中的中间轴轴径、中间轴承长径比以及后艉轴承跨距三目标因素的Pareto最优解,对船舶推进轴系进行多目标优化设计,协调、折中处理推进轴系多项性能间的优化问题,并获得推进轴系最佳性能参数如功耗、振动响应等,为多角度提升船舶推进轴系性能提供了理论支持.

1 推进轴系多目标优化方法

基于推进轴系功率传递匹配综合模型,以双点支撑实船长轴系为研究对象,采用智能算法,开展关于轴系机械功率传递匹配的多目标优化方法研究.以提高效率为主要目标,分别围绕轴系总功耗、后艉轴承振动响应两个方向展开研究,通过层次分析法依据各目标的重要程度设定其权重并确定最终目标函数;基于轴系功率匹配规律报告研究结果,以中间轴轴径、中间轴承长径比和后艉轴承跨距等关键设计要素为优化变量并初步确定其取值范围,通过CCD法得到各工况点数据结果,拟合响应值和因素间的函数关系并做方差分析.然后,采用GA实现多目标优化,得到最优解并对比优化前后传递效率的变化结果.最后,根据优化结果对结论进行概括总结.该研究相关方法对于其他推进轴系同样适用,其理论及结论可为轴系的设计、制造、安装和服役等方面提出优化方向建议.

船舶推进轴系多目标优化方法流程如图1所示.该方法根据RSM和GA原理,以轴系总功耗和轴承的振动响应作为优化设计评价指标,基于SimulationX和MATLAB软件联合仿真计算功耗和振动响应幅值,并运用CCD法选取实验点,回归拟合构建响应面模型.采用多目标GA,根据拟合后的响应面模型回归函数,求得Pareto最优解集并分析比较各组最优解,最终得出船舶推进轴系多目标最佳优化设计方案.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 推进轴系多目标优化方法流程图

Fig.1 Flow chart of multi-objective optimization method for propulsion shafting

1.1 响应面法星点设计

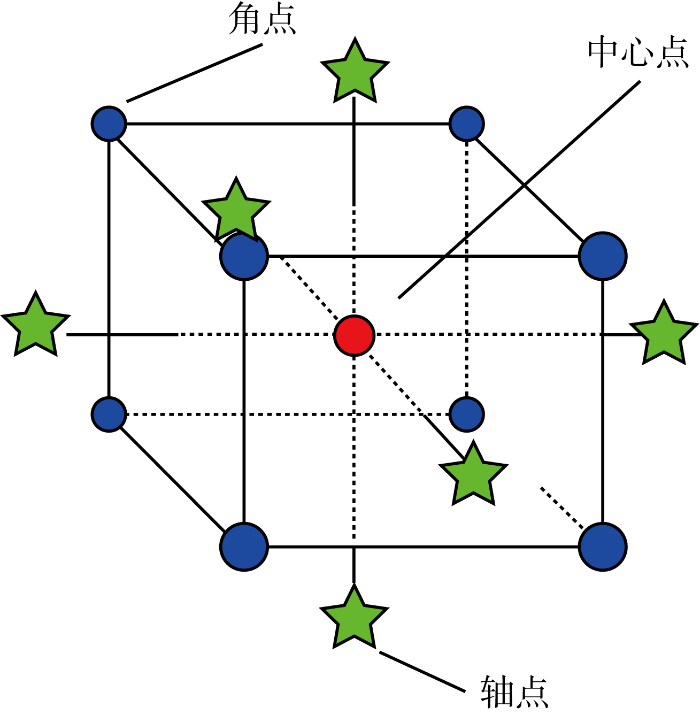
在构造推进轴系多目标优化模型时,首先需进行优化实验设计.RSM是由Box等^[14]提出的一种实验设计方法,与传统的正交实验设计和均匀实验设计相比,其可采用多元回归技术拟合因素变量与实验点参数值的函数表达式,从而建立近似数学模型,获得因素间最佳水平组合,具有实验次数少、回归方程精度高、可研究因素间的交互作用等优点^[15],可作为推进轴系多目标优化问题的实验设计方法.

作为一种常用的响应面实验设计方法,CCD法对各个因素选取5水平,以(0,±1,±α)编码,其中0为中心点,1为角点,α为轴点对应的极值($ \alpha= 2^{n / 4}$，n为因素数),实验点分布如图2所示.推进轴系多目标优化问题可基于RSM,对轴系轴径、轴承长径比、跨距等关键因素进行星点设计.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 CCD实验点分布

Fig.2 Distribution of CCD experiment site

1.2 多元回归拟合

在推进轴系多目标优化设计中,可使用RSM拟合过程中最常见的多元回归方法,解决如何建立推进轴系优化目标和设计变量间的近似函数问题.其中广泛运用的拟合方法是采用多项式拟合,简单的函数关系可以采用一次多项式拟合,对具有交互作用的函数关系可以采用二次多项式拟合.一次、二次多项式模型表达式分别如下:

(1)

y (x) = β_{0} + \sum β_{i} x_{i}

(2)

\begin{array}{l} y (x) = β_{0} + \sum β_{i} x_{i} + \sum β_{i j} x_{i} x_{j} + \sum β_{i i} x_{i}^{2} \end{array}

式中: m为变量数;y为响应值;i、j为1~m之间的整数; $β_{0}$ 为常数项; $β_{i}$ 为线性系数; $β_{i j}$ 为交互作用项系数; $β_{i i}$ 为二次项系数; $x_{i} 、 x_{j}$ 为各因素变量.

获取函数表达式后需分析验证多元回归模型的拟合程度,对模型进行显著性F检验,即方差分析.实验设计中实验值 $y_{i} (i = 1,2, \dots, n)$ 之间存在差异,可用实验值 $y_{i}$ 与其算数平均值 $\bar{y}$ 的偏差平方和来表示这种差异,即总离差平方和,其表达式如下:

(3)$S_{S T}=\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}=S_{S R}+S_{S E}$

造成实验值的波动的原因有两个.其一是由x的变化所引起的y的变化,即回归平方和 $S_{S R},$ 代表回归值 ${\hat{y}}_{i}$ 与算术平均值 $\bar{y}$ 之间的偏差平方和;其二是随机误差,即残差平方和 $S_{S E},$ 代表实验值 $y_{i}$ 与对应的回归值 ${\hat{y}}_{i}$ 之间偏差平方和,表达式分别如下:

(4)

\begin{matrix} S_{S R} = \sum_{i = 1}^{n} ({\hat{y}}_{i} {- \bar{y})}^{2} \end{matrix}

(5)

\begin{array}{l} S_{S E} = \sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})^{2} \end{array}

在多元回归拟合中,可用复相关系数R来反映构建模型的拟合精度,表达式如下:

(6)

\begin{matrix} R = \sqrt{S_{S R} / S_{S T}} \end{matrix}

当复相关系数R为1或接近1时,说明拟合效果好,响应面回归模型精度高.若R值远离1,达不到精度要求,可用更高阶的多项式模型或增加实验次数以提高拟合效果.

1.3 遗传算法

GA是基于“物竞天择、适者生存”的进化论思想,模拟在自然环境下,生物间遗传、进化过程的一种随机搜索的优化算法.其主要特点是从问题解的串集开始搜索,避免陷入局部最优解,实现全局择优.

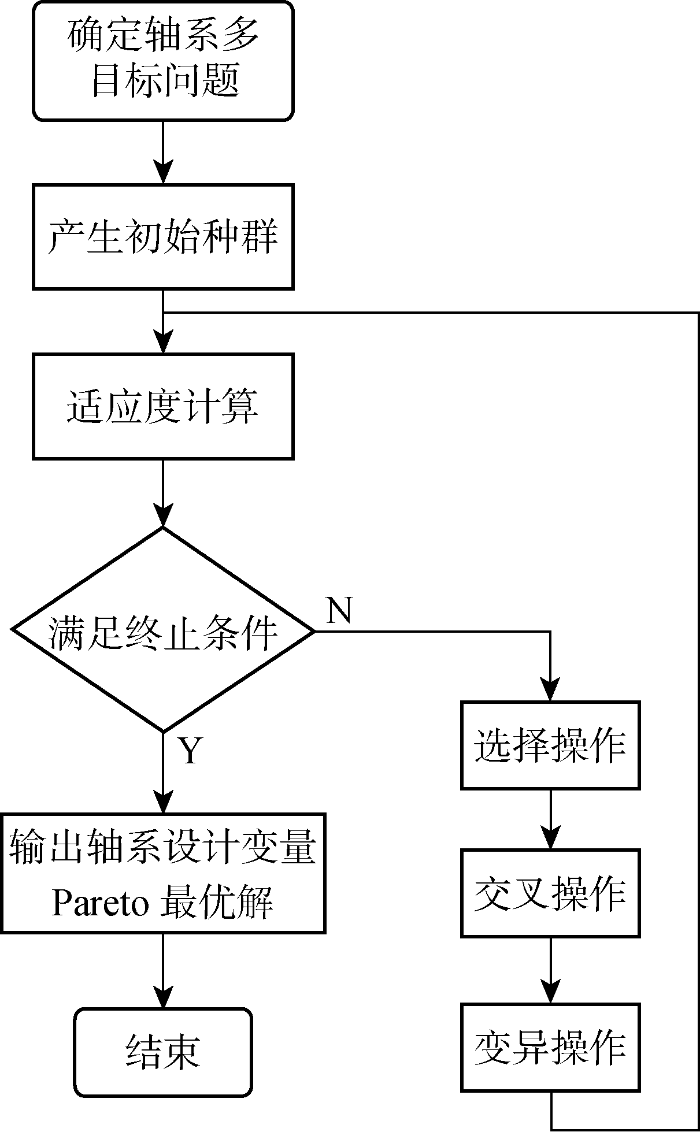
推进轴系多目标优化问题可基于GA,利用种群搜索技术将种群作为一组问题初始解,通过对当前种群施加类似生物遗传环境因素的选择、交叉、变异等一系列的遗传操作来产生新一代的种群,并逐步使种群优化到包含轴系设计变量Pareto最优解的状态,算法流程如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 推进轴系多目标GA流程图

Fig.3 Flow chart of multi-objective GA for propulsion shafting

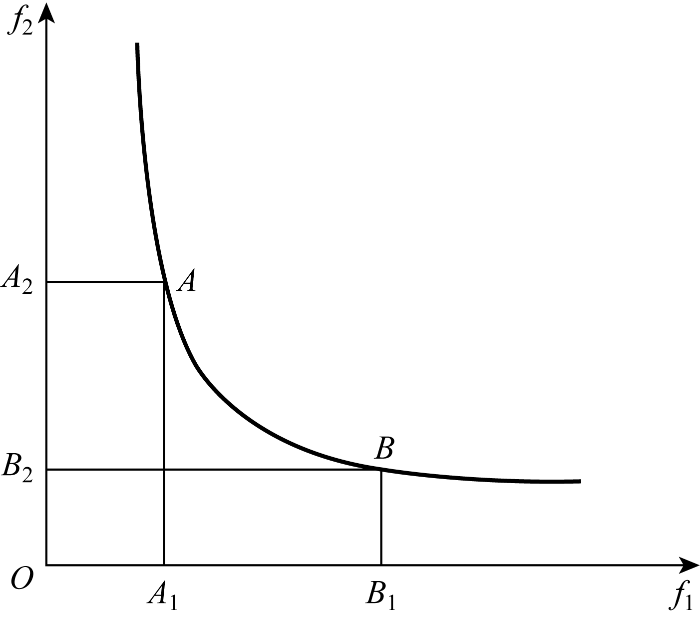
1.4 Pareto最优解

船舶推进轴系多目标优化问题如图4所示,以提高轴系功率传递效率、改善轴系振动性能为两优化目标:轴系振动性能 $f_{1} (x)$ 、轴系传递效率 $f_{2} (x)$ , A、B是优化问题的两个解.因为 $A_{1} B_{1}$ 且 $A_{2} B_{2}$ ,当选择解B时,优化目标 $f_{1} (x)$ 轴系传递效率接近最大值,但优化目标 $f_{2} (x)$ 改善轴系振动性能并没有达到最佳,需进行协调、折中处理,即轴系传递效率的提高需以轴系振动性能的降低作为代价,类似这样的解B是该问题的Pareto最优解^[16-17].

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 推进轴系多目标优化问题的Pareto最优解

Fig.4 Pareto optimal solution of multi-objective optimization problem of propulsion shafting

解决推进轴系多目标优化问题最终需要寻找Pareto 最优解,但优化结果并非唯一一组最优解,而是众多组最优解所组成的Pareto最优解集^[18].此外,Pareto最优解只是轴系多目标优化问题的一个可接受解,实际推进轴系优化设计方案可根据优化效果和决策偏好,从Pareto最优解集中比较筛选出一组或几组Pareto最优解做进一步研究分析^[19].

2 推进轴系优化设计

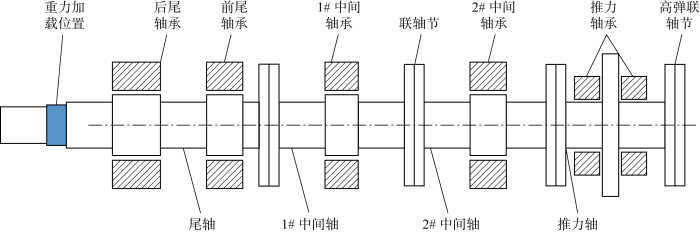
推进轴系优化设计以某船舶轴系综合性能实验台为研究对象,实验台主要包含加载装置、地基、机座、液压动力单元、齿轮减速器、电动机、两个推力轴承、轴系、水润滑单元、水箱和监测控制单元等设备装置,其中,驱动电动机55 kW,转速 1 480 r/min,减速箱传动比1.84,如图5所示.实验台的变频电动机连接扭矩传感器上,减速机后方有高弹联轴器平衡轴向和径向偏差,之后连接推力轴承,然后连接至轴系,轴系包括一根尾轴和两根中间轴,两中间轴之间以法兰连接,尾轴和中间轴间用液压联轴器连接,轴系末端的尾轴由两个尾轴承共同支撑,其中,一个润滑方式为油润滑,另一个为水润滑;在水润滑尾轴承后端有螺旋桨重力加载装置,可以加载脉动载荷,也可加载恒定载荷;水润滑轴承有水管连接至供水单元;水箱可以模拟艉部轴系及螺旋桨在水中运行时的情况;扭矩加载装置和力加载装置由液压油路连通并由液压动力单元提供动力;监测控制单元控制加载装置和变频电动机等设备完成实验的记录监控和汇总.该轴系台的组成与实际船舶推进轴系具有相似性,轴系台的运行性能能反映实船轴系的运行性能,保证该轴系实验台架与实际船舶推进轴系具有一定的契合度.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 船舶轴系综合性能实验台

Fig.5 Experiment bench for ship shafting comprehensive performance

实验台轴系结构如图6所示,包含两根中间轴、一根尾轴,用法兰连接两中间轴,而尾轴与中间轴间则用液压联轴器连接.轴系末端处的尾轴分别用油润滑、水润滑尾轴承共同支撑,并在水润滑尾轴承后端设置螺旋桨重力加载装置,加载脉动载荷或恒定载.各轴段的相关参数如表1所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 实验台架轴系示意图

Fig.6 Diagram of experiment bench shafting

表1 轴段相关参数

Tab.1 Related parameters of axis segment

轴段	内径/mm	长度/mm	润滑介质
艉轴	185	740	水
1#中间轴	165	730	油
2#中间轴	145	1 275	油
推力轴	125	1 200	油

新窗口打开| 下载CSV

将从后艉轴承至推力轴承分别编号为1~6.各轴承的相关参数和轴承的位置坐标如表2、3所示,其中后艉轴承标注为热态时的等效支点位置.

表2 轴承相关参数

Tab.2 Related parameters of bearing

轴承	内径/mm	长度/mm	润滑介质
后艉轴承	186	555	水
前尾轴承	150	156	油
中间轴承	160.5	130	油
推力径向轴承	160	101	油

新窗口打开| 下载CSV

表3 轴承位置坐标

Tab.3 Coordinate of bearing position

轴承编号	坐标位置/mm
1	1 360
2	4 048.75
3	6 180
4	8 380
5	9 725
6	10 060

新窗口打开| 下载CSV

基于SimulationX和MATLAB软件,根据实验台轴系构建轴系传递匹配综合模型,如图7所示,可进行联合仿真计算轴系的摩擦功耗、振动响应幅值等参数.图中:globalForce表示地球引力;freeMotion表示该轴是在自由运动的状态下;Motivation是施加在轴系上的激励;beam i (i=1,2,…,10)表示各段梁;EX_bearing i (i=1,2,…,6)表示轴系上的轴承;Coupling表示联轴器;Cylinder表示汽缸;seal为轴承密封;constraint为约束;tuili_bear表示推力轴承;preset表示预置值;actuatedRevoluteJoint表示启动的旋转关节.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 轴系传递匹配综合模型图

Fig.7 Synthetic model of shafting transfer matching

2.1 设计变量选取

根据实验台轴系实际结构及功率匹配的规律研究,选择1#中间轴轴径 $x_{1}$ 、1#中间轴承长径比 $x_{2}$ 和后艉轴承跨距 $x_{3}$ 作为设计变量,可表示为

(7)

\begin{matrix} x = {[\begin{array}{l} x_{1} & x_{2} & x_{3} \end{array}]}^{T} \end{matrix}

2.2 定义优化目标函数

2.2.1 传递效率

实验台轴系功率传递效率η表达式如下:

(8)

\begin{matrix} η = \frac{N_{i} - N_{f}}{N_{i}} η_{e} η_{f} \end{matrix}

式中:N_i为轴系输入功率;N_f为轴系总功耗;η_e为减速箱传递效率;η_f为隔音联轴器传递效率.由式(8)可知,为提高轴系功率传递效率,应减少整个传递过程中的功耗损失.因此选择总功耗y₁最小作为优化目标1,定义如下优化目标函数:

(9)

\begin{array}{l} f_{1} (x_{1}, x_{2}, x_{3}) = m i n y_{1} = \\ β_{0} + [\begin{array}{l} x_{1} & x_{2} & x_{3} \end{array}] [\begin{array}{l} β_{1} \\ β_{2} \\ β_{3} \end{array}] + \\ [\begin{array}{l} x_{1} & x_{2} & x_{3} \end{array}] [\begin{array}{l} β_{11} & β_{12} & β_{11} \\ β_{21} & β_{22} & β_{23} \\ β_{31} & β_{32} & β_{33} \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}] \\ s . t . \{\begin{array}{l} l_{b} \leq x \leq u_{b} \\ A_{e q} x = b_{e q} \\ A x \leq b \end{array} \end{array}

式中: $y_{1} = N_{i} - N_{i} η; \sum_{i = 1}^{3} β_{i}$ 为优化函数的线性系数; $\sum_{i = 1, j = 1}^{3} β_{i j}$ 为优化函数的交互作用项系数;x为待优化的变量;l_b和u_b分别为变量的下限和上限约束; $A_{e q} x = b_{e q} 为变量 x 的线性等式约束; A x \leq b 为变量 x$ 的线性不等式约束;A_eq和b_eq是等式约束条件的系数.

2.2.2 振动性能

为改善实验台轴系传递过程中振动性能,降低轴颈处的振动响应,选取后艉轴承的振动位移响应幅值y₂最小为优化目标2,定义如下优化目标函数:

(10)$\begin{array}{l}f_{2}\left(x_{1}, x_{2}, x_{3}\right)=\min y_{2}= \\\beta_{0}+\left[\begin{array}{lll}x_{1} & x_{2} & x_{3}\end{array}\right]\left[\begin{array}{l}\beta_{1}^{\prime} \\\beta_{2}^{\prime} \\\beta_{3}^{\prime}\end{array}\right]+ \\\\{\left[\begin{array}{lll}x_{1} & x_{2} & x_{3}\end{array}\right]\left[\begin{array}{lll}\beta_{11}^{\prime} & \beta_{12}^{\prime} & \beta_{13}^{\prime} \\\beta_{21}^{\prime} & \beta_{22}^{\prime} & \beta_{23}^{\prime} \\\beta_{31}^{\prime} & \beta_{32}^{\prime} & \beta_{33}^{\prime}\end{array}\right]\left[\begin{array}{l}x_{1} \\x_{2} \\x_{3}\end{array}\right]} \\\text { s. t. }\left\{\begin{array}{l}l_{\mathrm{b}} \leqslant x \leqslant u_{\mathrm{b}} \\A_{\mathrm{eq}} x=b_{\mathrm{eq}} \\A x \leqslant b\end{array}\right.\end{array}$

式中: $\sum_{i = 1}^{3} β'_{i}$ 为优化函数的线性系数; $\sum_{i = 1, j = 1}^{3} β'_{i j}$ 为优化函数的交互作用项系数.

2.3 轴系优化星点设计

为建立轴系响应面模型,以1#中间轴轴径 $x_{1} 、 1 # 中间轴承长径比 x_{2} 、后艉轴承跨距 x_{3}$ 这3个因素作为变量,每个因素取3个水平,以(-1,0,1)编码,如表4所示.

表4 CCD实验因素及水平

Tab.4 CCD experiment factors and levels

因素	水平
因素	-1	0	1
x₁/mm	144	160	176
x₂	0.45	0.70	0.95
x₃/mm	-269	0	269

新窗口打开| 下载CSV

根据定义的优化目标,以总功耗y₁、后艉轴承的振动响应y₂分别作为推进轴系传递效率、振动性能的评价指标.利用CCD法设计实验方案,对不同的变量组合进行SimulationX和MATLAB仿真计算,计算结果如表5所示.

表5 CCD实验数据

Tab.5 CCD experiment data

序号	x₁/mm	x₂	x₃/mm	y₁/W	y₂/μm
1	133	0.7	0	2 068.2	1.838 8
2	144	1.0	-269	2 166.5	1.903 7
3	144	1.0	269	2 165.1	1.810 0
4	176	0.5	-269	2 225.2	1.914 4
5	187	0.7	0	2 438.8	1.840 5
6	160	0.7	0	2 207.3	1.856 1
7	160	1.1	0	2 343.9	1.855 5
8	160	0.3	0	2 088.8	1.856 7
9	144	0.5	269	2 067.5	1.811 7
10	176	1.0	-269	2 450.3	1.913 1
11	144	0.5	-269	2 071.1	1.904 6
12	176	1.0	269	2 449.8	1.808 3
13	160	0.7	452	2 205.4	1.788 6
14	160	0.7	-452	2 209.8	1.944 7
15	176	0.5	269	2 221.6	1.809 4
16	160	0.7	0	2 209.1	1.846 1

新窗口打开| 下载CSV

2.4 回归拟合及方差分析

采用二次多项式模型表达式(2)拟合三因素与优化目标响应值之间的函数关系,分别得到如下总功耗、后艉轴承振动响应的多元回归方程:

(11)$0.0628 x_{1}^{2}+46.84 x_{2}^{2}-2.16 \times 10^{-6} x_{3}^{2}$

(12)$\begin{aligned}y_{2}= & 1.58 \times 10^{-6}+3.64 \times 10^{-9} x_{1}- \\& 6.94 \times 10^{-8} x_{2}-7.05 \times 10^{-11} x_{3}+ \\& 6.54 \times 10^{-12} x_{1} x_{2}-6.76 \times 10^{-13} x_{1} x_{3}- \\& 1.09 \times 10^{-12} x_{2} x_{3}-1.11 \times 10^{-11} x_{1}^{2}+ \\& 4.74 \times 10^{-8} x_{2}^{2}+9.23 \times 10^{-14} x_{3}^{2}\end{aligned}$

再对上述回归方程进行方差分析,结果如表6和表7所示.

表6 $y_{1}$ 方差分析

Tab.6 Variance analysis of $y_{1}$

来源	平方和	自由度	均方和	F值	P值
模型	260 879.91	9	28 986.66	2 052.04	<0.000 1
x₁	164 720.46	1	164 720.46	11 661.00	<0.000 1
x₂	84 684.96	1	84 684.96	5 995.07	<0.000 1
x₃	19.59	1	19.59	1.39	0.283 5
x₁x₂	8 475.08	1	8 475.08	599.97	<0.000 1
x₁x₃	0.086	1	0.086	0.006 11	0.940 2
x₂x₃	3.52	1	3.52	0.25	0.635 6
$x_{1}^{2}$	2 396.36	1	2 396.36	169.64	<0.000 1
$x_{2}^{2}$	79.40	1	79.40	5.62	0.055 5
$x_{3}^{2}$	0.23	1	0.23	0.016	0.903 6
残差	84.75	6	14.13
失拟项	83.06	5	16.61	9.80	0.237 7
纯误差	1.69	1	1.69
总和	260 964.66	15

新窗口打开| 下载CSV

表7 $y_{2}$ 方差分析

Tab.7 Variance analysis of $y_{2}$

来源	平方和	自由度	均方和	F值	P值
模型	3.270×10^-14	9	3.634×10^-15	126.85	<0.000 1
x₁	2.391×10^-17	1	2.391×10^-17	0.83	0.396 1
x₂	3.595×10^-18	1	3.595×10^-18	0.13	0.735 3
x₃	3.179×10^-14	1	3.179×10^-14	1 109.85	<0.000 1
x₁x₂	5.478×10^-21	1	5.478×10^-21	1.912×10^-4	0.989 4
x₁x₃	6.767×10^-17	1	6.767×10^-17	2.36	0.175 2
x₂x₃	4.333×10^-20	1	4.333×10^-20	1.513×10^-3	0.970 2
$x_{1}^{2}$	7.522×10^-17	1	7.522×10^-17	2.63	0.156 3
$x_{2}^{2}$	8.125×10^-17	1	8.125×10^-17	2.84	0.143 1
$x_{3}^{2}$	4.136×10^-16	1	4.136×10^-16	14.44	0.009 0
残差	1.719×10^-16	6	2.864×10^-17
失拟项	1.219×10^-16	5	2.438×10^-17	0.49	0.788 3
纯误差	4.996×10^-17	1	4.996×10^-17
总和	3.287×10^-14	15

新窗口打开| 下载CSV

由表6、7可知,模型显著性检验P均小于 0.000 1,显著;失拟项P均大于0.05,不显著,表明该模型合理、可靠性高.此外,复相关系数R分别为 0.997 6、0.965 9,接近1,也从另一个方面表明拟合效果好、模型可靠.通过比较三因素的F值大小可推断出,对总功耗的影响程度顺序为 $x_{1} x_{2} x_{3}$ ;对后艉轴承振动响应的影响程度顺序为 $x_{3} x_{1} x_{2} .$

图8为根据拟合回归模型绘制对总功耗、后艉轴承振动响应的三维响应面图,反映了影响程度较大的因素间的交互作用对优化目标响应值的影响.其中x₁和x₂对总功耗的交互作用较大如图8(a)所示,随着轴径减低,降低长径比将显著减少轴系功耗损失.此外,x₃和x₁对后艉轴承振动响应的交互作用较大,如图8(b)所示,随着轴径降低,增大跨距将显著降低后艉轴承的振动响应.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 交互作用响应面图

Fig.8 Interaction response surface diagram

2.5 优化结果

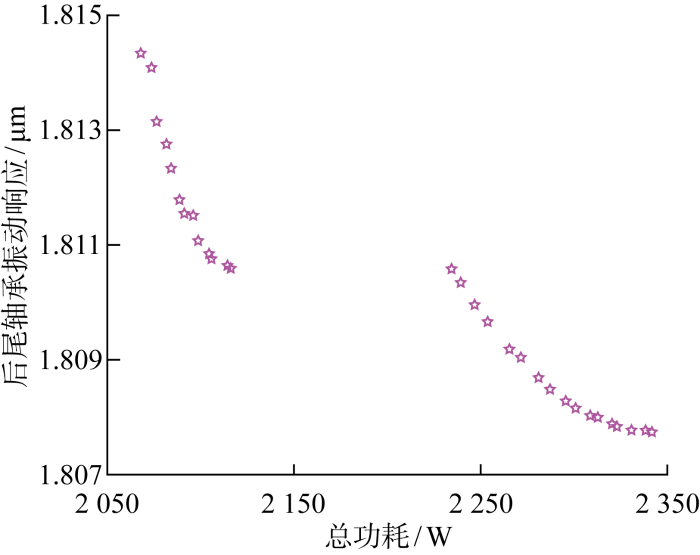
为获得上述响应面回归方程的Pareto最优解,根据GA原理,进行推进轴系多目标优化.针对所设定的传递效率、振动性能优化目标,利用MATLAB软件编写GA优化目标函数,设置相关参数,如最优个体系数为0.3,种群大小为100,最大进化代数为300,适应度函数偏差为1×10^-10,停止代数为300,进行多目标优化并绘制Pareto前端,优化结果见附录A,并且通过图9可以看出,前端的Pareto最优解分布均匀.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 Pareto前端

Fig.9 Pareto front end

经程序计算获得全局Pareto最优解集,从中选取了3组最优解,优化结果如表8所示.可以得出,通过GA多目标优化得能够获得更合理的x₁、x₂和x₃参数设计结果.相比而言,第1组最优解轴系所得总功耗和后艉轴承振动响应幅值的优化效果更好.

表8 Pareto最优解

Tab.8 Pareto optimal solution

最优解	x₁/mm	x₂	x₃/mm	y₁/W	y₂/μm
1	148.7	0.5	267.552 4	2 082.894 7	1.812 5
2	149.6	0.5	268.995 0	2 087.083 3	1.814 2
3	149.2	0.5	267.996 0	2 085.357 1	1.813 4

新窗口打开| 下载CSV

比较第1组最优解优化前后数据变化,如表9所示,优化目标轴系总功耗 2 082.89 W,减少7.10%,由式(8)可得,优化后轴系传递效率为96.17%,提高0.29百分点;而另一优化目标后艉轴承振动响应降低2.30%,两个优化目标均得以实现,这表明了所提出的优化设计方法是有效和可行的.

表9 优化前后数据对比

Tab.9 Comparison of data before and after optimization

类别	y₁/W	y₂/μm	传递效率/%
优化前	2 242.374 2	1.855 9	95.88
第1组解优化结果	2 082.894 7	1.812 5	96.17
变化率	-7.10%	-2.30%	+0.29百分点

新窗口打开| 下载CSV

3 实验验证

本文的数据来源于SimulationX和MATLAB软件仿真结果,为验证多目标优化方法的正确性和有效性,将船舶推进轴系实验结果与仿真结果进行对比分析.

3.1 优化前后振动响应结果验证

对比后艉轴承实验与仿真的轴系振动响应数据,由于轴系试验台实际运行工况较为复杂,且响应结果测量过程中设备干扰等因素的影响,为了更好地对比优化效果,将优化前的轴承振动响应结果设为1,优化后的结果即为优化后的响应值与优化前响应值的比值,进而才能对变化趋势进行对比分析,无量纲化操作后的数据如表10所示.

表10 无量纲化轴承优化前后振动响应幅值对比

Tab.10 Comparison of amplitude of vibration response of dimensionless bearings before and after optimization

支撑位置	振动响应
支撑位置	优化后	优化前
后艉轴承仿真结果	0.934 407	1
前艉轴承仿真结果	0.908 811	1
后艉轴承实验结果	0.995 977	1
前艉轴承实验结果	0.966 166	1

新窗口打开| 下载CSV

从表10中数据可以看出,对于前、后艉轴承而言,其实验和仿真所得的趋势相同,多目标优化后的振动响应幅值均有所减小.

3.2 优化前后总功耗和传递效率结果验证

由于轴系的总功耗是轴上各元件所产生的总和,所以需要得到轴系各元件的功耗数据.将实验所得轴系各元件功耗与仿真所得功耗进行对比,总功耗与传递效率对比如表11所示.

表11 优化前后轴系总功耗和传递效率对比

Tab.11 Comparison of total power consumption and transfer efficiency of shafting before and after optimization

数据	状态	总功耗/W	轴系功率传递效率/%
仿真数据	优化前	2 242.374 2	95.88
	优化后	2 082.894 7	96.17
实验数据	优化前	2 589.441 2	95.33
	优化后	1 813.922 4	96.67

新窗口打开| 下载CSV

从上述表格可以看出,实际实验的优化后结果要好于仿真优化后的结果,且优化后的效率高于96%,优化后的轴系功率传递效率提高了1.34百分点,从而验证了该轴系多目标优化的正确性和可行性.

根据上述的数据对比,可以看出实验与仿真数据在变化规律上基本一致,部分构件变化规律有一定差异,这是因为实验中模拟的水中轴系功耗的水箱对实验台架的影响很复杂,而仿真中的水中轴系功耗仅仅与转速有关,所以实验台架后端的功耗元件变化规律与仿真分析结果存在差异.

4 结论

本文采用RSM和GA相结合的优化方法对船舶推进轴系多目标优化设计问题进行了研究,可以得出如下结论.

(1) 应用RSM构建推进轴系多目标优化模型,能达到用多元拟合函数表示推进轴系的传递效率和振动性能函数关系的目的.同时采用GA对模型进行优化,能够快速求得目标函数的Pareto最优解集.对优化结果比较分析,选择某一组解作为最优解,轴系总功耗、后艉轴承振动响应分别降低了7.10%、2.30%,轴系传递效率提高0.29百分点,从而验证了该船舶推进轴系多目标优化方法的正确性和可行性.

(2) 本文提出的RSM和GA联合的多目标优化方法具有通用性,对船舶推进轴系结构的优化改进设计具有一定意义,类似复杂结构多目标优化问题也同样适用.

附录见本刊网络版(xuebao.sjtu.edu.cn/article/2025/1006-2467/1006-2467-59-04-0466.shtml)

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

龙周, 陈松坤, 王德禹.

基于SMOTE算法的船舶结构可靠性优化设计

[J]. 上海交通大学学报, 2019, 53(1): 26-34.

DOI:10.16183/j.cnki.jsjtu.2019.01.004 [本文引用: 1]

针对常规船舶结构可靠性优化设计由高度非线性带来的计算效率低、收敛困难的问题，提出了基于SMOTE (Synthetic Minority Oversampling Technique)算法的船舶结构可靠性优化设计方法.利用SMOTE算法建立了改进的BP (Back Propagation)神经网络模型，以较少的样本点完成了极限状态函数的高度近似，克服了以往代理模型不能同时满足精度和效率要求的缺点，并通过数学算例验证了使用SMOTE算法建立BP神经网络模型的可行性和有效性.将改进的BP神经网络模型和模拟退火法嵌入单循环优化策略，并将其用于船舶舱段的可靠性优化设计，验证了所提出的可靠性优化设计方法的求解效率和精度，为大型工程结构的可靠性优化设计提供了思路.

LONG

Zhou

, CHEN

Songkun

, WANG

Deyu

Ship structural reliability optimization design based on SMOTE algorithm

[J]. Journal of Shanghai Jiao Tong University, 2019, 53 (1): 26-34.