基于准比例谐振控制的模块化多电平矩阵变换器环流抑制策略

doi:10.16183/j.cnki.jsjtu.2023.193

基于准比例谐振控制的模块化多电平矩阵变换器环流抑制策略

姜亚峰¹, 李仪博¹, 吴秋伟^,²^,³, 刘沈全⁴, 吴小丹⁵, 周前⁶

1.山东大学电气工程学院,济南 250061

2.清华大学清华伯克利深圳学院, 广东深圳 518055

3.清华大学清华深圳国际研究生院,广东深圳 518055

4.华南理工大学电力学院,广州 510641

5.南京南瑞继保电气有限公司, 南京 211102

6.国网江苏省电力有限公司电力科学研究院,南京 211103

Circulating Current Suppression Strategy of Modular Multilevel Matrix Converter Based on Quasi-Proportional Resonant Control

JIANG Yafeng¹, LI Yibo¹, WU Qiuwei^,²^,³, LIU Shenquan⁴, WU Xiaodan⁵, ZHOU Qian⁶

1. School of Electrical Engineering, Shandong University, Jinan 250061, China

2. Tsinghua Berkeley Shenzhen Institute, Tsinghua University, Shenzhen 518055, Guangdong, China

3. Tsinghua Shenzhen International Graduate Institute, Tsinghua University, Shenzhen 518055, Guangdong, China

4. School of Electrical Engineering, South China University of Technology, Guangzhou 510641, China

5. NR Electric Co., Ltd., Nanjing 211102, China

6. State Grid Jiangsu Electric Power Co., Ltd. Research Institute, Nanjing 211103, China

通讯作者: 吴秋伟,教授,博士生导师;E-mail:qiuwu@sz.tsing.edu.cn.

收稿日期: 2023-05-12 修回日期: 2023-06-29 接受日期: 2023-08-9

基金资助:

国家电网公司总部科技项目(4000-202218073A-1-1-ZN)

Received: 2023-05-12 Revised: 2023-06-29 Accepted: 2023-08-9

作者简介 About authors

姜亚峰(1999—),硕士生,从事柔性低频输电研究.

摘要

模块化多电平矩阵变换器(M³C)是分频输电系统中的核心装置.由于缺乏直流环节,所以不同频率的电气量在M³C内部直接耦合,导致M³C内部出现非常复杂的谐波,造成子模块均压困难,影响M³C的稳定运行.提出一种基于准比例谐振(PR)控制器的闭环控制策略,实现对M³C内部环流的抑制.首先,研究稳态时子模块电容纹波电压,详细分析子模块纹波电压与开关函数耦合产生谐波电流的机理,推导谐波环流的解析式,指出抑制环流的必要性.然后,针对4种频率成分的谐波环流设计并联的准PR环流抑制器,在抑制环流的同时减少桥臂电流的畸变,保障桥臂间电容电压均衡并且具备良好的动态性能.最后,在MATLAB/Simulink中搭建仿真模型,通过仿真验证控制策略的有效性.

关键词： 模块化多电平矩阵变换器; 分频输电系统; 电容纹波电压; 准比例谐振控制; 环流抑制

Abstract

Modular multilevel matrix converter (M³C) is the core device of the fractional frequency transmission system. Due to the lack of direct current link, the electrical quantities of different frequencies are directly coupled inside the M³C, resulting in a complex harmonic condition, which makes it difficult to balance the capacitor voltage of the sub-module and affects the stable operation of the M³C. In this paper, a closed-loop control strategy based on quasi-proportional resonance (PR) controller is proposed to suppress the internal circulation of the M³C. First, the ripple voltage of the sub-module capacitor in steady state is studied. The mechanism of harmonic current generated by the coupling of sub-module ripple voltage and switching function is analyzed in detail. The analytical formula of harmonic circulating current is derived, and the necessity of suppressing the circulating current is pointed out. Then, a parallel quasi-PR circulation suppressor is designed for the harmonic circulation of four frequency components, which reduces the distortion of the bridge arm current while suppressing the circulating current, ensures the capacitor voltage balance between the bridge arms with a good dynamic performance. Finally, a simulation model is built in MATLAB / Simulink and the effectiveness of the control strategy is validated by simulation.

Keywords： modular multilevel matrix converter (M³C); fractional frequency transmission system; capacitors ripple voltage; quasi-proportional resonance (PR) control; circulating current suppression

PDF (2259KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

姜亚峰, 李仪博, 吴秋伟, 刘沈全, 吴小丹, 周前. 基于准比例谐振控制的模块化多电平矩阵变换器环流抑制策略[J]. 上海交通大学学报, 2025, 59(2): 242-251 doi:10.16183/j.cnki.jsjtu.2023.193

JIANG Yafeng, LI Yibo, WU Qiuwei, LIU Shenquan, WU Xiaodan, ZHOU Qian. Circulating Current Suppression Strategy of Modular Multilevel Matrix Converter Based on Quasi-Proportional Resonant Control[J]. Journal of Shanghai Jiaotong University, 2025, 59(2): 242-251 doi:10.16183/j.cnki.jsjtu.2023.193

海上风电因其资源丰富、可利用小时数高以及适合大规模开发等特点受到学术界的广泛关注^[1-2].目前近海的风电资源已经开发殆尽,随着海上风电技术的发展,未来海上风电场的建设必将向着中远海逐步迈进.但是大规模、远距离海上风电的开发给系统并网带来巨大的技术挑战.在此背景下,分频输电系统(fractional frequency transmission system,FFTS)通过降低输电频率、减少线路阻抗,来提高线路的传输能力,并且无需建设海上换流站,为中远海的海上风电并网提供了一种具有竞争力的输送方案^[3].

模块化多电平矩阵变换器(modular multilevel matrix converter,M³C)是分频输电系统中频率变换与功率传输的核心装置^[4].M³C可以实现高压大容量的功率转换,并且易于集成和拓展^[5],但是M³C复杂的拓扑结构大大增加了控制难度.针对M³C的数学模型和控制策略已有大量研究,目前最为广泛采用的是基于双αβO坐标变换的解耦控制方法^[6⇓-8],通过对M³C数学模型进行双αβO坐标变换,将工频侧与分频侧电流从桥臂电流中分离出来分别进行解耦控制.在此基础上,文献[9 ⇓-11]中采用层次化电容电压的控制方法, 对M³C的整体电压、相电压、桥臂电压以及子模块电压进行分层控制.但是这种控制方式比较复杂,桥臂电流经dq变换后,依然有多种频率的交流成分.

上述这些问题与M³C内部环流的存在有着密切关系.模块化多电平变换器(modular multilevel converter,MMC)的研究对环流产生机理与抑制方法进行了深入探索.文献[12 ⇓-14]中详细分析了子模块电容电压的波动以及子模块电容电压与内部环流之间通过开关函数相互影响的机制.文献[15 ⇓-17]中从不同角度设计MMC环流抑制控制器,有效地抑制桥臂电流中的2次谐波分量,显著降低桥臂电流波形的畸变程度.

与MMC相比,M³C内部谐波情况更加复杂,但是目前对M³C谐波特性的研究尚且不足.李峰等^[18]研究了稳态时子模块的电容纹波电压,得到电容纹波电压各频率成分的电压解析式,并对影响电容纹波电压的主要因素进行分析.孙玉巍等^[19]研究了M³C的谐波特性,推导了9个桥臂电流谐波的详细表达式,并且分析了谐波分布及影响谐波大小的因素.Luo等^[20]针对20 Hz与60 Hz的互联系统,详细分析M³C不同频率的谐波,但是由于互联系统频率存在整数倍的关系,忽视了部分频率信号,并且仅对工频、分频网侧电流进行控制,并未采取措施对环流进行抑制.文献[21 ⇓-23]中从桥臂间电容电压均衡的角度出发,采用比例控制器抑制环流,但是整体控制方式比较复杂,且对环流的抑制效果有限.相比之下,比例谐振(proportional resonance,PR)控制器可以实现对特定频率信号的有效控制, 在并网逆变器以及MMC的谐波抑制中取得良好效果^[24],但是尚未应用于M³C的环流抑制中.

在已有工作的基础上,研究子模块电容纹波电压与开关函数耦合产生谐波的机理,推导M³C内部谐波电流的解析式,针对M³C中的谐波环流,提出基于准PR控制的环流抑制策略.与常规比例控制器相比,并联的准PR控制器对环流抑制效果更加明显,减少了桥臂电流的畸变,降低了环流带来的功率损耗,有效提升了M³C的运行性能,并且整体控制结构简洁清晰易于实现.最后, 在MATLAB平台上搭建M³C的仿真模型,对所提环流抑制策略进行了仿真验证.

1 M³C基本原理

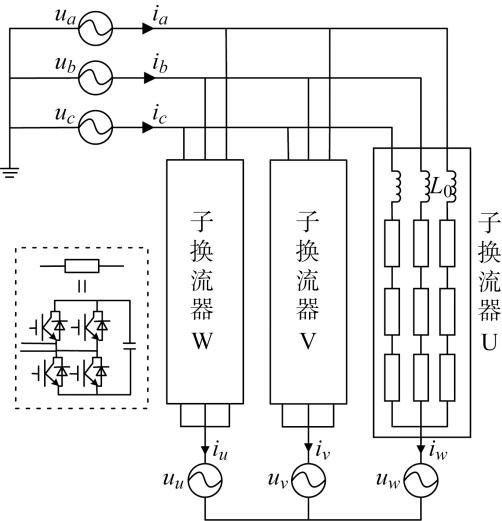
图1为M³C的主电路结构.图中,工频侧三相(a,b,c)与分频侧三相(u,v,w)通过9条桥臂相连,每条桥臂由N个全桥子模块和1个串级电感L₀组成.从分频侧相单元的角度,将M³C划分成3个星形连接的子换流器U、V、W.其中u_x、i_x(x=a,b,c)为工频侧的相电压与相电流;u_y、i_y(y=u,v,w)为分频侧的相电压和相电流.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 M³C主电路结构

Fig.1 Main circuit structure of M³C

假设各桥臂及子模块参数对称,稳态时各子模块电容电压相等,工频侧和分频侧电压和电流都为三相对称正弦波,每相电流平均分配在与之相连的3个桥臂中.以工频侧a相为例,其电压和电流分别为

(1)

\begin{array}{l} u_{a} = U_{a m} c o s (ω_{s} t + φ_{s}) \\ i_{a} = I_{a m} c o s (ω_{s} t + α_{s}) \end{array}\}

分频侧u相的电压和电流为

(2)

\begin{array}{l} u_{u} = U_{u m} c o s (ω_{l} t + φ_{l}) \\ i_{u} = I_{u m} c o s (ω_{l} t + α_{l}) \end{array}\}

式中:U_a_m、I_a_m分别为a相电压和电流的峰值;U_u_m、I_u_m分别为u相电压和电流的峰值;ω_s、ω_l分别为工频与分频侧的角频率;φ_s、α_s分别为a相电压和电流的初始相位角;φ_l、α_l分别为u相电压和电流的初始相位角;t为时间.

定义S_arm,_i为桥臂第i个子模块的开关函数,S_arm,_i值取1时表示该子模块正向投入,取-1时表示该子模块负向投入,取0表示将该子模块切除,由此定义桥臂平均开关函数为

(3)S_arm=

\frac{1}{N} \overset{N}{\sum_{i = 1}}

S_arm,_i

式中:S_arm表示桥臂中子模块的平均投入比.对于桥臂的第i个子模块,流过子模块电容的电流为

(4)S_arm,_ii_arm=C

\frac{d u_{d c}}{d t}

i_arm为桥臂电流;C为子模块电容值;u_dc为子模块电容电压.将该桥臂全部子模块电容电流求和并代入式(4),可得桥臂电流i_arm与子模块电容电压u_dc的关系为

(5)S_armi_arm=C

\frac{d u_{d c}}{d t}

由于稳态时各子模块直流侧电容电压相等,可得桥臂电压u_arm与子模块电容电压u_dc的关系式为

(6)$u_{\mathrm{arm}}=S_{\mathrm{arm}} N u_{\mathrm{dc}}$

2 M³C电容电压波动分析

根据式(5), 子模块电容电压可以表示为

(7)u_dc=

\frac{1}{C}

∫S_armi_armdt+

{\bar{u}}_{d c}

式中: ${\bar{u}}_{d c}$ 为子模块电容电压的直流分量.由此可得,子模块电容纹波电压为

(8)

{\tilde{u}}_{d c}

\frac{1}{C}

∫S_armi_armdt

根据式(8)可知,开关函数与桥臂电流的耦合导致电容纹波电压的产生.假设环流已经得到抑制,桥臂电流中仅含基频分量,基频包括工频和分频,将桥臂电流与开关函数代入式(8)即可得到稳态时的子模块电容纹波电压.

以桥臂au为例,附录A中的式(A1)为稳态时子模块电容纹波电压的瞬时表达式.分析该式可知, 由于M³C稳态运行时子模块电容纹波电压中直流分量为0^[18],所以子模块纹波电压中仅含4种频率的交流分量,分别为2ω_s、2ω_l、ω_s+ω_l、ω_s-ω_l.根据对称性可知,M³C中9个桥臂的电容纹波电压所含交流分量的频率成分一致,且相同频率的纹波电压幅值也相等.

3 M³C环流分析

分析M³C电容电压可知,子模块电容电压为直流电压 ${\bar{u}}_{d c}$ 与纹波电压 ${\tilde{u}}_{d c}$ 之和:

(9)u_dc=

{\bar{u}}_{d c}

{\tilde{u}}_{d c}

将式(9)代入式(6)中,可以得到桥臂电压的表达式:

(10)u_arm=NS_arm(

{\bar{u}}_{d c}

{\tilde{u}}_{d c}

)

由式(10)可知,子模块电容电压与开关函数耦合得到桥臂电压,其中子模块电容电压中直流分量的耦合成分为系统基频分量,而子模块纹波电压与开关函数的耦合成分则是桥臂内部谐波的来源.通过推导关系式可知,桥臂电压中含有8种频率成分的谐波分量,分别为ω_s、ω_l、3ω_s、3ω_l、2ω_s-ω_l、2ω_s+ω_l、ω_s-2ω_l、ω_s+2ω_l.

根据基尔霍夫电压定律可以得到每条桥臂的回路电压方程,桥臂中8种谐波电压会产生8种频率的谐波电流,通过求解电压方程可以得到相应频率的谐波电流解析式,进而能够分析谐波电流的特性^[20].

以2ω_s-ω_l频率的桥臂谐波电流为例,该频率谐波电流的解析式为

(11)

i_{x y, 2 ω_{s} - ω_{l}}

=k₁(

m_{x}^{2}

I_y_mcos((2ω_s-ω_l)t+θ₁)-m_xm_yI_x_mcos((2ω_s-ω_l)t+θ₂))-k₂(m_xm_yI_x_mcos((2ω_s-ω_l)t+θ₂))

式中:k₁、k₂为提取的公因式,k₁=(N/12)CL₀×(ω_s-ω_l)(2ω_s-ω_l),k₂=(N/24)CL₀ω_s(2ω_s-ω_l);I_x_m、I_y_m分别为M³C工频侧和分频侧相电流峰值;m_x、m_y分别为工频和分频侧的电压调制比,m_x=U_x_m/Nu_dc,m_y=U_y_m/Nu_dc,U_x_m、U_y_m分别为工频和分频侧相电压峰值;θ₁、θ₂为该频率电流的初始相位角,各桥臂中该频率电流初始相位角的表达式如表1所示.

表1 初始相位角θ₁和θ₂的表达式

Tab.1 Expressions of initial phase angles θ₁ and θ₂

xy	θ₁	θ₂
au, bw, cv	2φ_s-α_l	α_s+φ_s-φ_l
av, bu, cw	2φ_s-α_l+2π/3	α_s+φ_s-φ_l+2π/3
aw, bv, cu	2φ_s-α_l-2π/3	α_s+φ_s-φ_l-2π/3

新窗口打开| 下载CSV

根据推导结果,该频率成分的谐波电流在9个桥臂中幅值相等,但相位不同,根据其在9个桥臂中的分布情况可知,该频率成分的谐波电流仅在M³C内部流通,为谐波环流.

采用相同的计算方式,可以得到另外7种频率的桥臂谐波电流表达式和初始相位角,如附录式A(2)~A(8)所示.经分析,ω_s与ω_l频率的谐波电流为正序谐波,以正序基波的形式分别流入M³C的工、分频侧,不需要进行控制.3ω_s与3ω_l频率的谐波电流为零序谐波,会流入M³C的两侧;但在FFTS中M³C两侧变压器通常采用三角接线,能够直接切断零序电流的路径^[20],不再需要抑制零序电流.另外3种频率ω_s+2ω_l、2ω_s+ω_l、ω_s-2ω_l的谐波与 2ω_s-ω_l频率的谐波电流具有相同的特性,都为谐波环流,其中ω_s-2ω_l频率的谐波幅值最大.

环流叠加在桥臂电流上不仅会占用功率开关器件的额定电流容量,也会引起发热问题,导致器件老化.除此之外,桥臂中环流分量也会与开关函数进行耦合,子模块电容电压中将出现更加复杂的纹波,具体的频率成分如表2所示. 因此,如果不对M³C内部的环流进行抑制,不仅会增加额外的功率损耗,还会影响桥臂间电容电压的均衡,不利于M³C的稳定运行.

表2 子模块电容纹波电压的频率组成

Tab.2 Frequency composition of sub-module capacitor ripple voltage

环流频率	电容纹波电压中耦合频率成分
2ω_s-ω_l	3ω_s-ω_l、ω_s-ω_l、2ω_s、2ω_s-2ω_l
2ω_s+ω_l	3ω_s+ω_l、ω_s+ω_l、2ω_s、2ω_s+2ω_l
ω_s-2ω_l	2ω_s-2ω_l、ω_s-ω_l、ω_s-3ω_l、2ω_l
ω_s+2ω_l	2ω_s+2ω_l、2ω_l、ω_s+ω_l、ω_s+3ω_l

新窗口打开| 下载CSV

4 M³C环流抑制策略

根据环流分析的结果,M³C正常运行时桥臂电流中含有4种频率成分的谐波环流.由于频率成分并不单一,所以不能再采取MMC中将环流成分变换到dq坐标系下的比例积分(proportional integral, PI)控制方式.为此,提出一种并联的准PR控制器,在αβ静止坐标系下实现对谐波环流中4种频率分量的共同抑制.

4.1 准PR控制器

理想的PR控制器的传递函数为

(12)G_PR(s)=k_p+k_rs/(s²+

ω_{0}^{2}

)

式中:s为拉普拉斯算子;k_p为比例增益;k_r为谐振增益;ω₀为谐振角频率.

理想PR控制器在谐振角频率ω₀处有无穷大增益,但是在实际应用中,由于采样电路的误差以及控制系统精度的限制,信号频率可能出现偏移,因而无法有效地抑制交流信号.因此,选择准PR控制器抑制环流,其传递函数为

(13)G_QPR(s)=k_p+

\frac{2 k_{r} ω_{b} s}{s^{2} + 2 ω_{b} s + ω_{0}^{2}}

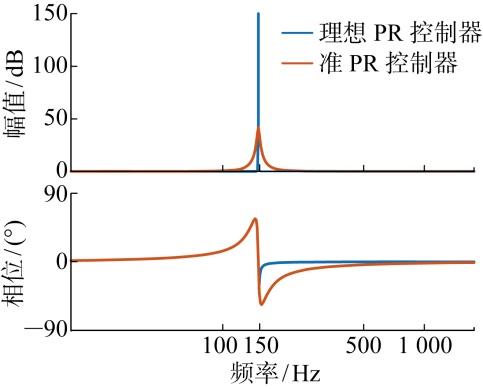
式中:ω_b为谐振带宽.图2为两种PR控制器的伯德图,其中参数设置为:k_p=1,k_r=10,ω₀=300π rad/s,ω_b=10 rad/s.由图可见,与理想PR控制器相比,准PR控制器在谐振频率ω₀处的增益减小,但对谐振频率处ω_b频率范围内的信号都具有控制作用,因此可以有效减小频率偏移带来的影响.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 理想PR控制器与准PR控制器伯德图

Fig.2 Bode diagram of ideal PR controller and quasi-PR controller

4.2 M³C环流抑制策略

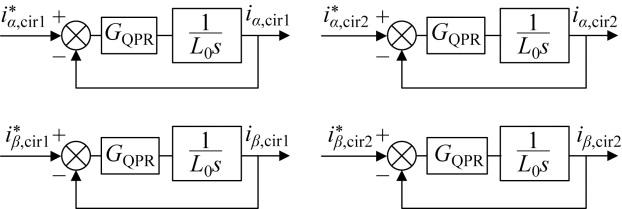
根据文献[25]中的推导,工频侧和分频侧以及内部环流在αβ静止坐标下的控制方程为

(14)

\begin{array}{l} (\frac{L_{0}}{3} \frac{d}{d t} + \frac{R_{0}}{3}) [\begin{array}{l} i_{i α} \\ i_{i β} \end{array}] + [\begin{array}{l} u_{s u m α} \\ u_{s u m β} \end{array}] = [\begin{array}{l} u_{i α} \\ u_{i β} \end{array}] \\ (\frac{L_{0}}{3} \frac{d}{d t} + \frac{R_{0}}{3}) [\begin{array}{l} i_{o α} \\ i_{o β} \end{array}] + [\begin{array}{l} u_{c o m α} \\ u_{c o m β} \end{array}] = [\begin{array}{l} u_{o α} \\ u_{o β} \end{array}] \end{array}\}

(15)

\begin{array}{l} (L_{0} \frac{d}{d t} + R_{0}) [\begin{array}{l} i_{α, c i r 1} \\ i_{β, c i r 1} \end{array}] + [\begin{array}{l} u_{α, c i r 1} \\ u_{β, c i r 1} \end{array}] = [\begin{array}{l} 0 \\ 0 \end{array}] \\ (L_{0} \frac{d}{d t} + R_{0}) [\begin{array}{l} i_{α, c i r 2} \\ i_{β, c i r 2} \end{array}] + [\begin{array}{l} u_{α, c i r 2} \\ u_{β, c i r 2} \end{array}] = [\begin{array}{l} 0 \\ 0 \end{array}] \end{array}\}

式中:R₀为串级电感L₀的等效电阻;i_i_α、i_i_β和i_o_α、i_o_β分别为工频侧和分频侧相电流在αβ静止坐标系下的分量;u_i_α、u_i_β和u_o_α、u_o_β分别为工频侧和分频侧相电压在αβ静止坐标系下的分量;u_sum_α、u_sum_β和u_com_α、u_com_β分别为工频侧和分频侧共模电压在αβ静止坐标系下的分量;i_α_,cri1、i_β_,cri1和i_α_,cri2、i_β_,cri2为环流1和环流2在αβ静止坐标系下的分量;u_α_,cri1、u_β_,cri1和u_α_,cri2、u_β_,cri2为环流电压1和环流电压2在αβ静止坐标系下的分量.

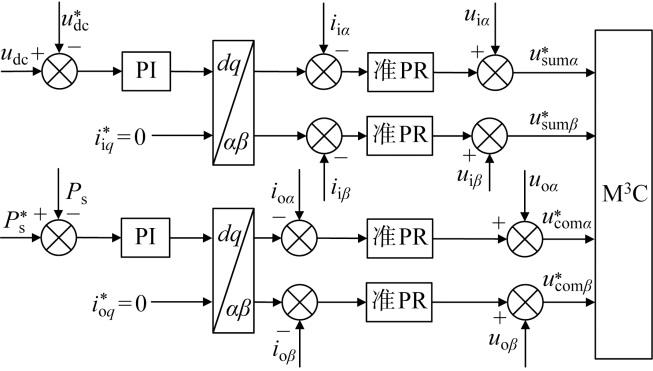
根据式(14),提出如图3所示的工频侧与分频侧的电压电流双闭环控制策略.图中:i_i_q、i_o_q分别为工频侧与分频侧相电流在q轴分量;P_s为分频测输出功率;*表示相应变量参考值.其中外环采用PI控制,电流内环采用准PR控制器.使用准PR控制后,不再需要进行耦合补偿就能实现对电流αβ分量的解耦控制,并且延时小,响应速度更快.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 工频侧与分频侧的控制框图

Fig.3 Control block of industrial frequency side and fractional frequency side

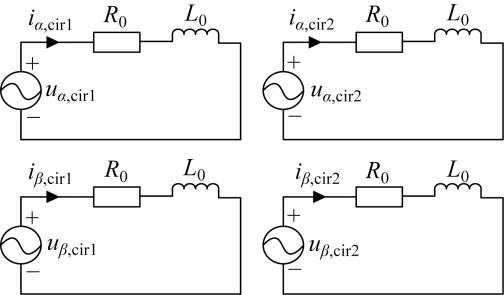
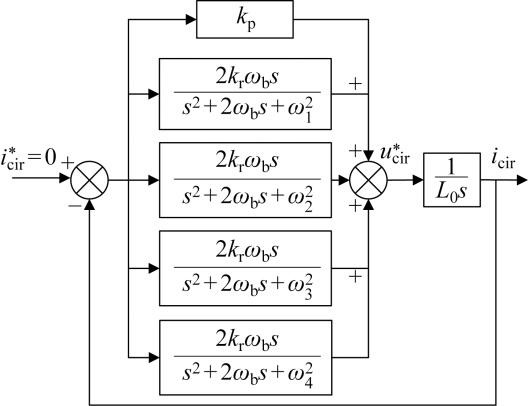
根据式(15),可以得到如图4所示的环流等效电路,据此提出M³C谐波环流抑制的闭环控制方式,如图5所示.根据推导的环流中4种频率成分设计如图6所示的环流抑制器.图中:i_cir、u_cir分别为环流和环流电压;ω₁、ω₂、ω₃、ω₄分别对应谐波环流中的4种频率成分.环流抑制器由一组并联的准PR控制器组成,谐振频率对应着M³C内部环流频率,能够对4种频率的谐波电流进行共同抑制,环流抑制器的传递函数为

(16)G_QPR(s)=k_p+2k_rω_bs/(s²+2ω_bs+

ω_{1}^{2}

\frac{2 k_{r} ω_{b} s}{s^{2} + 2 ω_{b} s + ω_{2}^{2}}

\frac{2 k_{r} ω_{b} s}{s^{2} + 2 ω_{b} s + ω_{3}^{2}}

+ 2k_rω_bs/(s²+2ω_bs+

ω_{4}^{2}

)

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 静止坐标系下M³C环流等效电路

Fig.4 M³C circulating current equivalent circuit in stationary coordinate system

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 M³C环流闭环控制方式

Fig.5 Circulation closed-loop control mode of M³C

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 环流抑制器结构框图

Fig.6 Structure of circulating current suppressor

环流抑制策略的具体方式为:检测桥臂电流并从中分离得到M³C的内部环流,经Clark变换得到环流的αβ分量,将环流送入并联的准PR控制器中进行跟踪处理,即可得到环流电压的参考值,与工频侧和分频侧控制得到的共模电压参考值一起经转换后得到M³C每条桥臂的电压参考值.

M³C桥臂单元的子模块数目较多,会产生桥臂内各子模块间的电容电压均衡问题^[5].因此,选择采用基于电容电压排序的最近电平逼近调制方法来实现给定电压参考值的调制输出.该方法简单,均压效果良好.

5 仿真分析

为了验证所提谐波环流抑制策略的有效性,在MATLAB/Simulink平台上搭建如图1所示电路的M³C仿真模型,采用第4节所提控制方案进行仿真研究.系统主要参数设置如表3所示;图7~10为仿真结果.

表3 M³C参数

Tab.3 Parameters of M³C

参数	数值
M³C额定容量/MW	11
C/mF	12
额定电容电压/V	800
桥臂模块数/个	29
桥臂电感/mH	30
工频侧频率/Hz	50
分频侧频率/Hz	20
工频侧额定线电压/kV	12
分频侧额定线电压/kV	12

新窗口打开| 下载CSV

图7

新窗口打开| 下载原图ZIP| 生成PPT

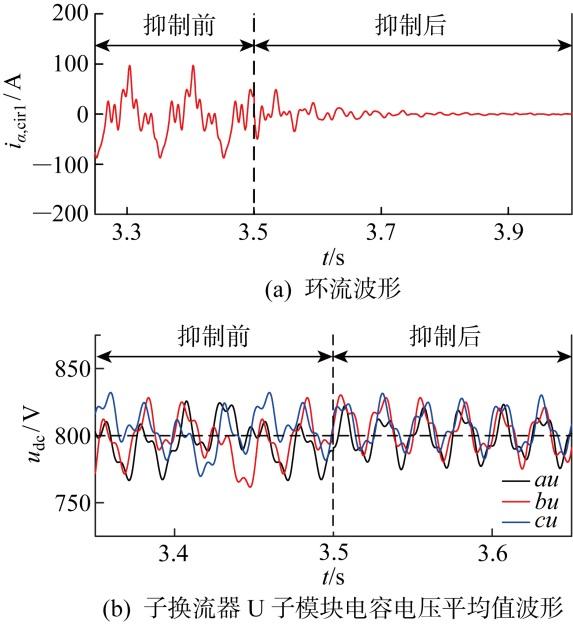
图7 环流抑制前后效果

Fig.7 Circulating current and capacitor voltage before and after circulation suppression

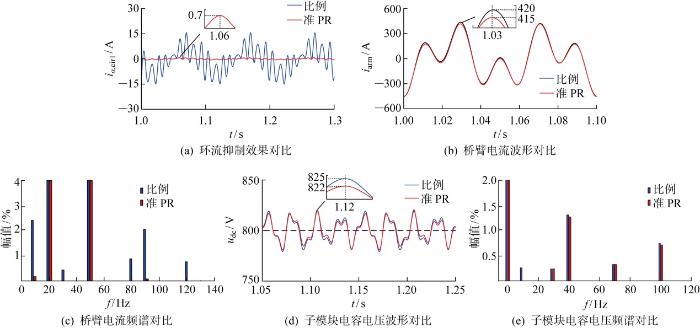
图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 比例控制与准PR控制效果对比

Fig.8 Effect comparison of proportional control and quasi-PR control

图9

新窗口打开| 下载原图ZIP| 生成PPT

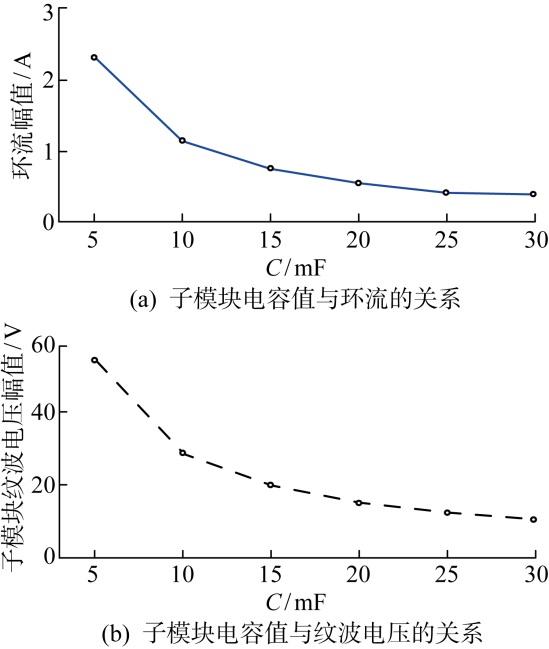
图9 子模块电容值与纹波电压和环流的关系

Fig.9 Sub-module capacitance versus ripple voltage and circulating current

图10

新窗口打开| 下载原图ZIP| 生成PPT

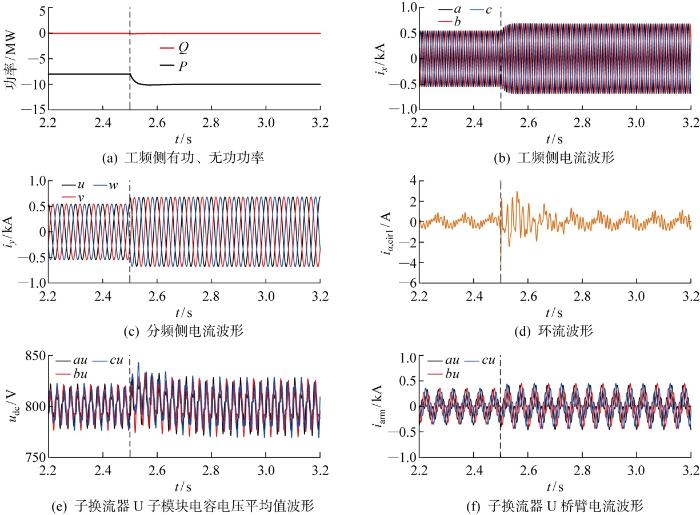
图10 M³C动态响应效果

Fig.10 Dynamic response effect of M³C

图7为环流抑制前后的效果图,M³C运行至3.5 s时开启环流抑制器.根据图7(a)中环流波形的变化,可以看出所提控制策略有效抑制了环流,环流幅值降至0 A左右,环流带来的功率损耗将大大降低;并且由于环流得到有效抑制,避免了与开关函数的耦合,因此子模块电容电压的波动幅值减小, M³C的运行性能也得到提升.

图8为环流抑制器采用比例控制与并联准PR控制器的仿真效果对比,两种控制中比例增益参数相同.图中:f为频率.环流抑制的效果如图8(a)所示,与比例控制器相比,采用准PR控制后,环流的幅值由15 A降到0.7 A,表明准PR环流抑制器对环流的抑制作用更加有效.

图8(b)、8(c)为桥臂au的电流波形与频谱的对比.由图可见,采用准PR控制后,桥臂电流的幅值从420 A降低至415 A.根据频谱分析结果,采用比例控制时,令f_s、f_l分别为工频侧与分频侧频率,桥臂电流中除50 Hz工频与20 Hz分频分量外,主要的谐波频率为: f_s-2f_l =10 Hz, 2f_s-f_l= 80 Hz,f_s+2f_l=90 Hz, 2f_s+f_l=120 Hz.其中,f_s-2f_l=10 Hz的谐波幅值最大,这与理论分析的一致.采用准PR控制器后,4种谐波分量都得到有效抑制,改善了桥臂电流的畸变程度.

图8(d)、8(e)为桥臂au子模块电容电压波形与频谱对比.由图可见,采用准PR抑制后,电容电压的波动幅度减小.根据频谱分析的结果,子模块电容电压除直流分量外,主要含有f_s-f_l=30 Hz、 2f_l= 40 Hz、f_s+f_l= 70 Hz、2f_s=100 Hz频率的纹波,与附录式(A1)推导的结果一致.除此之外,还存在幅值最大的f_s-2f_l=10 Hz频率的环流与开关函数耦合造成f_s-3f_l=10 Hz的纹波,由于准PR控制对环流抑制效果更好,避免了环流与开关函数的二次耦合,因而子模块纹波电压的幅值减小.

图9(a)、9(b)分别展示了子模块电容值与纹波电压幅值和环流幅值之间的关系.由图8可知,子模块电容越大纹波电压与环流的幅值越小,与式(11)和附录式(A1)中的推导结果相符,增大电容值能够有效抑制电容电压的波动和环流的大小,但是增大电容值既会增加电容器成本也会影响M³C的动态性能,实际应用中要在满足电容电压波动幅度的要求下,综合考虑成本、占地以及安全裕量等因素,来确定子模块电容的取值.

为了验证采用环流抑制器后M³C的动态性能,系统运行在单位功率因数模式下,在2.5 s分频侧的有功功率从8 MW跃升至10 MW,图10为动态响应的仿真结果.工频侧的功率曲线如图10(a)所示,有功功率(P)能够快速响应分频侧功率的变化,无功功率(Q)在阶跃中保持为0,表明M³C具有良好的动态响应特性.工频侧和分频侧的电流i_x、i_y波形分别如图10(b)、10(c)所示,两侧电流均为三相对称波形,能够迅速跟随系统能量的变化,实现工频、分频侧的解耦控制.图10(d)为环流i_α,_cri₁的波形,由图可知,M³C传输功率变化时,环流经过 0.2 s 的波动到达新的稳定值,并且环流波动范围在±3.5 A以内,表明环流抑制器在动态响应过程中能够保持良好的环流抑制效果.图10(e)、10(f)为子换流器中U子模块电容电压平均值和桥臂电流的波形,由图10(e)可知,电容电压稳定在800 V附近,整体控制策略能够实现桥臂间电容电压均衡.结合图10的仿真效果可知,采用并联准PR抑制器后,M³C的动态响应性能依然良好.

6 结论

详细分析M³C内部谐波电流产生机理,针对谐波环流提出基于准PR的环流抑制策略.通过理论分析与仿真验证,得到结论如下:

(1) 稳态运行时,子模块电容电压中将出现2ω_s、2ω_l、ω_s+ω_l和ω_s-ω_l这4种频率的纹波.如果不对环流进行抑制,子模块纹波电压中的频率成分会更加复杂.

(2) 子模块电容纹波电压与开关函数耦合在桥臂中产生8种频率成分的谐波,其中ω_s+2ω_l、2ω_s+ω_l、ω_s-2ω_l、2ω_s-ω_l这4种谐波只在M³C内部流通,为谐波环流,需要进行抑制.

(3) 采用并联的准PR控制器能够对4种频率成分的环流进行有效抑制,改善了桥臂电流的畸变程度,保障了桥臂间电容电压的均衡,并且动态响应性能良好.

(4) 所提环流抑制方案效果良好,控制结构清晰简洁,易于实现,具有一定的工程应用价值.

附录见本刊网络版(xuebao.sjtu.edu.cn/article/2025/1006-2467/1006-2467-59-02-0242.shtml)

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

余浩, 张哲萌, 彭穗,

等.

海上风电经柔性直流并网技术标准对比分析

[J]. 上海交通大学学报, 2022, 56(4): 403-412.

DOI:10.16183/j.cnki.jsjtu.2021.465 [本文引用: 1]

对国内外海上风电经柔性直流并网标准的现状进行介绍,选取具有代表性的海上风电经柔性直流并网标准,从功率控制、故障穿越、电能质量、稳定性等几个方面进行对比,分析海上风电经柔性直流并网标准的发展趋势.对中国海上风电经柔性直流并网标准的制修订提供合理建议,以促进海上风电行业的发展.

Hao

, ZHANG

Zhemeng

, PENG

Sui

et al.

Comparative analysis of technical standards for offshore wind power via VSC-HVDC

[J]. Journal of Shanghai Jiao Tong University, 2022, 56(4): 403-412.