考虑产消用户不确定性的售电公司购售电决策

doi:10.16183/j.cnki.jsjtu.2023.530

考虑产消用户不确定性的售电公司购售电决策

孙毅¹, 刘壮^,¹, 黄婷¹, 彭杰¹, 王晓甜², 刘创²

1 华北电力大学电气与电子工程学院, 北京 102206

2 国网河北省电力有限公司营销服务中心, 石家庄 050035

Decision-Making Model of Electricity Procurement and Sale for Electricity Retailers Considering the Uncertainty of Prosumers

SUN Yi¹, LIU Zhuang^,¹, HUANG Ting¹, PENG Jie¹, WANG Xiaotian², LIU Chuang²

1 School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China

2 Marketing Service Center, State Grid Hebei Electric Power Co., Ltd., Shijiazhuang 050035, China

通讯作者: 刘壮,硕士生;E-mail:2188886722@qq.com.

责任编辑: 王一凡

收稿日期: 2023-10-20 修回日期: 2024-01-27 接受日期: 2024-01-29

基金资助:

国网河北省电力有限公司科技项目(SGHEYX00DFJS2250130)

Received: 2023-10-20 Revised: 2024-01-27 Accepted: 2024-01-29

作者简介 About authors

孙毅(1972—),教授,博士生导师,从事能源互联网信息通信、需求侧管理相关研究.

摘要

新型电力系统背景下,传统的能源消费者正逐步转变为兼具电能消费与生产的“产消者”.产消用户的大量涌现使得售电公司的购售电决策变得更加复杂,与此同时,售电公司也将面临更多的不确定性因素,造成较大的市场风险.针对上述问题,本文充分考虑产消用户的发用电特点,并计及光伏、现货市场购售电价格不确定性因素的影响,提出一种不确定性环境下面向产消用户的售电公司购售电决策优化方法.首先,构建考虑不确定性因素的售电公司购售电决策双层优化模型:下层模型考虑产消用户光伏出力不确定性,以舒适度与用电成本为目标,建立产消用户鲁棒用能优化模型;上层模型针对现货市场购售电价格的不确定性,基于信息间隙决策理论(IGDT)构建售电公司鲁棒综合决策模型,并在售电公司侧引入储能和中长期购售电合约以增强售电公司的风险应对能力.随后,利用Karush-Kuhn-Tucker(KKT)条件将该双层优化问题转化为单层非线性规划问题进行求解.最后,通过仿真分析验证了所制定零售电价的经济性以及所建模型的有效性.

关键词： 产消用户; 不确定性因素; 信息间隙决策理论; KKT条件; 双层优化问题

Abstract

In the context of the new power system, traditional energy consumers are transforming into prosumers, entities that both consume and produce electricity. The emergence of a large number of prosumers has made the purchase and sale decisions of electricity retailers more complicated. At the same time, electricity retailers will also face more uncertainties, resulting in greater market risks. To address these challenges, this paper proposes an optimization method of power purchase and sales strategy for electricity retailers facing prosumers under uncertain factors. First, it establishes a two-tier optimization model for the purchase and sale of electricity by electricity retailers under uncertain conditions. The upper model focuses on the comfort and cost of prosumers, incorporates the uncertainty of photovoltaic output, and develops a robust energy optimization model for prosumers. For the uncertainty of electricity purchase and sale prices in the spot market, the lower model establishes a robust comprehensive decision-making model of electricity sales companies based on information gap decision theory (IGDT). Then, it uses the Karush-Kuhn-Tucker (KKT) condition to transform the two-tier optimization problem proposed in into a single-layer nonlinear programming problem. Finally, the simulation analysis demonstrates the economy of the retail electricity price obtained and the effectiveness of the proposed model.

Keywords： prosumers; uncertainty; information gap decision theory (IGDT); KKT condition; two-tier optimization problem

PDF (2928KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

孙毅, 刘壮, 黄婷, 彭杰, 王晓甜, 刘创. 考虑产消用户不确定性的售电公司购售电决策[J]. 上海交通大学学报, 2025, 59(10): 1476-1486 doi:10.16183/j.cnki.jsjtu.2023.530

SUN Yi, LIU Zhuang, HUANG Ting, PENG Jie, WANG Xiaotian, LIU Chuang. Decision-Making Model of Electricity Procurement and Sale for Electricity Retailers Considering the Uncertainty of Prosumers[J]. Journal of Shanghai Jiaotong University, 2025, 59(10): 1476-1486 doi:10.16183/j.cnki.jsjtu.2023.530

售电侧放开、培育独立售电主体是我国新一轮电力体制改革的重点内容^[1].售电公司作为衔接多元电力市场与电力用户的桥梁,通过上级市场购电再转售给电力用户盈利^[2-3].为实现利润最大化,售电公司需从购、售电两方面优化决策.

在“双碳”目标和新型电力系统背景下,分布式可再生能源在用户侧渗透率的不断提高,使得部分传统电力用户转变为产消者.产消用户利用自身储能设备,通过自平衡优化确定各时段购售电量来降低运行成本.产消用户的出现使得售电公司的优化决策不再仅仅针对用户侧用电,而应满足产消用户购、售电两方面的需求,同时也增加了售电公司决策时的不确定因素,使售电公司面临较大的市场风险.因此,如何在多样化电力需求和不确定因素下进行综合决策是售电公司亟需解决的关键问题.

目前,国内外学者对售电公司的购售电策略进行了大量研究.文献[4]中基于双层规划理论和时间序列最优聚类建立售电公司购售电决策模型,并通过Karush-Kuhn-Tucker (KKT)条件将双层模型转化为单层线性模型;文献[5]中在文献[4]的基础上,提出一种考虑用户自主选择的零售电价定价策略,建立以售电公司利润最大化为目标的决策模型;文献[6]中采用演化博弈理论分析电力用户对多类零售电价的选择行为,提出了一种考虑有限理性用户选择行为的售电公司运行策略;文献[7]中采用主从博弈的方法对售电公司与多元用户的关系进行建模,以售电公司效益最大化、用户综合满意度最大化为目标,构建售电公司决策模型.上述文献虽然对售电公司的优化决策进行了广泛研究,但缺乏对用户侧售电情况的考虑.产消用户的出现使得售电公司在用户侧和上级电力市场的单向能量交互变为双向.售电公司的购电和售电电价将综合影响产消用户的用能优化情况,忽略售电电价将难以实现产消用户和售电公司双方的经济最优.

在售电公司决策过程中不确定因素的考虑上,大多数文献只考虑到售电公司现货市场购电价格的不确定性.文献[8]中针对售电公司面临的现货市场购电价格的不确定性,建立了售电公司购售电决策和风险评估模型;文献[9]中考虑到中长期市场购电成本与现货市场零售风险之间的平衡问题,以综合效用最大化为目标,建立售电公司综合决策模型.不同于传统电力用户,由于产消用户的双向互动性,现货市场售电价格也会对售电公司的购售电决策产生影响.此外,由于产消用户光伏设备出力的波动性,光伏出力也是不可忽略的不确定因素.

在不确定因素的处理方法上,文献[10]中采用条件风险价值量化售电公司预期风险损失,并以风险损失最小为目标建立售电公司购售电决策模型,但场景法所得的优化结果仅为概率上的最优,在现货市场电价发生严重波动时,所得定价策略可能让售电公司收益大幅降低;文献[11]中为克服现货市场价格的不确定性,建立售电公司鲁棒双层优化模型,但应用鲁棒优化处理电价的不确定性存在决策偏保守的问题,不能满足售电公司对最低预期收益的要求,相反,由于鲁棒优化无需知道不确定变量的确切分布,更适合处理新能源出力的不确定性;信息间隙决策理论(information gap decision theory,IGDT)作为处理不确定性的一种有效方法,近年来在各研究领域得到了广泛应用^[12-13].IGDT输入售电公司的预期收益及偏差量,能够根据决策者的承受能力不断调整决策方案,可在保证系统鲁棒性的同时兼顾售电公司收益,因此其更适合处理现货市场价格的不确定性问题.上述文献采用场景法、鲁棒优化、IGDT对不同不确定性因素进行统一建模,但不同方法对不同不确定因素的适应性不同,实际则需根据不同场景选择不同的不确定性处理方法.

综上所述,本文提出了一种不确定因素下面向产消用户的售电公司购售电决策优化方法.首先,建立计及不确定性因素的售电公司购售电决策双层优化模型.下层模型考虑产消用户光伏出力的不确定性,建立产消用户鲁棒用能优化模型.上层模型针对现货市场购售电价格的不确定性,建立基于IGDT的售电公司鲁棒综合决策模型,并通过储能和中长期购售电合同的引入进一步提高售电公司的风险应对能力;其次,采用KKT条件将所建双层优化模型转化为单层模型统一求解;最后,通过仿真验证了所得售电公司决策的有效性.

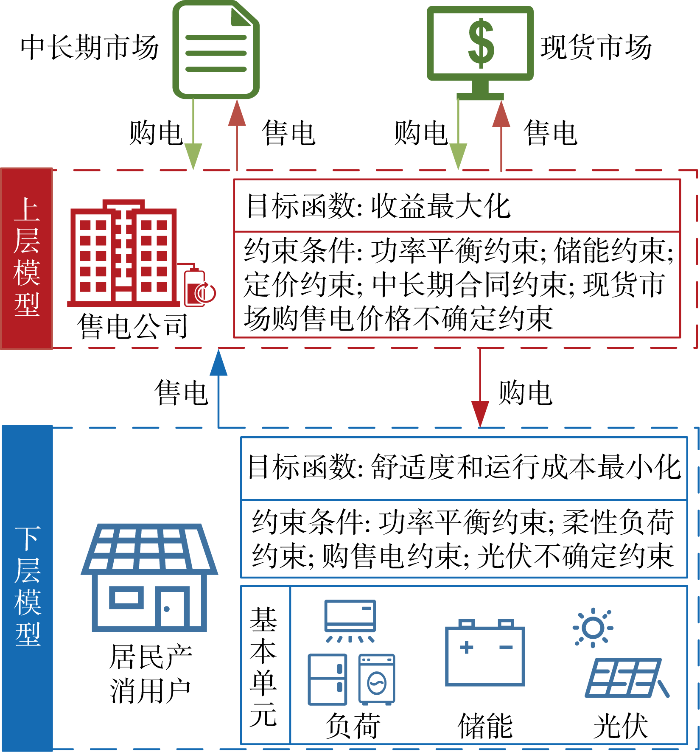
1 售电公司购售电决策双层优化模型

考虑到售电公司与产消用户属于不同的利益主体,故采用双层优化模型进行不确定因素下售电公司购售电决策,实现售电公司和产消用户双方的经济最优.产消用户通过售电公司代理参与上级市场;售电公司为实现产消用户的供需平衡,利用自身储能设备,参与中长期市场和现货市场购售电.在产消用户电价形式的设计上,由于实时电价在反映系统容量短缺和供需形势时具有独特的优势,相比其他电价形式,能够给售电公司带来更多的盈利空间,故本文采用的电价形式为实时电价.所建售电公司购售电决策双层优化模型如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 售电公司购售电决策双层优化模型

Fig.1 Bi-tier optimization model of retailers’ electricity procurement and sale decision-making

2 产消用户鲁棒优化模型

2.1 产消用户内部单元建模

2.1.1 负荷模型

产消用户的负荷由固定负荷、可转移负荷和可中断负荷构成.产消用户通过调整各时段负荷量,降低自身用电成本.产消用户负荷模型具体表达式如下:

(1)${L}^{0}\left(t\right)={L}^{\mathrm{n}\mathrm{l}}\left(t\right)+{L}_{0}^{\mathrm{i}\mathrm{l}}\left(t\right)+{L}_{0}^{\mathrm{s}\mathrm{l}}\left(t\right)$

(2)$0\le {L}^{\mathrm{i}\mathrm{l}}\left(t\right)\le {L}_{0}^{\mathrm{i}\mathrm{l}}\left(t\right)$

(3)${L}^{\mathrm{s}\mathrm{l}}\left(t\right)\ge -{L}_{0}^{\mathrm{s}\mathrm{l}}\left(t\right)$

(4)$\sum _{t\in T}{L}^{\mathrm{s}\mathrm{l}}\left(t\right)=0$

(5)$L\left(t\right)={L}^{\mathrm{n}\mathrm{l}}\left(t\right)+{L}^{\mathrm{i}\mathrm{l}}\left(t\right)+{L}_{0}^{\mathrm{s}\mathrm{l}}\left(t\right)+{L}^{\mathrm{s}\mathrm{l}}\left(t\right)$

式中:T为时段数;L⁰(t)为产消用户在t时段的原始负荷;${L}^{\mathrm{n}\mathrm{l}}\left(t\right)$为产消用户在t时段的固定负荷;${L}_{0}^{\mathrm{i}\mathrm{l}}\left(t\right)$、${L}_{0}^{\mathrm{s}\mathrm{l}}\left(t\right)$分别表示产消用户在t时段的原始可中断、可转移负荷;${L}^{\mathrm{i}\mathrm{l}}\left(t\right)$为产消用户在t时段实际可中断负荷;${L}^{\mathrm{s}\mathrm{l}}\left(t\right)$为产消用户在t时段实际负荷转移量;L(t)为产消用户在t时段的实际用电负荷.

2.1.2 储能模型

储能的加入赋予了产消用户更大的用能灵活性,促进了用户侧新能源的消纳.产消用户储能模型具体可表示为

(6)$0\le {P}^{\mathrm{c}\mathrm{h}}\left(t\right)\le {P}^{\mathrm{c}\mathrm{h}.\mathrm{m}\mathrm{a}\mathrm{x}}$

(7)$0\le {P}^{\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right)\le {P}^{\mathrm{d}\mathrm{i}\mathrm{s}.\mathrm{m}\mathrm{a}\mathrm{x}}$

(8)${S}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le S\left(t\right)\le {S}^{\mathrm{m}\mathrm{a}\mathrm{x}}$

(9)$S\left(1\right)=S\left(0\right)+{P}^{\mathrm{c}\mathrm{h}}\left(1\right){\eta }^{\mathrm{c}\mathrm{h}}-{P}^{\mathrm{d}\mathrm{i}\mathrm{s}}\left(1\right){\eta }^{\mathrm{d}\mathrm{i}\mathrm{s}}$

(10)$S\left(t\right)=S(t-1)+{P}^{\mathrm{c}\mathrm{h}}\left(t\right){\eta }^{\mathrm{c}\mathrm{h}}-{P}^{\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right){\eta }^{\mathrm{d}\mathrm{i}\mathrm{s}}$

(11)$S\left(t\right)={S}^{\mathrm{e}\mathrm{x}\mathrm{p}}, t=T$

式中:${P}^{\mathrm{c}\mathrm{h}.\mathrm{m}\mathrm{a}\mathrm{x}}$、${P}^{\mathrm{d}\mathrm{i}\mathrm{s}.\mathrm{m}\mathrm{a}\mathrm{x}}$分别为产消用户储能所允许的最大充、放电功率;${P}^{\mathrm{c}\mathrm{h}}\left(t\right)$、${P}^{\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right)$分别为产消用户在t时段储能的充、放电功率;${S}^{\mathrm{m}\mathrm{a}\mathrm{x}}$、${S}^{\mathrm{m}\mathrm{i}\mathrm{n}}$分别为产消用户储能所允许的最大、最小容量;S(t)为产消用户在t时段储能的容量;${\eta }^{\mathrm{c}\mathrm{h}}$、${\eta }^{\mathrm{d}\mathrm{i}\mathrm{s}}$分别为产消用户储能的充、放电效率;${S}^{\mathrm{e}\mathrm{x}\mathrm{p}}$为产消用户储能的预期容量.

2.1.3 光伏模型

光伏设备的存在使得传统负荷用户转变为产消用户,产消用户内部聚合的光伏主要为屋顶光伏,具体模型如下:

(12)$\begin{array}{c}0\le {P}^{\mathrm{p}\mathrm{v}}\left(t\right)\le {P}^{\mathrm{p}\mathrm{v}.\mathrm{m}\mathrm{a}\mathrm{x}}\end{array}$

式中:${P}^{\mathrm{p}\mathrm{v}}\left(t\right)$为产消用户的光伏实际出力值;${P}^{\mathrm{p}\mathrm{v}.\mathrm{m}\mathrm{a}\mathrm{x}}$为产消用户的光伏实际出力最大值.

2.2 产消用户用能优化模型

(1) 产消用户舒适度模型:

(13)$\begin{array}{c}{U}_{1}(t)=k({L}^{0}(t)-L{(t))}^{2}\end{array}$

式中:U₁(t)为产消用户在t时段的舒适度成本;k为产消用户的舒适度参数.

(2) 产消用户用电成本模型:

(14)$\begin{array}{l}{U}_{2}\left(t\right)={P}^{\mathrm{b}}\left(t\right){r}^{\mathrm{b}}\left(t\right)-{P}^{\mathrm{s}}\left(t\right){r}^{\mathrm{s}}\left(t\right)+\\ \epsilon ({P}^{\mathrm{c}\mathrm{h}}(t)+{P}^{\mathrm{d}\mathrm{i}\mathrm{s}}(t\left)\right)\end{array}$

式中:U₂(t)为产消用户在t时段的用电成本;P^b(t)、P^s(t)分别为产消用户在t时段的购、售电量;r^b(t)、r^s(t)分别为t时段售电公司向产消用户提供的购、售电价;$\epsilon $为产消用户储能的单位充放电成本.

(3) 产消用户用能优化目标函数:

(15)$\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{F}=\stackrel{T}{\sum _{t=1}}{U}_{1}\left(t\right)+{U}_{2}\left(t\right)$

(16)${P}^{\mathrm{p}\mathrm{v}}\left(t\right)+{P}^{\mathrm{b}}\left(t\right)+{P}^{\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right)=\mathrm{ }{P}^{\mathrm{s}}\left(t\right)+L\left(t\right)+{P}^{\mathrm{c}\mathrm{h}}\left(t\right)$

(17)$0\le {P}^{\mathrm{b}}\left(t\right)\le {P}^{\mathrm{b}.\mathrm{m}\mathrm{a}\mathrm{x}}$

(18)$0\le {P}^{\mathrm{s}}\left(t\right)\le {P}^{\mathrm{s}.\mathrm{m}\mathrm{a}\mathrm{x}}$

式中:F为产消用户用电总成本;${P}^{\mathrm{b}.\mathrm{m}\mathrm{a}\mathrm{x}}$、${P}^{\mathrm{s}.\mathrm{m}\mathrm{a}\mathrm{x}}$分别为产消用户允许的最大购、售电量.

2.3 计及不确定性的产消用户鲁棒用能优化模型

售电公司为了得到更稳健的决策,用户侧光伏出力的预测误差不可忽略^[11].本文采用鲁棒优化方法建立光伏出力不确定性模型.

由约束条件式(16)可知:

(19)$\begin{array}{l}{P}^{\mathrm{p}\mathrm{v}}\left(t\right)\ge {P}^{\mathrm{s}}\left(t\right)+L\left(t\right)+{P}^{\mathrm{c}\mathrm{h}}\left(t\right)-\\ {P}^{\mathrm{b}}\left(t\right)-{P}^{\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right)\end{array}$

根据鲁棒决策特点,可对式(19)进行等价简化并构造产消用户光伏出力不确定区间:

(20)$\mathrm{m}\mathrm{i}\mathrm{n}{P}^{\mathrm{p}\mathrm{v}}\left(t\right)\ge {P}^{\mathrm{s}}\left(t\right)+L\left(t\right)+\mathrm{ }{P}^{\mathrm{c}\mathrm{h}}\left(t\right)-{P}^{\mathrm{b}}\left(t\right)-{P}^{\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right)$

(21)${\overline{P}}^{\mathrm{p}\mathrm{v}}\left(t\right)-\Gamma \mathrm{\Delta }{P}^{\mathrm{p}\mathrm{v}}\left(t\right)\le {P}^{\mathrm{p}\mathrm{v}}\left(t\right):{\epsilon }_{1,t}$

(22)${\overline{P}}^{\mathrm{p}\mathrm{v}}\left(t\right)+\Gamma \mathrm{\Delta }{P}^{\mathrm{p}\mathrm{v}}\left(t\right)\ge {P}^{\mathrm{p}\mathrm{v}}\left(t\right):{\epsilon }_{2,t}$

式中:${\overline{P}}^{\mathrm{p}\mathrm{v}}\left(t\right)$为产消用户在t时段光伏出力预测值;$\Gamma $为不确定性参数,用于调整问题的鲁棒性;$\mathrm{\Delta }{P}^{\mathrm{p}\mathrm{v}}\left(t\right)$为产消用户在t时段光伏出力预测误差;${\epsilon }_{1,t}$、${\epsilon }_{2,t}$为相应拉格朗日乘子.

对$\mathrm{m}\mathrm{i}\mathrm{n}{P}^{\mathrm{p}\mathrm{v}}\left(t\right)$构建拉格朗日函数,并对不确定性变量${P}^{\mathrm{p}\mathrm{v}}\left(t\right)$应用对偶理论可得:

(23)$\underset{{\epsilon }_{1,t},{\epsilon }_{1,t}}{\mathrm{m}\mathrm{a}\mathrm{x}}{\overline{P}}^{\mathrm{p}\mathrm{v}}\left(t\right)-{\epsilon }_{1,t}\Gamma \mathrm{\Delta }{P}^{\mathrm{p}\mathrm{v}}\left(t\right)-\mathrm{ }{\epsilon }_{2,t}\Gamma \mathrm{\Delta }{P}^{\mathrm{p}\mathrm{v}}\left(t\right)$

(24)${\epsilon }_{1,t}-{\epsilon }_{2,t}=1$

(25)${\epsilon }_{1,t},{\epsilon }_{2,t}\ge 0$

故可写成如下形式:

(26)$\left.\begin{array}{l}{\overline{P}}^{\mathrm{p}\mathrm{v}}\left(t\right)-{\epsilon }_{1,t}\Gamma \mathrm{\Delta }{P}^{\mathrm{p}\mathrm{v}}\left(t\right)-{\epsilon }_{2,t}\Gamma \mathrm{\Delta }{P}^{\mathrm{p}\mathrm{v}}\left(t\right)\ge \\ {P}^{\mathrm{s}}\left(t\right)+L\left(t\right)+{P}^{\mathrm{c}\mathrm{h}}\left(t\right)-{P}^{\mathrm{b}}\left(t\right)-{P}^{\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right)\\ {\epsilon }_{1,t}-{\epsilon }_{2,t}=1, {\epsilon }_{1,t},{\epsilon }_{2,t}\ge 0\end{array}\right\}$

最后,计及光伏出力不确定性的产消用户鲁棒用能优化模型可由目标函数式(15)以及约束条件式(1)~(12)、式(17)~(18)、式(26)构成.

3 基于IGDT的售电公司鲁棒综合决策

在进行零售电价定价时,为得出具有针对性的零售电价,首先利用K-means聚类算法对产消用户的负荷曲线进行聚类分析,将售电公司服务区域内全部产消用户按照各自用电行为的不同分成I类^[14];随后,考虑到现货市场价格的不确定性,建立基于IGDT的售电公司鲁棒综合决策模型,协助售电公司进行购售电决策和零售电价定价;最后,为进一步提高售电公司的风险应对能力,在售电公司侧引入储能和中长期购售电合同.在现货市场价格波动时,售电公司通过合理决策现货市场和中长期市场的购售电量、储能的充放电量降低自身收益损失.

3.1 售电公司购售电决策模型

在满足产消用户用电需求的条件下,售电公司以自身收益最大化为目标,进行购售电决策.售电公司决策模型具体表达式如下:

(27)$\begin{array}{l}\mathrm{max}\mathrm{F}=\stackrel{T}{\sum _{t=1}}[\stackrel{I}{\sum _{i}}{N}_{i}{{P}^{\mathrm{b}}}_{i}(t\left){{r}^{\mathrm{b}}}_{i}\right(t)+\\ {P}^{\mathrm{s}\mathrm{p}.\mathrm{s}}\left(t\right){\lambda }^{\mathrm{s}\mathrm{p}.\mathrm{s}}\left(t\right)+{P}^{\mathrm{z}\mathrm{c}.\mathrm{s}}\left(t\right){p}^{\mathrm{z}\mathrm{c}.\mathrm{s}}-\\ \stackrel{I}{\sum _{i}}{N}_{i}{{P}^{\mathrm{s}}}_{i}\left(t\right){{r}^{\mathrm{s}}}_{i}\left(t\right)-{P}^{\mathrm{s}\mathrm{p}.\mathrm{b}}\left(t\right){\lambda }^{\mathrm{s}\mathrm{p}.\mathrm{b}}\left(t\right)-\\ {P}^{\mathrm{z}\mathrm{c}.\mathrm{b}}\left(t\right){p}^{\mathrm{z}\mathrm{c}.\mathrm{b}}-c({P}^{\mathrm{r}.\mathrm{c}\mathrm{h}}(t)+{P}^{\mathrm{r}.\mathrm{d}\mathrm{i}\mathrm{s}}(t\left)\right)]\end{array}$

式中:N_i为第i类产消用户的用户数量;${P}^{\mathrm{s}\mathrm{p}.\mathrm{b}}\left(t\right)$、${P}^{\mathrm{s}\mathrm{p}.\mathrm{s}}\left(t\right)$分别为t时段售电公司现货市场购售电量;${\lambda }^{\mathrm{s}\mathrm{p}.\mathrm{b}}\left(t\right)$、${\lambda }^{\mathrm{s}\mathrm{p}.\mathrm{s}}\left(t\right)$分别为t时段现货市场购、售电价;${P}^{\mathrm{z}\mathrm{c}.\mathrm{b}}\left(t\right)$、${P}^{\mathrm{z}\mathrm{c}.\mathrm{s}}\left(t\right)$分别为售电公司通过中长期合同分解到t时段的购售电量;${p}^{\mathrm{z}\mathrm{c}.\mathrm{b}}$、${p}^{\mathrm{z}\mathrm{c}.\mathrm{s}}$分别为中长期合同购、售电价;c为储能折旧系数;${P}^{\mathrm{r}.\mathrm{c}\mathrm{h}}\left(t\right)$、${P}^{\mathrm{r}.\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right)$分别为t时段售电公司储能的充、放电功率.

功率平衡约束:

(28)$\begin{array}{l}{P}^{\mathrm{s}\mathrm{p}.\mathrm{s}}+\stackrel{I}{\sum _{i}}{N}_{i}{{P}^{\mathrm{b}}}_{i}\left(t\right)+{P}^{\mathrm{r}.\mathrm{c}\mathrm{h}}\left(t\right)+{P}^{\mathrm{z}\mathrm{c}.\mathrm{s}}\left(t\right)=\\ {P}^{\mathrm{s}\mathrm{p}.\mathrm{b}}\left(t\right)+\stackrel{I}{\sum _{i}}{N}_{i}{{P}^{\mathrm{s}}}_{i}\left(t\right)+{P}^{\mathrm{r}.\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right)+{P}^{\mathrm{z}\mathrm{c}.\mathrm{b}}\left(t\right)\end{array}$

储能约束:

(29)$0\le {P}^{\mathrm{r}.\mathrm{c}\mathrm{h}}\left(t\right)\le {P}^{\mathrm{r}.\mathrm{c}\mathrm{h}.\mathrm{m}\mathrm{a}\mathrm{x}}$

(30)$0\le {P}^{\mathrm{r}.\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right)\le {P}^{\mathrm{r}.\mathrm{d}\mathrm{i}\mathrm{s}.\mathrm{m}\mathrm{a}\mathrm{x}}$

(31)${S}^{\mathrm{r}.\mathrm{m}\mathrm{i}\mathrm{n}}\le {S}^{\mathrm{r}}\left(t\right)\le {S}^{\mathrm{r}.\mathrm{m}\mathrm{a}\mathrm{x}}$

(32)${S}^{\mathrm{r}}\left(t\right)={S}^{\mathrm{r}}(t-1)+{P}^{\mathrm{r}.\mathrm{c}\mathrm{h}}\left(t\right){\eta }^{\mathrm{r}.\mathrm{c}\mathrm{h}}-{P}^{\mathrm{r}.\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right){\eta }^{\mathrm{r}.\mathrm{d}\mathrm{i}\mathrm{s}}$

(33)${S}^{\mathrm{r}}\left(t\right)={S}^{\mathrm{r}}\left(0\right), t=T$

式(29)和式(30)为售电公司储能充放电功率约束;式(31)为售电公司储能容量约束;式(32)为售电公司储能功率平衡约束;式(33)为售电公司储能初始容量约束.

定价约束:

(34)$\begin{array}{c}{{r}^{\mathrm{s}}}_{i}\left(t\right)\le {r}^{\mathrm{s}.\mathrm{m}\mathrm{a}\mathrm{x}}\left(t\right)\le {r}^{\mathrm{b}.\mathrm{m}\mathrm{i}\mathrm{n}}\left(t\right)\le {{r}^{\mathrm{b}}}_{i}\left(t\right)\end{array}$

(35)$\stackrel{T}{\sum _{t}}{{r}^{\mathrm{b}}}_{i}\left(t\right)/T\le {r}^{\mathrm{b}.\mathrm{a}\mathrm{v}\mathrm{e}}$

(36)$\stackrel{T}{\sum _{t}}{{r}^{\mathrm{s}}}_{i}\left(t\right)/T\ge {r}^{\mathrm{s}.\mathrm{a}\mathrm{v}\mathrm{e}}$

式中:${r}^{\mathrm{s}.\mathrm{m}\mathrm{a}\mathrm{x}}\left(t\right)$为t时段产消用户最高售电电价;${r}^{\mathrm{b}.\mathrm{m}\mathrm{i}\mathrm{n}}\left(t\right)$为t时段产消用户最低购电电价;${r}^{\mathrm{b}.\mathrm{a}\mathrm{v}\mathrm{e}}$、${r}^{\mathrm{s}.\mathrm{a}\mathrm{v}\mathrm{e}}$分别为产消用户购、售电价的平均值.

中长期合同约束:

(37)$\begin{array}{c}{P}^{\mathrm{z}\mathrm{c}.\mathrm{b}.\mathrm{m}\mathrm{i}\mathrm{n}}\le {P}^{\mathrm{z}\mathrm{c}.\mathrm{b}}\left(t\right)\le {P}^{\mathrm{z}\mathrm{c}.\mathrm{b}.\mathrm{m}\mathrm{a}\mathrm{x}}\end{array}$

(38)${P}^{\mathrm{z}\mathrm{c}.\mathrm{s}.\mathrm{m}\mathrm{i}\mathrm{n}}\le {P}^{\mathrm{z}\mathrm{c}.\mathrm{s}}\left(t\right)\le {P}^{\mathrm{z}\mathrm{c}.\mathrm{s}.\mathrm{m}\mathrm{a}\mathrm{x}}$

式中:P^zc.b.max、P^zc.b.min分别为分解到各时段的中长期购电合同电量上下限;P^zc.s.max、P^zc.s.min分别为分解到各时段的中长期售电合同电量上下限.

3.2 基于IGDT的售电公司购售电决策模型

IGDT是一种有效处理不确定性的非概率且非模糊的优化方法,其特点是不需要不确定参数的概率密度函数和大量历史数据.基于IGDT建立的决策模型,能根据决策者预期目标的不同,给出不同的决策方案^[15].一个典型的优化模型可表示为

(39)$\mathrm{m}\mathrm{a}\mathrm{x}B(X,d)$

$\begin{array}{c}\mathrm{s}.\mathrm{t}.H(X,d)=0\\ G(X,d)\le 0\end{array}$

式中: B(X,d) 为目标函数; H(X,d) 为等式约束; G(X,d) 为不等式约束; d为决策变量; X为售电侧不确定参数,对于确定性模型,各个不确定参数的值就等于其预测值,即$X=\overline{X}$.

在$\mathrm{I}\mathrm{G}\mathrm{D}\mathrm{T}$中, X围绕预测值上下波动,具体可描述为

(40)$\left.\begin{array}{l}X\in U(\xi,\overline{X})\\ U(\xi,X)=\left\{X:\left|\frac{X-\overline{X}}{\overline{X}}\right|\le \xi \right\}\end{array}\right\}$

式中:$ \xi $为波动系数,表征不确定性变量的波动幅度.

对于本文中售电公司所面临的现货市场购售电价格的不确定性,通过赋予不确定变量波动系数不同的权重,将多个不确定量归一为一个不确定量.设定现货市场购售电价格不确定变量对应的波动系数为ξ^sp.b、ξ^sp.s;对应波动系数权重为ω^sp.b、ω^sp.s,且有:

(41)$\left.\begin{array}{l}{\xi }^{\mathrm{s}\mathrm{p}.\mathrm{b}}={\omega }^{\mathrm{s}\mathrm{p}.\mathrm{b}}\xi \\ {\xi }^{\mathrm{s}\mathrm{p}.\mathrm{s}}={\omega }^{\mathrm{s}\mathrm{p}.\mathrm{s}}\xi \end{array}\right\}$

(42)${\omega }^{\mathrm{s}\mathrm{p}.\mathrm{b}}+{\omega }^{\mathrm{s}\mathrm{p}.\mathrm{s}}=1$

基于上述不确定变量的描述,对应不确定变量的取值如下:

(43)$\left.\begin{array}{l}{\lambda }^{\mathrm{s}\mathrm{p}.\mathrm{b}}\left(\mathrm{t}\right)\in \left[\right(1-{\xi }^{\mathrm{s}\mathrm{p}.\mathrm{b}}){\stackrel{-}{\lambda }}^{\mathrm{s}\mathrm{p}.\mathrm{b}}(t),\\ (1+{\xi }^{\mathrm{s}\mathrm{p}.\mathrm{b}}){\stackrel{-}{\lambda }}^{\mathrm{s}\mathrm{p}.\mathrm{b}}\left(t\right)]\\ {\lambda }^{\mathrm{s}\mathrm{p}.\mathrm{s}}\left(t\right)\in \left[\right(1-{\xi }^{\mathrm{s}\mathrm{p}.\mathrm{s}}){\stackrel{-}{\lambda }}^{\mathrm{s}\mathrm{p}.\mathrm{s}}(t),\\ (1+{\xi }^{\mathrm{s}\mathrm{p}.\mathrm{s}}){\stackrel{-}{\lambda }}^{\mathrm{s}\mathrm{p}.\mathrm{s}}\left(t\right)]\end{array}\right\}$

式中:${\stackrel{-}{\lambda }}^{\mathrm{s}\mathrm{p}.\mathrm{b}}\left(t\right)$、${\stackrel{-}{\lambda }}^{\mathrm{s}\mathrm{p}.\mathrm{s}}\left(t\right)$分别为t时段现货市场购、售电价预测值.

IGDT可分为机会模型、鲁棒模型两种,本文采用鲁棒模型.在该模型下,能够确保X在$\left[\right(1-\xi )\overline{X},(1+\xi )\overline{X}]$范围内波动时,所得策略的目标值都能满足售电公司最小预期收益的要求.IGDT鲁棒模型的具体表达式:

(44)$\underset{d}{\mathrm{m}\mathrm{a}\mathrm{x}}\xi $

$\begin{array}{c}\begin{array}{c}\mathrm{s}.\mathrm{t}.\xi,\delta \in \left(\mathrm{0,1}\right)\\ {B}_{C}=(1-\delta ){B}_{0}\end{array}\\ H(X,d)=0\\ \begin{array}{c}G(X,d)\le 0\\ B(X,d)\ge {B}_{C}\\ X\in U(\xi,\overline{X})\end{array}\end{array}$

式中:d为决策变量;B₀为确定性场景下售电公司的收益,其在不考虑现货市场电价不确定性,仅考虑产消用户光伏出力不确定性情况下优化确定;B_C为售电公司可接受的预期收益;$\delta $为偏差系数,表征B_C与B₀之间的偏差程度.

4 双层优化模型求解

本文构建的双层模型可通过KKT条件将下层优化模型转为上层优化模型的约束条件,进行统一求解,具体转化步骤详见附录A.上层模型的决策变量包括售电公司针对每一类产消用户的购售电价、储能充放电量、中长期和现货市场购售电量;下层模型的决策变量为各产消用户的购售电量、储能充放电量、各时段可削减负荷以及可转移负荷量.在将双层模型转化为单层模型后,模型仍为非线性优化模型,故采用非线性求解器IPOPT对其进行求解.

经过上述转化,本文不确定因素下面向产消用户的售电公司购售电决策优化方法具体流程详见附录B.

5 算例分析

5.1 参数设置

本文以电网企业的售电公司为研究对象,应用K-means聚类算法对某地区600户居民产消用户负荷曲线进行聚类分析,将产消用户分为双峰型、避峰型和平稳型3种类型.其中双峰型用户有380户,避峰型用户有40户,平稳型用户有180户;3类典型用户的负荷及光伏出力预测曲线见附录图C1^[16-18];$\mathrm{\Delta }{P}_{i}^{\mathrm{p}\mathrm{v}}\left(t\right)$取光伏出力预测值的5%;产消用户购售电电价的平均值分别为:r^b.ave=0.45元/(kW·h),r^s.ave=0.21元/(kW·h);双边合同的购售电价格分别为:p^zc.b=0.265元/(kW·h),p^zc.s=0.248元/(kW·h)^[5];现货市场购售电价见附录图C2^[5];3类典型用户和售电公司储能设备的运行参数如表1和表2所示^[19-21].

表1 3类典型用户储能设备运行参数

Tab.1 Operating parameters of energy storage equipment for three types of typical users

用户类型	S_i(0)/(kW·h)	${P}_{i}^{\mathrm{c}\mathrm{h}.\mathrm{m}\mathrm{a}\mathrm{x}}$/kW	${P}_{i}^{\mathrm{d}\mathrm{i}\mathrm{s}.\mathrm{m}\mathrm{a}\mathrm{x}}$/kW	${S}_{i}^{\mathrm{m}\mathrm{a}\mathrm{x}}$/(kW·h)	${S}_{i}^{\mathrm{m}\mathrm{i}\mathrm{n}}$/(kW·h)	${S}_{i}^{\mathrm{e}\mathrm{x}\mathrm{p}}$/(kW·h)	${\eta }_{i}^{\mathrm{c}\mathrm{h}}/{\eta }_{i}^{\mathrm{d}\mathrm{i}\mathrm{s}}$
双峰型	10	1.5	1.5	15	5	10	0.9/1.1
避峰型	10	1.5	1.5	15	5	10	0.9/1.1
平稳型	10	1.5	1.5	15	5	8	0.9/1.1

新窗口打开| 下载CSV

表2 售电公司储能设备运行参数

Tab.2 Operating parameters of energy storage equipment of electricity retailer

运行参数	取值
S^r(0)/(MW·h)	4
P^r.ch.max/MW	0.4
P^r.dis.max/MW	0.4
S^r.max/(MW·h)	6
S^r.min/(MW·h)	1
η^r.ch/η^r.dis	0.90/1.11

新窗口打开| 下载CSV

5.2 光伏鲁棒模型分析

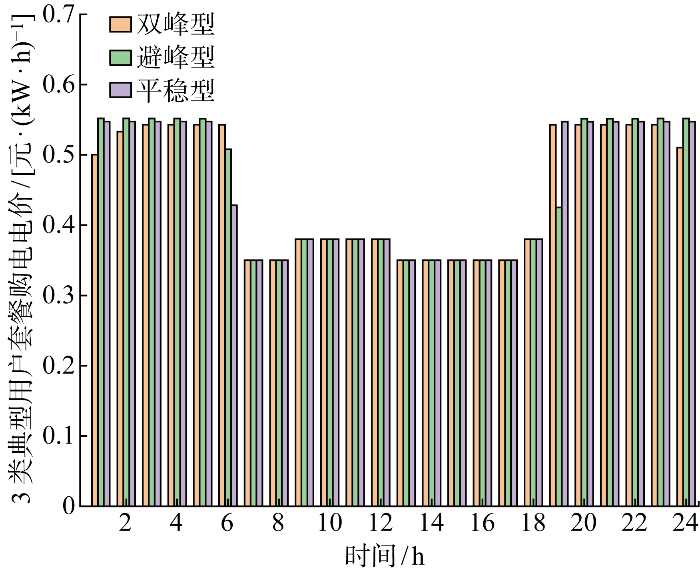
在用户侧不确定性参数Γ=1且不考虑现货市场电价不确定性时,3类典型用户的购售电价如图2、图3所示.对于双峰型用户,售电公司受到用户购电电价平均值约束的影响,在双峰型产消用户购电量较少的时段(23:00—2:00)提供较低的购电电价,进而提高双峰型用户高购电量时段的购电电价,增加自身收益;对于避峰型用户和平稳型用户,在 6:00—7:00、19:00—20:00 时段的光伏出力不足,购电量较少,购电电价较低,其余时段购电电价较高.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 3类典型产消用户的购电电价

Fig.2 Electricity purchase prices for three types of typical prosumers

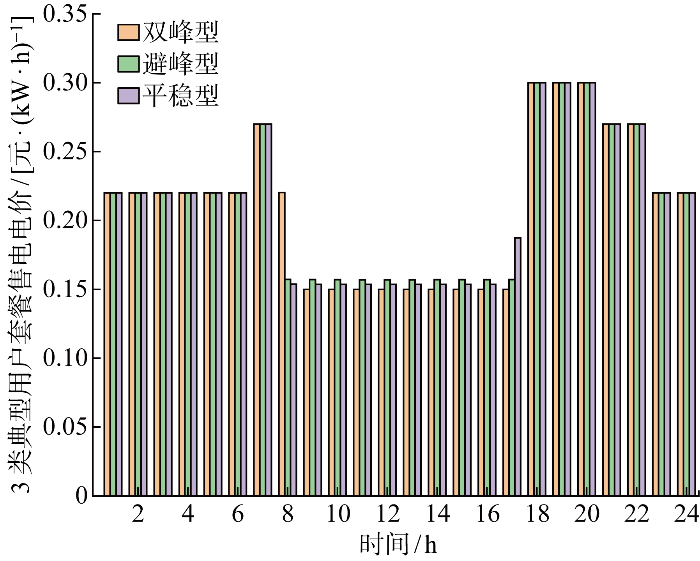
图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 3类典型产消用户的售电电价

Fig.3 Electricity selling prices for three types of typical prosumers

同理,在进行产消用户售电电价制定时,售电公司利用产消用户低售电量时段的高电价,降低产消用户在高售电量时段的售电电价.可见,售电公司能够通过合理调整产消用户不同购售电量时段的购售电价,尽可能提高自身收益.

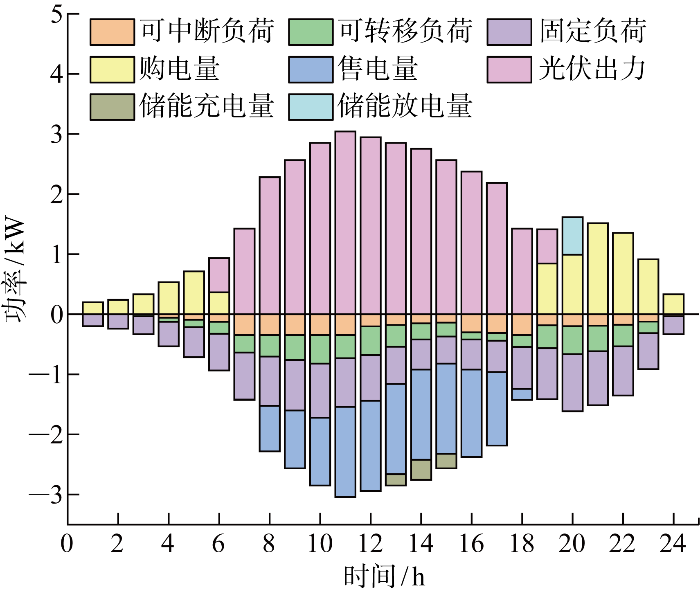
相应电价下,产消用户利用自身灵活性负荷和储能设备优化各时段购售电量.双峰型用户的自平衡优化情况如图4所示,由于午间光伏出力较大,双峰型用户将自身可转移负荷转移至午间时段,并利用储能设备将多余的光伏电量转移到晚间时段,以应对晚间时段的高电价,降低自身用电成本.避峰型和平稳型产消用户的自平衡优化情况见附录图C3、C4.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 双峰型用户自平衡优化情况

Fig.4 Auto-balancing optimization of dual-peak users

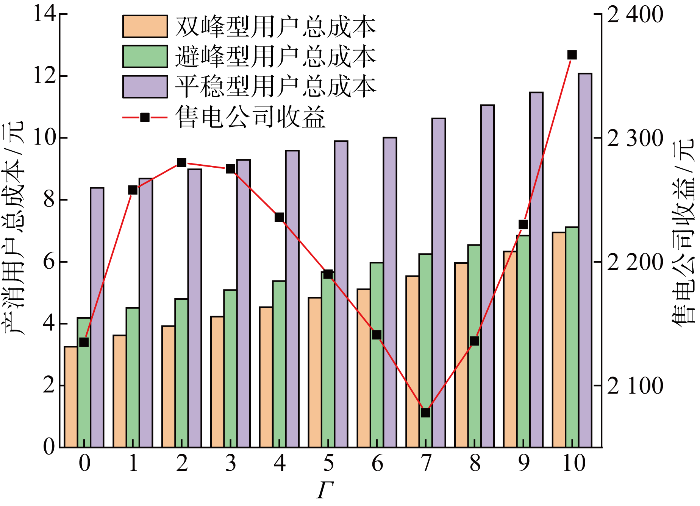
本文所建立的居民产消用户鲁棒用能优化模型能够通过不确定性参数$\Gamma $的调整,改变居民产消用户用能策略的保守性.不同保守性场景下,产消者用户用电总成本与售电公司收益变化情况如图5所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同Γ下各市场主体成本、收益情况

Fig.5 Costs and benefits of each market entity at different parameters Γ

由图5可知,对于3类典型产消用户,随着Γ的增加,产消用户盈缺/富余功率相应的越高/越低,用能优化策略的鲁棒性不断提高,总用电成本不断增加.

对于售电公司,当Γ在0~2变化时,售电公司收益有所上升.这是由于产消用户光伏出力预测偏差的增大,导致午间时段产消用户储能所存储的光伏电量减少,增加了产消用户晚间时段的购电量,使得售电公司收益增加;当Γ从2增大到7时,光伏出力预测偏差进一步增大,产消用户午间时段售电量减少,降低了售电公司在现货市场的售电量,售电公司获利减少;当Γ>7时,产消用户仅有少量售电,购电量不断增加,售电公司利用现货市场购电电价与产消用户购电电价的价差,不断增大自身收益.随着Γ的增加,可以发现,售电公司收益呈现先增加后减少再增大的趋势,售电公司可根据自身运行成本和运行风险合理选择决策方案.

5.3 IGDT鲁棒模型分析

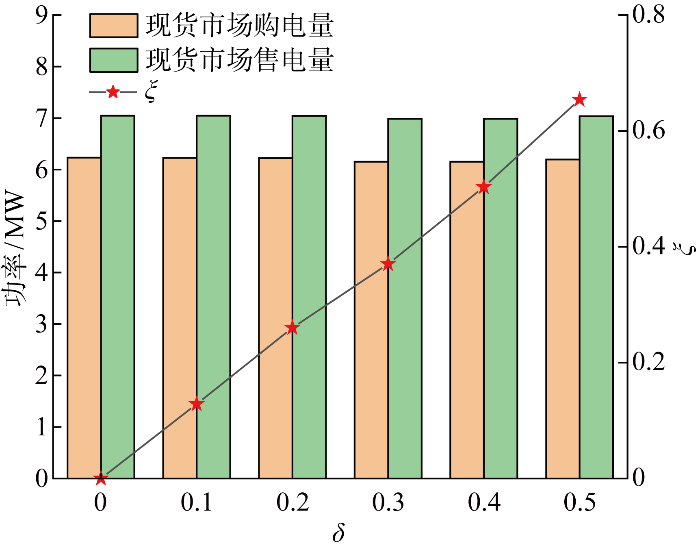
偏差系数δ是衡量售电公司预期收益与实际收益之间偏差的量,波动系数ξ表征了售电公司在现货市场购售电价格不断变化时的风险承受能力.本文以考虑光伏出力不确定情况下,Γ=1时售电公司的收益作为IGDT鲁棒模型下的基准收益B₀(下同),售电公司在不同δ下的风险承受能力及现货市场购售电变化情况如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 波动系数ξ与现货市场购售电情况分析

Fig.6 Volatility coefficient ξ and electricity purchase and sale in the spot market

由图6可知,随着δ的增大,ξ也相应增加,但售电公司的现货市场购售电量基本保持不变.说明售电公司并没有通过电价引导产消用户的购售电行为,来减少现货市场购售电量降低风险.而是仅仅通过降低自身收益,最大化现货市场购售电价的波动范围.因此,此时售电公司的风险承受能力较低.

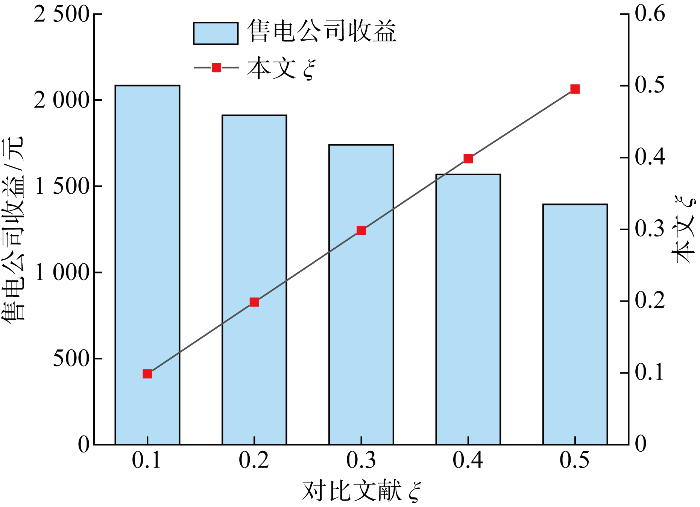
IGDT相较于鲁棒优化,鲁棒优化输入的是不确定变量的波动区间,并不能保证每次决策都能满足收益要求,而IGDT输入的是预期收益,能够在保证最低收益的同时最大化不确定变量的波动范围.由于二者同属区间优化方法,所以可采用文献[11]中所采用的鲁棒优化方法对本文IGDT鲁棒优化模型进行有效性分析.

在文献[11]鲁棒优化方法中,首先,将光伏不确定性参数Γ设为1,给定现货市场购售电价格的不确定性区间,计算出对比文献相较于本文IGDT模型的ξ;随后,采用鲁棒优化方法进行优化求解得出售电公司收益;最后,将售电公司收益代入本文所采用的IGDT鲁棒优化模型当中,优化得出本文ξ,将本文ξ与对比文献ξ进行对比.对比结果如图7所示,可以看出,本文ξ与对比文献ξ相差不大,曲线斜率近似为1,故本文所提IGDT鲁棒优化模型的有效性得证.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 IGDT鲁棒模型有效性分析

Fig.7 Validity analysis of IGDT robust model

5.4 经济性分析

鉴于现有研究中,产消用户的光伏上网电价多为固定电价,而本文所采用的产消用户售电电价形式为实时电价,为说明本文购售电价的经济性,将本文电价与产消用户购电电价为实时电价、售电电价为优化所得固定电价的情况进行对比分析.电价对比结果如图8所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 电价对比分析

Fig.8 Comparative analysis of electricity prices

由图8可以看出,本文所提电价相比产消用户固定售电电价,售电公司收益有明显的提升.在相同δ下,本文所提电价的ξ更大,说明本文电价有着更强的风险应对能力.

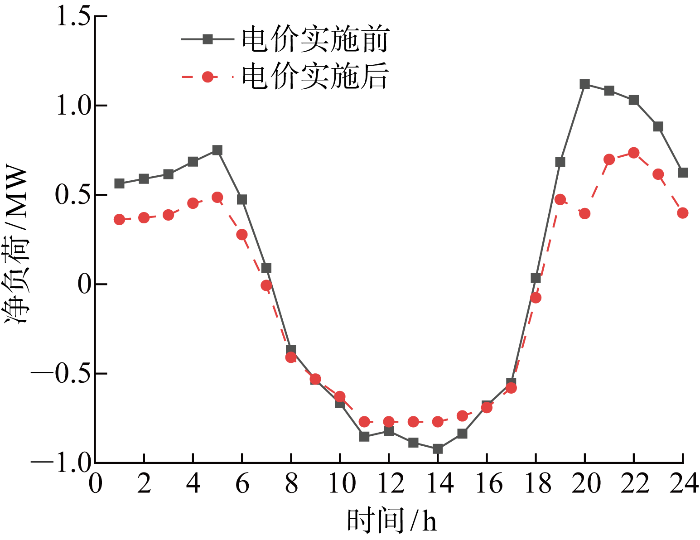
5.5 实施效果分析

购售电价实施前后产消用户净负荷曲线、各项指标如图9和表3所示.可见,本文电价分别使系统内净电量降低24.17%、峰谷差降低26.24%.产消用户购售电量的降低,表明产消用户通过储能将光伏发电量更多用于满足自身用能需求.因此,本文电价也提高了产消用户的光伏消纳率.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 产消用户净负荷曲线

Fig.9 Net load curves for prosumers

表3 电价实施前后各项指标对比

Tab.3 Comparison of various indicators before and after the implementation of electricity prices

指标	实施前	实施后	变化比例/%
系统净电量/(kW·h)	16 340.8	12 391.7	24.17
最大净负荷/kW	1 118.4	735.2	34.27
最小净负荷/kW	-921.8	-769.7	16.50
峰谷差/kW	2 040.2	1 504.9	26.24

新窗口打开| 下载CSV

5.6 不同场景下售电公司购售电决策分析

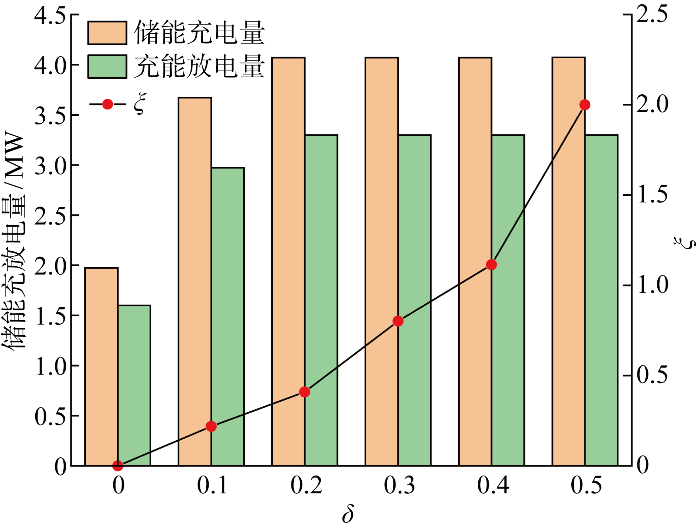
为了进一步提高售电公司对现货市场电价风险的应对能力,在售电公司侧引入储能.不同δ下,ξ以及售电公司储能充放电量的变化情况如图10所示.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 波动系数ξ与售电公司储能充放电情况

Fig.10 Volatility coefficient ξ and energy storage charging and discharging of electricity retailers

相比于图6,在相同$\delta $下,考虑储能后售电公司的$\xi $更大,可以容忍更高的现货市场购售电价预测误差.在储能充放电情况上,$\delta $在0~0.2内变化时,售电公司通过储能在购电时段放电、在售电时段充电最大化现货市场电价的波动系数,使其在相同收益损失时下,有更强的风险应对能力;$\delta $在0.2~0.4内变化时,由于储能运行约束,储能的充放电量达到极限,此时储能的充放电量不再发生变化;在$\delta $从0.4提高到0.5时,可以看出$\xi $增加到最大值,现货市场售电电价为0,现货市场购电电价变为原来的2倍.这是由于售电公司通过购售电价引导产消用户的用电行为,降低了其在现货市场的购售电量,使其通过储能基本满足了产消用户的购售电需求,因而$\xi $达到最大.$\delta $为0.4和0.5时,双峰型产消用户的自平衡优化情况见附录图C5、C6,售电公司的购售电情况见附录图C7、C8.

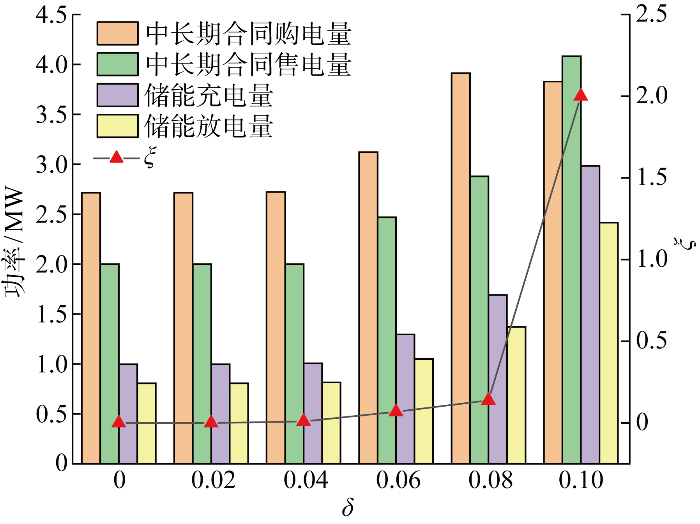
在图10的基础上进一步引入中长期购售电合同.不同$\delta $下,售电公司决策及$\xi $的变化情况如图11所示.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 波动系数ξ与售电公司中长期合同购售电情况

Fig.11 Volatility coefficient ξ and electricity purchase and sales of medium- to long-term contracts

分析图11可知,随着$\delta $的不断增加,售电公司储能的充放电量以及中长期合同购售电量不断增加,并在δ=0.1时,取到ξ最大值,如附录图C9所示,售电公司完全通过储能和中长期购售电合同满足产消用户购售电需求.相比图10售电公司侧仅有储能的情况,中长期购售电合同的引入极大提高了相同δ下ξ的数值,这主要是由于中长期购售电合同的引入增加了售电公司风险应对手段,售电公司通过储能和中长期购售电合同降低自身因现货市场价格波动造成的损失,实现风险对冲,使其在相同收益损失下具有更强的风险应对能力.

售电公司在无储能、有储能以及储能+中长期购售电合同下的基础收益情况如表4所示.结合图10和图11,可以看出储能和中长期购售电合同的引入不仅增加了售电公司的收益,还提高了售电公司的风险应对能力.

表4 不同场景下售电公司的基础收益

Tab.4 Basic income of electricity retailers in different scenarios

不同场景	售电公司基础收益/元
无储能	2 258
有储能	2 303
储能+中长期合同	2 371

新窗口打开| 下载CSV

5.7 决策方法分析

本文所得售电公司综合决策包括售电公司在中长期和日前阶段向上级市场提交的购售电计划,预测误差所引起的产消用户光伏预测出力与实际出力之间的不平衡电量需要在实时市场进行平衡.而实时市场的购售电价一般高于/低于日前现货市场的购售电价,导致售电公司最终收益降低.从这个角度出发,本文所得的综合决策更具有鲁棒性和抵御实时市场价格波动的能力.为验证上述结论,本文将在售电公司侧引入储能和中长期购售电合同,Γ=3、δ=0.04时的售电公司综合决策优化方法与确定性优化方法进行对比分析.其中,光伏出力预测误差表示以预测值为基准,实际值低于预测值的程度;对于日前现货市场电价,售电电价表示实际值低于预测值的程度;购电电价则相反.不同光伏出力及日前现货市场电价预测误差下本文优化方法和确定性优化方法的售电公司总收益如表5所示.两种优化方法下售电公司的购售电情况见附录图C10、C11.

表5 不同预测误差下优化方法的性能比较

Tab.5 Performance of optimization methods under different prediction errors

预测误差/%	确定性优化方法					本文优化方法
预测误差/%	增加收益/元	现货成本/元	平衡成本/元	日前收益/元	总收益/ 元	增加收益/元	现货成本/元	平衡成本/元	日前收益/元	总收益/ 元
-15	-503	-509	-353	2 135	2 494	-1 111	-160	-706	2 356	2 111
0	0	0	0		2 135	-555	0	-353		2 154
15	1 063	509	1 247		1 442	0	160	0		2 196
30	2 125	1 018	2 493		749	1 063	320	1 247		1 852

新窗口打开| 下载CSV

表5中,增加收益表示由于产消用户光伏出力误差售电公司所增加的收益,其中,取值为正表明产消用户光伏预测出力高于实际出力,售电公司售电量增加所获得的收益;现货成本表示由于现货市场购售电价波动给售电公司带来的成本偏差;平衡成本表示为平衡产消用户光伏出力预测误差售电公司在实时市场进行购售电的成本.

由表5可知,在预测误差小于0时,确定性优化的总收益要高于本文收益,本文优化方法存在偏保守的问题.这是由于本文优化方法在考虑了光伏出力和现货市场价格不确定性后,导致产消用户将更多的富余光伏出售给售电公司,此外现货市场购售电量的降低也减少了售电公司在现货市场获利的机会;在预测误差为0时,由于售电公司侧储能和中长期合同的引入,使得售电公司的日前收益较高,因而最终使得本文优化方法比确定性优化方法总收益高;在预测误差大于0时,由于本文优化方法考虑了产消用户光伏出力的不确定性,所以较确定性方法平衡成本更小,此外现货市场价格不确定性的考虑,也使得本文方法相较于确定性方法的现货成本更小,进而使得本文优化方法总收益更高.综上所述,可见,本文优化方法受预测误差的影响较小.

6 结论

本文面向“双碳”背景下的产消用户,考虑到产消用户光伏出力、售电公司现货市场购售电价格的不确定性,建立包含零售定价、现货市场购售电量、中长期市场购售电量以及储能充放电量等决策的售电公司综合决策双层优化模型,并通过KKT条件将双层模型转化为单层模型,进而开展不确定因素下面向产消用户的售电公司购售电策略研究.仿真结果表明:

(1) 随着不确定性参数的增加,产消用户用电总成本不断增加,售电公司收益呈现先增大后减少再增大的趋势;

(2) 本文购售电价与现有的固定用户售电电价相比,本文电价在提高售电公司经济性的同时,也增强了售电公司的风险应对能力;

(3) 购售电价的设计能够降低系统内产消用户净负荷,提高产消用户光伏消纳率;

(4) 储能和中长期购售电合同的引入,增加售电公司收益的同时,也减少了极端场景下售电公司从现货市场的购售电量,赋予了售电公司对现货市场价格风险更强的应对能力.

附录见本刊网络版(xuebao.sjtu.edu.cn/CN/10.16183/j.cnki.jsjtu.2023.530)

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

张晗, 韩冬, 刘坦, 等.

碳中和背景下分布式光伏渗透与售电市场耦合机制分析

[J]. 上海交通大学学报, 2023, 57(4): 464-472.

DOI:10.16183/j.cnki.jsjtu.2021.514 [本文引用: 1]

为评估碳中和背景下,售电商随分布式光伏的高水平渗透而面临“死亡螺旋”运营窘境的可能性,分析可能导致“死亡螺旋”的关键影响因素,采用系统动力学方法进行建模分析.首先建立销售电价等市场条件引导下的用户侧分布式光伏渗透模型,其次根据分布式光伏渗透水平与售电商盈余之间的负反馈关系,建立售电商盈余模型.算例分析从中长期视角评估了分布式光伏发电量、批发电价等因素对售电商盈余的灵敏度影响.结果表明:售电商盈余在中长期时间内呈缓慢下降趋势,若输配电量、批发电价、运维成本等多重影响因素同时发生较大变化,所形成的极端场景可能引起售电商运营的“死亡螺旋”.

ZHANG

Han

, HAN

Dong

, LIU

Tan

, et al.

Analysis of market coupling mechanism between distributed photovoltaic penetration and electricity market under background of carbon neutrality

[J]. Journal of Shanghai Jiao Tong University, 2023, 57(4): 464-472.