基于船舶-流场运动耦合的内河航道设计方法

doi:10.16183/j.cnki.jsjtu.2023.175

基于船舶-流场运动耦合的内河航道设计方法

张磊¹^,⁴, 封少雄¹^,⁴, 谭昆², 郭涛², 宋成果², 初秀民³, 苗洋^,¹^,⁴

1.武汉理工大学绿色智能江海直达船舶与邮轮游艇研究中心,武汉 430063

2.长江航道规划设计研究院,武汉 430040

3.武汉理工大学智能交通系统研究中心,武汉 430063

4.绿色智能江海直达船舶湖北省工程研究中心,武汉 430063

A Design Method of Inland River Channel Based on Hydrodynamic Response of Ship

ZHANG Lei¹^,⁴, FENG Shaoxiong¹^,⁴, TAN Kun², GUO Tao², SONG Chengguo², CHU Xiumin³, MIAO Yang^,¹^,⁴

1. Green and Smart River-Sea-Going Ship Cruise and Yacht Research Center, Wuhan University of Technology, Wuhan 430063, China

2. Changjiang Waterway Institute of Planning and Design, Wuhan 430040, China

3. Intelligent Transportation Systems Research Center, Wuhan University of Technology, Wuhan 430063, China

4. Hubei Province Engineering Research Center on Green and Smart River-Sea-Going Ship, Wuhan 430063, China

通讯作者: 苗洋,硕士生,电话(Tel.):027-86308715;E-mail:Vnisky@163.com.

责任编辑: 王一凡

收稿日期: 2023-05-6 修回日期: 2023-08-19 接受日期: 2023-09-7

基金资助:

海南省科技计划三亚崖州湾科技城联合项目(2021JJLH0035)
国家自然科学基金(52201377)
中央高校基本科研业务费专项资金(WUT:223173001)

Received: 2023-05-6 Revised: 2023-08-19 Accepted: 2023-09-7

作者简介 About authors

张磊(1988—),副研究员,主要从事计算流体力学、绿色智能船舶技术研究.

摘要

航道一般指江河及运河内可供船舶通航的水域,目前大多采用流场演化规律分析结合工程人员经验的方法开展规划设计,对通行船舶这一因素考虑不够全面.拟从河道中船舶与流场直接作用的角度提出一种内河航道设计方法.首先,基于Fluent二次开发,突破了船舶-流场相互作用的水动力响应解耦算法,对内河航段中船舶自由漂流运动进行模拟,其中,流场使用有限体积法进行求解,船舶运动控制方程通过用户自定义模块(UDF)输入并采用四阶Runge-Kutta法求解,动网格技术用于更新计算域;然后,考虑航行频率,给予通行船型不同权重,使用加权最小二乘法对漂流轨迹进行曲线拟合,得到航道边界线.选取了长江东流(从天生洲起)这一具有典型碍航结构物(弯道、分汊)航段开展航道设计验证.研究结果表明:设计的航道与现行规划航道趋势一致;同时,结合流场细节云图对船舶运动响应过程进行分析,发现设计的航道可使船舶有效规避风险急流、斜流,合理利用水流动能,提升航行安全性和经济性.

关键词： 内河; 航道设计; 船舶-流场运动耦合; 船舶; 水动力响应

Abstract

Channel is the navigable area for ships in rivers and canals. The analyses of flow details and experiences of engineers are extensively used for the design of channel nowadays, without thorough consideration of the fluid-structure interaction between flow and ships. In this paper, an inland channel design method based on ship hydrodynamic response is proposed. First of all, the secondary development is undertaken based on Fluent for the problem of ship-flow interaction, in which flow domain is simulated by using the finite volume method, and governing equations of ship are embedded through user defined function (UDF) and solved by using the fourth-order Runge-Kutta method. The dynamic mesh technique is adopted to update the changing computation domains. The hydrodynamic motion response of freely drifting ships in inland waterway is simulated, as well as trajectory. Then, the weighted least square method is used for curve fitting from the drifting trajectories of different ships, by which the channel boundaries are designed. The weight coefficients are obtained through the statistic of sailing frequencies of different ships. Dongliu route with typical navigation obstructions of curve and branch is chosen for the verification of the channel design method. It is found that the channel designed by the method with consideration of ship-flow interaction is consistent with the existing one. Besides, the analyses of flow details and ship responses indicate that ships sailing in this channel can avoid the influences of oblique flow and make use of the energy of flow, which maintains the sailing safety and economy.

Keywords： inland river; channel design; ship-flow interaction; ship; hydrodynamic response

PDF (4707KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张磊, 封少雄, 谭昆, 郭涛, 宋成果, 初秀民, 苗洋. 基于船舶-流场运动耦合的内河航道设计方法[J]. 上海交通大学学报, 2025, 59(1): 89-98 doi:10.16183/j.cnki.jsjtu.2023.175

ZHANG Lei, FENG Shaoxiong, TAN Kun, GUO Tao, SONG Chengguo, CHU Xiumin, MIAO Yang. A Design Method of Inland River Channel Based on Hydrodynamic Response of Ship[J]. Journal of Shanghai Jiaotong University, 2025, 59(1): 89-98 doi:10.16183/j.cnki.jsjtu.2023.175

我国内河众多,发展内河航运具有天然优势^[1].然而,自然河流大多弯曲且宽窄不一,同时包含绿洲和桥墩等典型碍航结构物.长江就是典型的弯曲河道,各处弯曲不一,形成了复杂的连续弯曲航道,弯曲航道水流本身具有一定纵向流速和横向流速,受到航道中不同形态碍航结构物的影响,流场规律变得更加复杂,给船舶航行带来了巨大挑战.

随着航道疏浚、径流调节等航道工程的开展,船舶通航的流场条件发生了变化,存在较多待规划航段或需要优化航道的航段.然而,当前内河航段航道规划设计研究还处在起步阶段,《航道工程设计规范》^[2]对天然河流航道选线进行了原则规定,实际操作时多依靠工程人员的综合评价方法^[3-4],同时关于航道设计的研究主要集中在采用数学方法确定航道尺度上^[5⇓-7].然而,船舶航行于复杂流场中,如何避免与碍航结构碰撞和有效利用流场动能是船舶航道设计需要考虑的关键因素,合理的航道规划能够提升船舶航行的安全性和经济性.曹民雄等^[8]使用水槽试验方法研究内河航道横流对船舶航行的影响,给出了横流对船舶横漂速度和漂距等影响的经验公式.孔宪卫^[9]对桥区水域船舶通航安全进行研究,给出了桥区航道设计建议.邹开明等^[10]采用平面二维水流数学模型与船模相结合的技术手段进行了弯道河流碍航特性研究,提出了急弯航道的优化方案.由上可知,学者多对航段局部如弯道、桥区等进行研究,据此给出航道设计建议,然而航段流场演化规律是全航段的;同时,航道设计过程中较少对船舶这一主体要素在流场中的行为进行讨论.因此,本文考虑航行船舶在航道设计中的影响,拟从船舶-流场相互作用角度进行全航段航道设计研究.

对于船舶-流场运动耦合问题研究而言,首先需要获得稳定的流场环境;对于流场的演化模拟,目前国内外已开展了大量研究,De Vriend^[11]在研究弯道水流数值模拟的基础上成功地计算了浅式弱弯曲低雷诺数弯道流,提出了计算浅水弯曲渠道的二维数学模型.李义天等^[12]采用数学计算的方法对沿河宽分布的糙率进行了研究.王平义等^[13]建立了分区三维水流流速计算模型并进行了求解.毕胜等^[14]使用二维数值模型对河道水流进了模拟,结果显示采用的模型可靠性良好.陈一帆等^[15]针对山区河流水位、流速变化剧烈的问题,提出了一套耦合计算方法,计算结果与试验吻合率较高.此外有多位研究者通过数值仿真方法对流场演化模拟进行研究^[16⇓-18].由上可知,数值模拟方法广泛应用于内河流场演化研究,能够获得可靠的河流水流运动规律.其次,进行船舶水动力响应计算.第1步为水动力系数的确定,目前船舶水动力系数常采用自由自航模试验法、约束模试验法和数值仿真计算法获得,前两者为试验方法,随着计算机性能水平的进步,考虑尺度效应、开展成本等因素,采用数值方法对船舶水动力响应开展的研究呈现增多的趋势^[19].胡伟等^[20]开发了船舶水动力数值计算程序,得到的水动力系数结果与试验吻合较好.邹璐^[21]在浅水中进行了低速斜航船舶的水动力数值预报.Kianejad等^[22]采用数值模拟与试验相结合的办法对横摇水动力系数与横摇之间的关系进行了研究.Kim等^[23]使用数值计算结合动网格方法对船舶在港口内的操纵性进行了综合分析.Song等^[24]基于数值仿真方法对有无尾翼船舶的水动力性能进行了综合研究.第2步为将上述获得水动力系数代入船舶运动控制方程的运动响应研究,多种船舶运动数学模型被提出.Abkowitz^[25]于1964年建立了整体型数学模型.随后,日本学者考虑螺旋桨力、舵力等外力之间的相互干扰,于1977年提出了分离型操纵模型(maneuvering model group,MMG)^[26].郭海鹏^[27]基于该分离思想建立了适用于双桨双舵船的船舶操纵运动模型.Yasukawa等^[28]基于MMG对大漂角下船舶舵力进行了研究.由此可以看出,目前大多通过水动力系数代入船舶运动控制方程的方法开展船舶水动力运动响应的计算,考虑船舶-流场实时运动耦合作用的研究较少.

综上所述,当前航道设计方法主要依赖规范和设计人员经验,规划设计中较少直接考虑船舶在流场中的运动行为,这将带来两方面的问题,一方面航段碍航结构物边界变化较大处不全面的流场-船舶耦合机制认知会直接影响船舶能否有效规避斜流和急流等风险,另一方面船舶对流场动能较低的利用程度将造成船舶航行经济性难达到较优的状态.此外,目前船舶水动力运动响应的研究多采用基于水动力系数的船舶运动控制方程求解方法,实时的船舶-流场耦合讨论较少.受上述分析启发,本文拟基于Fluent二次开发,突破船舶-流场运动耦合的解耦算法,对典型航段中多船型的自由漂流水动力响应运动进行模拟计算,并根据不同船型在目标航段上的航行频率,赋以运动轨迹不同权重,使用加权最小二乘法对得到的船舶航行轨迹进行拟合,得到航道边界线,从而构建一套考虑船舶-流场多物理场、多自由度运动耦合的航道设计方法.

1 基本介绍

1.1 航道设计流程

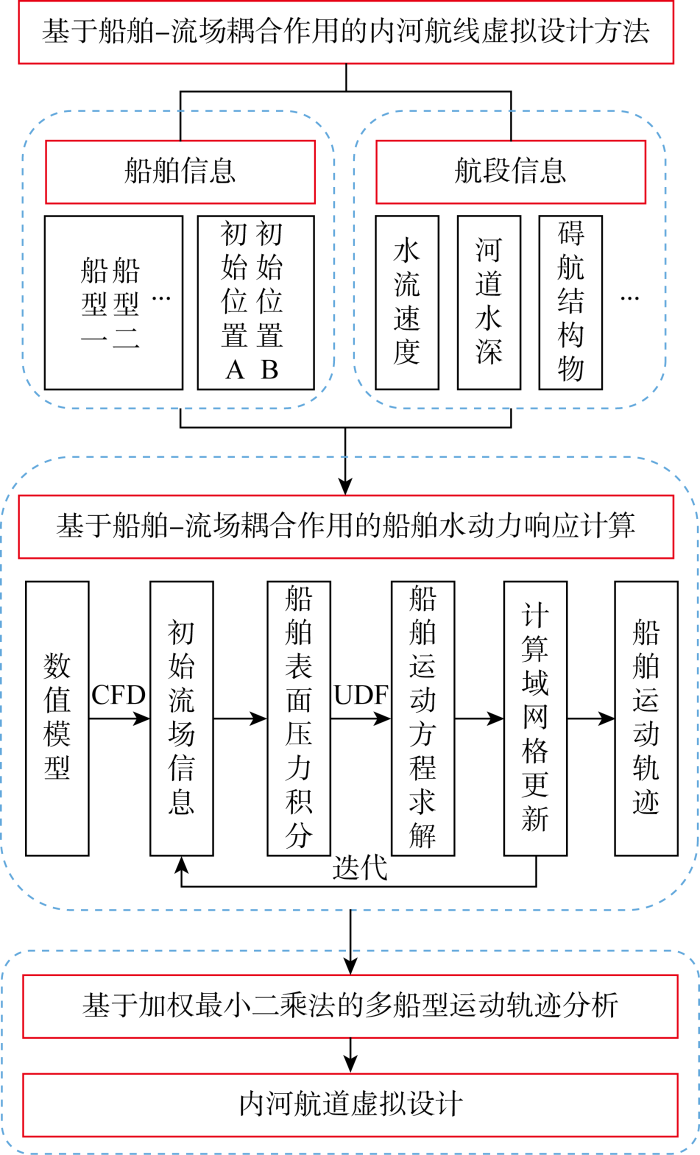
图1为本文航道设计方法的流程图.本航道设计方法从船舶-流场运动耦合的角度出发,利用船舶在流场下的水动力响应轨迹进行航道设计,主要分为3步.第1步是确定船舶和航段信息;船舶信息包括通航船型和船舶初始位置,航段信息包括入口水流速度、水深和碍航结构物等;由于桥梁限高等,内河航段对通航船型有一定限制,故所选船舶是目标航段内允许航行的典型船型;此外,为保证船舶的安全航行,需要满足吃水要求,而河道横截面常为两侧浅、中间深的形状,所以根据船舶吃水和航段水深确定船舶运动计算的两个初始限制位置A、B(分别距离河道两岸最近).第2步是船舶水动力响应计算,根据第1步确定的信息条件建立数值模型,使用计算流体力学(computational fluid dynamics,CFD)方法进行流场计算,待流场演化稳定后释放船舶,基于用户自定义函数(user defined function,UDF)将船舶运动控制方程嵌入Fluent,并采用四阶Runge-Kutta法求解,使用动网格方法更新船舶运动后的流场信息,监测包括速度、位移、船舶位置在内的船舶运动信息,得到两组船舶运动轨迹.第3步是基于加权最小二乘法的航道设计,根据各船型在目标航段的航行频率对其运动轨迹赋值,使用加权最小二乘法拟合A、B两组船舶运动轨迹曲线(即初始位置分别为A、B的轨迹集合),得到航道边界线.本设计方法具有两个特征:

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 设计流程图

Fig.1 Process of design

(1) 数值模拟得到的流场细节有助于揭示船舶-流场之间相互作用机理.

(2) 在航道设计时考虑不同通航船舶的航行频率,可提高航道整体利用率.

1.2 流体控制方程

对于船舶在内河中的航行运动问题,可将水视为不可压缩黏性流体,其质量和动量守恒表达式为

(1)

\frac{\partial v_{x}}{\partial x} + \frac{\partial v_{y}}{\partial y} + \frac{\partial v_{z}}{\partial z} = 0

(2)

\frac{\partial (ρ v_{x})}{\partial t} + \nabla \cdot (ρ v_{x} U) = - \frac{\partial p}{\partial x} + S_{x} + \nabla \cdot (μ \nabla v_{x})

(3)

\frac{\partial (ρ v_{y})}{\partial t} + \nabla \cdot (ρ v_{y} U) = - \frac{\partial p}{\partial y} + S_{y} + \nabla \cdot (μ \nabla v_{y})

(4)

\frac{\partial (ρ v_{z})}{\partial t} + \nabla \cdot (ρ v_{z} U) = - \frac{\partial p}{\partial z} + S_{z} + \nabla \cdot (μ \nabla v_{z})

式中:v为流体速度;U表示流域内流体的速度矢量,U= $[v_{x} v_{y} v_{z}]^{T}$ ;ρ为流体密度;p为作用在微元体上的压力;S为广义源项;μ为流体动力黏度.

1.3 船舶运动控制方程

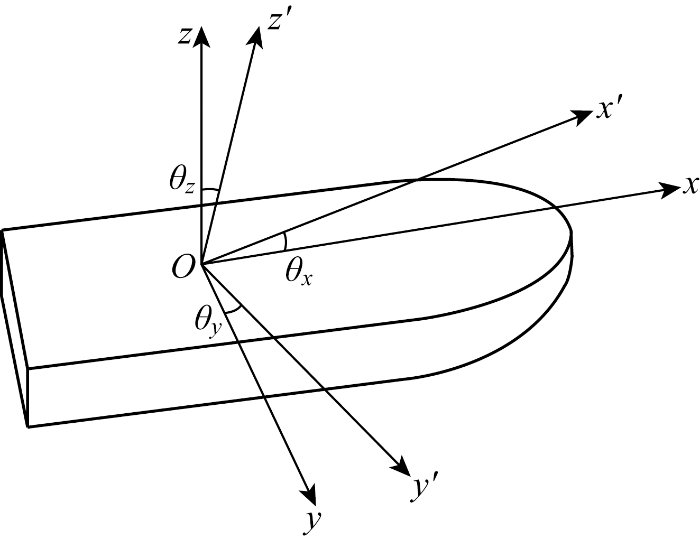
建立船舶附连坐标系O-x'y'z'和大地固定坐标系O-xyz如图2所示.船舶的线位移运动为随船运动坐标系相对固定坐标系的移动,定义为x,y和z,船舶的角位移为船舶坐标轴绕相应固定坐标系xyz轴的转角θx,θy,θz.基于附连坐标系构建船舶六自由度运动控制方程:

(5)

\begin{matrix} m ({\overset{\cdot}{v}}_{x'} + ω_{y'} v_{z'} - ω_{z'} v_{y'}) = F_{x'} \end{matrix}

(6)

m ({\overset{\cdot}{v}}_{y'} + ω_{z'} v_{x'} - ω_{x'} v_{z'}) = {F_{y}}^{'}

(7)

m ({\overset{\cdot}{v}}_{z'} + ω_{x'} v_{y'} - ω_{y'} v_{x'}) = F_{z'}

(8)

I_{x'} {\overset{\cdot}{ω}}_{x'} + (I_{z'} - I_{y'}) ω_{y'} ω_{z'} = M_{x'}

(9)

I_{y'} {\overset{\cdot}{ω}}_{y'} + (I_{x'} - I_{z'}) ω_{z'} ω_{x'} = M_{y'}

(10)

I_{z'} {\overset{\cdot}{ω}}_{z'} + (I_{y'} - I_{x'}) ω_{x'} ω_{y'} = M_{z'}

式中:m为船舶排水量;I为转动惯量;ω为角速度;F和M分别表示作用在船舶上的外力和外力矩.式(5)~(7)和式(8)~(10)分别表示船舶的平移和转动运动.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 坐标系

Fig.2 Coordinate system

由于拟对航段进行空间离散以及六自由度运动求解,所以计算资源需求极大.受此制约,同时也根据航道边界线主要限制船舶纵向和横向上的位置这一特点,拟作简化处理,将关注点放在船舶的横移、纵移和艏摇上,在水深方向上则采用预先考虑的处理方式,即在航道设计的第一步中对船舶吃水和河道水深条件进行调研和考量.基于此,本文开展二维数值模拟,主要关注船舶的横移、纵移和艏摇,拟采用二维数值模拟的方法进行研究,六自由度运动方程可简化为

(11)

m ({\overset{\cdot}{v}}_{x'} - ω_{z'} v_{y'}) = F_{H x'}

(12)

m ({\overset{\cdot}{v}}_{y'} + ω_{z'} v_{x'}) = F_{H y'}

(13)

I_{z'} {\overset{\cdot}{ω}}_{z'} = M_{H z'}

式中:F_H,M_H分别代表船舶受到的水动力和力矩.采用四阶Runge-Kutta法对上述运动控制方程进行求解,求解船舶横移、纵移和艏摇等响应运动,获得船速、位置等船舶运动参数.

1.4 流体-船舶运动耦合计算流程

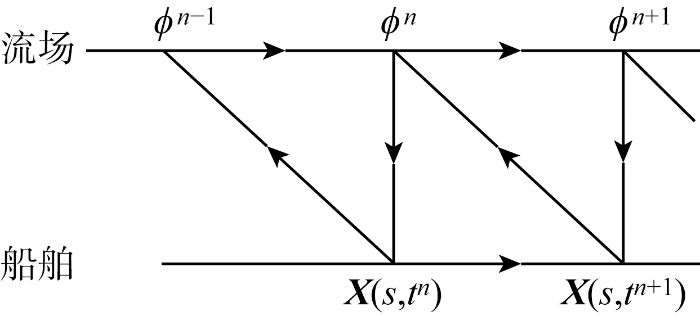
图3给出了流体-船舶运动耦合的计算流程^[29-30],ϕ为表示任意流体参量的通用变量.从时间步tⁿ到tⁿ⁺¹的具体计算流程叙述如下.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 船舶-流场耦合作用计算流程

Fig.3 Calculation process of ship-flow interaction

(1) 时间步tⁿ已知参量 $u^{f} = u^{f, n}$ ; 位置矢量X(s, t)=X(s, tⁿ); ∂X(s, t)/∂t=∂X(s, tⁿ)/∂t.

(2) 时间步tⁿ到tⁿ⁺¹:① 求解流体动力学方程积分获得作用在船舶上的流体力p^f,ⁿ;② 求解结构动力学方程获得tⁿ⁺¹时刻船舶的位置矢量X(s, tⁿ⁺¹);③ 根据船舶位置矢量采用动网格技术更新流体计算域.

2 船舶-流场运动耦合算法验证

2.1 流场演化可靠性验证

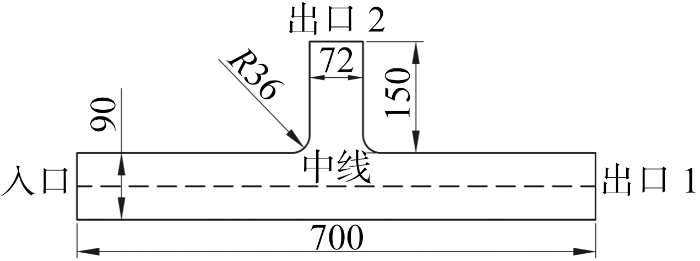
选取分汊典型特征航段^[16]对流场计算的可靠性进行验证.图4为T形分汊航段示意图.航段有一个来流段和两个去流段,干流宽90 m、长700 m,分流宽72 m、长150 m,分流区与干流之间角度为90°.边界条件为:速度入口0.858 m/s,主河道速度出口0.585 m/s,分流段速度出口0.273 m/s.选取标准k-ε模型(k为湍流动能;ε为湍流耗散率)配以标准壁面函数模拟流场中的湍流,使用SIMPLEC算法进行流场演化数值求解.图5 是T形分汊航段中轴线上合速度大小沿程的变化曲线.图中:L为中线上各位置与入口间的距离.验证结果表明,计算流速值与文献实验值、计算值都吻合较好,上、下游边界范围可以完整展现分流区水流变化,所用流场计算模型可较好地反映分流区水流运动,计算结果可靠.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 T形弯航段(m)

Fig.4 T-shaped channel (m)

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 T形航段验证算例结果对比

Fig.5 Comparison of flow evolution results of T-shaped channel

2.2 船舶水动力运动响应验证

内河弯曲航段较多,为验证本文船舶水动力响应运动模拟方法的可靠性,选择具有代表性的直角弯,验证船型选用航标船003,船型介绍如表1所示.流场进出口边界条件选择速度入口、压力出口,弯道边界及船体设为无滑移壁面条件;船舶运动导致的计算域变化,采用弹簧光顺和网格重构相结合的网格更新方法.仿真计算中网格尺寸、时间步长是关键的影响因素,考虑模拟时长较大,过小的时间步长将导致计算步数剧增,为保证计算效率,时间步长

表1 船舶主尺度

Tab.1 Main dimensions of ships

船型	总长/m	船宽/m	设计吃水/m
航标船003	25.9	4.6	1.0
重轮J3009	105.0	16.0	3.7
长航货轮001	130.0	16.2	3.6

新窗口打开| 下载CSV

统一取为0.1 s,选择了3种不同尺寸的网格(最小网格尺寸l分别为 0.01,0.05,0.5 m,网格数量分别为77万,25万,5万)进行网格无关性分析,图6为3种不同网格大小的网格划分示意图.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 网格划分示意图

Fig.6 Grid partition of fluid domain

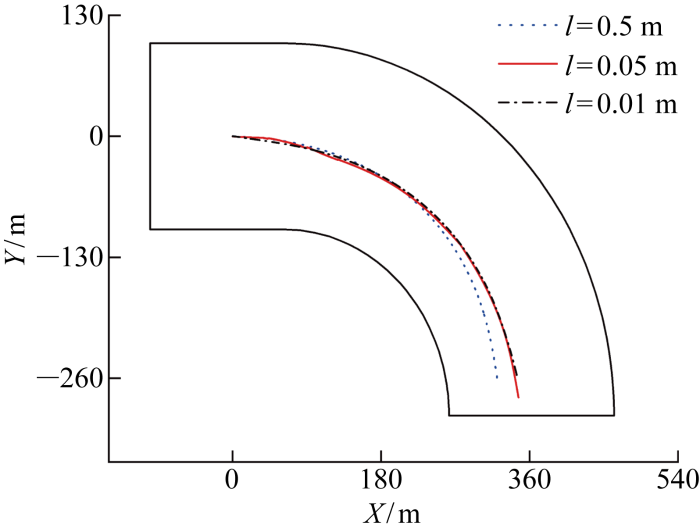
对于内河航段船舶航行运动仿真,保证航行轨迹收敛性是关键,因此将船舶运动轨迹作为判断指标.图7为某一相同工况船舶航行轨迹图.图中:X,Y分别表示船舶在x,y方向上的位移.可以看出,当最小网格尺寸选择l=0.05 m时,船舶运动轨迹与l=0.01 m相差较小,认为计算结果已收敛,不影响船舶运动轨迹结果,即仿真结果满足计算的工程精度要求,在接下来的仿真计算中采用相同设置.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 船舶水动力响应轨迹

Fig.7 Trajectories of ship

3 内河航道设计研究

3.1 计算模型介绍

航道设置水面航行标志(如航标)主要通过横向和纵向位置决定,此外水深也是重要的影响因素.考虑到基于航段复杂流场中船舶运动轨迹这一航道设计目标,船舶-流场耦合数值仿真的计算资源要求较高,设计中预先对航道水深和船舶吃水进行调研并约束.基于以上考虑,计算模型得到简化,拟采用二维数值模型对提出的航道设计方法进行验证.经过长江航道工程整治,武汉至安庆段水道通航水深已达6 m,选择其中包含弯道和分汊等典型碍航结构物的东流段(从天生洲起)进行航道设计,航段总长约30 km,图8所示为河道卫星平面图.根据目标航段的通航船型限制,选取了具有代表性的3种船型进行研究,目标船舶型号及其主尺度参数详见表1,其中,重轮J3009和长航货轮001为货轮.图9为船舶几何模型.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 东流航段

Fig.8 Dongliu route

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 船舶几何模型

Fig.9 Geometric model of ships

3.2 船舶运动响应计算

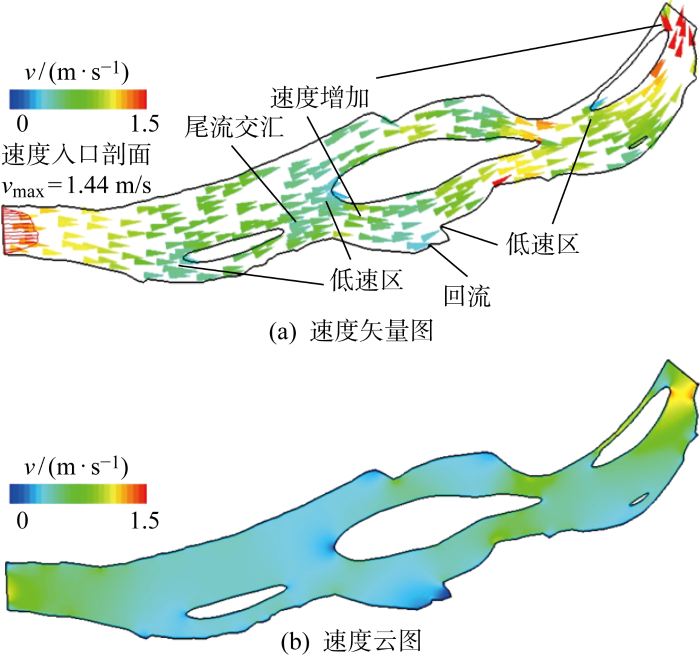
首先采用验证的方法进行流场计算,速度入口取自航段中水期流场,最大流速v_max可达1.44 m/s.图10展示了东流航段流场演化情况.图10(a)为速度矢量图,其中箭头表示速度方向,速度大小由颜色表征.此外,为更好地展示速度大小的分布情况,图10(b)给出了速度云图,从蓝色到红色速度大小依次增大.受航段前、中、后3处分汊碍航结构物和两侧河岸走势影响,航段流速变化较大.第1个分汊处,水流受到绿洲碍航结构物的作用,形成向上和向下的两股分流,碍航结构物迎流面速度急剧降低,形成低速高压区,由于上行通道过流断面变化较小,而下行过流断面增加,且上行通道位于来流主流区间,所以上行通道水流速度较下行通道水流速度大,同时,总体过流断面增大,使得上、下行通道流速均小于航段入口速度;第2个分汊处,第1分汊上、下行通道尾流形成交汇,并在短距离范围内遇到第2绿洲阻碍再次形成分流,碍航结构物迎流面流速同样降低,且该汇合流位置靠近下行通道,所以存在流速增大的区域,随后,航段下侧有一处较大的凸区域,水流通过该处时形成回流现象,流速明显下降;第3个分汊处,分汊前航段横断面较窄,不具备通航条件,这里不做分析,此外,绿洲下行通道河道具有较大的曲率,发生了流向的急剧偏转,航段出口处过水断面较入口处窄,根据流量守恒的原理,出口速度明显增大,在分汊后过流断面增大,流速有明显的降低.由上述分析可知,受河道走势和碍航结构物影响,水流速度方向和大小多变,存在交汇流和回流,给船舶安全航行带来了巨大挑战.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 东流航段流场演化

Fig.10 Flow of Dongliu route

得到稳定流场演化后,进行船舶的水动力响应计算.将3艘不同型号船舶置于航段起始位置,不对其施加任何主动力,使其在流场作用力下自由航行,记录船舶运动过程中的速度、位移等信息.为得到航道的两条边界线,对每一型船舶选取两个不同的初始位置(记为A、B位置),主要由水深、船舶吃水、水面上桥梁或其他通航约束条件决定,这两个位置是河道宽度方向上允许船舶航行的极限位置,由水深等限制条件决定.综上所述,3种船型各两个初始位置,共计6个船舶自由漂流模拟工况.

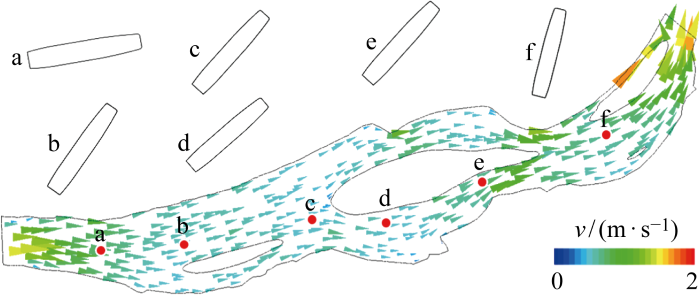
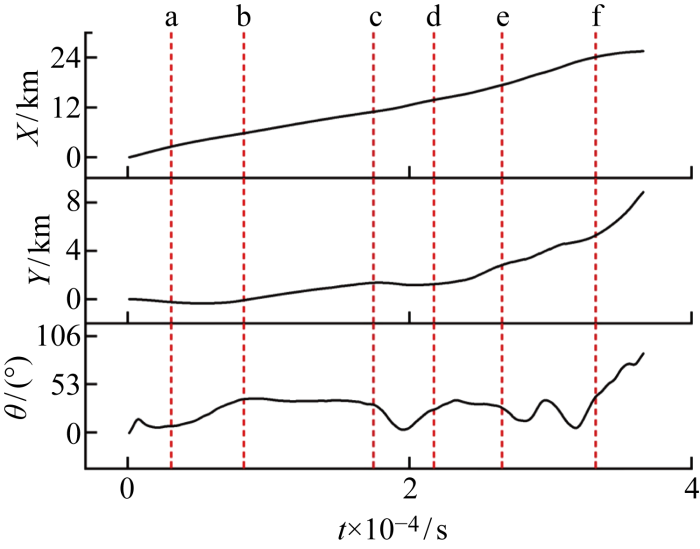
以航标船003初始位于A位置这一工况为例进行船舶-流场相互作用分析.图11为船舶水动力响应运动过程,为清晰展示船舶运动信息,使用红色圆点a~f表示船舶此刻位置,左上角放大图为对应位置处船舶姿态图.图12为其在运动过程中的速度和位移时历曲线.结合图11和图12,对船舶运动的分析如下:船舶开始时航向为0°,船尾在向下流场的作用下,受到逆时针转矩,船首向上偏转,此后向下流场力又作用于船首,船首角度逐渐减小,同时观察横向位移可以看出,船舶具有向下的偏移,与该段河岸向下的走势即流场演化规律一致;a点后,船舶相对于绿洲处于较上的位置,一方面受上行通道分流的影响,一方面根据伯努利原理可知,绿洲迎流面速度剧降处形成的高压区会将船舶推离,自动避开绿洲,船舶选择航线进入了上行通道,此后在向上分流的作用下船首角度逐步增大,到b位置航向角达到一个较大值;由左上角小图可知,船舶沿着碍航结构物上侧航行至c位置时艏摇角度较大,若继续保持此航向船舶将撞上绿洲,在流场作用下,船舶向下行通道转向,艏摇减小,避开第2个绿洲,随后受到通道内流场向上走势的影响,艏向角逐渐增大;c点至d点,受第1绿洲交汇尾流和第2个绿洲的分流作用,船舶移动主要体现在纵向上,横向基本保持水平,船舶航向角则呈现先剧减至水平然后随流场增加的趋势;d点至e点,受绿洲边界向上走势影响,艏摇角相应增大,期间船舶航向与流场一致,可充分利用水流动能运动,需要注意的是,d点后受到回流区的影响,船舶航向角快速增加,这也为开展航道设计需避开回流区的原则提供了科学依据,即船舶会在回流转矩作用下“打横”,船舶通航安全性受到挑战;e点至f点,船舶受第2绿洲后部地形角度减小和河段下边界向上流场的影响,航向角呈现先减小后变大的趋势,随后船舶运动至分汊口处,船首先受到上侧分汊来流的影响,使得航向角变小,船舶逐渐通过分汊,船尾受分汊上侧来流作用,导致航向角增大;f点后,船舶航向角继续增大,在流场的作用下,船舶充分利用流场动能,沿绿洲继续航行至目标航段末端.采取相同方法对另外5个工况进行计算,通过分析也发现了上述相似的过程,此处不再赘述,计算后共得到6条船舶运动轨迹曲线.从上述分析可以看出,船舶漂流运动与流场演化息息相关,总体而言:

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 东流航段无动力船舶水动力响应运动过程

Fig.11 Process of unpowered ship in Dongliu route

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 东流航段无动力船舶运动位移时历曲线

Fig.12 Displacement of unpowered ship in Dongliu route

(1) 船舶在流场作用下自主选择了航线,并成功避开绿洲碍航结构物以及由于河岸地形形成的回流区域,船舶通航的安全性可以得到保证.

(2) 船舶-流场耦合作用力下的船舶自由漂流运动基本沿着流场演化方向,可充分利用流场动能,有利于减少船舶能耗,提高营运经济性.

3.3 基于加权最小二乘法的航道设计

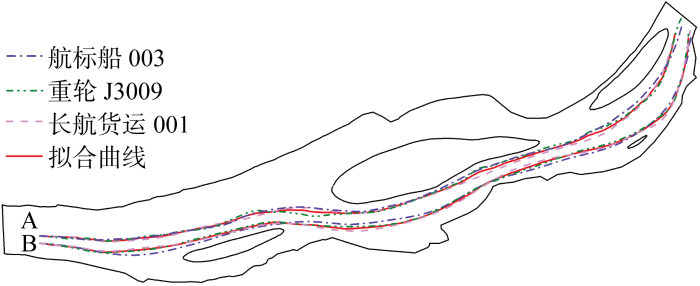
最小二乘法是一种数学优化技术,旨在通过将样本值与实际目标值之间的误差平方和最小化,从而寻找最佳未知的数据,可用于曲线拟合.长江上每一型船舶的日航次有所不同,本文提出的航道设计方法综合考虑每一型船舶对航道的使用比例,即考虑船舶的航行频率,根据航行频率对其航行轨迹赋以不同权重,从而保证航道整体适用性和利用率.使用最小二乘法将3.2节计算得到的6条轨迹曲线依据不同初始位置分组后进行加权拟合.长江上多航行大吃水的货轮,小型船舶如航标船003航行频率较低,对其航行轨迹赋以较小权重可提高航道的可靠性及利用率,选取的3条代表性船型在长江上的航行频率比为1∶4.5∶4.5.图13为拟合轨迹拟合示意图,彩色虚线为多船型不同初始位置计算得到的轨迹曲线,红色实线为使用加权最小二乘法拟合得到的曲线,A、B分别表示船舶初始位置为A、B.可以看出:

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 轨迹曲线拟合

Fig.13 Fitting curves

(1) 在流场作用下,3种不同船型船舶均安全绕航绿洲等碍航结构物,航行轨迹与航段边界保持一定距离,实现了全航段的安全航行,考虑到一般近岸处水深较浅,远离航段边界可在降低碰撞风险的同时满足船舶吃水条件,提高船舶航行的安全性.

(2) 两组不同初始位置下多船型船舶航行轨迹趋势一致,即选择了同样的通航路线,结合3.2中对流场演化的分析可以发现,船舶所选航行路线位于河道主流区域,较大的流场动能可以降低能耗,提高船舶燃油经济性.

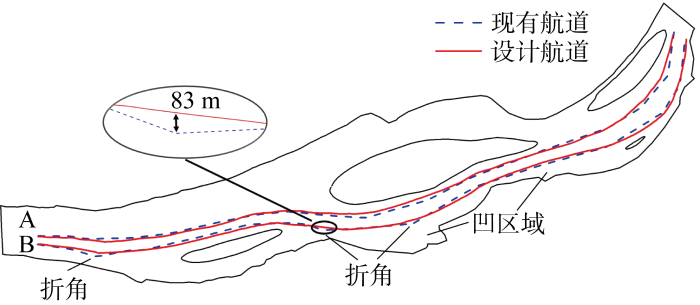
为说明航道设计方法可行性,将设计航道与现有航道进行对比.图14为东流航段航道设计对比图,蓝色虚线为现有规划设计的航道,红色实线为本文方法设计的航道.通过航道边界线对比可以看出:

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 航道对比

Fig.14 Comparison of channels

(1) 设计航道与现有航道趋势基本一致,证明了基于流场-船舶相互作用的航道设计方法的可行性,此外,二者均选择了第1个绿洲上侧通道、第2个绿洲下侧通道的主流区域作为通航路线,通过分析图11可以看出,这两处通道水流速度更大,则船舶可利用的流场动能更大.因此,航行于该航道区域内的船舶可利用流场助航,燃油消耗降低,航行经济性更加优良.

(2) 在航道宽度特征方面,相较于顺直和狭窄河段,航道在绿洲导致的分汊区域附近宽度较大.通过分析流场演化和船舶运动过程可知,较顺直航道或狭窄河段,分汊处流场将发生变化,在此复杂流场-船舶耦合水动力作用下,船舶航向角会发生较大变化,往往需要操舵以保持航向.因此,在该处为船舶操纵时带来的横移预留一定的空间,保证船舶与岸壁的距离,可以降低船舶撞岸风险.

(3) 设计航道与现有航道在细节处存在一定差别,主要体现在两个方面.一方面,相较于现有航道在分汊弯道处具有明显的折角,充分考虑船舶-流场相互作用的设计航道边界呈现光滑过渡的形态,受运动响应缓慢(由于船舶惯性大)这一特征影响,后者对于船舶操舵的时机和舵角大小判断更有参考价值;另一方面,设计航道整体上较现有航道更远离河岸走势出现凹的地方,在这些位置受回流的影响,船舶容易发生航向角的偏转,本设计安全性较优.需要指出的是,由于所选航段长约30 km,设计航道与现有航道边界在上述位置相差可达几十米.

4 结语

本研究突破了船舶-流场耦合作用的数值求解关键技术,并结合加权最小二乘法创新性地提出了基于船舶水动力响应的内河航道设计方法,以东流段为例进行了验证.研究发现,采用该方法设计的航道与现有航道规划吻合良好,说明了设计方法的可行性.分析流场演化和船舶运动过程发现,流场作用下自由漂流船舶具有避开碍航结构物的特点,利用此规律设计的航道可保证船舶航行的安全性;同时,船舶沿着速度较大的流场运动,保证了其对流场动能的利用率,有助于提高船舶燃油经济性;使用该方法设计的航道在安全性(避开碍航结构物)和经济性(流场助航)方面,较现有基于工程经验和流场演化分析规划的航道具有一定优势.本文还对实时的流场-船舶多物理场多自由度运动(船舶横移、纵移、首摇)耦合机理进行了揭示,该耦合机理可对现有设计原则(如分汊航道处设置较大的宽度及要远离回流区等)的科学性给予解释.此外,考虑航段船舶通行频次,提出的基于加权最小二乘法的航道设计方法对于提高航道的整体适用性和利用率具有重要意义.相关成果可为航道的科学设计提供理论和数据支撑,促进内河航运的高质量发展.

受制于计算资源,本文研究选择的船型、航段和水文工况较少,未来拟开展多船型、多航段和多水文工况的水动力响应计算;同时,本文虽然采用的是二维数模,但相关方法可直接拓展至三维数模的研究.为提高基于船舶水动力响应的航道设计方法的实用性,考虑航道生态、通航气象等因素的航道规划综合设计将是下一步的工作方向.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘怀汉, 杨胜发, 曹民雄.

长江黄金航道整治技术研究构想与展望

[J]. 工程科学与技术, 2017, 49(2): 17-27.