桩基础广泛应用于风电铁塔、铁路桥梁和海洋平台等工程项目中[1 ⇓ -3 ] .在风、波浪等随机荷载作用下,桩身除承受上部结构传递的水平荷载外,还可能承受由偏心荷载产生的扭矩[4 -5 ] .目前常规桩土相互作用研究多是基于Winkler弹性地基梁模型[6 ⇓ -8 ] ,鲜有考虑土体变形连续性对桩基承载特性的影响.同时,对于联合受荷桩,在多向荷载共同作用下,桩身响应之间的相互影响也是不可忽视的重要影响因素[9 ] .
Winkler模型[10 ] 将地基视为由若干互相独立的弹簧组成的弹性体,用弹性系数描述土体的变形特性,具有概念明确、计算简单的特点,但该理论忽略了土体变形连续性,不能很好地反映实际情况.Novak[11 ] 应用平面应变理论假设桩周土为一组无限薄的土层,解决了Winkler地基模型无法考虑土体连续性的问题,但不能表征土体位移和应力沿纵向的梯度变化.因此,Novak等[12 ] 将桩周土视为三维连续介质,通过偏微分方程描述土体各物理量沿纵向的变化规律,并推导了均质土中单桩水平振动解析解,然而该方法夸大了地基的深度和扩散能力.针对上述3种模型的缺陷,Pasternak模型[13 ] 引入了土体反力系数和土体切变模量这两个独立的地基参数,在考虑土体变形连续性的同时又满足了力学概念清晰、计算简便的工程需求.Fwa等[14 ] 统计了36组分别来自Pasternak地基模型和其他模型计算结果的平均误差,分析结果表明Pasternak模型计算误差最小.戴自航等[15 ] 、朱彦鹏等[16 ] 、江杰等[17 ] 、张玲等[18 ] 分别基于Pasternak地基模型研究了单桩水平承载特性,通过试验和有限元模拟验证了Pasternak模型应用于桩土相互作用研究中的合理性.
值得注意的是,上述研究多局限于水平荷载或扭矩的单一作用,实际工程中桩顶往往同时作用有水平力和扭矩,常规的桩基设计方法将不同形式的荷载简单叠加,不考虑多向荷载对桩身响应的影响,最终导致设计方案不合理,甚至造成安全事故[18 ] .为此,Hu等[19 ] 通过离心模型试验研究了水平荷载和扭矩共同作用下桩基的内力和位移,结果表明,水平荷载的存在会对桩身抗扭承载能力有一定的影响.孔令刚等[20 ] 利用经验性耦合因子量化了土体侧阻力对桩基抗扭承载力的耦合效应.Georgiadis等[21 ] 结合上限分析和有限元方法探讨了扭矩对单桩极限侧阻力的影响,并给出了扭矩作用下单桩侧向极限承载力系数.然而,当前已有联合受荷桩的研究多限于静力组合,实际工程中,风、水流等外荷载会使结构产生不容忽视的动力效应[22 ] ,且施工或使用过程中的偏心荷载会使桩身受扭,在处理这种复杂受荷情况时不应简化为单一静力或动力问题.
鉴于此,本文基于Pasternak地基模型,提出一种可考虑土体剪切效应和多向荷载耦合作用的 H (t )-T 受荷桩内力和位移计算数值解,并与相关理论解、模型试验以及有限元模拟结果进行对比验证.在此基础上通过参数分析探究土体剪切效应、桩土刚度比等相关参数对H (t )-T 受荷桩内力和位移的影响规律.
1 简化分析模型及基本假定
本文将桩-土相互作用问题适当简化,并引入以下基本假定:
(1) 桩身视为均质各向同性的线弹性连续介质,等效为圆形等截面Euler-Bernoulli梁,在外荷载作用下只发生小变形,忽略竖向位移,变形过程中保持桩-土位移协调.
(2) 由于自然界中的风、波浪等动荷载可通过傅里叶变换将其振动波形分解为多个正弦波的叠加,所以本文将水平动荷载简化为正弦简谐荷载,该荷载与扭矩共同作用于桩顶.
(3) 地基假定为Pasternak双参数模型,桩周土对桩的作用简化为一系列分布的弹簧、阻尼器和纯剪切单元.
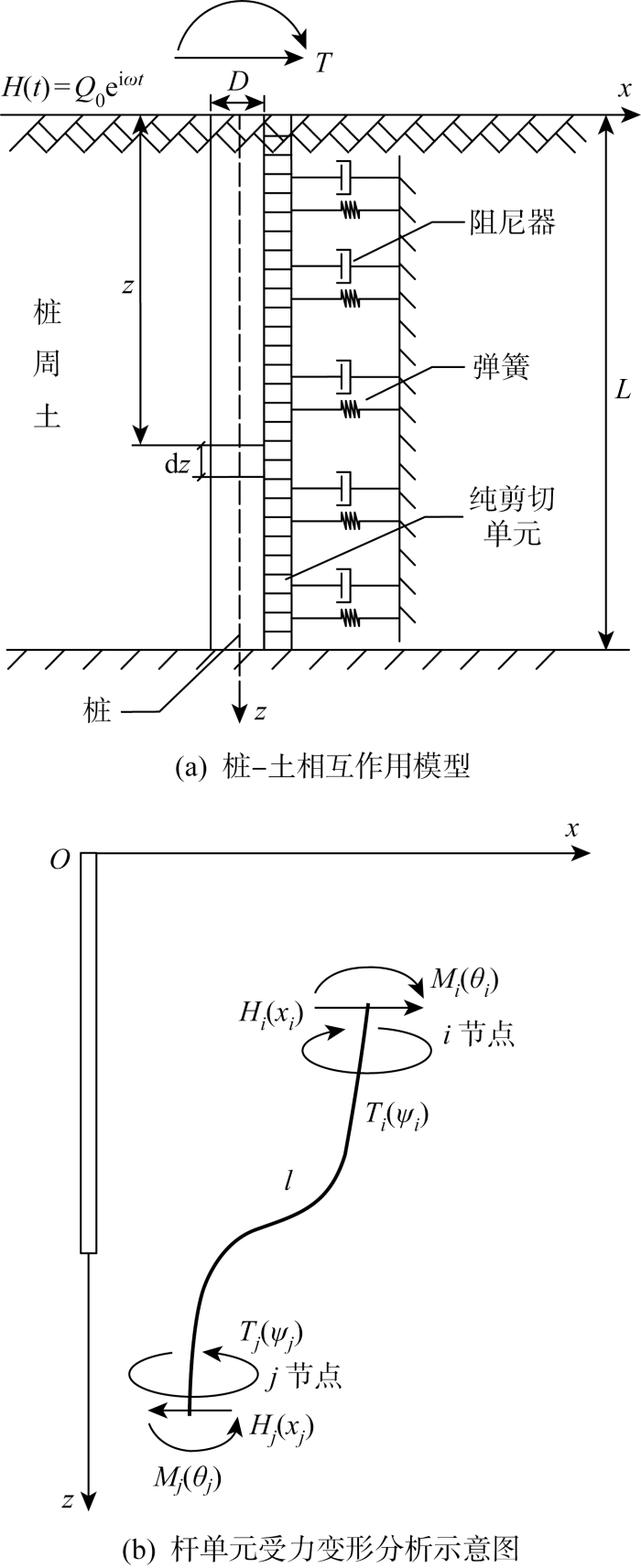
基于上述假定建立如图1 所示的桩-土相互作用模型.图中:L 、D 、z 和dz 分别为桩长、桩直径、桩入土深度以及桩身微元体;H (t )和T 分别为作用在桩顶的水平简谐荷载和扭矩;Q 0 为H (t )的幅值;虚数i=- 1 ω 为简谐荷载圆频率;Hi (Hj )、Mi (Mj )、Ti (Tj )、xi (xj )、θi (θj )、Ψi (Ψj )分别为单元i (j )节点的剪力、弯矩、扭矩、水平位移、转角和扭转角.
图1
图1
桩土体系简化分析模型
Fig.1
Simplified analysis model of pile-soil system
2 H (t )-T 联合受荷桩的综合刚度矩阵
2.1 传统桩身单元刚度矩阵
传统有限杆单元法假定桩身为小变形弹性体,其单元刚度矩阵[15 ] 为
(1) KE = 12 E p I l 3 6 E p I l 2 0 - 12 E p I l 3 6 E p I l 2 0 6 E p I l 2 4 E p I l 0 - 6 E p I l 2 2 E p I l 0 0 0 G p J l 0 0 - G p J l - 12 E p I l 3 - 6 E p I l 2 0 12 E p I l 3 - 6 E p I l 2 0 6 E p I l 2 2 E p I l 0 - 6 E p I l 2 4 E p I l 0 0 0 - G p J l 0 0 G p J l
式中:I 、J 分别为桩身截面惯性矩和极惯性矩;E p 、G p 分别为桩身弹性模量和切变模量;l 为离散单元长度.
2.2 考虑桩土相互作用的单元刚度矩阵
水平简谐荷载作用下桩周土反力由弹性力、阻尼力和惯性力组成,其与位移的关系在复数域的表达式为
(2) p (x )=(k s -ω 2 m p +iωc s )x
式中:p (x )为地基土反力;k s 为弹性系数,桩顶自由时可取k s ≈(1. 5~ 2. 5)E s [6 ] ;m p 和x 分别为单位桩长质量和桩身水平位移;c s 为辐射阻尼系数,c s =6a 0 - 1 / 4 ρ s v s D +2β s k s ω v s ={E s / [2ρ s (1+μ s )]}1 / 2 ;复刚度k s -ω 2 m p +iωc s 的实部代表动刚度,虚部代表阻尼;E s 、ρ s 、μ s 、β s 分别为桩周土的弹性模量、密度、泊松比及阻尼比;无量纲频率a 0 =ωD/v s .
由虚功原理可推导得到桩周土抗力等效换算为节点荷载的公式为
(3) F H =(k s -ω 2 m p +iωc s )∫ 0 l N v T N v x i θ i x j θ j z =
13 l 35 k 11 l 2 210 k 9 l 70 k - 13 l 2 420 k 11 l 2 210 k l 3 105 k 13 l 2 420 k - l 3 140 k 9 l 70 k 13 l 2 420 k 13 l 35 k - 11 l 2 210 k - 13 l 2 420 k - l 3 140 k - 11 l 2 210 k l 3 105 k x i θ i x j θ j
KH x i θ i x j θ j T
式中:K H 为H (t )产生的附加刚度矩阵;k =k s -ω 2 m p +iωc s ;N v 为单元受水平力时挠曲变形的形函数矩阵,其表达式为
(4) N v =[1-3 z 2 l 2 2 z 3 l 3 z -2 z 2 l z 3 l 2
3 z 2 l 2 2 z 3 l 3 - z 2 l z 3 l 2
扭矩作用下桩-土接触面产生环向侧摩阻力,此时桩身的控制方程[20 ] 为
(5) Gp J ∂ 2 θ ∂ z 2 θ θ=0
(6) f i i ( j j ) T T 2 π 1 G s D 2 l
式中:G s 为土体切变模量.本文采用Tanahashi[23 ] 提出的经验公式确定土体切变模量
(7) Gs = E s t 6 ( 1 + μ s )
式中:t 为地基土的剪切层厚度,可取11倍桩径[22 ] .
(8) Ti ( j ) = k i i ( j j ) T T i ( j ) = π G s D 2 l 2 i ( j )
将扭矩作用下桩身受到的环向侧摩阻力等效为节点荷载,从而获得受扭桩单元平衡方程
(9) T i T j k i i T T 0 0 k j j T T Ψ i Ψ j T Ψ i Ψ j
2.3 考虑H (t )-T 耦合作用的附加刚度矩阵
Kong[9 ] 通过离心模型试验分析了水平荷载和扭转荷载共同作用下的桩身内力和位移,并拟合出能反映水平荷载和扭矩相互作用规律的影响系数,其表达式为
(10) αTH = β P a D
式中:α TH 为H (t )-T 影响系数,表示受水平力和扭转联合作用的单桩与仅受扭矩作用的单桩在转角相同条件下对应节点上的扭矩比;P a 为标准大气压强;β 为H (t )-T 耦合因子,反映桩周水平土抗力对桩-土接触面上扭剪应力的增强效应.
因此,考虑水平动荷载和扭矩耦合作用的桩身单元平衡方程修正为
(11) T i T j 1 + β P a D k x i k i i T T 0 0 1 + β P a D k x j k j j T T Ψ i Ψ j HT Ψ i Ψ j
式中:K HT 为考虑H (t )-T 耦合作用的侧摩阻力附加刚度矩阵.
2.4 考虑土体剪切作用的附加刚度矩阵
二维平面应变条件下Pasternak地基模型的桩身挠曲微分方程[13 ] 可表示为
(12) Ep Ip d 4 x d 4 z s b d 2 x d 2 z
式中:E p I p 、K 和b 分别为桩身抗弯刚度、地基反力系数和桩身计算宽度.
(13) p (z )=Kbzx +G s bΨ
结合式(12)和(13),根据虚位移原理,可得双参数地基条件下桩周土抗力等效节点力表达式:
(14) F p =∫ 0 l n N v T K b z x + d N v d z T G s b Ψ z =
(KH +KGs )[x i θ i Ψ i x j θ j Ψ j
(15) KGs =Gs b 6 5 l 1 10 0 - 6 5 l 1 10 0 1 10 2 15 l 0 - 1 10 - l 30 0 0 0 0 0 0 0 - 6 5 l - 1 10 0 6 5 l - 1 10 0 1 10 - l 30 0 - 1 10 2 15 l 0 0 0 0 0 0 0
式中:l n 为土体单元的单位长度;K Gs 为土体剪切作用对单元刚度矩阵的修正矩阵.
综合式(1)、(11)、(13)、(15)可得考虑桩土相互作用的单元综合刚度矩阵为
(16) K =K E +K H +K HT +K Gs
3 联合受荷桩内力、位移求解
获得桩身单元综合刚度矩阵后通过编程求解桩身内力和位移,具体求解步骤如下.
(1) 建立计算模型.输入桩土参数和荷载情况,根据精度要求合理划分桩单元.
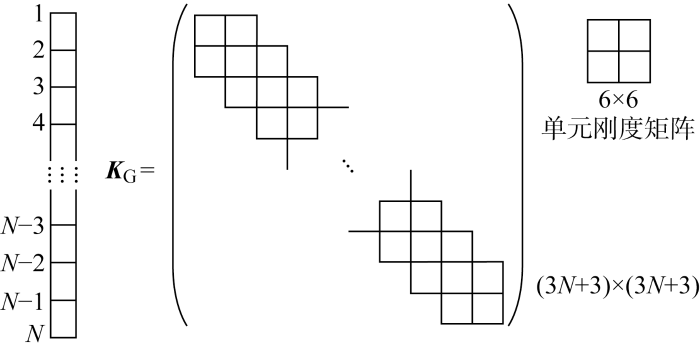
(2) 组装总体刚度矩阵.将式(16)表示的单元综合刚度矩阵按“首尾相连”原则组装为桩身总体刚度矩阵,如图2 所示.图中:K G 为桩身总体刚度矩阵;N 为桩单元划分总数.
图2
图2
组装总体刚度矩阵
Fig.2
Matrix of assembling global stiffness
(3) 引入边界条件.根据桩端约束条件和受荷情况在桩身总体刚度矩阵中引入边界条件,其中位移边界条件按“乘大数法”处理;桩顶自由,桩底嵌固,如下所示.
(17) E p I x ″ z = 0 = 0 , E p I x ‴ z = 0 = Q 0 G p J Ψ ' z = 0 = T π 2 - θ
(18) x z = L θ z = L Ψ z = L
(4) 求解位移.先利用矩阵方程Δ =K G - 1 F (Δ 为位移矩阵)求解桩身水平位移和转角,再将水平位移代入总体刚度矩阵中求解桩身扭转角,最终获得H (t )-T 联合受荷桩单元位移矩阵.
(5) 求解内力.将各单元位移矩阵和单元刚度矩阵相乘即可求出桩身各节点的弯矩、剪力和扭矩.
4 方法验证
目前水平动荷载和扭矩共同作用下的桩基受力变形分析相对较少,难以直接有效地验证本文方法的可靠性.为此分别考虑水平简谐荷载和扭矩单独作用两种情况,将其计算结果分别与文献[24 ⇓ -26 ]进行对比,再进行有限元建模,进一步验证本文方法的可靠性.
4.1 水平简谐荷载作用下单桩计算方法验证
基于文献[24 ]中桩土参数通过有限元软件建立三维实体单元模型,其中桩长L =20 m,桩径D =0.5 m,采用动力隐式分析步,水平简谐荷载幅值Q 0 =100 kN,频率f =16 Hz;桩顶自由,桩底嵌固.桩周土采用Mohr-Coulomb理想弹塑性模型,桩身采用C3D8单元模型,桩-土其他参数如表1 所示.
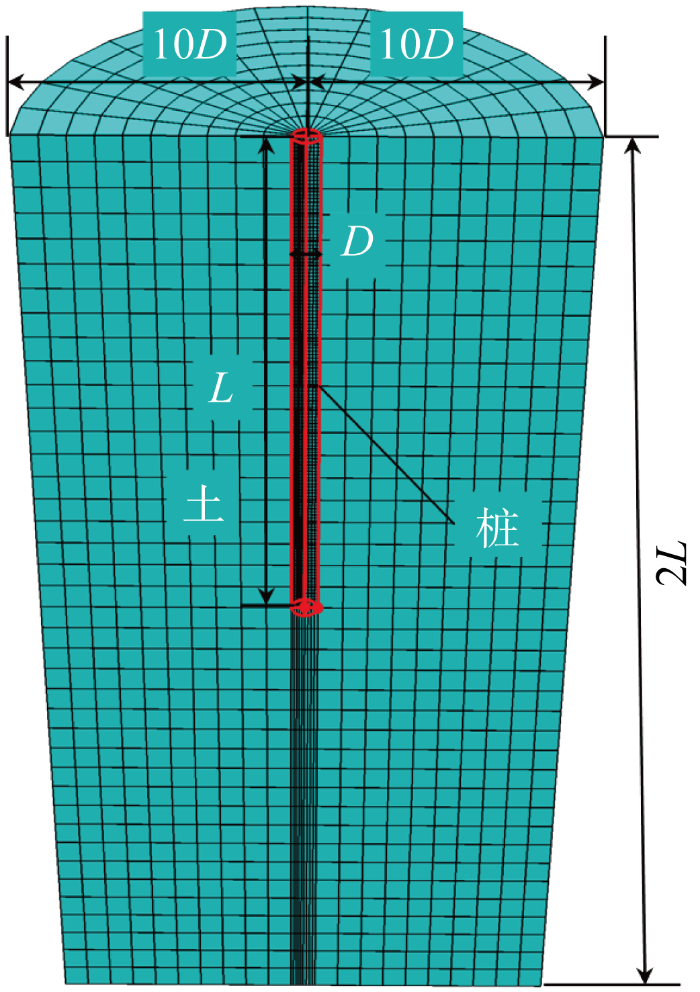
为消除边界条件的影响,模型的宽度取为桩径的20倍,深度取为桩长的2倍,土体侧面设置径向位移约束,土体底面和顶面分别设置为固定和自由.
通过两次自动应力平衡消除土体在自重作用下的变形,采用六面体扫掠进阶算法划分网格,总共划分 6 182 个单元网格,如图3 所示.
图3
图3
三维数值模型
Fig.3
3D numerical model
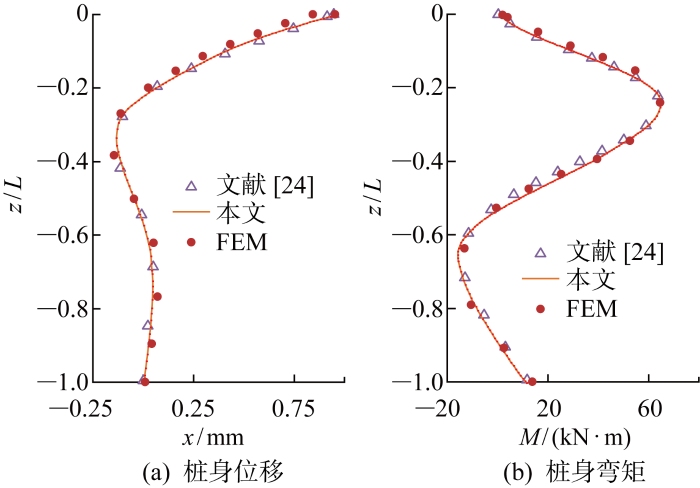
图4 给出了桩身水平位移和弯矩的分布曲线.由图4 可知,本文所提出的计算方法与文献[24 ]中的解析解以及有限元模拟(FEM)结果均吻合较好,表明本文方法能够较为准确地预测水平简谐荷载作用下桩基内力和位移.
图4
图4
桩身位移、内力对比
Fig.4
Comparison of displacement and internal force of pile
表2 给出了杆单元模型与三维实体单元模型所需计算时间的对比,从表2 可知三维实体单元模型计算时间为88.90 s,而本文杆单元模型计算时间仅为0.73 s;表明本文方法在保证计算结果准确性的同时又大幅提高了计算效率.考虑到实际工程中常涉及到大量桩基,当需要对数十乃至上百根桩基进行一体化分析时,本文计算方法所带来的计算效率和准确性优势将会更加明显.
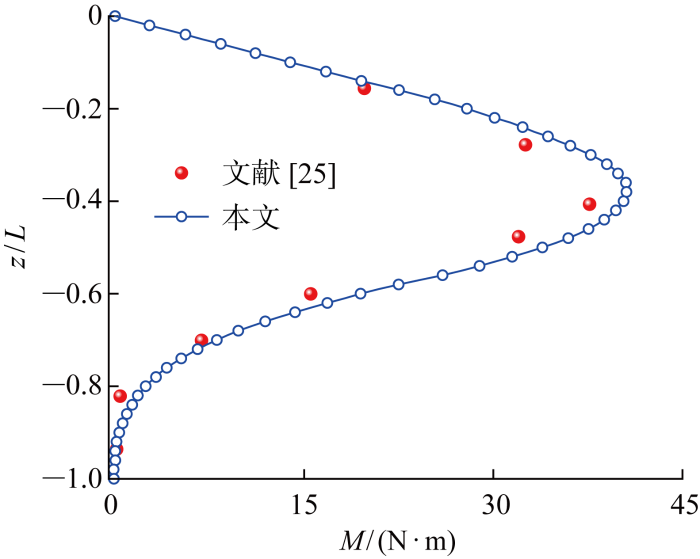
吕冰[25 ] 通过模型试验研究水平简谐荷载作用下单桩承载性能.试验地基土密度为 1 908 kg/m3 ;内摩擦角为36°;黏聚力为11.8 kPa;阻尼比为0.05;弹性模量为8.5 MPa.模型桩长900 mm;直径60 mm.水平荷载幅值H 0 =274.4 N;f =6 Hz;加载点位于泥面以上60 mm处.图5 给出了水平荷载作用下桩身弯矩计算结果和试验结果的对比.从图5 可以看出,桩身弯矩沿桩埋深先增大后减小,弯矩最大值出现在距离桩顶1/3深度处.总体上来看,本文方法计算结果与试验结果吻合较好.
图5
图5
桩身弯矩对比
Fig.5
Comparison of pile bending moment
4.2 扭矩作用下单桩计算方法验证
基于文献[26 ]中的桩土参数建立三维实体有限元数值模型,其中桩长L =9 m,桩径D =0.4 m,桩底嵌固,桩顶自由,桩顶作用T =40 kN·m的扭矩,桩周土体采用Mohr-Coulomb理想弹塑性模型,桩身采用C3D8单元,桩-土体系其他参数如表3 所示,数值建模方法同4.1节.
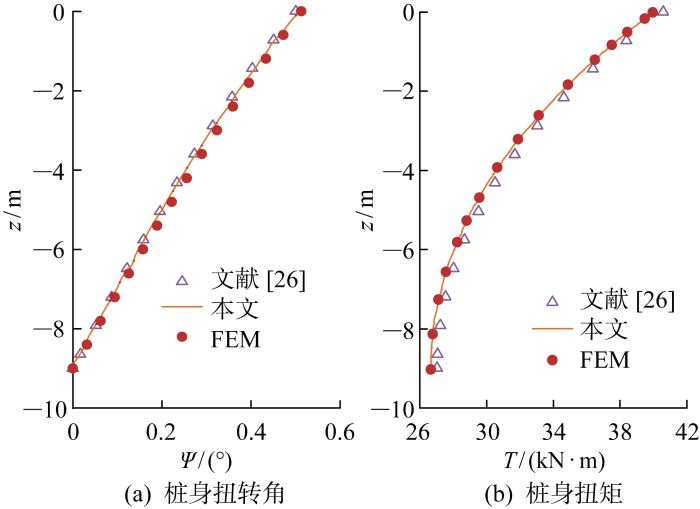
图6 给出了本文方法、有限元数值模拟以及文献[26 ]中计算结果的对比.从图中可以看出,本文提出的计算方法与有限元模拟值以及文献[26 ]中计算值均有较好的一致性,进一步证明了本文方法的可靠性.
图6
图6
桩身扭转角和扭矩对比
Fig.6
Comparison of pile torsion angle and torque
5 参数分析
影响H (t )-T 联合受荷桩内力和位移的因素很多,限于篇幅,结合本文方法特点,侧重讨论G s 、E p /E s 、L/D 、a 0 和Q 0 对桩身内力和位移的影响.
除另有说明,本节采用的桩土参数选取如下:L =15 m,D =0.5 m,E p =31.5 GPa,桩密度ρ p =2 500 kg/m3 ;桩顶自由,桩底嵌固;桩顶作用幅值Q 0 =100 kN和无量纲振动频率a 0 =0.4的水平简谐荷载;扭矩T =40 kN·m;E s =8 MPa,β s =0.05,μ s =0.3.
为客观描述桩土相互作用的内在规律,对计算结果进行如下无量纲归一化处理:
(19) x = x ( z ) / x m a x M = M ( z ) / M m a x Ψ = Ψ ( z ) / Ψ m a x T = T ( z ) / T m a x
式中:x (z )、M (z )、Ψ (z )及T (z )分别为桩身水平位移、弯矩、扭转角及扭矩的最大值;x max 、M max 、Ψ max 及T max 为同一变量下水平位移、弯矩、扭转角和扭矩的最大值.
5.1 土体切变模量G s 与桩土弹模比E p /E s 的影响
土体切变模量是描述土体抵抗剪切变形的参数,对桩土结构体系的稳定性、抗震性以及变形性能等具有重要影响.
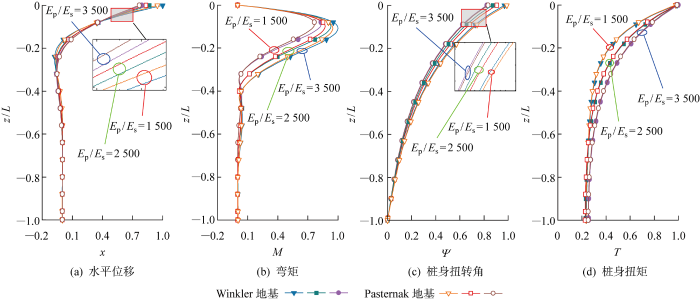
通过在合理区间内改变桩土弹性模量,使桩土弹模比E p /E s 分别为1 500、2 500、3 500.图7 给出了不同桩土弹模比下,基于Pasternak模型所得桩身内力变形与Winkler模型计算结果的对比.
图7
图7
不同桩土弹模比下桩身内力位移对比
Fig.7
Comparison of pile internal force and displacement at different pile-soil elastic modulus ratios
由图7 可知,在桩土弹模比为1 500、2 500和3 500时,对比Winkler模型计算结果,采用Pasternak地基模型的桩身最大弯矩分别减小了7.9%、6.1%和5.3%,桩顶最大位移分别减小了5.2%、4.1%和3.4%,而桩身扭转角和扭矩减小幅度均小于1%;表明土体剪切作用对桩身水平位移有显著的约束作用,而对扭转变形影响较小,同时,增加桩土弹模比会弱化土体剪切效应对桩身的约束作用.
当桩土弹模度比从 1 500 增加到 2 500 和 3 500 时,桩顶水平位移分别减小了13.1%和20.7%,桩身最大弯矩分别增加了13.6%和23.5%,桩身最大弯矩位置随桩土弹模比的增大而下降.从图7(a) 可知不同桩土弹模比下的桩身水平位移曲线在(0.07~0.32)L 之间的变化趋势与桩顶相反,这是因为桩土弹模比较小时,桩周土对桩的约束能力较弱,桩身位移曲线较为陡峭,桩身刚度偏小,出现变形局部集中的现象.
由图7(c) 可知,当桩土弹模比从 1 500 增加到 3 500 时,桩顶扭转角减小了15%,表明增加桩土弹模比可减小桩身扭转变形,提高桩身抗扭能力.
5.2 桩身长径比L/D 的影响分析
在实际工程中,桩身长径比对桩基的承载能力和变形控制都有重要的影响,选择合适的长径比既能够提高桩基的承载能力又可以获得最佳的经济效益.因此本节通过固定桩径、改变桩长的方式研究了桩身长径比L/D =5,15,25,50时的单桩承载特性.图8 给出了不同桩身长径比条件下桩身内力位移分布.
图8
图8
桩身长径比对桩身内力位移的影响
Fig.8
Influence of pile diameter ratio on displacement of internal force
由图8 可知,L/D =5时,桩身变形随埋深线性减小,桩身弯矩随埋深线性增加,桩身最大弯矩位置出现在桩底,此时桩身呈刚体运动.在工程实际中,应加强长径比较小的桩基底部嵌固,以避免桩底因抗弯能力不足而出现弯曲-屈曲失稳破坏.
随桩身长径比的增加,桩身水平位移由直线逐渐过渡为曲线,表现出柔性桩的性质,且位移减小至0的位置逐渐上移,桩身长径比从5增大到50,桩顶水平位移和扭转角分别增加了12.2%和41.4%;相同深度处,桩身扭转角随L/D 的增大而增大,桩身扭矩则随L/D 的增大而减小.
当L/D 从5增大到15时,桩顶水平位移和扭转角分别增加了12.3%和22.3%,表明通过固定桩径的方式增加长径比,实质上增加了桩身的柔度,减小了桩身抗弯和抗扭刚度.但当L/D 从15增大到50时,桩顶位移仅增加了1.5%,表明桩超过一定长度后,继续增加桩长对桩身抵抗水平变形能力并无显著影响.
5.3 水平动荷载无量纲频率a 0 的影响
为探讨水平动荷载振动频率对H (t )-T 受荷桩的影响,取无量纲频率a 0 =0.1,0.5,1.0这3种情况,求得桩身内力位移分布曲线如图9 所示.
图9
图9
简谐荷载无量纲频率对桩身内力位移的影响
Fig.9
Influence of simple harmonic load dimensionless frequency on the internal force displacement of pile body
从图9(a) 、9(b) 可知,增大a 0 可减小桩顶水平位移和桩身弯矩,当a 0 从0.1增大到1.0时,桩顶水平位移减小了17.42%,桩身最大弯矩减小了6.12%,随埋深增加,不同振频下的内力位移曲线趋于重合,表明外荷载的动力效应随埋深增加而逐渐减弱,土体阻尼有效地吸收了动荷载的能量.
从图9(c) 、9(d) 可知,桩身扭转角和扭矩随a 0 的增大而增大,当a 0 从0.1增大到1.0时,桩顶扭转角增大了18.4%.这是由于随a 0 增大,桩身水平位移减小,同时H (t )-T 耦合刚度也随之减小,所以在相同外荷载作用下,桩身扭转角和扭矩会增大.
5.4 水平动荷载幅值Q 0 的影响
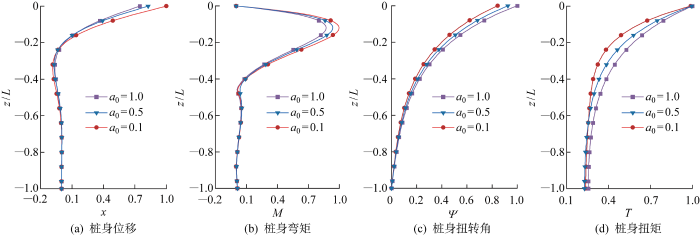
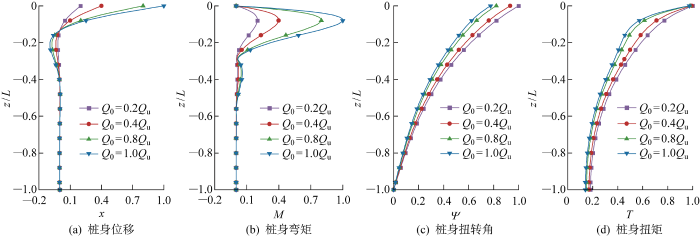
为分析水平简谐荷载幅值对H (t )-T 受荷桩的影响,取桩顶产生0.15D 水平位移时对应的荷载幅值为Q u ,固定桩顶扭矩T =40 kN·m,荷载幅值Q 0 分别取为0.2Q u 、0.4Q u 、0.8Q u 、1.0Q u 这4种工况,桩身内力位移计算结果如图10 所示.
图10
图10
简谐荷载幅值对桩身内力位移的影响
Fig.10
Influence of harmonic load amplitude on displacement of internal force of pile
荷载幅值Q 0 由0.2Q u 增大到1.0Q u 时桩顶水平位移增大了4.2倍,桩身最大弯矩增大了5倍,桩身最大弯矩位置不随Q 0 改变.
桩身扭转角和扭矩随水平荷载幅值增大而减小,桩顶扭转角最大减小了22.6%.这是由于在水平简谐荷载作用下桩基产生侧向位移,导致桩土之间的摩擦力增大,水平简谐荷载和扭矩之间的耦合刚度也随之增大,从而提高了单桩抗扭能力.
不难看出,水平简谐荷载幅值会对桩身最大内力位移产生较大影响,但桩身位移都在0.4倍桩长处降为0,表明水平动荷载幅值对当前工况下有效桩长影响较小.
6 结论
本文基于Pasternak地基模型,采用改进的有限杆单元法,考虑了土体剪切效应和多向荷载间的相互影响,得到了均质地基中水平简谐荷载和扭矩联合作用下桩基内力位移数值解,并获得以下结论:
(1) 土体剪切效应对桩身水平变形有约束作用,而对桩身扭转变形影响较小,对比不考虑土体剪切效应的Winkler模型计算结果,土体剪切效应可减小5.2%的桩顶水平位移和7.9%的桩身最大弯矩.
(2) 水平荷载能够增强桩身抗扭能力,水平简谐荷载幅值由0.2Q u 增大到1.0Q u ,桩顶扭转角减小了22.6%;增加桩土弹模比可减小桩身变形,但会增加桩身内力,桩土弹模比从 1 500 增加到 3 500 时,桩顶水平位移减小了20.7%,桩身最大弯矩增加了23.5%.
(3) 桩顶水平位移和桩身最大弯矩随简谐荷载无量纲频率a 0 的增大而减小,外荷载动力效应随桩埋深增加而逐渐减弱.增大桩身长径比会降低桩身刚度、扩大桩身变形,桩身长径比从5增大到50,桩顶水平位移和扭转角分别增加了12.2%和41.4%.工程设计中应加强刚性桩桩底嵌固.
(4) 与三维实体单元模型相比,杆单元模型在保证计算准确性的前提下可大幅减少单元划分数量和计算时间,有效提高了计算效率.
参考文献
View Option
[1]
金小凯 , 陈锦剑 , 廖晨聪 . 波浪荷载对单桩承载力影响的水槽模拟试验研究
[J]. 上海交通大学学报 2021 , 55 (4 ): 365 -371 .
DOI:10.16183/j.cnki.jsjtu.2019.268
[本文引用: 1]
针对浅海环境下的单桩基础,在水槽试验室中建立砂土-桩基-波浪缩尺模型,进行波浪作用下单桩静载荷试验.测试桩周海床土孔隙水压力和不同荷载作用下的桩基沉降,分析在波浪荷载下单桩和海床土相互作用机理和单桩荷载沉降曲线特性,探讨不同桩径下桩周海床土超静孔压(ps)对单桩竖向承载力的影响.结果表明:单桩的存在会增大桩周海床土ps,同时减小桩底海床土ps;桩径越大,桩周ps越大.与无波浪影响的情况相比,波浪荷载作用下的单桩承载力较小,相同荷载水平下的桩顶沉降增加显著,且沉降增大的趋势在桩径较大时更明显.研究表明在海洋桩基的设计过程中要关注波浪荷载对桩基承载力的影响.
JIN Xiaokai CHEN Jinjian LIAO Chencong . Wave flume simulation experiment on influence of wave load on bearing capacity of monopile
[J]. Journal of Shanghai Jiao Tong University 2021 , 55 (4 ): 365 -371 .
[本文引用: 1]
[2]
张驰 , 赖俊荣 , 阮芳伟 , 等 . 海洋钢管桩发生溜桩的地层条件及桩侧动摩阻力计算方法
[J]. 岩土力学 2022 , 43 (Sup.2): 355 -361 .
[本文引用: 1]
ZHANG Chi LAI Junrong RUAN Fangwei , et al Strata condition for steel pipe pile runs and calculation method of dynamic skin friction of pile in ocean engineering
[J]. Rock and Soil Mechanics 2022 , 43 (Sup.2): 355 -361 .
[本文引用: 1]
[3]
HE K P YE J H . Seismic dynamics of offshore wind turbine-seabed foundation: Insights from a numerical study
[J]. Renewable Energy 2023 , 205 (2023): 200 -221 .
[本文引用: 1]
[4]
BASILE F . Torsional response of pile groups
[C]// Proceedings of the 11th DFI & EFFC International Conference on Geotechnical Challenges in Urban Regeneration. London UK : Deep Foundations Institute , 2010 .
[本文引用: 1]
[5]
BASACK S NIMBALKAR S . Numerical solution of single pile subjected to torsional cyclic load
[J]. International Journal of Geomechanics 2017 , 17 (8 ): 04017016.
[本文引用: 1]
[6]
GAZETAS G DOBRY R . Horizontal response of piles in layered soils
[J]. Journal of Geotechnical Engineering, ASCE 1984 , 110 (1 ): 20 -40 .
[本文引用: 2]
[7]
吴君涛 , 王奎华 , 孙梵 , 等 . 水平振动桩周围半无限空间土体受迫振动响应理论解
[J]. 振动工程学报 2020 , 33 (6 ): 1272 -1281 .
[本文引用: 1]
WU Juntao WANG Kuihua SUN Fan , et al Dynamic response of a half-space soil model excited by the known lateral pile vibration
[J]. Journal of Vibration Engineering 2020 , 33 (6 ): 1272 -1281 .
[本文引用: 1]
[8]
黄茂松 , 边学成 , 陈育民 , 等 . 土动力学与岩土地震工程
[J]. 土木工程学报 2020 , 53 (8 ): 64 -86 .
[本文引用: 1]
HUANG Maosong BIAN Xuecheng CHEN Yumin , et al Soil dynamics and geotechnical earthquake engineering
[J]. China Civil Engineering Journal 2020 , 53 (8 ): 64 -86 .
[本文引用: 1]
[9]
KONG L G . Behavior of pile groups subjected to torsion [D]. Hong Kong, China : The Hong Kong University of Science and Technology , 2006 .
[本文引用: 2]
[10]
NOGAMI T NOVAK M . Resistance of soil to a horizontally vibrating pile
[J]. Earthquake Engineering and Structure Dynamics 1977 , 5 (3 ): 249 -261 .
[本文引用: 1]
[11]
NOVAK M . Dynamic stiffness and damping of pile
[J]. Canndian Geotechnical Journal 1974 , 11 (4 ): 574 -598 .
[本文引用: 1]
[12]
NOVAK M NOGAMI T . Soil-pile interaction in horizontal vibration
[J]. Earthquake Engineering and Structural Dynamics 1977 , 5 (3 ): 263 -281 .
[本文引用: 1]
[13]
PASTERNAK P L . Fundamentals of a new method of analyzing structures on an elastic foundation by means of two foundation onstants [M]. Moscow, Russia : Gosudarstvennoe Izdatelstro Liberaturi Po Stroitelstvui Arkhitekture , 1954 .
[本文引用: 2]
[14]
FWA T F SHI X P TAN S A . Use of Pasternak foundation model in concrete pavement analysis
[J]. Journal of Transportation Engineering 1996 , 122 (4 ): 323 -328 .
[本文引用: 1]
[15]
戴自航 , 王云凤 , 卢才金 . 水平荷载单桩计算的综合刚度和双参数法杆系有限元数值解
[J]. 岩石力学与工程学报 2016 , 35 (10 ): 2115 -2123 .
[本文引用: 2]
DAI Zihang WANG Yunfeng LU Caijin . Numerical solution of link finite element based on composite stiffness and bi-parameter method for computation of laterally loaded single pile
[J]. Chinese Journal of Rock Mechanics and Engineering 2016 , 35 (10 ): 2115 -2123 .
[本文引用: 2]
[16]
朱彦鹏 , 吴林平 , 施多邦 , 等 . 基于Pasternak地基模型的非线性土抗力-桩身侧向位移曲线在基坑支护桩中的应用
[J]. 岩土力学 2022 , 43 (9 ): 2581 -2591 .
[本文引用: 1]
ZHU Yanpeng WU Linping SHI Duobang , et al Application of nonlinear soil resistance-pile lateral displacement curve based on Pasternak foundation model in foundation pit retaining piles
[J]. Rock and Soil Mechanics 2022 , 43 (9 ): 2581 -2591 .
[本文引用: 1]
[17]
江杰 , 柴文成 , 欧孝夺 , 等 . 基于Timoshenko-Pasternak 模型的多向受荷桩水平动力响应分析
[J]. 岩石力学与工程学报 2022 , 41 (1 ): 172 -185 .
[本文引用: 1]
JIANG Jie CHAI Wencheng OU Xiaoduo , et al Horizontal dynamic response analysis of multi-directional loaded pile based on Timoshenko-Pasternak model
[J]. Chinese Journal of Rock Mechanics and Engineering 2022 , 41 (1 ): 172 -185 .
[本文引用: 1]
[18]
张玲 , 岳梢 , 赵明华 , 等 . 基于改进Pasternak地基模型的桩柱式桥墩受力变形分析
[J]. 岩土工程学报 2022 , 44 (10 ): 1817 -1826 .
[本文引用: 2]
ZHANG Ling YUE Shao ZHAO Minghua , et al Analysis of pile-column pier based on modified Pasternak foundation model
[J]. Chinese Journal of Geotechnical Engineering 2022 , 44 (10 ): 1817 -1826 .
[本文引用: 2]
[19]
HU Z H MCVAY M BLOOMQUIST D , et al Influence of torque on lateral capacity of drilled shafts in sands
[J]. Journal of Geotechnical and Geoenvironment Engineering 2006 , 132 (4 ): 456 -464 .
[本文引用: 1]
[20]
孔令刚 , 张利民 . 群桩扭转非线性模型
[J]. 岩土力学 2009 , 30 (8 ): 2231 -2236 .
[本文引用: 2]
KONG Linggang ZHANG Limin . Nonlinear analysis of pile groups subjected to torsion
[J]. Rock and Soil Mechanics 2009 , 30 (8 ): 2231 -2236 .
[本文引用: 2]
[21]
GEORGIADIS K SHEIL B . Effect of torsion on the undrained limiting lateral resistance of piles in clay
[J]. Géotechnique 2020 , 70 (8 ): 700 -710 .
[本文引用: 1]
[22]
WU W B YANG Z J LIU X , et al Horizontal dynamic response of pile in unsaturated soil considering its construction disturbance effect
[J]. Ocean Engineering 2022 , 245 : 110483 .
[本文引用: 2]
[23]
TANAHASHI H . Formulas for an infinitely long Bernoulli-Euler beam on the Pasternak model
[J]. Journal of the Japanese Geotechnical Society 2004 , 44 (5 ): 109 -118 .
[本文引用: 1]
[24]
CUI C Y LIANG Z M XU C S , et al Analytical solution for horizontal vibration of end-bearing single pile in radially heterogeneous saturated soil
[J]. Applied Mathematical Modelling 2023 , 116 : 65 -83 .
[本文引用: 3]
[25]
吕冰 . 水平振动荷载作用下支盘桩动力特性研究 [D]. 洛阳 : 河南科技大学 , 2015 .
[本文引用: 2]
LÜ Bing . Study on dynamic characteristics of squeezed branch pile under horizontal vibration load [D]. Luoyang : Henan University of Science and Technology , 2015 .
[本文引用: 2]
[26]
邹新军 , 徐洞斌 , 王亚雄 . 近海复杂环境下的H-M-T 受荷桩内力位移分析
[J]. 防灾减灾工程学报 2014 , 34 (6 ): 736 -741 .
[本文引用: 4]
ZOU Xinjun XU Dongbin WANG Yaxiong . Analysis of piles under H-M-T combined loading in offshore complex environment
[J]. Journal of Disaster Prevention and Mitigation Engineering 2014 , 34 (6 ): 736 -741 .
[本文引用: 4]
波浪荷载对单桩承载力影响的水槽模拟试验研究
1
2021
... 桩基础广泛应用于风电铁塔、铁路桥梁和海洋平台等工程项目中[1 ⇓ -3 ] .在风、波浪等随机荷载作用下,桩身除承受上部结构传递的水平荷载外,还可能承受由偏心荷载产生的扭矩[4 -5 ] .目前常规桩土相互作用研究多是基于Winkler弹性地基梁模型[6 ⇓ -8 ] ,鲜有考虑土体变形连续性对桩基承载特性的影响.同时,对于联合受荷桩,在多向荷载共同作用下,桩身响应之间的相互影响也是不可忽视的重要影响因素[9 ] . ...
Wave flume simulation experiment on influence of wave load on bearing capacity of monopile
1
2021
... 桩基础广泛应用于风电铁塔、铁路桥梁和海洋平台等工程项目中[1 ⇓ -3 ] .在风、波浪等随机荷载作用下,桩身除承受上部结构传递的水平荷载外,还可能承受由偏心荷载产生的扭矩[4 -5 ] .目前常规桩土相互作用研究多是基于Winkler弹性地基梁模型[6 ⇓ -8 ] ,鲜有考虑土体变形连续性对桩基承载特性的影响.同时,对于联合受荷桩,在多向荷载共同作用下,桩身响应之间的相互影响也是不可忽视的重要影响因素[9 ] . ...
海洋钢管桩发生溜桩的地层条件及桩侧动摩阻力计算方法
1
2022
... 桩基础广泛应用于风电铁塔、铁路桥梁和海洋平台等工程项目中[1 ⇓ -3 ] .在风、波浪等随机荷载作用下,桩身除承受上部结构传递的水平荷载外,还可能承受由偏心荷载产生的扭矩[4 -5 ] .目前常规桩土相互作用研究多是基于Winkler弹性地基梁模型[6 ⇓ -8 ] ,鲜有考虑土体变形连续性对桩基承载特性的影响.同时,对于联合受荷桩,在多向荷载共同作用下,桩身响应之间的相互影响也是不可忽视的重要影响因素[9 ] . ...
Strata condition for steel pipe pile runs and calculation method of dynamic skin friction of pile in ocean engineering
1
2022
... 桩基础广泛应用于风电铁塔、铁路桥梁和海洋平台等工程项目中[1 ⇓ -3 ] .在风、波浪等随机荷载作用下,桩身除承受上部结构传递的水平荷载外,还可能承受由偏心荷载产生的扭矩[4 -5 ] .目前常规桩土相互作用研究多是基于Winkler弹性地基梁模型[6 ⇓ -8 ] ,鲜有考虑土体变形连续性对桩基承载特性的影响.同时,对于联合受荷桩,在多向荷载共同作用下,桩身响应之间的相互影响也是不可忽视的重要影响因素[9 ] . ...
Seismic dynamics of offshore wind turbine-seabed foundation: Insights from a numerical study
1
2023
... 桩基础广泛应用于风电铁塔、铁路桥梁和海洋平台等工程项目中[1 ⇓ -3 ] .在风、波浪等随机荷载作用下,桩身除承受上部结构传递的水平荷载外,还可能承受由偏心荷载产生的扭矩[4 -5 ] .目前常规桩土相互作用研究多是基于Winkler弹性地基梁模型[6 ⇓ -8 ] ,鲜有考虑土体变形连续性对桩基承载特性的影响.同时,对于联合受荷桩,在多向荷载共同作用下,桩身响应之间的相互影响也是不可忽视的重要影响因素[9 ] . ...
Torsional response of pile groups
1
2010
... 桩基础广泛应用于风电铁塔、铁路桥梁和海洋平台等工程项目中[1 ⇓ -3 ] .在风、波浪等随机荷载作用下,桩身除承受上部结构传递的水平荷载外,还可能承受由偏心荷载产生的扭矩[4 -5 ] .目前常规桩土相互作用研究多是基于Winkler弹性地基梁模型[6 ⇓ -8 ] ,鲜有考虑土体变形连续性对桩基承载特性的影响.同时,对于联合受荷桩,在多向荷载共同作用下,桩身响应之间的相互影响也是不可忽视的重要影响因素[9 ] . ...
Numerical solution of single pile subjected to torsional cyclic load
1
2017
... 桩基础广泛应用于风电铁塔、铁路桥梁和海洋平台等工程项目中[1 ⇓ -3 ] .在风、波浪等随机荷载作用下,桩身除承受上部结构传递的水平荷载外,还可能承受由偏心荷载产生的扭矩[4 -5 ] .目前常规桩土相互作用研究多是基于Winkler弹性地基梁模型[6 ⇓ -8 ] ,鲜有考虑土体变形连续性对桩基承载特性的影响.同时,对于联合受荷桩,在多向荷载共同作用下,桩身响应之间的相互影响也是不可忽视的重要影响因素[9 ] . ...
Horizontal response of piles in layered soils
2
1984
... 桩基础广泛应用于风电铁塔、铁路桥梁和海洋平台等工程项目中[1 ⇓ -3 ] .在风、波浪等随机荷载作用下,桩身除承受上部结构传递的水平荷载外,还可能承受由偏心荷载产生的扭矩[4 -5 ] .目前常规桩土相互作用研究多是基于Winkler弹性地基梁模型[6 ⇓ -8 ] ,鲜有考虑土体变形连续性对桩基承载特性的影响.同时,对于联合受荷桩,在多向荷载共同作用下,桩身响应之间的相互影响也是不可忽视的重要影响因素[9 ] . ...
... 式中:p (x )为地基土反力;k s 为弹性系数,桩顶自由时可取k s ≈(1. 5~ 2. 5)E s [6 ] ;m p 和x 分别为单位桩长质量和桩身水平位移;c s 为辐射阻尼系数,c s =6 a 0 - 1 / 4 ρ s v s D +2β s k s ω v s ={E s / [2ρ s (1+μ s )]}1 / 2 ;复刚度k s -ω 2 m p +iωc s 的实部代表动刚度,虚部代表阻尼;E s 、ρ s 、μ s 、β s 分别为桩周土的弹性模量、密度、泊松比及阻尼比;无量纲频率a 0 =ωD/v s . ...
水平振动桩周围半无限空间土体受迫振动响应理论解
1
2020
... 桩基础广泛应用于风电铁塔、铁路桥梁和海洋平台等工程项目中[1 ⇓ -3 ] .在风、波浪等随机荷载作用下,桩身除承受上部结构传递的水平荷载外,还可能承受由偏心荷载产生的扭矩[4 -5 ] .目前常规桩土相互作用研究多是基于Winkler弹性地基梁模型[6 ⇓ -8 ] ,鲜有考虑土体变形连续性对桩基承载特性的影响.同时,对于联合受荷桩,在多向荷载共同作用下,桩身响应之间的相互影响也是不可忽视的重要影响因素[9 ] . ...
Dynamic response of a half-space soil model excited by the known lateral pile vibration
1
2020
... 桩基础广泛应用于风电铁塔、铁路桥梁和海洋平台等工程项目中[1 ⇓ -3 ] .在风、波浪等随机荷载作用下,桩身除承受上部结构传递的水平荷载外,还可能承受由偏心荷载产生的扭矩[4 -5 ] .目前常规桩土相互作用研究多是基于Winkler弹性地基梁模型[6 ⇓ -8 ] ,鲜有考虑土体变形连续性对桩基承载特性的影响.同时,对于联合受荷桩,在多向荷载共同作用下,桩身响应之间的相互影响也是不可忽视的重要影响因素[9 ] . ...
土动力学与岩土地震工程
1
2020
... 桩基础广泛应用于风电铁塔、铁路桥梁和海洋平台等工程项目中[1 ⇓ -3 ] .在风、波浪等随机荷载作用下,桩身除承受上部结构传递的水平荷载外,还可能承受由偏心荷载产生的扭矩[4 -5 ] .目前常规桩土相互作用研究多是基于Winkler弹性地基梁模型[6 ⇓ -8 ] ,鲜有考虑土体变形连续性对桩基承载特性的影响.同时,对于联合受荷桩,在多向荷载共同作用下,桩身响应之间的相互影响也是不可忽视的重要影响因素[9 ] . ...
Soil dynamics and geotechnical earthquake engineering
1
2020
... 桩基础广泛应用于风电铁塔、铁路桥梁和海洋平台等工程项目中[1 ⇓ -3 ] .在风、波浪等随机荷载作用下,桩身除承受上部结构传递的水平荷载外,还可能承受由偏心荷载产生的扭矩[4 -5 ] .目前常规桩土相互作用研究多是基于Winkler弹性地基梁模型[6 ⇓ -8 ] ,鲜有考虑土体变形连续性对桩基承载特性的影响.同时,对于联合受荷桩,在多向荷载共同作用下,桩身响应之间的相互影响也是不可忽视的重要影响因素[9 ] . ...
2
2006
... 桩基础广泛应用于风电铁塔、铁路桥梁和海洋平台等工程项目中[1 ⇓ -3 ] .在风、波浪等随机荷载作用下,桩身除承受上部结构传递的水平荷载外,还可能承受由偏心荷载产生的扭矩[4 -5 ] .目前常规桩土相互作用研究多是基于Winkler弹性地基梁模型[6 ⇓ -8 ] ,鲜有考虑土体变形连续性对桩基承载特性的影响.同时,对于联合受荷桩,在多向荷载共同作用下,桩身响应之间的相互影响也是不可忽视的重要影响因素[9 ] . ...
... Kong[9 ] 通过离心模型试验分析了水平荷载和扭转荷载共同作用下的桩身内力和位移,并拟合出能反映水平荷载和扭矩相互作用规律的影响系数,其表达式为 ...
Resistance of soil to a horizontally vibrating pile
1
1977
... Winkler模型[10 ] 将地基视为由若干互相独立的弹簧组成的弹性体,用弹性系数描述土体的变形特性,具有概念明确、计算简单的特点,但该理论忽略了土体变形连续性,不能很好地反映实际情况.Novak[11 ] 应用平面应变理论假设桩周土为一组无限薄的土层,解决了Winkler地基模型无法考虑土体连续性的问题,但不能表征土体位移和应力沿纵向的梯度变化.因此,Novak等[12 ] 将桩周土视为三维连续介质,通过偏微分方程描述土体各物理量沿纵向的变化规律,并推导了均质土中单桩水平振动解析解,然而该方法夸大了地基的深度和扩散能力.针对上述3种模型的缺陷,Pasternak模型[13 ] 引入了土体反力系数和土体切变模量这两个独立的地基参数,在考虑土体变形连续性的同时又满足了力学概念清晰、计算简便的工程需求.Fwa等[14 ] 统计了36组分别来自Pasternak地基模型和其他模型计算结果的平均误差,分析结果表明Pasternak模型计算误差最小.戴自航等[15 ] 、朱彦鹏等[16 ] 、江杰等[17 ] 、张玲等[18 ] 分别基于Pasternak地基模型研究了单桩水平承载特性,通过试验和有限元模拟验证了Pasternak模型应用于桩土相互作用研究中的合理性. ...
Dynamic stiffness and damping of pile
1
1974
... Winkler模型[10 ] 将地基视为由若干互相独立的弹簧组成的弹性体,用弹性系数描述土体的变形特性,具有概念明确、计算简单的特点,但该理论忽略了土体变形连续性,不能很好地反映实际情况.Novak[11 ] 应用平面应变理论假设桩周土为一组无限薄的土层,解决了Winkler地基模型无法考虑土体连续性的问题,但不能表征土体位移和应力沿纵向的梯度变化.因此,Novak等[12 ] 将桩周土视为三维连续介质,通过偏微分方程描述土体各物理量沿纵向的变化规律,并推导了均质土中单桩水平振动解析解,然而该方法夸大了地基的深度和扩散能力.针对上述3种模型的缺陷,Pasternak模型[13 ] 引入了土体反力系数和土体切变模量这两个独立的地基参数,在考虑土体变形连续性的同时又满足了力学概念清晰、计算简便的工程需求.Fwa等[14 ] 统计了36组分别来自Pasternak地基模型和其他模型计算结果的平均误差,分析结果表明Pasternak模型计算误差最小.戴自航等[15 ] 、朱彦鹏等[16 ] 、江杰等[17 ] 、张玲等[18 ] 分别基于Pasternak地基模型研究了单桩水平承载特性,通过试验和有限元模拟验证了Pasternak模型应用于桩土相互作用研究中的合理性. ...
Soil-pile interaction in horizontal vibration
1
1977
... Winkler模型[10 ] 将地基视为由若干互相独立的弹簧组成的弹性体,用弹性系数描述土体的变形特性,具有概念明确、计算简单的特点,但该理论忽略了土体变形连续性,不能很好地反映实际情况.Novak[11 ] 应用平面应变理论假设桩周土为一组无限薄的土层,解决了Winkler地基模型无法考虑土体连续性的问题,但不能表征土体位移和应力沿纵向的梯度变化.因此,Novak等[12 ] 将桩周土视为三维连续介质,通过偏微分方程描述土体各物理量沿纵向的变化规律,并推导了均质土中单桩水平振动解析解,然而该方法夸大了地基的深度和扩散能力.针对上述3种模型的缺陷,Pasternak模型[13 ] 引入了土体反力系数和土体切变模量这两个独立的地基参数,在考虑土体变形连续性的同时又满足了力学概念清晰、计算简便的工程需求.Fwa等[14 ] 统计了36组分别来自Pasternak地基模型和其他模型计算结果的平均误差,分析结果表明Pasternak模型计算误差最小.戴自航等[15 ] 、朱彦鹏等[16 ] 、江杰等[17 ] 、张玲等[18 ] 分别基于Pasternak地基模型研究了单桩水平承载特性,通过试验和有限元模拟验证了Pasternak模型应用于桩土相互作用研究中的合理性. ...
2
1954
... Winkler模型[10 ] 将地基视为由若干互相独立的弹簧组成的弹性体,用弹性系数描述土体的变形特性,具有概念明确、计算简单的特点,但该理论忽略了土体变形连续性,不能很好地反映实际情况.Novak[11 ] 应用平面应变理论假设桩周土为一组无限薄的土层,解决了Winkler地基模型无法考虑土体连续性的问题,但不能表征土体位移和应力沿纵向的梯度变化.因此,Novak等[12 ] 将桩周土视为三维连续介质,通过偏微分方程描述土体各物理量沿纵向的变化规律,并推导了均质土中单桩水平振动解析解,然而该方法夸大了地基的深度和扩散能力.针对上述3种模型的缺陷,Pasternak模型[13 ] 引入了土体反力系数和土体切变模量这两个独立的地基参数,在考虑土体变形连续性的同时又满足了力学概念清晰、计算简便的工程需求.Fwa等[14 ] 统计了36组分别来自Pasternak地基模型和其他模型计算结果的平均误差,分析结果表明Pasternak模型计算误差最小.戴自航等[15 ] 、朱彦鹏等[16 ] 、江杰等[17 ] 、张玲等[18 ] 分别基于Pasternak地基模型研究了单桩水平承载特性,通过试验和有限元模拟验证了Pasternak模型应用于桩土相互作用研究中的合理性. ...
... 二维平面应变条件下Pasternak地基模型的桩身挠曲微分方程[13 ] 可表示为 ...
Use of Pasternak foundation model in concrete pavement analysis
1
1996
... Winkler模型[10 ] 将地基视为由若干互相独立的弹簧组成的弹性体,用弹性系数描述土体的变形特性,具有概念明确、计算简单的特点,但该理论忽略了土体变形连续性,不能很好地反映实际情况.Novak[11 ] 应用平面应变理论假设桩周土为一组无限薄的土层,解决了Winkler地基模型无法考虑土体连续性的问题,但不能表征土体位移和应力沿纵向的梯度变化.因此,Novak等[12 ] 将桩周土视为三维连续介质,通过偏微分方程描述土体各物理量沿纵向的变化规律,并推导了均质土中单桩水平振动解析解,然而该方法夸大了地基的深度和扩散能力.针对上述3种模型的缺陷,Pasternak模型[13 ] 引入了土体反力系数和土体切变模量这两个独立的地基参数,在考虑土体变形连续性的同时又满足了力学概念清晰、计算简便的工程需求.Fwa等[14 ] 统计了36组分别来自Pasternak地基模型和其他模型计算结果的平均误差,分析结果表明Pasternak模型计算误差最小.戴自航等[15 ] 、朱彦鹏等[16 ] 、江杰等[17 ] 、张玲等[18 ] 分别基于Pasternak地基模型研究了单桩水平承载特性,通过试验和有限元模拟验证了Pasternak模型应用于桩土相互作用研究中的合理性. ...
水平荷载单桩计算的综合刚度和双参数法杆系有限元数值解
2
2016
... Winkler模型[10 ] 将地基视为由若干互相独立的弹簧组成的弹性体,用弹性系数描述土体的变形特性,具有概念明确、计算简单的特点,但该理论忽略了土体变形连续性,不能很好地反映实际情况.Novak[11 ] 应用平面应变理论假设桩周土为一组无限薄的土层,解决了Winkler地基模型无法考虑土体连续性的问题,但不能表征土体位移和应力沿纵向的梯度变化.因此,Novak等[12 ] 将桩周土视为三维连续介质,通过偏微分方程描述土体各物理量沿纵向的变化规律,并推导了均质土中单桩水平振动解析解,然而该方法夸大了地基的深度和扩散能力.针对上述3种模型的缺陷,Pasternak模型[13 ] 引入了土体反力系数和土体切变模量这两个独立的地基参数,在考虑土体变形连续性的同时又满足了力学概念清晰、计算简便的工程需求.Fwa等[14 ] 统计了36组分别来自Pasternak地基模型和其他模型计算结果的平均误差,分析结果表明Pasternak模型计算误差最小.戴自航等[15 ] 、朱彦鹏等[16 ] 、江杰等[17 ] 、张玲等[18 ] 分别基于Pasternak地基模型研究了单桩水平承载特性,通过试验和有限元模拟验证了Pasternak模型应用于桩土相互作用研究中的合理性. ...
... 传统有限杆单元法假定桩身为小变形弹性体,其单元刚度矩阵[15 ] 为 ...
Numerical solution of link finite element based on composite stiffness and bi-parameter method for computation of laterally loaded single pile
2
2016
... Winkler模型[10 ] 将地基视为由若干互相独立的弹簧组成的弹性体,用弹性系数描述土体的变形特性,具有概念明确、计算简单的特点,但该理论忽略了土体变形连续性,不能很好地反映实际情况.Novak[11 ] 应用平面应变理论假设桩周土为一组无限薄的土层,解决了Winkler地基模型无法考虑土体连续性的问题,但不能表征土体位移和应力沿纵向的梯度变化.因此,Novak等[12 ] 将桩周土视为三维连续介质,通过偏微分方程描述土体各物理量沿纵向的变化规律,并推导了均质土中单桩水平振动解析解,然而该方法夸大了地基的深度和扩散能力.针对上述3种模型的缺陷,Pasternak模型[13 ] 引入了土体反力系数和土体切变模量这两个独立的地基参数,在考虑土体变形连续性的同时又满足了力学概念清晰、计算简便的工程需求.Fwa等[14 ] 统计了36组分别来自Pasternak地基模型和其他模型计算结果的平均误差,分析结果表明Pasternak模型计算误差最小.戴自航等[15 ] 、朱彦鹏等[16 ] 、江杰等[17 ] 、张玲等[18 ] 分别基于Pasternak地基模型研究了单桩水平承载特性,通过试验和有限元模拟验证了Pasternak模型应用于桩土相互作用研究中的合理性. ...
... 传统有限杆单元法假定桩身为小变形弹性体,其单元刚度矩阵[15 ] 为 ...
基于Pasternak地基模型的非线性土抗力-桩身侧向位移曲线在基坑支护桩中的应用
1
2022
... Winkler模型[10 ] 将地基视为由若干互相独立的弹簧组成的弹性体,用弹性系数描述土体的变形特性,具有概念明确、计算简单的特点,但该理论忽略了土体变形连续性,不能很好地反映实际情况.Novak[11 ] 应用平面应变理论假设桩周土为一组无限薄的土层,解决了Winkler地基模型无法考虑土体连续性的问题,但不能表征土体位移和应力沿纵向的梯度变化.因此,Novak等[12 ] 将桩周土视为三维连续介质,通过偏微分方程描述土体各物理量沿纵向的变化规律,并推导了均质土中单桩水平振动解析解,然而该方法夸大了地基的深度和扩散能力.针对上述3种模型的缺陷,Pasternak模型[13 ] 引入了土体反力系数和土体切变模量这两个独立的地基参数,在考虑土体变形连续性的同时又满足了力学概念清晰、计算简便的工程需求.Fwa等[14 ] 统计了36组分别来自Pasternak地基模型和其他模型计算结果的平均误差,分析结果表明Pasternak模型计算误差最小.戴自航等[15 ] 、朱彦鹏等[16 ] 、江杰等[17 ] 、张玲等[18 ] 分别基于Pasternak地基模型研究了单桩水平承载特性,通过试验和有限元模拟验证了Pasternak模型应用于桩土相互作用研究中的合理性. ...
Application of nonlinear soil resistance-pile lateral displacement curve based on Pasternak foundation model in foundation pit retaining piles
1
2022
... Winkler模型[10 ] 将地基视为由若干互相独立的弹簧组成的弹性体,用弹性系数描述土体的变形特性,具有概念明确、计算简单的特点,但该理论忽略了土体变形连续性,不能很好地反映实际情况.Novak[11 ] 应用平面应变理论假设桩周土为一组无限薄的土层,解决了Winkler地基模型无法考虑土体连续性的问题,但不能表征土体位移和应力沿纵向的梯度变化.因此,Novak等[12 ] 将桩周土视为三维连续介质,通过偏微分方程描述土体各物理量沿纵向的变化规律,并推导了均质土中单桩水平振动解析解,然而该方法夸大了地基的深度和扩散能力.针对上述3种模型的缺陷,Pasternak模型[13 ] 引入了土体反力系数和土体切变模量这两个独立的地基参数,在考虑土体变形连续性的同时又满足了力学概念清晰、计算简便的工程需求.Fwa等[14 ] 统计了36组分别来自Pasternak地基模型和其他模型计算结果的平均误差,分析结果表明Pasternak模型计算误差最小.戴自航等[15 ] 、朱彦鹏等[16 ] 、江杰等[17 ] 、张玲等[18 ] 分别基于Pasternak地基模型研究了单桩水平承载特性,通过试验和有限元模拟验证了Pasternak模型应用于桩土相互作用研究中的合理性. ...
基于Timoshenko-Pasternak 模型的多向受荷桩水平动力响应分析
1
2022
... Winkler模型[10 ] 将地基视为由若干互相独立的弹簧组成的弹性体,用弹性系数描述土体的变形特性,具有概念明确、计算简单的特点,但该理论忽略了土体变形连续性,不能很好地反映实际情况.Novak[11 ] 应用平面应变理论假设桩周土为一组无限薄的土层,解决了Winkler地基模型无法考虑土体连续性的问题,但不能表征土体位移和应力沿纵向的梯度变化.因此,Novak等[12 ] 将桩周土视为三维连续介质,通过偏微分方程描述土体各物理量沿纵向的变化规律,并推导了均质土中单桩水平振动解析解,然而该方法夸大了地基的深度和扩散能力.针对上述3种模型的缺陷,Pasternak模型[13 ] 引入了土体反力系数和土体切变模量这两个独立的地基参数,在考虑土体变形连续性的同时又满足了力学概念清晰、计算简便的工程需求.Fwa等[14 ] 统计了36组分别来自Pasternak地基模型和其他模型计算结果的平均误差,分析结果表明Pasternak模型计算误差最小.戴自航等[15 ] 、朱彦鹏等[16 ] 、江杰等[17 ] 、张玲等[18 ] 分别基于Pasternak地基模型研究了单桩水平承载特性,通过试验和有限元模拟验证了Pasternak模型应用于桩土相互作用研究中的合理性. ...
Horizontal dynamic response analysis of multi-directional loaded pile based on Timoshenko-Pasternak model
1
2022
... Winkler模型[10 ] 将地基视为由若干互相独立的弹簧组成的弹性体,用弹性系数描述土体的变形特性,具有概念明确、计算简单的特点,但该理论忽略了土体变形连续性,不能很好地反映实际情况.Novak[11 ] 应用平面应变理论假设桩周土为一组无限薄的土层,解决了Winkler地基模型无法考虑土体连续性的问题,但不能表征土体位移和应力沿纵向的梯度变化.因此,Novak等[12 ] 将桩周土视为三维连续介质,通过偏微分方程描述土体各物理量沿纵向的变化规律,并推导了均质土中单桩水平振动解析解,然而该方法夸大了地基的深度和扩散能力.针对上述3种模型的缺陷,Pasternak模型[13 ] 引入了土体反力系数和土体切变模量这两个独立的地基参数,在考虑土体变形连续性的同时又满足了力学概念清晰、计算简便的工程需求.Fwa等[14 ] 统计了36组分别来自Pasternak地基模型和其他模型计算结果的平均误差,分析结果表明Pasternak模型计算误差最小.戴自航等[15 ] 、朱彦鹏等[16 ] 、江杰等[17 ] 、张玲等[18 ] 分别基于Pasternak地基模型研究了单桩水平承载特性,通过试验和有限元模拟验证了Pasternak模型应用于桩土相互作用研究中的合理性. ...
基于改进Pasternak地基模型的桩柱式桥墩受力变形分析
2
2022
... Winkler模型[10 ] 将地基视为由若干互相独立的弹簧组成的弹性体,用弹性系数描述土体的变形特性,具有概念明确、计算简单的特点,但该理论忽略了土体变形连续性,不能很好地反映实际情况.Novak[11 ] 应用平面应变理论假设桩周土为一组无限薄的土层,解决了Winkler地基模型无法考虑土体连续性的问题,但不能表征土体位移和应力沿纵向的梯度变化.因此,Novak等[12 ] 将桩周土视为三维连续介质,通过偏微分方程描述土体各物理量沿纵向的变化规律,并推导了均质土中单桩水平振动解析解,然而该方法夸大了地基的深度和扩散能力.针对上述3种模型的缺陷,Pasternak模型[13 ] 引入了土体反力系数和土体切变模量这两个独立的地基参数,在考虑土体变形连续性的同时又满足了力学概念清晰、计算简便的工程需求.Fwa等[14 ] 统计了36组分别来自Pasternak地基模型和其他模型计算结果的平均误差,分析结果表明Pasternak模型计算误差最小.戴自航等[15 ] 、朱彦鹏等[16 ] 、江杰等[17 ] 、张玲等[18 ] 分别基于Pasternak地基模型研究了单桩水平承载特性,通过试验和有限元模拟验证了Pasternak模型应用于桩土相互作用研究中的合理性. ...
... 值得注意的是,上述研究多局限于水平荷载或扭矩的单一作用,实际工程中桩顶往往同时作用有水平力和扭矩,常规的桩基设计方法将不同形式的荷载简单叠加,不考虑多向荷载对桩身响应的影响,最终导致设计方案不合理,甚至造成安全事故[18 ] .为此,Hu等[19 ] 通过离心模型试验研究了水平荷载和扭矩共同作用下桩基的内力和位移,结果表明,水平荷载的存在会对桩身抗扭承载能力有一定的影响.孔令刚等[20 ] 利用经验性耦合因子量化了土体侧阻力对桩基抗扭承载力的耦合效应.Georgiadis等[21 ] 结合上限分析和有限元方法探讨了扭矩对单桩极限侧阻力的影响,并给出了扭矩作用下单桩侧向极限承载力系数.然而,当前已有联合受荷桩的研究多限于静力组合,实际工程中,风、水流等外荷载会使结构产生不容忽视的动力效应[22 ] ,且施工或使用过程中的偏心荷载会使桩身受扭,在处理这种复杂受荷情况时不应简化为单一静力或动力问题. ...
Analysis of pile-column pier based on modified Pasternak foundation model
2
2022
... Winkler模型[10 ] 将地基视为由若干互相独立的弹簧组成的弹性体,用弹性系数描述土体的变形特性,具有概念明确、计算简单的特点,但该理论忽略了土体变形连续性,不能很好地反映实际情况.Novak[11 ] 应用平面应变理论假设桩周土为一组无限薄的土层,解决了Winkler地基模型无法考虑土体连续性的问题,但不能表征土体位移和应力沿纵向的梯度变化.因此,Novak等[12 ] 将桩周土视为三维连续介质,通过偏微分方程描述土体各物理量沿纵向的变化规律,并推导了均质土中单桩水平振动解析解,然而该方法夸大了地基的深度和扩散能力.针对上述3种模型的缺陷,Pasternak模型[13 ] 引入了土体反力系数和土体切变模量这两个独立的地基参数,在考虑土体变形连续性的同时又满足了力学概念清晰、计算简便的工程需求.Fwa等[14 ] 统计了36组分别来自Pasternak地基模型和其他模型计算结果的平均误差,分析结果表明Pasternak模型计算误差最小.戴自航等[15 ] 、朱彦鹏等[16 ] 、江杰等[17 ] 、张玲等[18 ] 分别基于Pasternak地基模型研究了单桩水平承载特性,通过试验和有限元模拟验证了Pasternak模型应用于桩土相互作用研究中的合理性. ...
... 值得注意的是,上述研究多局限于水平荷载或扭矩的单一作用,实际工程中桩顶往往同时作用有水平力和扭矩,常规的桩基设计方法将不同形式的荷载简单叠加,不考虑多向荷载对桩身响应的影响,最终导致设计方案不合理,甚至造成安全事故[18 ] .为此,Hu等[19 ] 通过离心模型试验研究了水平荷载和扭矩共同作用下桩基的内力和位移,结果表明,水平荷载的存在会对桩身抗扭承载能力有一定的影响.孔令刚等[20 ] 利用经验性耦合因子量化了土体侧阻力对桩基抗扭承载力的耦合效应.Georgiadis等[21 ] 结合上限分析和有限元方法探讨了扭矩对单桩极限侧阻力的影响,并给出了扭矩作用下单桩侧向极限承载力系数.然而,当前已有联合受荷桩的研究多限于静力组合,实际工程中,风、水流等外荷载会使结构产生不容忽视的动力效应[22 ] ,且施工或使用过程中的偏心荷载会使桩身受扭,在处理这种复杂受荷情况时不应简化为单一静力或动力问题. ...
Influence of torque on lateral capacity of drilled shafts in sands
1
2006
... 值得注意的是,上述研究多局限于水平荷载或扭矩的单一作用,实际工程中桩顶往往同时作用有水平力和扭矩,常规的桩基设计方法将不同形式的荷载简单叠加,不考虑多向荷载对桩身响应的影响,最终导致设计方案不合理,甚至造成安全事故[18 ] .为此,Hu等[19 ] 通过离心模型试验研究了水平荷载和扭矩共同作用下桩基的内力和位移,结果表明,水平荷载的存在会对桩身抗扭承载能力有一定的影响.孔令刚等[20 ] 利用经验性耦合因子量化了土体侧阻力对桩基抗扭承载力的耦合效应.Georgiadis等[21 ] 结合上限分析和有限元方法探讨了扭矩对单桩极限侧阻力的影响,并给出了扭矩作用下单桩侧向极限承载力系数.然而,当前已有联合受荷桩的研究多限于静力组合,实际工程中,风、水流等外荷载会使结构产生不容忽视的动力效应[22 ] ,且施工或使用过程中的偏心荷载会使桩身受扭,在处理这种复杂受荷情况时不应简化为单一静力或动力问题. ...
群桩扭转非线性模型
2
2009
... 值得注意的是,上述研究多局限于水平荷载或扭矩的单一作用,实际工程中桩顶往往同时作用有水平力和扭矩,常规的桩基设计方法将不同形式的荷载简单叠加,不考虑多向荷载对桩身响应的影响,最终导致设计方案不合理,甚至造成安全事故[18 ] .为此,Hu等[19 ] 通过离心模型试验研究了水平荷载和扭矩共同作用下桩基的内力和位移,结果表明,水平荷载的存在会对桩身抗扭承载能力有一定的影响.孔令刚等[20 ] 利用经验性耦合因子量化了土体侧阻力对桩基抗扭承载力的耦合效应.Georgiadis等[21 ] 结合上限分析和有限元方法探讨了扭矩对单桩极限侧阻力的影响,并给出了扭矩作用下单桩侧向极限承载力系数.然而,当前已有联合受荷桩的研究多限于静力组合,实际工程中,风、水流等外荷载会使结构产生不容忽视的动力效应[22 ] ,且施工或使用过程中的偏心荷载会使桩身受扭,在处理这种复杂受荷情况时不应简化为单一静力或动力问题. ...
... 扭矩作用下桩-土接触面产生环向侧摩阻力,此时桩身的控制方程[20 ] 为 ...
Nonlinear analysis of pile groups subjected to torsion
2
2009
... 值得注意的是,上述研究多局限于水平荷载或扭矩的单一作用,实际工程中桩顶往往同时作用有水平力和扭矩,常规的桩基设计方法将不同形式的荷载简单叠加,不考虑多向荷载对桩身响应的影响,最终导致设计方案不合理,甚至造成安全事故[18 ] .为此,Hu等[19 ] 通过离心模型试验研究了水平荷载和扭矩共同作用下桩基的内力和位移,结果表明,水平荷载的存在会对桩身抗扭承载能力有一定的影响.孔令刚等[20 ] 利用经验性耦合因子量化了土体侧阻力对桩基抗扭承载力的耦合效应.Georgiadis等[21 ] 结合上限分析和有限元方法探讨了扭矩对单桩极限侧阻力的影响,并给出了扭矩作用下单桩侧向极限承载力系数.然而,当前已有联合受荷桩的研究多限于静力组合,实际工程中,风、水流等外荷载会使结构产生不容忽视的动力效应[22 ] ,且施工或使用过程中的偏心荷载会使桩身受扭,在处理这种复杂受荷情况时不应简化为单一静力或动力问题. ...
... 扭矩作用下桩-土接触面产生环向侧摩阻力,此时桩身的控制方程[20 ] 为 ...
Effect of torsion on the undrained limiting lateral resistance of piles in clay
1
2020
... 值得注意的是,上述研究多局限于水平荷载或扭矩的单一作用,实际工程中桩顶往往同时作用有水平力和扭矩,常规的桩基设计方法将不同形式的荷载简单叠加,不考虑多向荷载对桩身响应的影响,最终导致设计方案不合理,甚至造成安全事故[18 ] .为此,Hu等[19 ] 通过离心模型试验研究了水平荷载和扭矩共同作用下桩基的内力和位移,结果表明,水平荷载的存在会对桩身抗扭承载能力有一定的影响.孔令刚等[20 ] 利用经验性耦合因子量化了土体侧阻力对桩基抗扭承载力的耦合效应.Georgiadis等[21 ] 结合上限分析和有限元方法探讨了扭矩对单桩极限侧阻力的影响,并给出了扭矩作用下单桩侧向极限承载力系数.然而,当前已有联合受荷桩的研究多限于静力组合,实际工程中,风、水流等外荷载会使结构产生不容忽视的动力效应[22 ] ,且施工或使用过程中的偏心荷载会使桩身受扭,在处理这种复杂受荷情况时不应简化为单一静力或动力问题. ...
Horizontal dynamic response of pile in unsaturated soil considering its construction disturbance effect
2
2022
... 值得注意的是,上述研究多局限于水平荷载或扭矩的单一作用,实际工程中桩顶往往同时作用有水平力和扭矩,常规的桩基设计方法将不同形式的荷载简单叠加,不考虑多向荷载对桩身响应的影响,最终导致设计方案不合理,甚至造成安全事故[18 ] .为此,Hu等[19 ] 通过离心模型试验研究了水平荷载和扭矩共同作用下桩基的内力和位移,结果表明,水平荷载的存在会对桩身抗扭承载能力有一定的影响.孔令刚等[20 ] 利用经验性耦合因子量化了土体侧阻力对桩基抗扭承载力的耦合效应.Georgiadis等[21 ] 结合上限分析和有限元方法探讨了扭矩对单桩极限侧阻力的影响,并给出了扭矩作用下单桩侧向极限承载力系数.然而,当前已有联合受荷桩的研究多限于静力组合,实际工程中,风、水流等外荷载会使结构产生不容忽视的动力效应[22 ] ,且施工或使用过程中的偏心荷载会使桩身受扭,在处理这种复杂受荷情况时不应简化为单一静力或动力问题. ...
... 式中:t 为地基土的剪切层厚度,可取11倍桩径[22 ] . ...
Formulas for an infinitely long Bernoulli-Euler beam on the Pasternak model
1
2004
... 式中:G s 为土体切变模量.本文采用Tanahashi[23 ] 提出的经验公式确定土体切变模量 ...
Analytical solution for horizontal vibration of end-bearing single pile in radially heterogeneous saturated soil
3
2023
... 目前水平动荷载和扭矩共同作用下的桩基受力变形分析相对较少,难以直接有效地验证本文方法的可靠性.为此分别考虑水平简谐荷载和扭矩单独作用两种情况,将其计算结果分别与文献[24 ⇓ -26 ]进行对比,再进行有限元建模,进一步验证本文方法的可靠性. ...
... 基于文献[24 ]中桩土参数通过有限元软件建立三维实体单元模型,其中桩长L =20 m,桩径D =0.5 m,采用动力隐式分析步,水平简谐荷载幅值Q 0 =100 kN,频率f =16 Hz;桩顶自由,桩底嵌固.桩周土采用Mohr-Coulomb理想弹塑性模型,桩身采用C3D8单元模型,桩-土其他参数如表1 所示. ...
... 图4 给出了桩身水平位移和弯矩的分布曲线.由图4 可知,本文所提出的计算方法与文献[24 ]中的解析解以及有限元模拟(FEM)结果均吻合较好,表明本文方法能够较为准确地预测水平简谐荷载作用下桩基内力和位移. ...
2
2015
... 目前水平动荷载和扭矩共同作用下的桩基受力变形分析相对较少,难以直接有效地验证本文方法的可靠性.为此分别考虑水平简谐荷载和扭矩单独作用两种情况,将其计算结果分别与文献[24 ⇓ -26 ]进行对比,再进行有限元建模,进一步验证本文方法的可靠性. ...
... 吕冰[25 ] 通过模型试验研究水平简谐荷载作用下单桩承载性能.试验地基土密度为 1 908 kg/m3 ;内摩擦角为36°;黏聚力为11.8 kPa;阻尼比为0.05;弹性模量为8.5 MPa.模型桩长900 mm;直径60 mm.水平荷载幅值H 0 =274.4 N;f =6 Hz;加载点位于泥面以上60 mm处.图5 给出了水平荷载作用下桩身弯矩计算结果和试验结果的对比.从图5 可以看出,桩身弯矩沿桩埋深先增大后减小,弯矩最大值出现在距离桩顶1/3深度处.总体上来看,本文方法计算结果与试验结果吻合较好. ...
2
2015
... 目前水平动荷载和扭矩共同作用下的桩基受力变形分析相对较少,难以直接有效地验证本文方法的可靠性.为此分别考虑水平简谐荷载和扭矩单独作用两种情况,将其计算结果分别与文献[24 ⇓ -26 ]进行对比,再进行有限元建模,进一步验证本文方法的可靠性. ...
... 吕冰[25 ] 通过模型试验研究水平简谐荷载作用下单桩承载性能.试验地基土密度为 1 908 kg/m3 ;内摩擦角为36°;黏聚力为11.8 kPa;阻尼比为0.05;弹性模量为8.5 MPa.模型桩长900 mm;直径60 mm.水平荷载幅值H 0 =274.4 N;f =6 Hz;加载点位于泥面以上60 mm处.图5 给出了水平荷载作用下桩身弯矩计算结果和试验结果的对比.从图5 可以看出,桩身弯矩沿桩埋深先增大后减小,弯矩最大值出现在距离桩顶1/3深度处.总体上来看,本文方法计算结果与试验结果吻合较好. ...
近海复杂环境下的H-M-T 受荷桩内力位移分析
4
2014
... 目前水平动荷载和扭矩共同作用下的桩基受力变形分析相对较少,难以直接有效地验证本文方法的可靠性.为此分别考虑水平简谐荷载和扭矩单独作用两种情况,将其计算结果分别与文献[24 ⇓ -26 ]进行对比,再进行有限元建模,进一步验证本文方法的可靠性. ...
... 基于文献[26 ]中的桩土参数建立三维实体有限元数值模型,其中桩长L =9 m,桩径D =0.4 m,桩底嵌固,桩顶自由,桩顶作用T =40 kN·m的扭矩,桩周土体采用Mohr-Coulomb理想弹塑性模型,桩身采用C3D8单元,桩-土体系其他参数如表3 所示,数值建模方法同4.1节. ...
... 图6 给出了本文方法、有限元数值模拟以及文献[26 ]中计算结果的对比.从图中可以看出,本文提出的计算方法与有限元模拟值以及文献[26 ]中计算值均有较好的一致性,进一步证明了本文方法的可靠性. ...
... ]中计算结果的对比.从图中可以看出,本文提出的计算方法与有限元模拟值以及文献[26 ]中计算值均有较好的一致性,进一步证明了本文方法的可靠性. ...
Analysis of piles under H-M-T combined loading in offshore complex environment
4
2014
... 目前水平动荷载和扭矩共同作用下的桩基受力变形分析相对较少,难以直接有效地验证本文方法的可靠性.为此分别考虑水平简谐荷载和扭矩单独作用两种情况,将其计算结果分别与文献[24 ⇓ -26 ]进行对比,再进行有限元建模,进一步验证本文方法的可靠性. ...
... 基于文献[26 ]中的桩土参数建立三维实体有限元数值模型,其中桩长L =9 m,桩径D =0.4 m,桩底嵌固,桩顶自由,桩顶作用T =40 kN·m的扭矩,桩周土体采用Mohr-Coulomb理想弹塑性模型,桩身采用C3D8单元,桩-土体系其他参数如表3 所示,数值建模方法同4.1节. ...
... 图6 给出了本文方法、有限元数值模拟以及文献[26 ]中计算结果的对比.从图中可以看出,本文提出的计算方法与有限元模拟值以及文献[26 ]中计算值均有较好的一致性,进一步证明了本文方法的可靠性. ...
... ]中计算结果的对比.从图中可以看出,本文提出的计算方法与有限元模拟值以及文献[26 ]中计算值均有较好的一致性,进一步证明了本文方法的可靠性. ...