早期疲劳失效是指远在设计寿命前就概率性地发生的疲劳破坏,这类失效会对设备以及人员生命构成严重的威胁.即使在满足设计规范及其关于安全系数的要求后,工程结构件仍会偶尔发生早期疲劳失效[1⇓-3].这引起了国内外研究人员的重视,并将其归因于结构材料在危险位置存在微小缺陷[4⇓-6],但如何避免该问题却一直缺少理论或机理上的依据.实际上,相比于常规试验所用的平板、圆棒等标准试验件(微观组织相对较为均匀),工程结构件的几何形状复杂,并且受加工工艺限制,材料内部微观组织结构(包含微观缺陷)的分布会存在较大的不均匀性[7⇓-9].另外,在结构件的加工、运输和使用过程中,一些表面划痕、腐蚀坑或其他概率性的微小缺陷往往是不可避免的[4].这些因素导致了结构材料的强度寿命特性的离散性.
在常规的结构强度或抗疲劳设计中,通常根据设计手册或规范要使用安全系数,以涵盖材料加工制造和服役期间的各种不确定性[10⇓⇓⇓-14].黄朝晖等[12]采用ANSYS热流固耦合方法对某型火箭发动机涡轮叶片进行改型设计分析,以满足规定的高周疲劳安全系数要求.Vaara等[13]认为将加工残余应力视为平均应力而忽略其释放(如在循环塑性或环境温度升高的情形下),将会导致所需安全系数的增加.Sola等[14]基于临界平面疲劳理论对曲轴进行有限元分析,评估了发动机功率增加对安全系数的影响.但是,总的来说,安全系数法在本质上只是利用材料强度寿命的中值特性,并暗中假定其离散范围,一旦材料的实际离散性过大,就容易引发结构的早期疲劳失效.因此,考虑到材料强度寿命特性的离散性对于实际结构的影响,可靠性在强度或抗疲劳设计中越来越被重视.丁然等[15]结合代数和计算可靠度保守估计的方法,建立了当损伤服从不同概率分布时的疲劳可靠度保守估计的条件.韦益夫等[16]提出确定响应面法样本点权重的改进移动最小二乘法,对结构的可靠性问题进行分析.Luo等[17]将机器学习和蒙特卡罗方法相结合,对复合材料层合板和涡轮叶片盘的可靠性和失效概率进行了高效预测.
另一方面,在一些设计手册或规范中,对于结构材料的强度特性,多以拉伸极限范围(一般是中值的±10%范围)来规定[10-11].需要注意的是,这些范围要求在本质上通常不是针对少量取样试验结果,而是对应于强度特性概率分布的3-sigma可靠性要求.只有根据实际材料的离散性和可靠性要求来规定所需的安全系数,才能有效避免结构的早期疲劳失效.考虑到材料的疲劳强度特性参数[7⇓⇓-10,18]通常有多个,如果对每个参数都通过试验来确定其离散性并计算可靠性,对于实际工程来说是繁琐的甚至是不现实的,必须依据相应的机理进行统一表征,才能便于工程应用.鉴于影响结构早期疲劳失效的因素较多[1⇓⇓⇓-5],如多轴应力状态、结构的几何尺寸、复杂的应力谱、材料的强度寿命特性的离散性等,本文以某柴油发动机曲轴为研究对象,主要关注材料的强度特性离散性对其早期疲劳失效的影响.在通过取样试验确定材料离散性时[10-11],虽然以疲劳或拉伸强度取样试验确定更直接,但是在实际工程中,现有材料离散性是通过冲击试验来获得的.因此,基于冲击功离散性进行曲轴强度可靠性和早期疲劳失效评价,具有现实应用背景和研究价值.
本文考虑到结构材料的强度寿命离散性的机理在于微观组织结构的不均匀性,用初始损伤的离散性来统一表征强度寿命特性的离散性.然后,对于某柴油发动机曲轴锻件开展冲击取样试验,并由冲击功的离散性估计疲劳极限和初始损伤的离散性,而疲劳极限均值则由曲轴单拐的结构疲劳试验确定.最后,建立了考虑材料实际离散性的安全系数与可靠性的定量关系,根据被测材料的疲劳极限离散性来分析其可靠性.结果表明,实际材料过大的离散性使得疲劳可靠性过低,这是导致曲轴发生概率性早期疲劳失效的主要原因.
1 强度寿命离散的机理及表征
材料力学特性通常可分为组织敏感和组织钝感两类[8].组织钝感类主要是变形特性,如弹性、塑性变形特性等,它们是某个区域内所有微观组织的整体行为,因此其离散性一般很小,例如不同工艺、型号的钢材,其弹性模量基本都在210 GPa左右.而疲劳强度、疲劳寿命等则是高度组织敏感的特性,因为它们主要决定于材料内的最弱点行为[4](weakest point theory).因此,在同一材料的不同部位,这类强度特性会由于微观组织的不均匀性而呈较大的离散性[7⇓-9].值得注意的是,由塑性变形导致的失效,其相应的强度特性如屈服强度、延伸率等则比较特殊,一方面,它们与晶粒粗细等微观结构形式密切相关,呈组织敏感的特征;另一方面,在变形过程中,它们又是某个区域内的整体行为,故而其离散性较小,呈组织钝感特性.本文主要关注由材料离散性导致的结构可靠性和安全性问题,故只考虑组织敏感的疲劳极限、拉伸极限、冲击功等强度寿命特性及其离散性的内在关联,为了方便,以下“强度寿命特性”指的是此类组织敏感量,它们共同的特点是具有较大的离散性,且都是由微观组织结构分布的不均匀性所导致,因此,可以用初始损伤的离散性进行统一表征.明确定量的材料离散性指标后,就可以用其来判断结构材料的均匀性是否合格,或者根据实际离散性指标来调整设计中的安全系数要求.
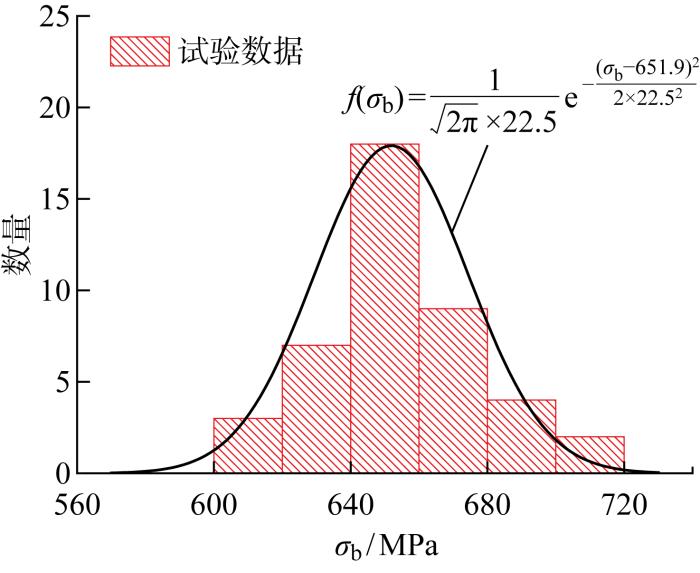
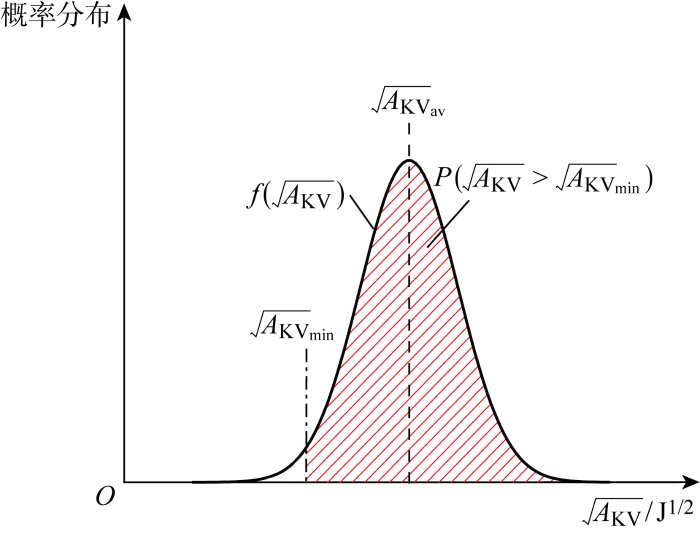
受材料成型及加工工艺的影响,复杂结构的材料内部微观组织(包含微观缺陷)分布通常是不均匀和随机的,使得不同位置的强度寿命各不相同且具有概率性和随机性的分布特征.正态分布被广泛应用于材料强度寿命特性的概率统计分析[10],以拉伸极限为例,其概率密度函数可被表示为
图1
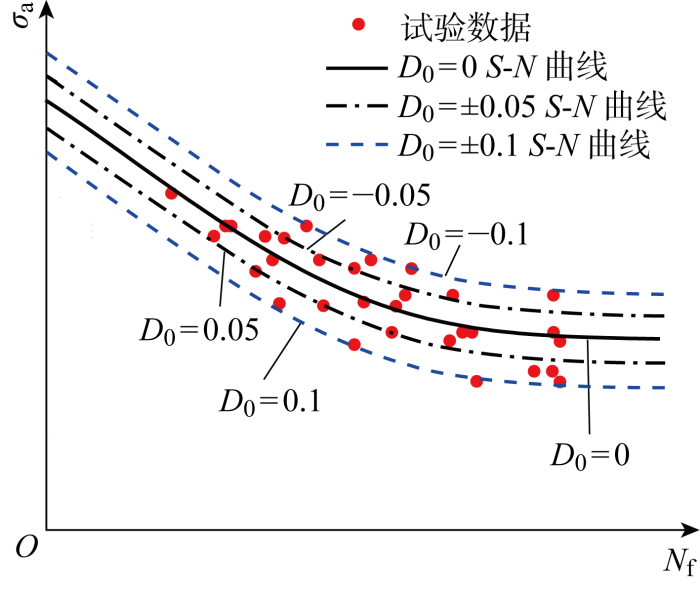
不同强度寿命特性的离散性是由微观组织分布的不均匀性所致,基于近期的研究[20],可用材料的初始损伤D0的离散性来统一表征.将强度取样试验结果的均值或期望记为材料名义强度,如果有取样试件的实测强度正好为名义强度,则意味着其微观组织结构(包含微观缺陷)就正好处于其平均或代表性状态.而实测强度与名义强度不同的取样试件,意味着微观组织结构与平均状态有所不同.用初始损伤来表示实测强度与名义强度(以拉伸极限和疲劳极限为例)的关系,则有:
式中:σ-1为对称疲劳极限;σ-1av为σ-1的均值.D0=0对应于实测强度值正好等于强度均值(即名义强度)的情况,此时材料内部仍然有微观缺陷,只不过其正好处于平均或代表性的状态.D0>0意味着微观组织比平均状态更弱,实测强度值比平均值小.而D0<0意味着微观组织比平均状态更强,实测强度值比平均值大.将初始损伤的0点定义在平均强度所对应的微观组织状态,称为初始损伤的相对性,即初始损伤是通过实测强度与其均值的差异来定义的,则:
图2
根据概率统计理论[21]和式(2)可知,初始损伤服从如下的正态分布:
式中:
2 由冲击试验确定疲劳极限的离散性
2.1 冲击功离散性和材料强度离散性的关联
在工程结构(如曲轴)的强度设计或抗疲劳设计中,对于不同供应商或批次的材料,通常需要获取它们的疲劳极限及离散性.考虑到工业效率和成本,直接进行大批量的取样疲劳试验是不现实的,通常可以采用少量疲劳试验确定疲劳极限的均值,进而采用简单快捷的冲击取样试验[22]来把握材料的离散性.需要说明的是,在按照相关工业标准[22-23]进行力学性能的取样试验时,拉伸试验的数量通常是冲击试验的1/3,拉伸强度数据过少,难以准确确定材料离散性.鉴于此,需要通过冲击取样试验结果确定材料离散性和初始损伤的概率分布.而如何由已有的冲击功离散性导出所关注的疲劳极限离散性,是工程实际中备受关注的,需要借助初始损伤建立两者之间的联系.
式中:a是裂纹长度;KI是I型裂纹应力强度因子;Y是无量纲的常数,取决于试样形状和加载模式;σ是拉应力.由此可得出:
结合式(2)、(3)、(6),为了方便,可简单假定:
式中:cb和C分别为
式中:sA和
式中:
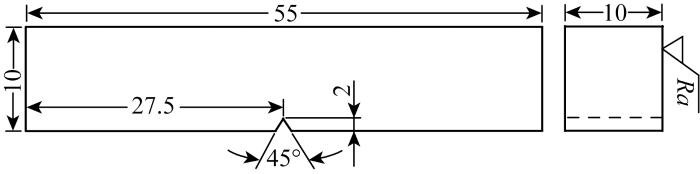
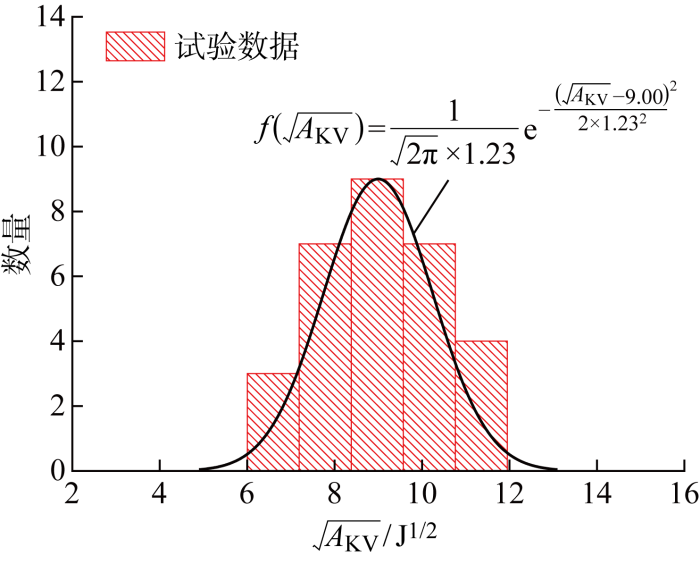
2.2 冲击试验方法和结果
图3
表1 冲击功试验数据
Tab.1
| 区域编号 | AKV/J |
|---|---|
| 1 | 77, 82, 82 |
| 2 | 49, 86, 65 |
| 3 | 92, 76, 68 |
| 4 | 100, 118, 107 |
| 5 | 94, 106, 106 |
| 6 | 116, 116, 117 |
| 7 | 65, 60, 60 |
| 8 | 80, 88, 96 |
| 9 | 49, 40, 61 |
| 10 | 86, 73, 57 |
图4
图5
图5
最小冲击功要求下的可靠度
Fig.5
Reliability under the requirement of minimum impact energy
2.3 疲劳极限概率分布的确定
对于疲劳极限的概率分布,其离散性可由冲击功的离散性估算,而其均值可由少量的疲劳极限试验获得.结合CCS规范[29]的改进升降法,对3个曲轴单拐(编号分别为#1、#2和#3)进行对称弯曲疲劳试验,然后,基于疲劳极限σ-1服从正态分布的前提,可根据Dixon-Mood法获得疲劳极限的均值σ-1av.单拐被安装在谐振式弯曲疲劳试验机上,与主动摆和从动摆组成音叉形的机械谐振机构,如图6所示,当试验件发生疲劳开裂时,试验机自动识别并终止试验.试验开始时,通过激振器施加正弦波形式的对称循环载荷,循环基数为1×107次,并观察试验件在达到指定循环基数前是否发生疲劳断裂,若未断裂,则提高应力幅,再次施加一个循环基数,直至该试验件断裂;若断裂,则对下一个试验件开展疲劳试验.
图6
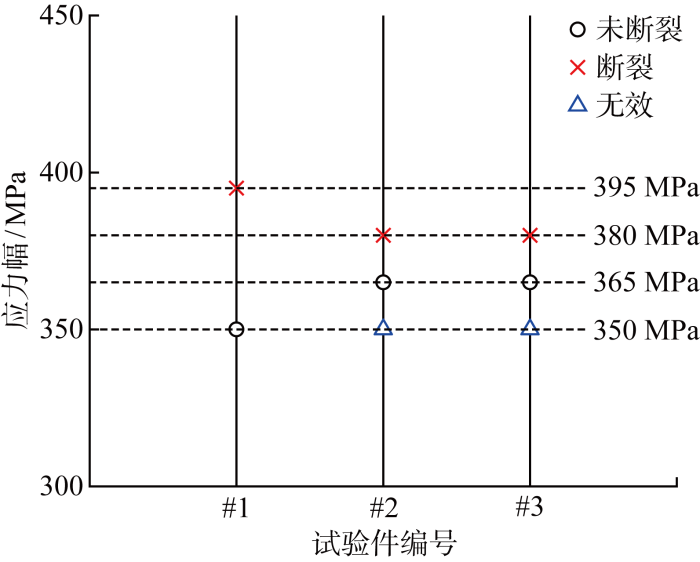
试验开始时的初始应力幅为350 MPa,在试验件#1的应力幅直接被提高至395 MPa而发生断裂后,设置每一级应力幅的增量为15 MPa,3个试验件的应力幅升降记录如图7所示.其中,由于试验件#2和#3的应力幅为365 MPa时均未断裂,两者升载前的350 MPa均被视为无效结果.
图7
表2 疲劳试验中的失效事件统计
Tab.2
| 应力幅/MPa | i | fi | ifi | i2fi |
|---|---|---|---|---|
| 395 | 1 | 1 | 1 | 1 |
| 380 | 0 | 2 | 0 | 0 |
则该样本的疲劳极限的均值Sav和标准差sS计算如下:
式中:S0为疲劳失效的最低应力幅;ΔS为每一级的应力幅增量.将表2数据代入式(12)、(13),可得Sav=377.5 MPa,sS=6.104 7 MPa.
式中:nS为样本总数,含失效事件数和未失效事件数,即nS=6;α为显著度,则
由式(9)可得该材料在3-sigma可靠性下的疲劳极限的标准差为50.9 MPa.由此可得相应的疲劳极限的概率密度函数为
由式(2)可知,
由此,利用初始损伤的离散性,就可以获得其他强度寿命特性的离散性[20],但其概率分布的均值需另由相应少量的强度寿命试验确定.
3 安全系数、可靠性和早期疲劳失效
3.1 安全系数和可靠性的关系
基于安全系数的常规强度设计方法通常依据的是材料强度的均值[10],而可靠性则与强度的离散性有关.对于同种牌号的金属材料,疲劳极限的均值一般相差不大,但离散性会由于厂家、批次的不同而出现明显的差异.材料品质的差异主要在于离散性的差异,取决于材料成型和零件加工工艺.这意味着,在同一安全系数下,不同厂家、批次的材料的可靠性会存在差异,而材料的离散性过大是导致工程结构(如曲轴)出现早期疲劳失效的主要原因.安全系数一般由设计规范或工程经验来确定,例如,取疲劳安全系数n,则所容许的最小疲劳极限σ-1s为
相应地,对于符合正态分布的疲劳极限σ-1,σ-1s的可靠性为
将其转换为标准正态分布下的随机变量X,即
令
对于工业设计常用的3-sigma可靠性,有:
所容许的最小疲劳极限为
因此,在一定的可靠性下,σ-1 s会随着材料的
将式(17)代入式(19),安全系数和标准正态随机变量X的关系可被表示为
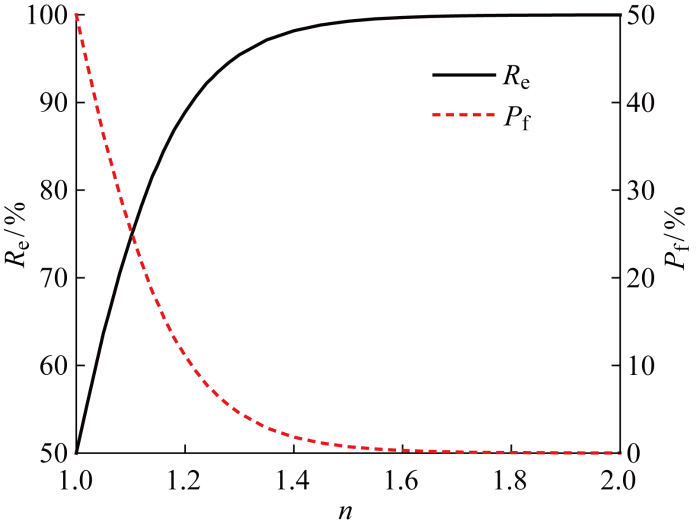
对于被测材料,安全系数与可靠性、疲劳失效概率间的定量关系如图8所示.例如,对于安全系数为1的情况,可靠性为50%,早期疲劳失效概率为50%.而对于3-sigma可靠性即可靠性为99.87%,相应的安全系数为1.70,其早期疲劳失效概率仅为0.13%,可以认为不会发生早期疲劳失效.需要说明的是,对于某个具体结构,并不意味有较大的Pf就必然发生早期疲劳失效,因为疲劳失效本身就是一种概率性发生的现象.
图8
图8
安全系数与可靠性、疲劳失效概率之间的关系
Fig.8
Safety factor versus reliability and probability of fatigue failure
3.2 可靠性与早期疲劳失效
一般来说,强度寿命设计的可靠性越低,就越易发生结构的早期疲劳失效,而这是与结构材料的具体离散性而不仅仅是设计方法相关的.对于n=1的情况,即仅按强度寿命中值进行设计时,发生早期疲劳失效的概率是50%.随着安全系数的增加,可靠性也增加,发生早期疲劳失效的概率降低.只有当可靠性大于一定值时,才可认为发生早期疲劳失效的概率足够小以至于不会发生.在常规工业设计中,该可靠性要求通常是3-sigma可靠性[10,21],对应于99.87%的安全可靠性.即当安全可靠性低于99.87%时,就可被认为有发生早期疲劳失效的较大可能性.对于本文所研究的材料,表3列举了在某些常见的可靠性下的安全系数的取值和早期疲劳失效概率,可知,若要满足3-sigma可靠性要求,安全系数需不小于1.70.
表3 不同可靠性下的安全系数、早期疲劳失效概率
Tab.3
| X | Re/% | n | Pf/% |
|---|---|---|---|
| 0 | 50.00 | 1.00 | 50.00 |
| 1.29 | 90.00 | 1.21 | 10.00 |
| 2.33 | 99.00 | 1.47 | 1.00 |
| 3.00 | 99.87 | 1.70 | 0.13 |
| 3.08 | 99.90 | 1.73 | 0.10 |
| 3.62 | 99.99 | 1.98 | 0.01 |
4 工程应用流程
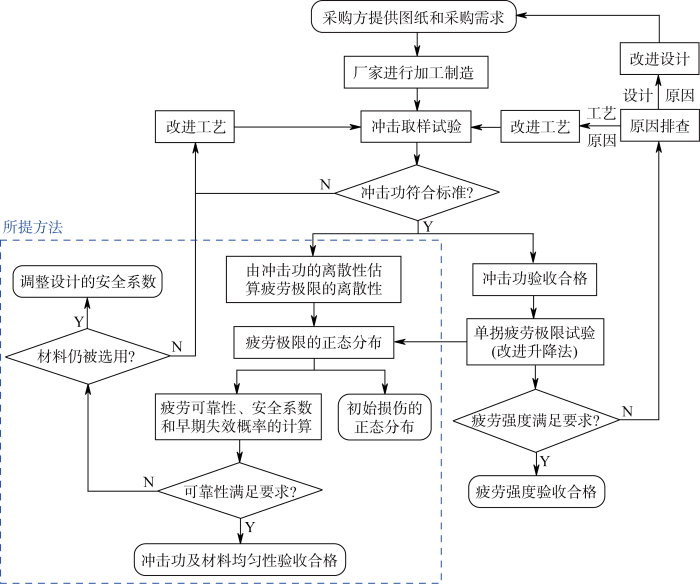
在实际工程中,上述方法可以用于判断材料均匀性是否合格,或者根据实际的离散性为可靠性设计提供一定的指导.冲击取样试验是工业标准[22-23]已规定的在曲轴验收流程中必须开展的试验,当冲击功不符合标准要求时,材料被判定为不合格,会导致零件的力学性能和可靠性的不足,需要厂家改进工艺,但是,未定量给出冲击功的离散性与可靠性之间的关系.而在强度设计过程中,设计师需对厂家生产的曲轴进行疲劳极限的抽检试验[29],并判断疲劳强度是否满足许用值,当实测强度不满足许用强度时,主要从工艺和设计两个角度排查原因.本文所提方法定量研究了冲击功离散性和疲劳可靠性之间的关联,在厂家的产品验收流程和设计师的强度设计流程之间建立了新的联系,如图9所示.当由冲击功离散性估算的可靠性不满足要求时,提供以下两个选择:① 当设计方法仍不变时,可以判定材料不合格,应改进工艺;② 当材料仍被选用时,需要调整设计的安全系数.本文所提方法可以为指导工艺或设计方法的改进以及预防早期疲劳失效提供一定的依据.
图9
图9
所提方法在工程实践中的应用流程图
Fig.9
Flow chart of application of proposed method in engineering practice
5 结论
本文基于材料强度寿命特性离散的微观机理,建立了冲击功离散性和初始损伤及强度离散性的关系,对于由34CrNi3MoA合金制成的曲轴锻件,通过冲击取样试验确定了材料的离散性,而通过曲轴单拐的结构疲劳试验确定了疲劳极限的均值.通过对比传统的安全系数设计方法,定量研究了材料离散性对于疲劳可靠性的影响.主要结论如下:
(1) 组织敏感的强度寿命特性的离散是由微观组织结构分布的不均匀性导致的,这可以用初始损伤的离散性进行统一表征.
(2) 为了便于工程应用,疲劳极限的离散性可由冲击试验数据的离散性估算,而疲劳极限概率分布的均值可由少量的疲劳试验确定.
(3) 传统设计手册的安全系数没有考虑实际材料具体的离散性,要避免曲轴的早期疲劳失效,需由材料的实际离散性计算可靠性,根据可靠性大小是否满足要求来判断.实际离散性较大的材料容易导致可靠性不足,进而有较大概率引发早期疲劳失效.
参考文献
Marine propulsion system failures—A review
[J].
Roles of microstructure, inclusion, and surface roughness on rolling contact fatigue of a wind turbine gear
[J].
Assessment of unusual failure in crankshaft of heavy-duty truck engine
[J].
Material defects as cause for the fatigue failure of metallic components
[J].
基于长短期记忆神经网络的板裂纹损伤检测方法
[J].
DOI:10.16183/j.cnki.jsjtu.2020.095
[本文引用: 2]

针对板不同位置裂纹损伤的智能分类问题,提出了一种基于长短期记忆(LSTM)神经网络的板裂纹损伤检测方法.采用Abaqus二次开发建立板裂纹损伤模型,计算高斯白噪声激励下板的加速度响应,并通过数据扩充方法生成数据集,同时考虑了噪声对损伤检测的影响.建立基于LSTM的板裂纹智能检测模型,直接将板的加速度响应作为输入,不需要额外的损伤特征提取,并以最小预测误差为目标,选择模型的超参数,优化模型配置.与多层感知机模型和基于小波包变换的多层感知机模型进行对比表明,本文提出的LSTM模型在板裂纹损伤检测中具有更高的损伤定位精度和更好的适用性.
Method for plate crack damage detection based on long short-term memory neural network
[J].
含缺陷轮盘失效概率分析流程与数值模拟
[J].
Analysis procedure and numerical simulation of failure probability of turbine disk caused by defects
[J].
结构疲劳百年研究的回顾与展望
[J].
DOI:10.3901/JME.2021.06.026
[本文引用: 3]

疲劳是机械结构最普遍的失效模式之一。自1854年第一次提出“Fatigue”(疲劳)概念以来,相关研究已有160余年的历程,逐步形成了以疲劳研究为基础的机械结构强度理论与技术,推动机械结构从经验设计走向安全设计。本文回顾了结构疲劳研究的缘起及发展历程,总结了典型失效案例对疲劳基础研究的促进作用和里程碑式成果,基于文献统计分析了最近50年本领域的代表性进展、研究热点与发展趋势。研究表明,尽管经历了百余年的不懈努力,疲劳极限、损伤易感基因、裂尖主控机制、蠕变-疲劳交互和安全系数的物理本质等仍是困扰人们的难题。数据科学和大数据技术的兴起,为突破数据驱动的疲劳寿命预测方法、诠释疲劳损伤物理机制和建立极端条件下的高端装备疲劳可靠性设计技术提供了新的途径。
Retrospect and prospect on century-long research of structural fatigue
[J].
DOI:10.3901/JME.2021.06.026
[本文引用: 3]

As one of the most common failure modes of mechanical structures, fatigue has been researched for more than 160 years since the term “fatigue” was first proposed in 1854, and the fatigue knowledge has laid a solid foundation for theory and modern technology in mechanical strength areas, and has promoted structural design from experience to safety concept. The paper presented a retrospect on the origin and development, and a summary of the milestones achieved in fatigue research that was driven by typical engineering failure cases. A thorough literature data mining was carried out to illustrate the highlighted achievements, hot topics, and new research trends in the past 50 years. The work showed that the fatigue limit, microstructural genetics, crack-tip driving force, creep-fatigue interaction, and safety factor, were still difficult topics to be solved, though explored for century-long period. The work also indicates that, the emergence of data science and big data technology can provide new pathways to make breakthroughs and establishments in data-driven fatigue life prediction, physical mechanisms of fatigue damage interpretation, and fatigue reliability design of high-end equipment at extreme working conditions.
Microstructure and fatigue behavior of 24CrNiMo low alloy steel prepared by selective laser melting
[J].
某型火箭发动机涡轮转子流热固耦合强度及疲劳寿命分析
[J].
Analysis of fluid-thermal-solid coupling strength and fatigue life of a certain rocket engine turbine rotor
[J].
Literature review of fatigue assessment methods in residual stressed state
[J].
Fatigue life assessment of crankshaft with increased horsepower
[J].
基于损伤累积模型的可靠度保守估计方法
[J].
DOI:10.16183/j.cnki.jsjtu.2019.10.012
[本文引用: 1]

提出一种通过代数和计算可靠度保守估计的方法,导出了损伤服从不同分布时可靠度保守估计的条件.结合应用实例,对比本文计算结果和 Monte-Carlo 模拟结果,验证了本文所提方法的可行性与合理性.
Method in conservative estimation of reliability based on damage accumulation model
[J].
改进移动最小二乘法及其在结构可靠性分析中的应用
[J].
DOI:10.16183/j.cnki.jsjtu.2018.04.010
[本文引用: 1]

基于移动最小二乘法的响应面法对结构可靠性问题进行分析.在确定样本点权重时,将样本点与中心点、响应面的距离同时作为判断其权重大小的依据,并考虑每次迭代得到的响应面函数对下一迭代的影响域的影响,由此提出改进移动最小二乘法.结果表明,改进方法可有效提高计算精度.
An improved moving least square method and application in structural reliability analysis
[J].
Hybrid enhanced Monte Carlo simulation coupled with advanced machine learning approach for accurate and efficient structural reliability analysis
[J].
一种新型的疲劳强度预测模型
[J].
DOI:10.16183/j.cnki.jsjtu.2021.051
[本文引用: 1]

疲劳破坏是工程应用构件失效的最主要原因之一.但由于疲劳实验成本过高,有必要用力学性能对疲劳强度进行预测.基于真实应力应变曲线,建立了一种新型的疲劳强度预测模型,并运用这种模型计算疲劳强度,与“升降法”和Basquin公式计算的疲劳强度作对比.结果表明:该模型仅需通过抗拉强度和加工硬化强度就可得到材料的疲劳强度,并且适用于其他钢种,极大地节约了成本,精确度也较高.
A novel prediction model for fatigue strength
[J].
Quantitative characterization of material uniformity and fatigue life reliability based on the initial damage discreteness
[J].
The quantitative relationship between fracture toughness and impact toughness in high-strength steels
[J].
Development of a method for extracting fracture toughness from instrumented Charpy impact tests in the ductile and transition regimes
[J].
Critical assessment of the Rolfe-Novak CVN-KIC upper shelf correlation
[J].