基于改进蜜獾算法的波能转换器阵列优化

doi:10.16183/j.cnki.jsjtu.2023.030

基于改进蜜獾算法的波能转换器阵列优化

杨博, 刘炳强, 陈义军, 武少聪, 束洪春, 韩一鸣^,

昆明理工大学电力工程学院,昆明 650500

Array Optimization of Wave Energy Converters via Improved Honey Badger Algorithm

YANG Bo, LIU Bingqiang, CHEN Yijun, WU Shaocong, SHU Hongchun, HAN Yiming^,

Faculty of Electric Power Engineering, Kunming University of Science and Technology, Kunming 650500, China

通讯作者: 韩一鸣,讲师;E-mail:2451250809@qq.com.

责任编辑: 王历历

收稿日期: 2023-02-1 修回日期: 2023-05-10 接受日期: 2023-05-26

基金资助:

国家自然科学基金(61963020)
国家自然科学基金(62263014)
国家自然科学基金(52207109)

Received: 2023-02-1 Revised: 2023-05-10 Accepted: 2023-05-26

作者简介 About authors

杨博(1988—),教授,博士生导师,从事基于人工智能的新能源系统优化与控制研究.

摘要

针对波浪能转换器(WEC)阵列发电效率提升问题,提出一种基于改进蜜獾算法的三系WEC阵列优化方法.首先,为克服原始蜜獾算法(HBA)收敛速度慢、收敛精度低等缺陷,引入佳点集初始化、混沌机制和蜜獾种群变异3种策略对原始HBA进行改进.此外,为了验证改进蜜獾算法(IHBA)的先进性和有效性,开展2个浮标、10个浮标和20个浮标3个不同规模的WEC阵列优化实验.2浮标阵列仿真结果表明,WEC阵列优化存在多组最优解,且IHBA、HBA、遗传算法和粒子群优化算法都能以不同速度找到最优解.然而,随着WEC阵列规模的增大,3种对比算法都会陷入局部最优解.相反地,IHBA依然表现出较强寻优能力并能搜寻到全局最优解.最后,IHBA所获10浮标和20浮标的阵列q因子分别高达1.059和0.968,远优于其他3种算法.

关键词： 海洋可再生能源; 波能转换器; 阵列优化; 改进蜜獾算法

Abstract

In order to enhance the generation efficiency of wave energy converter (WEC) arrays, an optimization method for three-tether WEC array based on an improved honey badger algorithm is proposed. First, to overcome the shortcomings of the primal honey badger algorithm (HBA), such as slow convergence speed and low convergence accuracy, three improvement strategies are introduced, i.e., good point set initialization, chaos mechanism, and honey badger population mutation. Then, three wave farms including 2-buoy, 10-buoy, and 20-buoy are tested to verify the advancement and effectiveness of the improved honey badger algorithm (IHBA). The simulation results of the 2-buoy array demonstrate that there are multiple groups of optimal solutions in WEC array optimization. Furthermore, IHBA, HBA, genetic algorithm, and particle swarm optimization can find these optimal solutions at different speeds. Nevertheless, with increasing size of the WEC array, three comparative algorithms fall into local optima solutions. On the contrary, IHBA still exhibits a strong optimization ability and can seek global optima solutions. Finally, the q-factor values obtained by IHBA in 10-buoy and 20-buoy arrays reach 1.059 and 0.968, respectively, which are dramatically larger than those of other algorithms.

Keywords： marine renewable energy; wave energy converter (WEC); array optimization; improved honey badger algorithm (IHBA)

PDF (3437KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨博, 刘炳强, 陈义军, 武少聪, 束洪春, 韩一鸣. 基于改进蜜獾算法的波能转换器阵列优化[J]. 上海交通大学学报, 2024, 58(9): 1465-1478 doi:10.16183/j.cnki.jsjtu.2023.030

YANG Bo, LIU Bingqiang, CHEN Yijun, WU Shaocong, SHU Hongchun, HAN Yiming. Array Optimization of Wave Energy Converters via Improved Honey Badger Algorithm[J]. Journal of Shanghai Jiaotong University, 2024, 58(9): 1465-1478 doi:10.16183/j.cnki.jsjtu.2023.030

随着工业的快速发展,煤、石油、天然气等资源逐渐枯竭,全球变暖、海平面上升等环境问题日益严重^[1].近年来,为了阻止环境退化和优化能源结构,太阳能、风能、海洋能等^[2]可再生能源在世界范围内得到广泛开发和利用.其中,海洋可再生能源约占世界能源总量的70%以上,海洋能位置条件便利,发展潜力巨大,已成为国际技术储备的战略资源^[3].目前海洋可再生能源主要可分为潮汐能、海流能、海水温差能和波浪能等^[4].其中,波浪能因其能量分布广和能量密度高等特点,已成为世界各国关注的焦点.据统计,全世界波浪能蕴藏量约为25亿 kW,中国海域波浪能密度可达15 kW/m,具有很大开发利用潜能^[5].

早在20世纪,就有不少国家开始探索和利用波浪能进行发电.其中,法国、英国、美国和日本等国家的波浪能发电技术较为领先.我国的中科院广州能源所、国家海洋技术中心、中国海洋大学等单位也在这方面开展了大量研究^[6⇓-8].相比于海上风电和潮汐能发电等,波浪能的开发和利用技术还不够成熟,仍然有很大研究空间.目前,波浪能发电技术正朝着智能化、直驱式、阵列化等方向发展^[9-10].

波浪能发电系统是将海洋波浪的动能转化为电能的装置, 整个装置由波浪能转换器(Wave Energy Converter, WEC)、功率输出(Power Take off, PTO)系统以及其他辅助系统组成^[11].其中,PTO系统包括中间转换系统(水力透平、空气透平、液压马达、增速齿轮箱等)和发电机^[12].迄今为止,WEC的类型主要包括振荡水柱式WEC、点吸收式WEC、截止式WEC等.完全浸没式CETO WEC^[13]也属于点吸收式,它能通过浮标的上下运动吸收波浪能.这类WEC在高密度海况下具有较长使用寿命,同时,设备视觉冲击和对海洋生态的影响都比较小,是目前WEC阵列优化中的重要研究对象.

单个WEC无法同时捕获不同海面位置的波浪能量,发电效率较低,而且能量输出不稳定,难以满足用电需求,不利于大规模发电.将WEC以阵列的形式布置进行发电,可以改善单一WEC发电的弊端.然而,与光伏阵列、风电场不同,WEC阵列中浮标之间存在比较复杂的水动力相互作用,这些相互作用对阵列的发电效率既是建设性的也是破坏性的^[14-15],主要与阵列中WEC的形状、位置和海况等因素有关.此外,这些相互作用使WEC阵列优化构成一个非凸、多模态、连续和具有约束的问题,目前采用q因子作为WEC阵列排布好坏的评价指标^[16].因此,如何对WEC尺寸、位置等进行优化,充分利用WEC之间的相互作用已成为波浪能发电工程的研究热点.WEC阵列的优化是一项极具挑战性的工作,Budal^[17]于20世纪70年代首先开始WEC阵列优化研究工作,对点吸收式WEC之间的互相作用进行简化计算.之后有很多学者在此基础上对WEC水动力模型进行修正和完善,提出各种方法来实现WEC阵列布局的优化,主要包含机器学习方法、数学方法和元启发式算法.传统的数学方法如抛物线交集法和蒙特卡罗方法,在提升q因子上具有较好性能^[18-19].然而,在解决非线性问题上,元启发式算法具有强大能力,因此被广泛应用于WEC阵列布局优化中^[16].文献[20]中利用改进差分进化算法,对含有3个、5个、8个浮标的小规模WEC阵列进行优化排布,其中,8浮标的阵列q因子提高到了1.898.文献[21]中提出基于遗传算法(Genetic Algorithm, GA)的二自由度浮标式WEC阵列的优化策略,对2个、3个、5个浮标组成的WEC阵列进行优化设计,显著提高WEC阵列捕获波浪能的效率.然而,上述研究工作波浪特性单一,且并未对大规模的WEC阵列进行研究.

Hashim等^[22]于2021年提出蜜獾优化算法(Honey Badger Algorithm, HBA).该算法主要受蜜獾觅食行为的启发,具有模型简单、易于实现、收敛速度快等特点.但HBA局部开发能力较弱,并且面对复杂问题时难以跳出局部最优.为了提高HBA的优化性能,研究人员主要从调整控制参数、更新搜索机制以及算法融合等多方面对HBA进行改进.文献[23]中引入逻辑映射和反向学习对蜜獾种群初始化进行了改进,提高了算法的随机性;文献[24]中在蜜獾捕食阶段引入交叉变异原则,提升了算法的收敛速度;文献[25]中在局部搜索阶段中引入维度学习策略,平衡了算法勘探与开发的能力.上述改进算法相比于原始HBA在性能上有一定提升,但仍存在一些不足,如部分改进算法的改进策略单一,仅对算法的某一阶段进行改进;改进策略并没有从根本上优化蜜獾的挖掘寻优机制,算法的寻优能力并未得到提升;改进算法的测试实验不够,并未对高纬度及复杂问题进行分析讨论,未能充分体现算法的优越性.

由于WEC阵列优化问题的复杂性,上述算法并未能精确、快速地解决此棘手问题,难以获得较合适的WEC阵列布局.通过合理改进HBA的寻优机制平衡算法的局部探索和全局搜索能力,有望成为高效解决上述难题的技术之一.因此,本文提出改进蜜獾算法(Improved Honey Badger Algorithm, IHBA),引入佳点集初始化、混沌机制和蜜獾种群变异3种策略对原始HBA进行改进.以WEC阵列q因子最大化为目标,利用IHBA对2个浮标、10个浮标和20个浮标3个不同规模的WEC阵列进行优化设计.同时,将HBA、GA和粒子群优化 (Particle Swarm Optimization, PSO)^[26]作为对比算法进行测试,实验结果验证了IHBA在WEC阵列优化问题上的先进性和有效性.

1 波浪能发电装置阵列模型

1.1 三系波浪能发电装置

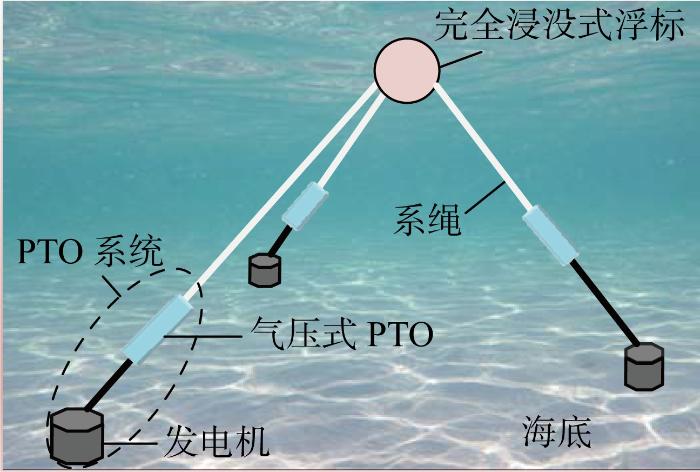
所研究的WEC为澳大利亚卡内基清洁能源公司开发的三系WEC,作为单系CETO WEC的替代技术.如图1所示,球形浮标完全浸没在海面下,可以通过自身的波涌、摇摆和升沉吸收波浪能量^[13].3条系绳平均地分布在浮标周围,每条系绳各自连接着PTO装置和旋转发电机,在海底产生的电能通过海底电缆传输到陆上.三系WEC的投资成本明显高于单系CETO WEC的成本,但在同一海况下,相同数量的三系WEC与单系WEC相比,前者因每个系绳都安装了独立的PTO装置和发电机,从而能够产生更多电能.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 三系WEC示意图

Fig.1 Schematic representation of three-tether WEC

1.2 三系WEC阵列数学模型

WEC在海中受到的力主要包括波浪激励力、波浪辐射力和PTO装置在浮标上的控制力^[27].假设N为WEC阵列中浮标个数,PTO装置可以等效为具有固定刚度系数K_pto和阻尼系数B_pto的弹簧阻尼控制器^[11].当WEC所处的海况中海水不可压缩、无粘性和无旋流动时,阵列中第i个WEC的运动方程在时域中可描述为

(1)M_i

{\ddot{x}}_{i}

(t)=F_exc,_i(t)+F_rad,_i(t)+F_pto,_i(t)

式中:M_i为第i个浮标的质量矩阵; ${\ddot{x}}_{i}$ (t)为浮标在浪涌、摇摆和升沉中的加速度矢量;F_exc,_i(t)、F_rad,_i(t)、F_pto,_i(t)分别为波浪激励力、波浪辐射力和PTO控制力;t为时间.

其中,第i个浮标受到的波浪辐射力为

(2)F_rad,_i=

\overset{N}{\sum_{j = 1}}

{\ddot{x}}_{i}

λ_i_,_j-

{\ddot{x}}_{i}

μ_i_,_j)

式中:λ_i_,_j为第j个浮标对第i个浮标作用的附加阻尼系数;μ_i_,_j第j个浮标对第i个浮标作用的附加质量系数.

根据无功控制理论,PTO控制力可近似为两个力的叠加,包括一个与速度成反比例的阻尼力和一个与位移成比例的弹簧力,因此:

(3)F_pto,_i=-B_pto,_i

{\hat{v}}_{i}

-K_pto,_i

{\hat{l}}_{i}

式中:B_pto,_i、K_pto,_i分别为第i个WEC装置的阻尼系数和刚度系数; ${\hat{v}}_{i}$ 、 ${\hat{l}}_{i}$ 分别为浮标在系绳正方向上的速度和位移矢量.

在WEC阵列中,多个WEC共存且彼此相对靠近,浮标之间的水动力相互作用不可忽视.此外,波浪的辐射情况也依赖于WEC在阵列中的布局.由于浮标是球形的,可以忽略由波浪引起的横滚、纵倾运动,所以在WEC吸收波浪能的过程中只考虑平移运动,即浪涌、摇摆和起伏.当一个频率为ω、入射角为0 rad、波高为H的规则海浪到达WEC场后,频域内含N个浮标的WEC场在海浪荷载作用下的运动可描述为^[13]

(4)

[(M_Σ+A_Σ(ω))jω+ ${\hat{B}}_{Σ}$ (ω)-

\frac{K_{p t o, Σ}}{ω}

j+B_{pto, Σ}]x_Σ=

{\hat{F}}_{e x c, Σ}

式中:M_Σ为N个浮标的广义质量矩阵;A_Σ (ω)为流体动力附加质量矩阵; ${\hat{B}}_{Σ}$ (ω)为辐射阻尼矩阵;K_pto,Σ、B_pto,Σ分别为PTO装置的刚度系数矩阵和阻尼系数矩阵;x_Σ为N个浮标的广义加速度矢量; ${\hat{F}}_{e x c, Σ}$ 为波浪激励力矩阵.

在确定波浪的频率ω、方向、入射角度、波高H和WEC的位置后,式(4)中的附加质量、辐射阻尼和波浪激励力等水动力系数可以通过半解析模型进行求解^[28].WEC阵列中第i个浮标所吸收波浪能的功率为

(5)P_i=

\overset{3}{\sum_{j = 1}} \frac{1}{2}

B_pto_,iω²H²

{|{\hat{l}}_{i, j}|}^{2}

式中: $|{\hat{l}}_{i, j}|$ 为浮标在系绳j正方向上的运动幅值.

含有N个WEC的阵列所吸收的波浪能总功率可通过下式计算:

(6)P_Σ=

\frac{1}{4}

(

{\hat{F}}_{e x c, Σ}^{T} {\hat{\overset{\cdot}{x}}}_{Σ}

{\hat{\overset{\cdot}{x}}}_{Σ}^{T} {\hat{F}}_{e x c, Σ}

\frac{1}{2} {\hat{\overset{\cdot}{x}}}_{Σ}^{T}

{\hat{\overset{\cdot}{x}}}_{Σ}

式中:B为PTO的阻尼系数.

根据式(6)计算出整个WEC阵列吸收的波浪能功率后,就可以估算出该阵列在特定海况下的年平均发电量,具体的计算方法可参考文献[21].

定义用阵列q因子来评估WEC阵列优劣:

(7)q=

\frac{P_{Σ}}{N P_{0}}

式中:P₀为仅有单个WEC工作时,其吸收的波浪能功率.

同样地,为了反映阵列中每个WEC波浪能吸收情况,也可以用相互作用系数q_i反映每个浮标的波浪能转换,定义为

(8)q_i=

\frac{P_{i}}{P_{0}}

1.3 波浪特性

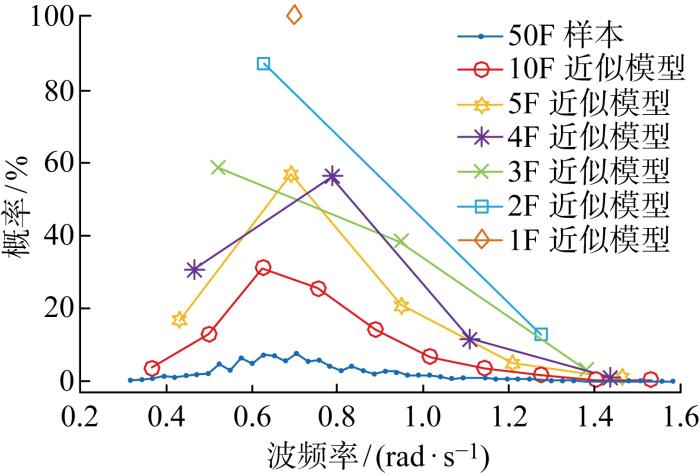
为了进一步降低计算成本,根据文献[29]中统计的悉尼海域波浪50个样本,文献[13]中提出悉尼海况的近似模型,如图2所示.该模型仅包括采样频率数为1F、2F、3F、4F、5F和10F的波浪特性,其中,1F波的频率为0.7 rad/s.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 波浪特性近似模型

Fig.2 Approximate model of wave characteristics

与原始50F海况模型相比,该近似海况模型可以显著减少计算成本,同时测试结果与50F模型的相似率可以保证在80%以上.因此,采用该近似模型模拟WEC阵列的海洋环境.

2 改进蜜獾算法设计

2.1 蜜獾算法

蜜獾主要采用两种方式觅食,一种是根据猎物的信息强度自主挖掘的模式,按照心形线轨迹挖掘蜂巢,简称挖掘模式;另一种是蜜獾通过导蜜鸟的指引到达蜂巢,简称采蜜模式.原始蜜獾算法的数学模型如下.

2.1.1 种群初始化

蜜獾种群的数量和位置根据下式进行初始化:

(9)A=

[\begin{array}{l} x_{1} \\ x_{2} \\ ︙ \\ x_{n} \end{array}]

[\begin{array}{l} x_{11} & x_{12} & x_{13} & \dots & x_{1 D} \\ x_{21} & x_{22} & x_{23} & \dots & x_{2 D} \\ \dots & \dots & \dots \\ x_{n 1} & x_{n 2} & x_{n 3} & \dots & x_{n D} \end{array}]

(10)x_m=l_m+r₁(u_m-l_m)

式中:A为整个蜜獾种群;x_m为第m只蜜獾的位置,m=1, 2, …, n;n、D分别为蜜獾个体总数及维度;u_m、l_m分别为搜索空间的上界和下界;r₁为(0, 1)内的随机数.

2.1.2 嗅觉强度定义

蜜獾觅食速度主要取决于嗅觉强度I_m的大小,I_m越大,则蜜獾运动速度越快.嗅觉强度的定义如下:

(11)I_m=r₂

\frac{S}{4 π d_{m}^{2}}

(12)S=(x_m-x_m₊₁)²

(13)d_m=x_prey-x_m

式中:r₂为(0, 1)内的随机数;S为猎物的集中强度;d_m为猎物与第m只蜜獾的距离;x_prey表示猎物的位置.

2.1.3 衰减因子更新

为了确保勘探到开发的平稳过渡,引入时变搜索衰减因子α,减少蜜獾觅食过程中随时间变化的随机性,定义如下:

(14)α=C

e^{\frac{- t}{t_{m a x}}}

, C=2

式中:t_max为最大迭代次数;C为参数.

2.1.4 蜜獾位置更新

包括以下两种模式.

(1) 挖掘模式.

在自主觅食挖掘过程中,蜜獾以心形线轨迹进行挖掘,可描述为

(15)

x_new=x_prey+FβIx_prey+

Fr₃αd_m

|c o s (2 π r_{4}) [1 - c o s (2 π r_{5})]|

式中:x_new为蜜獾更新后位置;β为蜜獾的捕猎能力,默认β=6;I为嗅觉强度;r₃、r₄、r₅均为(0, 1)内3个不同的随机数.蜜獾的搜索方向由F决定:

(16)F=

\{\begin{array}{l} 1, & 如 果 r_{6} \leq 0.5 \\ - 1, & 否 则 \end{array}

式中:r₆为(0, 1)内的随机数.

(2) 采蜜模式.

蜜獾通过导蜜鸟找到蜂巢,这一行为可以利用下式模拟:

(17)x_new=x_prey+Fr₇αd_m

式中:r₇为(0, 1)内的随机数.

2.2 改进蜜獾算法

和其他启发式算法一样,HBA在一些复杂问题上也会出现早熟、易陷入局部最优,限制了算法精度,具有较大改进空间.引入佳点集初始策略^[30]、混沌机制策略^[23]、种群变异策略对HBA进行改进.

2.2.1 佳点集初始化策略

对于GA、PSO和HAB等群体优化算法而言,初始化种群的质量好坏对算法收敛速度和全局优化效果有较大影响.然而,在原始HBA算法中,种群的初始化都是随机产生的,难以保证良好的种群多样性.因此,引入佳点集策略对蜜獾种群进行初始化,相对于随机初始化种群,佳点集策略产生的序列更加均匀,种群覆盖全局范围更广,有利于HBA的全局寻优.佳点集的定义如下:

设G_D为D维欧氏空间单位立方体,当γ∈G_D时,产生佳点集合:

(18)$ \begin{aligned} P_{n}(k)= & \left\{\left(\left\{\gamma_{1}^{(n)} k\right\},\left\{\gamma_{2}^{(n)} k\right\}, \cdots,\left\{\gamma_{D}^{(n)} k\right\}\right),\right. \\ & 1 \leqslant k \leqslant n\} \end{aligned}$

且集合P_n(k)各点之间的偏差满足:

(19)φ(n)=C(γ, ε)n^-1+^ε

式中:C(γ, ε)为仅与γ和ε有关的常数,ε>0;γ为佳点.

2.2.2 混沌机制策略

混沌机制根据混沌理论生成伪随机值而不是随机值,可以提高算法的全局探索能力.由于采用佳点集策略对HBA进行初始化,并不需要对r₁进行更新,所以基于混沌机制更新原始HBA的两个随机值r₂、r₃,如下:

(20)

r_{2}^{n e w}

=r₂+δ_tr₂

(21)

r_{3}^{n e w}

=r₃+δ_tr₃

(22)δ_t₊₁=4δ_t(1-δ_t)

式中: $r_{2}^{n e w}$ 、 $r_{3}^{n e w}$ 为更新后的随机值;δ_t为对应迭代次数的混沌值,初始值δ₁为(0, 1)之间的随机数.

2.2.3 变异策略

为解决HBA算法早熟、收敛精度等问题,同时不改变原始算法的复杂度,引入高斯变异策略,对式(15)和式(17)的蜜獾位置迭代给予相应的高斯变异算子,如下:

(23)x_new(t+1)=x_new(t)

[1 + \frac{|α|}{2} N (0, 1)]

式中:x_new(t+1)为下一次迭代蜜獾的位置;N(0, 1)为标准高斯分布.

变异策略可以使HBA在搜索初期获得足够扰动以增加算法的全局搜索能力,而在算法末期减少扰动以避免最优解的动荡,加快收敛速度.

3 基于改进蜜獾算法的波能转化器阵列优化设计

3.1 目标函数

利用IHBA对含N个浮标的WEC阵列进行优化,每个WEC装置包含横纵坐标2个分量.因此,需要优化的变量主要是浮标坐标位置,主要目标是在预定海域内找到每个浮标的最佳位置,最大限度地利用浮标之间相互作用提高WEC阵列的波浪能捕获,即实现q因子最大化.因此,构建的目标函数如下:

(24)

\begin{array}{l} m a x f = q ((x_{1}, y_{1}), (x_{2}, y_{2}), \dots, \\ (x_{N}, y_{N})) \\ q = \frac{P_{Σ}}{N P_{0}} \\ P_{Σ} = \frac{1}{4} ({\hat{F}}_{e x c, Σ}^{T} {\hat{\overset{\cdot}{x}}}_{Σ} + {\hat{\overset{\cdot}{x}}}_{Σ}^{T} {\hat{F}}_{e x c, Σ}) - \frac{1}{2} {\hat{\overset{\cdot}{x}}}_{Σ}^{T} B {\hat{\overset{\cdot}{x}}}_{Σ} \end{array}\}

式中:(x_i, y_i)代表第i个浮标的位置坐标.

3.2 约束条件

考虑到实际工程中WEC的安装以及维修,定义两个浮标之间的安全距离(d_save)为50 m,同时各个浮标之间的坐标要保证在所定义的海域内,故在整个WEC阵列优化过程中应满足以下约束条件:

(25)

\begin{array}{l} x_{i} \in (0, x_{U}), i = 1, 2, \dots, N \\ y_{i} \in (0, y_{U}), i = 1, 2, \dots, N \\ d_{s a v e} = \sqrt{(x_{i} - x_{j})^{2} + (y_{i} - y_{j})^{2}} \geq 50 \\ i, j = 1, 2, \dots, N, i \neq j \end{array}\}

式中:x_U和y_U为所定义海域的长度和宽度.

3.3 基于IHBA的WEC阵列优化框架

在确定好目标函数以及约束条件后,为保证起始蜜獾种群的多样性,增强搜索空间的覆盖程度,按式(9)、式(18)~(19)、式(25)在搜索空间内初始化蜜獾种群中的每个个体,并根据式(24)计算个体适应度值.接着根据式(11)~(17)、式(20)、式(23)进行迭代,更新个体位置和适应度值.此外,在每次迭代中不满足约束条件的个体会更新为上一代的最优个体,完成迭代后保留最优个体位置和适应度值.

4 算例分析

为验证所设计IHBA的有效性,以HBA、GA、以及PSO作为参照算法,分别对3个规模(2个浮标、10个浮标和20个浮标)的三系WEC阵列进行优化,各个算法的主要参数如表1所示.表中:p_c 为交叉概率;p_m 为变异概率;W_i为惯性因子;C₁为加速度常数;C₂为加速度常数.其中,在2浮标小规模阵列中,分别将5F波和1F波作为海浪条件进行实验,所有算法的种群大小和最大迭代次数分别为 n=60和t_max=400.在中规模10浮标和大规模20浮标阵列中,考虑到计算成本,只进行波浪条件为1F时的WEC阵列优化实验,同时设置各算法的种群大小和最大迭代次数分别为n=40和t_max=200,WEC装置以及环境条件的参数如表2所示.此外,当入射角为0 rad、波高为1.9 m、波的传播方向为从左至右时,计算出了单个WEC在5F波和1F波孤立工作下吸收的波浪能功率分别为 350.9 kW和 554.7 kW.所有仿真实验均在配置为2.90 GHz Intel(R) Core(TM) i5-9400 CPU,32.0 GB RAM,64位Windows 10的计算机上通过MATLAB 2019b环境运行.

表1 不同算法的主要参数

Tab.1 Main parameters of different algorithms

算法	参数	数值
IHBA	C	2
	β	6
HBA	C	2
	β	6
GA	p_c	0.5
	p_m	0.01
PSO	W_i	1.0
	C₁	1.49445
	C₂	1.49445

新窗口打开| 下载CSV

表2 WEC阵列优化实验主要参数

Tab.2 Main parameters of optimization experiment for WEC array

参数	数值
浮标半径/m	5
浮标质量/t	376
浮标下潜深度/m	6
海水深度/m	50
海水密度 /(kg·m^-3)	1020
重力加速度/(m·s^-2)	9.8
波高/m	1.9
入射角度/rad	0
K_pto/(kN·m^-1)	387
B_pto/(kN·m^-1)	161

新窗口打开| 下载CSV

4.1 小规模2浮标阵列优化

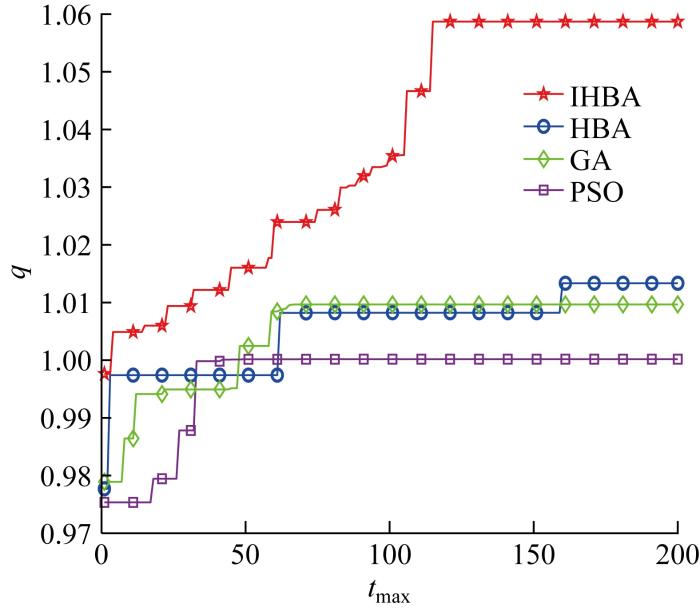
波浪特性为5F波、海域面积为100 m×100 m, 以阵列q因子为目标函数时,各个算法得到的2浮标阵列q因子收敛曲线如图3所示.不难看出,在变量维度较低的情况下,所有算法都能以不同速度找到最优解,但IHBA能够以最快速度找到最优解.同时,表3记录了各个算法最终优化结果,虽然各算法得到的最优WEC布局存在差异,但各算法之间的阵列吸收功率偏差仅在0.2 W以内,这也验证了WEC的阵列优化存在多组最优解.表中:X、Y分别为浮标的X、Y坐标.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 各算法优化2浮标阵列所得q因子收敛曲线

Fig.3 Convergence curves of q-factor obtained by various algorithms for 2-buoy array

表3 5F波下各算法优化后的2浮标阵列实验结果

Tab.3 Experimental results of 2-buoy array obtained by different algorithms with 5F wave source

算法	i	X/m	Y/m	P_Σ/W	q	仿真时间/h
IHBA	1	80	9	729129.63	1.0389	0.8
	2	80	100
HBA	1	63	8	729129.73	1.0389	0.9
	2	63	96
GA	1	100	100	729129.56	1.0389	0.9
	2	100	9
PSO	1	96	98	729129.65	1.0389	0.7
	2	96	7

新窗口打开| 下载CSV

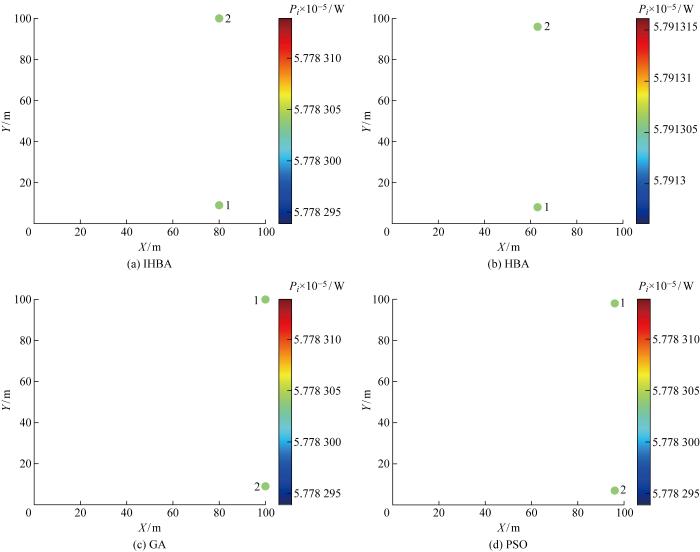
在上述4组2浮标最优布局的基础上,将波浪特性由5F改为1F,其他条件保持不变,对1F波下的2浮标阵列进行测试.测试结果如表4所示,可以看出在波浪特性为1F时各算法优化WEC阵列的q因子仍然大于1.这充分验证了相比于同样数目下的孤立浮标,WEC以阵列的形式布置能捕获更多波浪能.最后,根据表4中每个浮标的坐标以及吸收波浪能的功率.图4给出4种算法的2浮标的WEC阵列最优布局,其中,颜色深浅代表每个WEC吸收波浪能的功率大小.

表4 1F波下各算法优化后的2浮标阵列实验结果

Tab.4 Experimental results of 2-buoy array obtained by different algorithms with 1F wave source

算法	i	X/m	Y/m	P_i/W	P_Σ/W	q_i	q
IHBA	1	80	9	577830.38	1158261.22	1.04	1.043
	2	80	100	577830.38		1.04
HBA	1	63	8	579130.61	1155660.76	1.04	1.042
	2	63	96	579130.61		1.04
GA	1	100	100	577830.39	1155660.78	1.04	1.042
	2	100	9	577830.39		1.04
PSO	1	96	98	577830.41	1155660.82	1.04	1.042
	2	96	7	577830.41		1.04

新窗口打开| 下载CSV

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 各算法优化后的2浮标阵列最优布局

Fig.4 Optimal layouts of 2-buoy array obtained by different methods

4.2 中等规模10浮标阵列优化

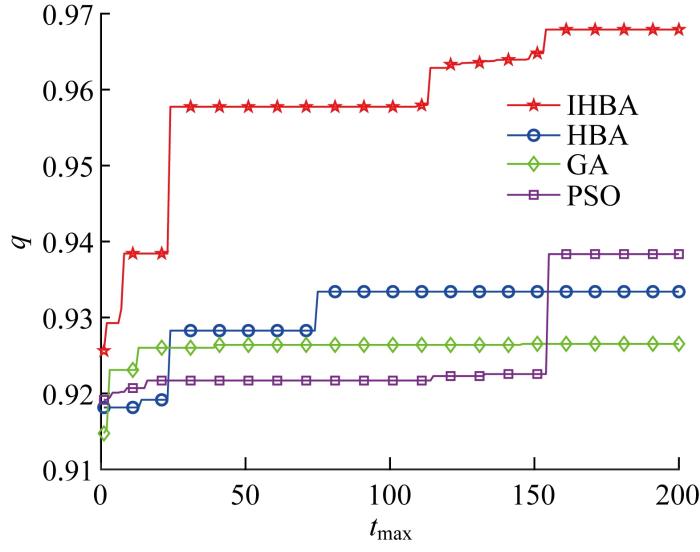
当波浪特性为1F,海域面积为 1 000 m×1 000 m 时,4种算法对10个浮标阵列优化过程中q因子收敛曲线图如图5所示.其中,4种算法在迭代50次后都能将阵列q因子提升到1以上.同时,从4条收敛曲线可以看出,利用佳点集策略进行初始化后的IHBA初期适应度值高于其他算法.3种对比算法在优化过程中陷入局部最优,原始HBA在阵列q因子的提升上相对GA和PSO的效果较好,但IHBA的寻优能力显著高于其他3种启发式算法,经IHBA优化后的阵列q因子比HBA、GA、PSO分别高出4.54%、4.64%、5.58%.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 各算法优化10浮标阵列所得q因子收敛曲线

Fig.5 Convergence curves of q-factor obtained by different algorithms for 10-buoy array

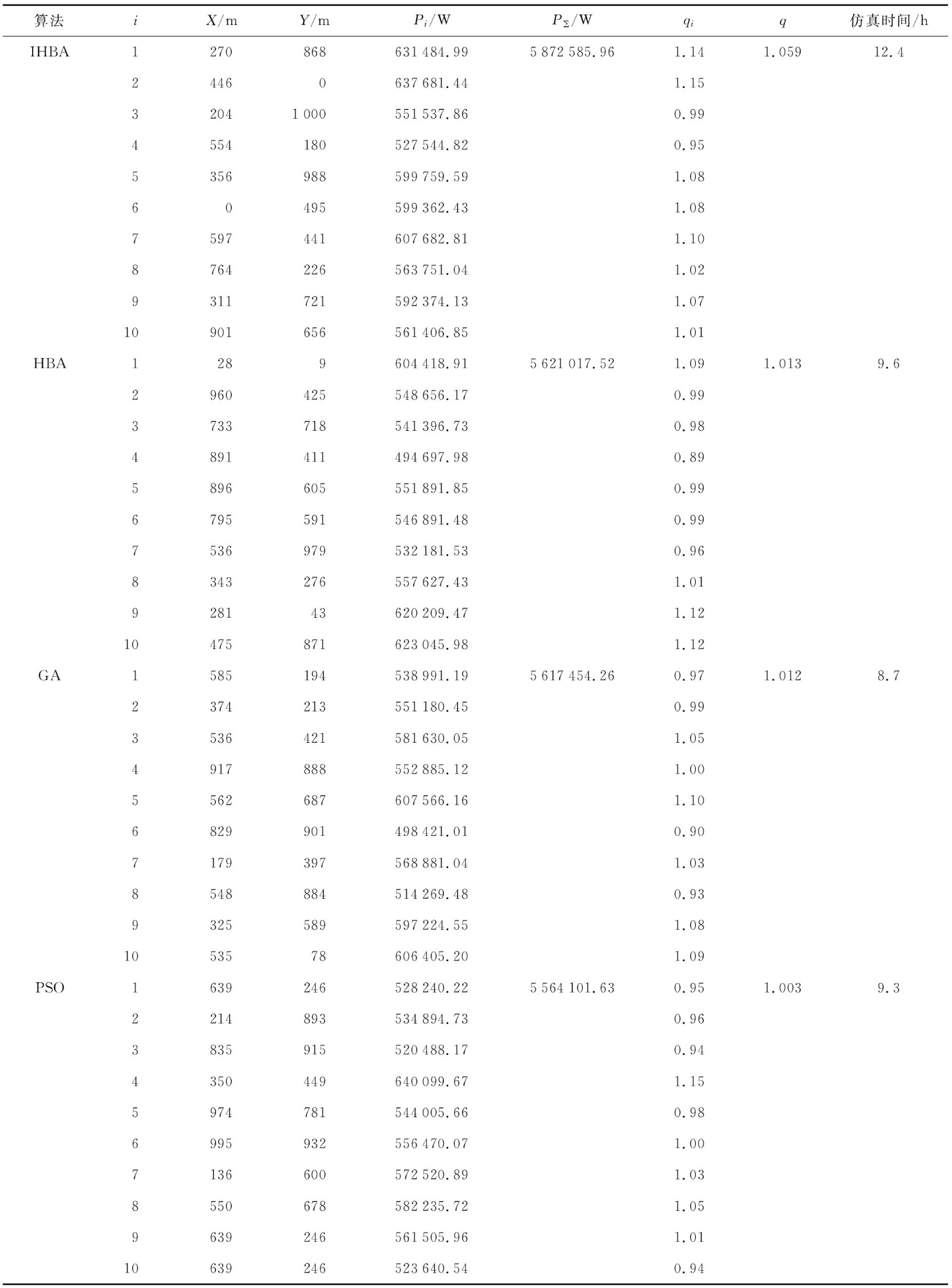
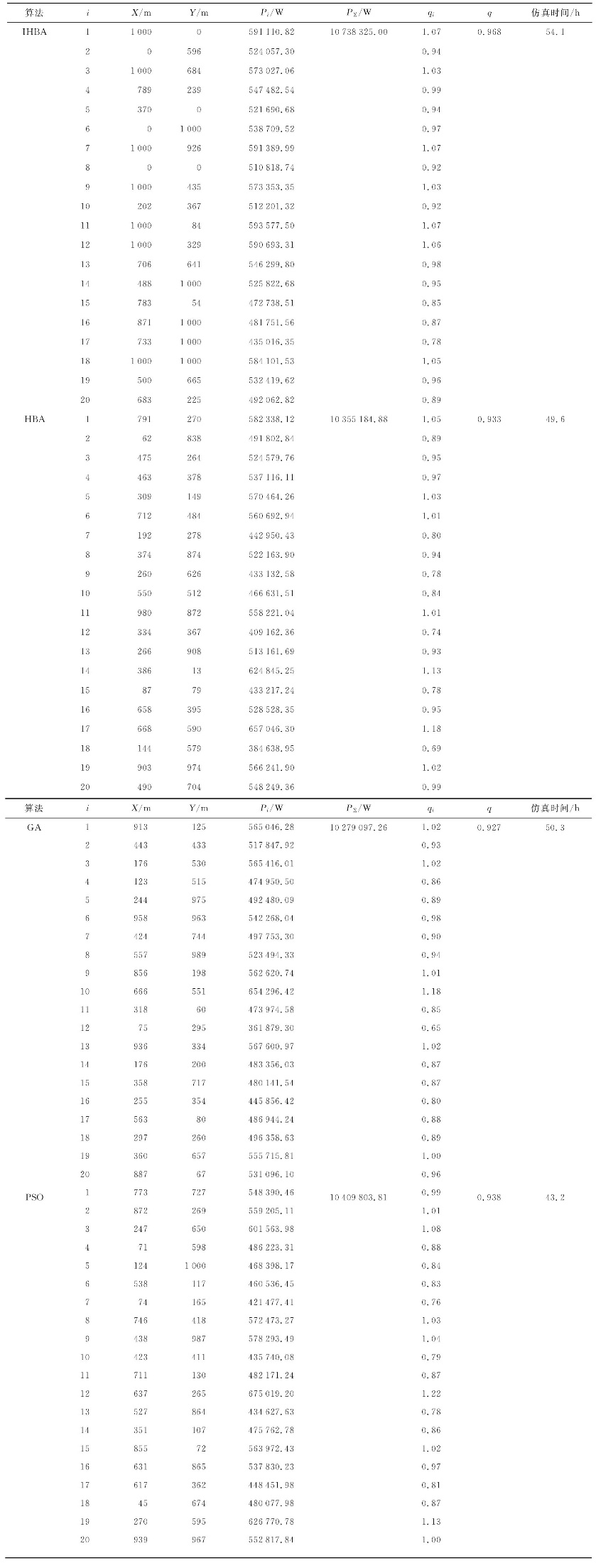
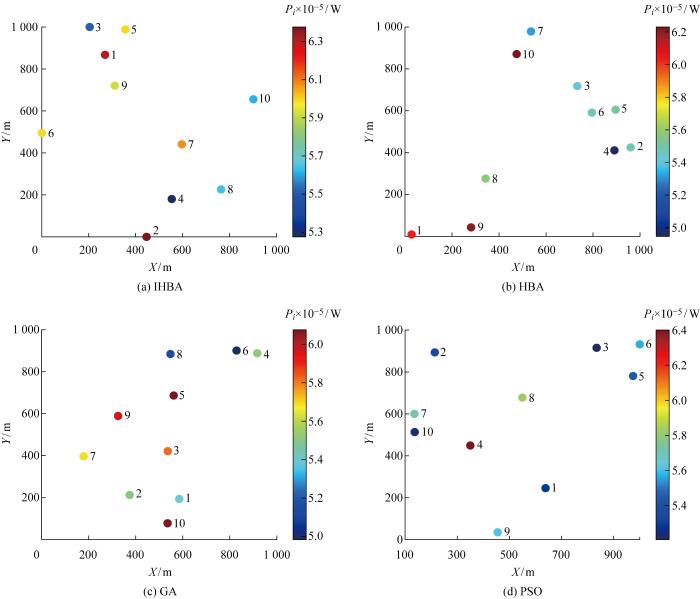
各个算法优化后的10浮标最优位置以及每个浮标的波浪能捕获情况如表5所示. 虽然IHBA在运算速度上有一定局限性, 但在IHBA优化后的WEC阵列中,相互作用系数q_i大于1的浮标个数多于其他3种算法所得,验证了IHBA可以在WEC阵列系统中有效且合理地利用浮标之间的相互作用,从而提升WEC阵列的波浪能捕获量.最后,根据表5中每个浮标的坐标以及吸收的波浪能功率,分别给出4种算法对10浮标阵列进行优化后的最优布局,如图6所示.

表5 各算法优化后的10浮标阵列实验结果

Tab.5 Experimental results of 10-buoy array obtained by different algorithms

新窗口打开| 下载CSV

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 各算法优化后的10浮标阵列最优布局

Fig.6 Optimal layouts of 10-buoy array obtained by different methods

4.3 大规模20浮标阵列优化

相比较于2个浮标和10个浮标组成的阵列,20个浮标阵列的优化工作更具挑战性,因为浮标之间相互作用变得更加复杂,搜索空间的复杂性要高很多.同样在波浪特性为1F和海域面积为1 000 m×1 000 m 下,利用前述4种算法对20个浮标组成的阵列进行优化,各算法的阵列q因子收敛曲线图如图7所示.不难看出4种算法优化后的20浮标阵列q因子都能达到0.9以上.同时,HBA、GA和PSO在优化过程中仍然陷入局部最优,经IHBA优化后的阵列q因子比HBA, GA和PSO所优化结果分别高3.75%、4.42%和3.20%,在4种方法中仍然处于最高水平,再次验证所提方法的先进性和有效性.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 各算法优化20浮标阵列所得q因子收敛曲线

Fig.7 Convergence curves of q-factor obtained by different algorithms for 20-buoy array

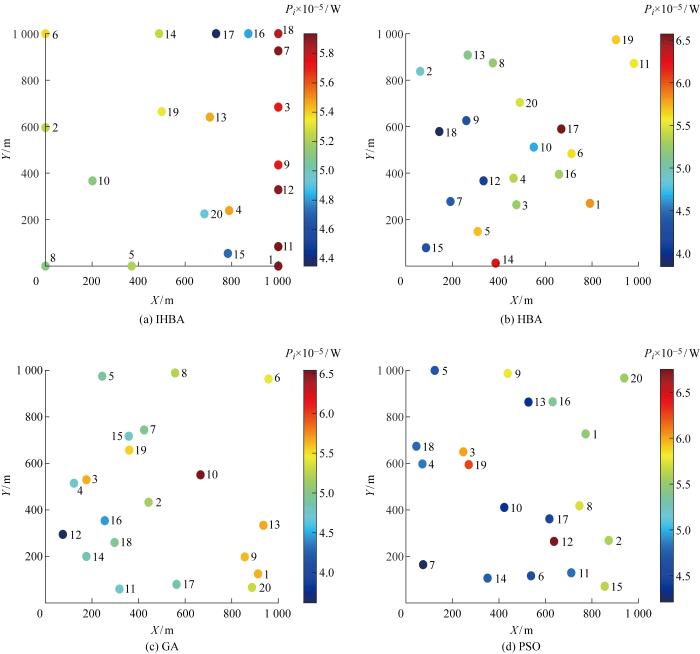
此外,表6记录了4种算法所得20个浮标阵列的最优布局以及各个浮标吸收波浪能的功率.可以看出,阵列规模越大,浮标之间相互作用也更加复杂,阵列q因子很难达到1以上,但部分浮标的相互作用系数q_i仍大于1.同样地,根据表6中统计的数据,图8给出了经4种算法优化后的20个浮标阵列最优布局图.

表6 各算法优化后的20浮标阵列实验结果

Tab.6 Experimental results of 20-buoy array obtained by different algorithms

新窗口打开| 下载CSV

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 各算法优化后的20浮标阵列最优布局

Fig.8 Optimal layouts of 20-buoy array obtained by different methods

5 结论

海洋中波浪的辐射和散射会严重影响WEC阵列发电效率.针对此问题,提出一种多策略改进的蜜獾优化算法,对不同规模WEC阵列进行布局优化和对比分析,主要研究成果和创新点可概括如下:

(1) 对原始HBA进行改进,利用佳点集策略初始化种群,增加了种群多样性.同时,引入混沌机制生成伪随机数,提高算法的全局探索能力.此外,在蜜獾挖掘和采蜜阶段引入种群变异策略,进一步提升解的质量.

(2) 建立基于IHBA的三系WEC阵列优化模型,利用IHBA对3个不同规模大小的WEC阵列进行布局优化.为了验证其先进性和有效性,在相同条件下对比验证了所提方法与原始HBA、GA和PSO算法的优化效果.

(3) 仿真结果表明,在小规模2个浮标的阵列优化中,4种算法中均能找到最优解,验证了WEC阵列优化问题含有多个最优解;在10浮标和20浮标WEC阵列优化中,HBA、GA和PSO都陷入局部最优,而采用佳点集初始化的IHBA在初始适应度值上占有优势,在优化过程中也表现出强大的寻优能力.其中,经IHBA优化后的10浮标阵列q因子比HBA、GA和PSO所得分别高出4.54%、4.64%和5.58%.经IHBA优化的20浮标阵列q因子比HBA、GA和PSO所优化结果分别高出3.75%、4.42%和3.20%.

本文主要研究WEC阵列吸收波能功率最大化,IHBA在WEC阵列优化上具有较好的优化效果,IHBA能够充分挖掘WEC之间的积极作用,从而提高WEC阵列的发电效率,对工程实践中波浪能的开发和利用具有一定的参考价值.未来将在此基础上综合考虑WEC的投资成本以及其建设对海洋环境的影响,海况模拟也将进一步丰富.同时,也将开展海上风能与波浪能发电装置科学集成的研究.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

CHEN

Y J

, YANG

, GUO

Z X

, et al.

Dynamic reconfiguration for TEG systems under heterogeneous temperature distribution via adaptive coordinated seeker

[J]. Protection & Control of Modern Power Systems, 2022, 7(1): 1-19.