不确定性条件下农业微电网与灌溉系统相结合的鲁棒优化调度

doi:10.16183/j.cnki.jsjtu.2023.035

不确定性条件下农业微电网与灌溉系统相结合的鲁棒优化调度

杨森, 郭宁, 张寿明^,

昆明理工大学信息工程与自动化学院,昆明 650500

Robust Optimal Scheduling of Agricultural Microgrid Combined with Irrigation System Under Uncertainty Conditions

YANG Sen, GUO Ning, ZHANG Shouming^,

Faculty of Information Engineering and Automation, Kunming University of Science and Technology, Kunming 650500, China

通讯作者: 张寿明,教授; E-mail:1740229323@qq.com.

责任编辑: 王历历

收稿日期: 2023-02-6 修回日期: 2023-07-8 接受日期: 2023-07-11

Received: 2023-02-6 Revised: 2023-07-8 Accepted: 2023-07-11

作者简介 About authors

杨森(1998—),硕士生,从事微电网优化运行与进化计算研究.

摘要

农业微电网以低成本的方式为偏远农村地区的能源供应提供了一种有前景的解决方案.综合考虑风光抽水蓄能一体化农业微电网满足用电负荷和用水负荷需求,在可再生能源出力及用电负荷需求的不确定性条件下,提出包含抽水蓄能(PHS)电站的孤岛型农业微电网和灌溉系统相结合的鲁棒优化调度模型,利用农村地区水资源富足的特点和风光抽蓄补偿的优势,在最小化系统总成本的同时提高可再生能源的消纳.所提模型考虑分布式发电、用电负荷和用水负荷需求、涡轮流量和灌溉流量,具有多样性、多约束、非连续的特点.提出一种引力鲸鱼优化算法(GWOA)求解该模型,在某农业微电网上的仿真结果表明,GWOA可以获得比CPLEX求解器及其他新开发算法更具竞争力的解.另外,探究了降水量不确定性引起灌溉系统用水负荷需求变化对系统运行成本的影响以及使用PHS电站的必要性.

关键词： 农业微电网; 抽水蓄能; 灌溉系统; 不确定性条件; 引力鲸鱼优化算法

Abstract

Agricultural microgrids offer a promising solution for energy supply in remote rural areas in a low-cost manner. In this paper, under uncertain conditions of renewable energy output and electricity load demand, a robust optimal scheduling model combined with the isolated agricultural microgrid and irrigation system containing a pumped hydro storage (PHS) power station is proposed, considering the factors that the wind-landscape pumped storage integrated agricultural microgrid can satisfy the uncertain fluctuations of power load demand and water load demand. By utilizing the abundant water resources in rural areas and the advantages of landscape drainage and storage compensation, the total cost of the system is minimized while the absorption of renewable energy is increased. Considering distributed generation, power load demand and water load demand, turbine flow, and irrigation flow, the proposed model is characterized by diversity, multi-constraint, and discontinuity. A gravitational whale optimization algorithm (GWOA) is proposed to solve the model. The simulation results of an agricultural microgrid show that the GWOA can obtain a more competitive solution than the CPLEX solver and other newly developed algorithms do. In addition, the impact of the change of water load demand caused by precipitation uncertainty on the operating cost of the irrigation system and the necessity of using PHS power station are explored.

Keywords： agricultural microgrid; pumped hydro storage (PHS); irrigation system; uncertainty condition; gravitational whale optimization algorithm (GWOA)

PDF (2680KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨森, 郭宁, 张寿明. 不确定性条件下农业微电网与灌溉系统相结合的鲁棒优化调度[J]. 上海交通大学学报, 2024, 58(9): 1432-1442 doi:10.16183/j.cnki.jsjtu.2023.035

YANG Sen, GUO Ning, ZHANG Shouming. Robust Optimal Scheduling of Agricultural Microgrid Combined with Irrigation System Under Uncertainty Conditions[J]. Journal of Shanghai Jiaotong University, 2024, 58(9): 1432-1442 doi:10.16183/j.cnki.jsjtu.2023.035

化石燃料在为全球提供大量电力的同时也造成温室气体的排放.目前,世界正面临能源短缺和环境污染的双重挑战,可再生能源凭借其巨大的可用性和清洁性成为传统燃料的理想替代品,并且可再生能源的使用正在显著增加^[1-2].国际能源署建议,到2022年,可再生能源在全球能源供应中的比例达30%.一些可再生能源,包括风能、太阳能、水能、潮汐能等,经常用于满足农村和城市地区的能源需求.与城市电气化相比,农村电气化面临人口地域分散、运营投资成本高、供电不足等挑战,这些挑战影响了电力消费和农业生产,从而制约农村经济发展,幸运的是,农村地区拥有丰富的可再生能源^[3].微电网可以将分布式电源、负荷、存储装置等有机整合在一起,提高能源的利用效率,缓解偏远地区的电力短缺^[4-5].因此,农业微电网成为解决农村地区电力消耗的有效手段.文献[6]中研究了智能微电网在尼日利亚离网农村电气化的潜力,建立包含太阳能光伏、储能电池和柴油发电机的离网微电网模型,考虑需求管理的同时与节能灯泡的使用相结合,确保该地区的可靠电力供应并显著降低系统总成本;文献[7]中建立包含太阳能光伏、微型水力发电、生物质能、电池和风能系统的独立微电网混合能源模型,并在印度一个农村社区进行测试,结果表明可以有效解决偏远地区电力供应缺口较小的问题;文献[8]中综合考虑农村地区负荷特性和气候条件等因素,以中国广东省某农村地区为研究对象,建立微电网光伏储能优化配置模型,显著提高并网条件下微电网的光伏吸收率;文献[9]中将由太阳能光伏、风力涡轮机、柴油发电机和储能电池组成的独立微电网在印度农村社区进行测试,结果表明可再生能源系统为农村人口的电气化提供了更有效的解决方案.

在所有可再生能源中,太阳能和风能被认为是最丰富、最发达、经济上可行和商业上可接受的^[10].然而,太阳能和风能固有的波动特性对系统可靠性提出更高要求,可再生能源在电力系统中的高渗透意味着需要以更加灵活的方式储存能量.考虑到农村地理的特殊性和水资源的丰富性,具有快速响应特点的抽水蓄能(PHS)电站成为最具吸引力的长期储能工具^[11].文献[12]中将抽水蓄能电站集成到小型浮动式太阳能光伏系统中,在印度的并网型微电网中进行验证,结果表明使用抽水蓄能电站可以最大限度地利用可再生能源,减少对主电网的压力,同时也能降低日运行成本;文献[13]中在所提孤岛型农村微电网日前能源管理优化框架中使用抽水蓄能电站和需求响应,结果表明实施抽水蓄能机组参与优化调度和需求响应后,经济技术性能指标显著提高.文献[14]中将抽水蓄能电站作为储能装置,提出考虑负荷响应的风-光-抽水蓄能的海岛微电网优化配置模型,算例验证了使用抽水蓄能代替蓄电池储能可以显著减少微电网投资成本.与孤岛型微电网相比,虽然并网型微电网的发展可以提高关键基础设施系统的可靠性和灵活性^[15],但是农村地区地理位置较为偏远的特殊性限制了并网型微电网的大规模使用.

微电网优化调度模型具有很强的非线性,诸如随机线性规划、混合整数规划、混合整数线性规划等传统数学方法难以取得令人满意的结果^[16⇓-18].因此,基于种群的元启发式算法,如粒子群算法、遗传算法、人工蜂群算法等凭借其强大的寻优能力被广泛应用于求解微电网优化调度问题^{[19⇓⇓⇓-23]}.文献[24]中针对微电网优化运行规划问题提出一种增强麻雀搜索算法,与其他算法的仿真结果比较发现所提方法能够有效降低系统运行成本;文献[25]中提出一种改进生物地理优化算法求解微电网并网运行问题,在综合考虑微电网环境效益和经济成本的同时计及可中断负荷对运行成本的影响,取得令人满意的结果;文献[26]中提出一种改进磷虾群算法,对装配太阳能光伏系统的微电网日前调度模型进行求解,并研究了光照各不相同的4个典型气候条件对调度结果的影响;文献[27]中提出一种改进自适应蝙蝠算法求解微电网最优能量调度问题,对一个离网微电网的仿真结果表明该算法具有优越性;文献[28]中提出一种混合粒子群-灰狼算法,用于求解建立在印度农村的微电网最优规划问题,实验结果验证了所提算法的优越性能.

上述文献研究了农村地区抽水蓄能电站的规模、管理和经济方法,但只将其作为储能装置进行抽水发电,忽视了抽水也可以用于灌溉,而这是农村地区储水的主要目的.针对有农田灌溉需求的偏远农村地区能源供应问题,将抽水蓄能电站与灌溉系统进行集成,不仅将抽水蓄能电站作为农业微电网的储能装置,还将其作为灌溉系统的储水装置;以系统总成本最低为目标,并考虑可再生能源发电及负荷波动和灌溉系统用水需求带来的不确定性因素,提出一种含抽水蓄能电站的农业微电网与灌溉系统相结合的鲁棒优化调度模型,在孤岛运行方式下研究该模型的可行性和有效性.所提模型考虑分布式发电、用电负荷需求和用水负荷需求、涡轮流量和灌溉流量,利用多个等式约束和不等式约束对其进行限制,并且存在柴油发电机启停状态的离散变量.因此,该模型具有多样性、多约束和不连续的特点.同时提出一种引力鲸鱼优化算法(GWOA)对其进行求解,为解决偏远农村地区的电力短缺问题提供理论依据.

1 系统模型

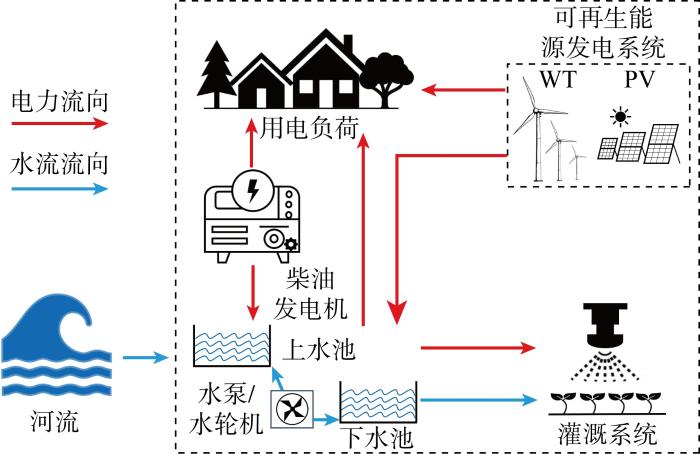
所提农业微电网模型如图1所示.农业微电网由风力涡轮机(WT)、太阳能光伏(PV)列阵、抽水蓄能电站、灌溉系统和两个位于不同水位的水池组成,由于无法与主电网进行功率交互,所以必要时可启动柴油发电机进行发电以补足缺额功率.其中,上水池与河流相连,下水池与灌溉系统相连,存储在上水池的水来自于河流和从下水池抽取的水,灌溉系统的用水需求由下水池提供.在该农业微电网中,当风力发电和光伏发电不足时由柴油发电机弥补电力缺额,反之则将过剩电能存储在抽水蓄能电站中.此外,若过剩的电能较少则无法存储在抽水蓄能电站中,此时将弃掉一部分风光以达到功率平衡.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 农业微电网模型

Fig.1 Model of agricultural microgrid

1.1 农业微电网模型

1.1.1 抽水蓄能电站模型

抽水蓄能电站包含一个用于从河流或者下水池抽水的水泵和一个连接在上水池与下水池之间用于发电的水力涡轮机.水泵和水力涡轮机的水电转换方程如下:

(1)P_PS_,_P=a_PS

Q_{P}^{2}

+b_PSQ_P+c_PS

(2)P_PS_,_S=a_PS

Q_{S}^{2}

+b_PSQ_S+c_PS

式中:a_PS、b_PS、c_PS为抽水蓄能水轮机的发电系数;P_{PS, P}为水泵消耗的电能;P_{PS, S}为水轮机生产的电能;Q_P为流经水泵的流量;Q_S为流经水轮机的流量.

1.1.2 灌溉系统模型

农村地区储存水的主要目的是对农田进行灌溉.灌溉系统的耗电公式如下:

(3)P_IS=a_IS

Q_{I S}^{2}

+b_ISQ_IS+c_IS

式中:P_IS为灌溉系统消耗的电能;a_IS、b_IS、c_IS为灌溉系统的耗电系数;Q_IS为灌溉系统的流量.

1.2 目标函数及约束条件

1.2.1 目标函数

农业微电网优化调度问题是指在满足系统负荷需求的前提下,合理调度各种资源发电,使系统运行成本最小,其目标函数为

(4)$ \begin{array}{l} \min F=\sum_{t=1}^{T}\left(\sum_{j=1}^{U} C\left(P_{j}\right)+C\left(P_{\mathrm{D}}\right)+\right. \\ \left.\phi_{\mathrm{G}} C\left(P_{\mathrm{PS}, \mathrm{P}}^{t}\right)+\phi_{\mathrm{S}} C\left(P_{\mathrm{PS}, \mathrm{~s}}^{t}\right)+C\left(P_{\mathrm{GU}}\right)\right) \end{array}$

式中:F为农业微电网系统运行成本;C(P_j) 为第j个可再生能源的发电成本,其中P_j为第j个可再生能源的输出功率;C(P_D)为柴油发电机运行成本;C( $P_{P S, P}^{t}$ )为水泵的启动成本,取35元;C( $P_{P S, S}^{t}$ )为水轮机的启动成本,取35元;ϕ_G、ϕ_S为二元整形变量,且0<ϕ_G+ϕ_S≤1;C(P_GU)为弃风弃光成本,取0.5元/(kW·h).

1.2.2 系统约束

具体如下.

(1) 功率平衡约束:

(5)P_load=

\overset{U}{\sum_{j = 1}}

P_j+P_DG+P_PS+P_IS

式中:P_load为系统负荷需求;P_DG为柴油发电机的输出功率;P_PS为抽水蓄能电站的功率,为正表示输出功率,为负表示吸收功率.

(2) 上下水池流速限制:

(6)

v_{U P}^{m i n}

≤

v_{U P}^{t}

≤

v_{U P}^{m a x}

(7)

v_{L O W}^{m i n}

≤

v_{L O W}^{t}

≤

v_{L O W}^{m a x}

式中: $v_{U P}^{t}$ 、 $v_{L O W}^{t}$ 分别为上、下水池t时刻放水或抽水流速; $v_{U P}^{m i n}$ 为上水池放水或抽水的最小流速; $v_{U P}^{m a x}$ 为上水池放水或抽水的最大流速; $v_{L O W}^{m i n}$ 为下水池放水或抽水的最小流速; $v_{L O W}^{m a x}$ 为下水池放水或抽水的最大流速.

(3) 上下水池容量限制:

(8)

Q_{U P}^{m i n}

≤

Q_{U P}^{t}

≤

Q_{U P}^{m a x}

(9)

Q_{L O W}^{m i n}

≤

Q_{L O W}^{t}

≤

Q_{L O W}^{m a x}

式中: ${Q^{t}}_{U P}$ 、 ${Q^{t}}_{L O W}$ 分别为上、下水池t时刻容量; $Q_{U P}^{m i n}$ 为上水池的容量下限; $Q_{U P}^{m a x}$ 为上水池的容量上限; $Q_{L O W}^{m i n}$ 为下水池的容量下限; $Q_{L O W}^{m a x}$ 为下水池的容量上限.

(4) 上下水池始末容量限制.为了保证抽水蓄能电站在第二天能够正常运行,在一天的运行结束时,上下水池中必须储存足够的水.水池容量限制如下:

(10)

Q_{U P}^{I n}

Q_{U P}^{F i n}

≥

Q_{U P}^{N o r}

(11)

Q_{L O W}^{I n}

Q_{L O W}^{F i n}

≥

Q_{L O W}^{N o r}

式中: $Q_{U P}^{I n}$ 为上水池的初始水量; $Q_{U P}^{F i n}$ 为上水池的终末水量; $Q_{U P}^{N o r}$ 为上水池始末规定水量; $Q_{L O W}^{I n}$ 为下水池的初始水量; $Q_{L O W}^{F i n}$ 为下水池的终末水量; $Q_{L O W}^{N o r}$ 为下水池始末规定水量.

(5) 灌溉系统流速限制:

(12)

v_{I r}^{m i n}

≤

v_{I r}^{t}

≤

v_{I r}^{m a x}

式中: $v_{I r}^{t}$ 为灌溉系统t时刻流速; $v_{I r}^{m i n}$ 为灌溉系统的流速下限; $v_{I r}^{m a x}$ 为灌溉系统的流速上限.

(6) 灌溉系统水量限制:

(13)

\overset{T}{\sum_{t = 1}} Q_{I r}^{t}

=Q_all

式中: $Q_{I r}^{t}$ 为t时刻灌溉系统用水量;Q_all为灌溉系统总用水量.

1.3 鲁棒优化调度模型

由于风力发电、光伏发电和用电负荷需求具有一定波动性和随机性,所以需考虑源荷不确定性对调度结果带来的影响.采用鲁棒优化的理论来建立可再生能源及用电负荷需求的出力模型,即源荷不确定性模型,如下:

(14)

\begin{array}{l} P_{i}^{t} = P_{f i}^{t} + u_{i}^{t} Δ P_{u i}^{t} - l_{i}^{t} Δ P_{l i}^{t} \\ 0 \leq u_{i}^{t} + l_{i}^{t} \leq 1 \\ u_{i}^{m i n} \leq \overset{T}{\sum_{t = 1}} u_{i}^{t} \leq u_{i}^{m a x} \\ l_{i}^{m i n} \leq \overset{T}{\sum_{t = 1}} l_{i}^{t} \leq l_{i}^{m a x} \end{array}\}

式中: $P_{i}^{t}$ 为风力涡轮机、光伏列阵或负荷需求的功率; $P_{f i}^{t}$ 为风力涡轮机、光伏列阵或负荷需求的预测功率值;Δ $P_{u i}^{t}$ 为波动范围的上限;Δ $P_{l i}^{t}$ 为波动范围的下限; $u_{i}^{t}$ 、 $l_{i}^{t}$ 为二元整型变量,当 $u_{i}^{t}$ =1时处于不确定性波动的上限,当 $l_{i}^{t}$ =1时处于不确定性波动的下限, $u_{i}^{t}$ = $l_{i}^{t}$ =1时则无波动; $u_{i}^{m i n}$ 为波动范围上限的最小个数; $u_{i}^{m a x}$ 为波动范围上限的最大个数; $l_{i}^{m i n}$ 为波动范围下限的最小个数; $l_{i}^{m a x}$ 为波动范围下限的最大个数.

考虑源荷不确定性的农业微电网鲁棒优化调度模型可以构造为min-max问题.将可再生能源出力和用电负荷需求作为不确定变量,定义在规定允许最大波动范围的不确定变量集合内,使得可再生能源发电成本和弃风弃光成本最大解所描述的场景为极端场景;然后在极端场景下得到的最优解即为农业微电网鲁棒优化调度方案.进一步可获得农业微电网鲁棒优化调度模型的目标函数如下:

(15)$ \begin{aligned} \min & \sum_{t=1}^{T}\left[\phi_{\mathrm{G}} C\left(P_{\mathrm{PS}, \mathrm{P}}^{t}\right)+\phi_{\mathrm{S}} C\left(P_{\mathrm{PS}, \mathrm{~s}}^{t}\right)+\right. \\ & \left.C\left(P_{\mathrm{D}}\right)+\max \left(\sum_{j=1}^{U} C\left(P_{j}\right)+C\left(P_{\mathrm{GU}}\right)\right)\right] \end{aligned}$

2 引力鲸鱼优化算法

2.1 鲸鱼优化算法

鲸鱼优化算法(WOA)是Mirjalili等^[29]在2016年提出的一种元启发式搜索算法,具有可调参数少、收敛速度快、寻优精度高等优点,目前已广泛应用于数据预测、路径规划和特征选择等多种工业和科学研究领域^[30⇓-32].WOA是一种模仿座头鲸狩猎策略的启发式搜索算法.主要包括包围猎物、气泡网攻击和搜索猎物3个阶段.

(1) 包围猎物.表示为

(16)D=

|C X^{*} (k) - X (k)|

(17)X(k+1)=X^*(k)-AD

式中:D为座头鲸与当前最优座头鲸的距离;k为迭代次数;X^*为到目前为止的最优位置;X为当前位置;A和C分别由下式计算,即

(18)A=2a'r-a'

(19)C=2r

r为[0,1]之间的随机数;a'随着迭代次数的增加从2线性减小到0,由下式计算,即

(20)a'=2-2

\frac{k}{k_{m a x}}

k_max为最大迭代次数.

(2) 气泡网攻击.座头鲸吐出气泡,并以螺旋线运动轨迹向猎物发动攻击,该行为由下式表示:

(21)X(k+1)=D_pe^blcos(2πl)+X^*(k)

(22)D_p=

|X^{*} (k) - X (k)|

式中:D_p为座头鲸与猎物之间的距离;b为常数,用于定义螺旋线的形状;l为[-1, 1]之间的随机数.

(3) 搜索猎物.在搜索猎物阶段,座头鲸在搜索空间中进行随机游走,该行为表示为

(23)D_r=

|C X_{r a n d} (k) - X (k)|

(24)X(k+1)=X_rand(k)-AD_r

式中:D_r为座头鲸与随机座头鲸的距离;X_rand为从种群中随机选取的个体.

值得注意的是,在WOA中,当收敛因子 $|A|$ <1时,算法进行局部搜索,此时座头鲸以概率P^*进行包围猎物行为,以概率1-P^*的概率向猎物发起气泡网攻击;当收敛因子 $|A|$ ≥1时,算法进行全局搜索,此时座头鲸随机游走以搜索猎物.

2.2 引力鲸鱼优化算法

Rashedi等^[33]受到牛顿的重力和运动理论启发而开发的引力搜索算法(GSA)将种群中的粒子视为空间中运动个体,这些个体在引力的作用下彼此吸引,质量越大的个体吸引其他粒子的作用力也越强,其解的质量也越好,整个种群依靠粒子间的相互作用力进行运动从而向最优区域进行搜索.GSA的操作步骤如下.

计算在第k次迭代时,第z个粒子作用在第i个粒子上的的引力大小 $F_{i, z}^{d}$ (k):

(25)

\begin{array}{l} F_{i, z}^{d} (k) = G (k) \frac{m_{i} (k) m_{z} (k)}{R_{i, z} (k) + ε} (x_{z}^{d} (k) - x_{i}^{d} (k)) \\ G (k) = G_{0} e^{- γ \frac{k}{K}} \end{array}\}

式中:G(k)为第k次迭代的万有引力常数,γ=20,G₀=100;K为最大迭代次数;m_i(k)、m_z(k)分别为粒子i和粒子z的惯性质量; R_{i, z}(k)为粒子i和粒子z之间的欧氏距离;ε为一个极小的常数; $x_{z}^{d}$ (k)、 $x_{i}^{d}$ (k)分别为第k次迭代时粒子z、i在第d维的位置.

第i个粒子的加速度 $a_{i}^{d}$ (k)由下式计算:

(26)

\begin{array}{l} F_{i}^{d} (k) = \overset{N_{P}}{\sum_{z = 1, z \neq i}} R F_{i, z}^{d} (k) \\ m_{i} (k) = \frac{f_{n, i} (k) - W (k)}{B (k) - W (k)} \\ M_{i} (k) = \frac{m_{i} (k)}{\overset{N_{P}}{\sum_{z = 1}} m_{z} (k)} \\ a_{i}^{d} (k) = \frac{F_{i}^{d} (k)}{M_{i} (k)} \end{array}\}

式中: $F_{i}^{d}$ (k)为在第d维上其他粒子对第i个粒子引力的合力;N_P为粒子个数;R为[0,1]之间的随机数;f_{n, i}(k)为第k次迭代时第i个粒子的适应度值;B(k)、W(k)分别为当前种群中的最优适应度值和最差适应度值.

对于WOA而言,个体在包围猎物和搜索猎物阶段的位置更新都与收敛因子a的取值有关:a的值越大,算法的全局搜索能力越强;a的值越小,算法的局部搜索能力越强.如何设计合适的参数a对于WOA性能的提升至关重要.算法前期应加强全局搜索,在整个搜索空间中尽可能对勘探出最优解所在的区域,算法后期应该注重局部搜索,在锁定的最优解区域进行开发,从而寻到最优解.然而,WOA中的收敛因子a随着迭代次数从2线性减小到0,并不能完全体现出WOA的勘探和开采过程.

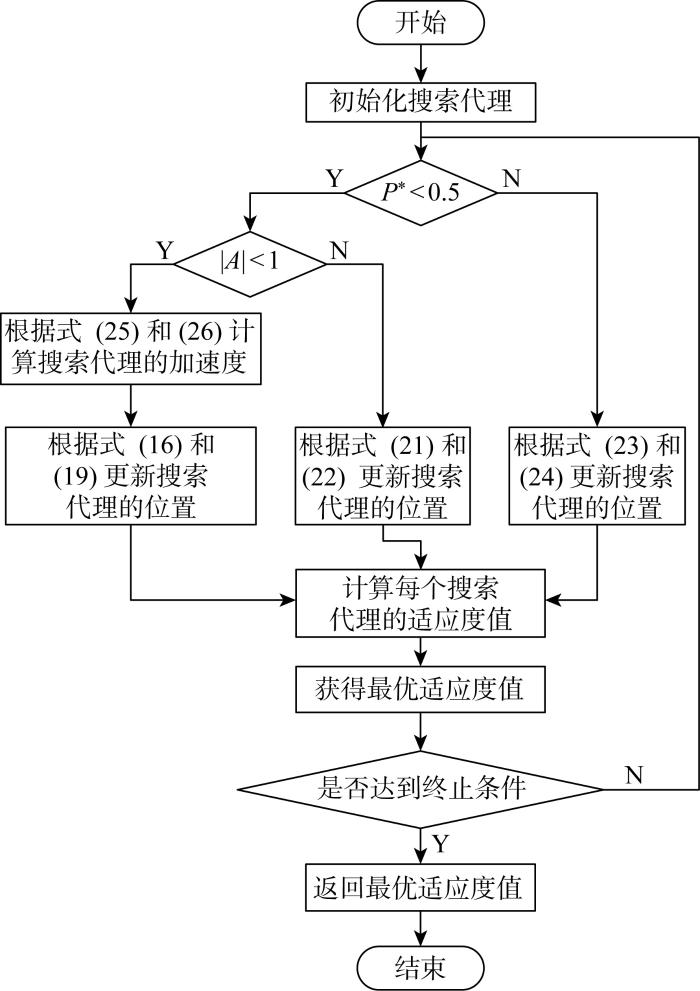
受GSA启发,将加速度因子a^*引入位置更新公式中用于取代收敛因子a.个体间引力的作用使得惯性质量小的个体具有较小加速度,此时算法更倾向于局部搜索;惯性质量大的个体具有较大加速度,此时算法更注重全局搜索.在迭代过程中,加速度因子a^*会受到其他个体引力以及自身其他维度引力的引导,将呈现非线性变化,自适应调整全局搜索和局部搜索的程度,驱使算法向着最优区域进行搜索,进而搜索到最优值.GWOA的算法流程图如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 GWOA算法流程图

Fig.2 Flow chart of GWOA

3 算例分析

3.1 系统参数设置

在考虑源荷不确定性的条件下,利用GWOA对农业微电网的鲁棒优化调度问题进行研究,调度周期为24 h,时间间隔为1 h.农业微电网系统参数设置^[34-35]如下.

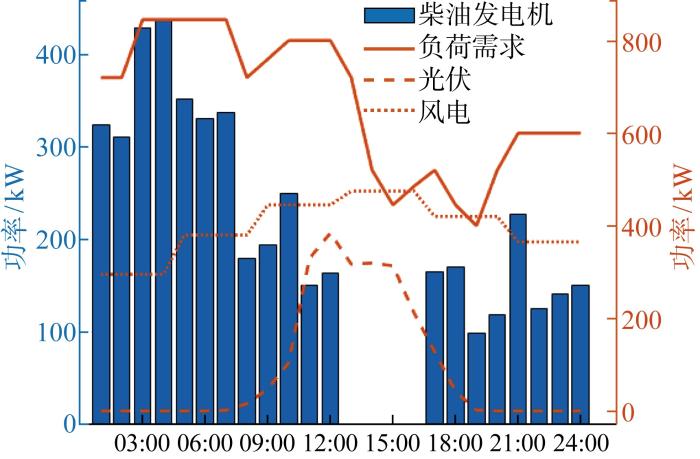
负荷需求:农业微电网的负荷需求、光电功率和风电功率如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 可再生能源功率及负荷需求

Fig.3 Renewable energy power and load requirements

抽水蓄能电站:抽水蓄能电站上水池的水来自河流或下水池,下水池满足灌溉系统用水需求.抽水蓄能水轮机发电系数为a_PS=-0.033 W·h²/(m³)²,b_PS=5 W·h/m³,c_PS=0 W.抽水蓄能电站上下水池参数设置如表1所示.

表1 蓄水池参数

Tab.1 Parameters of reservoir

水池	流速上限/ (m³·h^-1)	流速下限/ (m³·h^-1)	容量上限/m³	容量下限/m³	始末规定容量/m³
上水池	60	10	450	50	350
下水池	60	10	600	150	100

新窗口打开| 下载CSV

灌溉系统:该农业微电网中,灌溉系统功耗系数为a_IS=-0.033 W·h²/(m³)²,b_IS=5 W·h/m³,c_IS=0 W.灌溉系统的流速下限 $v_{I r}^{m i n}$ =5 m³,流速上限 $v_{I r}^{m a x}$ =20 m³.

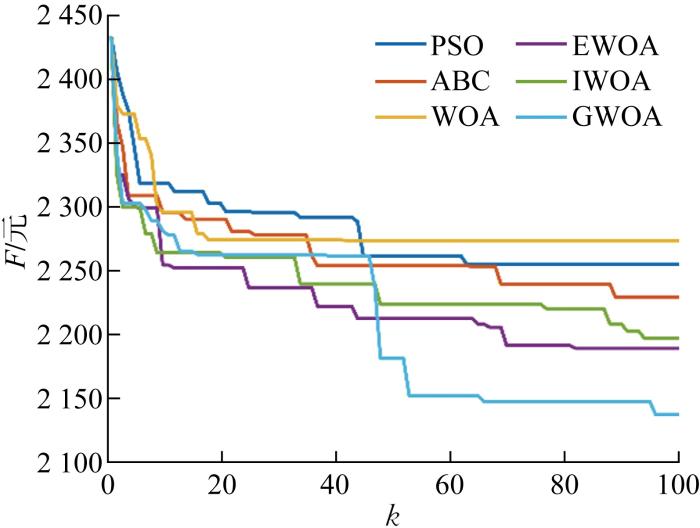
为验证所提GWOA的有效性,将GWOA与粒子群算法(PSO)、人工蜂群算法(ABC)、WOA、增强鲸鱼优化算法(EWOA)和改进鲸鱼优化算法(IWOA)的优化结果进行分析对比^[36-37].PSO、ABC、WOA的参数参考相关文献设置,EWOA和IWOA的参数参考原文设定,如表2所示.表中:C₁、C₂分别为自学习因子、互学习因子;W为惯性权重;L为侦查蜂转换阈值;p为选择攻击方式概率;α为阶跃尺度因子;β为Levy分布随机数的参数.

表2 算法参数设置

Tab.2 Parameter setting of algorithms

算法	参数
PSO	C₁=1.5,C₂=1.5,W=0.75
ABC	L=5
WOA	b=1, p=0.5
EWOA	p=0.5
IWOA	b=1, p=0.5, α=0.01,β=1.5
GWOA	b=1, p=0.5

新窗口打开| 下载CSV

3.2 智能算法的有效性分析

为探究智能算法求解该农业微电网的有效性,将常用于求解电力系统经济调度问题的CPLEX求解器与WOA、EWOA、IWOA和GWOA的优化结果进行对比,分别从求解精度和求解速度两个角度进行分析对比,在灌溉系统用水需求量为300 m³的春季进行验证.

如表3所示,CPLEX求解器的求解速度最快,仅用0.6 s就得到结果;GWOA求解时间最长,需要1.5 s才能完成求解.从求解精度来看,GWOA的精度最高,没有任何改进的WOA求解精度最低,其次是CPLEX求解器.对于优化调度问题而言,在求解速度相差不大的情况下,会更侧重于求解精度.本次验证中求解最长时间为1.5 s,最短时间为 0.6 s,同属于一个量级且求解速度相差不大.CPLEX求解器的综合性能略好于WOA,但相较于有改进的EWOA、IWOA和GWOA,CPLEX求解器的综合性能略显不足,故智能算法更加适合求解该农业微电网经济优化运行模型.

表3 不同求解方法的结果对比

Tab.3 Comparison of results of different solution methods

求解方法	最优成本/元	所用时间/s
CPLEX求解器	2254.7	0.6
WOA	2269.5	0.7
EWOA	2236.4	1.1
IWOA	2221.1	0.9
GWOA	2147.7	1.5

新窗口打开| 下载CSV

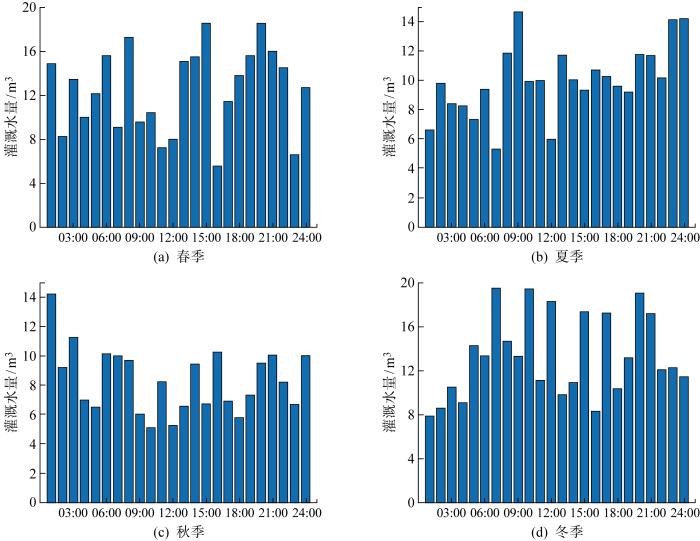
3.3 不同季节的仿真结果分析

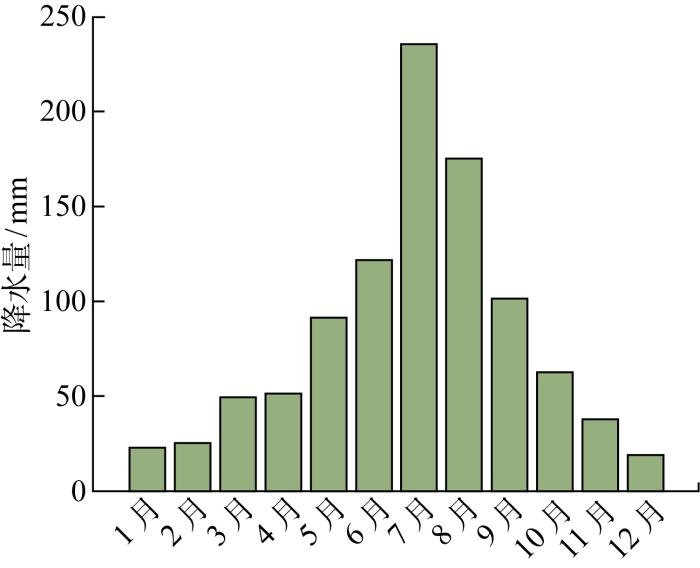
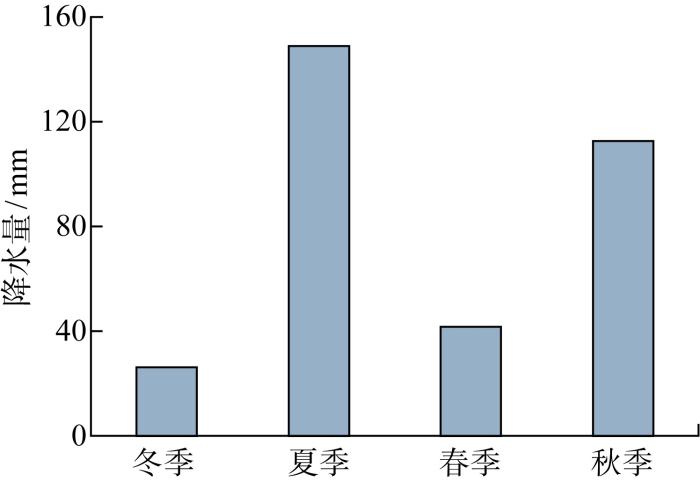
为研究季节降水量引起灌溉系统水负荷变化对农业微电网运行成本的影响,选择一年中4个不同季节的平均降水量作为灌溉系统用水需求量变化指标.某地年均降水量和4个不同季节平均降水量分别如图4和图5所示,灌溉系统在春季、夏季、秋季和冬季的用水需求量分别为300、200、240和 320 m³.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 年均降水量

Fig.4 Average annual precipitation

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 季节平均降水量

Fig.5 Average seasonal precipitation

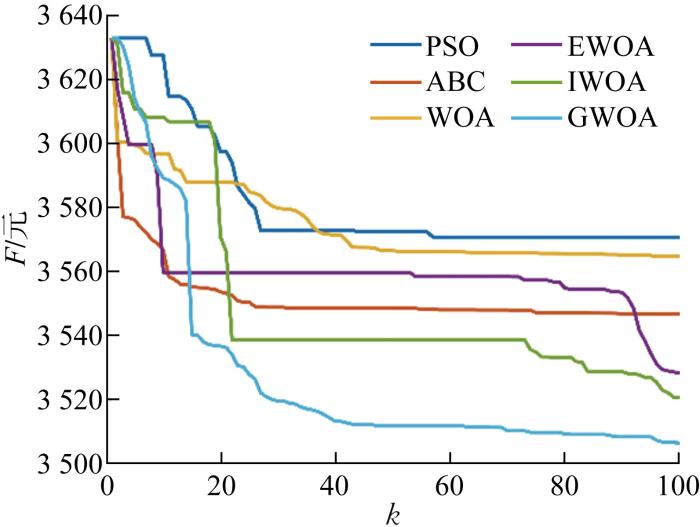
图6为灌溉系统在4个不同季节里的灌溉计划,表4为6种算法分别在降水量各不相同的4个不同季节里的最优运行成本.由表可知,与WOA、PSO和ABC相比,EWOA和IWOA可以取得更好的解,而GWOA得到的解是6种算法中最佳.此外,值得注意的是,夏季的系统运行成本低于另外3个季节,这是由于夏季的降水量最多,意味着灌溉系统的用水负荷需求最低,则农业微电网的运行成本也最低.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 最佳灌溉计划

Fig.6 Optimal irrigation plan

表4 不同算法季节最优成本对比

Tab.4 Comparison of seasonal optimal cost of different algorithms元

季节	WOA	PSO	ABC	EWOA	IWOA	GWOA
春	2256.5	2345.6	2303.4	2230.2	2224.4	2186.8
夏	2134.2	2141.3	2120.6	2065.4	2076.5	2001.7
秋	2182.8	2231.5	2151.4	2128.5	2134.2	2105.7
冬	2304.8	2408.4	2339.4	2265.2	2252.6	2222.5

新窗口打开| 下载CSV

3.4 仿真结果分析

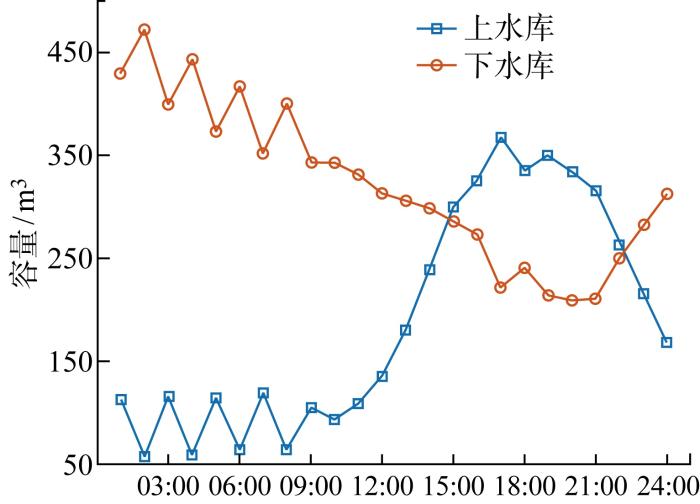
以该农业微电网为分析对象,选择灌溉系统水负荷为300 m³的春季进行仿真实验,经过GWOA优化后的农业微电网系统上下水池容量变化和柴油发电机功率分别如图7、图8所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 蓄水池容量变化

Fig.7 Reservoir capacity versus time

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 柴油机发电功率

Fig.8 Generation power of diesel engine

由图7和图8可知,在0:00—9:00时段,光伏出力较少,可再生能源的输出功率不足以满足该时间段的负荷需求,因此需要柴油发电机大量发电补足缺额电能以满足功率平衡.柴油发电机的成本函数为二次函数形式,如在某一时刻柴油发电机发电过多,则柴油发电机在该时刻的发电成本会急速上升.为避免这种情况而导致系统总成本过高,抽水蓄能电站的上水池在满足约束条件的前提下遵循“能放则放”的原则,从而尽可能多地发电以降低柴油发电机的发电成本,因此上水池在 1:00、3:00、5:00、7:00、9:00 放水驱动水力涡轮机发电.在 10:00—17:00 时段,随着可再生能源输出功率增加以及负荷需求降低,柴油发电机的发电量逐渐减少;在 13:00—16:00 时段柴油发电机处于停机状态,可再生能源的输出功率能够满足负荷需求并将盈余电能转化为水的重力势能储存在上水池中.在 18:00—24:00 时段,可再生能源的输出功率无法满足负荷需求,上水池放水驱动水力涡轮机发电补足部分负荷需求,剩余较少缺额电能由柴油发电机补足.

为进一步验证所提农业微电网模型的合理性和可行性,同时进一步验证所提算法的有效性,设定农业微电网模型中含PHS和不含PHS电站两种场景,利用PSO、ABC、WOA、EWOA、IWOA、GWOA这6种算法对两种场景进行仿真,获取系统弃风弃光率和最小成本实验数据进行分析.两种场景下农业微电网系统总成本的仿真结果分别如图9和图10所示,具体优化结果如表5所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 含PHS场景

Fig.9 Scenario with PHS

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不含PHS场景

Fig.10 Scenario without PHS

表5 2种场景下微电网运行成本

Tab.5 Operation cost of microgrid in two scenarios

场景	算法	弃风弃光率/%	弃风弃光率均值/%	最优成本/元	最优成本均值/元
含PHS	WOA	8.75	7.78	2272.9	2212.9
	PSO	8.58	7.78	2254.5	2212.9
	ABC	8.16	7.78	2228.3	2212.9
	EWOA	7.24	7.78	2188.5	2212.9
	IWOA	7.15	7.78	2196.6	2212.9
	GWOA	6.85	7.78	2136.6	2212.9
不含PHS	WOA	18.34	18.18	3564.9	3539.7
	PSO	20.56	18.18	3571.0	3539.7
	ABC	17.98	18.18	3546.9	3539.7
	EWOA	17.52	18.18	3528.4	3539.7
	IWOA	17.41	18.18	3521.0	3539.7
	GWOA	17.26	18.18	3506.2	3539.7

新窗口打开| 下载CSV

由图9~10和表5可知在含PHS场景下,WOA、PSO、ABC、EWOA、IWOA和GWOA这6种算法求得的最优成本分别为 2272.9、2254.5、2228.3、2188.5、2196.6 和 2136.6 元,不含PHS场景下的最优成本则为 3564.9、3571.0、3546.9、3528.4、3521.和 3506.2元,由此可见,无论在何种场景下,GWOA算法所求目标函数的最优值均好于其余5种算法,表明该算法的寻优精度高,具有一定优越性.由表5可知,含PHS场景下该农业微电网模型的最优成本均值为 2212.9 元,明显低于不含PHS场景下的 3539.7 元,减少37.5%;可再生能源的利用率即弃风弃光率均值也比不含PHS场景的高10.4个百分点.这是因为含PHS场景下可将盈余电能储存在PHS电站中,在出现供需不平衡的时候将电能释放以满足负荷需求,降低柴油发电机的发电量,也能降低弃风弃光成本,从而使得整个农业微电网系统成本降低.

3.5 考虑源荷不确定性时的调度结果对比

优化调度结果根据历史数据得到,但源荷不确定性波动可能会导致难以满足负荷需求的情况发生,故应将源荷不确定性对调度结果的影响考虑在内.根据式(14)给出的模型,设风、光出力和负荷的波动范围为预测值的±20%.由于表5已论证含PHS的农业微电网系统总成本最低,故对该模型进行源荷不确定性分析.在实际优化过程中,考虑不同波动情况下出现的极端情况,Case1,可再生能源出力波动为预测值的+20%和负荷波动为预测值的+20%;Case2,可再生能源出力波动为预测值的 +20% 和负荷波动为预测值的-20%;Case3,可再生能源出力波动为预测值的-20% 和负荷波动为预测值的 +20%;Case4,可再生能源出力波动为预测值的-20%和负荷波动为预测值的-20%.以上4种场景均采用GWOA进行求解,结果如表6所示.

表6 源荷波动下运行成本

Tab.6 Operation costs under load source fluctuation

场景	弃风弃光率/%	最优成本/元
Case1	7.54	3011.9
Case2	14.34	2230.5
Case3	3.32	4363.2
Case4	8.03	1488.2

新窗口打开| 下载CSV

由表6可知,Case1场景下系统成本为 3011.9 元,比源荷不波动场景的成本略高,可再生能源出力增加及负荷需求提高,但光伏不出力的时段,柴油发动机会生产更多的电能以维持功率平衡,致使系统总成本增加;Case2场景下系统成本为 2230.5 元,与源荷不波动场景的成本相当,由于PHS的容量有限,无法储存过多盈余电能,产生弃风弃光成本的同时,柴油发电机成本也会降低,所以此场景下可再生能源的消纳率最低;Case3场景下系统成本为 4363.2 元,明显高于源荷不波动场景的成本,可再生能源出力的减少以及负荷需求的增加,为满足功率平衡,柴油发电机必须发更多的电能,致使柴油发电机成本急剧增加,但该场景下可再生能源的利用率最高;Case4场景下系统成本为 1488.2 元,略低于源荷不波动场景的成本,可再生能源出力及负荷需求的降低使得柴油发电机的发电量减少,从而系统总成本降低.故将Case1的调度方案作为考虑源荷不确定性时的最佳调度方案.

4 结语

针对含有农田灌溉需求的偏远农村地区能源供应问题,依据农村地区水资源的丰富性和地理位置的特殊性,在可再生能源及用电负荷需求的不确定性条件下,综合考虑光伏发电、风力发电、用电负荷需求和灌溉系统用水需求等因素,提出含PHS电站的孤岛型农业微电网与灌溉系统相结合的鲁棒优化调度模型,将PHS电站作为储能装置的同时也将其作为储水装置,满足农业微电网的部分用电负荷需求和灌溉系统的用水负荷需求.为验证所提模型的可行性,分别在源荷不确定性和降水不确定性的条件下对该模型进行可行性分析,利用所提GWOA求解该模型.与CPLEX求解器的对比证明了智能算法求解农业微电网优化调度问题的必要性;同时,与其余5种算法对比,验证了所提算法的有效性.最后,设定含PHS和不含PHS两种场景,分析对比调度结果可知,含PHS的农业微电网可减少37.5%的最优成本均值,并降低10.4个百分点的弃风弃光率均值,以低成本的方式为偏远农村地区的能源供应提供了一种有前景的解决方案.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

ISHRAQUE

M F

, SHEZAN

S A

, ALI

M M

, et al.

Optimization of load dispatch strategies for an islanded microgrid connected with renewable energy sources

[J]. Applied Energy, 2021, 292: 116879.

[本文引用: 3]

[2]

陆秋瑜, 于珍, 杨银国, 等.

考虑源荷功率不确定性的海上风力发电多微网两阶段优化调度

[J]. 上海交通大学学报, 2022, 56(10): 1308-1316.

DOI:10.16183/j.cnki.jsjtu.2021.409 [本文引用: 1]

针对海上风力发电多微网源荷功率不确定性大、经济效益低的问题,提出考虑源荷不确定性的海上风力发电多微网两阶段优化调度方法,以提升海上风力发电多微网的日运行收益.所提两阶段优化调度方法包括日前和时前两个阶段.在日前阶段,所提方法基于风力发电出力和负荷需求预测数据,考虑预测误差的分布特征,建立随机优化模型,制定燃油发电机组组合计划和电池储能荷电状态值,从而最大化日运行收益的期望值.在日前优化的基础上,依托时前风力发电出力和负荷需求的预测数据,建立确定性优化模型,通过调节燃油发电机组出力、风力发电出力和电池储能充放电功率,最大化每小时的运行收益.以实际工程中的海上风力发电多微网源荷预测数据为基础,建立仿真模型,对所提方法进行验证.仿真结果表明,与传统调度方法相比,所提两阶段优化调度方法可以提高运行收益和风力发电资源整体消纳率.

Qiuyu

, YU

Zhen

, YANG

Yinguo

, et al.

Two-stage optimal scheduling of offshore wind power generation in multi-microgrid considering source-load power uncertainty

[J]. Journal of Shanghai Jiao Tong University, 2022, 56(10): 1308-1316.