考虑多维影响因素的改进Transformer-PSO短期电价预测方法

doi:10.16183/j.cnki.jsjtu.2023.065

考虑多维影响因素的改进Transformer-PSO短期电价预测方法

孙欣^,, 王思敏, 谢敬东, 江海林, 王森

上海电力大学电气工程学院,上海 200090

Improved Transformer-PSO Short-Term Electricity Price Prediction Method Considering Multidimensional Influencing Factors

SUN Xin^,, WANG Simin, XIE Jingdong, JIANG Hailin, WANG Sen

College of Electrical Engineering, Shanghai University of Electric Power, Shanghai 200090, China

责任编辑: 王历历

收稿日期: 2023-02-27 修回日期: 2023-05-4 接受日期: 2023-05-19

基金资助:

国家自然科学基金(U2066214)

Received: 2023-02-27 Revised: 2023-05-4 Accepted: 2023-05-19

作者简介 About authors

孙欣(1980—),博士,副教授,从事电力市场、能源互联网等方面研究;E-mail:sunxin@shiep.edu.cn.

摘要

随着多元化电力市场的建设,电价影响因素日益增加,市场环境变化也更加剧烈.为提高市场短期电价的预测精度,提出一种考虑多种电价影响因素的改进Transformer-粒子群优化(PSO)算法短期电价预测方法.首先,在考虑历史电价、负荷的基础上进一步分析电价形成的相关因素,利用自相关函数分析电价的多周期特性并在此基础上调整输入序列,克服了仅采用历史数据以及经验调整输入序列导致预测精度受限的问题.其次,结合长短期记忆(LSTM)、自注意力机制与多层注意力机制并采用多输入结构建立改进Transformer模型,进一步提升LSTM模型捕获不同时间步信息间的长短期依赖关系的能力,克服LSTM的信息利用瓶颈,适应包括历史电价及多种电价成因的复杂多序列输入.此外,还利用PSO智能算法搜索模型不同学习阶段的最佳学习率克服手动调整学习率的局限性.最后,采用PJM市场电价进行算例分析,结果表明所提短期电价预测模型能应用于电价影响因素多、变化剧烈的市场环境,并有效提升短期电价预测精度.

关键词： 短期电价预测; 多维影响因素; 自相关分析; 改进Transformer模型; 粒子群优化

Abstract

With the construction of a diversified electricity market, the factors affecting electricity prices are gradually increasing, and the market environment has undergone more drastic changes. In order to improve the accuracy of short-term electricity price prediction, an improved Transformer-particle swarm optimization (PSO) short-term electricity price prediction method considering multiple factors affecting electricity prices is proposed. First, based on the consideration of historical electricity prices and historical loads, the relevant factors of electricity price formation are further analyzed. The autocorrelation function is used to analyze the multi-cycle characteristics of electricity price and adjust input sequence, which overcomes the problem of limited prediction accuracy caused by using historical data only and adjusting the input sequence by experience. Then, by combining long short-term memory (LSTM), self-attention mechanism, multi-layer attention mechanism, and adopting a multi-input structure, an improved Transformer model is established to further enhance the ability of the LSTM model to capture long short-term dependencies between different time step information, to overcome the information utilization bottleneck of LSTM, and to adapt to complex multiple sequence inputs including historical electricity prices and various electricity price causes. In addition, the PSO intelligent algorithm is utilized to search for the optimal learning rate of the model at different learning stages, overcoming the limitations of manually adjusting the learning rate. Finally, the PJM market electricity price is used for example analysis. The results show that the proposed short-term electricity price prediction model can be applied to the market environment where electricity prices are affected by various factors and drastic changes, and effectively improve the accuracy of short-term electricity price prediction.

Keywords： short-term electricity price prediction; multidimensional influencing factors; autocorrelation analysis; improved Transformer model; particle swarm optimization (PSO)

PDF (3027KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

孙欣, 王思敏, 谢敬东, 江海林, 王森. 考虑多维影响因素的改进Transformer-PSO短期电价预测方法[J]. 上海交通大学学报, 2024, 58(9): 1420-1431 doi:10.16183/j.cnki.jsjtu.2023.065

SUN Xin, WANG Simin, XIE Jingdong, JIANG Hailin, WANG Sen. Improved Transformer-PSO Short-Term Electricity Price Prediction Method Considering Multidimensional Influencing Factors[J]. Journal of Shanghai Jiaotong University, 2024, 58(9): 1420-1431 doi:10.16183/j.cnki.jsjtu.2023.065

全球电力行业的普遍趋势是引入竞争与放松管制,随着我国电力市场改革逐渐深化,电力行业也逐渐由垄断走向市场化,而电力市场环境下各方交易均建立在电价基础之上,因此预测电价能为电力市场各方决策提供参考^[1].由于近些年“双碳”目标的提出,电力市场的多元化建设对电价造成冲击,影响电价的因素较传统电力市场更多且市场环境变化更为剧烈,而预测电价能作为各方能源结构转型、能源配比调整从而使电力市场运行效率更高的一个重要参考,受到市场各方的广泛关注.因此,在传统电价预测方法仅考虑历史电价与历史负荷的基础上进一步考虑多种电价影响因素,研究适应变化剧烈的市场环境的高精度短期电价预测方法具有十分重要的意义.

现有电价预测模型主要包括统计或经济学模型以及人工神经网络模型,其中统计或经济学模型^[2⇓-4]一般采用数学理论以及数学方程组合,利用电价以及电价相关影响因素的历史数据并估计参数建立回归模型来预测电价,导致其对非线性关系的建模能力有限,因此电价预测精度有限.人工神经网络则模拟人脑神经元的结构,采用自下而上的学习策略,大大降低建模难度且能较好地拟合复杂的非线性数据^[5].其中,应用广泛的长短期记忆(Long Short-Term Memory, LSTM)^[6-7]在基本循环神经网络(Recurrent Neural Network, RNN)模型的基础上增加一条携带信息的轨道,使得网络能记忆较长时间步之前的内容,但随时间延长仍会逐渐丢失部分信息,导致预测精度受损.为提升LSTM网络的预测精度,部分学者分解输入序列简化序列成分使得序列分量更易于网络学习,或利用相关性算法分析输入序列信息的相关性从而进一步选择输入序列提升高相关性信息的密度.文献[8]中利用快速集成经验模态分解以及变分模态分解建立两层分解技术,实现对复杂输入序列的高效简化.文献[9]中利用最大信息系数分析电价影响因素序列与电价序列间的相关性,从而选择输入序列中与待预测电价高相关性数据.但若相关性算法过度分析,选择输入序列往往会导致模型泛化性能下降,而分解序列易造成数据泄露,导致高精度预测假象,滚动分解则需增加数倍乃至数十倍预测运算时间,需要较高的算力支撑^[10].因此,除上述针对输入序列进行处理外,也有学者对基本LSTM模型进行改进或利用复合模型提升模型的信息利用能力从而取得更高预测精度.文献[9]中改进了基本LSTM的门控结构,采用多层级门控结构,提升对输入序列中部分频率信息的学习效果.文献[11]中采用图卷积神经网络将域外信息传导到待研究区域内再利用LSTM网络模型进行预测,从而学习跨区域电力市场各区域间交流对电价的影响.除上述模型外,近些年在语言翻译领域已经取得良好应用效果的Transformer模型^[12-13]已逐渐应用至时间序列预测领域,但关于其在电价预测领域应用的相关研究还比较匮乏.为利用Transformer模型取得较高的电价预测精度,需对模型进行改进.此外,由于神经网络模型不直接根据原始数据建立模型,模型中众多超参数往往没有正式成文的规则来进行计算.学习率作为控制模型收敛特性的关键超参数,手动调整局限性较大,可利用智能算法^[14-15]搜索不同学习阶段的最佳学习率以改善模型的收敛特性以及泛化性能.

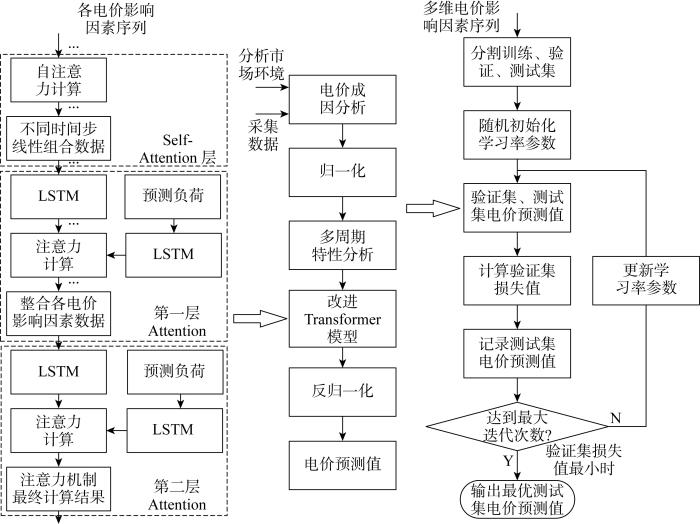
综上,提出一种考虑电价多维影响因素的改进Transformer-粒子群优化(Transformer-Particle Swarm Optimization, Transformer-PSO)短期电价预测方法.首先,分析电价形成的市场机理,获取电价形成的相关因素,并利用自相关函数分析电价的多周期特性,根据电价的多周期特性调整输入序列.其次,结合LSTM、自注意力(Self-Attention)机制、多层注意力(Attention)机制采用多输入结构建立改进Transformer模型,并利用粒子群优化算法^[16]对不同学习阶段的最优学习率进行优化.最后,采用PJM(Pennsylvania-New Jersey-Maryland)市场2020年电价数据以及2022年上半年数据验证所提模型预测精度.结果表明,该短期电价预测模型能有效应用于电价影响因素多、变化剧烈的市场环境,并有效提升短期电价预测精度.

1 电价多维影响因素

在市场环境下影响电价的因素众多,盲目选择电价影响因素往往会造成数据冗余,导致网络运算速度下降以及预测精度下降.因此除历史电价、负荷数据外,需分析电价的市场成因以及日前市场出清机制,提炼出电价多维影响因素,利用电价序列与多个电价相关的序列“交叉学习”来提升模型的预测精度^[17-18].PJM市场规模较大,运行稳定,且PJM官网披露了各项市场运营数据以及运营政策,是理想的电价预测数据来源.PJM日前市场发电商需申报发电资源和发电意愿,用户侧则需申报其购电量和价格,PJM则根据最经济的发电组合对次日24 h电能需求和日前计划备用联合出清^[19].此外,PJM将根据需求调用额外资源满足负荷预测与日前计划备用,其中发电组合中还需考虑机组爬坡等约束问题.因此,为准确预测短期电价,需综合考虑发电资源与用户需求,引入负荷与可用装机容量的比值、预测负荷;考虑发电资源足够但电力设施压力较大时带来的电价上升,引入负荷描述电力设施压力;考虑机组爬坡问题,引入负荷波动的程度.此外,电价作为价格序列,同样具有金融序列的某些特性,如波动聚集性、均值回复性^[20],还应引入电价的波动特性.

综上所述,选取电价、电价波动度、负荷与可用装机容量的比值、负荷、负荷波动度、预测负荷组合作为输入序列预测短期电价.

1.1 电价波动度

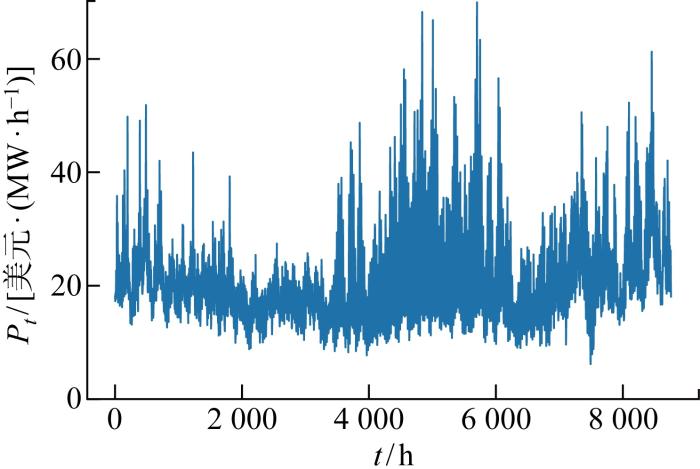
电价的波动聚集性指电价当前时期与前一时期的波动呈正相关,电价的均值恢复性指电价在市场环境下虽会受各种因素影响导致波动变化,但总是围绕着一个相对固定的值波动.电价的上述特性往往说明了近期的市场情绪,预示着近期电价的大致水平和波动程度,选取PJM市场2020年电价进行分析,如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 PJM市场2020年电价

Fig.1 Electricity price of PJM market in 2020

为使网络能够学习电价的此类特性,除历史电价外引入电价波动度:

(1)ΔP_t=P_t-P_t-1

式中:ΔP_t为t时刻电价波动度;P_t为t时刻的电价;P_t-1为t-1时刻的电价.

1.2 负荷可用装机容量比

在电力市场的背景下,电能作为一种特殊商品其价格同样也符合商品的价格变化规律.从整个市场的宏观角度分析,电能的供给为可用装机容量,需求则为负荷,二者需综合考虑.为此,引入负荷可用装机容量比作为电价影响因素:

(2)R=

\frac{D}{S}

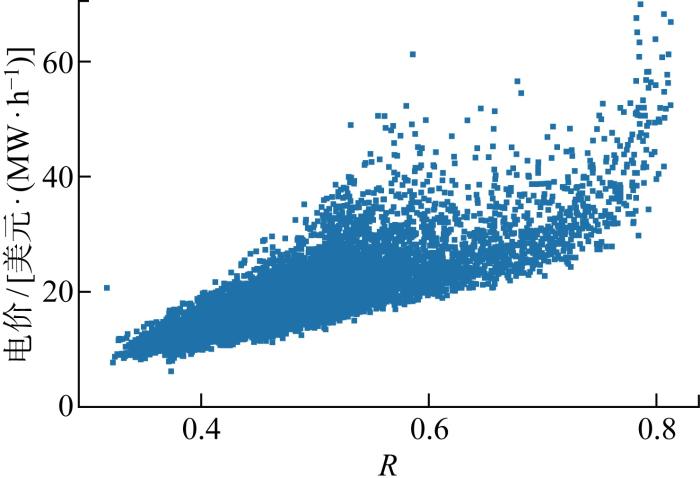
式中:R为负荷可用装机容量比;D为负荷;S为可用装机容量.以PJM市场2020年数据为例,R与电价的关系如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 负荷可用装机容量比与电价分布关系

Fig.2 Available installed capacity ratio of load versus distribution of electricity price

当负荷可用容量比相同时,高负荷较低负荷场景下对输、配电设施有更大压力,也可能导致电价升高,因此将负荷也作为影响电价的因素输入模型.

1.3 负荷波动度

电能作为一种特殊商品,与其他常规商品最大的区别是电能要求时刻供需平衡,且发电机组改变出力需要时间.若负荷变化剧烈,往往会因为机组爬坡时间问题导致高电价.为量化负荷变化的程度,引入负荷波动度作为电价影响因素:

(3)ΔD_t=D_t-D_t-1

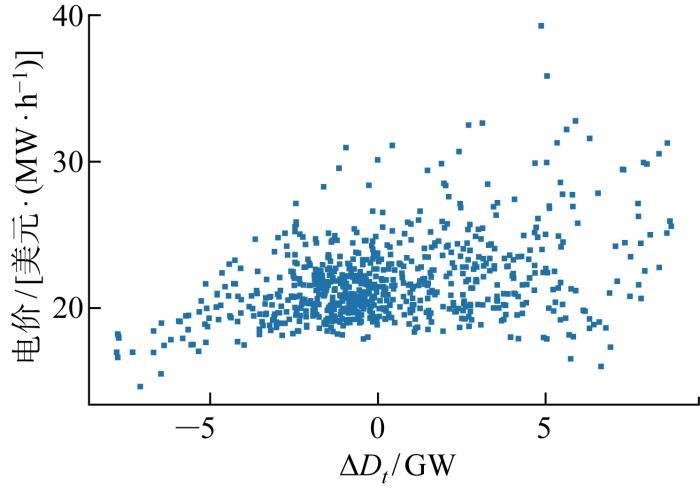
式中:ΔD_t为t时刻负荷变化的程度;D_t为t时刻的负荷;D_t-1为t时刻前一时刻的负荷.电价受负荷可用装机容量比影响较大,选取负荷可用装机容量比近似为0.5时,以PJM市场2020年数据为例,负荷波动度与电价关系如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 负荷波动度与电价分布关系

Fig.3 Comprehensive load factors versus distribution of electricity price

1.4 预测负荷

上述变量均采用历史数据,无法描述已知的未来事件如已知的负荷变化,且PJM市场通常利用日前预测负荷作为日前市场出清满足的目标之一,仅采用历史数据进行电价预测可能由于缺乏学习数据导致预测与实际偏差较大.而负荷周期性较强,通常可被较准确地预测到^[21],将预测负荷也作为输入可以进一步提升电价预测的准确度.

1.5 时间属性

电价在用电高峰时段与用电低谷时段的变化规律一般存在差异,工作日与休息日电价变化规律也往往不一致,而分割数据集则易导致数据量不足,破坏数据的连贯性导致电价预测精度下降.因此,可利用日期及时间编码变量标记输入序列的电价时间与其周内特征,使得神经网络在训练时可适应电价的日内、周内规律.

2 输入序列预处理

由于组成输入序列的各电价影响因素子序列的量纲、取值范围存在较大差异,未经处理直接输入电价预测模型往往会导致模型学习困难造成电价预测精度下降^[22],所以需对各子序列数据进行归一化处理.此外,电价往往存在一定的周期性,若仅根据经验决定输入序列可能会违背电价自身的变化趋势,造成模型学习效果差.因此,可利用自相关函数对电价的多周期特性进行分析,并根据分析结果对输入序列数据进行调整,提升模型的学习效果.

2.1 归一化

为缩小输入序列各子序列的取值范围,消除数据量纲影响,实现模型中层权重的平稳调整以及不受子序列量纲的影响进行“交叉学习”,对各子序列进行归一化处理,公式如下:

(4)x'=

\frac{x - x_{m i n}}{x_{m a x} - x_{m i n}}

式中:x'为归一化后的数据值;x为待归一化的数据值;x_min、x_max分别为x的最小、最大值.

2.2 多周期特性分析

由于电价存在一定的周期性,若能根据电价的多周期特性对输入序列进行调整,往往能提升电价预测模型对输入序列的学习效果,从而提升电价的预测精度.采用PJM市场2020年前4周电价进行示例分析,如图4所示.图中,虚线框内日期为周六、周日.由图可见,PJM市场周内各日期的电价变化趋势、时刻大致相同.周末电价并非总是一周内最低,但较一周中最后一个工作日周五的电价明显下降,周日后半日临近周一电价呈现上升趋势.综上所述,电价一般存在两种变化周期——周内规律与日内规律,即当前时刻电价受到一周内同时刻电价以及同一日当前时刻前数小时电价的影响较大.因此,在预测电价时可考虑电价的多重周期特性以获得较准确的预测精度.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 PJM市场2020年前4周电价

Fig.4 PJM market electricity prices in the first four weeks of 2020

为量化当前时刻电价受不同时刻电价的影响,采用自相关函数对电价序列进行分析,自相关系数的计算公式如下:

(5)ρ_k=

\frac{\frac{1}{N - k} \overset{N}{\sum_{t = k + 1}} (x_{t} - \bar{x}) (x_{t - k} - \bar{x})}{\frac{1}{N} \overset{N}{\sum_{t = 1}} (x_{t} {- \bar{x})}^{2}}

式中:ρ_k为当前时刻t与滞后k小时电价的自相关系数;N为选取电价数据集的时间跨度;x_t为当前时刻电价; $\bar{x}$ 为选取电价数据值的平均值.

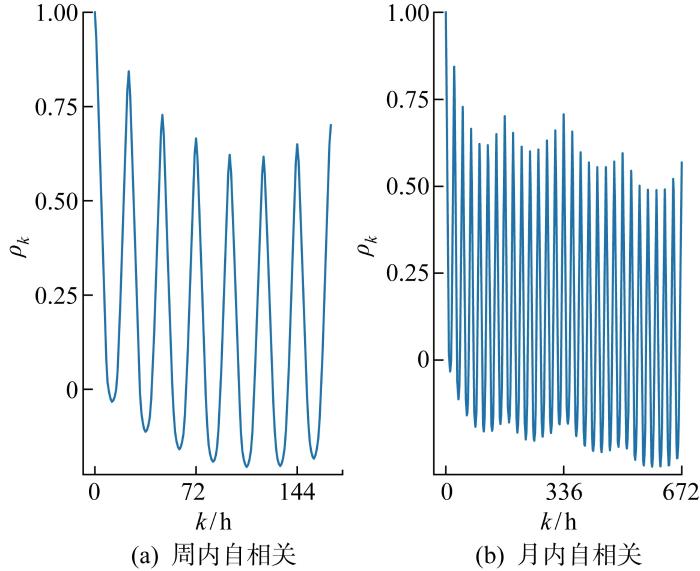
利用式(5)对PJM市场2020年电价前4周电价进行分析,结果如图5所示.由图5(a)可知,PJM市场一周内当前时刻电价与滞后时间约24 h及其整数倍电价的自相关系数,除极接近当前时刻电价的数小时电价外,显著高于其他时刻电价,且当前时刻电价与一周后同时刻电价的自相关系数高于间隔 2 d 以上日期的同时刻电价.由图5(b)可知,PJM市场电价的自相关系数以日、周为周期进行双周期变化,且随着滞后小时数增大,自相关系数整体上不断减小.综上分析,对于提前一天的短期电价预测,采用前一周同时刻电价作为输入序列预测未来电价.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 电价序列自相关系数

Fig.5 Autocorrelation coefficient of electricity price series

3 改进Transformer-PSO模型

3.1 LSTM模型

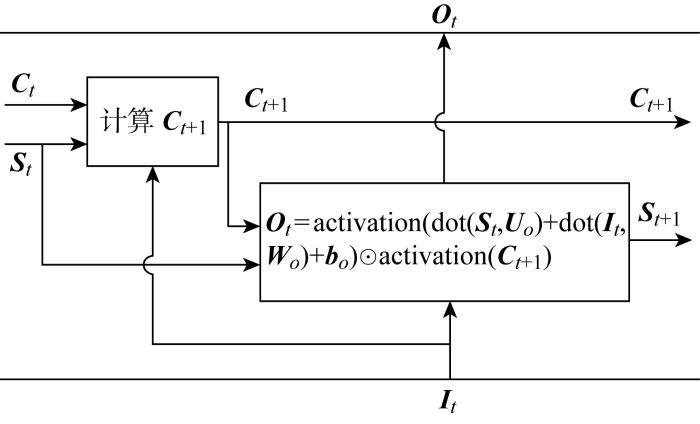
由于时间序列数据的特殊性,一般利用循环神经网络处理,但基本RNN由于梯度消失问题无法保留时间跨度较大的重要信息,而LSTM神经网络在基本RNN模型的基础上增加了可以将信息长时间携带的信息轨道,使LSTM能保留多个时间步以前的重要信息,结构如图6所示.图中:C_t为经过上一个时刻单元处理后轨道内的值;S_t为当前时刻t的状态,即t-1时刻的输出;I_t为当前时刻的输入;O_t为当前时刻的输出,也为下一时刻的状态S_t₊₁;C_t₊₁为经过当前时刻单元处理后轨道内的值.计算公式如下:

(6)O_t=activation (dot (S_t, U_o)+dot(I_t, W_o)+b_o)☉activation(C_t₊₁)

(7)C_t₊₁=G_tH_t+C_tF_t

(8)F_t=activation (dot(S_t, U_f)+dot(I_t, W_f)+b_f)

(9)G_t=activation (dot(S_t, U_g)+dot (I_t, W_g)+b_g)

(10)H_t=activation (dot (S_t, U_h)+dot (I_t, W_h)+b_h)

式中:activation为选取的激活函数;dot为矩阵相乘函数;U_o、W_o、U_f、W_f、U_g、W_g、U_h、W_h为权重矩阵;b_o、b_f、b_g、b_h为偏置项;C_tF_t是为了忘记携带信息轨道中的不重要信息;G_tH_t更新当前信息轨道中的信息,记住当前时间步中重要的信息.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 LSTM单元的结构

Fig.6 Structure of LSTM unit

综上可知,LSTM模型利用前一时刻轨道内的值、状态信息以及当前时刻输入不断更新轨道中的信息,使LSTM能保留多个时间步以前的重要信息.但随着时间的延长,仍会有部分信息在传递过程中逐渐丢失,导致LSTM的预测精度仍受到限制.

3.2 改进Transformer模型

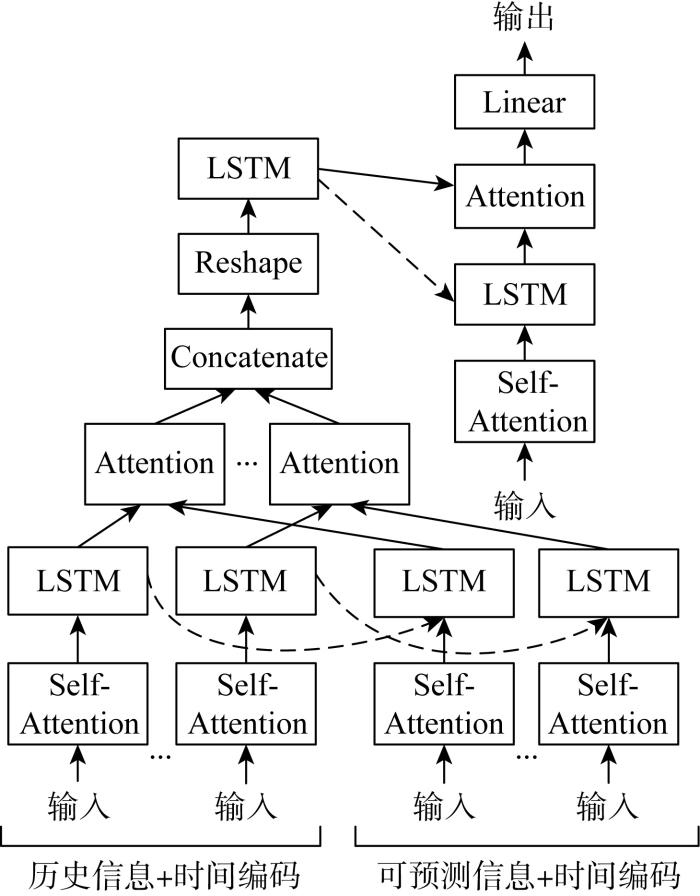
在历史电价、历史负荷的基础上考虑市场环境下的多种电价影响因素,由各电价影响因素子序列组成模型的输入序列,但各子序列的形式以及输入时机不完全相同,单输入网络结构不能满足要求,且LSTM模型存在信息利用瓶颈等问题.因此,结合LSTM模型、Self-Attention机制以及多层Attention机制对基本Transformer模型进行改进,并采用多输入结构,模型结构如图7所示.图中:Concatenate、Reshape、Linear分别代表拼接函数、张量维度变换函数、Pytorch线性层.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 改进Transformer模型

Fig.7 Improved Transformer model

由图7可见,改进Transformer模型的多输入结构能适应形式差异大的子序列构成的多输入序列组合,有利于根据市场环境灵活调整输入序列.Self-Attenion层根据输入序列进行自注意力计算,自适应调整不同时间步信息权重,关注其中的重要信息并整合不同时间步信息.双层Attention机制结合可预测信息对输入数据经LSTM处理后的隐藏状态信息进行注意力计算,自适应调整不同时间步隐藏状态信息权重,关注其中的重要信息并整合不同时间步隐藏状态信息;两层分别针对同一电价影响因素的不同时间步数据以及不同电价影响因素数据经LSTM处理后的隐藏状态信息,最终实现对包含大量信息的输入序列的高效学习.

3.2.1 自注意力机制

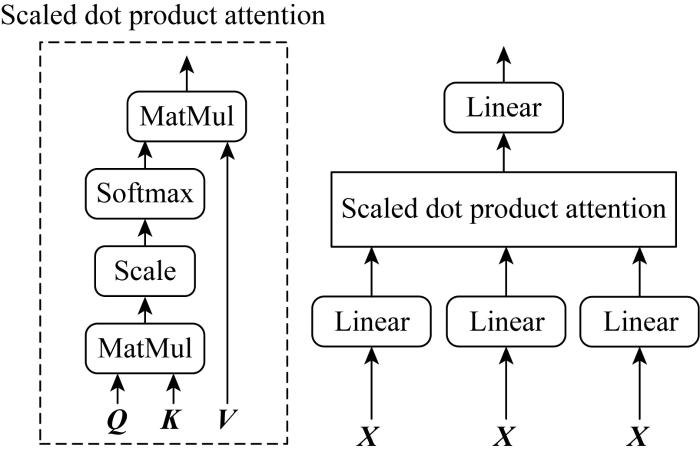
改进Transformer模型的单个输入通道内不同时间步数据对未来电价的影响程度不同,因此可利用Self-Attention^[12]层对输入序列进行自注意力计算,自适应调整子序列中不同时间步信息的权重,关注其中的重要信息并整合不同时间步信息,提升模型的学习效率与效果.此外,self-attention机制并行处理输入序列所有时间步信息并进行自注意力计算的方式提供了一种较短路径捕获输入序列不同时间步信息间的局部依赖关系,进一步提升LSTM模型捕获不同时间步信息间的长短期依赖关系的能力,Self-Attention机制结构如图8所示.图中:Scaled dot product attention表示按比缩放的点积注意力;Scale表示缩放操作;MatMul 为矩阵相乘函数.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 Self-attention机制

Fig.8 Self-attention mechanism

图8中,X为输入序列,经线性层处理后得到Q、K、V这3个矩阵,即

(11)

\begin{array}{l} Q = a c t i v a t i o n (d o t (X, W_{Q}) + b_{Q}) \\ K = a c t i v a t i o n (d o t (X, W_{K}) + b_{K}) \\ V = a c t i v a t i o n (d o t (X, W_{V}) + b_{V}) \end{array}\}

式中:W_Q、W_K、W_V为Q、K、V的权重矩阵;b_Q、b_K、b_V为Q、K、V的偏置项.

注意力计算公式为

(12)attention (Q, K, V)=softmax

(\frac{Q K^{T}}{\sqrt{d_{k}}})

式中:d_k为Q以及K的向量维度.

3.2.2 注意力机制

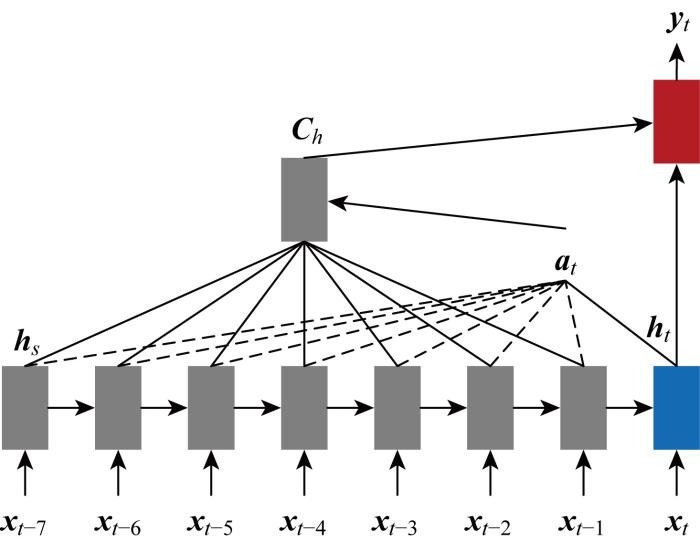
LSTM在处理时间序列时会有部分信息随着时间延长丢失,导致对包含大量信息的输入序列的信息利用瓶颈,造成预测精度下降.而Attention层能根据可预测信息对LSTM历史时间步隐藏状态信息进行注意力计算^[23],自适应调整历史时间步隐藏状态中的信息权重,关注其中的重要信息并整合不同时间步隐藏状态信息,采用双层堆叠结构,两层分别处理同一序列不同时间步数据以及不同序列数据经LSTM处理后的隐藏状态信息,从而克服LSTM的信息利用瓶颈问题,其结构如图9所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 Attention机制

Fig.9 Attention mechanism

由图9可见,以电价序列作示例分析,输入序列x_t_-7~x_t_-1经LSTM处理后,历史时间步状态为h_t_-7~h_t_-1, 根据当前时间步状态h_t建立score函数:

(13)score(h_t, h_s)=

{h^{T}}_{s}

W_sh_s

式中:h_s为历史时间步状态;W_s为权重矩阵.

历史时间步状态经score函数处理后,利用softmax函数进行归一化形成权重向量:

(14)a_t=softmax(score(h_s, h_t))

历史时间步状态的加权和为

(15)C_h=∑a_th_s

注意力向量为

(16)y_t=tanh(W_c[C_h, h_t])

式中:tanh为激活函数;W_c为权重矩阵;[C_h, h_t]为将C_h、h_t进行拼接.

3.3 粒子群学习率优化算法

学习率作为优化器的一个重要超参数,控制着模型的学习速度以及最后的收敛特性.不同学习阶段对学习率的要求不同,手动调整局限性较大^[24].因此,利用PSO搜索不同学习阶段的最佳学习率,将模型的学习率作为PSO的优化参数,网络的最小损失值作为PSO的优化目标.

PSO是一种群体优化算法,在d维空间中,粒子仅具有位置和速度两个属性:

(17)

\begin{array}{l} X_{j} = [x_{j}^{1} x_{j}^{2} \dots x_{j}^{d}] \\ V_{j} = [v_{j}^{1} v_{j}^{2} \dots v_{j}^{d}] \end{array}\}

式中: $x_{j}^{d}$ 为第j个粒子在第d维的位置; $v_{j}^{d}$ 为第j个粒子在第d维的速度;X_j、V_j分别为第j个粒子的位置、速度.

根据目标函数F(X_j)评价第j个粒子的位置参数,第j个粒子找到的最优位置为

(18)p_j=min F(X_j)

在任一维中,根据粒子自身找到的最优值以及其他粒子共享的最优值来调整自己的速度与位置:

(19)

\begin{array}{l} v_{j}^{q + 1} = m_{f} v_{j}^{q} + l_{1} r_{1} (p_{j}^{q} - x_{j}^{q}) + l_{2} r_{2} (p_{b e s t}^{q} - x_{j}^{q}) \\ x_{j}^{q + 1} = x_{j}^{q} + v_{j}^{q} \end{array}\}

式中: $v_{j}^{q + 1}$ 为q+1次迭代时第j个粒子在此维度上的速度; $x_{j}^{q + 1}$ 为q+1次迭代时第j个粒子在此维度的坐标;m_f为惯性因子,是非负数;l₁为粒子的个体学习因子;l₂为粒子的群体学习因子;r₁、r₂为[0,1]上的随机数; $p_{j}^{q}$ 为第q次迭代时第j个粒子寻找到的最优位置; $p_{b e s t}^{q}$ 为第q次迭代粒子群中所有粒子寻找到的最优位置.

结合实际模型,粒子位置参数的维度为学习率的阶段数,粒子群优化变量为不同阶段的学习率取值,则第j个粒子的属性参数为

(20)X_j=[

l_{j}^{1}

l_{j}^{2}

…

l_{j}^{d}

]

式中: $l_{j}^{d}$ 为第j个粒子在第d阶段的学习率参数.

损失函数采用均方误差(MSE),每个粒子的优化目标均为验证集最小损失值即粒子的最优位置:

(21)min F(X_j)=min

\frac{1}{n} \overset{n}{\sum_{i = 1}}

(

y_{r}^{i}

y_{p j}^{i}

)²

式中:n为测试集样本数量; $y_{r}^{i}$ 为测试集中第i个样本的电价实际值; $y_{p j}^{i}$ 为使用第j个粒子参数时测试集第i个样本电价预测值.

4 算例分析

为准确预测市场日前电价,考虑电价多维影响因素并建立改进Transformer模型,基本技术路线如图10所示.考虑电价数据的特殊性,验证集、测试集均预测未来一周或两周日前市场电价.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 电价预测模型基本技术路线

Fig.10 Basic technical route of electricity price prediction model

4.1 误差评价损失函数

模型学习预测误差可利用损失函数衡量,对于预测电价这类回归问题,可采用均方根误差(Root Mean Squared Error, RMSE)损失函数、平均绝对误差(Mean Absolute Error, MAE)、对称平均绝对百分比误差^[9](Symmetric Mean Absolute Percentage Error, SMAPE),计算方式分别为

(22)y_RMSE=

\sqrt{\frac{1}{n} \overset{n}{\sum_{i = 1}} (y_{r}^{i} - y_{p}^{i})^{2}}

(23)y_MAE=

\frac{1}{n} \overset{n}{\sum_{i = 1}} |y_{r}^{i} - y_{p}^{i}|

(24)y_SMAPE=

\frac{100}{n} \overset{n}{\sum_{i = 1}} \frac{| y_{r}^{i} - y_{p}^{i} |}{0.5 (| y_{r}^{i} | + | y_{p}^{i} |)}

式中: $y_{p}^{i}$ 为测试集中第i个样本的电价预测值.其中y_RMSE损失值侧重对于预测值与实际值偏差较大的点的评估,y_MAE则侧重于评估预测的整体平均误差,y_SMAPE则侧重于考虑预测电价值与实际值大小影响后预测的整体平均误差.

4.2 不同模型电价预测精度对比分析

为验证所提预测方法的准确性,设置5种模型A~E.模型A采用改进Transformer;模型B采用LSTM网络;模型C采用LSTM网络且仅采用时间编码标记的历史电价、历史负荷;模型D采用反向传播(Back Propagation, BP)神经网络;模型E采用反向传播神经网络且仅采用时间编码标记的历史电价、历史负荷.利用损失函数RMSE、MAE、SMAPE对电价预测误差进行评估,各模型预测误差如表1所示,均使用PJM市场2020年数据,均以反归一化后的实际值计算.

表1 2020年数据集各模型误差分析

Tab.1 Analysis of prediction errors of different models in dataset of 2020

模型	y_RMSE	y_MAE	y_SMAPE
A	2.399	1.760	7.014
B	3.072	2.412	9.569
C	4.592	3.534	14.366
D	3.345	2.648	10.617
E	4.131	3.138	12.796

新窗口打开| 下载CSV

此外,为避免仅采用损失值造成的评估结果误判,采用结合Harvey修改的Diebold-Mariano检验^[25].检验值若小于0, 则说明前一个模型预测精度高于后一个模型,通常P值小于等于0.01时,拒绝原假设两模型预测精度一致的依据高度显著.不同模型间预测结果的Diebold-Mariano 检验评估值如表2所示.

表2 2020年数据集各模型预测误差Diebold-Mariano 检验结果

Tab.2 Diebold-Mariano test results of prediction errors of different models in dataset of 2020

模型	检验值	P
A、B	-3.813	1.9×10^-4
B、C	-6.755	2.3×10^-10
B、D	-5.020	1.3×10^-6
D、E	-5.595	8.9×10^-8

新窗口打开| 下载CSV

由表1可知,模型A较模型B在测试集中RMSE损失值降低,即精度提升21.908%,MAE降低27.032%,SMAPE降低26.701%,说明所提改进Transformer模型较LSTM模型预测精度有全面提升.模型B较模型C在测试集中的RMSE损失值降低33.101%,RMSE降低31.749%,SMAPE降低33.391%,说明考虑电价多维影响因素较仅利用历史电价、负荷数据的模型电价预测精度有全面提升.同时可以看出在数据集不够充分的情况下,由于过拟合等原因,LSTM的预测精度可能落后于反向传播;但在数据集充分的情况下,过拟合问题得到解决,LSTM的预测精度则要优于反向传播.由表2可知,模型A、B以及模型B、C的检验值均小于0,所有检验的P值均小于0.01,拒绝原假设的依据非常显著.

综上,由各模型预测误差值和Diebold-Mariano 检验结果可知,考虑多维电价影响因素与采用改进Transformer模型均能有效提升日前电价预测精度,平均提升幅度分别超过30%、25%.

4.2.1 改进Transformer模型对预测精度的影响

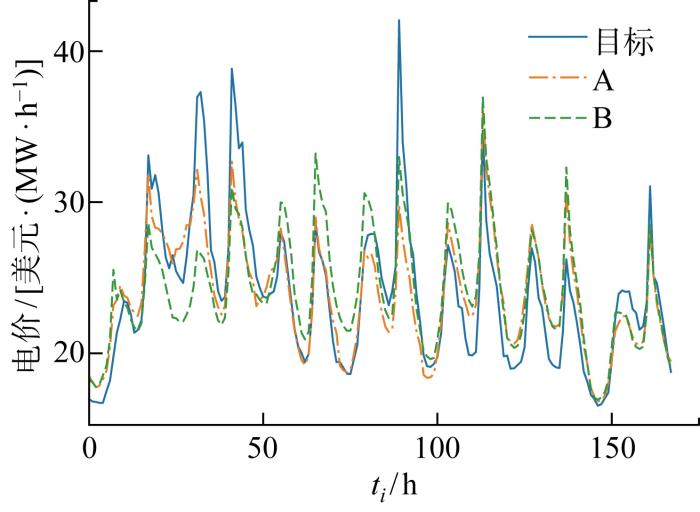
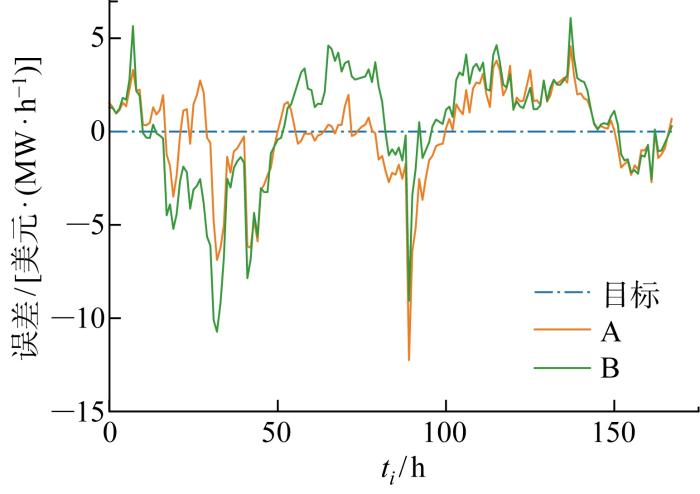
为对比采用改进Transformer模型对电价预测精度的影响,进一步分析模型A与模型B电价预测值,模型A、B电价预测结果与实际电价值如图11所示,预测值与实际值误差如图12所示.图中:t_i为测试集中的时刻.由图可见,LSTM模型对非剧烈波动的电价已有很高的预测精度,但测试集第1日、第2日、第3日即圣诞节前后,电价变化趋势与常规日期差异较大,LSTM模型预测误差较大;而改进Transformer模型这3日的电价预测精度显著高于LSTM模型精度.这是由于所采用的多维电价影响因素包含不同时间步的大量信息,电价也存在波动聚集性以及均值回复性,即不同时间步信息间往往存在较强长短期依赖关系,当大量且波动剧烈的信息作为输入序列时,LSTM模型的电价预测精度往往受到限制;而改进Transformer模型能进一步提升LSTM模型捕获不同时间步信息间的长短期依赖关系的能力,并克服LSTM模型的信息利用瓶颈,从而在与常规日期电价变化趋势差异较大的节日前后取得较高的电价预测精度.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 模型A与B电价预测结果对比

Fig.11 Comparison of electricity price prediction results between Models A and B

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 模型A与B电价预测误差对比

Fig.12 Comparison of price prediction errors between Models A and B

4.2.2 考虑电价多维影响因素对预测精度的影响

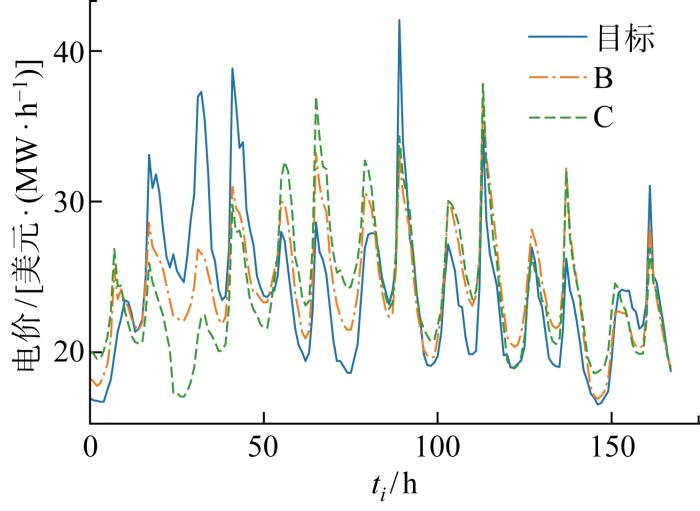
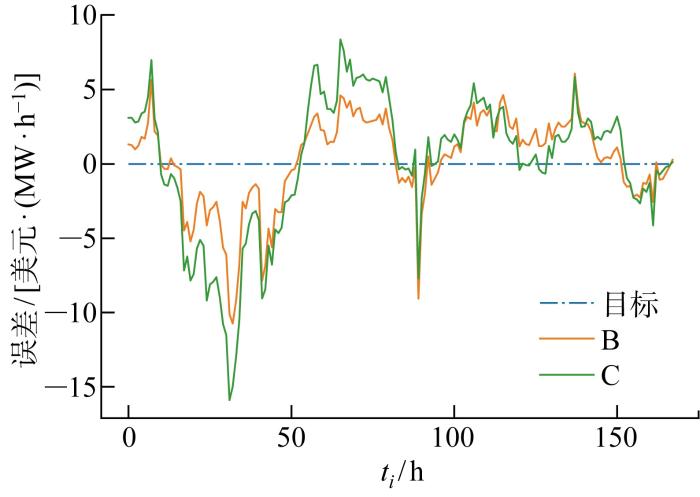
为对比考虑电价多维影响因素对电价预测精度的影响,进一步分析模型B与模型C电价预测值,模型B、C电价预测结果与实际电价值如图13所示,预测值与实际值误差如图14所示.由图可见,模型C在非节日前后有一定预测精度,但与常规日前电价变化趋势差异较大的节日前后模型C预测精度较差,且预测电价的变化趋势与实际电价的变化趋势也有较大差异;而模型B虽在节假日前后预测乏力,但预测精度高于模型C,且模型B预测电价的变化趋势基本与实际电价的变化趋势一致.这是由于模型C缺乏电价影响因素的相关数据,只能根据电价以及负荷的历史特征对未来电价进行预测,导致其对节日前后电价变化趋势的预测产生较大误差.而模型B虽存在信息利用瓶颈,但仍可以通过分析电价的波动聚集性、电价供需关系、负荷波动情况以及预测负荷等电价影响因素来综合分析、交叉学习以增强对电价形成机理的描述,从而在与常规日前电价变化趋势差异较大的节日前后取得更高的电价预测精度.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 模型B与C电价预测结果对比

Fig.13 Comparison of electricity price prediction results between Models B and C

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 模型B与C电价预测误差对比

Fig.14 Comparison of price prediction errors between Models B and C

4.3 不同数据下各模型预测精度表现

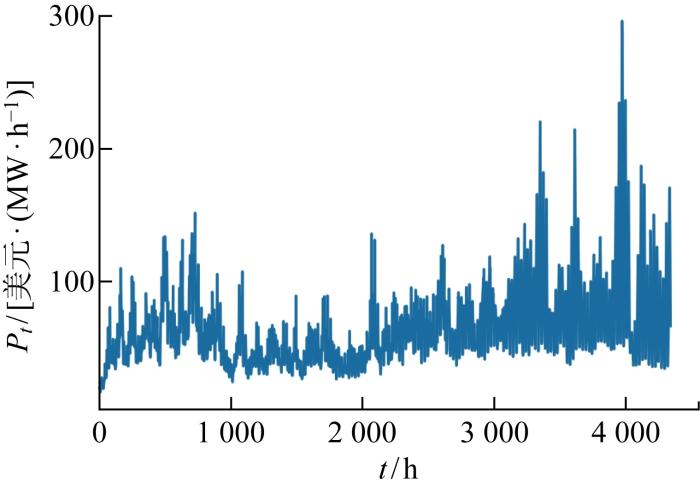
为进一步说明模型在不同数据集以及不同价格段下的表现,选取2022年PJM市场上半年数据验证,选取最后两周电价数据作为测试集,倒数第3、4周电价数据作为验证集.PJM市场2022年上半年电价如图15所示,预测精度如表3所示,Diebold-Mariano 检验评估值如表4所示.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 PJM市场2022年上半年电价

Fig.15 Electricity price of PJM market in the first half of 2022

表3 2022年数据集各模型误差分析

Tab.3 Analysis of prediction errors of different models in dataset of 2022

模型	y_RMSE	y_MAE	y_SMAPE
A	10.510	8.333	11.083
B	13.053	9.944	12.880
C	19.820	14.664	18.130
D	16.578	11.772	14.635
E	19.895	14.462	17.771

新窗口打开| 下载CSV

表4 2022年数据集各模型预测误差Diebold-Mariano 检验结果

Tab.4 Diebold-Mariano test results of prediction errors of different models in dataset of 2022

模型	检验值	P
A、B	-4.999	9.328×10^-7
B、C	-6.635	1.300×10^-10
B、D	-5.125	5.000×10^-7
D、E	-8.959	2.300×10^-17

新窗口打开| 下载CSV

由图15可知,测试集即2022上半年电价绝大多数超过100美元/(MW·h),远超2020年末的40美元/(MW·h),也大幅超过2020年同时期的不到60美元/(MW·h).

由表3可知,采用模型A较模型B在测试集中RMSE损失值降低,即精度提升19.482%;MAE降低16.201%;SMAPE降低13.952%.模型B较模型C在测试集中RMSE损失值降低34.142%,RMSE降低 32.188%,SMAPE降低28.958%.说明即使在不同市场环境以及不同价格段下,所提模型以及电价多维影响因素仍能较大幅度提升电价预测精度.由表4可知,各检验的检验值均小于0,P值均小于0.01,拒绝原假设的依据非常显著.

综上可知,即使受新冠疫情发展以及气温影响,2022年电价较2020年同时期电价有大幅提升,波动也更加剧烈,考虑多维电价影响因素与采用改进Transformer模型仍能有效提升日前电价预测精度,平均提升幅度超30%、15%.

5 结论

提出一种考虑电价多维影响因素的改进Transformer-PSO短期电价预测方法,采用PJM市场2020年以及2022上半年日前市场数据验证所提方法的预测精度,分析不同模型的电价预测结果,得到以下结论.

(1) 所提电价预测方法对电价较为平稳的PJM市场2020年日前电价以及电价较高且波动较为剧烈的PJM市场2022上半年电价均有较高的预测精度,说明所提电价预测方法不仅适用于平稳的市场环境也能适用于变化较为剧烈的市场环境.

(2) 在采用历史电价、历史负荷的基础上,进一步分析市场环境下的电价影响因素,并对市场电价的多周期特性进行简要分析,克服仅采用历史电价、历史负荷难以充分描述电价形成机理导致模型预测精度受限以及经验调整输入序列的局限性的问题.

(3) 所提改进Transformer模型能适应包括电价及其成因的复杂多序列输入,进一步提升LSTM模型捕获不同时间步信息间的长短期依赖关系的能力,克服LSTM的信息利用瓶颈,实现对包含大量信息的输入序列的高效学习,从而取得较高的电价预测精度.

(4) 为提升电价的预测精度,可在历史电价的基础上进一步分析市场环境下的电价影响因素;为避免模型信息利用瓶颈,可采用多输入结构并能根据输入信息重要程度自适应调整信息权重,且可对不同时间步信息进行整合的电价预测模型,从而进一步提升电价预测精度.

综上所述,所提考虑多维影响因素的改进Transformer-PSO短期电价预测方法日前电价预测精度较高,可灵活地随市场环境进行适应性变化,实现对包含大量信息的输入序列的高效学习.模型思想适应多种场景预测需求,易于迁移至其他领域.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

蒋锋, 何佳琪, 曾志刚, 等.

基于分解-优化-集成学习方法的电价预测

[J]. 中国科学: 信息科学, 2018, 48(10): 1300-1315.

[本文引用: 2]

JIANG

Feng

, HE

Jiaqi

, ZENG

Zhigang

, et al.

Decomposition-optimization-ensemble learning approach for electricity price forecasting

[J]. Scientia Sinica (Informationis), 2018, 48(10): 1300-1315.

[本文引用: 2]

[2]

HUANG

, YANG

Y B

, ZHAO

H L

, et al.

Time series modeling and filtering method of electric power load stochastic noise

[J]. Protection & Control of Modern Power Systems, 2017, 2(1): 25.