生产调度与可靠性耦合的变工况再制造系统维护建模

doi:10.16183/j.cnki.jsjtu.2023.113

生产调度与可靠性耦合的变工况再制造系统维护建模

肖常胜, 周晓军^,, 祝米鑫

上海交通大学机械与动力工程学院,上海 200240

Maintenance Modeling of Remanufacturing Systems in Variable Working Condition with Coupling of Production Scheduling and Reliability

XIAO Changsheng, ZHOU Xiaojun^,, ZHU Mixin

School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 周晓军,副教授,博士生导师;E-mail:zzhou745@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-03-31 修回日期: 2023-05-11 接受日期: 2023-06-25

基金资助:

国家自然科学基金(52075336)

Received: 2023-03-31 Revised: 2023-05-11 Accepted: 2023-06-25

作者简介 About authors

肖常胜(1999-),硕士生,从事复杂制造系统设备预防维护研究.

摘要

针对变工况下的多工序再制造系统,提出生产、设备衰退和系统维护之间的耦合建模方法.首先引入考虑设备可靠性的动态生产优先级并据此生成生产调度计划,进而基于变动生产计划建立设备的变工况故障率模型,在此基础上,考虑生产的动态性和设备衰退的不确定性,构建基于双生产周期优化的再制造系统动态维护决策模型.算例分析表明,该模型可有效提高系统生产净收益且相对于传统生产和维护决策方法更具优势.

关键词： 再制造系统; 预防维护; 变工况; 动态生产优先级; 耦合建模方法

Abstract

For the multi-process remanufacturing system under variable working conditions, a modeling method considering the coupling among equipment deterioration, maintenance, and production is proposed. First, a dynamic production priority considering equipment reliability is introduced, based on which, a production scheduling plan is generated. Then, an equipment hazard rate model under variable production plan is established. On this basis, a dual-cycle dynamic maintenance decision-making method is constructed, considering the dynamic nature of production scheduling plan and the uncertainty of equipment failure. The illustrative example shows that the model can effectively improve the net profit of the system and has more advantages than traditional production and maintenance decision-making methods.

Keywords： remanufacturing system; preventive maintenance; variable working condition; dynamic production priority; coupled modeling methods

PDF (2389KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

肖常胜, 周晓军, 祝米鑫. 生产调度与可靠性耦合的变工况再制造系统维护建模[J]. 上海交通大学学报, 2024, 58(8): 1211-1220 doi:10.16183/j.cnki.jsjtu.2023.113

XIAO Changsheng, ZHOU Xiaojun, ZHU Mixin. Maintenance Modeling of Remanufacturing Systems in Variable Working Condition with Coupling of Production Scheduling and Reliability[J]. Journal of Shanghai Jiaotong University, 2024, 58(8): 1211-1220 doi:10.16183/j.cnki.jsjtu.2023.113

随着循环经济兴起,再制造产业成为制造业重要组成部分.再制造生产模式下,企业回收不同类型产品进行加工,加工工序不同.回收市场波动影响生产调度决策,导致系统不同生产工况,给各工序设备带来不同生产负荷,影响设备衰退进程,进而影响后续生产计划和维护方案.在该生产模式下,各设备衰退进程难以预知,且生产与维护相互制约.为保障再制造系统可靠性,描述设备生产与衰退的耦合关系,解析设备衰退进程,进而制定合理维护计划是再制造企业面临的新问题.

目前,系统预防维护的相关研究^{[1⇓⇓⇓⇓⇓-7]}较多,传统制造系统预防维护领域已有的研究多假设系统工况完全已知且稳定.夏唐斌等^[8]引入失效率调整因子,建立双目标优化维护决策模型.陆志强等^[9]综合考虑缓冲区对系统生产和维护成本的影响,求解最优预防性维护周期和最佳缓冲区库存量.Chen等^[10]提出基于期望可用度和维护成本率的预防维护综合评估方法.Lai等^[11]针对双组件失效率交互影响系统,引入关联成本作为主要评估指标优化系统最佳预防替换时间.以上研究均基于稳定工况,无法解决变动工况下的设备维护决策问题.

部分研究考虑变动生产环境下的设备维护决策,Zhou等^[12]针对多品种小批量生产模式建立了维护力度决策模型.Zhang等^[13]采用更新过程描述任务执行成功概率,提出了预防替换方案选择策略.Li等^[14]考虑不同工况下环境因素对设备衰退的影响,建立了混合变量衰退模型.禄智鸿等^[15]以有效开动时间为核心建立了集成质量与可靠性的变工况设备维护模型.Rezaei-Malek等^[16]提出了一种基于线性化和鲁棒概率规划的多目标维护决策模型.以上研究大多侧重变动工况对设备衰退和维护决策的单向影响,其无法解决设备衰退、维护与生产三者之间存在相互影响下的再制造场景维护决策问题.

目前,有关再制造系统维护的研究还相对较少.Polotski等^[17]针对新产品与回收产品混合生产场景进行生产维护联合规划建模;Hajej等^[18]针对制造与再制造混合生产系统进行维护与排产的联合规划.陈竹等^[19]考虑产品质量与再制造生产率对设备衰退的影响,提出基于成本节约的动态机会维护策略.上述研究均侧重再制造环境下生产对设备衰退的影响,事实上,在维护决策对系统生产影响方面,Li等^[20]将维护机会安插在生产空闲期以联合优化生产与维护计划.Baykasoğlu 等^[21]提出一种贪婪随机自适应搜索方法以同时调度工作车间的加工和维护活动.周炳海等^[22]则考虑加工速度和设备衰退的相互影响,提出了最小化完工时间和维护成本的双目标调度方法.Ghaleb等^[23]在综合考虑加工时间、能耗对设备衰退的影响下,提出一种联合优化单设备生产、检查和维护活动的模型.以上研究仍未深入分析设备衰退、维护与生产三者的相互制约关系,且无法解决长期工况未知时的生产调度与维护决策问题.

本文以变工况下的多工序再制造系统为研究对象,在综合考虑产品生产动机与设备生产动机的基础上,引入基于动态生产优先级的生产调度计划,考虑设备衰退、维护与生产间的制约关系,构建以净收益率为目标函数的单设备维护模型,以及基于生产的系统动态维护决策模型,以最终获取再制造系统整体的维护方案.

1 问题描述

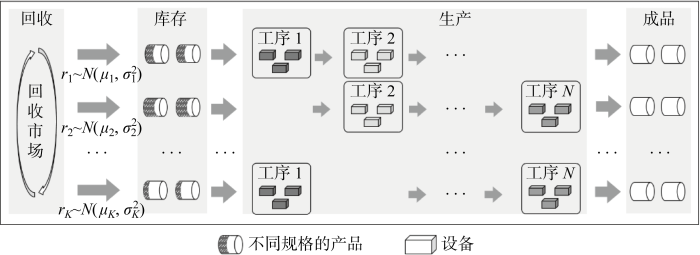
考虑一含N道工序的再制造系统,工序内设备数量不一.系统加工不同规格的回收产品,并将成品销售到下游市场,如图1所示.系统从回收市场定期回收K种规格的产品进入库存,每种产品的周期回收数量r_i~N(μ_i, $σ_{i}^{2}$ ),其中:μ_i, $σ_{i}^{2}$ 分别为产品i周期回收数量分布的均值和方差.系统每一个生产周期对应一个回收周期,新的生产调度计划在每次库存更新之后制定.由于回收的产品数量不稳定,每周期生产产品的数量将出现较大波动,部分产品可能无法及时参与生产而滞留在库存中,系统工况总体呈现较大波动性.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 多品种多工序再制造生产模式

Fig.1 Multi-product and multi-process remanufacturing production mode

随着运行时间推移,设备老化易导致系统故障停机,小修可使停机设备恢复运行状态但不改变设备故障率.为降低设备故障停机的影响,需及时对设备实施预防维护.通常,预防维护并非对所有部件修复,无法使设备恢复到全新状态.同时,为减少预防维护对系统生产的影响,预防维护只在生产周期间隔实施.

系统工况的波动导致设备负荷的动态变化,设备衰退速度也随之不断改变,不同衰退速度下的设备状态将影响后续生产安排和维护动作,而维护决策需要考虑其对后续设备衰退进程和生产调度的影响,这意味着系统生产、设备衰退和系统维护呈现相互干涉的耦合特性.

系统的其他假设如下:不同产品的回收数量分布相互独立;设备小修时间和换模时间忽略不计;同一生产周期内设备生产保持稳定;设备维护决策时,下一生产周期的产品信息已知;维护资源充足,可以同时对多台设备实施预防维护.

2 动态生产调度下的维护决策建模

动态生产调度下的维护决策建模主要分成两个阶段.首先是再制造场景中动态生产调度下的单设备维护建模,以获取单设备最佳预防维护时间,并作为系统决策的基础输入;其次是基于随机规划的系统动态机会维护建模,以得到系统整体维护方案.

2.1 动态生产调度下的单设备维护建模

在每个生产周期的开始时间点,首先根据回收产品的数量更新库存,然后判断是否对设备实施预防维护,进而规划下一周期的生产任务.由于实施预防维护会影响下一周期的生产调度,所以提出基于动态优先级的生产调度规则,并据此构建设备维护周期收益率模型,进而优化维护决策.

2.1.1 基于动态优先级的生产调度

(1) 产品生产动机与设备生产动机联合驱动的动态优先级建模.

在该再制造场景下,设备的生产能力(加工时间和加工速度)有限,并且各产品利润不同,通常需要优化各产品的生产数量以获取最大的生产效益.为此,可基于动态生产优先级排定生产计划.生产优先级主要构成要素包括收益能力和资金成本,则回收产品i的第j期库存产品在第n个生产周期的生产优先级定义为

(1)P_ijn=ω_p

{P^{p}}_{i j n}

+ω_o

{P^{o}}_{i j n}

式中: ${P^{p}}_{i j n}$ 表示收益能力优先级; ${P^{o}}_{i j n}$ 表示资金成本优先级;ω_p,ω_o分别表示收益能力优先级和资金成本优先级的权重;j表示产品在库存中的滞留周期数,

(2)j=

[\frac{t - t^{i n i}}{T}]

式中: $[\cdot]$ 表示向下取整;t为当前时刻;tⁱⁿⁱ表示产品进入库存的时刻;T表示生产周期时长.另外,始终假设系统处于第n-1个生产周期与第n个生产周期的间隔,即t=(n-1)T.

收益能力优先级 ${P^{p}}_{i j n}$ 由产品生产动机和设备生产动机组成.产品生产动机与产品消耗单位生产能力带来的净利润成正比,设备生产动机则与产品的加工工序中设备下一次失效的期望时间的平均水平成正比.综合以上两方面, ${P^{p}}_{i j n}$ 定义为

(3)

{P^{p}}_{i j n}

\frac{\sum_{k \in C^{p d} (i)}^{} \sum_{s = 1}^{M_{k}} {L^{r}}_{k s} (t) / \sum_{k \in C^{p d} (i)}^{} M_{k}}{\underset{k, s}{m a x} {L^{r}}_{k s} (t)}

\frac{P_{i}^{p r} / \sum_{k \in C^{p d} (i)}^{} E_{i k}}{\underset{i}{m a x} (P_{i}^{p r} / \sum_{k \in C^{p d} (i)}^{} E_{i k})}

式中:C^pd(i)为产品i的加工工序集合;M_k为工序k中设备数量;令设备(k, s)表示工序k中设备s,则 ${L^{r}}_{k s}$ (t)为设备(k, s)在t时刻距离下一次失效的期望时间; $P_{i}^{p r}$ 为生产单个产品i的利润,即产品售价减去购买与制造成本;E_ik为生产单个产品i在工序k上所需的生产能力.由于系统采用小修策略保持设备工作状态,所以可以假设设备此前始终保持工作,则 ${L^{r}}_{k s}$ (t)可表征为

(4)

{L^{r}}_{k s}

(t)=

\frac{\int_{t}^{\infty} R_{k s} (τ) d τ}{R_{k s} (t)}

式中:R_ks(τ)为设备可靠度函数,

(5)R_ks(τ)=exp

(- \int_{0}^{τ} λ_{k s} (μ) d μ)

λ_ks(μ)为设备失效率函数.

类似地, ${P^{o}}_{i j n}$ 也由产品生产动机和设备生产动机组成.产品不参与生产所产生的投资资金成本越高,产品生产动机越强;产品的加工工序中设备下一次失效的期望时间的平均水平相对其他设备越高,设备生产动机越强.因此, ${P^{o}}_{i j n}$ 定义为

(6)

{P^{o}}_{i j n}

\frac{\sum_{k \in C^{p d} (i)}^{} \sum_{s = 1}^{M_{k}} {L^{r}}_{k s} (t) / \sum_{k \in C^{p d} (i)}^{} M_{k}}{\underset{k, s}{m a x} {L^{r}}_{k s} (t)}

\frac{c_{i}^{p c} {(1 + o)}^{j} - \underset{i, j}{m i n} [c_{i}^{p c} {(1 + o)}^{j}]}{\underset{i, j}{m a x} [c_{i}^{p c} {(1 + o)}^{j}] - \underset{i, j}{m i n} [c_{i}^{p c} {(1 + o)}^{j}]}

式中: $c_{i}^{p c}$ 表示产品i的单位回收成本;o表示以每个生产周期为一期的投资资金成本率.

(2) 生产调度规则.

每个生产周期开始时间点,基于动态优先级模型安排生产任务.生产调度规则如下:

步骤1 计算产品优先级,设置设备最大生产能力A_ks为剩余生产能力.

步骤2 选择优先级最大的产品,根据工序剩余生产能力尽可能多地安排生产.

步骤3 生产任务分配至设备,相同工序中设备按 ${L^{r}}_{k s}$ (t)大小依次承担生产任务.

步骤4 更新工序和设备的剩余生产能力.

步骤5 更新未调度产品集合,若非空,回步骤2;若为空,结束.

不同滞留周期的产品在生产调度阶段视为不同种类,但在设备维护决策阶段,同一类型产品的加工工序、收益和成本相同,无需考虑滞留周期的影响.

2.1.2 设备故障与维护建模

(1) 变动工况下设备故障率建模.

再制造生产模式下,设备需在每个生产周期承担不同的生产负荷以完成不同产品组合的生产需求,比例故障率模型^[24-25]能有效描述变工况环境下的设备故障率,不失一般性,假设设备处于第m个维护周期,设备(k, s)的故障率表示为

(7)λ_ksm(τ)=

λ_{k s m}^{0}

(τ)exp

(γ_{k s} \frac{W_{k s n} - W_{k s}^{0}}{W_{k s}^{0}})

式中: $λ_{k s m}^{0}$ (τ)为第m个维护周期的基准故障率函数;γ_ks为协变量系数,表征生产负荷对故障率函数的影响程度; $W_{k s}^{0}$ 为基准故障率下设备的生产负荷;W_ksn为设备在第n个生产周期内的生产负荷,

(8)W_ksn=

\sum_{i \in C^{a s} (k, s, n)}^{}

O_iksnE_ik

C^as(k, s, n)表示设备(k, s)在第n个生产周期内生产的产品类型集合;O_iksn表示第n个生产周期内设备(k, s)生产产品i的数量.

(2) 单设备维护决策建模.

由于预防维护通常只对设备部分部件进行维护,无法使设备恢复到全新状态,同时可能改变设备原本的装配特性,使得设备衰退加速.基于双调整因子的修复非新模型^[8]可有效描述维护对设备衰退的影响,据此,设备(k, s)第m个维护周期的基准故障率函数为

(9)

λ_{k s m}^{0}

(τ)=b_ks

λ_{k s, m - 1}^{0}

(τ+a_ks

T_{k s, m - 1}^{P M}

)

式中: $T_{k s, m - 1}^{P M}$ 表示设备第m-1个维护周期时长;a_ks为役龄衰减因子;b_ks为失效加速因子.

设备维护逐生产周期决策,若设备当前维护周期的净收益率最大值出现在当前生产周期结束时间点,设备不预防维护;否则,设备在当前周期预防维护.假设设备处于第m个维护周期,则设备在此维护周期内的净收益率为

(10)

P_{k s m}^{n r}

\frac{P_{k s m}^{p f} - c_{k s m}^{i n} - c_{k s}^{m r} \int_{t_{k s, m - 1}^{P M}}^{t_{k s m}^{P M}} λ_{k s m} (τ) d τ - {c^{p}}_{k s}}{t_{k s m}^{P M} - t_{k s, m - 1}^{P M}}

, (n-1)T≤

t_{k s m}^{P M}

≤nT

式中:自变量 $t_{k s m}^{P M}$ 表示设备第m次预防维护时间点; $P_{k s m}^{p f}$ 为设备在第m个维护周期内产生的生产收益; $c_{k s m}^{i n}$ 为设备在第m个维护周期内承担的库存成本; $c_{k s}^{m r}$ 为设备单次小修成本; ${c^{p}}_{k s}$ 为设备单次预防维护成本.

生产收益 ${P^{p}}_{f k s m}$ 由维护周期内生产产品总数与设备生产单位产品所得收益决定.假设其他设备的衰退进程不改变,可得到当前生产周期的生产优先级和调度计划,进而得到产品i在设备(k, s)上的生产数量.设备生产单位产品所得收益根据产品生产全流程中该设备提供的生产能力占整体所需生产能力的比例分配.设备在此周期生产产品数按维护周期在生产周期所占时长比例计算,则

(11)

P_{k s m}^{p f}

\sum_{i}^{}

{

\frac{E_{i k} {P^{p}}_{r i}}{\sum_{κ \in C^{p d} (i)}^{} E_{i κ}}

[

{O^{h}}_{i k s}

{O^{d}}_{i k s} \frac{(t_{k s m}^{P M} - t)}{T}

]}

式中: ${O^{h}}_{i k s}$ , ${O^{d}}_{i k s}$ 分别表示时段[ $t_{k s, m - 1}^{P M}$ , (n-1)T]和[(n-1)T, $t_{k s m}^{P M}$ ]内产品i在设备(k, s)上的生产数量.

库存成本 $c_{k s m}^{i n}$ 由维护周期内各生产周期平均库存与单位产品为设备带来的库存成本决定,此项成本由生产工序中的全部设备平均分担,则

(12)

c_{k s m}^{i n}

\sum_{i \in C^{w k} (k)}^{} (\frac{c_{i}^{p c} o}{\sum_{κ \in C^{p d} (i)}^{} M_{κ}} \sum_{r \in C_{k s}^{p r} (m)}^{} {I^{a}}_{i r})

式中:C^wk(k)表示需要工序k参与生产的产品集合; $C_{k s}^{p r}$ (m)表示设备第m个维护周期所涉及到的生产周期集合,即有 $t_{k s, m - 1}^{P M}$ ≤(r-1)T< $t_{k s m}^{P M}$ ; ${I^{a}}_{i r}$ 表示产品i在第r个生产周期内的平均库存,即

(13)

{I^{a}}_{i r}

\{\begin{array}{l} I_{i r} - \frac{O_{i r}}{2}, & r \leq n - 1 \\ I_{i r} - \frac{O_{i r} [t_{k s m}^{P M} - (r - 1) T]}{2 T}, & r = n \end{array}

I_ir表示在第r个生产周期开始前回收产品进入系统后产品i的库存量;O_ir表示产品i在第r个生产周期的生产量.

2.2 基于双周期优化的系统动态机会维护建模

预防维护会改变设备衰退进程,且各设备衰退进程联合影响系统下一周期内的生产任务,进而改变各设备当前维护周期收益率.因此,系统中各设备的预防维护决策互相影响,需要统筹决策当前生产周期内的多设备维护方案.

在当前生产周期内维护的设备形成系统决策组合G_sys,由于预防维护只在生产周期间隔实施,系统可提前或推后使G_sys中设备的预防维护时机.传统单周期动态机会维护方法仅关注系统维护决策在当前生产周期的实施效果,不考虑维护动作的长期影响,系统长期优化效果并不显著.因此,考虑预防维护动作在当前生产周期与后续生产周期的总实施效果,综合评估决策的直接影响与后续影响,从而获取最佳决策方案.系统优化目标为当前周期和后续周期内的系统净收益之和,维护方案给出后,系统维护动作将改变设备衰退进程,根据生产调度规则得到当前周期的生产计划,获取当前生产周期的净收益,同时利用随机规划方法获取后续周期的预期净收益,通过最大化双周期总净收益可确定最佳维护方案.

由此,系统机会维护决策模型定义为

(14)

P_{n, n + 1}^{s y s}

P_{n}^{p f, s y s}

c_{n}^{i n, s y s}

c_{n}^{m r, s y s}

+E(

P_{n + 1}^{p f, s y s}

c_{n + 1}^{i n, s y s}

c_{n + 1}^{m r, s y s}

\sum_{(k, s) \in G_{s y s}}^{} {c^{p}}_{k s}

式中: $P_{n}^{p f, s y s}$ , $c_{n}^{i n, s y s}$ , $c_{n}^{m r, s y s}$ 分别表示系统在第n个生产周期内的总生产收益、库存成本和小修成本;E( $P_{n + 1}^{p f, s y s}$ - $c_{n + 1}^{i n, s y s}$ - $c_{n + 1}^{m r, s y s}$ )表示第n+1个生产周期内净收益的期望值,

(15)

P_{n}^{p f, s y s}

\sum_{i}^{} P_{i}^{p r}

O_in

(16)

c_{n}^{i n, s y s}

\sum_{i}^{} [c_{i}^{p c} o (I_{i n} - \frac{O_{i n}}{2})]

(17)

c_{n}^{m r, s y s}

\sum_{k, s}^{} c_{k s}^{m r} \int_{(n - 1) T}^{n T}

λ_ks(τ)dτ

设决策变量x=[x₁x₂ … $x_{X (G_{s y s})}$ ],其中:X(A)表示集合A中的元素个数;x_i为0-1变量,且有

x_i=

\{\begin{array}{l} 1, & G_{s y s} 中 第 i 个 设 备 在 t = (n - 1) T \\ 时 刻 执 行 预 防 维 护 \\ 0, & G_{s y s} 中 第 i 个 设 备 在 t = n T \\ 时 刻 执 行 预 防 维 护 \end{array}

由式(15)~(17)可知,在获取决策变量对应的维护动作之后,可根据生产调度规则得到总生产收益 $P_{n}^{p f, s y s}$ 、总库存成本 $c_{n}^{i n, s y s}$ 和总小修成本 $c_{n}^{m r, s y s}$ .对于第n+1个生产周期,设该周期开始前,全体设备故障率为λ(nT)=[ $λ_{1, 1, m_{1, 1}}$ (nT) $λ_{1, 2, m_{1, 2}}$ (nT) … $λ_{N, M_{N} m_{N}, M_{N}}$ (nT)],其中,若设备(k, s)在G_sys中且对应决策变量为0, $λ_{k s m_{k s}}$ (nT)为在生产周期间隔执行预防维护后的故障率,表征为

(18)

λ_{k s m_{k s}}

(nT)=b_ks

λ_{k s m_{k s}}^{0}

(a_ks

T_{k s m_{k s}}^{P M}

)exp

(γ_{k s} \frac{W_{k s n} - W_{k s}^{0}}{W_{k s}^{0}})

否则,λ_ks(τ)为未执行预防维护的故障率,表征为

(19)λ_ks(nT)=b_ks

λ_{k s, m_{k s} - 1}^{0} (n T - \sum_{i = 1}^{m_{k s} - 1} T_{k s, m_{k s} - 1}^{P M} + a_{k s} T_{k s, m_{k s} - 1}^{P M})

×exp

(γ_{k s} \frac{W_{k s n} - W_{k s}^{0}}{W_{k s}^{0}})

由于产品回收量呈正态分布,设第n+1个生产周期开始前,回收市场新流入的产品数量为I= $[I_{1} I_{2} \dots I_{K}]$ ,其概率密度为

(20)f(I)=

\prod_{i = 1}^{K} \{\frac{1}{\sqrt{2 π} σ_{i}} e x p [- \frac{(I_{i} - μ_{i})^{2}}{2 σ_{i}^{2}}]\}

类似于第n个生产周期,基于动态优先级的调度方法,可获得在任意回收数量组合I下,第n+1个生产周期内的生产安排,进而得到总生产收益 $P_{n + 1}^{p f, s y s}$ 、总库存成本 $c_{n + 1}^{i n, s y s}$ 和总小修成本 $c_{n + 1}^{m r, s y s}$ .令 $P_{n + 1}^{e, s y s}$ (λ(nT), I)表示设备失效率为λ(nT)且回收量为I时系统在第n+1个生产周期内的总生产收益与库存成本和小修成本之差.由此

(21)E(

P_{n + 1}^{p f, s y s}

c_{n + 1}^{i n, s y s}

c_{n + 1}^{m r, s y s}

\int_{0}^{\infty}

…

\int_{0}^{\infty} P_{n + 1}^{e, s y s}

(λ(nT), I)

\prod_{i = 1}^{K}

f(I_i)dI₁…dI_K

然而 $P_{n + 1}^{e, s y s}$ (λ(nT), I)无解析表达式,式(21)中积分无法直接计算.可对f(I_i)进行离散化近似,假设将分布区间分为q_i段,区间端点为x_i₀, x_i₁, …, $x_{i q_{i}}$ ,则有

(22)I_il=

\frac{\int_{x_{i, l - 1}}^{x_{i l}} I_{i} f (I_{i}) d I_{i}}{\int_{x_{i, l - 1}}^{x_{i l}} f (I_{i}) d I_{i}}

, i=1, 2, …, K

(23)P(I_il)=

\int_{x_{i, l - 1}}^{x_{i l}}

f(I_i)dI_i, i=1, 2, …, K

式中:I_il表示离散近似第l段的回收量取值;P(I_il)表示回收量取值为I_il的概率.考虑到正态分布的集中性和对称性以及回收数量的非负特性,可按如下方法设置分布区间:

(24)

\begin{array}{l} q_{i} = 2 θ_{i} + 1 \\ x_{i 0} = 0 \\ x_{i 1} = μ_{i} - 3 σ_{i} \\ x_{i l} = x_{i, l - 1} + \frac{6 σ_{i}}{q_{i} - 2}, l = 2, \dots, q_{i} - 1 \\ x_{i_{q i}} = \infty \end{array}\}

式中:θ_i为任意正整数,i=1, 2, …, K.θ_i取值越大,该离散近似就越接近原分布,则有

(25)E(

P_{n + 1}^{p f, s y s}

c_{n + 1}^{i n, s y s}

c_{n + 1}^{m r, s y s}

\sum_{I}^{}

(

P_{n + 1}^{e, s y s}

(λ(nT), I)

\prod_{i = 1}^{K}

P(I_i))

因此,通过最大化式(14)所示目标函数,可求得最佳的维护决策组合.

3 算例分析

3.1 算例概述

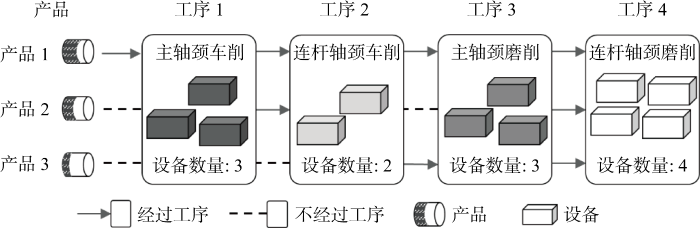
以某公司发动机曲轴再制造生产系统为对象,该系统加工3种规格产品并有主轴颈车削、连杆轴颈车削、主轴颈磨削和连杆轴颈磨削4道连续工序,每类产品的加工工序和各工序设备数量如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 产品加工工序

Fig.2 Production process

通常,曲轴在机加工之前需基于增材制造工艺进行修复,假设其生产能力足够,不影响后续机加工生产安排,因此在该实例中不考虑该工序.根据系统日常生产状况可得生产周期T=224 h,单生产周期下的机会成本率o=0.08.设备最大生产能力A_ks和基准故障率下的生产负荷 $W_{k s}^{0}$ 如表1所示.表中:A_ks通过统计各个设备在生产周期内的历史最大工作时间得到; $W_{k s}^{0}$ 根据工序中全部设备的历史工况下平均加工时间计算得到.

表1 设备生产能力参数

Tab.1 Production capacity of equipment

k	A_k₁/min	A_k₂/min	A_k₃/min	A_k₄/min	$W_{k s}^{0}$
1	12 145	12 582	11 890		4 536
2	12 548	12 876			10 414
3	12 021	12 072	12 103		9 731
4	12 740	12 558	12 022	11 934	10 383

新窗口打开| 下载CSV

在设备衰退方面,设备基准故障率可用威布尔分布描述,即 $λ_{k s}^{0}$ (t)= $\frac{α_{k s}}{β_{k s}} {(\frac{t}{β_{k s}})}^{α_{k s} - 1}$ ,衰退参数和修复参数如表2和表3所示.表中:α_ks,β_ks等参数均基于设备历史故障信息,采用极大似然法计算得到;b_ks,a_ks则可根据设备历史故障维护信息拟合得到;成本相关参数 $c_{k s}^{m r}$ , ${c^{p}}_{k s}$ 通过设备历史维护数据计算平均值得到.

表2 设备衰退相关参数

Tab.2 Degradation related parameters of equipment

k	(α_k₁, β_k₁)	(α_k₂, β_k₂)	(α_k₃, β_k₃)	(α_k₄, β_k₄)	γ_k₁	γ_k₂	γ_k₃	γ_k₄
1	(1.73, 577)	(1.84, 565)	(1.78, 583)		0.76	0.78	0.68
2	(1.96, 625)	(1.99, 632)			0.83	0.85
3	(1.87, 594)	(1.88, 612)	(1.80, 601)		1.01	1.12	1.02
4	(1.85, 704)	(1.96, 691)	(1.67, 722)	(1.91, 688)	0.92	0.99	0.87	0.85

新窗口打开| 下载CSV

表3 设备修复相关参数

Tab.3 Maintenance related parameters of equipment

k	(b_k1, a_k1)	(b_k2, a_k2)	(b_k3, a_k3)	(b_k4, a_k4)	( $c_{k 1}^{m r}$ , ${c^{p}}_{k 1}$ )/元	( $c_{k 2}^{m r}$ , ${c^{p}}_{k 2}$ )/元	( $c_{k 3}^{m r}$ , ${c^{p}}_{k 3}$ )/元	( $c_{k 4}^{m r}$ , ${c^{p}}_{k 4}$ )/元
1	(1.008, 0.04)	(1.008, 0.03)	(1.009, 0.03)		(2 782, 1 453)	(2 977, 1 495)	(2 932, 1 525)
2	(1.012, 0.06)	(1.009, 0.03)			(3 088, 2 321)	(3 054, 2 366)
3	(1.017, 0.04)	(1.016, 0.05)	(1.014, 0.03)		(2 643, 1 943)	(3 012, 2 176)	(2 712, 1 958)
4	(1.004, 0.04)	(1.004, 0.02)	(1.003, 0.06)	(1.004, 0.03)	(4 658, 2 416)	(4 031, 2 643)	(4 872, 2 298)	(4 652, 2 511)

新窗口打开| 下载CSV

该系统加工的3类产品的生产利润 $P_{i}^{p r}$ 、回收成本 $c_{i}^{p c}$ 和回收量r_i如表4所示.表中:回收成本 $c_{i}^{p c}$ 和回收量r_i根据产品历史回收价格和数量统计得到;生产利润 $P_{i}^{p r}$ 通过历史销售数据、制造成本数据和回收价格计算得到.另外,根据历史回收数据高频分布,取离散近似参数θ₁=θ₂=θ₃=1.

表4 产品生产利润、回收成本和回收量

Tab.4 Production margins, recovery costs, and recovery volumes of products

i	$P_{i}^{p r}$ /元	$c_{i}^{p c}$ /元	r_i
1	281	318	N(431, 45.32)
2	289	318	N(222, 54.12)
3	312	329	N(318, 35.62)

新窗口打开| 下载CSV

产品在不同工序内加工所需产能根据日常生产中单位产品在工序内生产平均耗时得到,具体参数如表5所示.另外,收益能力和资金成本优先级的权重可分别根据历史生产周期内产品加工量与滞留量占回收量的平均比例得到,本例中取ω_p=ω_o=0.5.

表5 产品生产所需产能

Tab.5 Capacity required for production of the products

k	E₁_k/min	E₂_k/min	E₃_k/min
1	68
2	46	54
3	61		71
4	55	63	69

新窗口打开| 下载CSV

依据以上参数,基于提出的动态机会维护模型,可得到每个生产周期间隔的系统组合维护方案.表6给出了前6个回收周期的产品回收序列.表7给出了此生产序列下前6个生产周期的系统维护方案,“A”表示设备从最佳维护时点提前预防维护,“D”则表示推迟预防维护,以t=224 h为例,设备(1, 1),(2, 2),(4, 2)将全部提前执行预防维护.表7说明系统层维护存在提前与推后的动态决策结果,系统具备显著的优化能力.

表6 产品回收数量序列

Tab.6 Quantity series of product recovery

i	t=0 h	t=224 h	t=448 h	t=672 h	t=896 h	t=1 120 h	t=1 344 h
1	431	419	374	407	293	382	429
2	222	245	170	204	197	272	231
3	318	331	291	318	362	330	262

新窗口打开| 下载CSV

表7 前6个生产周期的系统维护方案

Tab.7 System maintenance plan for the first 6 production cycles

设备	维护计划
设备	t=224 h	t=448 h	t=672 h	t=896 h	t=1 120 h	t=1 344 h
(1, 1)	A		D
(1, 2)			D		A
(1, 3)			D		D
(2, 1)		D	A		D
(2, 2)	A			A		D
(3, 1)		A		D		A
(3, 2)		D		A		D
(3, 3)		D		D		D
(4, 1)		D		D		D
(4, 2)	A			A		D
(4, 3)		D			A
(4, 4)		D		A		A

新窗口打开| 下载CSV

3.2 策略对比

为探究考虑生产调度与可靠性耦合的动态生产调度和维护决策策略的有效性,将其定义为动态耦合策略,同时根据企业常用生产与维护方法,选择3种对比策略如下.

(1) 提前维护策略,以对比验证双周期维护决策的有效性.该策略与动态耦合策略的不同在于:在预防维护决策时,不考虑设备维护动作对后续生产的影响,直接通过最小化设备维护周期内的小修和预防维护成本率获取最佳维护时间点,随后系统提前对维护时间点落在当前生产周期的全部设备实施预防维护.此外,生产调度方法与动态耦合策略一致.

(2) 产能均衡策略,以对比验证动态生产调度方法的有效性.在该策略下,生产调度不考虑产品生产优先级与库存期数,采用产能平均分配原则安排生产,生产调度策略为:基于库存产品种类,将系统产能平均分配至每种产品.在此过程中,优先分配库存数量最少的产品种类直至达到平均分配产能,若针对该种产品的产能有剩余,则剩余产能再次平均分配至其他产品种类.除此之外,维护决策模型与动态耦合策略保持一致.

(3) 分部决策策略,以进一步验证考虑耦合机制的有效性.在该策略下,生产调度与可靠性独立决策,生产调度采用产能平均分配原则,设备维护决策方法则与提前维护策略相同.

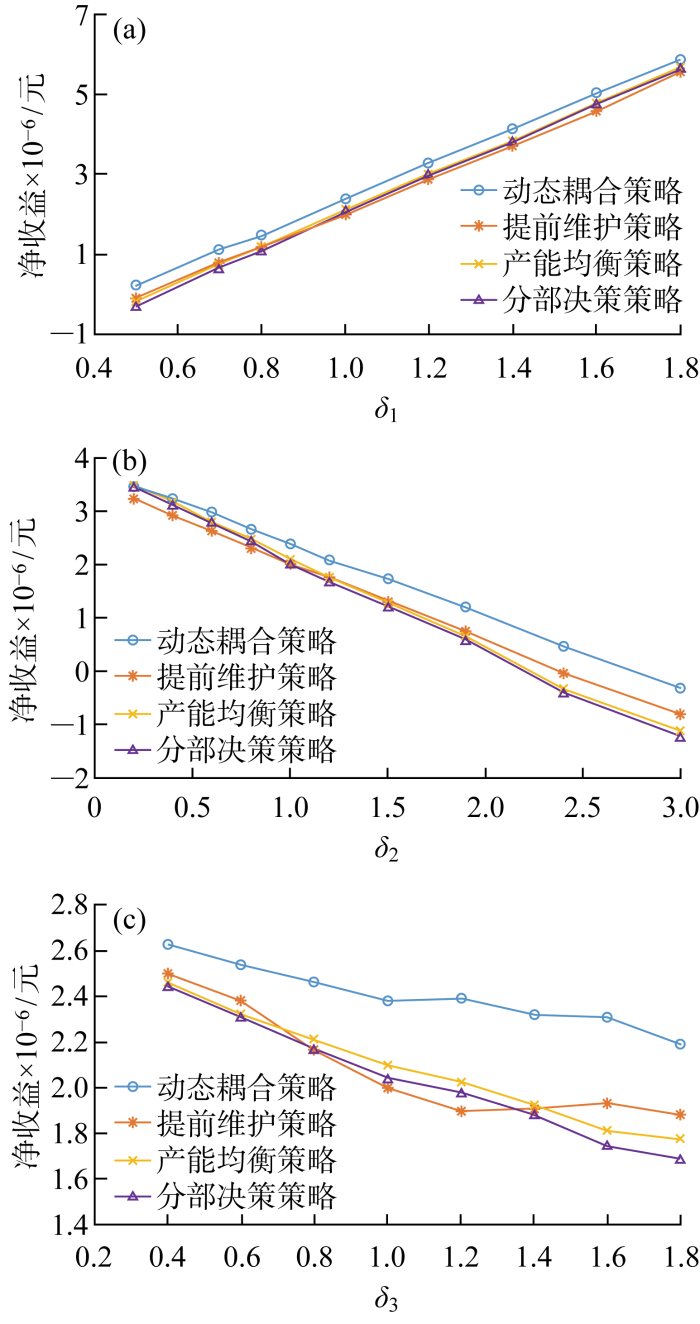
考虑到经济因素对系统决策的影响,改变产品利润、产品回收成本和设备小修成本,对比不同策略下系统生产净收益变化.引入比例因子δ₁, δ₂, δ₃,令参数 $P_{i}^{p r'}$ =δ₁ $P_{i}^{p r}$ , $c_{i}^{p c'}$ =δ₂ $c_{i}^{p c}$ , $c_{k s}^{m r'}$ =δ₃ $c_{k s}^{m r}$ ,通过调节比例因子得到不同大小的参数,分析参数变化下系统在20个生产周期内的净收益,重复模拟10次,计算结果均值如图3所示,在δ₁, δ₂, δ₃的各种取值下,动态耦合策略下的系统净收益始终高于其他3种策略,体现了该策略的有效性.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 经济因素变化的净收益对比分析

Fig.3 Comparative analysis of net benefits from changes in economic factors

进一步对比发现,δ₂增大时,产品库存成本增大,动态耦合策略下净收益下降速度低于其他策略,说明该策略更适用于库存成本较高的情境.δ₁,δ₃变动时,动态耦合策略始终保持最优,说明该策略可以较稳定地保证系统净收益.

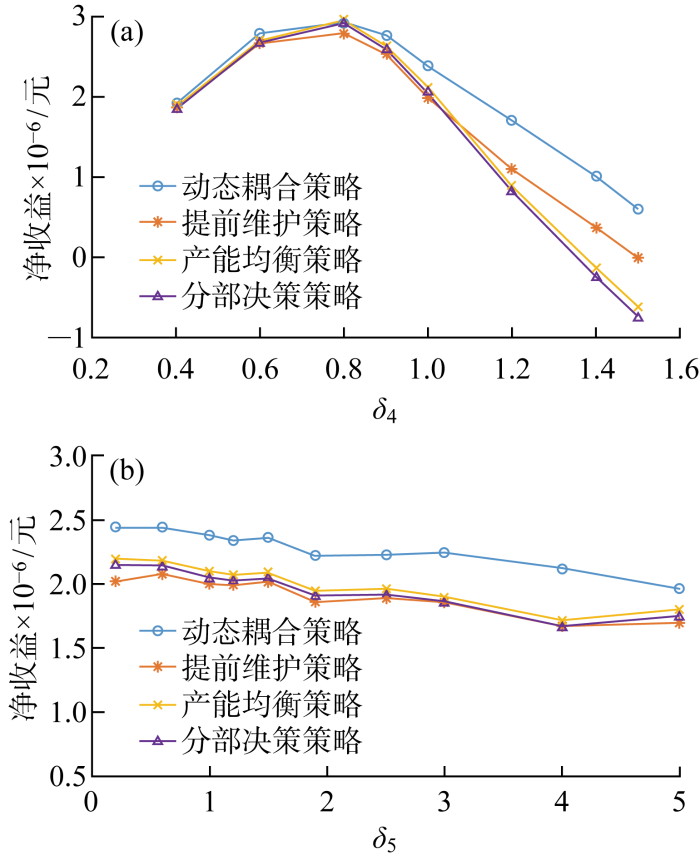
考虑回收因素的影响,改变产品回收量的均值和方差,对比分析4种策略下系统生产净收益的变化情况.引入比例因子δ₄,δ₅,令参数μ'_i=δ₄μ_i, $σ_{i}^{2'}$ =δ₅ $σ_{i}^{2}$ ,调节比例因子,分析参数变化下系统在20个生产周期内的净收益,重复模拟10次,计算结果均值如图4所示.参数δ₄=0.8时,系统净收益达到峰值,此时系统可以最大化生产且不会留有过多库存,随着δ₄逐渐增大,动态耦合策略逐渐优于其他策略,说明该策略更适用于回收量较高的场景.δ₅变化时,4种策略下的系统净收益均呈现下降趋势,说明回收市场的波动性对系统生产存在负面影响,与生产事实相符.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 回收因素的净收益对比分析

Fig.4 Comparative analysis of net benefits from changes in recovery factors

动态耦合策略综合考虑了生产、设备衰退和维护相互影响,与提前维护策略相比,能够根据未知工况的变化,更合理地安排设备的维护时间点,从而减少了后续生产过程中的设备失效次数和维护成本;与产能均衡策略相比,能够根据设备的衰退程度和产品的生产动机,更合理地调整生产调度方案,从而增加了生产收益;与分部决策策略相比,能够充分考虑生产调度与可靠性之间的耦合关系,在此基础上更有效地决策生产与维护,显著提升了系统的净收益.

4 结语

本文以变工况下的多工序再制造系统为研究对象,综合考虑设备衰退、维护与生产间的耦合关系,提出基于动态优先级的生产调度方法,并构建基于双周期优化的动态维护决策模型.基于实际生产场景的算例分析结果表明,相较于提前维护或产能均衡的策略,考虑设备衰退、维护与生产间耦合关系的动态调度方法与维护决策模型更适用于再制造生产环境,且随着回收量的增大,该模型的优势更加明显.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

LEVITIN

, XING

, XIANG

Optimizing preventive replacement schedule in standby systems with time consuming task transfers

[J]. Reliability Engineering & System Safety, 2021, 205: 107227.

i	t=0 h	t=224 h	t=448 h	t=672 h	t=896 h	t=1 120 h	t=1 344 h
1	431	419	374	407	293	382	429
2	222	245	170	204	197	272	231
3	318	331	291	318	362	330	262

i	t=0 h	t=224 h	t=448 h	t=672 h	t=896 h	t=1 120 h	t=1 344 h
1	431	419	374	407	293	382	429
2	222	245	170	204	197	272	231
3	318	331	291	318	362	330	262