浅海质点振速场强度的深度分布特性

doi:10.16183/j.cnki.jsjtu.2023.073

浅海质点振速场强度的深度分布特性

张海刚¹^,²^,³, 谢金怀¹^,²^,³, 刘佳琪⁴, 龚李佳^,¹^,²^,³, 李智¹^,²^,³

1.哈尔滨工程大学水声技术全国重点实验室,哈尔滨 150001

2.哈尔滨工程大学海洋信息获取与安全工业和信息化部重点实验室,哈尔滨 150001

3.哈尔滨工程大学水声工程学院,哈尔滨 150001

4.上海船舶电子设备研究所,上海 201108

Depth Distribution Characteristics of Particle Velocity Field Intensity in Shallow Sea

ZHANG Haigang¹^,²^,³, XIE Jinhuai¹^,²^,³, LIU Jiaqi⁴, GONG Lijia^,¹^,²^,³, LI Zhi¹^,²^,³

1. National Key Laboratory of Underwater Acoustic Technology, Harbin Engineering University, Harbin 150001, China

2. Key Laboratory of Marine Information Acquisition and Security of the Ministry of Industry and Information Technology, Harbin Engineering University, Harbin 150001, China

3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China

4. Shanghai Marine Electronic Equipment Research Institute, Shanghai 201108, China

通讯作者: 龚李佳,副教授;E-mail:lijia.gong@hrbeu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-03-3 修回日期: 2023-05-6 接受日期: 2023-06-16

基金资助:

国家自然科学基金(11904292)
国家自然科学基金(12174048)

Received: 2023-03-3 Revised: 2023-05-6 Accepted: 2023-06-16

作者简介 About authors

张海刚(1981-),教授,博士生导师,主要从事海洋声场建模与应用研究.

摘要

质点振速场强度的深度分布特性对水声探测与估计具有重要影响.基于简正波非相干模态和变换到角度积分的近似条件,推导出质点振速的非相干简正波的角度积分形式,避免了本征值和本征函数的复杂计算,并揭示了质点振速强度在声源深度及对称深度具有显著变化特性的物理机理.数值结果表明:非相干质点振速的角度积分解析式可实现快速计算,并可较好地表征出质点振速强度的深度分布特性;同时,由于简正波模态幅度函数的叠加效应,垂直质点振速与水平质点振速的深度分布存在显著差异性;随后,以质点振速强度差为研究对象,分析了水平距离、声源频率、声速剖面及海水深度等参数对质点振速场强度的深度分布特性的影响.相关结论可为基于矢量场的被动目标深度估计提供理论依据.

关键词： 质点振速; 深度分布; 声源深度; 简正波模态叠加

Abstract

The depth distribution characteristics of particle velocity field intensity have had a significant impact on underwater acoustic detection and estimation. In this paper, based on the approximate conditions of the incoherent normal modes sum transformation to angular integration, the angular integration form of incoherent normal modes of particle velocity was derived, which avoided the complex calculations of eigenvalues and eigenfunctions while revealing the physical mechanism behind the significant variations in particle velocity intensity with source depth and symmetrical depth. The numerical results demonstrate that the analytical expression of the angular integration of incoherent particle velocity can facilitate fast computation and effectively characterize the depth distribution characteristics of particle velocity intensity. Additionally, due to the superposition effect of the amplitude function of normal modes, there are notable differences in the depth distribution of vertical and horizontal particle velocity. Subsequently, focusing on the intensity difference of particle velocity, the study analyzed the effects of parameters such as horizontal distance, source frequency, sound speed profile, and water depth on the depth distribution characteristics of particle velocity field intensity. The findings provide a theoretical basis for passive target depth estimation based on vector fields.

Keywords： particle velocity; depth distribution; source depth; normal mode superposition

PDF (6512KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张海刚, 谢金怀, 刘佳琪, 龚李佳, 李智. 浅海质点振速场强度的深度分布特性[J]. 上海交通大学学报, 2024, 58(7): 995-1005 doi:10.16183/j.cnki.jsjtu.2023.073

ZHANG Haigang, XIE Jinhuai, LIU Jiaqi, GONG Lijia, LI Zhi. Depth Distribution Characteristics of Particle Velocity Field Intensity in Shallow Sea[J]. Journal of Shanghai Jiaotong University, 2024, 58(7): 995-1005 doi:10.16183/j.cnki.jsjtu.2023.073

水下声道中声场的深度分布一直受国内外学者的广泛关注.20世纪80年代,Weston^[1⇓-3]利用经典波动理论解释了在理想等声速的Pekeris波导中,声源深度和其近似对称深度位置声场强度最强且几乎相等,并称此深度为最佳接收深度.随后,国内外众多学者对声传播最佳接收深度进行了大量研究.Ferla等^[4]利用声纳的优质因数研究了不同环境剖面下被动声纳最佳接收深度,得出在已知声源深度情况下,最佳的接收深度为声源深度或共轭深度的经验规律;Gershfeld等^[5]通过数值模拟研究海洋环境参数及声源参数对最佳接收深度位置的影响,发现频率在200 Hz以上时,最佳深度几乎与频率和沉积物类型无关;An等^[6]为了克服传播模型计算最佳接收深度时间成本高这一问题,利用模拟退火法进行最佳接收深度寻取,实现声纳探测性能最大化.国内对声纳最佳工作深度选择的研究工作主要局限于数值仿真^[7⇓-9],缺乏深入的理论解析研究.近年来,Harrison^[10]利用简正波的非相干模态解析表达式研究波导传播的声场特性,清晰地描述了声场的深度依赖特性.Sertlek等^[11-12]通过将简正波模态和转换为角度积分,推导了Faddeeva函数的解析解并用于表征最佳接收深度,进一步分析浅海Pekeris波导中声压非相干传输因子深度方向的分布特性.

根据已有研究表明,大多数声传播的最佳接收深度研究仅考虑了声压强度的深度分布特性,而针对质点振速场强度的深度分布特性研究鲜有报道.随着矢量传感器在水声测量的广泛应用,声矢量场特性研究可为水下目标探测与定位、海洋环境参数反演等应用提供可靠的理论参考^[13⇓-15].在声矢量场特性研究中,质点振速场往往是通过声压场数值差分获取,其中声压场可由简正波方法、抛物方程方法或射线方法等数值模型计算.因此,质点振速场的计算精度取决于数值差分步长.当差分步长较小时,计算量大导致计算速度慢,不适合声矢量场的快速计算^[16-17].因此,利用数值计算模型进行质点振速场强度的深度分布特性研究时,会存在计算效率低、计算结果受模型适用性条件限制等问题.

为此,本文将声压的非相干模态和的角度积分形式扩展到质点振速的角度积分,获得质点振速场强度的深度分布特性,避免了本征值和本征函数的复杂计算,同时提高计算效率.进一步理论解释质点振速场强度的深度分布特性的原因,为矢量传感器的应用提供理论基础.接着,以水平质点振速与垂直质点振速的非相干强度差作为研究对象,分析波导环境参数的改变对浅海质点振速场强度的深度分布特性的影响.最后,从简正波模态叠加的角度分析质点振速场强度的深度分布特性,直观地揭示了质点振速场强度的深度分布特性的物理机理.

1 质点振速场的深度分布特性

1.1 等声速波导环境解析推导

在声纳性能建模、水声通信、环境风险评估和海洋学等诸多声学问题中,都需要精确计算传播损失,传播损失L_T可以定义为

(1)L_T=-10lg

\frac{F}{F_{r e f}}

式中: $\frac{F}{F_{r e f}}$ 为传播因子^[18],F_ref为参考距离1 m处的声压值,F为声压.根据简正波理论,在与水平距离无关波导环境中,利用欧拉公式,由点源声场声压可进一步表示出声场中水平质点振速v_r和垂直质点振速v_z:

(2)v_r=

\frac{i}{ρ_{w}^{2} ω \sqrt{8 π r}} e^{- i \frac{π}{4}} \overset{N}{\sum_{n = 1}}

ϕ_n(z_s)ϕ_n(z)

\sqrt{k_{n}} e^{i k_{n} r}

(3)v_z=

\frac{1}{ρ_{w}^{2} ω \sqrt{8 π r}} e^{- i \frac{π}{4}} \overset{N}{\sum_{n = 1}}

ϕ_n(z_s)ϕ'_n(z)

\frac{e^{i k_{n} r}}{\sqrt{k_{n}}}

式中:z为深度;z_s为声源深度;ϕ_n(z)是第n阶归一化的本征函数;ϕ'_n(z)是第n阶归一化本征函数在深度方向的偏导数;k_n=κ_n+iδ_n是实部表征为水平波数、虚部为简正波衰减的复本征值,δ_n为衰减系数;ρ_w为海水介质密度;ω为角频率;N为最大阶数;r为水平距离.相应地,可得出声矢量场中水平质点振速与垂直质点振速的传播损失如下^[19]:

(4)

\begin{array}{l} L_{T v_{r}} = - 10 l g {|\frac{v_{r} (r, z)}{{v_{r e f}|}_{r = 1}}|}^{2} \\ L_{T v_{z}} = - 10 l g {|\frac{v_{z} (r, z)}{{v_{r e f}|}_{r = 1}}|}^{2} \end{array}\}

式中:v_ref为参考振速,由文献[14]可知v_ref= $\frac{k_{0}}{ρ_{w} ω}$ × $\frac{e^{i k_{0} r}}{4 π r}$ ,k₀为波数.根据传播因子 $\frac{F}{F_{r e f}}$ 定义,可类似地定义 ${|\frac{v_{r}}{v_{r e f}}|}^{2}$ 和 ${|\frac{v_{z}}{v_{r e f}}|}^{2}$ 为声矢量场水平质点振速与垂直质点振速的传播因子,对此进一步将相干质点振速传播因子展开为

(5)$\begin{aligned}\left|\frac{v_{r}}{v_{\text {ref }}}\right|^{2}= & \frac{2 \pi}{k_{0}^{2} \rho_{\mathrm{w}}^{2} r}\left\{\sum_{n=1}^{N} \phi_{n}^{2}\left(z_{\mathrm{s}}\right) \phi_{n}^{2}(z) k_{n} \mathrm{e}^{-2 \delta_{n} r}+\right. \\& \sum_{n=1}^{M} \sum_{m=1}^{n-1} \phi_{n}\left(z_{\mathrm{s}}\right) \phi_{n}(z) \phi_{m}\left(z_{\mathrm{s}}\right) \phi_{m}(z) \times \\& \left.\sqrt{k_{n} k_{m}} \cos \left[\left(k_{n}-k_{m}\right) r\right]\right\}=F_{r 1}+F_{r 2}\end{aligned}$

(6)$\begin{array}{l}\left|\frac{v_{z}}{v_{\text {ref }}}\right|^{2}=\frac{2 \pi}{k_{0}^{2} \rho_{\mathrm{w}}^{2} r}\left\{\sum_{n=1}^{N} \phi_{n}^{2}\left(z_{\mathrm{s}}\right) \phi_{n}^{\prime 2}(z) \frac{\mathrm{e}^{-2 \delta_{n} r}}{k_{n}}+\right. \\\sum_{n=1}^{M} \sum_{m=1}^{n-1} \phi_{n}\left(z_{\mathrm{s}}\right) \phi_{n}^{\prime}(z) \phi_{m}\left(z_{\mathrm{s}}\right) \phi_{m}^{\prime}(z) \times \\\left.\frac{\cos \left[\left(k_{n}-k_{m}\right) r\right]}{\sqrt{k_{n} k_{m}}}\right\}=F_{z 1}+F_{z 2}\end{array}$

式(5)~(6)等号右边第1项为非相干求和项,其表征为声波传播的平均强度;第2项为交叉作用项,主要通过简正波干涉对声波传播产生影响.由于浅海实际海洋环境的复杂性,其声场干涉结构与实验结果难以相吻合;而且当距离很远时,声速分布的微小变化就可能使简正波之间的相对相位发生改变,这种情况下精确地计算声场的细微结构往往失去实际意义^[20].因此,本文利用简正波非相干模态和研究质点振速场强度的深度分布特性,暂不考虑简正波相干模态和的交叉作用项在深度方向的影响.Pekeris波导环境下,水平质点振速和垂直质点振速传播因子F_r₁, F_z₁为

(7)F_r₁=

\frac{2 π}{k_{0}^{2} ρ_{w}^{2} r} \overset{N}{\sum_{n = 1}} ϕ_{n}^{2}

(z_s)

ϕ_{n}^{2}

(z)k_n

e^{- 2 δ_{n} r}

(8)F_z₁=

\frac{2 π}{k_{0}^{2} ρ_{w}^{2} r} \overset{N}{\sum_{n = 1}} ϕ_{n}^{2}

(z_s)

ϕ_{n}^{' 2}

(z)

\frac{e^{- 2 δ_{n} r}}{k_{n}}

等声速波导环境下,本征函数可利用半经典计算方法WKB近似表示为^[10]

(9)ϕ_n(z)=

\frac{A_{n} s i n (γ_{n} z)}{(k_{0}^{2} (z) - k_{n}^{2})^{1 / 4}}

式中:A_n为归一化幅值;γ_n为垂直波数,对于有效深度为H的压力释放波导,垂直波数可由γ_nH=nπ给出.其中有效深度H是通过考虑声波在界面反射导致的相位变化时,引入的有效深度概念^[21-22],其主要受海底参数和频率的影响,等声速半无限海底波导环境下可表示为

(10)H=h+

\frac{{[1 - 2 {(\frac{c_{s}}{c_{w}})}^{2}]}^{2} g}{k_{0} s i n θ_{c}}

式中:h为实际深度;ρ_b为海底介质密度;密度比g= $\frac{ρ_{b}}{ρ_{w}}$ ;c_s为海底剪切波声速;c_w为水中声速,临界掠射角θ_c=arccos $(\frac{c_{w}}{c_{p}})$ ,c_p为海底横波声速;波数k₀= $\frac{2 π f}{c_{w}}$ ,f为频率.该环境下 $k_{0}^{2}$ (z)为随深度不变的常数.根据本征函数的正交完备性,

∫

ϕ_{n}^{2}

(z)dz=1

可得出本征函数的归一化幅值^[23]:

(11)

A_{n}^{2}

\frac{2}{\int \frac{1}{\sqrt{k_{0}^{2} - k_{n}^{2}}} d z}

水平质点振速与垂直质点振速传播因子F_r₁, F_z₁可进一步写成:

(12)F_r₁=

\frac{2 π}{k_{0}^{2} ρ_{w}^{2} r}

\overset{N}{\sum_{n = 1}} A_{n}^{4} \frac{s i n^{2} (γ_{n} z_{s}) s i n^{2} (γ_{n} z)}{\sqrt{k_{0}^{2} (z_{s}) - k_{n}^{2}} \sqrt{k_{0}^{2} (z) - k_{n}^{2}}}

k_n

e^{- 2 δ_{n} r}

(13)F_z₁=

\frac{2 π}{k_{0}^{2} ρ_{w}^{2} r}

\overset{N}{\sum_{n = 1}} A_{n}^{4} \frac{s i n^{2} (γ_{n} z_{s}) γ_{n}^{2} c o s^{2} (γ_{n} z)}{\sqrt{k_{0}^{2} (z_{s}) - k_{n}^{2}} \sqrt{k_{0}^{2} (z) - k_{n}^{2}}} \frac{e^{- 2 δ_{n} r}}{k_{n}}

当相邻项的变化很小时,简正波的非相干离散模态和可以近似为以下积分形式,用F_r₀, F_z₀表示:

(14)F_r₀=

\frac{2 π}{k_{0}^{2} ρ_{w}^{2} r}

\int_{0}^{\infty} A_{n}^{4} \frac{s i n^{2} (γ_{n} z_{s}) s i n^{2} (γ_{n} z)}{\sqrt{k_{0}^{2} (z_{s}) - k_{n}^{2}} \sqrt{k_{0}^{2} (z) - k_{n}^{2}}}

k_n

e^{- 2 δ_{n} r}

(15)F_z₀=

\frac{2 π}{k_{0}^{2} ρ_{w}^{2} r}

\int_{0}^{\infty} A_{n}^{4} \frac{s i n^{2} (γ_{n} z_{s}) γ_{n}^{2} c o s^{2} (γ_{n} z)}{\sqrt{k_{0}^{2} (z_{s}) - k_{n}^{2}} \sqrt{k_{0}^{2} (z) - k_{n}^{2}}} \frac{e^{- 2 δ_{n} r}}{k_{n}}

通过对模态求和的积分转换,正整数n可近似表示为与掠射角相关的函数n≈n(θ),利用WKB相位积分给出简正波的模态阶数n与水平波数k_n的关系^[24]π(n+ε)= $\int_{0}^{H} \sqrt{k_{0}^{2} (z) - k_{n}^{2}}$ dz,ε为由边界条件引起相位变化的附加值.同时,水平波数与波数的几何关系满足k_n=k₀cos θ,并根据射线循环距离与水平波数满足关系式r_c=2∫k_n/ $\sqrt{k_{0}^{2} (z) - k_{n}^{2}}$ dz,整理可得出模态阶数n的积分与角度θ的积分关系式:

(16)

\begin{array}{l} \frac{d n}{d k_{n}} = - \frac{k_{n}}{π} \int_{0}^{H} \frac{1}{\sqrt{k_{0}^{2} (z) - k_{n}^{2}}} d z \\ \frac{d n (θ)}{d θ} = \frac{d n}{d k_{n}} \frac{d k_{n}}{d θ} = \frac{r_{c}}{2 π} k_{0} s i n θ \end{array}\}

另外,简正波水平方向上的衰减项 $e^{- δ_{n} r}$ 中衰减系数δ_n与海底反射系数相关:δ_n=-ln( $|V (θ_{n})|$ )/r_c,考虑指数型反射系数 $|V|$ =exp(-ηθ²/tan θ).将式(11)和式(16)代入简正波模态阶数n的积分式(14)和式(15),整理可得出声矢量场中水平质点振速与垂直质点振速传播因子的解析表达式:

(17)F_r₀(z_s, z)=

\frac{2}{ρ_{w}^{2} r h}

\int_{0}^{θ_{c}}

(1-W(z_s, z, θ))

e^{- \frac{η r}{h} θ^{2}}

cos²θdθ

(18)F_z₀(z_s, z)=

\frac{2}{ρ_{w}^{2} r h}

\int_{0}^{θ_{c}}

(1-G(z_s, z, θ))

e^{- \frac{η r}{h} θ^{2}}

sin²θdθ

$\begin{array}{l}W\left(z_{\mathrm{s}}, z, \theta\right)= \\\cos \left(2 k_{0} z_{\mathrm{s}} \sin \theta\right)+\cos \left(2 k_{0} z \sin \theta\right)- \\\frac{\cos \left[2 k_{0} \sin \theta\left(z_{\mathrm{s}}-z\right)\right]+\cos \left[2 k_{0} \sin \theta\left(z_{\mathrm{s}}+z\right)\right]}{2} \\G\left(z_{\mathrm{s}}, z, \theta\right)= \\\cos \left(2 k_{0} z_{\mathrm{s}} \sin \theta\right)-\cos \left(2 k_{0} z \sin \theta\right)+ \\\frac{\cos \left[2 k_{0} \sin \theta\left(z_{\mathrm{s}}-z\right)\right]+\cos \left[2 k_{0} \sin \theta\left(z_{\mathrm{s}}+z\right)\right]}{2}\end{array}$

式中:η是海底密度、声速和衰减系数的函数.式(17)~(18)将质点振速的非相干简正波模态和转化到角度积分形式,可避免简正波的本征值和本征函数的复杂计算,为研究浅海质点振速场强度的深度分布特性提供有效的解析方法.由于在推导非相干质点振速传播因子的角度积分解析表达式过程中,利用正弦函数形式近似表示本征函数,所以有必要进一步讨论解析表达式在深度方向的周期性问题.由WKB相位积分给出模态阶数与水平波数的关系^[24] (n+ε)π= $\int_{0}^{H} \sqrt{γ_{n}^{2}}$ dz,且本文利用简正波的非相干项进行质点振速场强度的深度分布特性研究,不考虑交叉作用项相位的影响,因此忽略ε,可得出垂直波数满足γ_n=nπ/H,将其代入式(12)和式(13)得:

(19)F_r₁=

\frac{2 π}{k_{0}^{2} ρ_{w}^{2} r}

\overset{\infty}{\sum_{n = 1}} A_{n}^{4} \frac{s i n^{2} (\frac{n π}{H} z_{s}) s i n^{2} (\frac{n π}{H} z)}{\sqrt{k_{0}^{2} (z_{s}) - k_{n}^{2}} \sqrt{k_{0}^{2} (z) - k_{n}^{2}}}

k_n

e^{- 2 δ_{n} r}

(20)F_z₁=

\frac{2 π}{k_{0}^{2} ρ_{w}^{2} r}

\overset{\infty}{\sum_{n = 1}} A_{n}^{4} \frac{s i n^{2} (\frac{n π}{H} z_{s}) {(\frac{n π}{H})}^{2} c o s^{2} (\frac{n π}{H} z)}{\sqrt{k_{0}^{2} (z_{s}) - k_{n}^{2}} \sqrt{k_{0}^{2} (z) - k_{n}^{2}}} \frac{e^{- 2 δ_{n} r}}{k_{n}}

在均匀介质环境下 $k_{0}^{2}$ (z)为常数,根据三角函数的周期性性质,接收深度z和声源深度z_s均满足sin²[nπ(H-z)/H]=sin²(nπz/H)和cos²[nπ(H-z)/H]=cos²(nπz/H)的恒等关系,整理可知质点振速的传播因子在深度方向满足如下对称关系:

(21)

\begin{array}{l} F_{r 1} (z_{s}, z) = F_{r 1} (z_{s}, H - z) = \\ F_{r 1} (H - z_{s}, z) \\ F_{z 1} (z_{s}, z) = F_{z 1} (z_{s}, H - z) = \\ F_{z 1} (H - z_{s}, z) \end{array}\}

可进一步得出:

(22)

\begin{array}{l} F_{r 1} (z_{s}, z) = F_{r 1} (H - z_{s}, H - z) \\ F_{z 1} (z_{s}, z) = F_{z 1} (H - z_{s}, H - z) \end{array}\}

因此,在等声速波导环境下,可利用非相干质点振速场的深度对称性进行对称深度区域非相干声场计算,避免计算所有接收深度的传播因子,以此提高计算效率.同时,为研究质点振速场强度的深度分布特性提供简单直观且物理意义清晰的数学表达式.

1.2 数值仿真对比

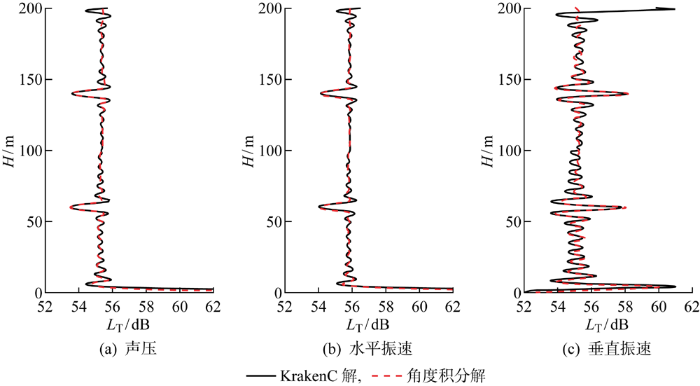
为了验证等声速波导环境下质点振速的角度积分形式用于表征质点振速场强度的深度分布特性的有效性,以及该解析式的计算效率,以KrakenC声场计算软件^[25]计算结果作为标准解,仿真计算声矢量场传播损失L_T=-10lg(F/F_ref)随深度的分布.仿真海水深度为200 m,水中声速 1 500 m/s,海底声速 1 800 m/s的波导环境,计算声源深度为 60 m,频率为200 Hz,在距离声源2 km处的深度分布曲线如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 等声速波导环境的深度分布

Fig.1 Depth distribution of waveguide environment with isospeed

可以看到,利用声矢量各分量的角度积分解析式计算的深度分布结果与KrakenC声场计算软件计算结果基本吻合,且利用声场计算软件计算本征值和本征函数,进一步计算质点振速强度的深度分布特性需耗时 3 314.854 ms,而利用上文推导解析式进行相关计算仅需 11.756 ms,计算效率显著提高.由此,验证了非相干质点振速角度积分解析式用于表征深度分布特性的有效性及高效性.同时,图1中所示声压与水平质点振速强度的深度分布规律基

本相似;水平质点振速相比垂直质点振速强度总体大10 dB左右,声源深度及声源对称深度强度大15 dB左右.除此之外,声压和水平质点振速相比垂直质点振速强度在深度方向起伏平缓.

1.3 声源深度及对称深度现象的物理机理解释

质点振速的深度依赖性完全包含在简正波模态和中:

(23)

\begin{array}{l} S_{r} = \overset{N}{\sum_{n = 1}} s i n^{2} (γ_{n} z_{s}) s i n^{2} (γ_{n} z) \\ S_{z} = \overset{N}{\sum_{n = 1}} s i n^{2} (γ_{n} z_{s}) c o s^{2} (γ_{n} z) \end{array}\}

利用三角函数积化和差公式可转化为

(24)

\begin{array}{l} S_{r} = \frac{1}{4} \overset{N}{\sum_{n = 1}} {1 - c o s (2 γ_{n} z_{s}) - c o s (2 γ_{n} z) + \\ \frac{c o s [2 γ_{n} (z_{s} - z)] + c o s [2 γ_{n} (z_{s} + z)]}{2}} \\ S_{z} = \frac{1}{4} \overset{N}{\sum_{n = 1}} {1 - c o s (2 γ_{n} z_{s}) + c o s (2 γ_{n} z) - \\ \frac{c o s [2 γ_{n} (z_{s} - z)] + c o s [2 γ_{n} (z_{s} + z)]}{2}} \end{array}\}

对于海底软边界环境,垂直波数满足γ_n=nπ/H,可令x=2πz/H,根据欧拉公式变换,余弦函数求和可转化为如下格式:

(25)

\overset{N}{\sum_{n = 1}}

cos nx=

\frac{1}{2} \{\frac{s i n \frac{(2 N + 1) x}{2}}{\frac{s i n x}{2}} - 1\}

因此,可将水平质点振速的模态幅度函数进一步表示为

(26)$\begin{aligned}S_{r}= & \frac{1}{4}\left\{N-\frac{1}{2}\left[\frac{\sin \left[(2 N+1) \frac{\pi z_{\mathrm{s}}}{H}\right]}{\sin \frac{\pi z_{\mathrm{s}}}{H}}-1\right]-\right. \\& \frac{1}{2}\left[\frac{\sin \left[(2 N+1) \frac{\pi z}{H}\right]}{\sin \frac{\pi z}{H}}-1\right]+ \\& \frac{1}{4}\left[\frac{\sin \left[(2 N+1) \frac{\pi\left(z_{\mathrm{s}}-z\right)}{H}\right]}{\sin \frac{\pi\left(z_{\mathrm{s}}-z\right)}{H}}-1\right]+ \\& \left.\frac{1}{4}\left[\frac{\sin \left[(2 N+1) \frac{\pi\left(z_{\mathrm{s}}+z\right)}{H}\right]}{\sin \frac{\pi\left(z_{\mathrm{s}}+z\right)}{H}}-1\right]\right\}\end{aligned}a$

当声源深度或接收深度位于海表界面时z=0或z_s=0及z=z_s=0,水平质点振速模态幅度函数的强度值S_r=0;当声源深度等于接收深度或声源深度与接收深度对称时z_s=z或z_s+z=H,模态幅度函数的强度值S_r=3N/8;当声源深度等于接收深度且位于半波导深度时z=z_s=H/2,模态幅度函数的强度值S_r=N/2;当接收深度与声源深度不在同一深度或对称深度时z≠z_s且z+z_s≠H,模态幅度函数的强度值S_r=N/4为参考强度.因此,通过分析声源与接收位于4种不同情况位置的水平质点振速模态幅度函数表明:在等声速波导环境下,当接收与声源同一深度时,其模态幅度函数的强度在声源深度和对称深度有N/8增强效应;声源位于波导中间深度时,同一深度接收信号具有N/4增强效应.

同理,可得出垂直质点振速的模态幅度函数正弦形式:

(27)$\begin{aligned}S_{z}= & \frac{1}{4}\left\{N-\frac{1}{2}\left[\frac{\sin \left[(2 N+1) \frac{\pi z_{\mathrm{s}}}{H}\right]}{\sin \frac{\pi z_{\mathrm{s}}}{H}}-1\right]+\right. \\& \frac{1}{2}\left[\frac{\sin \left[(2 N+1) \frac{\pi z}{H}\right]}{\sin \frac{\pi z}{H}}-1\right]- \\& \frac{1}{4}\left[\frac{\sin \left[(2 N+1) \frac{\pi\left(z_{\mathrm{s}}-z\right)}{H}\right]}{\sin \frac{\pi\left(z_{\mathrm{s}}-z\right)}{H}}-1\right]- \\& \left.\frac{1}{4}\left[\frac{\sin \left[(2 N+1) \frac{\pi\left(z_{\mathrm{s}}+z\right)}{H}\right]}{\sin \frac{\pi\left(z_{\mathrm{s}}+z\right)}{H}}-1\right]\right\}\end{aligned}$

利用式(27)可分析垂直质点振速场强度的深度分布情况.接收深度位于海表界面时z=0,垂直质点振速的模态幅度函数的强度值S_z=N/2;声源深度等于接收深度或声源深度与接收深度对称时z_s=z或z_s+z=H,模态幅度函数的强度值S_z=N/8;声源深度等于接收深度且位于半波导深度时z=z_s=H/2,模态幅度函数的强度值S_z=0;接收深度与声源深度不在同一深度或对称深度时z≠z_s且z+z_s≠H,参考强度S_z=N/4.因此,当接收与声源同一深度时,垂直质点振速的模态幅度函数的强度在声源深度和对称深度有N/8弱化效应;当声源位于波导中间深度时,同一深度接收信号强度减弱N/4,且在海表界面接收的垂直质点振速信号最强.

综上所述,将质点振速的模态幅度函数进行三角函数转化,可定性分析声源及接收在特定深度时的强度分布情况,由此揭示了质点振速在声源深度及对称深度显著特性的物理机理.

2 环境参数对质点振速场强度深度分布特性的影响

由前文可知,等声速波导环境下的质点振速强度在声源深度和对称深度具有显著特性,其中水平质点振速强度明显增强而垂直质点振速强度明显衰弱,且当研究质点振速场强度的深度分布特性时,仅需考虑质点振速的强度特征.因此,可通过计算水平质点振速和垂直质点振速的非相干强度差(ΔL_Inc= $L_{T v_{r}}^{I n c}$ - $L_{T v_{z}}^{I n c}$ ),进一步分析环境参数对质点振速在声源深度和对称深度的强度特性产生的影响.该物理量可同时表达出水平质点振速强度在特定深度明显增强而垂直质点振速减弱的深度分布特性,而且避免了信号声源级起伏所带来的误差.其非相干强度差可表示为

(28)ΔL(r, z)_Inc=-10lg

\frac{\int_{0}^{θ_{c}} (1 - W (z_{s}, z, θ)) e^{(- \frac{η r}{H} θ^{2})} c o s^{2} θ d θ}{\int_{0}^{θ_{c}} (1 - G (z_{s}, z, θ)) e^{(- \frac{η r}{H} θ^{2})} s i n^{2} θ d θ}

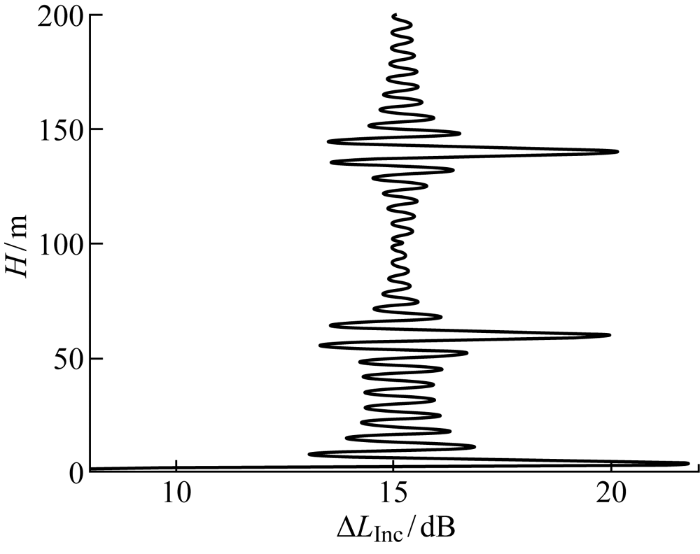
在海水深度为200 m,水中声速 1 500 m/s,海底声速 1 800 m/s的等声速波导环境下,声源深度60 m,频率200 Hz的质点振速强度差计算结果如图2所示.在声源深度和声源对称深度的强度差起伏高达5 dB,而图1(b)中的水平质点振速强度起伏为2 dB,且强度差的深度分布缓和了垂直质点振速在其他深度的振荡性.另一方面,利用非相干质点振速强度差进行质点振速场强度的深度分布特性研究,仅仅需要水平质点振速和垂直质点振速信号的非相干传播损失差值,避免了信号声源强度起伏所带来的误差.因此,可利用非相干质点振速强度差描述浅海质点振速场强度的深度分布特性,进一步分析水平距离、声源参数、声速剖面和海水深度等环境对质点振速深度分布特性的影响.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 等声速波导环境强度差的深度分布

Fig.2 Depth distribution of environmental intensity difference of isospeed waveguide

2.1 水平距离对深度分布特性的影响

针对流体层为均匀介质,下层为半无限软弹性海底的波导环境,分析水平距离对质点振速场强度的深度分布特性产生的影响.其中环境参数如表1所示.表中:横、纵波衰减分别为α_sλ和α_pλ,λ为波长;ρ为介质密度.

表1 仿真环境

Tab.1 Simulation environment

介质层	H/ m	c_p/ (m·s^-1)	c_s/ (m·s^-1)	ρ/ (g·cm^-3)	α_pλ/ dB	α_sλ/ dB
流体层	200	1 500	—	1.0	0.1	—
半无限软弹性海底	—	1 800	900	1.5	0.1	0.1

新窗口打开| 下载CSV

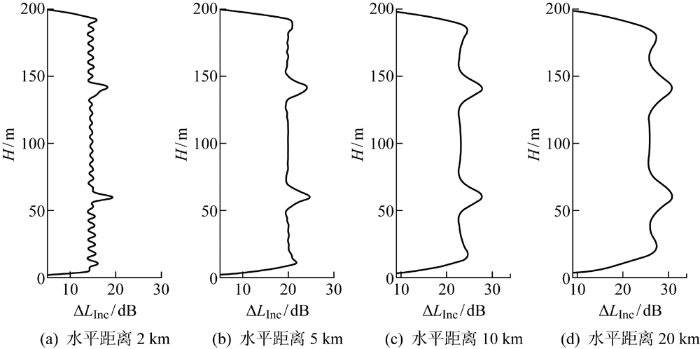
图3给出了上述波导环境下,频率为200 Hz,声源深度为60 m,水平距离为2、5、10和20 km的质点振速强度差的深度分布曲线.可以看到,质点振速强度差在声源深度和对称深度具有明显增强现象,且随着水平距离的增大,质点振速强度差明显增强的深度范围逐渐变宽.根据传播距离的远近,简正波的模态可分为传播模态与泄露模态,其中声源激发的低阶模态为主要传播模态,泄露模态主要为高阶模态.因此,在较远水平距离处,质点振速场强度差主要由低阶模态作用决定,使其深度分布幅值变化频率低, 质点振速强度差明显增强的深度范围逐渐变宽.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 强度差的深度分布

Fig.3 Depth distribution of strength difference

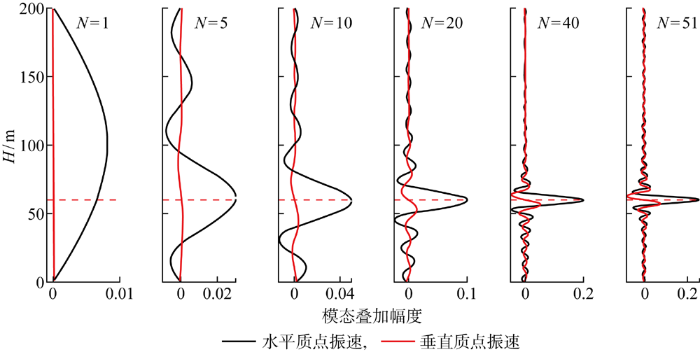
为此,利用水平质点振速与垂直质点振速的简正波的模态幅度函数 $\overset{N}{\sum_{n = 1}}$ ϕ_n(z_s)ϕ_n(z)和 $\overset{N}{\sum_{n = 1}}$ ϕ_n(z_s)ϕ'_n(z),分析质点振速场强度在声源深度显著特性的物理机理.该环境下声源共激发出51阶模态,图4给出了多阶模态叠加效果随深度的分布曲线,其中红色虚线为声源深度.当仅有1阶模态时,水平质点振速的模态叠加幅度峰值不在声源深度位置;随着模态叠加阶数增多,水平质点振速的模态叠加幅度峰值逐渐聚焦于声源深度,而垂直质点振速在声源深度没有明显幅度峰值.同时,由于高阶模态为泄露模态,传播过程中衰减快、对质点振速场强度的贡献较小,所以40阶模态与51阶模态叠加效果差异不大.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 模态叠加幅度效果

Fig.4 Amplitude effect of modal superposition

2.2 声源参数对深度分布特性的影响

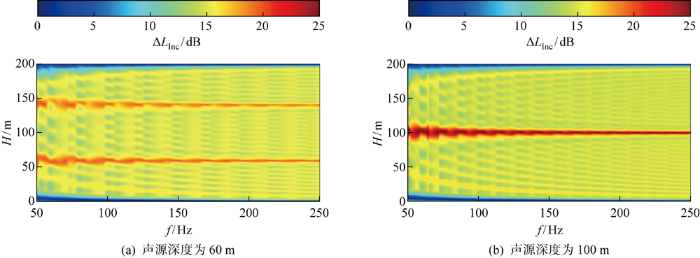
声源参数(声源深度、声源频率)直接决定声场能量的分布,为此有必要分析声源频率及声源深度对质点振速场强度差的深度分布特性产生的影响.在水平距离2 km处,计算50~250 Hz频带内,声源深度为60 m和100 m的质点振速强度差的深度-频率(f)分布情况,结果如图5所示.在均匀介质环境下,由于简正波模态的位移幅值在深度方向上近似关于H/2对称,非相干质点振速强度差在声源对称深度表现出声源深度的特性.如声源深度为60 m时,在对称声源深度140 m处产生相同的声场效应;而声源深度为100 m时,声源在相同的深度产生声场能量叠加.同时,随着频率的升高,点声源激发声场的简正波个数增多,由各阶模态叠加引起的声能深度分布会更加聚焦于声源深度,且同时考虑水平质点振速的叠加增强和垂直质点振速叠加减弱效应,将会使得质点振速强度差的峰值随着频率的升高更加聚焦于声源深度.如图5(a)、5(b)中质点振速场强度差在50~250 Hz频段内随频率的增大,质点振速强度差明显增强的深度范围随着频率的升高逐渐变窄.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 强度差的深度-频率域分布

Fig.5 Depth-frequency domain distribution map of intensity difference

2.3 声速剖面对深度分布特性的影响

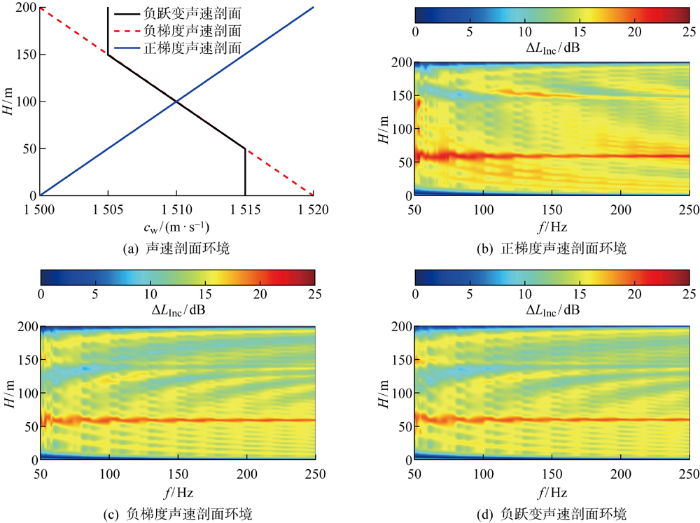
声速剖面环境及强度差的深度-频率域分布如图6所示.声速剖面对声场的分布具有重要影响,本节通过讨论如图6(a)所示的正梯度、负梯度及负跃变3种典型声速剖面对质点振速分布的影响,探究不同声速剖面环境质点振速场强度的深度分布特性.在水平距离2 km处,计算深度为60 m声源在3种声速剖面波导环境的非相干质点振速强度差深度-频率分布情况,结果如图6(b)~6(d)所示.正梯度、负梯度和负跃变声速剖面环境的非相干质点振速强度差仅在声源深度具有显著增强效果,而在对称深度处的非相干质点振速强度差有弱化现象.同时,声速剖面通过影响声能量向声速小的深度范围传输,进而影响了质点振速深度方向的分布特性,故该条件下声源所在深度区域的质点振速强度差值更大,正梯度声速剖面环境下的该区域的差值尤为显著.根据声传播理论分析:在非均匀介质环境中,声波激发的简正波模态幅度函数在深度方向并不对称,且各阶简正波叠加后的峰值均在声源深度位置,因此非相干质点振速强度差仅在声源深度具有显著增强.同时,声源位于声速较小深度时,其声线弯曲程度比声源位于声速较大深度发出的声线弯曲程度大,部分声线未到达界面就发生了反转,导致声能集中在声速小的深度区域,但声源深度位移幅值大的简正波量级也很大.因此声速剖面环境会改变质点振速强度差的空间分布,而声源深度处的质点振速强度差依旧具有强度最强的特性.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 声速剖面环境及强度差的深度-频率域分布

Fig.6 Depth-frequency domain distribution of acoustic speed profile environment and strength difference

2.4 海水深度对深度分布特性的影响

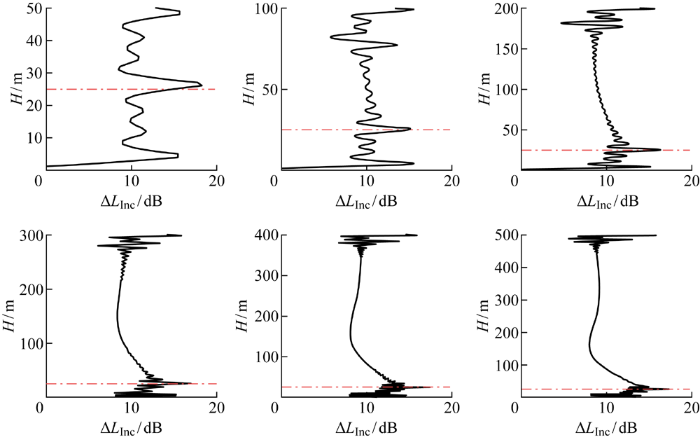
海水深度是影响声传播特性的重要参数之一,分析讨论海水深度对质点振速深度分布特性的影响,对理解质点振速强度的深度分布及其特性的普遍性具有重要意义.考虑在海水深度分别为50、100、200、300、400和500 m这6种深度环境的负梯度声速剖面波导环境下,计算声源频率为200 Hz,声源深度25 m,水平距离2 km处接收的非相干质点振速强度差深度分布曲线,结果如图7所示.图中黑色实线为强度差深度分布曲线,红色虚线为声源深度,在不同深度环境下,在海面海底界面处受海面海底边界不连续性影响较大,导致非相干质点振速强度差起伏比较剧烈,而声源深度的强度差总是呈现增强效应.在50 m和100 m海深环境存在1 m深度误差,其他海深环境的振幅峰值深度为声源深度.由简正波理论可知,在声源频率不变的前提下,水中波导简正波的个数将随着海水深度的增加而增多,且质点振速强度差的深度分布由声源激发的简正波个数决定.简正波叠加个数越多,质点振速强度差在声源深度越尖锐,而其他深度的强度分布随着深度的增加逐渐平滑.由此可认为,浅海海水深度对质点振速强度差峰值始终分布在声源深度这一特性的影响较小.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 不同海深环境强度差的深度分布

Fig.7 Depth distribution of environmental intensity difference at different depths

3 结论

本文基于简正波理论,将声压的非相干简正波模态和的角度积分形式扩展到了质点振速,得到了等声速波导环境下声矢量场振速传播损失与深度的关系,并以质点振速强度差作为研究对象,进一步分析了浅海环境参数对质点振速场强度深度分布特性产生的影响,得到如下结论:

(1) 由于简正波模态幅度函数的叠加效应,水平质点振速强度在声源深度具有明显增强效应,而垂直质点振速强度在该深度明显减弱,所以声源深度处的质点振速场强度差最大,且环境参数的改变会使这个差值有一定影响.质点振速场强度差在声源深度表现的特性,可为利用矢量传感器振速通道进行水下目标深度估计提供新思路.

(2) 随着水平距离的增大,质点振速强度差明显增强的深度范围逐渐变宽,而声源频率的升高使得峰值的深度范围逐渐聚焦于声源深度.同时,声速剖面通过影响声场能量的空间分布,导致非均匀介质环境在对称深度没有显著增强特性;而浅海海水深度对质点振速声源深度的分布特性影响不明显.因此,在海上水声探测实验设计时,应充分考虑环境参数对目标探测的影响.

研究过程中仅推导了浅海等声速波导环境下质点振速的角度积分公式,且只分析了浅海环境及相对低频质点振速场强度的深度分布特性,而实际海洋环境极其复杂,深入研究复杂海洋环境矢量场的深度分布特性非常必要.目前由于条件限制,本研究仅局限于仿真和理论工作,下一步的研究计划将利用海上实验对相关特性进行验证.同时,随着研究人员对深海超低频矢量特性的广泛关注,相关领域的深度分布特性仍需进一步研究.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

WESTON

D E

Acoustic flux formulas for range-dependent ocean ducts

[J]. The Journal of the Acoustical Society of America, 1980, 68(1): 269-281.