地铁车站深基坑开挖变形智能多步预测方法

doi:10.16183/j.cnki.jsjtu.2022.419

地铁车站深基坑开挖变形智能多步预测方法

刘俊城, 谭勇^,, 张生杰

同济大学地下建筑与工程系,上海 200092

Multi-Step Prediction of Excavation Deformation of Subway Station Based on Intelligent Algorithm

LIU Juncheng, TAN Yong^,, ZHANG Shengjie

Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China

通讯作者: 谭勇,教授,博士生导师;E-mail:tanyong21th@tongji.edu.cn.

责任编辑: 王一凡

收稿日期: 2022-10-24 修回日期: 2022-11-23 接受日期: 2022-12-1

基金资助:

国家自然科学基金(42177179)

Received: 2022-10-24 Revised: 2022-11-23 Accepted: 2022-12-1

作者简介 About authors

刘俊城(1997-),博士生,从事基坑工程变形预测、事故分析等方面的研究.

摘要

为更好预测深基坑开挖期间地下连续墙的侧向位移变形,基于长短期记忆神经网络(LSTM)智能算法理论构建了LSTM多步预测模型.首先对多步预测模型的多输出策略进行论述,其次详细介绍了LSTM多步预测模型的构建方法,并对模型输入集空间维度和时间维度两项超参数进行探究,以提高模型的预测准确度.最后依托某富水砂土深基坑工程实例,分析了模型预测值与实际监测值的差异.3个典型监测点的数据分析结果表明LSTM多步预测模型具有较强的泛化能力,相关算法对深基坑开挖变形预测方法的改进优化具有参考价值.

关键词： 基坑工程; 开挖变形预测; 长短期记忆神经网络智能算法; 多步预测模型

Abstract

To better predict the lateral displacements of diaphragm walls during deep excavation, a long short-term memory (LSTM) multi-step prediction model is developed in this paper based on the LSTM algorithm. First, the multi-output strategy of multi-step prediction model is discussed. Then, the construction method of the LSTM multi-step prediction model is introduced in detail, and the two hyperparameters, i.e., the space and time dimensions of the model input set, are explored to improve the prediction accuracy of the model. Finally, the errors between the predicted values and the field monitoring data are analyzed based on an excavation project buried in water-rich sandy strata. The analysis results of three typical monitoring points indicate that the LSTM prediction model is characterized by solid generalization ability, and the relevant algorithm is practically helpful for improving and optimizing deformation prediction methods of deep excavation.

Keywords： excavation; deformation prediction; long short-term memory (LSTM) intelligent algorithm; multi-step prediction model

PDF (2005KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘俊城, 谭勇, 张生杰. 地铁车站深基坑开挖变形智能多步预测方法[J]. 上海交通大学学报, 2024, 58(7): 1108-1117 doi:10.16183/j.cnki.jsjtu.2022.419

LIU Juncheng, TAN Yong, ZHANG Shengjie. Multi-Step Prediction of Excavation Deformation of Subway Station Based on Intelligent Algorithm[J]. Journal of Shanghai Jiaotong University, 2024, 58(7): 1108-1117 doi:10.16183/j.cnki.jsjtu.2022.419

随着我国城市建设和经济的快速发展,越来越多的城市开始进行大规模的地铁建设,城市地铁车站基坑工程不仅面临越来越深的挑战,周边环境也愈发复杂,基坑周边往往建(构)筑物密集.一旦发生基坑事故,不仅会影响工程进度,还可能造成人员伤亡和巨大经济损失.因此,保证基坑工程的施工安全至关重要.基坑和邻近建(构)筑物变形可以直观反映基坑本体和周边环境安全状态,对基坑开挖变形及邻近建(构)筑物变形做出可靠的预测,是施工安全的重要保证^[1⇓-3].

基坑开挖变形受到地质参数、施工方式等多种因素的综合影响,实际变形机制远比理论复杂,地质条件的复杂性也使得地层的土力学性质存在较大的变异性,因此准确预测开挖期间围护结构水平变形始终较为困难.传统基坑研究领域中,多采用有限元等方法建立数值模型对基坑变形进行分析,但由于这些方法存在一些局限,比如有限元模型中地层力学参数大多需进行一定简化,所采用的材料本构模型很多时候无法准确反映工程实践中材料的应力-应变关系,实际施工过程也往往比数值模型中所模拟的施工工况更为复杂,所以有限元模型在多数情况下难以完全真实反映基坑开挖变形状态.其次,数值计算结果通常对应于较长时间区间内或者笼统施工步骤下的变形数据,难以精准定位到每一天的基坑变形,因此无法准确得到未来几天的基坑变形数据,对工程实践中开挖变形控制的参考意义也相对有限.

近年来,随着计算机处理能力的显著提升,神经网络模型、智能算法等新技术得到快速发展,在土木工程领域也逐渐得到广泛应用.长短期记忆神经网络(Long Short-Term Memory,LSTM)最早由两位计算机科学家提出^[4],该智能算法对非线性数据和时间序列具有独特的优势,非常适合进行时间序列方面的数据预测,在变形预测上的表现优于传统反向传播(BP)神经网络等方法.众多因素对基坑变形的影响本质上都已体现在历史变形数据上,LSTM智能算法特有的记忆单元则能够考虑历史数据对当前的影响^[5],可通过学习基坑已有变形数据时间序列的内在规律,得出抽象的权重集和映射关系,适用于基坑开挖变形预测.

Xie等^[6]以中国西南地区陡坡为研究对象,建立LSTM动态预测模型,对陡坡发生的滑坡位移进行预测,结果表明,与传统的力学模型相比,LSTM预测模型具有更好的动态特征;Zhang等^[7]建立LSTM模型用于预测盾构机掘进引起的最大地表沉降和纵向沉降分布曲线,结果表明,LSTM模型较强的鲁棒性可适用于不同类型的地下工程;钱建固等^[8]建立LSTM组合预测模型,对基坑开挖诱发的地表沉降进行预测,发现当工况稳定时,LSTM模型的预测误差相对较小;赵华菁等^[9]以苏州某地铁基坑工程为背景,分别采用BP神经网络和LSTM智能算法建立预测模型,对地下连续墙侧向变形进行预测,并对模型预测稳定性进行验证,结果表明LSTM模型预测精度相较于传统神经网络模型更高.

但是,以上研究内容均基于LSTM单步预测模型,单步预测模型实际上每次仅输出一期数据,若要连续输出多期的预测值,需要向模型不断输入新的实际监测值进行滚动预测,最后再将多次预测结果进行汇总,因此对实际工程的参考价值相对有限.

针对单步预测模型单次输出一期预测值的局限性,本文进一步研究了单次输出多期预测值的方法,构建出LSTM多步预测模型,以期扩大LSTM模型的时间预测范围从而提高该模型的实践价值.建立的LSTM多步预测模型可基于基坑已有的变形监测数据,在当前工况下,预测基坑未来几天的开挖变形量,从而实现单次输出更长时间的基坑开挖变形预测结果,为实际工程提供有效指导.

1 多步预测策略

多步预测策略指的是LSTM模型实现一次预测输出多期预测值的策略,目前较为通用的多步预测策略有直接策略、递归策略和多输出策略.选择依据主要为策略合理性、建模实现难度、易用性和灵活性等.

直接策略具有理论简单但灵活性极差的特点,递归策略的建模难度极大,对模型构建者的建模水平要求较高.直接策略和递归策略本质上都属于单步预测的特殊情况,其存在的原因主要归结于一些较为传统的机器学习算法无法直接处理多输出的问题,所以只能采用直接策略或者递归策略间接地构建多步预测模型^[10].

理想情况下,真正的多步预测是模型一次预测便可以实现多输出的效果.LSTM作为近年来比较新的机器学习算法,可以调整模型输出值的维度不再为1,直接实现多输出功能^[11].因此本文选择多输出策略用于多步预测模型的构建,下面将对多输出策略进行详细介绍.

假设有表1所示的一段时间序列样本,需要预测未来3个时间步的数据,也就是第10、11、12步的数据.

表1 假设的时间序列样本

Tab.1 Hypothetical time series sample

时间步	数据
1	x₁
2	x₂
3	x₃
4	x₄
5	x₅
6	x₆
7	x₇
8	x₈
9	x₉

新窗口打开| 下载CSV

假设时间窗口大小为4,即用过去4个时间步的数据去预测未来3个时间步的数据,则对于多输出策略来说,需要构建出如表2所示有监督的数据关系.

表2 多输出策略

Tab.2 Multi-output strategy

数据样本	输入	输出
训练-1	[x₁x₂x₃x₄]	[x₅x₆x₇]
训练-2	[x₂x₃x₄x₅]	[x₆x₇x₈]
训练-3	[x₃x₄x₅x₆]	[x₇x₈x₉]
预测	[x₆x₇x₈x₉]	[ ${\hat{x}}_{10}$ ${\hat{x}}_{11}$ ${\hat{x}}_{12}$ ]

新窗口打开| 下载CSV

可见,多输出策略的原理并不复杂,建立模型时也仅需将模型输出值的维度进行调整即可,属于理论直白且操作难度较低的策略,易用性强.

多输出策略认为,表2中所输出的3个数据之间是互相独立、互不依赖的.该策略让所输出的多个时间步数据失去依赖性质归因于其输出结果并非严格意义上的数据值,而是一个向量.这种数据处理方式也会带来正反两方面的影响:一方面,时间序列中各时间步的数据确实存在一定的依赖、关联等,而多输出策略没有考虑多个输出数据值之间的关系;另一方面,通过忽略多个输出值之间的关联,一定程度上可以提高预测结果的精度,如果前一个时间步的预测值会影响到下一个时间步的预测值,那么可能会产生误差累积的问题,导致模型预测精度的下降.

综上,从实际应用的角度考虑,相较其他两种策略而言,多输出策略易用性强、建模逻辑清晰,是一种优秀的策略,非常适合用于本文中LSTM多步预测模型的构建.

2 LSTM多步预测模型构建

本文构建LSTM多步预测模型主要包括以下几个步骤.

(1) 模型框架建立.

本文所探究的LSTM多步预测模型基于TensorFlow.js框架构建.TensorFlow.js框架属于TensorFlow系列框架中的一种,由Google公司于2018年推出,提供了建模、模型训练与预测一整套完整的开发接口,其最大的特点是环境配置和数据操作上的易用性^[12].

(2) 数据样本处理.

由于原始数据通常无法直接用于模型训练,尤其是对于本文所分析的基坑工程变形数据,考虑到监测期间可能存在诸多因素对数据监测准确度进行干扰,所以需先对原始数据样本进行处理.数据样本处理包括数据预处理、数据归一化和数据转换划分3项工作.

数据预处理指的是剔除明显错误或重复的数据,再使用插值方法^[8]对缺失的数据进行补足,来尽量避免原始数据缺陷对后续模型训练的影响.数据归一化指的是将模型训练用到的数据样本统一为[0,1]区间内的无量纲数,以提高模型收敛速度.数据转换指的是将数据形式转换为具有监督关系的数据,有监督的数据指的是模型输入值和输出值之间具有已知确定关系.对于本文探讨的多步预测而言,有监督的数据关系即为表2所示的输入数据与输出数据之间的关系.

(3) 模型结构搭建.

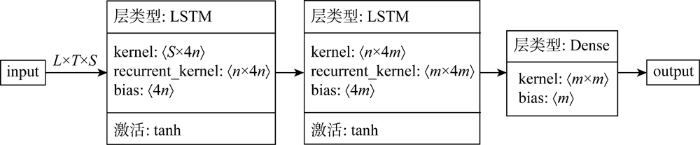
LSTM多步预测模型包括输入层、隐藏层、全连接层和输出层,使用的是TensorFlow.js框架提供的tf.sequential ()序贯方法堆叠出模型结构.本研究中,构建出的LSTM多步预测模型通用结构如图1所示.图中:L×T×S即为前述的输入数据样本的张量维度,L表示输入数据样本总数量,T表示每个数据样本的时间维度,S表示每个数据样本的空间维度.L会根据输入到模型中的训练样本数据个数生成,T和S需要手动赋值,具体取值会影响到模型最终的训练和预测效果.kernel、recurrent_kernel和bias为LSTM结构的3个关键参数,其中kernel和recurrent_kernel是两种权值矩阵,bias是偏置向量,3个参数后面的数值分别代表其维度大小.这3个参数的赋值包括两个过程:①模型训练前的初始化赋值;②训练过程中不断学习已有变形数据时间序列的内在规律来持续更新参数值,最终得到可用于基坑变形预测的最优权重集和映射关系.因此,

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 LSTM多步预测模型结构

Fig.1 Structure of LSTM multi-step prediction model

本模型对其进行初始化参数赋值时,将kernel按“VarianceScaling”进行设置,即初始化器能够根据权值的尺寸调整其规模;将recurrent_kernel按“Orthogonal”进行设置,即生成一个随机正交矩阵的初始化器;将bias按“Zeros”进行设置,即将张量初始值设为0.n为第1层LSTM结构的单元个数,n的取值也会对模型的训练和预测产生一定的影响;m为第2层LSTM结构的单元个数,同时也是模型一次输出的数据个数,即m为模型预测得到的未来变形的时间步长度.

(4) 模型训练.

在数据样本处理和模型结构搭建完成之后,便可开始进行模型训练.该工作的目的是生成最优的神经元权重集,学习数据样本输入-输出之间的关系.模型训练过程中,判断模型训练情况最主要的依据便是训练集损失Loss和验证集损失Val_loss.当训练集损失和验证集损失均不断减小时,则表明模型训练正常^[13].

(5) 模型预测结果评价.

对于单个预测值来说,本文所采用的误差评价指标是绝对误差ε_i.绝对误差存在正负,可以表示为下式:

(1)ε_i=

{\hat{y}}_{i}

-y_i

式中:ε_i为第i项的绝对误差; ${\hat{y}}_{i}$ 为第i项的预测值;y_i为第i项的真实值.

对于所有预测项来说,需要评价预测结果的整体准确性,本文采用两种评价指标:平均绝对误差和中位绝对误差.

平均绝对误差ε_MAE,指的是所有单项预测值与真实值的差值绝对值的均值.平均绝对误差将单项绝对误差进行绝对值处理,避免出现正负绝对误差相互抵消的问题,能真实反映预测结果的整体情况,可以表示为下式:

(2)ε_MAE(y,

\hat{y}

\frac{1}{N} \overset{n}{\sum_{i = 1}} |{\hat{y}}_{i} - y_{i}|

式中:N为预测值的数量.

中位绝对误差ε_MedAE,指的是所有单项预测值与真实值的差值绝对值的中值.通过综合中位绝对误差和平均绝对误差两项指标的结果,可以解决平均绝对误差受极大值、极小值影响较大的问题,从而更为全面地反映预测结果情况,可以表示为下式:

(3)ε_MedAE(y,

\hat{y}

)= median

(|{\hat{y}}_{1} - y_{1}|, \dots, |{\hat{y}}_{N} - y_{N}|)

3 LSTM多步预测模型超参数探究

模型的超参数指的是诸如模型隐藏层的单元个数、迭代次数、学习速率、输入集维度等需要人为设置的模型参数.超参数的取值对模型结构、模型训练以及模型最终预测结果都有着直接或间接的影响,因此设置合适的超参数是建立LSTM多步预测模型极其重要的工作.

对于LSTM多步预测模型而言,有一些超参数的取值通用性较强或现有取值经验较为成熟^{[14⇓⇓-17]},本文模型对这类超参数的取值具体如下:损失函数选择方根差函数MSE,模型优化器选择Adam算法,激活函数为tanh激活函数,批次大小设置为4,单元个数设置为32,学习速率α设置为0.001.

重点对输入集空间维度和时间维度两项超参数进行探究,其均与模型应用场景高度相关.对本研究而言,重点开展基坑开挖变形预测应用背景下的两项超参数取值优化工作.

用于超参数探究的数据样本来自江苏省南通市地铁1号线某地铁深基坑工程实例,该地铁车站位于富水砂性地层,为12 m岛式站台地下两层框架结构,车站底板埋深16.75 m,净长180 m,净宽19.3 m.基坑标准段采用明挖顺作法施工,800 mm厚地下连续墙作为围护结构,竖向设1道混凝土支撑(0.8 m×1 m)和3道钢支撑(⌀609 mm,圆环厚度 t=16 mm),标准段基坑开挖深度为16.95 m.为及时获取基坑施工期间围护结构变形情况,该项目选用YT-610F活动式垂直测斜仪对墙体水平变形进行监测,监测频率为1 次/d,即1天1期.该基坑平面示意图及本文后续研究中涉及到的关键监测点CX14、CX17、CX19的位置如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 基坑平面布置

Fig.2 Plan layout of the excavation site

超参数探究部分所使用的数据样本来自CX14测点,该测点开挖期共有74期变形监测数据,将已有的变形数据输入LSTM多步预测模型进行训练,模型预测及验证的目标是基坑开挖期内CX14测点最后5期的墙体水平变形值.对基坑围护结构侧向变形量进行控制时,通常以最大墙体水平变形值作为控制基准.此外,既有研究^[18-19]也表明多支撑深基坑围护结构最大水平变形值所在深度通常位于开挖面附近.因此,尽管本研究仅对测斜点的最大水平变形值进行预测分析,但也能反映出围护结构整体变形情况及基坑安全状态.

3.1 输入集空间维度

多步预测输入的是一个维度为(L, T, S)的三维数组.其中S为每个数据样本的空间维度,也就是数据窗口的大小,可以理解成最里层的向量长度,取值需满足一个大于等于1的整数.作为直接影响输入集结构的超参数之一,空间维度的取值直接影响到了第1层LSTM的结构维度,对模型训练及最终预测的结果均有直接影响.针对输入集空间维度的探究共设置了6组对比试验,如表3所示.

表3 不同空间维度下关键超参数设置情况

Tab.3 Settings of key hyperparameter in different space dimensions

试验编号	S	T	n	α
1-a	1	5	32	0.001
1-b	2	5	32	0.001
1-c	3	5	32	0.001
1-d	4	5	32	0.001
1-e	5	5	32	0.001
1-f	6	5	32	0.001

新窗口打开| 下载CSV

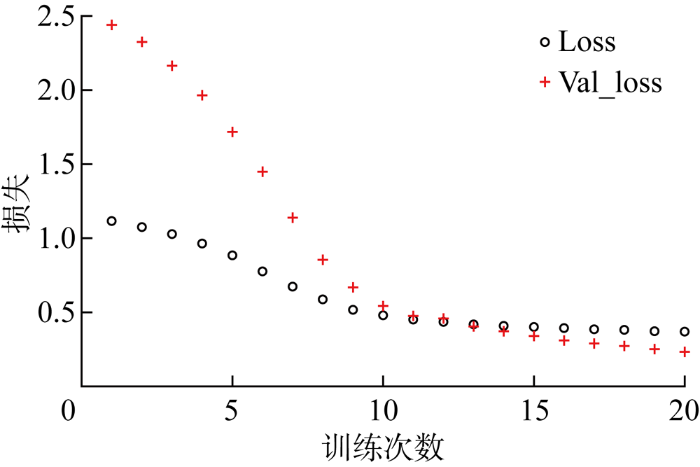
在训练次数(epoch)为20的情况下,当验证集损失和训练集损失均达到最小值附近时停止模型训练.在不同空间维度条件下,6组试验的收敛过程基本一致,具体可参考图3.模型整体训练过程均表现较为平滑,说明模型的输入集空间维度不会对模型训练过程造成明显影响.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 模型训练时的损失值变化(空间维度)

Fig.3 Loss change during model training (space dimension)

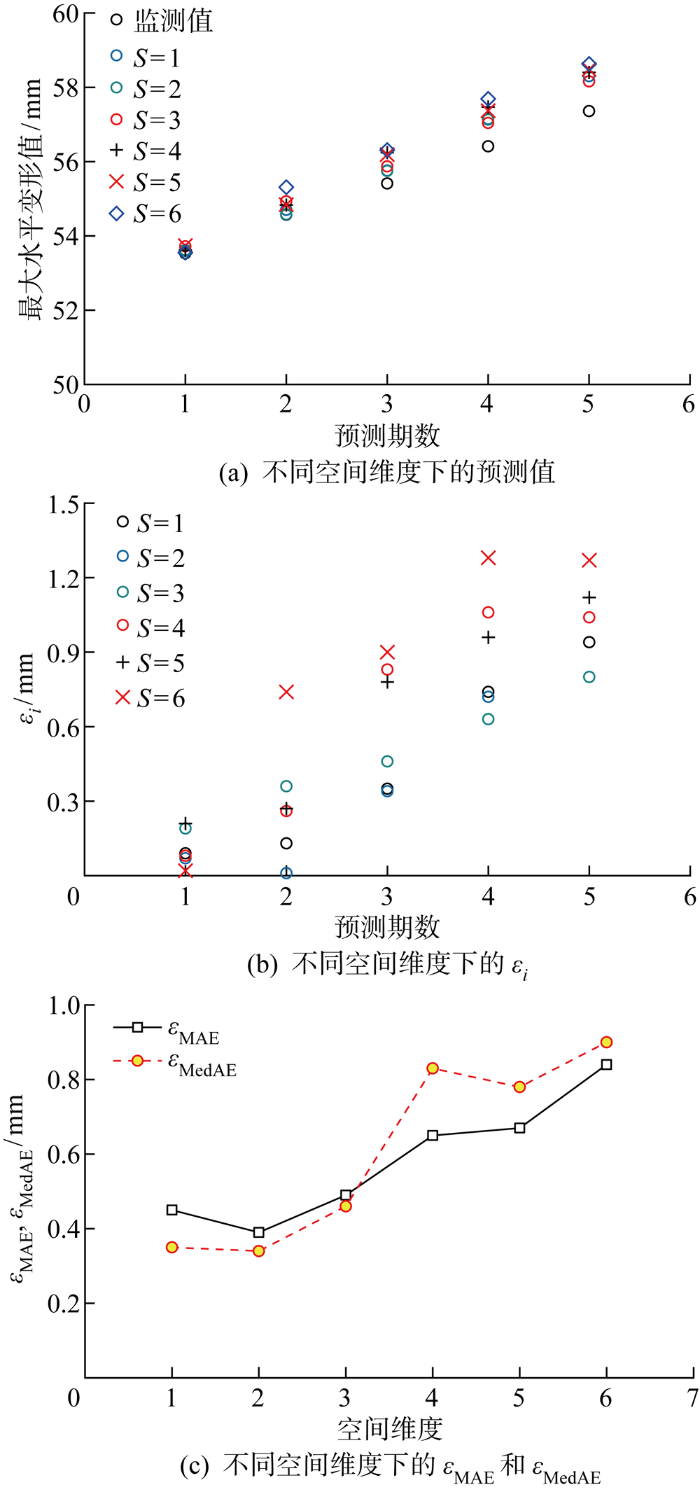
需要说明的是,模型训练表现接近并不能代表最终预测结果同样接近,这两者之间并无绝对关联.在本次探究中,6种空间维度下的模型预测结果如图4所示.可见,当空间维度为1、2、3时,模型得到的预测值较为接近,没有明显的预测差距并且预测结果和监测值较为接近;而随着空间维度逐渐增大,模型预测值和实际监测值的误差也随之增大.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同空间维度下的预测效果对比

Fig.4 Comparison of predictions in different space dimensions

由图4(c)可知,在不同空间维度下模型预测结果的ε_MAE和ε_MedAE存在一定变化规律:当空间维度为1或2时,ε_MAE和ε_MedAE是十分接近的,波动较小;而随着空间维度进一步增大,ε_MAE和ε_MedAE也明显增大.

结合模型原理和数据样本情况可知,由于基坑开挖期较短,所以模型训练中可用的数据样本量相对较小,当样本的特征量过多,即空间维度较大时,模型学习较多特征的能力不足.数据样本量和样本的特征量匹配度不佳,较小的数据样本不足以拟合出包含较多特征自变量的合理映射关系,因此导致模型最终应用时预测效果并不理想.而当数据量不是特别大时,空间维度设置较小可使得样本的特征数量相对较少,模型就能在少量数据条件下充分学习已知的特征,得到既简单又更为合理的映射关系,从而在应用时取得更好的预测效果.综上,当空间维度较小时,模型预测效果相对更好,可认为本模型输入集空间维度取2时的预测效果较为理想.

3.2 输入集时间维度

输入数据样本的维度(L, T, S)中,T表示时间维度,即每个数据样本内要包含T个向量,数据样本每次前进T个时间步,时间维度取值需满足一个不小于1的整数.针对输入集时间维度,共设置6组对比试验,如表4所示.

表4 不同时间维度下关键超参数设置情况

Tab.4 Settings of key hyperparameter in different time dimensions

试验编号	S	T	n	α
2-a	2	2	32	0.001
2-b	2	3	32	0.001
2-c	2	4	32	0.001
2-d	2	5	32	0.001
2-e	2	6	32	0.001
2-f	2	7	32	0.001

新窗口打开| 下载CSV

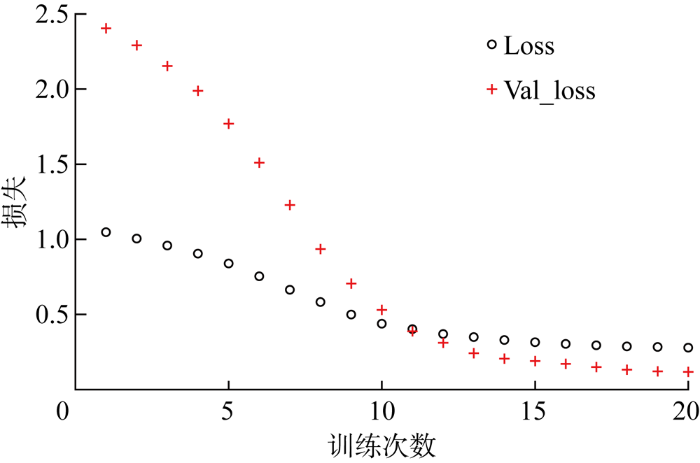
在epoch为20 次的情况下,当验证集损失和训练集损失均达到最小值附近时停止模型训练.与不同空间维度条件下的训练表现相似,在不同时间维度下,6组对比试验的收敛过程基本一致,如图5所示,这表明模型的输入集时间维度对模型训练过程同样不会有明显影响.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 模型训练时的损失值变化(时间维度)

Fig.5 Loss change during model training (time dimension)

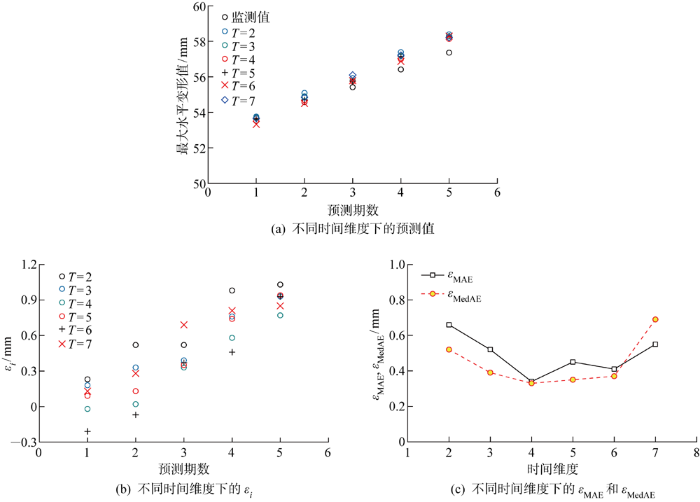
6种时间维度下的模型预测结果如图6所示.可见,时间维度从2增加到4时,预测误差逐渐变小;时间维度从4增加到7时,预测误差则逐渐变大.这种预测结果差异主要是由数据样本与超参数之间的匹配关系决定的,基坑开挖期内总的原始监测数据量基本是固定或者相差不大的,时间维度是转换这些原始数据的关键超参数之一,将原始数据转换成三维的张量用于模型训练.时间维度控制的是单个张量的时间步长度,如果时间长度过短,模型则无法充分学习出时间序列的关系;如果时间长度过长,总的张量个数则会变少,模型的学习能力同样会受到影响.因此,有必要找出较为适中的时间维度值,以期平衡单个张量内时间序列的长度与总的张量个数之间的关系,使得模型能够充分利用已有的训练数据,实现更好的预测效果.综上,在基坑开挖变形预测的模型应用背景下,可认为输入集时间维度取4时,模型预测效果较好.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同时间维度下的预测效果对比

Fig.6 Comparison of predictions in different time dimensions

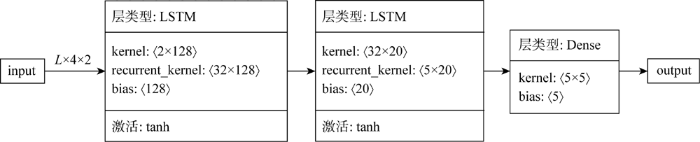
通过对输入集空间维度和时间维度两项超参数的最优值探究,本文解决了LSTM多步预测模型的关键超参数设置问题,得到了可用于基坑开挖变形预测的完整LSTM多步预测模型,模型超参数设置如图7所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 LSTM多步预测模型结构的超参数设置

Fig.7 Hyperparameter settings of LSTM multi-step prediction model

4 LSTM多步预测模型泛化能力验证

在上一章节中,模型训练的数据样本使用的是图2所示CX14测点基坑开挖期共74期的监测数据,模型预测及后续验证的目标是基坑开挖期内CX14测点最后5期的墙体最大水平变形.考虑到基坑开挖期间尺寸效应的显著影响,同一基坑不同位置的墙体侧向位移规律存在差异.为充分验证LSTM多步预测模型的稳定性与通用性,同时证明该模型具有较强的泛化能力,除上述位于基坑标准段跨中的CX14测点外,下文还将对该基坑开挖至一定深度时位于基坑标准段边缘的CX17测点及基坑端头井的CX19测点未来5期地下连续墙最大水平变形进行预测,两测点位置分布如图2所示.预测所基于的数据样本是对应测点过去时间内已有的变形监测数据.

4.1 CX17测点未来5期的最大水平变形预测

CX17测点位于该基坑标准段边缘,该段基坑处于正常开挖状态且后续施工继续保持当前工况,已有监测数据81期(前76期作为数据样本),监测频率为1 次/d.通过本文构建的LSTM多步预测模型,对该测点未来5期的最大水平变形进行预测,然后与实测值进行对比.

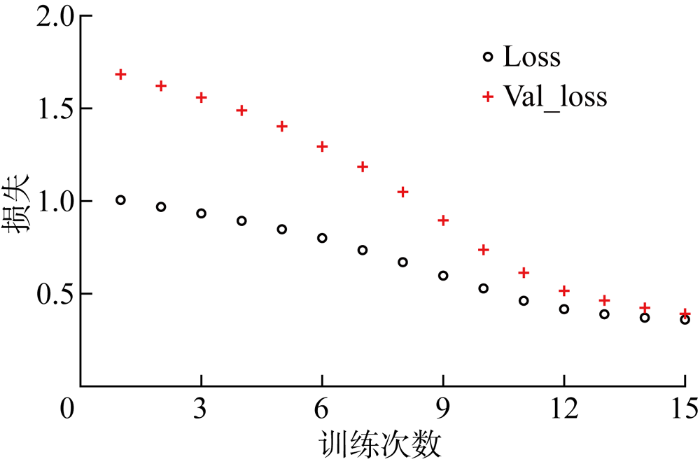
将已有的76期监测数据输入到LSTM多步预测模型中进行训练,训练过程中训练集和验证集的损失值变化情况如图8所示.可见,模型训练进行顺利,进行10 次完整的训练便可实现较好的收敛,即10个epoch.随着每个epoch的进行,训练集损失和验证集损失平稳下滑,最终两者均降至最小值附近.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 模型训练时的损失值变化(CX17测点)

Fig.8 Loss change during model training (point CX17)

模型预测结果如图9所示,其中图9(a)为预测的5期最大水平变形值与实际监测值的对比结果,图9(b)则为预测值的绝对误差结果,可见预测值与监测值非常接近.受累计误差影响,前4期预测结果的绝对误差逐渐增加,但该误差值仍不超过 0.2 mm;对于第5期预测结果而言,实际变形值较之前增幅较小,而预测值绝对误差却出现较大幅度增长,但该误差值也仅0.6 mm左右,这样的误差水平在实际工程中是允许的.综上,5期预测值的平均绝对误差为0.19 mm,中位绝对误差为0.09 mm.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 CX17测点预测结果

Fig.9 Prediction results at CX17

4.2 CX19测点未来5期的最大水平变形预测

CX19测点位于该基坑端头井,该基坑段同样处于正常开挖状态且后续施工继续保持当前工况,已有监测数据52期(前47期作为数据样本),监测频率为1 次/d.相较于CX17测点而言,该测点的原始数据相对较少.将已有的47期监测数据同样输入到LSTM多步预测模型中进行训练,训练期间训练集和验证集的损失值变化情况如图10所示.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 模型训练时的损失值变化(CX19测点)

Fig.10 Loss change during model training (point CX19)

可见模型训练正常,仅进行15 次完整的训练便可实现较好的收敛,即15个epoch.随着每个epoch的进行,训练集损失和验证集损失平稳下滑,最终两者均降至最小值附近.模型预测结果如图11所示,其中图11(a)为预测的5期最大水平变形值与实际监测值的具体对比结果,图11(b)为预测值的绝对误差结果.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 CX19测点预测结果

Fig.11 Prediction results at CX19

可见,预测值与实际监测值非常接近.对于这5期预测值而言,绝对误差值并未逐渐增大,而是始终在波动,这主要归因于CX19的最大水平变形监测数据在整个开挖期内始终存在增速上的波动.模型学习到了该特点,并在预测值增速变化上体现出了波动行为,因此预测值的绝对误差存在很大波动.此外,变形增速的波动消除了线性增长中累计误差的不利影响,绝对误差值始终较小,最大绝对误差仅0.5 mm左右,该误差水平在实际工程中是允许的.综上,5期预测值的平均绝对误差为 0.18 mm,中位绝对误差为0.12 mm.

综合上述两组工程实例验证来看,CX17测点未来5期预测值的平均绝对误差是0.19 mm,中位绝对误差是0.09 mm,最大绝对误差是0.61 mm;CX19测点未来5期预测值的平均绝对误差是0.18 mm,中位绝对误差是0.12 mm,最大绝对误差是0.46 mm.可见,即使对同一基坑不同位置的地下连续墙最大水平变形进行预测,预测结果的误差指标仍非常接近,且均处于可被实际工程接受的误差范围内.这表明LSTM多步预测模型精度较高,稳定性、通用性较好,模型泛化能力强,实际验证效果好.

5 结论

(1) 为实现基坑开挖变形的多期预测,本文基于LSTM智能算法理论,结合多输出策略,构建了LSTM多步预测模型,并对模型构建方法进行了较为详细的论述.

(2) 以江苏省南通市某富水砂土地铁基坑工程为实例,基于变形监测数据,对模型输入集空间维度和时间维度这两项与模型应用场景高度相关的超参数进行优化分析,得到最适用于基坑开挖变形预测的超参数,有效提高了LSTM多步预测模型的精度.

(3) 进一步的工程实例验证表明,LSTM多步预测模型可对基坑不同位置开挖变形进行准确预测,预测效果稳定可靠,泛化能力极强,模型可基于已有监测数据进行预测得到未来一段时间的开挖变形值,这对实际施工具有较强参考价值.

(4) 本文研究内容和结论适用于较规范施工条件下的基坑开挖变形预测.当实际施工存在部分流程不规范时,可能会诱发相关风险,从而导致本文提出的LSTM多步预测模型的适用性和准确性受到影响.鉴于基坑施工的不确定性,使用该模型对开挖变形进行预测还需更多实践的优化和改进.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

ZHENG

, YANG

, ZHOU

, et al.

A simplified prediction method for evaluating tunnel displacement induced by laterally adjacent excavations

[J]. Computers and Geotechnics, 2018, 95: 119-128.

[本文引用: 2]

[2]

ZHENG

, DU

, CHENG

, et al.

Characteristics and prediction methods for tunnel deformations induced by excavations

[J]. Geomechanics and Engineering, 2017, 12(3): 361-397.