上海交通大学学报

上海交通大学学报, 2024, 58(7): 1036-1046 doi: 10.16183/j.cnki.jsjtu.2023.023

船舶海洋与建筑工程

不同水力集矿模型的矿粒采集及环境扰动特性数值研究

李雨瑶1,2, 赵国成,1,2, 肖龙飞1,2

1.上海交通大学 海洋工程国家重点实验室,上海 200240

2.上海交通大学三亚崖州湾深海科技研究院,海南 三亚 572024

Numerical Study on Collection and Environmental Disturbance Characteristics of Different Nodule Collecting Models

LI Yuyao1,2, ZHAO Guocheng,1,2, XIAO Longfei1,2

1. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. SJTU Yazhou Bay Institute of Deepsea SCI-TECH, Sanya 572024, Hainan, China

通讯作者: 赵国成,助理研究员,电话(Tel.): 021-34207184;E-mail:guocheng.zhao@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-01-19   修回日期: 2023-03-22   接受日期: 2023-04-6  

基金资助: 上海市科技创新行动计划启明星项目(扬帆专项)(23YF1419800)

Received: 2023-01-19   Revised: 2023-03-22   Accepted: 2023-04-6  

作者简介 About authors

李雨瑶(2002-),本科生,从事深海水力集矿研究.

摘要

实现高效、低扰动海底集矿是深海多金属结核矿产资源开发面临的关键技术挑战.海底矿粒采集过程的力学行为十分复杂,是一个涉及三维紊动流动、离散粗颗粒运动与细颗粒土体破坏的流固土多物理场耦合过程.针对吸扬式、附壁射流式、射流冲采式3种主流的深海水力集矿方法,基于K-Epsilon两层模型和离散元模型分别模拟集矿液相湍流和固相矿粒,进行矿粒采集性能和环境扰动的数值模拟研究,分析集矿流量qm和集矿头拖曳速度v对矿粒采集率η、集矿流场湍动能k和海水-沉积物混合物体积分数φ的影响,探究集矿流场中流速、压力和矿粒的分布特征.结果表明:在相同qm和v下,射流冲采式模型获得的η最大,吸扬式模型获得的η最小;射流冲采式模型对近底流场扰动程度最大,深海沉积物扩散现象也最为明显,而吸扬式和附壁射流式模型造成的环境扰动程度较小,更有利于环保要求;附壁射流式模型的η对qm和v最不敏感,且该集矿模型可以较好地兼顾高效矿粒采集和低环境扰动.研究结果可为揭示集矿机理和设计研发高效低扰动集矿装置提供科学依据.

关键词： 深海采矿; 多金属结核; 流固土多场耦合; 矿粒采集效率; 环境扰动

Abstract

It is a significant technical challenge to exploit deep-sea polymetallic nodules with high efficiency and low disturbance. The mechanical behavior of seabed nodule collecting is very complicated, which is a multi-physical coupling process involving three-dimensional turbulent flow, discrete particle movement, and fine particle soil failure. In this paper, three main deep-sea hydraulic nodule collecting methods, i.e., the suck-up-based method, the Coandă-effect-based method, and the double-jet hydraulic method, are investigated by numerical simulation on the performance of nodule collecting and environmental disturbance. The realizable K-Epsilon two-layer model and the discrete element method are used to simulate the turbulent flow of the liquid phase and nodule particles in the solid phase respectively. The effect of collection flow qm and drag velocity v on collection rate η, turbulent kinetic energy k, and volume fraction φ of the seawater-sediment mixture in the collecting flow field is analyzed. The flow velocity, pressure, and nodule distribution are explored. The results indicate that, at the same qm and v, the double-jet hydraulic model will achieve the largest η, while the suck-up-based model will achieve the least η. The double-jet hydraulic model has the most significant disturbance to the near-bottom flow field and the most obvious sediment spreading phenomenon. In contrast, the suck-up-based model and the Coandăeffect-based model have less environmental disturbance, which is more conducive to the requirements of environmental protection. The Coandă-effect-based model shows minor sensitivity to qm and v and a good balance between high nodule collecting efficiency and low environmental disturbance. This paper will provide a scie.pngic basis for revealing the nodule collecting mechanism and designing and developing a nodule collecting device.

Keywords： deep-sea mining; polymetallic nodules; multi-field coupling of fluid-solid-soil; nodule collection efficiency; environmental disturbance

PDF (6683KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

李雨瑶, 赵国成, 肖龙飞. 不同水力集矿模型的矿粒采集及环境扰动特性数值研究[J]. 上海交通大学学报, 2024, 58(7): 1036-1046 doi:10.16183/j.cnki.jsjtu.2023.023

LI Yuyao, ZHAO Guocheng, XIAO Longfei. Numerical Study on Collection and Environmental Disturbance Characteristics of Different Nodule Collecting Models[J]. Journal of Shanghai Jiaotong University, 2024, 58(7): 1036-1046 doi:10.16183/j.cnki.jsjtu.2023.023

深海多金属结核是分布最广、储量最大的海底矿产资源,富含锰、镍、铜、钴等新能源和国防工业亟需的金属元素[1],被认为是21世纪陆地矿产未来重要的接替资源.多金属结核多以半埋状颗粒的形式广泛赋存于深海表层沉积物中[2],开采难度大.当今主流的深海水力集矿方式主要包括吸扬式、附壁射流式和射流冲采式,如何实现技术经济性和环保性[3]是目前深海矿产商业化开采面临的最严峻挑战.

为具体分析各种集矿原理的作业性能,国内外学者开展了多项研究.对于吸扬式集矿原理,夏建新等[4]通过管流中粗颗粒浓度分布的粒子图像测速(PIV)试验研究,分析了颗粒垂向最大浓度点出现的相对高度与水流平均流速、颗粒粒径、管径等参数间的关系;赵国成等[5]通过圆球矿粒在圆管抽吸流场中受力特性的试验研究,发现集矿头离底高度与矿粒直径比、集矿头与矿粒底部端点之间的偏转角度、集矿头拖曳速度等参数会对矿粒受力特性产生显著影响;Xiong等[6]使用流体动力学-离散元(CFD-DEM)耦合数值方法研究了不同直径的球形颗粒在垂直管道内的漂浮运动及流场变化,揭示了颗粒尺寸与圆管内颗粒漂浮速度间的关系.对于附壁射流式集矿原理,Lim等[7]采用CFD方法分析了其作业过程中的流线分布和湍流动能变化,发现集矿流场特性易受到流量和颗粒行为的影响;Cho等[8]通过在室内水槽清水环境中开展集矿头机构静态实验和动态实验,研究了射流喷嘴尺寸、集矿头曲率半径、离底高度和射流流量对颗粒采集率的影响.对于射流冲采式集矿原理,Yang等[9]研究了射流挡板的形状、尺寸等主要参数对采集效果和功耗的影响;Hong等[10]通过水力集矿性能实验,在不同射流流量、集矿头移动速度和离底高度工况下,分析了不同参数对矿粒采集率的影响,发现集矿头的几何外形和底部压力分布是影响采集率的关键因素;黎蔚杰等[11]通过数值方法模拟了水流作用下的海床局部冲刷过程,研究了不同水流参数和海床参数下的冲刷深度;Chen等[12]通过开展不同海底岩土特性中的冲刷试验,分析了水力冲刷的机理和海底岩土特性参数对冲刷深度的影响.总的来说,尽管针对3种主流水力集矿方式的研究日益深入,但已有成果大多只针对其中一种方式进行数值模拟或实验分析,鲜有学者针对3种不同水力集矿方式开展综合、定量的对比研究.

针对现有研究的不足,以及国际海底管理局(ISA)提出的在深海采矿技术的选取上需要执行最佳可得技术(the Best Available Technology,BAT)原则[13],本文基于前人海试集矿样机的几何形状分别建立了吸扬式、附壁射流式、射流冲采式集矿模型,采用数值模拟方法研究了3种模型的采集性能和环境扰动程度,旨在定量对比分析3种不同水力集矿原理的集矿特性,揭示不同集矿模型的工作原理,为未来深海水力集矿装备的设计研发提供参考.

1 数值模拟方法

本研究使用的数值模拟软件为STAR-CCM+12.02,采用可实现的K-Epsilon两层模型(RKE 2L)模拟集矿液相湍流,采用离散元(DEM)模型模拟矿粒.

1.1 液相湍流模型

在水力集矿物理模型中,集矿头和深海底质共同组成了复杂的几何固体壁面,集矿流场可看作是复杂壁面下的湍流问题.RKE 2L模型是可实现的K-Epsilon模型与两层方法的结合[14],其系数与K-Epsilon 模型的系数相同,但RKE 2L模型能更加灵活地解决复杂壁面的问题.模型中动能k和湍流耗散率ε的输运方程分别为

∂∂t(ρk)+Δ·(ρ kv-)=Δ· μ+μtσkΔk+ Pk-ρ(ε-ε0)+Sk
∂∂t(ρε)+Δ(ρ kv-)=Δ· μ+μtσεΔε+ 1TεCε1Pε-Cε2f2ρ εTε-ε0T0+Sε

湍流黏度μt表达式为

μt=λμt|k-ε+(1-λ)μμtμ2L

式中:ρ为流体密度;v-为流体质点平均速度;μ为流体动力黏度;Cε1=maxξ5+ξ, 0.43,ξ=Skε,S=12(Δ·v-+Δ·v-T);Cε2=1.9;f2=kk+με/ρ;σε=1.2;σk=1;Tε=kε为大涡时间尺度;T0=maxk0ε0,v-ε0,ε0为初始湍流耗散率,k0为初始湍动能;Pk和Pε为K-Epsilon模型相关项;Sk和Sε是用户定义项;λ与雷诺数Re相关.

1.2 颗粒仿真模型

在水力集矿物理模型中,赋存于深海底质上的矿粒可看作是离散粗颗粒.DEM将离散体看作有限个离散单元的组合,根据每一时步各颗粒间的相互作用和牛顿运动定律的交替迭代预测散体群的行为,DEM与计算流体力学结合模型(DEM-CFD)的模拟结果与实际试验的结果吻合度较高,能够对离散粗颗粒流相关的工程问题做出较为合理的解释[15].该模型中,离散颗粒由于具有方向性,需同时满足动量守恒和角动量守恒方程为

msdvsdt=msg+Ffs+Fct
Isdωsdt=Mfs+Mct

式中:ms为颗粒质量;vs为颗粒速度;g为重力加速度;Ffs为流体对颗粒的作用力;Fct为颗粒间的相互作用力;Is为颗粒转动惯量;ωs为颗粒角速度;Mfs是流体作用于颗粒的阻力矩;Mct是颗粒间相互作用产生的力矩.

2 水力集矿数值模拟

2.1 水力集矿模型

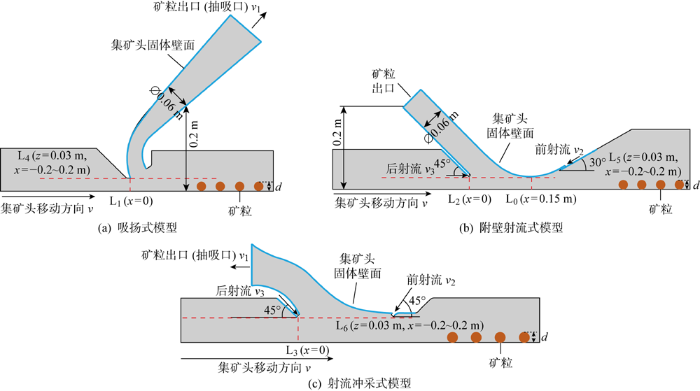
吸扬式、附壁射流式和射流冲采式模型的设计分别依据1978年OMA海试中使用的样机形状[16]、2018年GSR环评报告中的几何参数[8]和1999年韩国KRISO测试中的样机参数[17].3种模型的主视图(xOz平面)如图1所示.图中:v为集矿头拖曳速度; v1为抽吸流速度; v2为前射流速度;v3为后射流速度;d为矿粒直径;L0~L6为模型监测线.统一将集矿头喷嘴的横截面形状设为矩形,集矿头后口处设为x=0,模型对称平面设为y=0,颗粒接触的底部平面设为z=0.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   3种水力集矿模型剖面图

Fig.1   Profile of three hydraulic nodule collecting models


深海表层沉积物颗粒粒径较小,易与海水充分混合,且其含水率较高、抗剪切强度较低,因此为简化问题,将矿粒模型设为表面光滑、直径为0.02 m的球体,清水环境底部设为光滑平面,海底表层沉积物设为具有恒定密度的可溶于水的液体,忽略矿粒和沉积物之间的黏性作用.数值计算中的主要参数如表1所示,其中矿粒丰度An为单位面积上的矿粒数量.

表1   数值模拟中的主要参数

Tab.1  Main parameters in numerical simulation

参数取值
ρ/(kg·m-3)1 025
μ/(Pa·s)1.08×10-3
沉积物-海水混合物密度,ρm/(kg·m-3)1 400
d/mm20
矿粒密度,ρn/(kg·m-3)2 100
An/(kg·m-2)5.864
集矿头离底高度,h/m0.03
集矿范围宽度,w/m0.3

新窗口打开| 下载CSV


2.2 计算域和边界条件

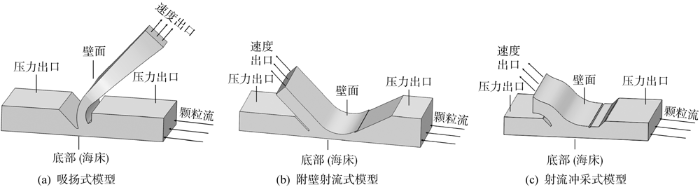
数值模拟中3种模型的计算域和边界条件如图2所示.为更好地体现流场状态,将集矿头固定,底部设置为以速度v匀速运动的无滑移壁面,以此模拟集矿头在海底的拖曳过程.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   数值模拟中的计算域和边界条件

Fig.2   Computational domain and boundary conditions in numerical simulation


2.3 网格收敛性分析

对网格分辨率和时间步长进行收敛性分析,确定最合适的网格和时间步长组合,结果如表2所示.以集矿头稳定作业后输矿管出口的平均矿粒质量流量qmn作为判定依据,当相邻网格数或时间步长的计算结果差异小于0.7%时认为算例已经收敛.最终确定吸扬式集矿模型的网格数为2 082 416、时间步长为0.04 s,附壁射流式集矿模型的网格数为2 238 371、时间步长为0.04 s,射流冲采式集矿模型的网格数为1 847 882、时间步长为0.04 s.

表2   3种模型的网格和时间步长收敛性分析

Tab.2  Mesh and time step convergence analysis of three models

集矿模型分析参数网格数时间
步长/s		qmn/
(kg·s-1)
吸扬式网格收敛性分析1 216 8920.050.171 008
1 375 0340.050.174 044
1 561 1690.050.177 083
2 082 4160.050.180 143
2 837 5730.050.181 357
时间步长收敛性分析2 082 4160.060.177 987
2 082 4160.050.180 143
2 082 4160.040.181 370
2 082 4160.030.181 452
2 082 4160.020.181 604
附壁射流式网格收敛性分析1 582 6510.050.176 716
1 906 0520.050.179 113
2 238 3710.050.180 306
2 376 2120.050.180 706
2 526 4080.050.181 037
2 777 7460.050.181 384
时间步长收敛性分析2 238 3710.060.178 097
2 238 3710.050.180 306
2 238 3710.040.181 666
2 238 3710.030.182 000
2 238 3710.020.182 149
射流冲采式网格收敛性分析253 1430.050.166 392
582 2050.050.177 978
1 114 1080.050.183 515
1 847 8820.050.184 726
时间步长收敛性分析1 847 8820.060.183 722
1 847 8820.050.184 263
1 847 8820.040.184 726
1 847 8820.030.184 982

新窗口打开| 下载CSV


2.4 数值模型的实验验证

将数值计算的速度分布结果与Hu等[18]使用PIV技术得到的实验结果进行比较,从而验证基于RKE 2L湍流模型预报集矿流场流速分布的准确性.以附壁射流式模型为例,在集矿流量qm=34.9 t/h时,图1(b)中监测线L0上取16个监测点,其流体质点的平均速度v-与PIV实验结果对比如图3所示.可以发现数值结果与实验结果吻合度高,证明了基于RKE 2L湍流模型可以准确地预报集矿流场中的流速分布.

图3

新窗口打开| 下载原图ZIP| 生成PPT

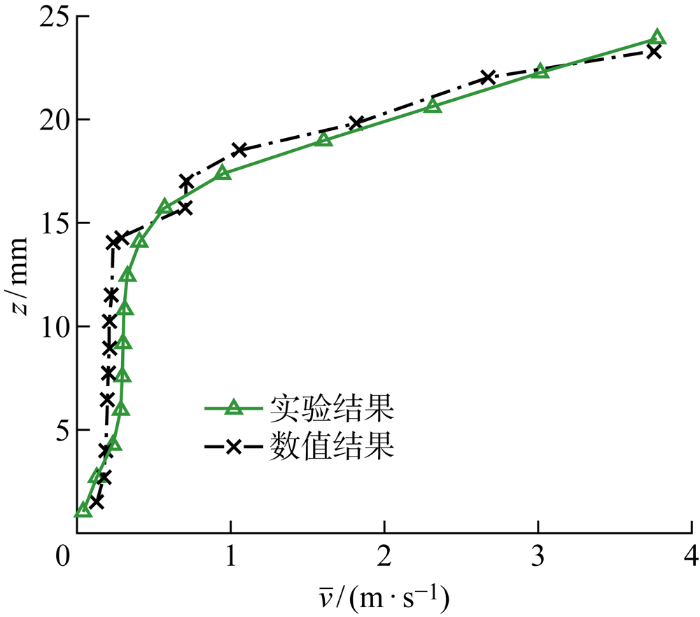
图3   基于CFD和PIV获得的监测线上的速度分布比较

Fig.3   Comparison of velocity distributions on monitoring lines based on CFD and PIV


以吸扬式和附壁射流式模型为例,分别在监测线L1和L0(见图1)上设置5个等距监测点,各监测点对应的流体质点速度时历曲线如图4所示.可以发现,吸扬式模型监测点上的流体质点速度几乎不随时间变化而改变,附壁射流式模型监测点上的流体质点速度随时间近似呈周期性变化,但其均值和幅值已达到稳定状态.这表明集矿流场均已得到充分发展,瞬时流场特征可以反映矿粒采集效率研究过程中的整体规律.

图4

新窗口打开| 下载原图ZIP| 生成PPT

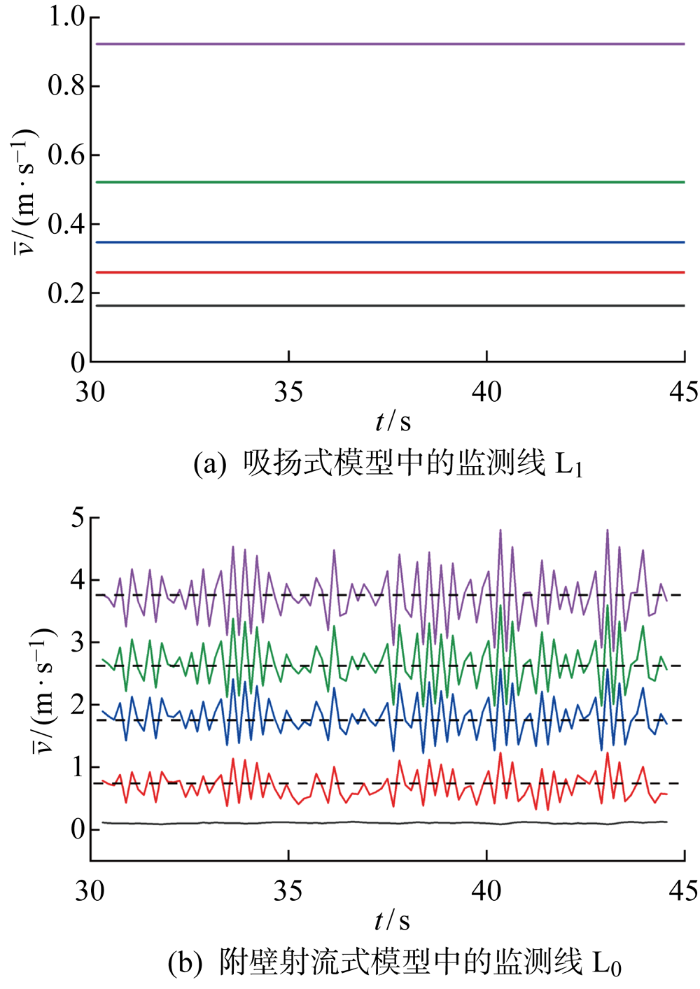
图4   监测线上各流体质点的速度时历曲线

Fig.4   Time-series of the flow velocities at each point on monitoring lines


2.5 数值模拟内容

矿粒采集性能研究在清水环境中开展,通过改变集矿头拖曳速度v和流量qm,研究3种模型在不同v-qm组合下的采集率η,采集率η可表示为η=M0/M,其中M0为进入输矿管内的矿粒质量,M为释放的矿粒总质量.环境扰动程度的研究在清水和海水-沉积物混合环境中开展.实际深海多金属结核大多以半埋状为主,因此将海水-沉积物混合物的厚度设为0.5d,以模拟矿粒的半埋赋存态.深海表层稀软底质物理特性复杂,因此以集矿区域内的流场流速分布、湍动能分布以及沉积物的扩散过程表征集矿过程对底质的扰动程度.具体工况设计如表3所示.

表3   具体工况设置

Tab.3  Specific working condition

集矿头种类环境条件颗粒状态v/(m·s-1)qm/
(t·s-1)
吸扬式清水多颗粒0.05,0.15,0.250~85
附壁射流式0.05,0.15,0.250~70
射流冲采式0.05,0.15,0.250~65
吸扬式海水-沉积物多颗粒(半埋态)0.150~85
附壁射流式0.150~80
射流冲采式0.150~75

新窗口打开| 下载CSV


3 结果与分析

3.1 矿粒采集率对比

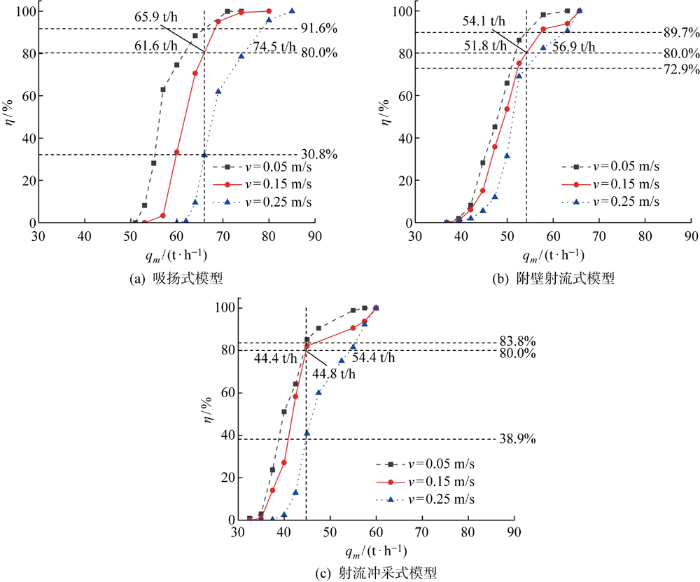
不同v下的η-qm曲线如图5所示.吸扬式模型的qm表示抽吸管的流量,附壁射流式和射流冲采式模型的qm为前、后射流喷嘴的射流流量之和.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   3种模型的η-qm曲线

Fig.5   η-qm curves of three models


对于吸扬式模型,当v=0.05 m/s时,随着qm的增加,η先缓慢增加至8.2%,然后在qm=53 t/h时迅速增加直至88.5%;随着qm的进一步增大,η继续增大.v=0.15 m/s和v=0.25 m/s时,发现了相似的特征,η-qm曲线均呈现“S”形.当v从0.05 m/s增加至0.15 m/s和从0.15 m/s增加至0.25 m/s时,qm值分别需要增加7%和13%以保持η=80%.拖曳速度越大,保持相同采集率所需的流量增值也越大.由此可见,吸扬式模型的η对v和qm均比较敏感,且敏感程度随着v的增加而增大.

对于附壁射流式模型,前、后射流喷嘴的射流流速比设为8.当v=0.05 m/s时,随着qm的增加,η的增速呈现先迅速增加、再缓慢减小的趋势,3种v下的η-qm曲线也均呈“S”形.当v从0.05 m/s增加至0.15 m/s和从0.15 m/s增加至0.25 m/s时,qm值分别需要增加4%和5%以保持η=80%.相比吸扬式,附壁射流式模型η对v和qm的敏感程度较小.

对于射流冲采式模型,输矿管的抽吸流速和前、后射流喷嘴的射流流速比设为v1∶v2∶v3=0.7∶2∶1.6.随着qm的增加,η先缓慢增加;当35 t/h<qm<45 t/h时,η随qm的增加快速增大至85%;当qm继续增加时,η的增加速率减缓.3种v下的η-qm曲线变化趋势相似.当v从0.05 m/s增加至0.15 m/s和从0.15 m/s增加至0.25 m/s时,qm值分别需要增加1%和21%以保持η=80%.相比吸扬式和附壁射流式模型,在一定范围内射流冲采式方法η对v和qm的敏感程度最大.

对比相同v下3种模型的η-qm曲线,分析采集率η达到80%所需要的流量qm.当v=0.05 m/s时,吸扬式模型的qm值约为附壁射流式的1.2倍,射流冲采式的1.4倍;当v=0.15 m/s时,吸扬式模型的qm值约为附壁射流式的1.2倍,射流冲采式的1.5倍;当v=0.25 m/s时,吸扬式模型的qm值约为附壁射流式的1.3倍,射流冲采式的1.4倍.达到相同的η时,吸扬式模型所需的qm最大,而射流冲采式模型所需的qm最小.随着v的增大,附壁射流式和射流冲采式模型的η-qm曲线越来越接近,说明二者采集性能的差异随v的增大而逐渐缩小.

3.2 集矿流场和矿粒分布特征

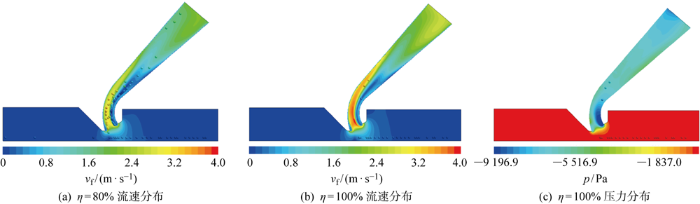
v=0.15 m/s时在达到η=80%和η=100%的qm作用下,经过60 s稳定发展后,3种模型y=0平面上的流场速度、矿粒和压力分布分别如图6~8所示.图中:vf为流体流速;p为流体压强.对于吸扬式模型,越接近输矿管入口,流场流速越大,矿粒通常在输矿管入口正下方产生垂向初始起动;进入输矿管后,越靠近后管壁,流场流速越大.对于附壁射流式模型,可以明显观察到Coandă效应,即前射流喷嘴射出的流体贴附着模型凸曲壁流动,靠近凸曲壁处流场流速大、压力小,而靠近底部的流场流速小、压力大,流速差异造成流场内压力分布的变化,在上下压差作用下矿粒发生垂向初始起动,该流速分布有利于降低集矿过程对底质的扰动;此外可以发现,由于后排射流喷嘴是水平方向的,而附近的附壁射流流动是斜向上方向的,所以当两种水流交汇后,在后排喷嘴上方发生了流动分离,造成压差阻力,形成了旋涡状回流区域,导致局部流场紊乱,不利于提升矿粒,需进一步优化该区域的几何形状.对于射流冲采式模型,矿粒在前、后射流喷嘴附近发生垂向初始起动;与附壁射流式模型不同,射流并未贴附在凸曲壁上,而是直接作用于矿粒和底质.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   吸扬式模型流场流速、矿粒和压力分布

Fig.6   Flow field velocity, nodule, and pressure distribution of suck-up-based model


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   附壁射流式模型流场流速、矿粒和压力分布

Fig.7   Flow field velocity, nodule, and pressure distribution of Coandă-effect-based model


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   射流冲采式模型流场流速、矿粒和压力分布

Fig.8   Flow field velocity, nodule, and pressure distribution of double-jet hydraulic model


达到η=80%和η=100%时,输矿管处垂向监测线L1~L3(见图1)上湍动能k的分布如图9所示.随着监测线上监测点z的增加,即距输矿管入口的垂向距离越大,吸扬式和附壁射流式模型中流体质点的k值逐渐变小;而射流冲采式模型在靠近底部时(z越小),反而会出现值增大的情况,这是由于射流冲采式模型的前、后射流直接作用于矿粒和底质,对近底流场造成了直接扰动.达到相同η时,射流冲采式模型对近底流场的整体扰动程度最大,附壁射流式模型的扰动程度最小.3种模型达到η=80%时的扰动程度约为达到η=100%时扰动程度的1/4~1/3,因此必要时可通过适当降低采集率来显著降低作业过程对近底流场的扰动.

图9

新窗口打开| 下载原图ZIP| 生成PPT

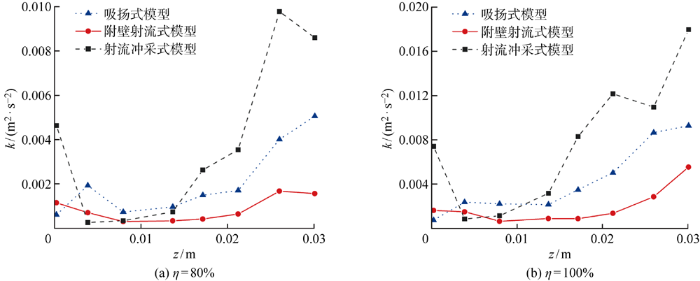
图9   η=80%和η=100%时3种模型监测线上的湍动能

Fig.9   Turbulent kinetic energy on monitoring line of the three models at a η of 80% and 100%


3.3 海底表层沉积物扩散特性

本研究中,将海底矿区表层稀软沉积物简化为密度为1 400 kg/m3的可溶于水的液体,以其扩散特征表征集矿过程对深海底质的扰动程度.图10~12给出了v=0.15 m/s时在达到η=100%的qm作用下,3种模型前20 s作业过程中的海水-沉积物混合物扩散情况,图中φ为海水-沉积物体积分数.对于吸扬式模型,大多数混合物沿着管道后壁被吸入输矿管中.对于附壁射流式模型,流场稳定后,少量混合物扩散至集矿头后方.对于射流冲采式模型,射流的高速冲刷使得向管外扩散和吸入管内的沉积物体积相当,沉积物悬浮扩散现象较为明显.

图10

新窗口打开| 下载原图ZIP| 生成PPT

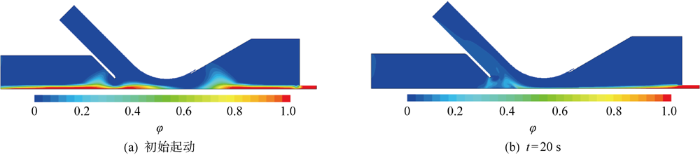
图10   吸扬式模型中海水-沉积物混合物扩散情况

Fig.10   Dispersion of seawater-sediment mixtures in suck-up-based model


图11

新窗口打开| 下载原图ZIP| 生成PPT

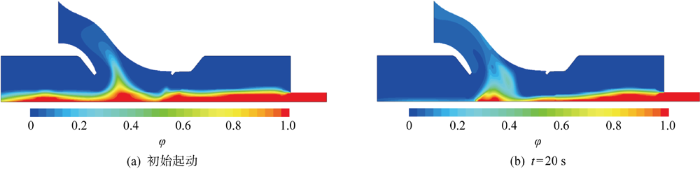
图11   附壁射流式模型中海水-沉积物混合物扩散情况

Fig.11   Dispersion of seawater-sediment mixtures in Coandă-effect-based model


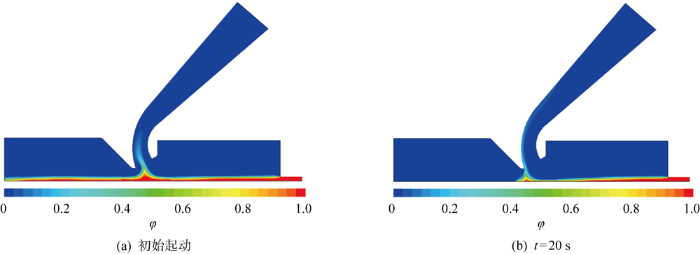
图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   射流冲采式模型中海水-沉积物混合物扩散情况

Fig.12   Dispersion of seawater-sediment mixtures in double-jet hydraulic model


t=20 s时输矿管入口处横向监测线L4~L6(见图1)上的φ结果如图13所示.吸扬式和附壁射流式模型中,φ的极值位于输矿管入口附近;而射流冲采式模型φ的极值偏向集矿头前方, 且数值远大于吸扬式和附壁射流式集矿模型.

图13

新窗口打开| 下载原图ZIP| 生成PPT

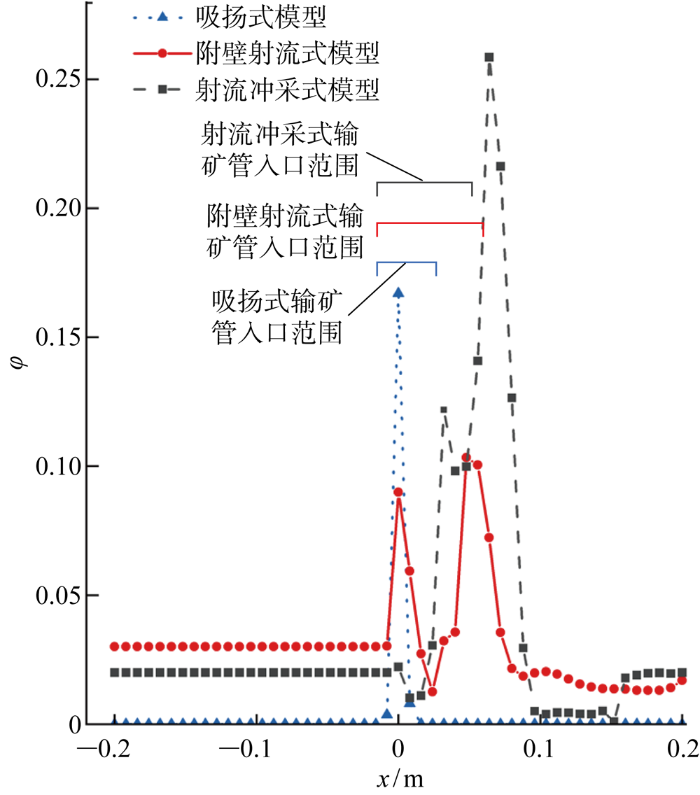
图13   3种模型监测线上的φ值分布

Fig.13   Distribution of φ on monitoring lines of three models


进一步研究附壁射流式和射流冲采式模型在不同qm下的混合物扩散情况,如图14所示.当qm增加20%时,附壁射流式模型中的φ峰值更集中于集矿头,说明在大流量作用下,附壁射流式方法可以更快达到稳定,且不会显著增加对周围沉积物的扰动程度.对于射流冲采式模型,当qm增加20%时,集矿头前方的φ显著增大,沉积物有明显向集矿头前方加剧扩散的趋势.综合来看,取得相同η时,水力集矿过程对海水-沉积物混合物的扰动程度最大的是射流冲采式集矿模型,其次为附壁射流式和吸扬式集矿模型.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14   不同qm下附壁射流式和射流冲采式模型监测线上的混合物扩散情况

Fig.14   Diffusion of mixtures on the monitoring line at different qm values in Coandă-effect-based and double-jet hydraulic model


4 结论

本文基于前人海试集矿样机的几何参数设计模型,分别从矿粒采集性能和环境扰动程度两个方面,对吸扬式、附壁射流式、射流冲采式3种主流的深海水力集矿方法进行数值模拟研究,提出了比较不同集矿模型作业特性的数值模拟方法.通过与PIV实验数据比较,论证了基于K-Epsilon两层模型模拟三维复杂集矿流场的准确性和可行性;分析了不同集矿模型中集矿流场流速、压力及海水-沉积物混合物的分布特征,揭示了集矿机理,为高效、低扰动集矿装备的设计研发提供了理论基础.主要结论如下:

(1) 揭示了水力集矿方法的集矿机理,3种不同的集矿模型中,固体矿粒均处在非均匀流场中,上部流体质点流速大、压力小,下部流体质点流速小、压力大,矿粒在上下压力差作用下发生初始垂向起动,最终被采集到输矿管中.

(2) 在矿粒采集特性方面,达到相同采集率η时,射流冲采式模型所需的流量qm最小,吸扬式模型所需的qm最大;拖曳速度v越大,相同流量qm下3种集矿模型可达到的采集率η越小,其中附壁射流式模型的η-qm曲线对v的变化最不敏感.

(3) 在流场扰动方面,以湍动能k为指标,达到相同η时,射流冲采式模型对近底流场扰动程度最大,附壁射流式模型的扰动程度最小.以海水-沉积物混合物体积分数φ为指标,达到相同η时,吸扬式和附壁射流式模型对近底流场扰动较小,射流冲采式模型中海水-沉积物混合物则有明显的向外扩散的趋势,且扩散趋势随qm增加而加剧.

(4) 在进行深海多金属结核矿产资源开发的过程中,建议结合不同矿区各自的生态环境参数选择合适的水力集矿方法.对于生物种类丰富、环保要求更为苛刻的矿区,可采用附壁射流式、吸扬式等对近底流场扰动较小的集矿方法;对于生物密度较低的矿区,可采用射流冲采式等低能耗高作业经济性的集矿方法.

参考文献

ALVARENGA R A F, PRÉAT N, DUHAYON C, et al.

Prospective life cycle assessment of metal commodities obtained from deep-sea polymetallic nodules

[J]. Journal of Cleaner Production, 2022, 330: 1-10.

[本文引用: 1]

邱显焱. 深海采矿系统扬矿子系统纵向振动被动减振研究[D]. 长沙: 中南大学, 2014.

[本文引用: 1]

QIU Xianyan. Research for passive control for longitudinal vibration of lifting pipe in deep sea mining system[D]. Changsha: Central South University, 2014.

[本文引用: 1]

ELERIAN M, VAN R C, HELMONS R.

Experimental and numerical modelling of deep-sea-mining-generated turbidity currents

[J]. Minerals, 2022, 12(5): 1-23.

[本文引用: 1]

夏建新, 吴优, 邹燚, 等.

基于PIV技术粗颗粒在管流断面浓度分布试验研究

[J]. 应用基础与工程科学学报, 2017, 25(6): 1086-1093.

[本文引用: 1]

XIA Jianxin, WU You, ZOU Yi, et al.

Experimental study on the concentration distribution in pipe flow based on PIV technology

[J]. Journal of Basic Science and Engineering, 2017, 25(6): 1086-1093.

[本文引用: 1]

赵国成, 肖龙飞, 杨建民, 等.

深海水力集矿球形颗粒受力特性试验研究

[J]. 上海交通大学学报, 2019, 53(8): 907-912.

[本文引用: 1]

ZHAO Guocheng, XIAO Longfei, YANG Jianmin, et al.

Experimental research on force characteristics of a spherical particle in deep sea hydraulic collecting

[J]. Journal of Shanghai Jiao Tong University, 2019, 53(8): 907-912.

[本文引用: 1]

XIONG H, CHEN Y, YANG N, et al.

Numerical study on settling and floating movements of a sphere particle flowing in a vertical pipe

[C]//The 28th International Ocean and Polar Engineering Conference. Sapporo, Japan:The 28th International Ocean and Polar Engineering Conference, 2018: 176-182.

[本文引用: 1]

LIM S J, KIM J W, JUNG S T, et al.

Deep-seawater flow characteristics around the manganese nodule collecting device

[J]. Procedia Engineering, 2015, 116: 544-551.

[本文引用: 1]

CHO S, PARK S, OH J, et al.

Design optimization of deep-seabed pilot miner system with coupled relations between constraints

[J]. Journal of Terramechanics, 2019, 83: 25-34.

[本文引用: 2]

YANG N, TANG H.

Several considerations of the design of the hydraulic pick-up device

[J]. Environmental Health Perspectives, 2003, 32(11): 267-271.

[本文引用: 1]

HONG S, CHOI J S, KIM J H, et al.

A note on design and operation of waterjet nodule lifter of manganese nodule collector

[J]. International Journal of Offshore and Polar Engineering, 2001, 11(3): 237-239.

[本文引用: 1]

黎蔚杰, 张琪, 廖晨聪, 等.

孤立波和海流作用下单桩基础局部冲刷及保护的数值分析

[J]. 上海交通大学学报, 2021, 55(6): 631-637.

DOI:10.16183/j.cnki.jsjtu.2020.108      [本文引用: 1]

采用数值模拟的方法研究了孤立波和海流共同作用下单桩周围海床的局部冲刷.通过求解RNG k-&#x003b5;湍流模型封闭的N-S方程,准确地模拟了桩周流场的变化情况.泥沙输运模型考虑泥沙的夹带、悬移质输送、沉积以及推移质输送的泥沙冲刷机制.对于斜坡床面,考虑重力对泥沙颗粒的影响,并对临界希尔兹数进行修正.将数值结果与实验数据进行比较,验证了数值模型的准确性.在此基础上,详细分析在不同波高条件下的桩基冲刷发展过程,初步研究了桩基保护层对冲刷的影响.结果表明:波-流共同作用下桩基周围海床的冲刷深度比单纯流或孤立波作用下冲刷深度更大;倾斜海床下的局部冲刷深度更大;保护层的设置可以有效地降低桩周局部冲刷深度,保护层粒径的大小对防护效果的影响较大.

LI Weijie, ZHANG Qi, LIAO Chencong, et al.

Numerical analysis of local scour and protection of a single pile around a seabed under solitary wave and current

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(6): 631-637.

[本文引用: 1]

CHEN X, LIU X, LI H, et al.

Effects of seabed geotechnical properties on scour mechanism at the pile in non-cohesive soils: Experimental study

[J]. Ocean Engineering, 2022, 254: 1-15.

[本文引用: 1]

DURDEN J M, MURPHY K, JAECKEL A, et al.

A procedural framework for robust environmental management of deep-sea mining projects using a conceptual model

[J]. Marine Policy, 2017, 84: 193-201.

[本文引用: 1]

SHIH T H, LIOU W W, SHABBIR A, et al.

A new k-ε eddy viscosity model for high Reynolds number turbulent flows

[J]. Computers & Fluids, 1995, 24(3): 227-238.

[本文引用: 1]

徐泳, 孙其诚, 张凌, 等.

颗粒离散元法研究进展

[J]. 力学进展, 2003, 33(2): 251-260.

[本文引用: 1]

XU Yong, SUN Qichen, ZHANG Ling, et al.

Advances in discrete element methods for particulate materials

[J]. Advances in Mechanics, 2003, 33(2): 251-260.

[本文引用: 1]

KAUFMAN R, LATIMER J P, TOLEFSON D C.

The design and operation of a pacific ocean deep-ocean mining test ship: R/V Deepsea Minner II

[C]//Offshore Technology Conference. Houston, Texas, USA: Offshore Technology Conference, 1985: 33-43.

[本文引用: 1]

HONG S, CHOI J S, KIM J H, et al.

Experimental study on hydraulic performance of hybrid pick-up device of manganese nodule collector

[C]//The 3rd ISOPE Ocean Mining Symposium. Goa, India: The Third ISOPE Ocean Mining Symposium, 1999: 69-77.

[本文引用: 1]

HU J, ZHAO G, XIAO L, et al.

Experimental investigation on characteristics of flow field in ‘Suck-up-based’ and ‘Coandă-Effect-based’ nodule pick-up devices

[C]//The 30th International Ocean and Polar Engineering Conference. Virtual:The 30th International Ocean and Polar Engineering Conference, 2020: 34-44.

[本文引用: 1]

/

〈 〉