管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计.
上述研究对管路自动布置问题做出了积极贡献,对于核动力舰船而言,其内部布置环境则更为复杂.本文结合核动力舰船的工程背景,在经典蚁群算法(ACO)的基础上改进,提出更适用于三维空间管路布置优化的信息素高斯扩散多蚁群优化(Pheromone Gaussian diffusion Multi Ant Colony Optimization,PG-MACO)算法,由于ACO的核心在于利用信息素启发蚂蚁间的协作,因此引入基于高斯分布[18 ] 的信息素扩散机制、改进蚂蚁寻路过程的空间状态转移策略以及面向混合管路布置工况设计的协同进化机制,使得算法的自动化程度、计算效率、求解效果得到提升,开发管路自动布置软件系统实现算法的工程应用,在核级一回路管道布置工程案例和船舶机舱燃油管路布置案例中验证PG-MACO算法的有效性.
1 管道布置优化模型
舰船管路布置需要在复杂的舱室空间中寻找到连通管路接口的路径,属于三维空间中路径规划问题,可将布置空间离散成若干网格节点进行寻路,其过程要遵循经济性、美观性、可施工性等原则,因此可抽象为多目标优化问题.其设计变量为从起点管路接口到终点管路接口的三维空间中路径信息P ,具体表达为空间中若干网格节点坐标的集合,设起点为n s ,终点为n e :
(1) P ={ns , …, ni , …, ne }, 0≤i ≤I
式中:ni 代表某网格节点,由三维坐标xi 、yi 、zi 确定,即ni (xi , yi , zi );I 为路径中网格节点的个数.
考虑到管路与设备不得发生干涉、管路不得逾越布置空间等硬性要求,在约束条件中将设备视为障碍物,管路的节点集合均在布置空间中,且不得与障碍物存在交集.为降低计算复杂度,采用轴平行包围盒法[19 ] 适当简化设备,即对设备轮廓进行规则几何体包络,简化为由对角点坐标确定的长方体,有如下表达:
(2) M ={n (x , y , z )|x ∈[0, X ], y ∈[0, Y ], z ∈[0, Z ]}
(3) O =o 1 ∪o 2 …∪oj …∪oJ , 0≤j ≤J
(4) oj ={n (x , y , z )|x ∈(x j, min x j, max y ∈(y j, min y j, max z ∈(z j, min z j, max
(5) s.t. P ⋃ M = M P ⋂ O = ⌀
式中:M 为布置空间离散后的全部网格节点集合;X 、 Y 、 Z 分别为布置空间三维方向上最大网格数;O 为所有障碍物节点集合;oj 为第j 个障碍物所覆盖节点的集合;(x j, min y j, min z j, min x j, max y j, max z j, max j 个障碍物包络后的极小对角点和极大对角点;J 为障碍物个数;式(5)为约束条件.
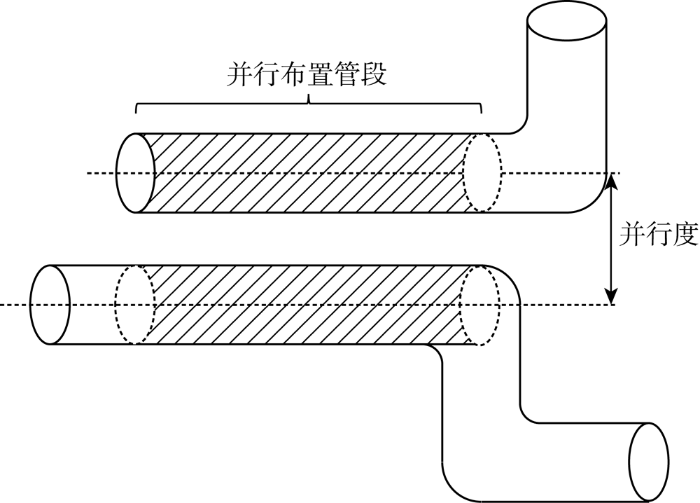
除硬性要求外,管路布置还需要考虑降低建造成本、协调布置管路,尽量美观且符合施工要求等,因此优化目标f 需考虑经济性指标f ec 、可操作性指标f op 及协调性指标f co .f ec 主要受管路长度及所需弯头数量影响;可操作性通常考虑管路是否符合施工要求,例如管路通常沿着设备表面或舱壁布置以便于获取足够的支撑,本文引入能量区[6 ] 概念,即对网格节点赋予能量值属性,引导管路向特定区域探索并辅助量化可操作性指标;协调性是指多条管路并行布置程度,本文提出管路并行度概念D par ,即管段轴线在其正交截面上投影点的距离.管道并行布置示意图如图1 所示,有如下表达:
(6) min f =ln[c 1 (fec +fop +fco )]+c 2
(7) fec =w1 ∑ i = 1 n - 1 i , ni+1 )+w2 ∑ i = 2 n - 1 i -1 , ni , ni +1 )
(8) fop =w 3 ∑ i = 1 n i )
(9) f co =w 4 L p a r D p a r + c 3 5 Blap
式中:L (ni , ni +1 )为路径中两个相邻节点的距离;B (ni -1 , ni , ni +1 )表示对管路节点是否为折弯点的判断,当ni 和ni -1 组成的矢量与ni 和ni +1 组成的矢量正交时,则ni 点为折弯点,需要添加一个弯头;E 表示能量矩阵,是X ×Y ×Z 的三维矩阵;E (ni )为ni 点坐标对应的能量值;L par 为并行布置的管路长度;B lap 表示管路重合时重复计算的折弯点个数;w 1 、w 2 、w 3 、w 4 、w 5 为权重系数,权重的设置需要综合考虑各优化目标,使得各变量影响程度合理,本文设置为1、1 000、0. 5、-0. 3、-600,也可对需要突出考虑的因素赋予较大权重;c 1 、c 2 、c 3 为常数,用于调整目标函数图像的形状和位置,本文中c 1 =1,c 2 =0,为避免分母为0取c 3 =1.
图1
图1
管路并行布置示意图
Fig.1
Schematic diagram of pipeline parallelism
2 PG-MACO算法设计
核动力舰船内部的管路布置工况较为复杂,除了单独布置的管路外,还需要考虑性质相同的同组管路协同布置、多接口分支管路布置以及相互混合的工况,因此其复杂度及计算难度较高,传统蚁群算法的求解效率和效果不足以满足要求.本文在该算法基础上改进,设计提出PG-MACO算法,算法架构包括3个方面,首先改进产生设计变量的机制,即路径可行解的搜索方式,提高计算效率,其次改进对设计变量的优化过程,引入信息素高斯扩散机制,加速算法收敛,最后结合混合管路布置工况设计多蚁群协同进化机制.
2.1 环境信息初始化
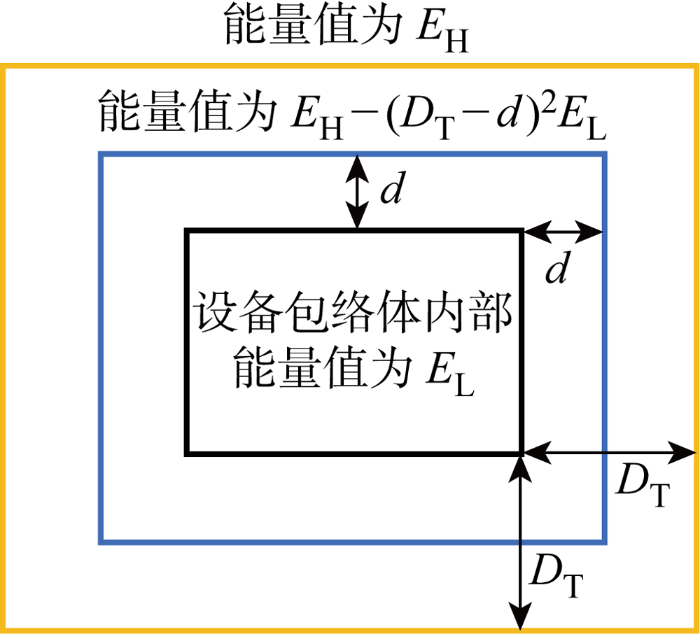
在探索路径前需要初始化蚂蚁周围环境信息,包括布置空间M' 、能量值矩阵E 和信息素矩阵T ,三者初始化为X ×Y ×Z 单位矩阵,而后E 乘以能量值上限E H , M' 根据M 集合中节点的属性对相应元素0-1赋值,0视为障碍物不可穿越;为细化能量区分布且易于程序实现,采用二次函数递减分布策略,在一定距离范围能量值沿着障碍物表面向外逐层递减,以长方体的形状进行能量区的嵌套,如图2 所示.首先根据下式计算:
(10) D T = ( E H - E L ) / E L
式中:E L 为能量值下限;D T 为能量减弱的范围,由E H 和E L 确定,本文设定E H =1和E L =0.1.
图2
图2
设置能量区示意图
Fig.2
Schematic diagram of energy zone setting
在障碍物向外扩展距离为d 的能量区内,其各节点处能量值为E H -(D T -d )2 E L ,在超过D T 范围后,将不再设置能量区.
2.2 空间状态转移策略
蚂蚁搜索路径的过程是从起点出发,按照特定规则不断选择下一节点,直至抵达终点,其选择下一节点的过程即为状态转移.传统蚁群算法的思想是从当前节点转移到邻接节点,由于三维空间中节点过多,此方法容易出现大量折弯,不满足管路设计需求.本文提出基于环境信息的空间状态转移策略,根据蚂蚁当前位置的环境信息,如信息素浓度T 、能量值E 、可行域信息F 及相对位置信息D ,首先进行方向决策,设当前节点为n c ,n c 到终点n e 的矢量为V ,ek 为三维正交空间中沿坐标轴正负方向的单位矢量,k 为整数且k ∈[1 ,6 ],相对位置信息Dk 为V 在该方向上的投影距离,距离终点越远越值得探索. 为提升解的随机性,若投影为负,则该方向上仅保留余量ξ ;可行域信息主要考虑各方向上可行节点数量Fk 和信息素的平均浓度Tk ,可行节点越多、信息素浓度越高,则该方向越值得选择.根据下式计算选择各方向的概率:
(11) φ (x )= 1 , x > 0 0 , x < 0
(12) Dk =φ (V ·ek )|V ·ek |+ξ , 1≤k ≤6
(13) p k D D k F k T k ∑ k = 1 6 D k F k T k
确定方向后进行步长决策,获取该方向上各节点信息素浓度TN 、能量值EN 和与终点n e 间的曼哈顿距离dN ,曼哈顿距离计算方法为dN (ni , nj )=|nix -njx |+|niy -njy |+|niz -njz |,按照下式计算各节点伪随机概率并进行状态转移:
(14) p N F T N α E N - 1 d N - β ∑ N = 1 F k T N α E N - 1 d N - β k
式中:φ (x )为分段函数;ξ 取值为1;α 为信息素启发因子;β 为距离启发因子;p k D p N F
2.3 信息素扩散机制
蚁群算法在迭代中不断更新设计变量并筛选出较优的可行解,其中信息素的更新是重要的一环.传统蚁群算法中蚂蚁会在经过的路径上释放信息素,后续蚂蚁参考信息素浓度选择转移节点,但在三维空间中节点数量较多,信息素对后续蚂蚁寻路的启发性较弱.本文提出基于高斯分布的信息素扩散机制,即在已布置管路周围空间扩展信息素影响范围,高斯分布的概率密度函数曲线呈钟形,符合蚂蚁信息素的扩散强度随扩散距离增大而衰减的物理机制,借助该函数的这一特性,实现信息素浓度的空间扩散和衰减.此外,方差参数影响曲线的形状,方差越大则数据分布越分散、曲线越扁平,该特点可用于模拟信息素衰减的剧烈程度.将个体适应度与方差建立联系,实现越优的个体信息素衰减的越缓慢,即扩散范围更大、吸引力更强.
设高斯分布的概率密度函数为G (x ),则在期望μ 处取得最大值G (μ ),在算法每次迭代中会得到多只蚂蚁搜索的多个可行解,每个可行解根据式(6)计算出个体适应度值,即优化目标函数值.根据下式计算方差θ :
(15) θ = g m a x - g c g m a x - g m i n θ b , θ > θ 0 θ 0 , θ ≤ θ 0
式中:g max 为当次迭代中个体最大适应度值;g min 为最小适应度值;g c 为当前个体适应度值;θ b 为方差基值;θ 0 为方差下限. 为降低参数敏感性,将方差的取值限定在两者之间,θ b 和θ 0 设置的越大则信息素衰减程度越弱,本文中取θ b =3,θ 0 =1.
而后各路径节点沿径向向外扩展信息素,由下式计算出扩展各节点处信息素浓度增量Δτ :
(16) ϕ (d ex )= G ( μ + d e x ) G ( μ )
(17) Δτ = Q ϕ ( d e x ) L c
(18) τ (t +1)=(1-ρ )τ (t )+Δτ
式中:ϕ (d ex )为信息素衰减因子,表征扩展节点处相比于最大值G (μ )的下降程度;d ex 为扩展距离;Q 为当前个体的信息素总量;L c 为当前个体路径长度;τ (t )和τ (t +1)为第t 次和第t +1次迭代时的信息素浓度;ρ 为信息素挥发系数.
2.4 混合管路并行度计算
通常布置单管路仅需考虑经济性指标和可操作性指标,而多管路和分支管路需要考虑协调性指标,从工程的角度来看,对于同组的多管路希望尽量并排铺设,便于施工和添加支撑,同时要考虑管路的管径,留出适当的安全距离避免干涉,对于分支管路则要求分支点尽量少且位置合理,减小总长和折弯次数等,因此多管路和分支管路的布置相较于单管路更为复杂,且性质不同.为实现混合管路布置一体化,本文改进协同进化机制,首先将多接口的分支管路分解为起点相同而终点不同的同组多条管道,选取与其他接口距离之和最小的接口为起点;其次将各条管路视为种群,每个种群中包含若干优化问题的可行解,种群间结合协调性指标f co 协同优化,最终得到整体布置方案.在布置当前管路时,将已布置的管路视为障碍物,结合管径和安全距离要求,将管路周围可能发生干涉的节点标记为障碍物.
3 案例验证
3.1 验证方法
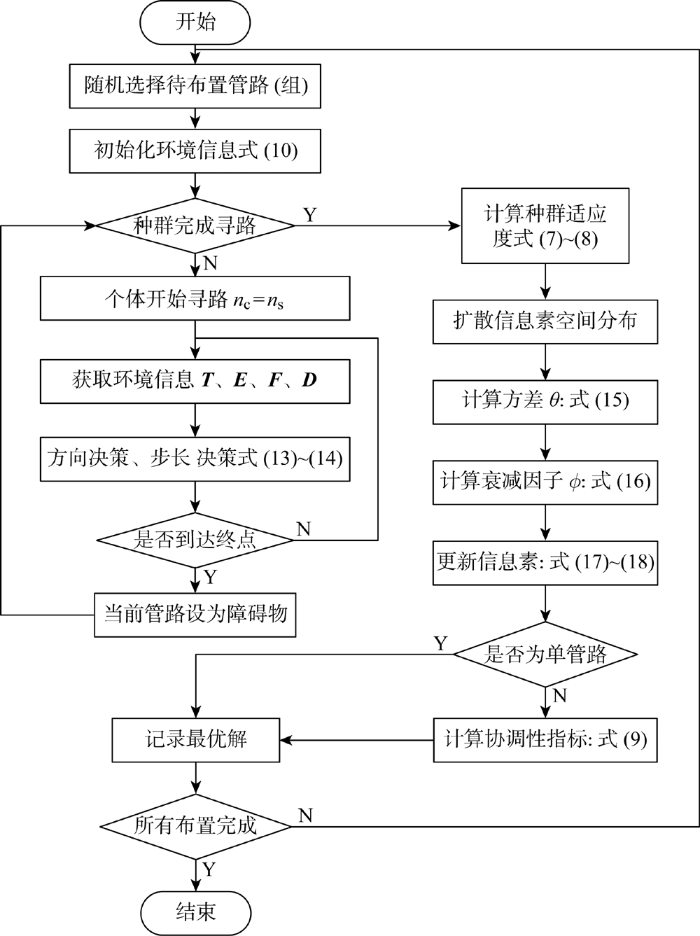
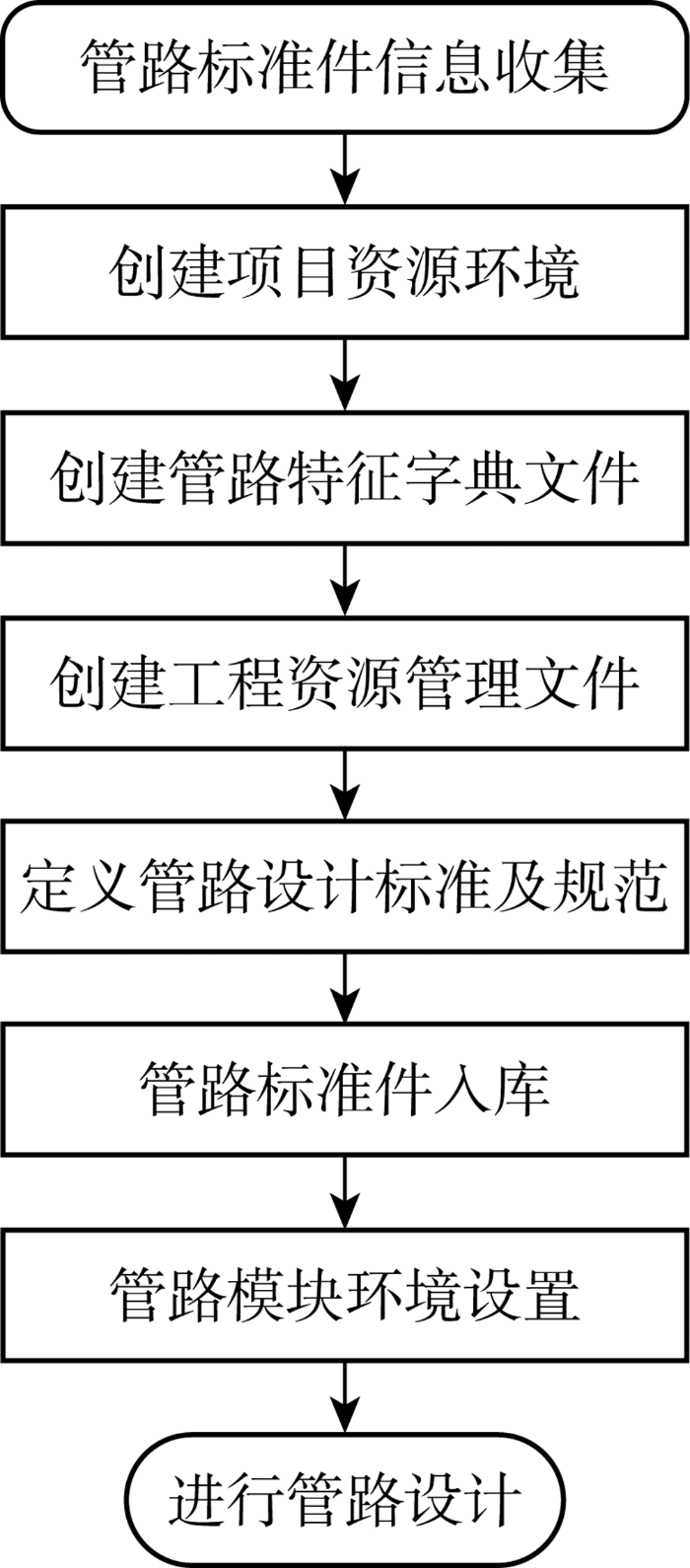
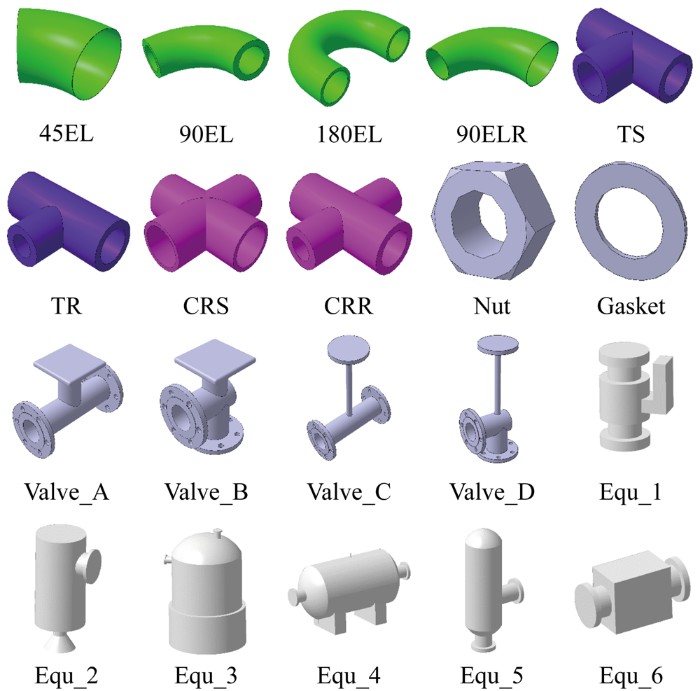
由算法计算得到混合管路的整体流程图如图3 所示,该算法已公开申请发明专利[20 ] .管路布置算法的计算结果需要转化为工程设计成果,本文基于COM二次开发技术[21 ] 将算法应用于第三方设计软件,使用Python语言开发管路自动布置功能,输入信息包括管路接口坐标信息、设备坐标信息、管径及算法参数等,程序调用内部函数接口实现管路自动绘制,此部分研究现获得软件著作授权[22 ] ,绘制完成后需为其添加附件,如弯头、三通等、阀门等.为提高设计效率,可客户化定制专属管路零件库,存储常用附件及设备模型供装配时调用.定制方法如图4 所示,零件库示意图如图5 所示.
图3
图3
PG-MACO算法流程图
Fig.3
Flow chart of PG-MACO algorithm
图4
图4
管道标准件库客户化定制流程
Fig.4
Customized process of pipe standard parts database
图5
图5
管路零件库示意图
Fig.5
Example of pipeline standard parts database
3.2 验证案例
为验证算法适用于核动力舰船管路布置,采用核级一回路管路布置工程案例进行实验,案例中包含9个设备,由零件库中Equ_1~Equ_6组成,需布置P1~P6管路和两条三接口分支管路P7和P8,真实坐标信息如表1 和表2 所示.为提高计算效率,算法需将真实坐标等比例缩小100倍并取整,设置全部管路的管径为 80 mm,安全距离为 10 mm.
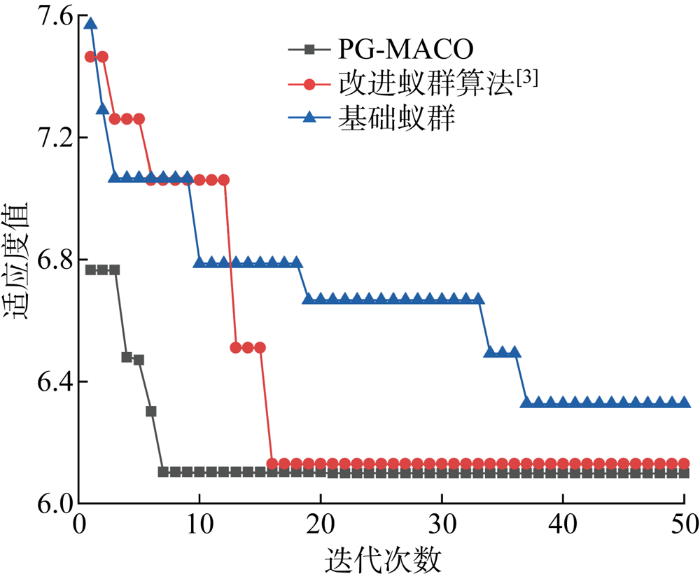
(1) 为验证算法改进后的性能提升,以P7-1管路为例进行测试,对比传统蚁群算法与PG-MACO算法的路径搜索效率和算法收敛性,并引用文献[3 ]中的改进蚁群算法为参考,参数设置如表3 所示,图6 为3种算法的收敛对比图.由于3种算法在50~100代间适应度值不变,图6 仅展示0~50代的适应度值, 测试结果表明相比于传统蚁群算法,PG-MACO算法的单次寻路时间缩短58.38%,收敛代数缩短43.24%;相比于参考算法,虽收敛代数稍大,但整体适应度值下降更快.
图6
图6
算法收敛性对比折线图
Fig.6
Comparison of algorithm convergences
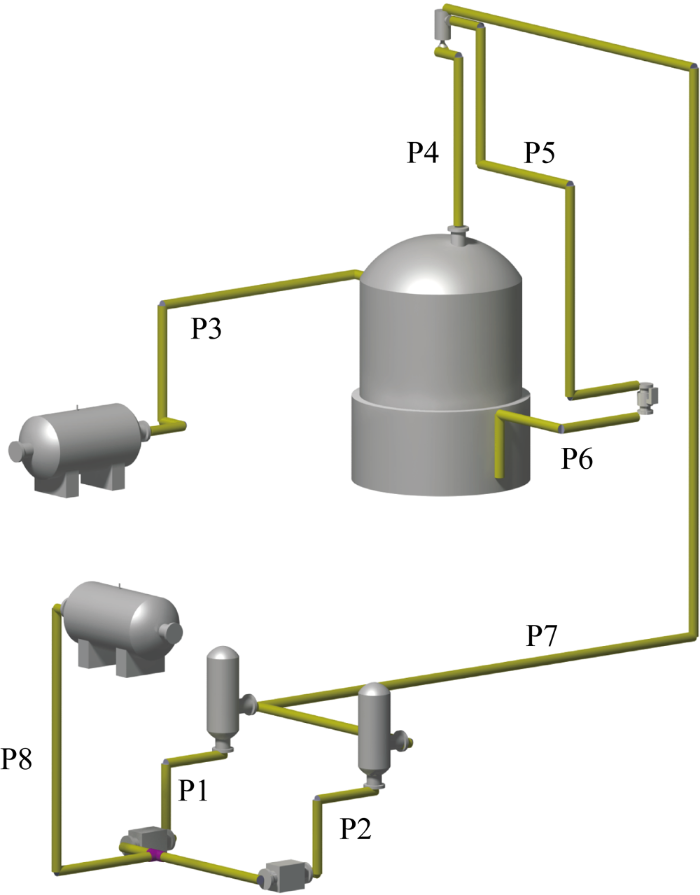
(2) 为验证PG-MACO算法能够有效布置混合管路,将本案例中P1~P8管路同时布置,布置结果如图7 所示.图中显示管路能够沿着设备表面布置,如P3、P6、P8等,符合可操作性要求;从P1与P2以及P4、P5、P6之间可看出管路能够沿着已布置管路并行布置,符合协调性布置要求.表4 为布置方案的数据统计,PG-MACO算法相较于传统蚁群算法缩短管路长度33.88%,减少管路折弯次数41.67%,符合经济性要求,验证了PG-MACO算法的有效性.
图7
图7
案例布置结果
Fig.7
Result of case layout
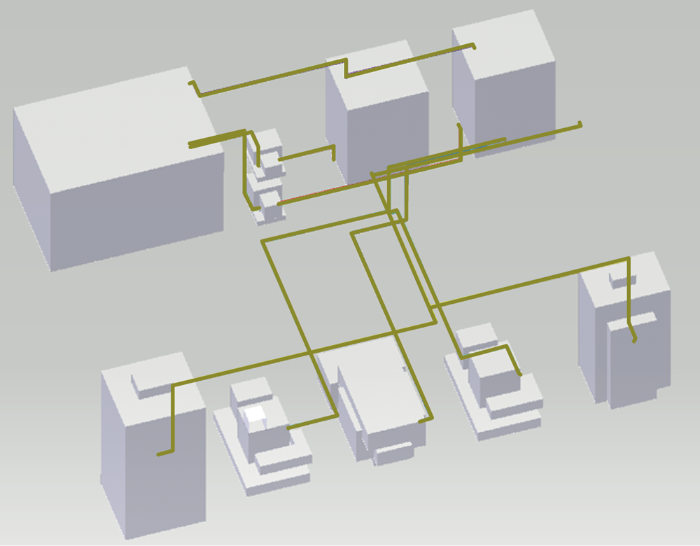
(3) 为进一步验证本算法的有效性,与其他类型的算法进行比较,参照文献[15 ]中提出的GA-A* 算法,使用该文献中的船舶机舱燃油管路布置算例进行验证, 案例中包含燃油舱、燃油输送泵、燃油储罐、船用主机、柴油发电机和锅炉等设备,需要布置8条燃油管道P1~P8,具体坐标信息参照文献[15 ],PG-MACO算法的测试结果如图8 所示,数据统计结果如表5 所示.从图中可看出PG-MACO算法能够协同布置多条管路、分支管路的重叠性良好、能够沿着舱壁及设备表面布置,虽然在折弯次数方面PG-MACO略多于GA-A* ,但PG-MACO算法整体长度更短,通过对比验证了PG-MACO算法具备较强的有效性,工程应用价值较高.
图8
图8
案例布置结果
Fig.8
Case layout result
4 结论
本文研究蚁群算法在舰船管路布置优化上的应用,针对传统蚁群算法的缺陷结合工程实际改进,提升算法性能并实现混合管路的布置优化,在三维设计平台上实现PG-MACO算法的布管应用:
(1) 结合舰船管路布置要求,建立相应优化数学模型,综合考虑管路布置过程中安全性、经济性、可操作性、协调性等工程要求,确定设计变量、约束条件及目标函数,提升优化方法的计算结果的实用性.
(2) 针对传统蚁群算法不适用于管路布置的工程背景、搜索效率低且容易出现大量折弯的问题,提出空间状态转移策略,采用环境信息指引下的方向决策与步长决策,提升搜索路径可行解的效率及结果质量,实验结果显示PG-MACO相比于传统蚁群算法的单次寻路时间缩短58.38%,管路布置结果长度缩短33.88%,折弯次数减少41.67%.
(3) 针对传统蚁群算法收敛速度慢的问题,提出信息素扩散机制,沿路径向周围的节点扩散信息素,增强信息素对后续蚂蚁寻路过程的启发程度,加速算法收敛,实验结果显示PG-MACO相比于传统蚁群算法收敛代数缩短43.24%.
(4) 针对混合管路布置工况设计多蚁群协同进化机制,实现多种类型的混合管路自动布置,结合核级一回路管路布置案例和船舶机舱燃油管路布置案例进行算法的实例验证,证实了本方法具有较高的工程实用价值,使用Python语言对第三方设计平台二次开发,实现从算法到设计成果的进一步转化,为舰船管道布置问题提供有益参考.
参考文献
View Option
[1]
DONG Z R BIAN X Y ZHAO S Ship pipe route design using improved multi-objective ant colony optimization
[J]. Ocean Engineering , 2022 , 258 : 1 -14 .
[本文引用: 3]
[2]
WANG Y L YU Y Y LI K et al A human-computer cooperation improved ant colony optimization for ship pipe route design
[J]. Ocean Engineering , 2018 , 150 : 12 -20 .
[本文引用: 2]
[3]
JIANG W Y LIN Y CHEN M et al A co-evolutionary improved multi-ant colony optimization for ship multiple and branch pipe route design
[J]. Ocean Engineering , 2015 , 102 : 63 -70 .
[本文引用: 3]
[4]
陈杨 . 基于改进蚁群算法和SolidWorks二次开发的船舶管路规划研究 [D]. 镇江 : 江苏科技大学 , 2019 .
[本文引用: 2]
CHEN Yang Research on ship pipeline planning based on improved ant colony algorithm and secondary development of SolidWorks [D]. Zhenjiang : Jiangsu University of Science and Technology , 2019 .
[本文引用: 2]
[5]
范小宁 , 林焰 , 纪卓尚 . 多蚁群协进化的船舶多管路并行布局优化
[J]. 上海交通大学学报 , 2009 , 43 (2 ): 193 -197 .
[本文引用: 2]
FAN Xiaoning LIN Yan JI Zhuoshang Multi ant colony cooperative coevolution for optimization of ship multi pipe parallel routing
[J]. Journal of Shanghai Jiao Tong University , 2009 , 43 (2 ): 193 -197 .
[本文引用: 2]
[6]
范小宁 , 林焰 , 纪卓尚 . 船舶管路三维布局优化的变长度编码遗传算法
[J]. 中国造船 , 2007 (1 ): 82 -90 .
[本文引用: 4]
FAN Xiaoning LIN Yan JI Zhuoshang A variable length coding genetic algorithm to ship pipe path routing optimization in 3D space
[J]. Shipbuilding of China , 2007 (1 ): 82 -90 .
[本文引用: 4]
[7]
董宗然 , 楼偶俊 , 管官 . 基于改进遗传算法的船舶管路布局设计
[J]. 计算机工程与应用 , 2020 , 56 (19 ): 252 -260 .
DOI:10.3778/j.issn.1002-8331.1906-0251
[本文引用: 2]
针对船舶管路布局设计中的路径规划问题提出一种改进型遗传算法求解方法。建立船舶管路布局设计问题的模型空间、约束条件和优化目标;提出一种基于连接点网格的定长编码方法,结合该编码方法设计了适合改进遗传算法应用的适应度函数和交叉、变异算子,定长编码可降低遗传算子设计复杂度和非法个体修补代价;提出在进化流程中嵌入以“去折弯”和“改模式”两种改善型变异方法构建的爬山操作,以提升算法收敛性和寻优能力。通过仿真实验验证所提算法具有可行性和先进性。
DONG Zongran LOU Oujun GUAN Guan Ship pipe route design based on improved genetic algorithm
[J]. Computer Engineering and Applications , 2020 , 56 (19 ): 252 -260 .
DOI:10.3778/j.issn.1002-8331.1906-0251
[本文引用: 2]
<p>In order to solve the Ship Pipe Route Design(SPRD) problem, an improved Genetic Algorithm(GA) optimization method is proposed. Firstly, the model space, constraint conditions and optimization objectives are established for the SPRD problem. Then a fixed-length encoding method based on connection-grids is proposed. Combined with this method, the fitness function and genetic operators such as crossover and mutation are designed for the improved GA. The fixed-length encoding simplifies the implementation of the genetic operators, and can reduce the cost of illegal individual repair. In addition, two improved mutation methods, i.e., “bend-remove” and “mode-change”, are embedded in the evolutionary process as the hill-climbing operator to improve the convergence and optimization abilities of the algorithm. Finally, a simulation experiment is conducted to verify the feasibility and advancement of the proposed algorithm.</p>
[8]
王运龙 , 王晨 , 韩洋 , 等 . 船舶管路智能布局优化设计
[J]. 上海交通大学学报 , 2015 , 49 (4 ): 513 -518 .
[本文引用: 2]
WANG Yunlong WANG Chen HAN Yang et al Intelligent layout optimization design of ship pipe
[J]. Journal of Shanghai Jiao Tong University , 2015 , 49 (4 ): 513 -518 .
[本文引用: 2]
[9]
DONG Z R LIN Y A particle swarm optimization based approach for ship pipe route design
[J]. International Shipbuilding Progress , 2017 , 63 (1-2 ): 59 -84 .
[本文引用: 2]
[10]
LIN Y BIAN X Y DONG Z R A discrete hybrid algorithm based on Differential Evolution and Cuckoo Search for optimizing the layout of ship pipe route
[J]. Ocean Engineering , 2022 , 261 : 1 -13 .
[本文引用: 1]
[11]
BIAN X LIN Y DONG Z Auto-routing methods for complex ship pipe route design
[J]. Journal of Ship Production and Design , 2022 , 38 (2 ): 100 -114 .
[本文引用: 1]
[12]
董宗然 , 林焰 . 基于协同进化和并行计算的船舶管路布置方法
[J]. 大连理工大学学报 , 2016 , 56 (4 ): 367 -374 .
[本文引用: 1]
DONG Zongran LIN Yan Method of ship pipe routing based on co-evolution and parallel computing
[J]. Journal of Dalian University of Technology , 2016 , 56 (4 ): 367 -374 .
[本文引用: 1]
[13]
邢佳鹏 . 基于改进A-star算法的船舶三维管路布局优化设计 [D]. 大连 : 大连理工大学 , 2021 .
[本文引用: 1]
XING Jiapeng Optimal design of ship three-dimensional pipeline layout based on improved A-star algorithm [D]. Dalian : Dalian University of Technology , 2021 .
[本文引用: 1]
[14]
熊勇 , 张加 , 余嘉俊 , 等 . 船舶三维管路智能布局优化算法
[J]. 计算机应用 , 2020 , 40 (7 ): 2164 -2170 .
DOI:10.11772/j.issn.1001-9081.2020010075
[本文引用: 2]
针对船舶在三维环境下管路布局约束多,工程规则难以量化,难以确定合适的优化评价函数等问题,提出一种新的船舶管路自动布局方法。首先,采用轴平行包围盒法(AABB)对船体和船内设备进行简化,将其离散成空间节点并赋予初始信息素和能量值,对空间障碍物进行标记,并对主要的敷管规则给出了具体的量化形式;其次,将快速扩展随机树(RRT)算法和蚁群优化(ACO)算法进行结合,引入方向选择策略、避障策略和变步长策略,提升了算法搜索效率和成功率,通过建立优化评价函数,利用ACO对路径进行循环迭代优化,以期得到满足工程规则的综合最优解;最后,采用计算机模拟的船舱空间布局环境进行管路自动敷设仿真实验,验证了所提方法的有效性和实用性。
XIONG Yong ZHANG Jia YU Jiajun et al Intelligent layout optimization algorithm for 3D pipelines of ships
[J]. Journal of Computer Applications , 2020 , 40 (7 ): 2164 -2170 .
DOI:10.11772/j.issn.1001-9081.2020010075
[本文引用: 2]
In the ship pipeline layout at three-dimensional environment, aiming at the problems that there are too many constraints, the engineering rules are difficult to quantify and the appropriate optimization evaluation function is hard to determine, a new ship pipeline automatic layout method was proposed. Firstly, the hull and ship equipments were simplified by the Aixe Align Bounding Box (AABB) method, which means that they were discretized into space nodes, and the initial pheromones and energy values of them were given, the obstacles in the space were marked, and the specific quantitative forms for the main pipe-laying rules were given. Secondly, with the combination of Rapidly-exploring Random Tree (RRT) algorithm and Ant Colony Optimization (ACO) algorithm, the direction selection strategy, obstacle avoidance strategy and variable step strategy were introduced to improve the search efficiency and success rate of the algorithm, and then the ACO algorithm was used to optimize the path iteratively by establishing the optimization evaluation function, so as to obtain the comprehensive optimal solution that meets the engineering rules. Finally, the computer simulated cabin space layout environment was used to carry out automatic pipe-laying simulation experiments, which verified the effectiveness and practicability of the proposed method.
[15]
DONG Z BIAN X Ship pipe route design using improved A* algorithm and genetic algorithm
[J]. IEEE Access , 2020 , 8 : 153273 -153296 .
[本文引用: 4]
[16]
董宗然 , 王法胜 , 楼偶俊 , 等 . 基于改进NSGA-II 的船舶管路路径设计
[J]. 计算机集成制造系统 , 2022 , 28 (4 ): 1129 -1142 .
[本文引用: 2]
DONG Zongran WANG Fasheng LOU Oujun et al Ship pipe route design based on improved NSGA-II
[J]. Computer Integrated Manufacturing Systems , 2022 , 28 (4 ): 1129 -1142 .
[本文引用: 2]
[17]
WANG Y WEI H ZHANG X et al Optimal design of ship branch pipe route by a cooperative co-evolutionary improved particle swarm genetic algorithm
[J]. Marine Technology Society Journal , 2021 , 55 (5 ): 116 -128 .
[本文引用: 2]
[18]
徐浩天 , 季伟东 , 孙小晴 , 等 . 基于正态分布衰减惯性权重的粒子群优化算法
[J]. 深圳大学学报(理工版) , 2020 , 37 (2 ): 208 -213 .
[本文引用: 2]
XU Haotian JI Weidong SUN Xiaoqing et al A PSO algorithm with inertia weight decay by normal distribution
[J]. Journal of Shenzhen University (Science & Engineering ), 2020 , 37 (2 ): 208 -213 .
[本文引用: 2]
[19]
邹玉堂 , 任光 , 路慧彪 . 船舶管路布置仿真模型简化
[J]. 上海海事大学学报 , 2010 , 31 (1 ): 72 -76 .
[本文引用: 1]
ZHOU Yutang REN Guang LU Huibiao Simulation model simplification for pipe route design of ship
[J]. Journal of Shanghai Maritime University , 2010 , 31 (1 ): 72 -76 .
[本文引用: 1]
[20]
林焰 , 金庭宇 . 一种基于PG-MACO算法的舰船管路布置设计: CN 202211218580.2 [P].2022-12-16[2022-12-09].
[本文引用: 1]
LIN Yan JIN Tingyu A ship pipeline layout design based on PG-MACO algorithm: CN 202211218580.2 [P]. 2022-12-16[2022-12-09].
[本文引用: 1]
[21]
罗朝阳 . 基于CATIA游艇机舱可视化设计 [D]. 武汉 : 武汉理工大学 , 2013 .
[本文引用: 1]
LUO Chaoyang The yacht cabin visual design based on CATIA [D]. Wuhan : Wuhan University of Technology , 2013 .
[本文引用: 1]
[22]
大连理工大学 . 舰船管道自动布置设计PD-MACO算法软件 [M]. 辽宁 : 中华人民共和国国家版权局 , 2022 .
[本文引用: 1]
Dalian University of Technology . PD-MACO algorithm software for automatic layout design of ship pipelines [M]. Liaoning : People’s Republic of China (PRC) National Copyright Administration , 2022 .
[本文引用: 1]
Ship pipe route design using improved multi-objective ant colony optimization
3
2022
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... [1 ]改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... 蚂蚁搜索路径的过程是从起点出发,按照特定规则不断选择下一节点,直至抵达终点,其选择下一节点的过程即为状态转移.传统蚁群算法的思想是从当前节点转移到邻接节点,由于三维空间中节点过多,此方法容易出现大量折弯,不满足管路设计需求.本文提出基于环境信息的空间状态转移策略,根据蚂蚁当前位置的环境信息,如信息素浓度T 、能量值E 、可行域信息F 及相对位置信息D ,首先进行方向决策,设当前节点为n c ,n c 到终点n e 的矢量为V ,ek 为三维正交空间中沿坐标轴正负方向的单位矢量,k 为整数且k ∈[1 ,6 ],相对位置信息Dk 为V 在该方向上的投影距离,距离终点越远越值得探索. 为提升解的随机性,若投影为负,则该方向上仅保留余量ξ ;可行域信息主要考虑各方向上可行节点数量Fk 和信息素的平均浓度Tk ,可行节点越多、信息素浓度越高,则该方向越值得选择.根据下式计算选择各方向的概率: ...
A human-computer cooperation improved ant colony optimization for ship pipe route design
2
2018
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... [2 ]提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
A co-evolutionary improved multi-ant colony optimization for ship multiple and branch pipe route design
3
2015
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... [3 ]对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... (1) 为验证算法改进后的性能提升,以P7-1管路为例进行测试,对比传统蚁群算法与PG-MACO算法的路径搜索效率和算法收敛性,并引用文献[3 ]中的改进蚁群算法为参考,参数设置如表3 所示,图6 为3种算法的收敛对比图.由于3种算法在50~100代间适应度值不变,图6 仅展示0~50代的适应度值, 测试结果表明相比于传统蚁群算法,PG-MACO算法的单次寻路时间缩短58.38%,收敛代数缩短43.24%;相比于参考算法,虽收敛代数稍大,但整体适应度值下降更快. ...
2
2019
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... [4 ]改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
2
2019
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... [4 ]改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
多蚁群协进化的船舶多管路并行布局优化
2
2009
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... [5 ]面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
Multi ant colony cooperative coevolution for optimization of ship multi pipe parallel routing
2
2009
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... [5 ]面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
船舶管路三维布局优化的变长度编码遗传算法
4
2007
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... 除硬性要求外,管路布置还需要考虑降低建造成本、协调布置管路,尽量美观且符合施工要求等,因此优化目标f 需考虑经济性指标f ec 、可操作性指标f op 及协调性指标f co .f ec 主要受管路长度及所需弯头数量影响;可操作性通常考虑管路是否符合施工要求,例如管路通常沿着设备表面或舱壁布置以便于获取足够的支撑,本文引入能量区[6 ] 概念,即对网格节点赋予能量值属性,引导管路向特定区域探索并辅助量化可操作性指标;协调性是指多条管路并行布置程度,本文提出管路并行度概念D par ,即管段轴线在其正交截面上投影点的距离.管道并行布置示意图如图1 所示,有如下表达: ...
... 蚂蚁搜索路径的过程是从起点出发,按照特定规则不断选择下一节点,直至抵达终点,其选择下一节点的过程即为状态转移.传统蚁群算法的思想是从当前节点转移到邻接节点,由于三维空间中节点过多,此方法容易出现大量折弯,不满足管路设计需求.本文提出基于环境信息的空间状态转移策略,根据蚂蚁当前位置的环境信息,如信息素浓度T 、能量值E 、可行域信息F 及相对位置信息D ,首先进行方向决策,设当前节点为n c ,n c 到终点n e 的矢量为V ,ek 为三维正交空间中沿坐标轴正负方向的单位矢量,k 为整数且k ∈[1 ,6 ],相对位置信息Dk 为V 在该方向上的投影距离,距离终点越远越值得探索. 为提升解的随机性,若投影为负,则该方向上仅保留余量ξ ;可行域信息主要考虑各方向上可行节点数量Fk 和信息素的平均浓度Tk ,可行节点越多、信息素浓度越高,则该方向越值得选择.根据下式计算选择各方向的概率: ...
A variable length coding genetic algorithm to ship pipe path routing optimization in 3D space
4
2007
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... 除硬性要求外,管路布置还需要考虑降低建造成本、协调布置管路,尽量美观且符合施工要求等,因此优化目标f 需考虑经济性指标f ec 、可操作性指标f op 及协调性指标f co .f ec 主要受管路长度及所需弯头数量影响;可操作性通常考虑管路是否符合施工要求,例如管路通常沿着设备表面或舱壁布置以便于获取足够的支撑,本文引入能量区[6 ] 概念,即对网格节点赋予能量值属性,引导管路向特定区域探索并辅助量化可操作性指标;协调性是指多条管路并行布置程度,本文提出管路并行度概念D par ,即管段轴线在其正交截面上投影点的距离.管道并行布置示意图如图1 所示,有如下表达: ...
... 蚂蚁搜索路径的过程是从起点出发,按照特定规则不断选择下一节点,直至抵达终点,其选择下一节点的过程即为状态转移.传统蚁群算法的思想是从当前节点转移到邻接节点,由于三维空间中节点过多,此方法容易出现大量折弯,不满足管路设计需求.本文提出基于环境信息的空间状态转移策略,根据蚂蚁当前位置的环境信息,如信息素浓度T 、能量值E 、可行域信息F 及相对位置信息D ,首先进行方向决策,设当前节点为n c ,n c 到终点n e 的矢量为V ,ek 为三维正交空间中沿坐标轴正负方向的单位矢量,k 为整数且k ∈[1 ,6 ],相对位置信息Dk 为V 在该方向上的投影距离,距离终点越远越值得探索. 为提升解的随机性,若投影为负,则该方向上仅保留余量ξ ;可行域信息主要考虑各方向上可行节点数量Fk 和信息素的平均浓度Tk ,可行节点越多、信息素浓度越高,则该方向越值得选择.根据下式计算选择各方向的概率: ...
基于改进遗传算法的船舶管路布局设计
2
2020
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
Ship pipe route design based on improved genetic algorithm
2
2020
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
船舶管路智能布局优化设计
2
2015
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
Intelligent layout optimization design of ship pipe
2
2015
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
A particle swarm optimization based approach for ship pipe route design
2
2017
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
A discrete hybrid algorithm based on Differential Evolution and Cuckoo Search for optimizing the layout of ship pipe route
1
2022
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
Auto-routing methods for complex ship pipe route design
1
2022
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
基于协同进化和并行计算的船舶管路布置方法
1
2016
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
Method of ship pipe routing based on co-evolution and parallel computing
1
2016
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
1
2021
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
1
2021
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
船舶三维管路智能布局优化算法
2
2020
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... [14 ]将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
Intelligent layout optimization algorithm for 3D pipelines of ships
2
2020
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... [14 ]将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
Ship pipe route design using improved A* algorithm and genetic algorithm
4
2020
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... [15 -16 ]将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... (3) 为进一步验证本算法的有效性,与其他类型的算法进行比较,参照文献[15 ]中提出的GA-A* 算法,使用该文献中的船舶机舱燃油管路布置算例进行验证, 案例中包含燃油舱、燃油输送泵、燃油储罐、船用主机、柴油发电机和锅炉等设备,需要布置8条燃油管道P1~P8,具体坐标信息参照文献[15 ],PG-MACO算法的测试结果如图8 所示,数据统计结果如表5 所示.从图中可看出PG-MACO算法能够协同布置多条管路、分支管路的重叠性良好、能够沿着舱壁及设备表面布置,虽然在折弯次数方面PG-MACO略多于GA-A* ,但PG-MACO算法整体长度更短,通过对比验证了PG-MACO算法具备较强的有效性,工程应用价值较高. ...
... 算法,使用该文献中的船舶机舱燃油管路布置算例进行验证, 案例中包含燃油舱、燃油输送泵、燃油储罐、船用主机、柴油发电机和锅炉等设备,需要布置8条燃油管道P1~P8,具体坐标信息参照文献[15 ],PG-MACO算法的测试结果如图8 所示,数据统计结果如表5 所示.从图中可看出PG-MACO算法能够协同布置多条管路、分支管路的重叠性良好、能够沿着舱壁及设备表面布置,虽然在折弯次数方面PG-MACO略多于GA-A* ,但PG-MACO算法整体长度更短,通过对比验证了PG-MACO算法具备较强的有效性,工程应用价值较高. ...
基于改进NSGA-II 的船舶管路路径设计
2
2022
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... -16 ]将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
Ship pipe route design based on improved NSGA-II
2
2022
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... -16 ]将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
Optimal design of ship branch pipe route by a cooperative co-evolutionary improved particle swarm genetic algorithm
2
2021
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... [17 ]将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
基于正态分布衰减惯性权重的粒子群优化算法
2
2020
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... 上述研究对管路自动布置问题做出了积极贡献,对于核动力舰船而言,其内部布置环境则更为复杂.本文结合核动力舰船的工程背景,在经典蚁群算法(ACO)的基础上改进,提出更适用于三维空间管路布置优化的信息素高斯扩散多蚁群优化(Pheromone Gaussian diffusion Multi Ant Colony Optimization,PG-MACO)算法,由于ACO的核心在于利用信息素启发蚂蚁间的协作,因此引入基于高斯分布[18 ] 的信息素扩散机制、改进蚂蚁寻路过程的空间状态转移策略以及面向混合管路布置工况设计的协同进化机制,使得算法的自动化程度、计算效率、求解效果得到提升,开发管路自动布置软件系统实现算法的工程应用,在核级一回路管道布置工程案例和船舶机舱燃油管路布置案例中验证PG-MACO算法的有效性. ...
A PSO algorithm with inertia weight decay by normal distribution
2
2020
... 管路设计是船舶设计中非常重要的一环,传统的设计方式依赖人工,设计过程繁琐且效率低下.随着计算机技术的发展,管路设计工作向数字化和自动化的方向发展,管路自动布置算法成为近些年来研究的热点,文献[1 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -9 ]中采用启发式算法进行管路布局,Dong等[1 ] 改进蚁群算法的关键技术,提出人工解与Pareto解组合的方法;Wang等[2 ] 提出一种人机合作机制下的改进蚁群算法,将人工解和算法解有机结合,有效利用设计人员经验及计算机算力;Jiang等[3 ] 对蚁群算法的信息素赋予方向属性,提出方向和距离选择相结合的路径搜索方法,提高算法的搜索效率;陈杨[4 ] 改进了信息素的表达与更新方式以及路径点的选取规则,提高了蚁群算法的性能;范小宁等[5 ] 面向多管路布置工况设计多蚁群协同进化算法;文献[6 ⇓ -8 ]中将改进遗传算法应用于船舶管路布置;文献[9 ]和文献[10 ]中则分别对粒子群算法以及布谷鸟算法改进,实现船舶管路优化布置.文献[11 ⇓ -13 ]中采用确定性算法中典型的A* 算法为基础,研究船舶单管路、多管路及分支管路的布置方法.启发式算法和确定性算法各有优劣,文献[14 ⇓ ⇓ ⇓ -18 ]中将不同的算法融合,熊勇等[14 ] 将快速扩展随机树算法与蚁群算法相结合,提出变步长搜索策略并利用蚁群算法优化路径,提升了算法的效率和鲁棒性;Dong等[15 -16 ] 将A* 算法与遗传算法融合提出GA-A* 算法和改进NSGA-II算法;Wang等[17 ] 将粒子群算法和遗传算法融合应用于船舶分支管路的路径设计. ...
... 上述研究对管路自动布置问题做出了积极贡献,对于核动力舰船而言,其内部布置环境则更为复杂.本文结合核动力舰船的工程背景,在经典蚁群算法(ACO)的基础上改进,提出更适用于三维空间管路布置优化的信息素高斯扩散多蚁群优化(Pheromone Gaussian diffusion Multi Ant Colony Optimization,PG-MACO)算法,由于ACO的核心在于利用信息素启发蚂蚁间的协作,因此引入基于高斯分布[18 ] 的信息素扩散机制、改进蚂蚁寻路过程的空间状态转移策略以及面向混合管路布置工况设计的协同进化机制,使得算法的自动化程度、计算效率、求解效果得到提升,开发管路自动布置软件系统实现算法的工程应用,在核级一回路管道布置工程案例和船舶机舱燃油管路布置案例中验证PG-MACO算法的有效性. ...
船舶管路布置仿真模型简化
1
2010
... 考虑到管路与设备不得发生干涉、管路不得逾越布置空间等硬性要求,在约束条件中将设备视为障碍物,管路的节点集合均在布置空间中,且不得与障碍物存在交集.为降低计算复杂度,采用轴平行包围盒法[19 ] 适当简化设备,即对设备轮廓进行规则几何体包络,简化为由对角点坐标确定的长方体,有如下表达: ...
Simulation model simplification for pipe route design of ship
1
2010
... 考虑到管路与设备不得发生干涉、管路不得逾越布置空间等硬性要求,在约束条件中将设备视为障碍物,管路的节点集合均在布置空间中,且不得与障碍物存在交集.为降低计算复杂度,采用轴平行包围盒法[19 ] 适当简化设备,即对设备轮廓进行规则几何体包络,简化为由对角点坐标确定的长方体,有如下表达: ...
1
... 由算法计算得到混合管路的整体流程图如图3 所示,该算法已公开申请发明专利[20 ] .管路布置算法的计算结果需要转化为工程设计成果,本文基于COM二次开发技术[21 ] 将算法应用于第三方设计软件,使用Python语言开发管路自动布置功能,输入信息包括管路接口坐标信息、设备坐标信息、管径及算法参数等,程序调用内部函数接口实现管路自动绘制,此部分研究现获得软件著作授权[22 ] ,绘制完成后需为其添加附件,如弯头、三通等、阀门等.为提高设计效率,可客户化定制专属管路零件库,存储常用附件及设备模型供装配时调用.定制方法如图4 所示,零件库示意图如图5 所示. ...
1
... 由算法计算得到混合管路的整体流程图如图3 所示,该算法已公开申请发明专利[20 ] .管路布置算法的计算结果需要转化为工程设计成果,本文基于COM二次开发技术[21 ] 将算法应用于第三方设计软件,使用Python语言开发管路自动布置功能,输入信息包括管路接口坐标信息、设备坐标信息、管径及算法参数等,程序调用内部函数接口实现管路自动绘制,此部分研究现获得软件著作授权[22 ] ,绘制完成后需为其添加附件,如弯头、三通等、阀门等.为提高设计效率,可客户化定制专属管路零件库,存储常用附件及设备模型供装配时调用.定制方法如图4 所示,零件库示意图如图5 所示. ...
1
2013
... 由算法计算得到混合管路的整体流程图如图3 所示,该算法已公开申请发明专利[20 ] .管路布置算法的计算结果需要转化为工程设计成果,本文基于COM二次开发技术[21 ] 将算法应用于第三方设计软件,使用Python语言开发管路自动布置功能,输入信息包括管路接口坐标信息、设备坐标信息、管径及算法参数等,程序调用内部函数接口实现管路自动绘制,此部分研究现获得软件著作授权[22 ] ,绘制完成后需为其添加附件,如弯头、三通等、阀门等.为提高设计效率,可客户化定制专属管路零件库,存储常用附件及设备模型供装配时调用.定制方法如图4 所示,零件库示意图如图5 所示. ...
1
2013
... 由算法计算得到混合管路的整体流程图如图3 所示,该算法已公开申请发明专利[20 ] .管路布置算法的计算结果需要转化为工程设计成果,本文基于COM二次开发技术[21 ] 将算法应用于第三方设计软件,使用Python语言开发管路自动布置功能,输入信息包括管路接口坐标信息、设备坐标信息、管径及算法参数等,程序调用内部函数接口实现管路自动绘制,此部分研究现获得软件著作授权[22 ] ,绘制完成后需为其添加附件,如弯头、三通等、阀门等.为提高设计效率,可客户化定制专属管路零件库,存储常用附件及设备模型供装配时调用.定制方法如图4 所示,零件库示意图如图5 所示. ...
1
2022
... 由算法计算得到混合管路的整体流程图如图3 所示,该算法已公开申请发明专利[20 ] .管路布置算法的计算结果需要转化为工程设计成果,本文基于COM二次开发技术[21 ] 将算法应用于第三方设计软件,使用Python语言开发管路自动布置功能,输入信息包括管路接口坐标信息、设备坐标信息、管径及算法参数等,程序调用内部函数接口实现管路自动绘制,此部分研究现获得软件著作授权[22 ] ,绘制完成后需为其添加附件,如弯头、三通等、阀门等.为提高设计效率,可客户化定制专属管路零件库,存储常用附件及设备模型供装配时调用.定制方法如图4 所示,零件库示意图如图5 所示. ...
1
2022
... 由算法计算得到混合管路的整体流程图如图3 所示,该算法已公开申请发明专利[20 ] .管路布置算法的计算结果需要转化为工程设计成果,本文基于COM二次开发技术[21 ] 将算法应用于第三方设计软件,使用Python语言开发管路自动布置功能,输入信息包括管路接口坐标信息、设备坐标信息、管径及算法参数等,程序调用内部函数接口实现管路自动绘制,此部分研究现获得软件著作授权[22 ] ,绘制完成后需为其添加附件,如弯头、三通等、阀门等.为提高设计效率,可客户化定制专属管路零件库,存储常用附件及设备模型供装配时调用.定制方法如图4 所示,零件库示意图如图5 所示. ...