基于倾斜关联筛选的船舶分区消磁绕组部署及消磁电流优化策略

doi:10.16183/j.cnki.jsjtu.2022.417

基于倾斜关联筛选的船舶分区消磁绕组部署及消磁电流优化策略

田野¹, 余墨多^,¹, 黄文焘¹, 邰能灵¹, 牛璐²

1.上海交通大学电子信息与电气工程学院, 上海 200240

2.中国船舶工业公司第七〇八研究所, 上海 200011

Degaussing Coil Deployment and Degaussing Current Optimization Strategy for Ship Partition Based on Tilted Correlation Screening

TIAN Ye¹, YU Moduo^,¹, HUANG Wentao¹, TAI Nengling¹, NIU Lu²

1. School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. Marine Design and Research Institute of China, Shanghai 200011, China

通讯作者: 余墨多,助理研究员;E-mail:379440278@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2022-10-20 修回日期: 2022-12-6 接受日期: 2023-01-10

Received: 2022-10-20 Revised: 2022-12-6 Accepted: 2023-01-10

作者简介 About authors

田野(1996-),硕士生,从事船舶消磁研究.

摘要

在现代舰船消磁系统中,消磁绕组主要基于舰船舱壁的形状进行分布,难以保证每个消磁绕组的消磁效果.为解决这一问题,引入一种高维变量筛选中的倾斜关联筛选方法,选择合适的阈值,将原有绕组进行拆分重组,对原有消磁区段进行重新划分,进而改善每个绕组的单位绕组磁感应强度.针对绕组重组后消磁电流计算时存在的参数向量稀疏和多重共线的问题,提出了倾斜关联筛选-部分岭回归算法,通过仿真可知,在阈值为0.73和0.91时,该算法相较最小二乘法消磁误差最大幅值分别减小了10.08%和17.59%,而剩余均方根误差分别减小了10.45%和12.17%.根据仿真结果可知,采用该算法后消磁效果得到明显提升.

关键词： 船舶消磁; 倾斜关联筛选; 最小二乘法; 部分岭回归; 区段划分

Abstract

In modern ship degaussing systems, degaussing windings are mainly distributed based on the shape of ship bulkhead, which is difficult to ensure the degaussing effect of magnetic induction intensity of unit winding of each degaussing winding. In order to solve this problem, this paper introduces a tilted correlation screening in high-dimensional variable filter, which splits and recombines the original coils, and re-divides the original degaussing sections, so as to improve the degaussing efficiency of each coil. Aiming at the problem of sparse parameter vectors and multiple collinearity in the calculation of degaussing current after winding restructuring, this paper proposes a slant correlation screening and partial ridge regression algorithm. Through simulation, when the threshold is 0.73 and 0.91, the algorithm reduces 10.08% and 17.59% respectively compared with the least square method, while the residual root mean square error decreases by 10.45% and 12.17%. The simulation results show that the degaussing effect is significantly improved after the algorithm is adopted.

Keywords： ship degaussing; tilted correlation screening; least square method; partial ridge regression; section partition

PDF (3102KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

田野, 余墨多, 黄文焘, 邰能灵, 牛璐. 基于倾斜关联筛选的船舶分区消磁绕组部署及消磁电流优化策略[J]. 上海交通大学学报, 2024, 58(7): 1018-1026 doi:10.16183/j.cnki.jsjtu.2022.417

TIAN Ye, YU Moduo, HUANG Wentao, TAI Nengling, NIU Lu. Degaussing Coil Deployment and Degaussing Current Optimization Strategy for Ship Partition Based on Tilted Correlation Screening[J]. Journal of Shanghai Jiaotong University, 2024, 58(7): 1018-1026 doi:10.16183/j.cnki.jsjtu.2022.417

现代舰船船体及船上设备一般都是由铁磁材料制成,在舰船制造和航行的过程中不可避免地会受到地磁场的影响,产生水下异常感应磁场.同时,磁探技术及磁引信武器的发展对舰船的磁性防护提出了更高的要求,基于消磁绕组的感应磁场补偿方法成为提高舰船磁隐身能力的关键^[1⇓-3].为了有效提升舰船的磁隐身防护,需要分析舰船磁特征,并对舰船消磁系统的消磁绕组进行仿真建模,设计合适的绕组配置,以达到有效消除舰船磁场的目的^[4].

随着舰船的尺寸不断增加,舰船的磁场分布越来越复杂,需要更多的消磁绕组来对感应磁场进行补偿.传统的舰船消磁系统多采用单一消磁回路进行消磁,但由于如今舰船尺寸较大,单一回路消磁方法消磁效果不甚理想.针对单一回路消磁方法的弊端,唐申生等^[5]首次提出了分区消磁的思想.其研究表明,与单一回路消磁相比,分区消磁不仅能减轻消磁系统的质量,提高消磁系统的可靠性和可维修性,还能适应舰船分段建造要求.但是分区消磁的消磁区段主要基于船舱壁的形状划分,导致每个区段消磁绕组的单位绕组磁感应强度存在较大的差异,无法保证整体的消磁效果.

目前,针对分区消磁绕组部署不合理而导致消磁效果较差的问题,研究人员提出了消磁绕组部署优化的方法.左超等^[6]提出了一种基于遗传算法的消磁绕组部署优化方法,通过有限元仿真软件建立船舶的静态磁场等效模型,结合逐步遍历法以及遗传算法对消磁绕组的安匝量以及位置分布进行了优化设计.结果表明,消磁绕组部署优化之后,消磁效果得到明显提升.然而,当消磁绕组数量较多时,由于变量较多,该方法难以得到最优解.

针对以上问题,研究人员又提出了消磁绕组电流优化方法来提升消磁效果.Kim等^[7]将最小二乘法运用到舰船消磁中:首先求解出各个消磁绕组的单位绕组磁感应强度,然后采用所有的消磁绕组去拟合舰船的感应磁场,最后计算出各个消磁绕组的电流大小,以此来最大程度降低舰船下方异常感应磁场.然而这种方法仅考虑了剩余磁场均方根误差最小的情况,不能实现剩余磁场峰值误差最小的目的.针对以上问题,研究人员采用群体智能算法对消磁绕组电流进行优化,例如遗传算法、随机粒子群算法、多种群粒子群算法、线性递减权重的粒子群.还有部分研究人员考虑计算消磁绕组的电感大小^[8⇓⇓-11],进而实现对消磁电流的优化.上述方法在消磁绕组数量较少的情况下可以取得较好的效果,但是考虑到现代大型舰船上的消磁绕组数量较多,采用上述智能算法,存在计算效率较低、优化结果不理想的缺点.针对现代大型舰船消磁绕组数量较多的问题,Vishal等^[12]提出了一种基于广义岭回归的消磁绕组计算方法,结果表明该方法消磁效果良好.但是广义岭回归具有以下局限性:未考虑多重共线性的程度,对所有回归变量都施加了偏差,进而导致均方根误差稳定性下降.综上所述,现有的消磁绕组电流计算方法大多未考虑消磁绕组数量较多时的消磁问题,在消磁绕组较多的情况下,绕组部署不合理且数量较多,因此不能保证消磁电流求解的效率及准确性.

针对消磁绕组位置优化和消磁电流求解的难题,本文提出了基于倾斜关联筛选-部分岭回归算法的消磁绕组优化策略,该方法先将分布式消磁系统的绕组进行拆分,对消磁绕组进行相关性筛选,将相关性高的绕组进行合并,并对原有消磁绕组的部署优化,进而改善每个绕组的单位绕组磁感应强度,使得整体的消磁效果得到提升,并可兼顾求解效率.同时,针对现代舰船消磁绕组数量较多的问题,提出了一种消磁电流计算方法,首先通过倾斜关联筛选筛选出与残差关联度高的变量,去除掉关联度较低的变量,并在每次迭代过程中采用部分岭回归计算出回归系数.

在消磁绕组部署优化时,通过分析各个绕组之间的关联度,对关联度高的相邻绕组进行合并,在保证消磁绕组单位绕组磁感应强度的前提下,大幅降低消磁绕组部署优化求解步骤与时间,提高绕组优化效率.针对大型舰船消磁绕组数量多的问题,通过高维变量筛选,筛选出与感应磁场关联度较高的绕组,以提高求解效率.针对广义岭回归算法稳定性较差的问题,对筛选后的变量进行部分岭回归,尽可能降低剩余磁场均方根值,进而提高整体计算稳定性.

1 分区消磁原理及流程

1.1 消磁理论

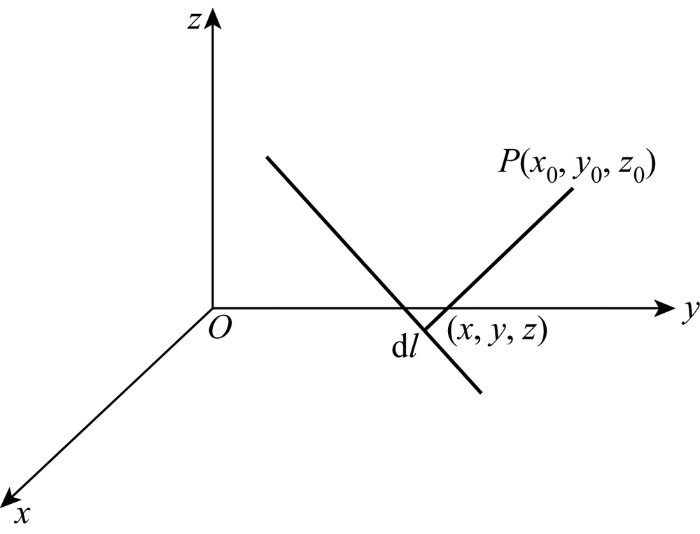
根据静磁场理论,图1所示的载流导线在距离为r的点P(x₀, y₀, z₀)处所产生的磁感应强度和磁场强度由Biot.Savart定理可得:

(1)dH=

\frac{I d l \times r}{4 π r^{3}}

式中:H为磁场强度;I为源电流;dl是源电流的微小线元素;r为空间点(x₀, y₀, z₀)到(x, y, z)之间的距离,r=[(x₀-x)²+(y₀-y)²+(z₀-z)²]¹^/².

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 电流元磁场

Fig.1 Magnetic field of current element

由式(1)可得,单根直导线在周围空间所产生的磁场强度:

(2)H(x₀, y₀, z₀)=

\frac{I}{4 π} \int_{A}^{B} \frac{d l \times r}{r^{3}}

\frac{I}{4 π} \int_{x_{1}}^{x_{2}} \frac{(y_{0} - y) \hat{k} - (z_{0} - z) \hat{j}}{[(x_{0} {- x)}^{2} + (y_{0} {- y)}^{2} + (z_{0} {- z)}^{2}]^{3 / 2}}

dx+

\frac{I}{4 π} \int_{y_{1}}^{y_{2}} \frac{(z_{0} - z) \hat{i} - (x_{0} - x) \hat{k}}{[(x_{0} {- x)}^{2} + (y_{0} {- y)}^{2} + (z_{0} {- z)}^{2}]^{3 / 2}}

dy+

\frac{I}{4 π} \int_{z_{1}}^{z_{2}} \frac{(x_{0} - x) \hat{j} - (y_{0} - y) \hat{i}}{[(x_{0} {- x)}^{2} + (y_{0} {- y)}^{2} + (z_{0} {- z)}^{2}]^{3 / 2}}

式中:I为源电流;A, B分别表示单根导线的起点和终点; $\hat{i}$ , $\hat{j}$ , $\hat{k}$ 分别x,y,z轴上的单位向量.

消磁系统产生的总磁场可以看作所有消磁绕组产生磁场的叠加,而单个绕组的磁场又可以视为各段直导线的叠加,因此整个消磁系统产生的磁场其实是各段直导线磁场的叠加.

1.2 分区消磁原理及流程

现有的消磁绕组部署区段划分时需要遵循以下原则^[3]:

(1) 各绕组电缆应尽量敷设在一起,进而提高空间利用率,降低施工难度.

(2) 为使绕组的磁场在纵向与舰船磁场形状吻合,各绕组应从首至尾分成若干区段,并根据舰船磁场变化剧烈程度,调整区段划分的疏密程度.

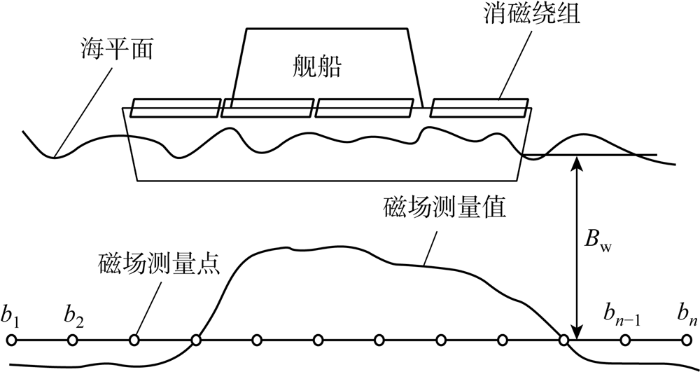
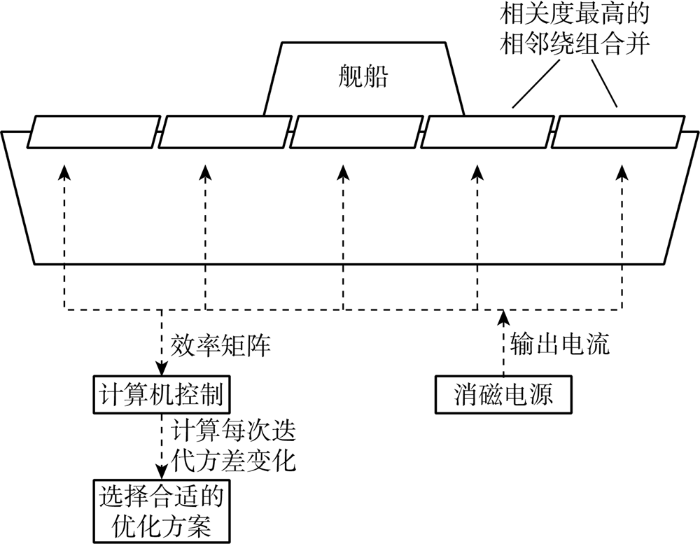
基于以上原则,从技术与实际合理性角度可以选择合适的分区方案,并设计消磁绕组的安装位置.采用分区消磁技术的舰船消磁系统,每个消磁绕组电流可单独进行控制,图2展示了一种典型消磁系统原理图.舰船共有若干消磁绕组且每个绕组都单独供电.在不同通电条件下,可测量舰船感应磁场及每个消磁绕组的单位绕组磁感应强度大小.磁场测量点一般设定在龙骨下方B_w(B_w表示船体宽度)的位置,共设置n个测量点b₁~b_n.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 典型消磁系统原理图

Fig.2 Schematic of a typical degaussing system

首先,在各个绕组均未通电的情况下,测量舰船在地磁场激励下产生的感应磁场大小,并形成向量B,记为

(3)B=[b₁b₂ … b_n]^T

然后依次对每个绕组通入1 A的电流,测出每个消磁绕组的单位绕组磁感应强度,形成效率矩阵G,记为

(4)G=

[\begin{array}{l} g_{11} & g_{12} & g_{13} & \dots & g_{1 p} \\ g_{21} & g_{22} & g_{23} & \dots & g_{2 p} \\ g_{31} & g_{32} & g_{33} & \dots & g_{3 p} \\ ︙ & ︙ & ︙ & ︙ \\ g_{n 1} & g_{n 2} & g_{n 3} & \dots & g_{n p} \end{array}]

式中:g_ij表示绕组j在第i个测量点的单位绕组磁感应强度,i=1, 2,…,n,j=1, 2,…,p,n表示测量点数量,p表示绕组的数量.通过计算优化绕组电流I=[I₁I₂ … I_p]^T,使得所有绕组的产生的磁场正好能够抵消舰船产生的感应磁场:

(5)GI+B=0

式(5)可以看成一个多元回归方程,该方程一般不能直接求解,I可以通过求解目标函数的均方根误差的最小值来计算得出,计算方程如下:

(6)f_RMS(I)=min

\overset{n}{\sum_{i = 1}}

(

\overset{p}{\sum_{j = 1}}

g_ijI_j-b_i)²

通过式(6)得到求解最优的消磁电流I,并将求得的电流I通入消磁绕组中,以产生与感应磁场磁场大小相同、方向相反的磁场,进而减小舰船的磁场信号特征,提升舰船安全性能^[13-14].

2 绕组部署优化策略

根据1.1节所描述的消磁理论可知,整个消磁系统产生的磁场其实是由各段直导线磁场的叠加而成,可以将每根导线的单位绕组磁感应强度视为变量,将舰船的感应磁场视为响应,对每根导线进行筛选和重组,从而提高消磁绕组的单位绕组磁感应强度.但是考虑到消磁绕组的实际安装过程,消磁绕组导线之间的组合存在一定限制.因此本文提出以下策略:选取所有船舱壁宽度的最小公约数为单位宽度,将原有绕组拆分为单位宽度,这样尽可能保证拆分后的绕组依旧沿着舱壁分布,减小绕组安装的难度,并将拆分后的绕组按照设定的阈值进行重组,从而提升消磁绕组的单位绕组磁感应强度.基于以上因素,本文提出的优化算法在工程实践运用中具有广泛的应用前景.

首先对原有绕组进行拆分.根据上述的拆分策略,可将原有绕组拆分为单位宽度的绕组,拆分前后如图3、图4 所示.根据消磁理论,若保证拆分前后的绕组通入相同的电流,两者产生的磁场效果完全相同.因此,此拆分策略对绕组产生的磁场效果不产生影响.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 拆分前绕组图

Fig.3 Coil diagram before split

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 拆分后绕组图

Fig.4 Coil diagram after split

在绕组部署优化过程中,可以将原绕组拆分为m个单位宽度的新绕组,对新绕组通入1 A电流,测量新绕组在各个测量点的效率矩阵R:

(7)R=

[\begin{array}{l} r_{11} & r_{12} & \dots & r_{1 m} \\ r_{21} & r_{22} & \dots & r_{2 m} \\ ︙ & ︙ & ︙ \\ r_{n 1} & r_{n 2} & \dots & r_{n m} \end{array}]

式中:r_ij'表示拆分后的绕组j'在第i个测量点的单位绕组磁感应强度,j'=1, 2,…,m.将消磁矩阵R单位化后,计算各个消磁绕组之间的关联度A:

(8)A=R^TR=

[\begin{array}{l} a_{11} & a_{12} & a_{13} & \dots & a_{1 m} \\ a_{21} & a_{22} & a_{23} & \dots & a_{2 m} \\ a_{31} & a_{32} & a_{33} & \dots & a_{3 m} \\ ︙ & ︙ & ︙ & ︙ \\ a_{m 1} & a_{m 2} & a_{m 3} & \dots & a_{m m} \end{array}]

式中:a_ij表示第i个绕组与第j个绕组之间的单位绕组磁感应强度关联度,a₂₁,a₃₂,…,a_m₍_m_-1)则表示相邻绕组之间的关联度.若相邻绕组单位的磁感应强度关联度大于设定的阈值V,则表明两个绕组的单位绕组磁感应强度相近,可以将单位绕组磁感应强度相近的绕组合并为一个新绕组.

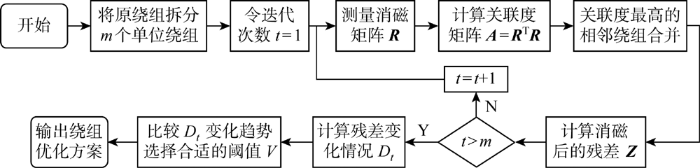
具体绕组的筛选重组流程如下.

(1) 选取船舱壁宽度的最小公约数为单位宽度,将原有消磁绕组拆分为m个单位宽度的消磁绕组.

(2) 测量拆分后各个消磁绕组的单位绕组磁感应强度,形成消磁矩阵R.消磁矩阵R是一个n×m的矩阵,表明共有m个线圈,每个消磁绕组有n个测量点.

(3) 将消磁矩阵单位化,计算各消磁绕组之间的关联度矩阵A,其中a_ij表示第i个绕组与第j个绕组之间的单位绕组磁感应强度关联度,则a₂₁,a₃₂,…, a_m₍_m_-1)则可以表示相邻绕组之间的关联度.

(4) 比较关联度矩阵A中a₂₁,a₃₂,…, a_m₍_m_-1)的大小,选取其中数值最大的量a₍_k₊₁₎_k,此时消磁绕组k与消磁绕组k+1是关联度最高的相邻线圈,对这两个相邻绕组进行合并.

(5) 测量合并之后绕组的单位绕组磁感应强度,计算绕组的消磁电流,并计算残差大小Z_t:

(9)Z_t=[

\begin{array}{l} z_{1 t} & z_{2 t} & \dots & z_{n t} \end{array}

]^T

式中:z_it表示第t次迭代时,在第i个测量点的残余的磁场大小,t=1, 2,…,m.

(6) 重复步骤(2)~(5),直到所有绕组都进行了合并.

(7) 计算每次迭代残差变化的情况:

(10)D_t=

\overset{n}{\sum_{i = 1}}

(z_it-z_i₍_t₊₁₎)²

式中:D_t表示第t次迭代时,残差平方差之和的变化情况.

(8) 比较每次残差变化的情况,选取在整个迭代过程中残差变化较为明显时对应的阈值,表明此时绕组相较上一次迭代,其安装成本变化不大,但消磁效果却发生了明显变化.分别选取这个阈值对绕组的部署进行优化,并对比不同阈值下消磁效果,结合实际情况选择合适的阈值进行优化重组.

绕组部署优化的示意图如图5所示,绕组筛选重组流程图如图6所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 绕组位置优化示意图

Fig.5 Schematic of coil position optimization

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 绕组筛选重组流程图

Fig.6 Flow chart of coil screening recombination

3 消磁绕组电流计算

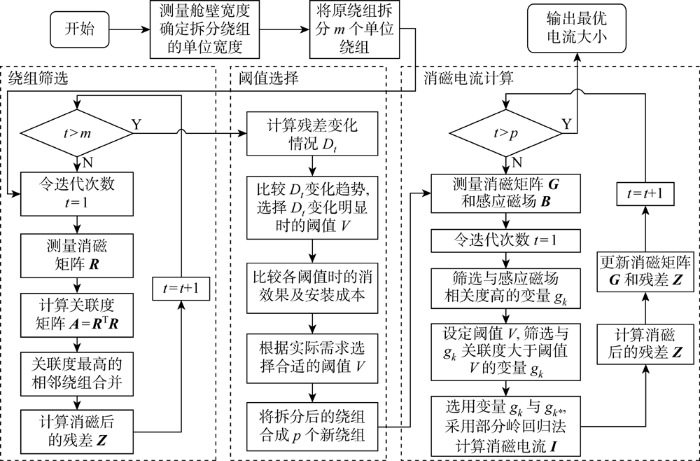
通过第2节的优化策略,消磁绕组在拆分后,绕组数量得到明显提升,数据量显著增加,导致计算消磁绕组电流时产生以下问题.

(1) 参数向量稀疏.由于绕组的数量p较大,通常只有少量的预测因子对响应有贡献.

(2) 多重共线问题.当对相同的或对称的绕组进行测量,或测量网格距离船的龙骨线非常远时,会出现多重共线性的问题.

为了解决以上两个问题,需要对消磁电流计算方法进行改进.本文采用高维变量筛选中的倾斜相关筛选方法来解决参数向量稀疏的问题,并用部分岭回归的方法来解决多重共线的问题.消磁电流计算过程的具体步骤如下.

(1) 测量绕组效率矩阵G及感应磁场大小B.

(2) 筛选出与感应磁场关联度较高的消磁绕组.

(3) 再筛选出与步骤(2)中选中的消磁绕组关联度较高的消磁绕组.

(4) 采用部分岭回归法计算筛选出的消磁绕组的电流大小.

(5) 计算残差大小,再根据残差重复(1)~(4),直到计算出所有消磁绕组的电流大小.

3.1 基于倾斜关联筛选的绕组选择

倾斜关联筛选为每个变量提供了一个在使用边际相关和倾斜相关之间的自适应选择,其中变量选取与设计矩阵的硬阈值相关,可成功地区分相关和不相关的变量,从而作为变量选择的工具.倾斜关联筛选算法可描述为以下步骤.

(1) 定义集合F为空集,当前残差为Z和设计矩阵为M,则线性回归模型为Z=Mβ+ε, 其中β为回归系数,ε为误差量.

(2) 找到M中与Z达到最大边际相关性的变量m_k,使得k=arg max_j_∉_F| ${m^{T}}_{j}$ Z|.

(3) 找到M中与m_k关联度大于设定阈值V_n的变量,使得C_k={j∉F, j≠k∶| ${m^{T}}_{k}$ m_j|>V_n},如果C_k=⌀,则令k^*=k.

(4) 如果C_k=⌀,找到k^*= $a r g m a x_{j \in C_{k} ⋃ {k}} |c_{j}^{*}|$ , $c_{j}^{*}$ 为C_k中的向量.

(5) 将k^*添加到F中,并更新当前残差和当前设计矩阵z←(I_n-X_F( ${X^{T}}_{F}$ X_F)^-1 ${X^{T}}_{F}$ )y,和M←(I_n-X_F( ${X^{T}}_{F}$ X_F)^-1 ${X^{T}}_{F}$ )X, 之后将M的每一列重新调整为1范数.其中X为设计矩阵;X_F为特征向量.

3.2 基于部分岭回归原理电流计算

由于消磁绕组电流的计算过程存在多重共线的问题,若在倾斜关联筛选的每次迭代中,将所选变量对应的系数设置为最小二乘估计,则会导致结果很差.因此在每次迭代过程中,采用岭回归来进行估计.但由于岭回归在最小二乘法的目标函数加上了收缩惩罚项,这种方法具有局限性^[15-16]:① 偏差适用于所有的回归变量,而不考虑多重共线性的程度;② 稳定性是以增加均方根误差为代价来实现的;③ k值的选择方法较为随意.而采用广义岭回归计算消磁电流时,由于未考虑变量的共线性水平,k的加入会导致对所有回归变量的偏差.因此本文采用部分岭回归来进行消磁电流的计算.

在部分岭回归中,k只被添加到部分回归变量中.此方法的优势:① 偏差将被减少,估计值预计将比岭回归回归更接近真实的β;② 总体方差将显著减少.部分岭回归可以描述为以下步骤.

(1) 对X^TX进行奇异值分解,其中X=[X₁ … X_p]^T是一个p×n设计矩阵.

(2) 计算回归系数β_R,

(11)β_R=(UΔU^T+kH)^-1X^Ty=

{\{U [\begin{array}{l} λ_{1} & \dots & 0 \\ ︙ & ︙ \\ 0 & \dots & λ_{p} \end{array}] U^{T} + [\begin{array}{l} k_{1} & \dots & 0 \\ ︙ & ︙ \\ 0 & \dots & k_{p} \end{array}]\}}^{- 1}

X^Ty

式中:U为特征向量;λ₁,…,λ_p为X^TX的特征向量,其大小依次递减.设定阈值为特征向量最大值λ₁的千分之一.若特征值小于阈值,则设定偏差值k=0;若特征值大于阈值,则按照广义岭回归计算偏差值k.

综上所述,舰船分区消磁绕组部署及消磁电流优化的具体流程图如图7所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 消磁绕组部署及消磁电流优化流程图

Fig.7 Flow chart of degaussing winding deployment and degaussing current optimization

4 算例分析

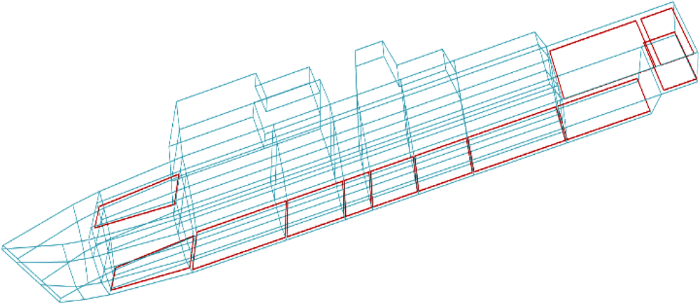
图8给出了舰船简化模型,船长为150 m,船宽为14 m,测量线为龙骨下方14 m处,测量线上均匀分布101个测量点,船上共分布12个垂向消磁绕组,具体参数如表1所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 简化舰船模型及绕组布置示意图

Fig.8 Simplified ship model and schematic diagram of winding arrangement

表1 磁性模型参数表

Tab.1 Parameters of magnetic model

参数	取值
长度/m	150
宽度/m	14
高度/m	23
船壳厚度/mm	7
船壳相对磁导率,μ_r	260
地磁场大小,B_Earth/μT	50

新窗口打开| 下载CSV

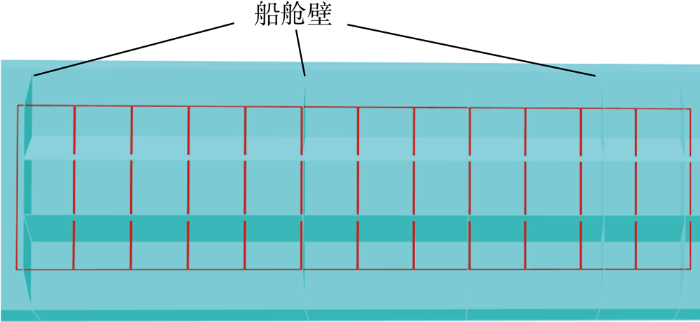
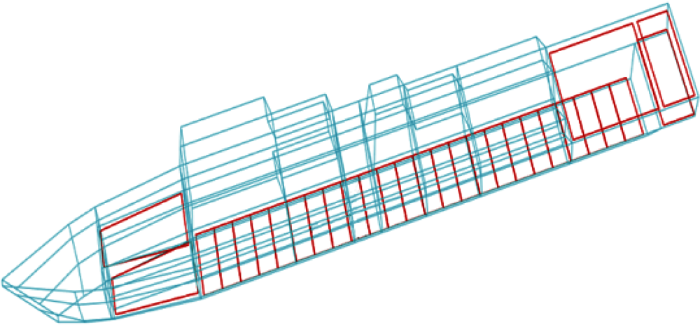
首先是对底部绕组部署进行优化.为了保证拆分重组后的绕组不会出现安装问题,选择原绕组宽度的最小公约数为单位绕组宽度,对舰船下方的消磁绕组进行拆分,拆分后的消磁绕组如图9所示.拆分后的绕组共有24个,从右到左依次命名为L1, L2, …, L24.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 消磁绕组拆分后绕组示意图

Fig.9 Schematic diagram of the winding after the split of degaussing coil

首次测量拆分后绕组的单位绕组磁感应强度,计算各绕组单位绕组磁感应强度关联度如表2所示.

表2 相邻绕组单位绕组磁感应强度关联度表

Tab.2 Correlation of magnetic induction intensity of unit winding of adjacent winding

绕组序号	关联度	绕组序号	关联度
L1-L2	0.769 362	L13-L14	0.962 847
L2-L3	0.591 805	L14-L15	0.781 647
L3-L4	0.910 071	L15-L16	0.536 287
L4-L5	0.613 498	L16-L17	0.419 504
L5-L6	0.872 680	L17-L18	0.873 163
L6-L7	0.640 723	L18-L19	0.918 340
L7-L8	0.749 592	L19-L20	0.714 019
L8-L9	0.829 750	L20-L21	0.953 347
L9-L10	0.696 601	L21-L22	0.826 416
L10-L11	0.797 570	L22-L23	0.530 558
L11-L12	0.943 900	L23-L24	0.945 969
L12-L13	0.701 524

新窗口打开| 下载CSV

根据表2所示的结果,将关联度最高的绕组L13和L14进行合并,采用最小二乘法计算消磁电流大小,并计算残差大小.之后重新测量合并后绕组的单位绕组磁感应强度,并计算合并后绕组单位绕组磁感应强度之间的关联度,选择关联度最高的绕组进行合并.经过23次迭代后,所有绕组完成合并,每次迭代后残差平方差之和增长的情况如图10所示.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 残差平方差变化情况

Fig.10 Changes in the residual squared error

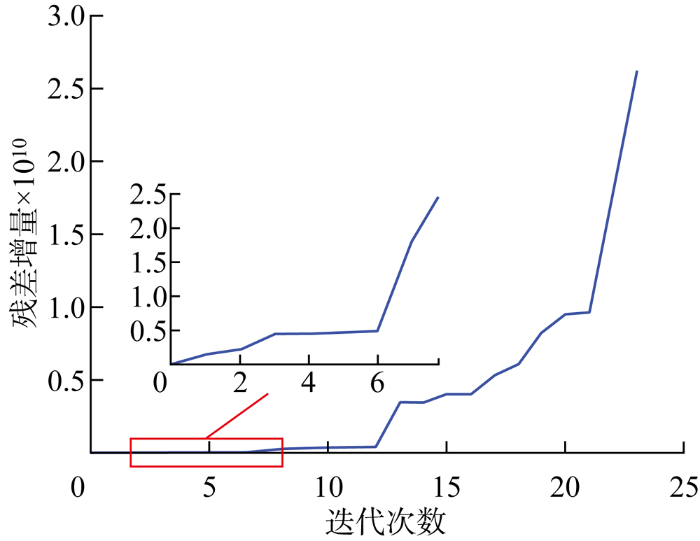
图10结果表明,在迭代第6次、第12次时,残差的增量明显得到提升,说明与迭代前的结果相比,安装成本变化不大,而消磁效果发生明显变化.取这两次迭代结果对应的阈值,分别对消磁绕组部署进行优化,其对应的阈值分别为0.91和0.73.

为了对比绕组优化前后及不同电流计算方法之间的消磁效果差别,对舰船施加z方向50 μT时的地磁场进行测试,并对结果进行了详细的分析.图11为消磁绕组优化前后的消磁效果对比图.图中:测量点在船首为正,船尾为负.由图可知,消磁绕组在优化后消磁效果比原绕组得到明显提升.但若绕组进行继续合并,则会导致消磁效果明显降低.优化前后具体的数据如表3所示.

图11

新窗口打开| 下载原图ZIP| 生成PPT

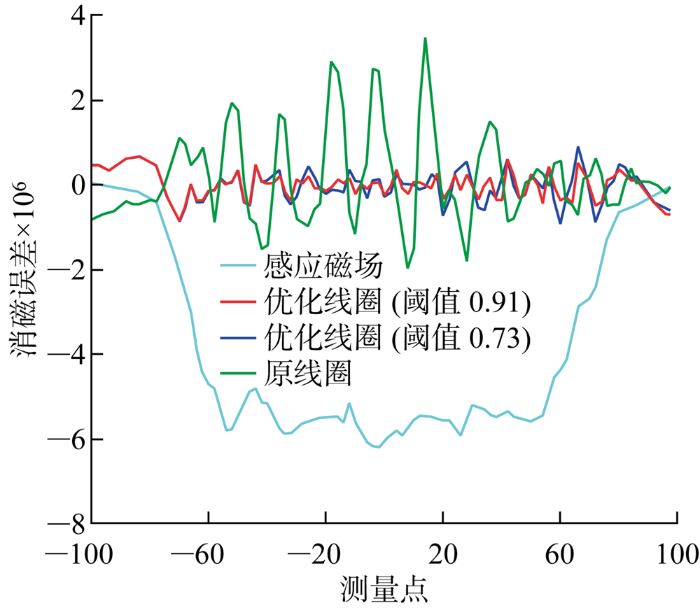
图11 绕组位置优化前后消磁效果对比

Fig.11 Comparison of demagnetization efficiency before and after coil position optimization

表3 绕组优化前后消磁效果对比

Tab.3 Comparison of degaussing effect before and after winding optimization

绕组分类	消磁误差最大幅值/T	剩余均方根误差/T	线圈数量
原绕组	3.48×10^-6	1.13×10^-10	12
第6次迭代结果(阈值0.91)	8.47×10^-7	1.15×10^-11	23
第12次迭代结果(阈值0.73)	9.22×10^-7	1.53×10^-11	17

新窗口打开| 下载CSV

由表3结果可知,当阈值设定为0.91时,其消磁效果优于阈值设定为0.73时的消磁效果,但此时线圈合并数量较少,安装成本较大,因此可以根据实际情况合理选择阈值.设定阈值为0.73和0.91分别完成绕组位置优化后,采用倾斜关联筛选-部分岭回归算法计算消磁绕组中的消磁电流.图12、图13分别表示阈值为0.91和0.73时,优化后的消磁绕组在3种电流计算方法下的消磁效果对比图.优化后的具体数据如表4所示.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 不同电流计算方法消磁效果对比图(阈值0.91)

Fig.12 Comparison of demagnetization efficiency of different current calculation methods (at a threshold of 0.91)

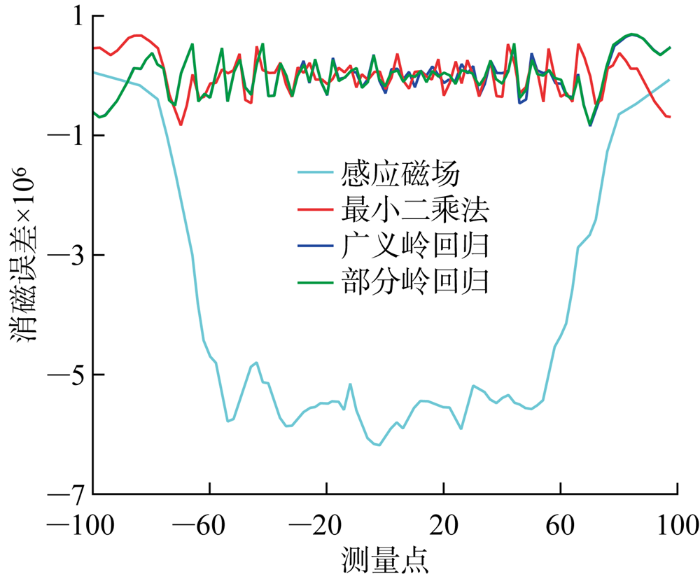
图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 不同电流计算方法消磁效果对比图(阈值0.73)

Fig.13 Comparison of demagnetization efficiency of different current calculation methods (at a threshold of 0.73)

表4 不同电流计算方法消磁效果对比

Tab.4 Comparison of degaussing effects of different current calculation methods

消磁电流计算方法	阈值0.91		阈值0.73
消磁电流计算方法	消磁误差最大幅值/T	剩余均方根误差/ T	消磁误差最大幅值/T	剩余均方根误差/ T
最小二乘法	8.47×10^-7	1.15×10^-11	9.22×10^-7	1.53×10^-11
广义岭回归	8.02×10^-7	1.08×10^-11	9.01×10^-7	1.45×10^-11
部分岭回归	6.98×10^-7	1.01×10^-11	8.29×10^-7	1.37×10^-11

新窗口打开| 下载CSV

从表4可以看出,部分岭回归法相对于最小二乘法和广义岭回归法,消磁误差最大幅值和剩余均方根误差都有明显提升.在阈值为0.73时,部分岭回归法将消磁误差最大幅值减小至8.29×10^-7 T,相较最小二乘法的9.22×10^-7 T,减小了10.09%,而广义岭回归对比最小二乘法只减少了2.28%.

部分岭回归法将剩余均方根误差减小至1.37×10^-11 T,相较最小二乘法的1.53×10^-11 T,减小了10.46%,而广义岭回归对比最小二乘法只减少了5.23%.在阈值为0.91时,部分岭回归法将消磁误差最大幅值减小至6.98×10^-7 T,相较最小二乘法的8.47×10^-7 T,减小了17.59%,而广义岭回归对比最小二乘法只减少了5.31%.部分岭回归法将剩余均方根误差减小至1.01×10^-11 T,相较最小二乘法的1.15×10^-11 T,减小了12.17%,而广义岭回归对比最小二乘法只减少了6.09%.由此可知,在阈值较大情况下,由于消磁绕组合并次数较少,消磁绕组数量更多,部分岭回归法的消磁效果更为出色.

5 结论

以舰船感应磁场补偿为研究对象,结合消磁绕组的位置选择及区段划分原则,提出基于绕组关联度的筛选重组方法,可以在保证消磁效果的前提下,大幅降低绕组位置优化求解步骤与时间,提高绕组优化效率.针对多消磁绕组电流计算存在的问题,提出基于倾斜关联筛选的绕组选择方法以及基于部分岭回归的电流计算方法,提升了电流计算的效率与稳定性.通过理论分析和算例验证可得出如下结论:

(1) 本文提出的基于绕组关联度的绕组筛选重组方法可以在保证消磁效果的前提下,大幅降低绕组位置优化求解步骤与时间,提高绕组优化效率.

(2) 本文针对大型舰船消磁绕组数量多的问题,通过高维变量筛选,筛选出与感应磁场关联度较高的绕组,提高求解效率.

(3) 针对广义岭回归算法的稳定性较差的问题,采用筛选后的变量进行部分岭回归的方式,尽可能降低均方根值,提高计算稳定性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

夏建超, 徐正喜, 左超, 等.

基于改进型粒子群算法的舰船消磁电流调整方法研究

[J]. 船电技术, 2015, 35(4): 18-21.