基于联邦强化学习的电热综合能源系统能量管理策略

doi:10.16183/j.cnki.jsjtu.2022.418

基于联邦强化学习的电热综合能源系统能量管理策略

王金锋¹, 王琪^,², 任正某¹, 孙晓晨¹, 孙毅², 赵一伊²

1.国网陕西省电力有限公司经济技术研究院,西安 710065

2.华北电力大学电气与电子工程学院,北京 102206

Energy Management Strategy of Integrated Electricity-Heat Energy System Based on Federated Reinforcement Learning

WANG Jinfeng¹, WANG Qi^,², REN Zhengmou¹, SUN Xiaochen¹, SUN Yi², ZHAO Yiyi²

1. Economic Research Institute, State Grid Shaanxi Electric Power Company, Xi’an 710065, China

2. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China

通讯作者: 王琪,硕士生;E-mail:455951466@qq.com.

责任编辑: 王历历

收稿日期: 2022-10-20 修回日期: 2023-03-6 接受日期: 2023-03-9

基金资助:

国网陕西省电力有限公司科技项目(5226SX21N036)

Received: 2022-10-20 Revised: 2023-03-6 Accepted: 2023-03-9

作者简介 About authors

王金锋(1984-),博士,高级工程师,从事电力需求侧管理、综合能源服务、电力市场、碳资产管理研究.

摘要

电热综合能源系统(IES)的能量管理关系到园区的经济效益与多能互补能力,但面临新能源出力随机性和用户负荷不确定性的挑战.首先,构建电热IES能量管理问题的数学模型,将各供能子系统赋能为智能体,基于深度确定性策略梯度(DDPG)算法建立综合考虑子系统实时用能负荷、分时电价及各设备出力的系统能量管理模型.然后,采用联邦学习技术,在训练过程中交互3个子系统的能量管理模型梯度参数对模型的训练效果进行协同优化,打破数据壁垒的同时保护各子系统数据隐私.最后,通过算例分析验证了所构建基于联邦学习框架的DDPG能量管理模型能有效提升园区IES经济效益.

关键词： 综合能源系统; 联邦学习; 能量管理; 深度确定性策略梯度

Abstract

The energy management of the electricity-heating integrated energy system (IES) is related to the economic benefits and multi-energy complementary capabilities of a park, but it faces the challenges of the randomness of renewable energy and the uncertainty of load. First, in this paper, a mathematical model of the energy management problem for the electricity-heating IES is conducted, and each energy supply subsystem is empowered as an agent. Based on the deep deterministic policy gradient (DDPG) algorithm, a system energy management model is established that comprehensively considers the real-time energy load of the subsystem, the time-of-use pricing, and the output of each equipment. Then, the federated learning technology is used to interact with the gradient parameters of the energy management model of the three subsystems during the training process to synergistically optimize the training effect of the model, which can protect the data privacy of each subsystem while breaking the data barriers. Finally, an example analysis verifies that the proposed federated-DDPG energy management model can effectively improve the economic benefits of the park-level IES.

Keywords： integrated energy system (IES); federated learning; energy management; deep deterministic policy gradient (DDPG)

PDF (4615KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王金锋, 王琪, 任正某, 孙晓晨, 孙毅, 赵一伊. 基于联邦强化学习的电热综合能源系统能量管理策略[J]. 上海交通大学学报, 2024, 58(6): 904-915 doi:10.16183/j.cnki.jsjtu.2022.418

WANG Jinfeng, WANG Qi, REN Zhengmou, SUN Xiaochen, SUN Yi, ZHAO Yiyi. Energy Management Strategy of Integrated Electricity-Heat Energy System Based on Federated Reinforcement Learning[J]. Journal of Shanghai Jiaotong University, 2024, 58(6): 904-915 doi:10.16183/j.cnki.jsjtu.2022.418

在能源转型及“双碳”背景下,能源的高效利用和可持续发展引起全球广泛关注和高度重视.综合能源系统(Integrated Energy System,IES)兼具多能耦合、协同供应的优势,在提高能源利用效率的同时满足多样化用能需求,是能源领域的重要发展趋势之一^[1].在工业生产领域,IES的表现形式为集合园区电、气、热等能源形式的园区IES(Park-Level Integrated Energy System,PIES).PIES在能源综合利用^[2]、节能减排^[3]、可再生能源就地消纳^[4]等方面具有重要意义.

IES具备大规模区域互联的特性,并逐渐形成大型高维系统,风光等不确定出力的新能源和以分布式储能设备为代表的柔性负荷的接入进一步加强了IES的复杂动态特性^[5].此外,能源多样性和多能间存在复杂多变的耦合特性也使现代化能源管理面临巨大挑战^[6].

传统的IES能量管理方法,诸如混合整数规划^[7]、非线性规划^[8]、线性规划^[9],都基于模型驱动,是充分运用系统成熟机理的优化调度方法.高比例可再生能源的接入提高了系统实时调度决策的性能需求.此外,系统的源荷不确定性使机理建模面临困境,即使针对此类问题进行随机规划^[10]、鲁棒优化^[11],依旧无法摆脱不确定性因素的刻画,模型驱动方法因而陷入瓶颈.

为了摆脱机理建模的制约,并通过离线训练缩短实时调度决策时间,引入数据驱动,采用无模型的强化学习(Reinforcement Learning,RL)方法.强化学习通过智能体与环境的迭代交互,依靠奖励回报自适应学习生成最优策略,不受精确的模型信息和预测准确性的制约.此外,强化学习还可以与具备良好数据处理能力的深度学习相结合形成较传统优化算法更易实现的深度强化学习(Deep Reinforcement Learning,DRL)^[12]算法.

许多专家学者已经开始利用DRL来处理IES管理问题并取得一定研究成果.文献[13]中采用深度Q网络建立微网能源系统优化管理模型,管理电、热、冷3种能源系统的能源生产、转换与存储操作,实现微网经济调度.文献[14]中提出一种基于柔性行动器-评判器的强化学习框架,解决电气IES的多能流协同优化问题.文献[15]中提出深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)算法求解电气IES优化调度问题.文献[16]中采用一种改进型深度确定性策略梯度(DDPG-AD)算法来优化文中所提分布式清洁能源发电系统模型的发电效率.

此外,当前机器学习模型构建多依托集中式框架进行分布式学习优化,需要各智能体之间进行信息交互,随着IES规模的不断扩大,数据隐私的地位逐步提高.伴随着用户对数据隐私的重视,分布式学习的隐私保护逐步成为当前研究重点.国内外学者提出联邦强化学习方法来解决此类问题.在联邦强化学习中,各智能体通过向聚合中心发送模型参数替代数据,进而保护了用户的隐私安全.文献[17]中将纵向联邦学习与深度强化学习算法相结合,协同优化电、热、气3种能源系统实时管理能力的同时保护各参与方的数据安全.文献[18]中将联邦学习与能源需求学习相结合,有效保护用户数据隐私的同时预测电动汽车的能源需求.文献[19]中提出一种联邦强化学习(Federated Reinforcement Learning,FRL)方法用于多智能家庭的能源管理.当前,针对IES的能量管理过程中的隐私问题,多采用多智能体强化学习方法,尚缺乏联邦强化学习的研究与应用.FRL框架中,各参与方间交互DRL模型中间参数,协同优化各参与方DRL模型的训练速度^[20⇓-22].此外,FRL在各参与方中采用间接交互模型中间参数的方式替代了原始数据的直接交换,使各参与方的数据隐私得到有效保护.

以工业园区为研究场景构建一个包含3个供能子系统的电热IES模型,同时基于DDPG算法设计一种能兼容于3个异构供能子系统的能量管理模型.对于3个异构供能子系统,该模型能够综合考虑园区实时电负荷、热负荷、分时电价,朝着经济效益最大化方向自适应地对供能子系统内部各设备的出力进行调整.此外,提出一种基于联邦学习框架的DDPG算法(Federated-Deep Deterministic Policy Gradient,F-DDPG)对园区IES能量进行管理.在F-DDPG框架中,各供能子系统利用内部数据,独立地对DDPG能量管理模型进行训练.在模型训练过程中,F-DDPG采用联邦学习算法交互各供能子系统能量管理模型的梯度参数,协同优化各子系统能量管理模型训练速度.最后,通过算例仿真验证了所构建基于联邦强化学习的园区IES能量管理方法对系统经济效益的显著提升.

1 园区IES结构及设备模型

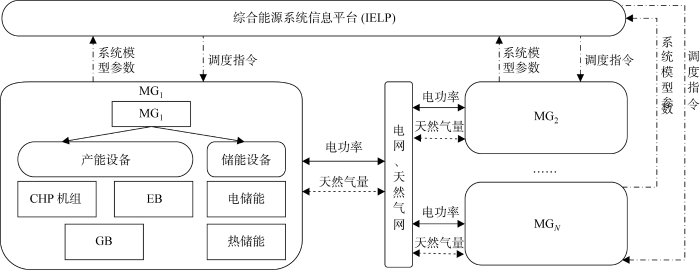
园区IES内部通常包含多个供能子系统,其典型架构如图1所示.各供能子系统分别用MG₁、MG₂、MG_N来表示,其内部分为产能设备、储能设备、用能负荷3部分.其中,产能设备主要包括热电联产机组(Combined Heat and Power,CHP)、燃气锅炉(Gas Boiler,GB)、电锅炉(Electric Boiler,EB)等设备,储能设备主要包括电储能、热储能,用能负荷主要包括电、热等固定负荷以及可控负荷.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 园区IES结构

Fig.1 Structure of IES for the park

各供能子系统内部设置智能体,负责收集本系统内部可再生能源出力、电热负荷需求以及各设备状态信息,并调节各可控设备出力.各智能体可通过数据传输链路实现与IEIP的信息交互,各智能体上传能源系统模型参数等信息,经IELP分析处理后,平台下发调度指令.

各供能子系统既可实现本系统内部自治,又可协作运行.一方面,各智能体都包含策略网络和价值网络,可实现各供能子系统的就地数据处理;另一方面,各智能体上传各网络特征参数至IELP,最终通过IELP的调度实现协同优化.该架构避免了调度过程中大量隐私数据传输.

1.1 供能子系统设备模型

各供能子系统内元件特性详述如下:

(1) CHP模型.CHP机组作为IES的核心设备,以天然气为主要燃料,可输出热、电能,具有较高的综合用能效率.

CHP机组的发电功率为

(1)

\begin{matrix} P_{C H P} (t) = V_{C H P} (t) H_{N G} η_{C H P} \end{matrix}

式中: $V_{C H P} (t) 为 t$ 时段CHP机组单位时间内天然气消耗量;H_NG为天然气的热值;η_CHP为CHP机组的发电效率.

CHP机组发电功率满足约束条件:

(2)

\begin{matrix} P_{C H P}^{m i n} \leq P_{C H P} (t) \leq P_{C H P}^{m a x} \end{matrix}

式中: $P_{C H P}^{m i n}$ 、 $P_{C H P}^{m a x}$ 分别为CHP机组发电功率的最小值、最大值.

此外,CHP机组在输出电能的同时,也会放出大量热能.CHP机组输出热功率与电功率比值为热电比β,CHP机组t时段输出热功率可表示为

(3)

\begin{matrix} H_{C H P} (t) = β P_{C H P} (t) η_{H E} \end{matrix}

式中:η_HE为余热回收效率.

(2) 燃气锅炉模型.燃气锅炉消耗天然气为IES提供热能,其输出热功率为

(4)

\begin{matrix} H_{G B} (t) = η_{G B} H_{N G} V_{G B} (t) \end{matrix}

式中:η_GB为燃气锅炉的效率;V_GB(t)为t时段内燃气锅炉的单位时间天然气消耗量.

燃气锅炉输出热功率满足约束条件:

(5)

\begin{matrix} H_{G B}^{m i n} \leq H_{G B} (t) \leq H_{G B}^{m a x} \end{matrix}

式中: $H_{G B}^{m i n}$ 、 $H_{G B}^{m a x}$ 分别为燃气锅炉输出热功率的最小值、最大值.

(3) 电锅炉模型.电锅炉消耗电能为IES提供热能,其输出热功率为

(6)

\begin{matrix} H_{E B} (t) = P_{E B} (t) η_{E B} \end{matrix}

式中: $P_{E B} (t) 为 t$ 时段制热电锅炉消耗电功率;η_EB为制热电锅炉的制热效率.

制热电锅炉输出热功率满足约束条件:

(7)

\begin{matrix} H_{E B}^{m i n} \leq H_{E B} (t) \leq H_{E B}^{m a x} \end{matrix}

式中: $H_{E B}^{m i n}$ 、 $H_{E B}^{m a x}$ 分别为制热电锅炉输出热功率的上下限.

(4) 电储能模型.电储能设备作为IES的重要组成部分,可在一定程度上对IES中源荷不确定性进行缓解.建立典型电储能设备-蓄电池的数学模型.蓄电池的储电状态受上一时段储电状态和充放电功率影响,满足以下公式:

(8)

\begin{matrix} B_{s o c} (t) = B_{s o c} (t - 1) - \frac{η_{B A} P_{B A} (t) Δ t}{Q_{B A}} \end{matrix}

式中:B_soc(t)为蓄电池在t时段的储电状态;P_BA(t)为蓄电池的运行功率,为正时表示其处于放电状态,为负时表示其处于充电状态;Q_BA为蓄电池的最大容量;η_BA为蓄电池的充放电系数,表示为

(9)

\begin{matrix} η_{B A} = \{\begin{array}{l} η_{c h}, & P_{B A} < 0 \\ 1 / η_{d i s}, & P_{B A} \geq 0 \end{array} \end{matrix}

式中:η_ch∈(0, 1]为蓄电池的充电系数;η_dis∈(0, 1]为蓄电池的放电系数.

蓄电池的运行功率满足约束条件:

(10)

\begin{matrix} P_{B A}^{m i n} \leq P_{B A} (t) \leq P_{B A}^{m a x} \end{matrix}

式中: $P_{B A}^{m i n}$ 、 $P_{B A}^{m a x}$ 分别为蓄电池充、放电功率的最小值、最大值.

(5) 热储能模型.热储能设备与电储能设备同为IES的重要组成部分,对IES的意义与作用与电储能设备一致.以蓄热罐为典型热储能设备为例进行建模.蓄热罐t时段的储热状态满足下式:

(11)

Q_{H S} (t) = Q_{H S} (t - 1) (1 - σ_{x}) + η_{H S} P_{H S} (t) Δ t

式中:P_HS(t)为蓄热罐的运行功率,为正时表示其处于放热状态,为负时表示其处于吸热状态;σ_x为蓄热罐的自损率;η_HS为蓄热罐的吸放热系数,表示为

(12)

\begin{matrix} η_{H S} = \{\begin{array}{l} η_{c h r}, & P_{H S} < 0 \\ 1 / η_{d c h}, & P_{H S} \geq 0 \end{array} \end{matrix}

式中:η_chr∈(0, 1]为蓄热罐的放热功率;η_dch∈(0, 1]为蓄热罐的吸热效率.

1.2 约束条件

IES的约束条件分为各设备自身约束条件和热电功率平衡约束条件,设备的自身约束如1.1节所示.根据IES结构,供能子系统能源平衡约束如下.

(1) 电功率平衡约束方程:

(13)

\begin{array}{l} P_{M G} (t) + P_{N E} (t) + P_{B A} (t) + P_{C H P} (t) = \\ P_{E B} (t) + P_{l o a d} (t) \end{array}

式中:P_MG(t)、P_NE(t)分别为t时段电网流入IES的电功率、新能源发电功率; P_load(t)为电负荷.

(2) 热功率平衡约束方程:

(14)

\begin{array}{l} H_{C H P} (t) + H_{G B} (t) + H_{E B} (t) + H_{H S} (t) = \\ H_{l o a d} (t) \end{array}

式中:H_load(t)为t时段热负荷;H_HS(t)为t时段蓄热罐的热功率.

(3) 外部能源供应约束.t时段电网流入IES的电功率满足以下约束条件:

(15)

\begin{matrix} P_{M G}^{m i n} < P_{M G} (t) < P_{M G}^{m a x} \end{matrix}

式中: $P_{M G}^{m i n}$ 、 $P_{M G}^{m a x}$ 分别为流入IES电功率的最小值、最大值.

t时段天然气供应商对IES的天然气供应量满足以下约束条件:

(16)

\begin{matrix} v_{N G} (t) = V_{C H P} (t) + V_{G B} (t) \end{matrix}

(17)

v_{N G}^{m i n} \leq v_{N G} \leq v_{N G}^{m a x}

式中:v_NG(t)为t时段供应商天然气供应总量; $v_{N G}^{m i n}$ 、 $v_{N G}^{m a x}$ 分别为供应商天然气供应量的最小值、最大值.

1.3 目标函数

在电热IES中,系统运行成本主要包括购电成本、购气成本、弃风弃光成本.奖励函数只考虑购能成本以及弃风弃光成本,忽略设备启停成本和维护成本.以最小化系统运行成本为目标,日前经济调度的运行成本为

(18)

\begin{matrix} m i n C (t) = C_{E} (t) + C_{N E} (t) \end{matrix}

式中:C_E为购能成本;C_NE为弃风弃光成本.

(19)

\begin{array}{l} C_{E} (t) = λ_{M G} P_{M G} (t) + \\ λ_{N G} (\frac{P_{C H P} (t)}{η_{C H P} H_{N G}} + \frac{H_{G B} (t)}{η_{G B} H_{N G}}) \end{array}

式中:λ_MG(t)为t时段电价;λ_NG(t)为天然气的单位热量价格;P_MG(t)为正表示系统向主电网购电,为负表示系统向主电网售电,产生弃风弃光行为.

弃风弃光成本公式如下所示:

(20)

\begin{matrix} C_{N} = \overset{T}{\sum_{t = 1}} c_{N c u r t} P_{N c u r t} (t) \end{matrix}

式中:T为日前调度的时间段数;c_Ncurt为弃光成本系数;P_Ncurt(t)为弃风弃光量.

2 供能子系统系统的DDPG能量管理模型

2.1 DDPG能量管理模型

基于DDPG算法构建一种能自适应地对供能子系统设备出力进行调整的优化管理模型.各供能子系统中,DDPG能量管理模型观测电负荷需求、热负荷需求以及各设备运行状态等信息并汇总至子系统,由子系统对各设备出力的动作进行调整.DDPG能量管理模型基于子系统内是否存在弃风弃光等情况,对子系统所执行策略的经济效果进行量化分析,并通过迭代寻优不断更新策略.

2.2 状态空间

电热IES模型中,智能体观测的环境信息为新能源发电功率、负荷需求、蓄电池的荷电状态、蓄热罐的储热状态.任意时段t下,3种能源系统的状态空间定义为

$S^{i} = (P_{N E}^{i} (t), P_{l o a d}^{i} (t), H_{l o a d}^{i} (t), H_{H S}^{i} (t), P_{M G}^{i} (t))$

其中: $P_{N E}^{i}$ (t)为i系统新能源在t时段的输出功率; $P_{l o a d}^{i}$ (t)为i系统内t时段电负荷; $H_{l o a d}^{i}$ (t)为i系统在t时段热负荷; $H_{H S}^{i}$ (t)为i系统在t时段蓄热罐的热功率; $P_{M G}^{i}$ (t)为i系统在t时段与电网交换的功率.

2.3 动作空间

智能体收集到环境状态后,经由策略集π进行决策,执行动作空间A内存储的一个动作.在时段t,选用设备的出力情况表示IES中的动作.由于P_CHP(t)确定后,H_CHP(t)可由式(3)计算得到;P_EB(t)确定后,H_EB(t)可根据式(6)确定,此外,H_GB(t)确定后,H_HS(t)可由式(14)确定;进而P_MG(t)也通过式(13)计算确定.即在P_CHP(t)、P_EB(t)、H_GB(t)、P_BA(t)确定后,其他量可以迅速得到.故IES的动作可表示为

$A^{i} = (P_{C H P}^{i} (t), P_{E B}^{i} (t), H_{G B}^{i} (t), P_{B A}^{i} (t))$

2.4 奖励函数

经济运行成本的最小化是电热IES的最终目标.强化学习算法中,将最小化问题转换成最大化奖励函数问题,因此,智能体i在时段t输出的奖励表示为

$R_{i} (s_{i}, a_{i}) = - \frac{1}{1000} (C_{E} + C_{N E})$

通过与 $\frac{1}{1000}$ 相乘对奖励函数进行缩放.

在IES某一确定状态s_i下,可通过动作-值函数Q_π(s_i, a_i)^[23]对动作a_i的优劣程度进行评估,其目标是找到最优策略π以最大化状态-动作值函数:

$\begin{array}{l} \begin{matrix} Q_{π} (s_{i}, a_{i}) = E_{π} (R_{i} (s_{i}, r_{i})) \end{matrix} \\ π = a r g \underset{a \in A}{m a x} Q_{π} (s_{i}, a_{i}) \end{array}$

其中:r_i为动作空间.

3 基于F-DDPG的系统能量管理方法

3.1 基于MADDPG的系统能量管理

传统的强化学习方法在解决单智能体问题时都能取得较好的学习效果,但当面对多智能体相互合作或竞争的环境时,由于状态与动作空间随着智能体的增加而成倍增长,模型无法有效学习,所以引入多智能体DDPG(Multi-Agent Deep Deterministic Policy Gradient,MADDPG).

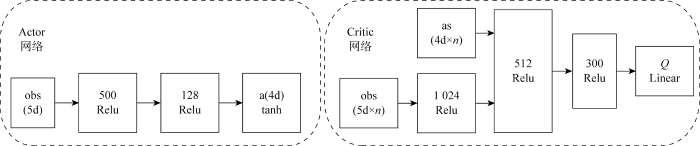
在MADDPG模型内,各智能体分为观测全局环境状态的评论家(Critic)网络和观测局部环境状态的演员(Actor)网络^[24].MADDPG算法依托集中训练的Critic网络来应对环境的非稳定状态,在训练阶段,Critic网络传递全局信息至各智能体,同步各智能体策略状态,保证MADDPG的训练稳定性.Actor网络和Critic网络均为采用线性整流函数激活的多层全连接网络.建立的Actor和Critic网络的结构如图2所示.obs用来表示输入层的五维(5d)观测值,Actor网络经过两个神经元分别为500、128的隐藏层后在输出层输出四维(4d)的决策值,并采用双曲正切函数tanh作为激活函数控制动作输出,避免过大或过小的动作值对系统的影响.n为数组个数.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 Actor网络和Critic网络结构

Fig.2 Structure of Actor network and Critic network

Critic网络则分别经过 1024、512、300的隐藏层,最后Linear即全连接层输出网络评估参数Q值,各隐藏层通过选取整流函数Relu作为激活函数来应对训练过程中梯度消失对神经网络学习率的冲击.

建立的园区IES模型中,各供能子系统赋能为智能体,单独计算子系统收益.各智能体由Actor网络、Critic网络、目标Actor网络、目标Critic网络构成.在训练阶段,Critic网络观测全局信息并基于此评估当前联合状态和联合动作的价值,对Actor网络的策略进行调整;训练好的Actor网络仅利用局部观测信息即可输出最优动作.各网络参数更新方法如下所示:

(1) Critic网络参数更新.Actor网络通过最小化损失函数以更新网络参数,即

(21)

m i n L_{k} (θ_{k, i}^{Q}) = \frac{1}{B} \sum_{i} (y_{k}^{i} - Q_{k} (s_{k}^{i}, a^{i} | θ_{k}^{Q} {))}^{2}

式中: $L_{k} (θ_{k, i}^{Q})$ 为Critic网络的损失函数,采用1/B来表征均方误差损失函数形式,即时间差分误差值的累计平方值的均值; $Q_{k} (s_{k}^{i}, a^{i} | θ_{k}^{Q})$ 为Critic网络估算出的联合状态动作价值,设 $y_{k}^{i} 为目标 Q$ 值,则

(22)

\begin{matrix} y_{k}^{i} = r_{k}^{i} + γ Q'_{k} (s_{k}^{i + 1}, a^{i + 1} | θ_{k}^{Q'}) |_{a^{i + 1} = μ'_{k} (s_{k}^{i + 1})} \end{matrix}

式中: $r_{k}^{i}$ 为经验回放池中参数;γ为联合状态动作价值的权重;$Q^{\prime}{ }_{k}\left(s_{k}^{i+1}, a^{i+1} \mid \theta_{k}^{Q^{\prime}}\right)$为Critic目标网络输出的下一步联合状态动作价值;μ'_k表示目标网络当前时段的策略,即Critic网络下一步的动作与状态.

损失函数的梯度计算公式为

(23)

\begin{matrix} Δ θ_{k, i}^{Q} = \frac{2}{B} (y_{k}^{i} - Q_{k} (s_{k}^{i}, a^{i}) | θ_{k}^{Q}) \end{matrix}

根据损失函数的梯度更新Critic网络参数为

(24)

\begin{matrix} θ_{k + 1, i}^{Q} = θ_{k, i}^{Q} + α Δ θ_{k, i}^{Q} \end{matrix}

式中:α为Critic网络的学习率.

(2) Actor网络参数更新.训练过程中,Actor网络更新其参数 $J (μ_{k} | θ_{k}^{μ})$ 以获取最大预期的长期折扣奖励,确定性策略梯度为

(25)

\begin{array}{l} Δ_{θ_{k}^{μ}} J (μ_{k} | θ_{k}^{μ}) = \frac{1}{B} [\sum_{i} Δ_{a_{k}} Q_{k} (s_{k}^{i}, a^{i} | θ_{k}^{Q}) \times \\ Δ_{θ_{k}^{μ}} μ_{k} (s_{k}^{i} | θ_{k}^{μ})]_{| a_{i} = μ_{k} (s_{k}^{i})} \end{array}

根据确定性策略梯度更新Actor网络参数为

(26)

\begin{matrix} θ_{k + 1, i}^{μ} = θ_{k, i}^{μ} + μ Δ θ_{k, i}^{μ} \end{matrix}

式中:μ为Actor网络的学习率.

(3) 目标网络参数更新.利用软更新技术更新目标网络的参数来进一步保证学习过程的稳定性^[25]:

(27)

\begin{matrix} θ_{k}^{μ'} \leftarrow τ θ_{k}^{μ} + (1 - τ) θ_{k}^{μ'} \end{matrix}

(28)

θ_{k}^{Q'} \leftarrow τ θ_{k}^{Q} + (1 - τ) θ_{k}^{Q'}

式中:τ为软更新系数,且τ≪1.

MADDPG算法中引入Ornstein-Uhlenbeck噪声来强化供能子系统训练过程中算法探索环境的能力,从而输出更优的动态调度策略.

3.2 基于F-DDPG的系统能量管理

将DDPG算法扩展到FRL,用于解决连续动作任务,称为F-DDPG.DDPG算法训练过程的关键在于通过训练Critic网络来估计准确的长期回报,进而指导Actor网络调整策略获取良好的回报.F-DDPG的主要目的在于提供一个全局的Critic网络指导智能体调整策略以获取最优整体回报.采用F-DDPG算法的单供能子系统与采用MADDPG算法单供能子系统以及采用传统DDPG方法的独立供能子系统相比,具有更好的通信效率和计算效率.

相较于MADDPG,F-DDPG的Critic网络参数更新中,由于 $r_{k}^{i}$ 为智能体的隐私数据,直接传递其指全局Critic网络具有隐私泄露风险,所以在训练过程中,各智能体上传损失函数梯度 $Δ θ_{k, i}^{Q}$ 至中央服务器,中央服务器对其进行平均输出全局梯度,并在传输过程中执行加法同态加密以提供安全保护,如下式所示:

(29)

\begin{matrix} [[G]] = \sum_{i} \frac{[[Δ θ_{k, i}^{Q}]]}{3} \end{matrix}

式中:[[·]]表示Paillier加密;G为3个系统聚合后的平均梯度.在F-DDPG算法中,Paillier加密的引入保证各子系统都不能在交互损失函数时,获得其它子系统的损失函数信息.该项措施有效保证园区IES在进行 F-DDPG能量优化管理过程中的数据隐私.

中央服务器下发全局梯度至各智能体,更新本地Critic网络参数,如下所示:

(30)

\begin{matrix} θ_{k + 1, i}^{Q} = θ_{k, i}^{Q} + G \end{matrix}

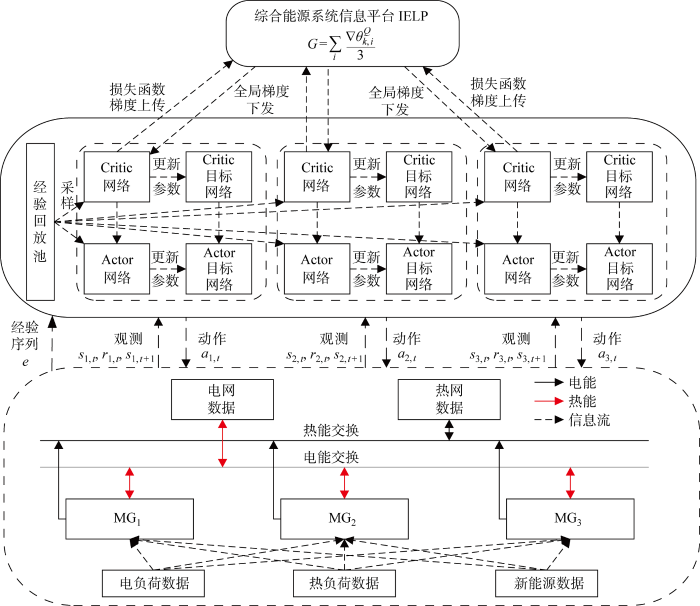
建立基于F-DDPG算法的IES能量管理框架如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 基于F-DDPG的IES能量管理框架

Fig.3 Energy management framework of IES based on F-DDPG

该算法通过经验回放机制,采用历史的电负荷、热负荷、新能源出力、蓄热罐运行功率及入网电功率数据作为系统状态输入,离线训练F-DDPG算法网络.离线训练结束后得到的F-DDPG算法参数直接代入IES的能量管理问题进行求解.在调度执行阶段,各智能体观测当前系统状态信息并输入训练好的F-DDPG算法网络,迭代寻优后经由内部Actor网络输出调度策略.随后,执行策略并更新环境状态,输出当前策略奖励值.然后输入时段t+1系统的状态信息,并做出该时段的决策.不断迭代最终输出动态调度动作.

4 算例分析

以某一台区下的园区IES为例对所提基于FRL的电热IES能量管理策略的有效性进行验证,该园区可分为3个供能子系统,各供能子系统内具体设备信息如表1所示.

表1 供能子系统资源配置

Tab.1 Resource configuration of power subsystem

供能子系统	所包含设备
MG₁	风力发电机、光伏、CHP机组、电、热储能系统、燃气锅炉、电热锅炉及电、热负荷
MG₂	风力发电机、光伏、CHP机组、电、热储能系统、燃气锅炉及电、热负荷
MG₃	风力发电机、光伏、电、热储能系统、燃气锅炉、电热锅炉及电、热负荷

新窗口打开| 下载CSV

园区各设备运行参数如表2所示,并基于开源的CREST模型^[26]生成各用能子系统的热负荷、电负荷及新能源出力数据.该模型经由拉夫堡大学研究团队提出并通过有效性验证,现已被大规模使用^[27-28].系统以15 min为间隔将调度时段划分为96个时隙.

表2 供能子系统中设备运行参数

Tab.2 Operating parameters of equipment in energy supply subsystem

设备	P^min, H^min/MW	P^max, H^max/MW
CHP机组	0	1.2
电热锅炉	0	1.4
燃气锅炉	0	1.2
蓄电池	-0.2	0.2

新窗口打开| 下载CSV

系统与主电网交换功率的范围为 [-1.5 MW,3.0 MW],其他参数如表3所示.园区电价为分时电价如表4所示,峰时段为12:00—16:00、19:00—22:00,谷时段为0:00—8:00,平时段为8:00—12:00、16:00—19:00、22:00—24:00.天然气价格固定为0.450 元/(kW·h).

表3 供能子系统中其他参数

Tab.3 Other parameters in energy supply subsystem

参数	数值	参数	数值
η_CHP	0.32	η_EB	0.94
β	1.25	η_GB	0.82
η_HE	0.73	C_Ncurt	0.20

新窗口打开| 下载CSV

表4 分时电价

Tab.4 Time-of-use electricity price

时段	购电电价/ [元·(kW·h)^-1]	售电电价/ [元·(kW·h)^-1]
峰时段	0.922	0.500
平时段	0.540	0.200
谷时段	0.382	0

新窗口打开| 下载CSV

以CREST模型生成的5月份和6月份的历史数据作为训练数据.在进行系统动态能量管理之前,预先对联邦强化学习网络进行训练,确定网络参数.为了展现所提方法的收敛性能,给出智能体训练过程中每100个周期的平均奖励值曲线如图4所示.该算法经过约 20000 个周期后收敛,得到最优动态经济调度策略.在日内调度开始前,智能体观测供能子系统的新能源发电功率、用能需求,随后依据前文所述的训练过程输出奖励值,并朝着最大化奖励值方向不断调整执行策略.如图4所示,可观测到在训练过程中奖励值出现振荡,其振荡受各周期中的日训练数据中如负荷数据和光伏发电数据的变化影响.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 奖励函数收敛曲线

Fig.4 Convergence curve of reward function

4.1 动态调度结果

调度开始前,F-DDPG算法网络经由历史数据进行离线训练,调整网络性能,训练好的算法网络用于调度阶段系统的动态能量管理.为了更好地阐释系统的动态能量管理结果,基于所提F-DDPG算法输出的P_CHP(t)、v_GB(t)、P_BA(t)、H_GB(t)以及相应计算得到的H_CHP(t)、H_EB(t)、H_HS(t)、P_MG(t),以该园区2016年6月15日的调度情况为例进行分析.

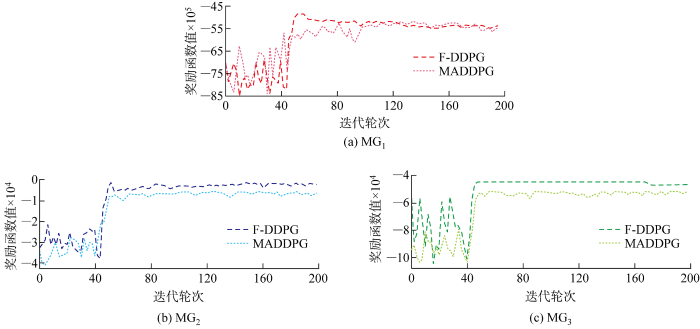
首先验证3种供能子系统DDPG能量管理模型的奖励函数收敛性,以及F-DDPG 方法对3种供能子系统DDPG能量管理模型奖励函数收敛曲线的改善效果.3种供能子系统的 DDPG能量管理模型在各训练回合下的奖励函数收敛曲线如图5所示.由图可见,各供能子系统能量管理模型奖励函数都在迭代训练过程中实现收敛.由于所提算法在各DDPG能量管理模型训练过程中经由联邦学习加密,所以利用交互各能源系统的损失函数来计算园区IES的综合损失函数,从而对各DDPG能量管理模型的训练水平进行量化;此外,F-DDPG方法通过计算各DDPG能量管理模型对于当前园区IES损失函数的梯度信息,独立地更新和优化各DDPG能量管理模型的评估网络参数.因此所提F-DDPG方法能够有效提升各供能子系统的DDPG能量管理模型训练效率.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 各供能子系统能量管理模型奖励函数收敛曲线

Fig.5 Convergence curves of reward function of energy management model of each energy supply subsystem

此外,F-DDPG依托Paillier全同态加密算法,减轻了各供能子系统DDPG能量管理模型梯度信息以及子系统原始数据的泄露风险.因此,F-DDPG方法能够有效打破异构供能子系统之间数据壁垒,在保护数据隐私的前提下协同训练各供能子系统能量管理模型.

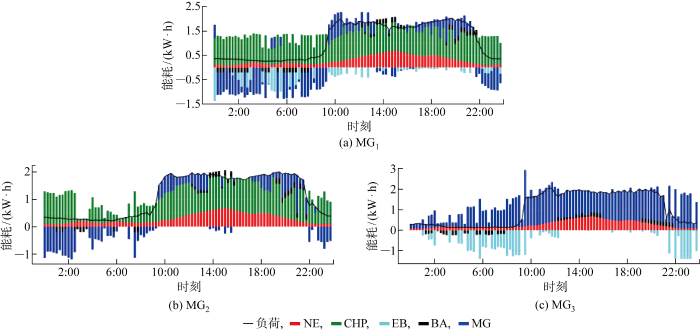
模型训练完成后,DDPG能量管理模型所决策的各设备出力情况如图6和图7所示.其中,图6为电功率调度结果,图7为热功率调度结果.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 基于F-DDPG算法的电功率调度结果

Fig.6 Result of electrical power scheduling based on F-DDPG algorithm

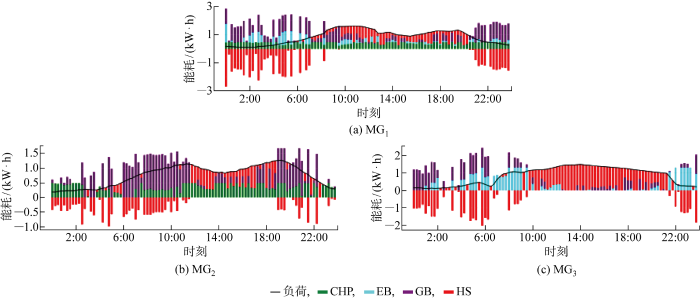
图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 基于F-DDPG算法的热功率调度结果

Fig.7 Result of thermal power scheduling based on F-DDPG algorithm

由图6可见,MG₁、MG₂、MG₃子系统内整体趋势为:主要由CHP机组、蓄电池产生电能,其中蓄电池受分时电价引导充放电.以MG1为例,蓄电池在谷电价且电负荷较小时充电以备后续的高峰时段,如 1:15—2:45、5:30—6:45 等时段;在峰电价且电负荷较高时放电以减少运行成本,如 12:00—13:00、14:00—15:00 等时段.在谷电价时电能出力供电热锅炉消耗,反向向电网售电;平电价阶段,系统向主电网购电以满足用电需求.

由图7可见,MG₁、MG₂、MG₃整体趋势为:蓄热罐受分时电价影响,谷电价和平电价时蓄热为后续的高峰时刻做准备,如 0:00—2:00、4:45—5:00 等时段,在峰电价且热负荷较高时放热以减少运行成本.MG₁中,CHP机组持续供热,在谷电价且热需求高于0.5 MW时,机组制热不能满足热负荷需求,采用电热锅炉购电制热以及燃气锅炉制热进行补充.峰电价时CHP机组、蓄热罐、燃气锅炉以及少量电热锅炉制热满足热负荷需求.MG₂中,CHP机组持续供热,在谷电价且热需求高于0.5 MW时,机组制热无法满足热负荷需求,采用燃气锅炉制热进行补充.峰电价时CHP机组、蓄热罐、燃气锅炉制热满足热负荷需求.平电价时,CHP机组和燃气锅炉联合供热满足热需求和供蓄热罐吸热.MG₃中,谷电价且低负荷时主要由电热锅炉制热,当热需求高于0.9 MW时,电锅炉制热不能满足热负荷需求,燃气锅炉制热进行补充,如 4:45—5:15 等时段;峰电价时主要由蓄热罐放热,少量燃气锅炉、电热锅炉制热满足热负荷需求.

综上,所提基于F-DDPG算法的能量管理策略能够在满足用能需求的前提下不断调整各子系统设备出力以提升系统经济效益.

4.2 对比分析

为进一步对所提算法有效性进行验证,首先选取传统的基于模型预测控制的调度方法与所提基于F-DDPG的调度方法进行对比.此外,如文献[12]所述,对于多主体系统,直接使用传统DDPG进行独立训练和决策,其面对的环境不稳定,这种不稳定打破了强化学习算法所遵循的马尔可夫假设^[29],无法输出稳定的策略,因此额外采用基于MADDPG的调度方法进行对比.

表5给出3种能量管理方法的经济效益和有效训练时长.有效训练时长指利用相同数据集开展100次实验,不忽略管理模型所出现的不收敛、过拟合等不成功训练情况, 统计其成功训练收敛的平均用时.

表5 不同能量管理方法的日运行成本统计结果

Tab.5 Statistics of the daily operation costs of different methods

优化方法	成本/元			有效训练时长/s
优化方法	MG₁	MG₂	MG₃	有效训练时长/s
传统方法	19342.00	16786.00	49560.00	14228.00
MADDPG	18424.00	16629.00	47892.00	10634.20
F-DDPG	12973.02	13845.09	41469.00	6121.80

新窗口打开| 下载CSV

由表可见,对于上述园区IES,采用所提方法计算结果优于传统调度方法与MADDPG算法,验证了该方法的求解有效性;同时该算法的有效训练时长远小于上述两种算法,表明F-DDPG算法具有较高的计算效率.

在传统调度方法中,在IES管理的各时隙下,都需要针对热、电负荷与新能源出力进行精准预测并基于预测结果重新计算系统在后续1 h的管理方案;而所提算法无需对源荷信息进行预测,只需要将源荷信息作为智能体观察到的状态信息输入算法网络,大大缩短有效训练时间.此外,相较于所提算法,传统调度方法对各部分数据进行集中处理因而无法保证数据隐私.相较于MADDPG算法,所提 F-DDPG 方法基于联邦学习技术,在训练过程中通过各供能子系统模型梯度参数的交互而相互影响,使各智能体的模型训练效率和效果朝着更优的方向提升,更快速、更高效地实现系统的优化调度.

5 结论

面向工业园区电热IES,本文提出一种基于联邦强化学习的园区IES能量管理方法.F-DDPG算法通过在3个供能子系统中分别构建DDPG能量管理模型来管理各系统内设备的实时出力值.同时 F-DDPG 方法采用间接交互各子系统DDPG能量管理模型的梯度信息替代原始数据的直接交互,协作进行能量管理.最后,通过算例仿真对F-DDPG方法的有效性进行验证,并得到以下主要结论:

(1) 基于DDPG构建的供能子系统能量管理模型,综合考虑供能子系统内的新能源出力、实时热、电负荷、分时电价,动态地管理3个供能子系统在日内各状态下的设备出力.

(2) 所提基于联邦强化学习的园区IES能量管理方法能够使各供能子系统DDPG能量管理模型的训练效率和效果朝着更优的方向提升,并收获优良的经济效益.

(3) 由于能量管理过程中,各供能子系统避免了原始数据的直接交互,所提F-DDPG方法能够有效地对各供能子系统内部用能数据隐私进行保护.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

苏慧玲, 杨世海, 陈铭明.

考虑能源效率的综合能源系统多目标优化调度

[J]. 电力系统及其自动化学报, 2022, 34(2): 130-136.