上海交通大学学报

上海交通大学学报, 2024, 58(6): 798-805 doi: 10.16183/j.cnki.jsjtu.2022.476

新型电力系统与综合能源

计及尾流效应的风电场短路故障动态等值建模

余浩1, 黎灿兵,2, 叶志亮2, 彭穗1, 任万鑫1, 陈思捷2, 唐彬伟3, 陈达伟2

1.广东电网有限责任公司 电网规划研究中心, 广州 510080

2.上海交通大学 电子信息与电气工程学院, 上海 200240

3.明阳智慧能源集团股份公司, 广东 中山 528437

Dynamic Equivalence Modeling of Short-Circuit Faults in Wind Farms Considering Wake Effects

YU Hao1, LI Canbing,2, YE Zhiliang2, PENG Sui1, REN Wanxin1, CHEN Sijie2, TANG Binwei3, CHEN Dawei2

1. Power Grid Planning and Research Center, Guangdong Power Grid Co., Ltd., Guangzhou 510080, China

2. School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

3. Mingyang Smart Energy Group Co., Ltd., Zhongshan 528437, Guangdong, China

通讯作者: 黎灿兵,教授,博士生导师;E-mail:licanbing@sjtu.edu.cn.

责任编辑: 孙伟

收稿日期: 2022-11-25   修回日期: 2023-05-29   接受日期: 2023-07-31  

基金资助: 国家自然科学基金(51977062)

Received: 2022-11-25   Revised: 2023-05-29   Accepted: 2023-07-31  

作者简介 About authors

余浩(1986-),高级工程师,从事电网规划、系统仿真及新能源并网技术研究.

摘要

快速、准确分析大型风电场短路特性具有重要的工程应用价值,而尾流效应影响下风电场各机组短路特性差异大,需建立风电场短路故障时等值模型.提出一种考虑尾流效应影响的风电场短路故障动态等值方法,首先定义尾流效应因子反映机组受尾流效应影响程度,并采用尾流效应因子作为分组依据,缩小尾流效应影响下组内各机组运行状态差异性.为提高非对称短路故障下的等值模型有效性,分析风电场短路时正、负、零三序网络的构成,提出适用于零序集电网络的等值方法,搭建平台并加以验证.仿真结果表明,该风电场短路故障动态等值模型能准确反映尾流效应影响下风电场有功、无功短路输出特性.

关键词： 尾流效应; 风电场; 短路故障; 聚类算法; 动态等值模型

Abstract

Fast and accurate analysis of the short-circuit characteristics of large wind farms has important engineering application value, and the short-circuit characteristics of wind farms under the influence of the wake effect vary greatly. Therefore, it is necessary to establish a wind farm short-circuit fault time equivalence model. A wind farm short-circuit fault dynamic equivalence method considering the effect of wake effect is proposed. First, the wake effect factor is defined to reflect the degree of the unit affected by the wake effect. Then, the wake effect factor is used as the grouping basis to reduce the variability of operating state of the units within the group under the influence of the wake effect. A positive- negative- zero-sequence network equivalence method is analyzed to improve the effectiveness of the equivalence model in asymmetric short-circuit faults. An equivalence method suitable for zero-sequence network is proposed and a platform is built for verification. The simulation results show that the dynamic short-circuit fault equivalence model proposed can accurately reflect the active and reactive short-circuit output characteristics of wind farms under the influence of the wake effect.

Keywords： wake effect; wind farm; short-circuit fault; clustering algorithm; dynamic equivalence model

PDF (2071KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

余浩, 黎灿兵, 叶志亮, 彭穗, 任万鑫, 陈思捷, 唐彬伟, 陈达伟. 计及尾流效应的风电场短路故障动态等值建模[J]. 上海交通大学学报, 2024, 58(6): 798-805 doi:10.16183/j.cnki.jsjtu.2022.476

YU Hao, LI Canbing, YE Zhiliang, PENG Sui, REN Wanxin, CHEN Sijie, TANG Binwei, CHEN Dawei. Dynamic Equivalence Modeling of Short-Circuit Faults in Wind Farms Considering Wake Effects[J]. Journal of Shanghai Jiaotong University, 2024, 58(6): 798-805 doi:10.16183/j.cnki.jsjtu.2022.476

大型风电场由数百台风电机组组成,受风场分布与尾流效应影响,各机组风速差异大,其短路特性也存在较大差异.风电场短路故障动态等值建模时采用风速、有功输出、电压作为分组指标可能导致分组数过多[1],仿真计算量大,不利于实际工程应用.因此,需合理考虑尾流效应影响下机组风速差异对集群故障动态等值模型结构和参数影响.

风电场动态等值方法主要分为单机等值法、半机等值法和多机等值法[2⇓-4].风电场单机等值模型拟合精度难以满足要求[5];半机等值法对仿真软件不具有普适性[6];多机等值法基于分组指标对风电场机组进行分组,并将同组机组等值为单台机组,从而采用少量机组替代整个风电场[7],其等值模型精度较高且计算量小.多机等值法的关键在于分组指标的选取,现有文献主要以地理位置分布和反映机组运行状态的特征参数作为分组指标.文献[8]中依据机组所处地理位置,按照行、列的方式对风电场分组等值.文献[9]中根据威布尔分布计算各风电机组的权重因子,并建立动态加权聚合等效模型.文献[10]中提出一种基于机组低电压穿越特性的倍乘等值方法.文献[5,11⇓⇓⇓-15]中选取机组的特征量作为分组指标,如风速[11]、桨距角动作情况[12]、状态变量矩阵[5]、机端暂态电压[13]、故障切除转速[14]、机组运行控制区域[15].

然而,在尾流效应影响下,风电场各机组间风速差异大,且机组间风速变化往往具有连续性,因此若以风速等特征参数为分群指标可能导致分组指标不明显且分组数较多问题[16].文献[17]中采用单-双高斯拟合算法对单台机组的尾流效应建模.文献[18]中分析了风电场内风电机组的尾流相互作用.文献[19]中假设尾流效应影响下同排机组风速相同,并将同排机组分为一组.文献[20-21]中基于尾流效应影响下机组运行状态的差异,以每台风电机组的风轮位于几个尾流影响区域作为分群指标.文献[22]中考虑风向与尾流效应的情况下,采用机组、风向、风速三维相关系数矩阵进行分群.大型风电场内各机组受尾流效应影响程度不同,位置相近的机组间运行状态可能相差较大,现有文献依据地理位置对机组进行区域划分或以受几台机组尾流效应影响为分组指标,可能造成同群机组运行状态存在显著差异,参数聚合时产生较大误差.

综上,目前研究主要集中在风电场稳态运行、低压穿越或三相对称故障风电场等值建模,考虑尾流效应对机组运行状态的影响,提出一种适用于非对称短路故障的风电场动态等值模型.首先以下游机组风速与上游机组风速比值为基准,定义尾流效应因子反映机组受尾流效应影响程度,并采用尾流效应因子作为分组指标.同时分析非对称短路故障时风电场正、负、零序网络的构成,并提出适用于零序集电网络的等值方法,提升非对称故障情况下等值模型的有效性.在PSCAD/EMTDC仿真平台上搭建风电场短路故障动态等值模型,验证了所提方法有效性.

1 基于尾流效应影响因子的风电机组聚类算法

1.1 尾流效应因子

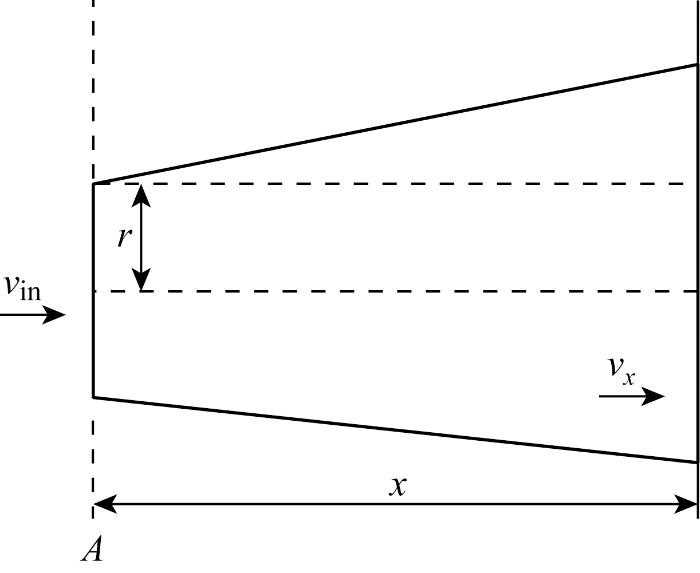
在同一风速、风向下,风电场中各台机组的运行状态受尾流效应影响程度不同[20],尾流效应是导致风电场内风速差异的主要原因.关于尾流效应的建模分析,文献[23]中指出比较成熟的是Jensen模型,其基本原理如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   尾流效应Jensen模型示意图

Fig.1   Diagram of Jensen model of wake effect


在偏航系统的作用下,机组风轮面垂直于风向,此时机组风速取决于机组受尾流效应影响程度.图1中,在A处的上游机组尾流效应影响下,x处的风速为

　vx=vin1-1-1-CT1/2rr+ζx2

式中:r为涡轮机的转子半径;x为沿风向的水平距离;vin为A处的来流风速;vx为尾流效应影响下的实际风速;ζ为衰减常量;CT为推力系数. 可知,下游机组风速vx与距离上游机组的水平距离x成反比,x值越大,则受上游机组尾流效应程度越小.在同一风场下,当x足够大时,下游机组风速vx接近上游机组风速vin,此时可以忽略尾流效应影响.

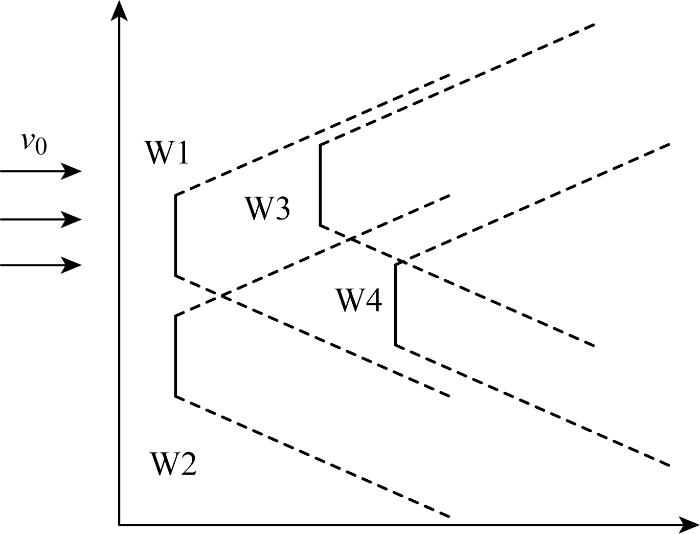
如图2所示,v0为初始风速,机组W1对机组W3风速影响高于对机组W4,但机组W4同时受机组W1和机组W2尾流效应影响.因此,机组W3与机组W4受尾流效应影响程度无法准确比较,其运行状态和短路故障特性差异也不确定.若按尾流效应影响对机组进行区域划分,将机组W3、W4归为同一分组,可能造成同组机组运行状态存在显著差异,其短路故障等值模型误差较大.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   机组间尾流效应示意图

Fig.2   Diagram of inter-unit wake effect


为量化每台风电机组受其他机组尾流效应程度,需定义尾流效应因子:

 δi=∑j≠iδij

式中:δi为机组i的尾流效应因子;δij为机组i受机组j的尾流效应程度.

尾流效应因子δi反映了机组i风速受尾流效应影响程度,其区间分界点用σ表示.若机组i位于上游,则不受其他机组尾流效应影响,δi值取0;若机组i不位于机组j尾流效应影响范围内,则δij同样为0;若机组i位于机组j尾流效应影响范围内,σ值越小,说明下游机组风速与上游机组风速相差越大,则机组i受机组j尾流效应程度越高,则δij值越大.当机组i位于机组j尾流效应影响范围内时,σ的取值区间为(0, 1),可将σ值化分为n个区间(0, σn-1), [σn-1, σn-2), …, [σ1, 1),δij由σ值基准决定,其取值方式如下式所示:

 δij=0,σ∈[σ1, 1)1,σ∈[σ2,σ1)n-1,σ∈(0,σn-1)

1.2 基于尾流效应因子的风电机组分群算法

分群的目的是将符合相似特征的数据尽可能归为一类,不符合相似特征的数据尽可能分开.已有文献[5,13]中通常采用一种高效简便的聚类分群方法,即k均值算法,但是由于要人为给定聚类的个数,可能会导致无法得到最优分类结果.本文以每台风力发电机的尾流效应因子作为分群的指标,采用自动选取最优分群数目的k均值算法对风电场机组进行分群.当聚类后的风力发电机组集群数为m时,需要根据各个风力发电机的差异分为m个集群,相同集群风力发电机的相似程度高、不同集群风力发电机的相似程度低.因此需要定义相似性指标:

ε(m)=∑n=1m∑j=1Ni(xn, j-yn)2/Nn∑n=1m(yn-Y)2/m

式中:xn, j为第n个集群中的第j个风力发电机;yn为第n个风力发电机集群的聚类中心值;Y为整个风力发电机群的聚类中心值;Nn为第n个集群的风力发电机个数;m为风力发电机聚类集群总个数.

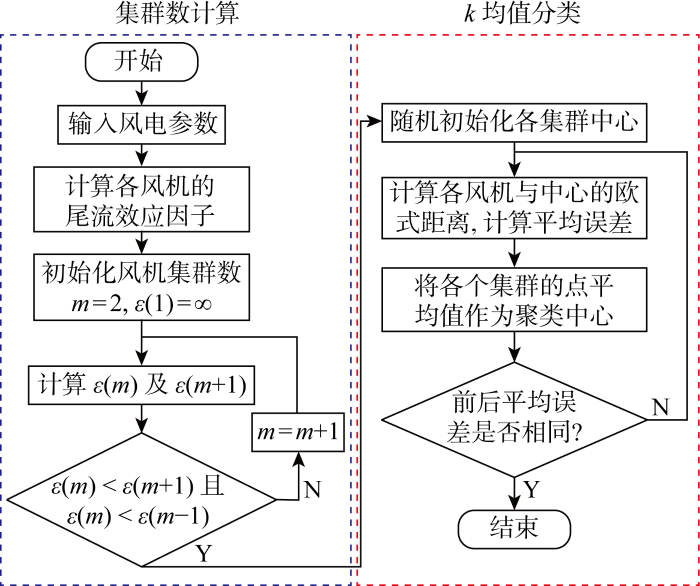
为实现聚类过程中,集群数的优化计算,避免人为确定集群数带来的应用局限性,采用以下的动态k均值分类算法,如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   分群算法流程图

Fig.3   Flow chart of binning algorithm


2 聚合参数等值

风电场分组后,采用基于容量加权的参数聚合法计算风力发电机等值模型参数[21],其中传动链、发电机、变压器聚合参数计算方法参考文献[18].

2.1 风速等值

设Peq为组内k台风力发电机捕获风功率之和,则

Peq=∑i=1kPi=∑i=1k12ρSiCpivi3

式中:Pi为第i台风力发电机捕获功率;Si为第i台风力发电机扫风面积;Cpi为第i台风力发电机风能利用系数;ρ为空气密度;vi为第i台风力发电机输入风速.

设等值风力发电机风能利用系数Cpeq为各台风力发电机风能利用系数平均值:

Cpeq=1n∑i=1mCpi

令:

Peq=12kCpeqρSiveq3

可得输入到等值风力发电机的等值风速,用veq表示:

veq3=1kCpeq∑i=1kCpivi313

对于恒转速区,由于对应该区的风速区间很小,通过仿真分析可知各机组的风能利用系数Cp差异不大,稳定在Cpmax附近.而对于恒功率区,变桨环节参与控制,各机组的Cp差异较大,使等值前后出现功率误差.因此,该风速等值方法适用于最大风能跟踪区(MPPT区)及恒转速区的机组聚合.对于恒功率区,此方法计算出的等值风速略有误差,但是只要等值风速对应的输入最大风能大于功率上限,即可保证机组运行在恒功率区,因此对于恒功率区该方法同样适用.风力发电机输出功率采用标幺值表示时,风力发电机尺寸无需变化,相应的齿轮箱变比、最大风能跟踪曲线系数也不变.

2.2 集电线路参数等值

依据等值损耗功率法[24],可得等值集电线路阻抗为

Zeq=∑i=1n(∑j=1iSj/Uj)2Zi+∑i=1n(Si/Ui)2ZTi∑i=1n(Si/Ui)2

式中:Zi为第i台机组的线路阻抗;Ui, Si, ZTi分别为第i台风力发电机的机端电压、容量以及升压变压器阻抗.

2.3 控制环节等值

等值风力发电机控制参数按下式参数聚合:

KG=∑∀j∈GSjSGKj

式中:Kj、KG分别为等值前后风力发电机比例-积分(PI)环节中的参数;Sj、SG分别为等值前后机组容量;G为风电场中的风力发电机集合.

3 负序、零序聚合参数等值

变压器和集电线路为静止原件,故前文所述的变压器和集电线路的正序参数等值方法同样适用于负序参数等值.而风力发电机为旋转元件,其正、负序阻抗参数计算方法不同.由于风电机组网侧换流器通常采用负序电流抑制策略消除机组非对称短路故障时产生的负序电流,故负序网络中通常将风力发电机的负序等值阻抗近似为无穷大[7].然而风力发电机在故障情况下,其正负序阻抗计算方式不同,因此需要对风电场序阻抗网络进行分析.

撬棒电路投入后,风力发电机负序等效阻抗将受到撬棒电阻及转差率影响,可由下式表达:

Z-=jωsLs[Rcb+j(2-s)(Lr-Lm2/Ls)ωs]Rcb+j(2-s)ωsLr

式中:ωs为同步角速度;Ls、Lr、Lm分别为风力发电机定、转子电感和互感;s为转差;Rcb为撬棒投入后的等效转子电阻.

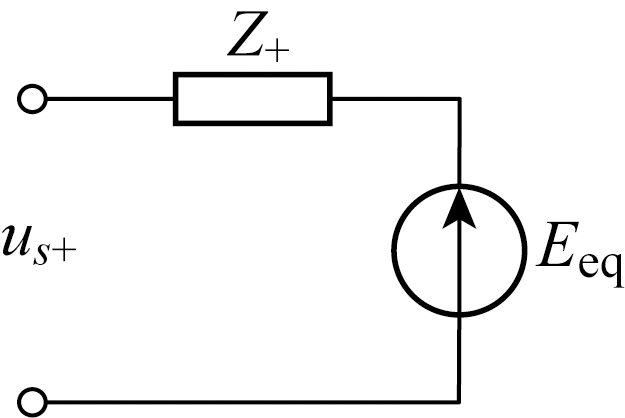
由于故障状态下,风力发电机正序电流存在基频分量和衰减的转速频率分量,所以风力发电机正序等值网络包含一个内阻抗Z+及一个衰减的电压源Eeq,如图4所示.图中,us+为风力发电机正序电压.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   风力发电机正序暂态网络

Fig.4   Positive sequence transient network of wind generator


当电流中的转速频分量衰减完之后,其无源阻抗表达式为

Z+=jωsLs[Rcb+jsωs(Lr-Lm2/Ls)]Rcb+jsωsLr

对于风力发电机零序阻抗,由于风电场正负序阻抗远大于零序阻抗,所以可忽略不计[24].综上所述,由于风力发电机直接与升压变压器相连接,其正负序阻抗与变压器串联,所以在风电场序阻抗网络等值中,只需将风力发电机正负序阻抗加上变压器阻抗,再代入式(9)中的ZTi,则可求得等值损耗功率下的风电场等效序阻抗网络.

4 算例分析

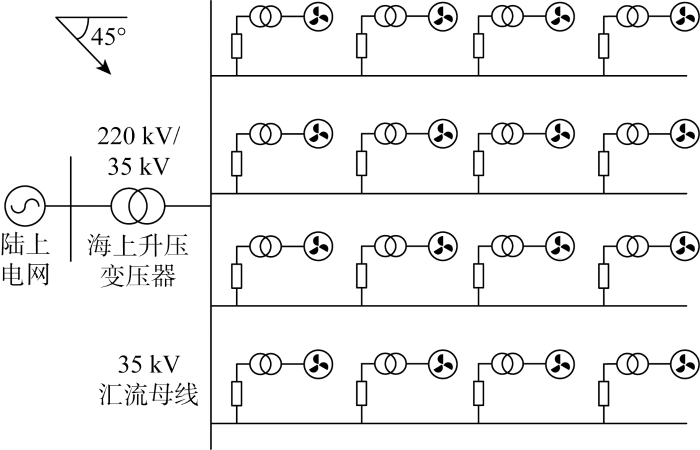
以某地区风电场的16台双馈风电机组为基础,在PSCAD/EMTDC仿真平台上搭建16台额定功率为5.5 MW双馈机组风电场,出口电压为690 V,经0.69/35 kV箱式变电站升压至35 kV,每3~5台风电机组成一个联合单元后,由35 kV海底电缆汇流至海上升压站,升压至220 kV后由送出海底电缆送至220 kV陆上集控站,再经一回220 kV架空线路接入阳江电网.将σ值化分为4个区间,区间分界点σ1、σ2、σ3按照风速分布阶梯,依次取0.95、0.7、0.4,并以各机组的尾流效应因子为分群指标.在三相短路故障、单相接地故障、两相接地故障情况下,对比四机等值模型、详细模型、单机倍乘模型输出响应曲线,结果如图5所示.其中四机等值模型采用本文所述分群等值方法,将风电场分为4个集群,每个集群等值为1台机组;详细模型中16台风力发电机均采用全阶电磁模型搭建;单机倍乘模型即未经过分群、所有风力发电机等值为1台机组.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   风电场模型

Fig.5   Diagram of wind farm model


4.1 三相短路故障

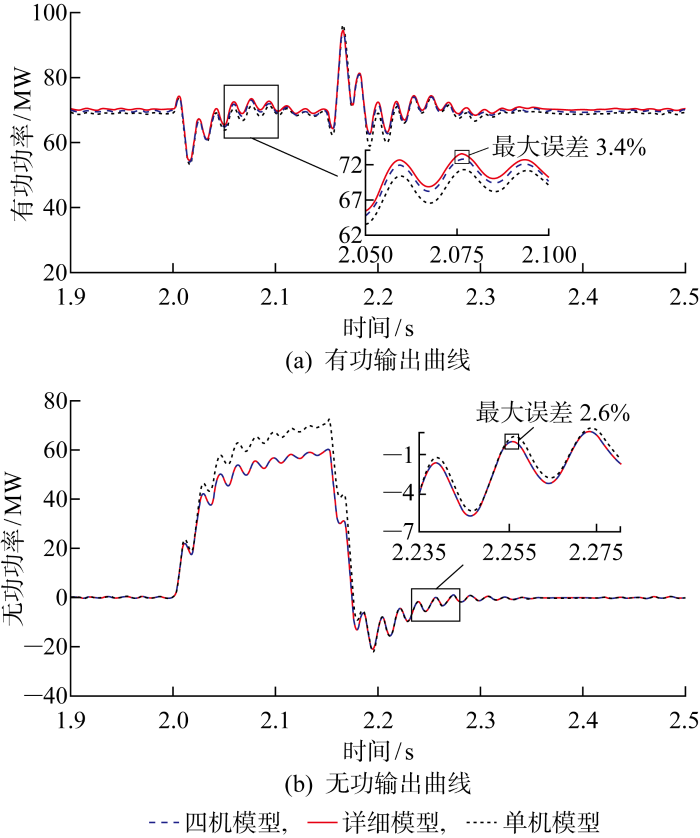
在风电场汇集母线(Point of Common Coupling,PCC)点设置三相接地短路故障,考察等值方法在三相故障情况下的适应性.假定暂态期间风速不变,图6为四机等值模型、详细模型、单机倍乘模型三相接地故障下风电场出口有功功率、无功功率输出曲线比较情况.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   PCC点三相接地故障输出曲线

Fig.6   Three-phase ground fault output of PCC point


由图6可以看出,三相接地故障下四机模型的输出有功功率、无功功率误差更小,准确反映了风电场有功、无功特性.因此,采用本文考虑尾流效应的风电场短路故障动态等值模型能够相对准确地反映风电场在PCC点三相接地故障情况下的动态响应,四机模型与详细模型仿真结果基本一致,最大误差低于2.6%.

4.2 单相接地故障

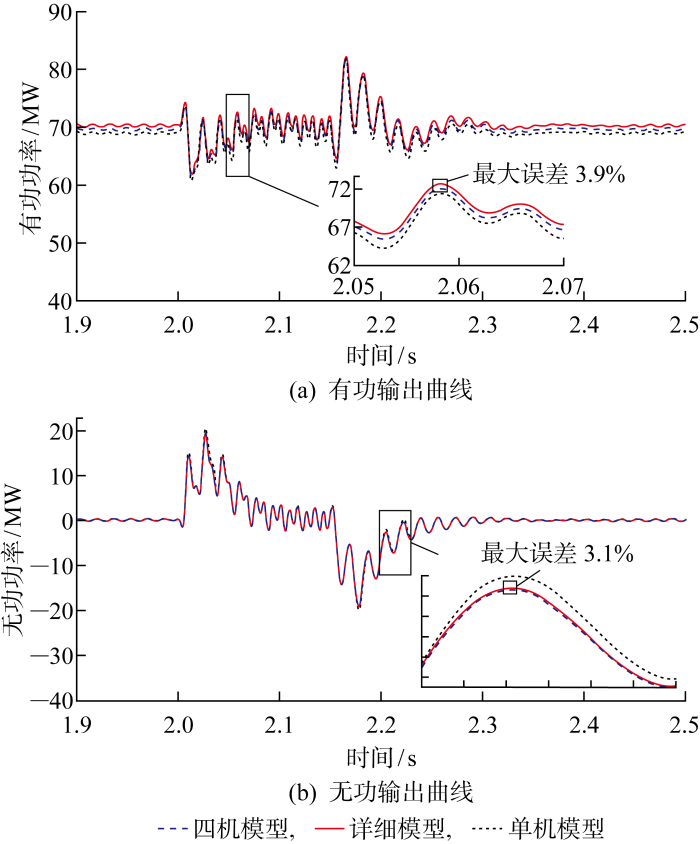
对PCC点单相接地故障仿真,假定暂态期间风速不变,图7为四机等值模型、详细模型、单机倍乘模型单相接地故障下风电场出口有功功率、无功功率输出曲线对比情况.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   PCC点单相接地故障输出曲线

Fig.7   Single-phase ground fault output of PCC point


从图7可以看出,相比于单机倍乘模型,四机模型输出有功功率与详细模型误差更小,能准确反映详细模型的有功、无功变化趋势.因此,本文短路故障动态等值模型能够相对准确地反映风电场在PCC点单相接地故障情况下的动态响应.

4.3 两相接地故障

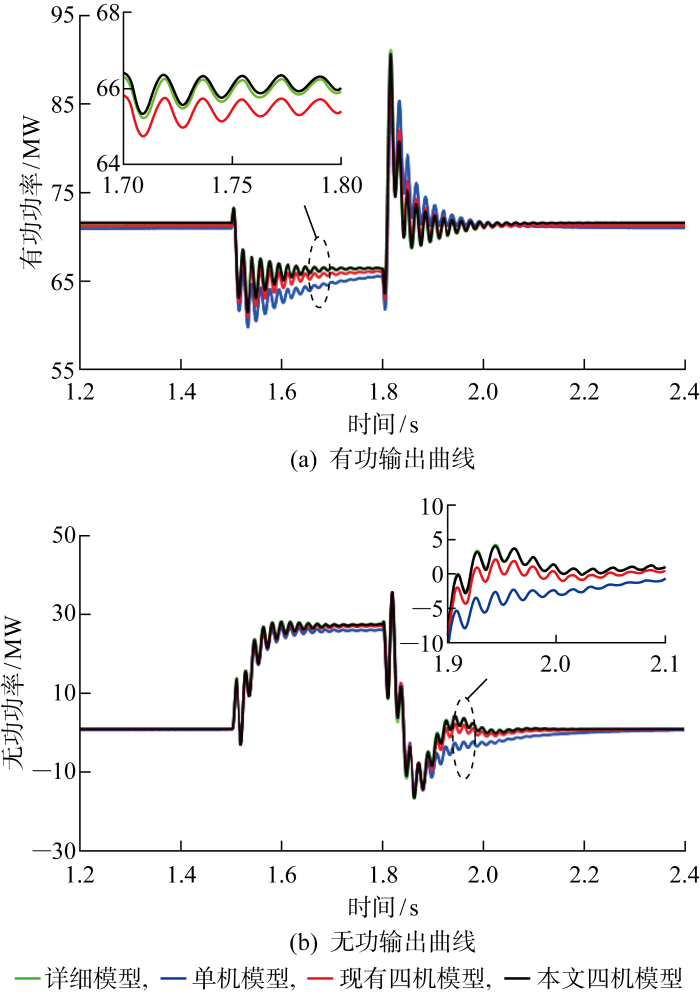
工程应用中,常见因三相交流系统绝缘特性下降而引发相间短路,其危害性相较于单相接地短路故障更为严重.相间短路故障中,又以两相接地短路故障最为严重.因此进一步分析PCC点两相接地故障的特性,如图8所示.两相接地短路引起定子绕组中出现较大不对称电流分量,导致功率波动剧烈.图中所示现有四机模型采用文献[22]中所提基于K-means的风速分群等值方法,由于分群时需确定聚类中心和聚类数量,所以当风电场经历较大扰动后,原来确定的参数将不再适应.相比而言,本文基于尾流效应因子的动态分群方法,风速仅作为初始化的条件输入,其分群结果动态优化,更适用于运行工况多变的风电场,具有更低等值误差.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   PCC点两相接地故障输出曲线

Fig.8   Double-phase ground fault output of PCC point


综合仿真结果表明,本文短路故障动态等值模型能准确模拟风电场PCC处发生对称或非对称接地短路故障期间各电气量的动态特性,与单机等值模型相比精度有所提升,从而验证了所提动态等值方法的有效性.

5 结语

考虑尾流效应对机组运行状态影响,提出一种适用于短路故障分析的风电场多机动态等值建模方法.该方法以尾流效应因子为分群指标,反映风电场各机组受尾流效应影响后运行状态的差异性,并且避免风电场采用风速、有功输出作为分群指标可能导致分组过多问题.分析风电场短路时正、负、零三序网络的构成,并提出适用于零序集电网络的等值方法,提升非对称故障情况下等值模型的有效性.仿真结果表明,该方法能准确反映风电场故障期间有功功率和无功功率响应特性,适合风电场对称和非对称短路故障的暂态分析,具有重要的工程应用价值.

参考文献

奚鑫泽, 邢超, 覃日升, 等.

含双馈风力发电系统的配电网短路电流特性

[J]. 上海交通大学学报, 2023, 57(7): 921-927.

DOI:10.16183/j.cnki.jsjtu.2022.011      [本文引用: 1]

双馈异步风力发电机(DFIG)作为分布式电源接入配电网,能将辐射状的单电源系统变为双电源系统,改变配电网的拓扑结构.当配电网发生短路故障时,配电网的短路电流会受到风力发电接入的影响.针对DFIG作为分布式电源接入配电网,配电网中不同点发生三相短路故障时短路电流受到风力机接入容量及接入点位置影响的问题,结合DFIG的控制策略进行理论推导和仿真分析.首先,从理论上推导含风力发电的配电网短路故障电流关系式,对风力机提供的短路电流进行分析.然后,引入模型预测控制,与经典的矢量控制进行对比分析得出不同控制策略对短路电流的影响,并在此基础上分析配电网在不同点发生三相短路故障时,短路电流随风力机接入容量及位置的变化情况,分析总结DFIG对配电网短路电流及电流保护的影响.

XI Xinze, XING Chao, QIN Risheng, et al.

Characteristics of short-circuit current in distribution network with doubly-fed wind power system

[J]. Journal of Shanghai Jiao Tong University, 2023, 57(7): 921-927.

[本文引用: 1]

林俐, 赵会龙, 陈迎, 等.

风电场建模研究综述

[J]. 现代电力, 2014, 31(2): 1-10.

[本文引用: 1]

LIN Li, ZHAO Huilong, CHEN Ying, et al.

Research summary of wind farm modeling

[J]. Modern Electric Power, 2014, 31(2): 1-10.

[本文引用: 1]

CHOWDHURY M A, SHEN W X, HOSSEINZADEH N, et al.

A novel aggregated DFIG wind farm model using mechanical torque compensating factor

[J]. Energy Conversion and Management, 2013, 67: 265-274.

[本文引用: 1]

LIU H Z, CHEN Z.

Aggregated modelling for wind farms for power system transient stability studies

[C]//2012 Asia-Pacific Power and Energy Engineering Conference. Shanghai, China: IEEE, 2012: 1-6.

[本文引用: 1]

陈树勇, 王聪, 申洪, 等.

基于聚类算法的风电场动态等值

[J]. 中国电机工程学报, 2012, 32(4): 11-19.

[本文引用: 4]

CHEN Shuyong, WANG Cong, SHEN Hong, et al.

Dynamic equivalence for wind farms based on clustering algorithm

[J]. Proceedings of the CSEE, 2012, 32(4): 11-19.

[本文引用: 4]

徐玉琴, 刘丹丹.

基于两步分群法的双馈机组风电场等值建模

[J]. 电力系统保护与控制, 2017, 45(6): 108-114.

[本文引用: 1]

XU Yuqin, LIU Dandan.

Equivalence of wind farms with DFIG based on two-step clustering method

[J]. Power System Protection and Control, 2017, 45(6): 108-114.

[本文引用: 1]

余浩, 张哲萌, 彭穗, 等.

海上风电经柔性直流并网技术标准对比分析

[J]. 上海交通大学学报, 2022, 56(4): 403-412.

DOI:10.16183/j.cnki.jsjtu.2021.465      [本文引用: 2]

对国内外海上风电经柔性直流并网标准的现状进行介绍,选取具有代表性的海上风电经柔性直流并网标准,从功率控制、故障穿越、电能质量、稳定性等几个方面进行对比,分析海上风电经柔性直流并网标准的发展趋势.对中国海上风电经柔性直流并网标准的制修订提供合理建议,以促进海上风电行业的发展.

YU Hao, ZHANG Zhemeng, PENG Sui, et al.

Comparative analysis of technical standards for offshore wind power via VSC-HVDC

[J]. Journal of Shanghai Jiao Tong University, 2022, 56(4): 403-412.

[本文引用: 2]

YE L, RAO R S, ZHANG Y L, et al.

Dynamic equivalent modeling approach of wind power plant with PMSG-WTGs

[C]//2017 IEEE Power & Energy Society General Meeting. Chicago, USA: IEEE, 2017: 1-5.

[本文引用: 1]

ZHOU Y H, ZHAO L, MATSUO I B M, et al.

A dynamic weighted aggregation equivalent modeling approach for the DFIG wind farm considering the weibull distribution for fault analysis

[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 5514-5523.

[本文引用: 1]

魏娟, 黎灿兵, 黄晟, 等.

大规模风电场高电压穿越控制方法研究综述

[J/OL]. 上海交通大学学报. https://doi.org/10.16183/j.cnki.jsjtu.2022.416.

[本文引用: 1]

WEI Juan, LI Canbing, HUANG Sheng, et al.

Review on high voltage ride-through control method of large-scale wind farm

[J/OL]. Journal of Shanghai Jiao Tong University. https://doi.org/10.16183/j.cnki.jsjtu.2022.416.

[本文引用: 1]

高永强, 梅勇, 王晗玥, 等.

基于机组聚合与线路等值影响因子的风电场等值优化

[J]. 广东电力, 2023, 36(6): 11-22.

[本文引用: 2]

GAO Yongqiang, MEI Yong, WANG Hanyue, et al.

Equivalent optimization of wind farm based on influencing factors of wind turbine aggregation and collector line equivalence

[J]. Guangdong Electric Power, 2023, 36(6): 11-22.

[本文引用: 2]

袁超, 颜全椿, 顾文, 等.

考虑尾流效应及连接架构的风电场等值方法研究

[J]. 可再生能源, 2023, 41(6): 794-803.

[本文引用: 2]

YUAN Chao, YAN Quanchun, GU Wen, et al.

Study on the wind farm equivalent method considering wake effect and connection structure

[J]. Renewable Energy Resources, 2023, 41(6): 794-803.

[本文引用: 2]

徐玉琴, 王娜.

基于聚类分析的双馈机组风电场动态等值模型的研究

[J]. 华北电力大学学报(自然科学版), 2013, 40(3): 1-5.

[本文引用: 3]

XU Yuqin, WANG Na.

Study on dynamic equivalence of wind farms with DFIG based on clustering analysis

[J]. Journal of North China Electric Power University (Natural Science Edition), 2013, 40(3): 1-5.

[本文引用: 3]

张剑, 崔明建, 何怡刚.

基于PMU实测数据的DFIG风电场等值模型鲁棒性与适应性分析

[J]. 太阳能学报, 2023, 44(10): 320-328.

DOI:10.19912/j.0254-0096.tynxb.2022-0867      [本文引用: 2]

对传统聚合方法无法解决风电场长期运行过程中产生的参数变化问题,该文基于实测数据建立双馈感应发电机（DFIG）风电场详细等值模型与初始化方法,分析时变参数的轨迹灵敏度,提出首先将非时变参数固定为聚合值,然后利用风电场公共并网点相量测量单元（PMU）数据针对时变参数采用基因学习粒子群（GLPSO）混合算法进行参数辨识的策略。采用WECC标准算例分析不同风速、尾流效应、部分风电机组离线、风速未知、不同短路故障位置与电压暂降深度情形下等值模型的鲁棒性与适应性。仿真算例表明所提出的参数辨识方法全局寻优能力远高于标准粒子群与遗传算法。而且,对于高灵敏度参数,参数辨识结果与真实值的最大偏差小于10%,远优于目前技术水平。

ZHANG Jian, CUI Mingjian, HE Yigang.

Robustness and adaptability analysis of equivalent model of DFIG wind farm based on measured data of PMU

[J]. Acta Energiae Solaris Sinica, 2023, 44(10): 320-328.

DOI:10.19912/j.0254-0096.tynxb.2022-0867      [本文引用: 2]

In this paper, in view of the fact that the traditional aggregation method cannot solve the problem of parameters variation after long-term operation of wind farms, a detailed equivalent model of Doubly Fed Induction Generators （DFIGs） wind farm and initialization method are developed. The trajectory sensitivity of parameters is analyzed. Parameters identification strategy is proposed that the non-time-varying parameters are fixed as aggregated values, while the Genetic Learning Particle Swarm Optimization （GLPSO） hybrid algorithm is used to identify time-varying parameters based on Phasor Measurement Unit （PMU） data at the common interconnection point of wind farm. The robustness and adaptability of the equivalent model of DFIG wind farm under different wind speeds, wake effects, unknown wind speed, different short-circuit fault locations and voltage sags depth and some DFIGs off-line are analyzed. The simulation results using the Western Electricity Coordinating Council benchmark test system show that the global searching capability to find the optimal solution of the proposed method is much higher than that of canonical particle swarm optimization （PSO） and genetic algorithm （GA）. Further, the maximum deriation between the identification results using the proposed method and the true values is less than 10% with high sensitivity parameters, which is much better than previous state-of-art work.

高峰, 赵东来, 周孝信, 等.

直驱式风电机组风电场动态等值

[J]. 电网技术, 2012, 36(12): 222-227.

[本文引用: 2]

GAO Feng, ZHAO Donglai, ZHOU Xiaoxin, et al.

Dynamic equivalent algorithm for wind farm composed of direct-drive wind turbines

[J]. Power System Technology, 2012, 36(12): 222-227.

[本文引用: 2]

董文凯, 任必兴, 王海风, 等.

适用于系统次同步振荡分析的风电场等值建模方法综述

[J]. 电力工程技术, 2022, 41(4): 33-43.

[本文引用: 1]

DONG Wenkai, REN Bixing, WANG Haifeng, et al.

Small-signal equivalent modeling methods of the wind farm and its application in sub-synchronous oscillations analysis of gird-connected wind power systems

[J]. Electric Power Engineering Technology, 2022, 41(4): 33-43.

[本文引用: 1]

白雁翔, 王德林, 马宁宁, 等.

大型风电场的动态等值方法研究

[J]. 电工技术, 2018(13): 46-49.

[本文引用: 1]

BAI Yanxiang, WANG Delin, MA Ningning, et al.

Study on dynamic equivalence method of large scale wind farm

[J]. Electric Engineering, 2018(13): 46-49.

[本文引用: 1]

刘清媛, 吴松华, 张凯临, 等.

基于单-双高斯模型拟合法的测风激光雷达海上风电机组尾流特征分析

[J]. 大气与环境光学学报, 2021, 16(1): 44-57.

[本文引用: 2]

LIU Qingyuan, WU Songhua, ZHANG Kailin, et al.

Offshore wind turbine wake characteristics analysis using single-double Gaussian model based on wind lidar measurements

[J]. Journal of Atmospheric and Environmental Optics, 2021, 16(1): 44-57.

[本文引用: 2]

SUN H Y, GAO X X, YANG H X.

A review of full-scale wind-field measurements of the wind-turbine wake effect and a measurement of the wake-interaction effect

[J]. Renewable and Sustainable Energy Reviews, 2020, 132: 110042.

[本文引用: 1]

徐玉琴, 张林浩, 王娜.

计及尾流效应的双馈机组风电场等值建模研究

[J]. 电力系统保护与控制, 2014, 42(1): 70-76.

[本文引用: 2]

XU Yuqin, ZHANG Linhao, WANG Na.

Study on equivalent model of wind farms with DIFG considering wake effects

[J]. Power System Protection and Control, 2014, 42(1): 70-76.

[本文引用: 2]

黄梅, 万航羽.

在动态仿真中风电场模型的简化

[J]. 电工技术学报, 2009, 24(9): 147-152.

[本文引用: 2]

HUANG Mei, WAN Hangyu.

Simplification of wind farm model for dynamic simulation

[J]. Transactions of China Electrotechnical Society, 2009, 24(9): 147-152.

[本文引用: 2]

曹娜, 于群.

风速波动情况下并网风电场内风电机组分组方法

[J]. 电力系统自动化, 2012, 36(2): 42-46.

[本文引用: 2]

CAO Na, YU Qun.

A grouping method for wind turbines in a grid-connected wind farm during wind speed fluctuation

[J]. Automation of Electric Power Systems, 2012, 36(2): 42-46.

[本文引用: 2]

袁飞.

风电场常用工程尾流模型对比与分析

[J]. 能源与节能, 2023(11): 37-41.

[本文引用: 1]

YUAN Fei.

Comparison and analysis of commonly used engineering wake models in wind farms

[J]. Energy and Energy Conservation, 2023(11): 37-41.

[本文引用: 1]

蔺红, 晁勤.

等值损耗功率法在风电场等值计算中的应用

[J]. 电测与仪表, 2011, 48(8): 5-9.

[本文引用: 2]

LIN Hong, CHAO Qin.

Application of equivalent power loss in equivalence calculation of wind farms

[J]. Electrical Measurement & Instrumentation, 2011, 48(8): 5-9.

[本文引用: 2]

/

〈 〉