基于量子蚁群算法的配电网故障区段快速定位技术

doi:10.16183/j.cnki.jsjtu.2023.004

基于量子蚁群算法的配电网故障区段快速定位技术

毕忠勤¹, 余晓婉¹, 王宝楠^,¹^,², 黄文焘², 张丹³, 董真⁴

1.上海电力大学计算机科学与技术学院,上海 201306

2.上海交通大学电力传输与功率变换控制教育部重点实验室,上海 200240

3.上海海事大学物流科学与工程研究院,上海 201306

4.国网上海市电力公司电力科学研究院,上海 200437

Fast Fault Location Technology for Distribution Network Based on Quantum Ant Colony Algorithm

BI Zhongqin¹, YU Xiaowan¹, WANG Baonan^,¹^,², HUANG Wentao², ZHANG Dan³, DONG Zhen⁴

1. College of Computer Science and Technology, Shanghai University of Electric Power, Shanghai 201306, China

2. Key Laboratory of Control of Power Transmission and Conversion of the Ministry of Education, Shanghai Jiao Tong University, Shanghai 200240, China

3. Institute of Logistics Science and Engineering, Shanghai Maritime University, Shanghai 201306, China

4. State Grid Shanghai Electric Power Research Institute, Shanghai 200437, China

通讯作者: 王宝楠,讲师;E-mail:wbn_shu0099@163.com.

责任编辑: 王历历

收稿日期: 2023-01-4 修回日期: 2023-04-4 接受日期: 2023-05-8

基金资助:

电力传输与功率变换控制教育部重点实验室开放课题(2022AA02)

Received: 2023-01-4 Revised: 2023-04-4 Accepted: 2023-05-8

作者简介 About authors

毕忠勤(1977-),教授,从事云计算、数据处理和智能电网中的质量控制等研究.

摘要

分布式电源并入配电网已成为新型电力系统重要特征之一,分布式电源的接入与发电的不确定性使配电网潮流复杂多变,对配电网故障快速定位提出更高的技术要求.然而,现有智能优化算法在解决配电网故障区段定位问题时会出现收敛速度慢、易陷入局部最优等问题.针对这些挑战与问题,提出一种基于量子蚁群算法(QACA)的配电网故障区段快速定位技术.首先,根据状态逼近思想和最小故障集理论构建配电网故障定位的数学模型;其次,针对馈线终端单元上传信息缺失情况提出信息自修正方法,并提出分级定位模型来缩短定位时间;然后,提出3种改进技术对QACA进行针对性改进,改进量子旋转门更新机制,以函数控制形式动态调整旋转角大小,同时引入精英策略加快算法收敛速度.最后,在关键参数确定后验证了改进技术、信息自修正法、分级定位模型的有效性.将所提算法与7种不同算法进行对比,结果表明:改进的QACA可有效完成故障区段定位,具有良好的收敛速度、准确率以及容错性能.

关键词： 配电网故障区段定位; 量子蚁群算法; 信息自修正法; 分级定位模型

Abstract

Integration of distributed generations into distribution networks has become one of the important features of new power systems. The integration of distributed generation and the uncertainty of power generation make the power flow in distribution networks complex and variable, which poses higher technical requirements for rapid fault location in distribution networks. However, existing intelligent optimization algorithms may encounter problems such as slow convergence speed and susceptibility to local optimization when solving the problem of fault section location in distribution networks. To address these challenges and problems, a rapid fault section location technology based on quantum ant colony algorithm (QACA) is proposed. First, a location mathematical model is constructed based on the state approximation idea and the minimum fault set theory. Then, an information self-correction method is proposed for the missing information uploaded by feeder terminal unit, and a hierarchical location model is proposed to shorten the location time. Afterwards, three improvement techniques are proposed to improve the QACA. The update mechanism of the quantum rotary gate is improved, the rotation angle is dynamically adjusted in the form of function control, and the elite strategy is introduced to accelerate the convergence speed of the algorithm. Finally, after the key parameters are determined, the effectiveness of the improved technique, the information self-correction method, and the hierarchical positioning model is verified. A comparison with 7 different algorithms indicates that the improved QACA can effectively locate the fault section, and has a fast convergence speed, great accuracy, and fault tolerance.

Keywords： location of fault section in distribution network; quantum ant colony algorithm (QACA); information self-correction method; hierarchical location model network

PDF (2880KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

毕忠勤, 余晓婉, 王宝楠, 黄文焘, 张丹, 董真. 基于量子蚁群算法的配电网故障区段快速定位技术[J]. 上海交通大学学报, 2024, 58(5): 693-708 doi:10.16183/j.cnki.jsjtu.2023.004

BI Zhongqin, YU Xiaowan, WANG Baonan, HUANG Wentao, ZHANG Dan, DONG Zhen. Fast Fault Location Technology for Distribution Network Based on Quantum Ant Colony Algorithm[J]. Journal of Shanghai Jiaotong University, 2024, 58(5): 693-708 doi:10.16183/j.cnki.jsjtu.2023.004

配电网主要担负分配电能的任务,是连接输电网与电力用户的纽带.快速准确的故障区段定位有利于迅速定位隔离故障和恢复供电,对提高电力系统电能质量至关重要^[1-2].现已存在多种配电网故障定位方法,按照定位结果分类主要包括3个方面:故障选线、故障测距和故障区段定位^[3-4].随着配电网自动化技术的快速发展,基于沿线装设现场设备馈线终端单元的故障区段定位方法成为当前研究热点.目前,基于馈线终端单元(Feeder Terminal Unit, FTU)的故障定位算法可分为两类:直接算法和间接算法.直接算法根据图论知识,结合线路的电流信息和配电网的拓扑结构对故障进行诊断,经典方法为矩阵算法^[5⇓-7].矩阵算法是将网络描述矩阵和故障信息向量相乘形成判据矩阵,实现对故障区段的准确定位^[8].矩阵算法原理简单且定位快速,但当配电网拓扑发生改变时要重新生成网络矩阵或数据库,因此算法通用性差,且对于FTU上传故障信息精准度依赖较强,容错性差.间接算法包含智能优化算法、数学类优化算法、人工智能方法.其中,数学类优化算法是一种以代数关系建模为基础的故障定位方法,可用数值稳定性高的非线性规划进行决策,克服了逻辑模型对群体智能算法的依赖,但是该类方法建模复杂,求解效率问题还有待考察^[9-10].人工智能方法如专家系统、神经网络等通过构建考虑多种因素的历史故障知识模型,结合从数据采集与监视控制(Supervisory Control and Data Acquisition, SCADA)系统获取的数据信息,从而实现故障定位,但是该类方法通用性不强,对于不同拓扑结构的配电网需要完全不同的数据支撑.目前的研究热点为将配电网故障定位问题转换为二进制优化问题,以馈线区段状态作为决策变量来建立配电网故障定位的数学模型,使用智能优化算法迭代寻优找到故障区段^[11].文献[12]中使用一种改进的突变二值获取知识共享算法,有效地解决了配电网故障定位问题,算例验证所提算法可以准确定位单点故障、多点故障以及信息畸变等情况.文献[13]中提出一种改进的仿电磁学算法解决配电网故障区段定位问题,根据分层及全局寻优思想对传统定位方法的一体化结构进行优化,成功验证算法在大规模复杂配电网上的定位有效性.文献[14]中使用多元宇宙算法进行配电网故障定位,引入自适应精英策略和自适应突变操作改进算法,实验结果表明改进的多元宇宙算法具有很高的准确率和收敛速度.文献[15]中提出基于秃鹰搜索算法的配电网故障定位,通过引入交叉算子、非均匀变异算子和翻筋斗觅食策略来提高算法寻优能力,改进后算法的准确率、求解速度均有提升.智能优化算法在求解配电网故障定位问题时具备一定的容错性,且自适应能力较强,算法通用性好,能够适应复杂的配电网结构,但是算法存在收敛速度慢、易陷入局部最优解的问题.因此,避免甚至解决这些问题成为该领域的新研究方向.

量子人工智能提供了一种不同于经典算法的新量子计算模式^[16].已有学者证明使用量子计算与智能优化算法相结合的方法能够避免传统智能优化算法寻优效率低、准确率不高的问题.文献[17]中采用量子免疫算法解决配电网故障定位问题,用量子比特编码方式体现量子的并行性提高算法收敛速度,并优化克隆扩增和变异操作过程,帮助算法的全局搜索.文献[18]中将量子计算与遗传算法结合,成功应用于配电网故障定位问题,构建动态自适应角策略优化量子旋转门,避免算法陷入局部最优.当前,基于量子计算与智能优化算法相结合的配电网故障定位问题的研究处于初期阶段,成果较少,值得深入探索.

量子蚁群算法(Quantum Ant Colony Algorithm,QACA)是结合量子计算高效并行性及蚁群算法正反馈性、强鲁棒性等优势的一种可靠、有前景的算法,目前已成功在路径规划、0-1背包等问题上应用,QACA相比其他智能优化算法在寻优性能上的优势也已被证明^[19-20].使用QACA解决配电网故障定位问题,并对模型及算法进行合理改进,旨在设计一种配电网故障区段快速定位技术.首先,建立配电网故障定位数学模型,提出信息自修正法并介绍以对外等效原理为基础的分级定位模型;然后,介绍QACA基本原理并对算法进行针对性地改进,通过故障定位问题转换实现QACA的应用;最后,在IEEE33节点配电网、三电源环网开环运行配电网以及含分布式电源69节点的配电网上进行仿真,验证前期工作的有效性,通过不同实例下的分析与不同算法的对比,体现改进量子蚁群算法(Improved QACA, IQACA)优秀的寻优能力.

1 配电网故障定位问题数学模型

1.1 开关函数

配电网发生故障后,SCADA接收到FTU上传的过流信息,在利用算法进行故障区段定位时,必须建立一个从开关故障电流越限情况到馈线区段状态的转换,开关函数可实现这样的转换.

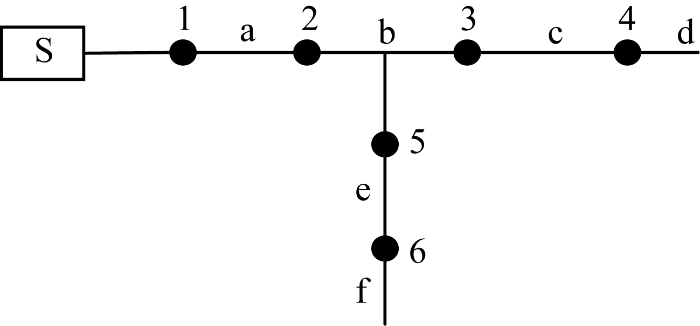
如图1所示为单电源辐射状配电网,S表示主电源,1~6为馈线开关,a~f为馈线区段.规定从系统电源到馈线末端为正方向,如果FTU在某节点处监测到过电流,则节点上开关的状态上传值为1,反之为0.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 简单配电网拓扑图

Fig.1 Topology diagram of a simple distribution network

开关函数即期望状态信息 $I_{j}^{*}$ 与区段状态值的数学逻辑关系如下:

(1)

I_{j}^{*}

\overset{n}{\prod_{i = 1}}

C_i

式中:“∏”表示逻辑或相乘;n为开关j下游馈线区段总数;C_i为开关j下游第i个馈线区段状态值,状态值取1表示区段发生故障,取0表示未发生故障.

以图1配电网为例, $I_{j}^{*}$ 可表示为

(2)

\begin{array}{l} I_{1}^{*} = I_{2}^{*} \lor C_{a} \\ I_{2}^{*} = I_{3}^{*} \lor I_{5}^{*} \lor C_{b} \\ I_{3}^{*} = I_{4}^{*} \lor C_{c} \\ I_{4}^{*} = C_{d} \\ I_{5}^{*} = I_{6}^{*} \lor C_{e} \\ I_{6}^{*} = C_{f} \end{array}\}

式中:“∨”表示逻辑或运算; $I_{1}^{*}$ ~ $I_{6}^{*}$ 为馈线开关状态;C_a~C_f为馈线区段状态.

分布式电源接入后配电网潮流由原来的单向变成双向流动,故障电流的编码需要考虑潮流方向.若检测到与正方向一致的故障电流,编码为1,若与正方向相反则编码为-1,无故障电流产生则编码为0.开关函数的设置需要同时考虑节点上游及下游的开关状态,定义如下:

(3)

I_{j}^{*}

[\prod_{s_{1}} K_{s_{1}} (1 - \sum_{i_{1}} x_{j, s_{1}} (i_{1}))] \prod_{n}

x_j₁(n)-

[\prod_{s_{2}} K_{s_{2}} (1 - \sum_{i_{2}} x_{j, s_{2}} (i_{2}))] \prod_{m}

x_j₂(m)

式中: $K_{s_{1}}$ 、 $K_{s_{2}}$ 为电源开关系数,分别用来表示第j个开关上游区、下游区的电源是否接入配电网,若电源接入配电网则对应的电源系数取1,否则取0; $x_{j, s_{1}}$ 、 $x_{j, s_{2}}$ 分别为从第j个开关到上游区电源、下游区电源路径上所经过的馈线区段状态值;s₁、s₂分别为第j个开关上游电源、下游电源;x_j₁、x_j₂分别为从第j个开关到上游区段、下游区段状态值;m、n分别为第j个开关上游区段序号、下游区段序号.

1.2 目标函数

目标函数是评价测控点的期望状态信息与实际状态信息差异的重要指标,其表达式直接影响故障定位的准确性.根据状态逼近思想和最小故障集理论,目标函数构造如下:

(4)F=

\overset{N}{\sum_{j = 1}} |I_{j} - I_{j}^{*} (S_{B})|

\overset{M}{\sum_{k = 1}} |C_{k}|

式中:N为配电网节点数;I_j为各测控点的实际状态; $I_{j}^{*}$ (S_B)为各测控点的期望状态;S_B为馈线区段的状态;w为权重系数;M为配电网区段数量;C_k为区段k的状态值.式(4)中 $\overset{N}{\sum_{j = 1}} |I_{j} - I_{j}^{*} (S_{B})|$ 依据状态逼近思想建立,若实际状态与期望状态一致则为0,但是会出现不同故障诊断结果对应相同目标函数值的情况,会因“一对多”的关系造成误判;依据故障最小集理论,增加式(4)中w $\overset{M}{\sum_{k = 1}} |C_{k}|$ ,为了在可能的故障诊断结果中选取故障线路数目最小的解,可避免发生误判.

1.3 信息自修正法

恶劣环境、电磁干扰等不定因素可能导致FTU上传的信息出现缺失或畸变的情况,增加配电网故障定位的难度,是算法准确定位故障的一大挑战.目前,许多研究针对信息畸变情况进行修正判别,且大多针对矩阵算法容错率低的缺陷.对于信息缺失情况,多数研究直接将缺失点状态定为0,利用算法容错性定位故障区段.针对FTU上传信息发生缺失情况提出信息缺失自修正法.规定配电网中开关至系统电源方向为该开关节点的上游(用u表示),与该方向相反的方向称为下游(用d表示),假设信息缺失节点为f,则信息自修正法可由下式表示:

(5)I_f=

\{\begin{array}{l} I_{f u} I_{f d}, & 同 时 含 有 上 下 节 点 状 态 信 息 \\ 且 不 同 时 为 - 1 时 \\ I_{f d}, & 不 含 上 游 节 点 状 态 信 息 \\ - 1, & 上 下 游 节 点 状 态 信 息 同 时 为 - 1 时 \\ 0, & 其 他 \end{array}

其中,I_f_u由节点f的上游节点信息状态决定,I_f_d由节点f的下游节点信息状态决定,分别按下式取值:

(6)I_f_u=

\{\begin{array}{l} 1, & 上 游 节 点 状 态 信 息 含 1 时 \\ - 1, & 上 游 节 点 状 态 不 含 1 含 - 1 时 \\ 0, & 上 游 节 点 状 态 信 息 全 为 0 时 \end{array}

(7)I_f_d=

\{\begin{array}{l} 1, & 下 游 节 点 状 态 信 息 含 1 时 \\ - 1, & 下 游 节 点 状 态 信 息 不 含 1 含 - 1 时 \\ 0, & 下 游 节 点 状 态 信 息 全 为 0 时 \end{array}

信息自修正法基于配电网拓扑结构,由节点的上游及下游节点信息决定该节点状态的修正值.若在上传节点信息前增加信息自修正环节,尽可能还原真实故障过流信息,可最大程度地避免信息缺失带来的影响.

1.4 分级定位模型

传统单级定位模型定位故障时算法耗时与配电网规模呈正比关系,对于大型结构复杂的配电网,算法定位耗时长,实时性无法保证.可考虑分级定位模型,根据对外等效原理对配电网进行分区,降低定位维度,从而缩短定位时间.

以图1简单配电网为例,由于3、4节点状态对其他节点的期望状态值影响相同,根据对外等效原理可将这些节点划分为一个区域,由此图1的配电网被划分成3个独立区域,如图2所示.规定每个区域的端节点状态代表整个区域状态.分级定位模型第一级根据区域状态使用算法定位故障区段所在区域,第二级在定位得到的区域内定位具体故障区段.

图2

新窗口打开| 下载原图ZIP| 生成PPT

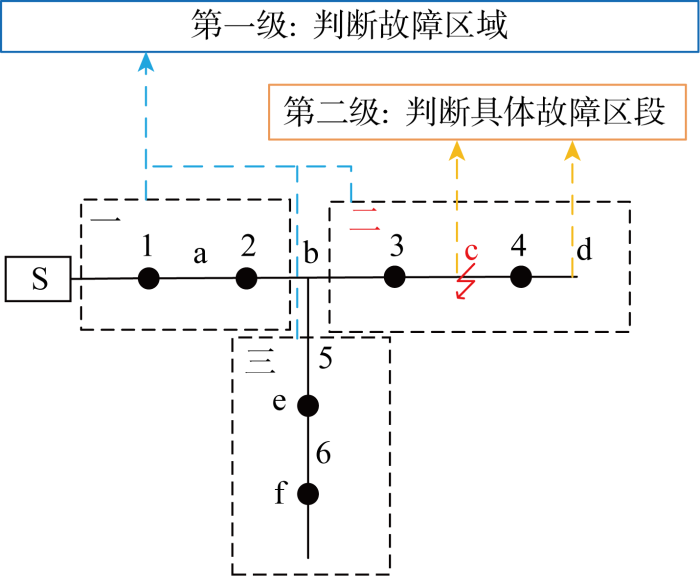
图2 分级定位模型下的简单配电网

Fig.2 Simple distribution network in a hierarchical positioning model

如图2所示,配电网中区段c发生故障.第一级启动区域定位,算法根据各区域状态I_q=[1 1 0],得到定位结果为区域二发生故障;第二级启动具体区段定位,根据区域二中c、d区段状态I_j=[1 0]判断故障区段,最终算法定位区段c发生故障.

在单级定位模型中算法定位维度为6,等于配电网节点数,在分级定位模型中算法定位维度即区域个数与故障区域包含的区段数之和为5.在单极定位模型下有2⁶=64个可能解,而在分级定位模型下有2³+2²=12个可能解.对于节点数目越多的配电网,该模型降低定位维度方面的优势越明显,因此该模型通过对配电网分层减少定位维度,缩短算法定位时间.

2 QACA及其应用

2.1 QACA基本原理

QACA是量子计算与蚁群算法相结合的一种新型优化算法,最早由Narayanan和Moore定义^[21].其算法核心是将量子计算中的态矢量和量子旋转门引入蚁群算法中,利用量子比特编码得到量子信息素,其信息素的更新通过量子旋转门实现.

(1) 量子比特编码. 与经典比特仅能表示2种状态不同,量子比特中一个量子位可以处于|0>、|1> 之间的任一中间态,一个量子位的状态可以表示为如下叠加态:

(8)|ψ>=|α>+|β>

式中:|α>、|β>分别为状态α和β的概率幅,且满足 |α|²+|β|²=1^[22].

于是,包含t个量子位的第r个个体的概率幅可表示为

(9)q_r=

[\begin{array}{l} α_{1} & α_{2} & \dots & α_{t} \\ β_{1} & β_{2} & \dots & β_{t} \end{array}]

设蚁群种群数目为a,其量子信息素编码可表示为

(10)Q=(q₁, q₂, …, q_a)

式中:q_a为个体a的概率幅,表达式如式(9)所示.

(2) 量子旋转门. 与蚁群算法使用公式更新信息素的方式不同,在QACA中量子信息素更新通过量子旋转门来实现,其操作如下式所示:

(11)

[\begin{array}{l} α'_{x} \\ β'_{x} \end{array}]

[\begin{array}{l} c o s θ_{x} & - s i n θ_{x} \\ s i n θ_{x} & c o s θ_{x} \end{array}] [\begin{array}{l} α_{x} \\ β_{x} \end{array}]

(12)θ_x=s(α_x, β_x)Δθ_x

式中:α_x、β_x为量子旋转门更新前的概率幅;α'_x、β'_x为更新后的概率幅;θ_x为旋转角;Δθ_x、s(α_x, β_x)分别为旋转角的大小和旋转方向.旋转角的大小和方向可以根据旋转角选择策略表表1查询得到.表中:x_x、c_x分别为当前解和当代最优解的第x位的比特位;F(x)、F(c)分别为解x和c对应的目标函数值.s(α_x, β_x)=-1表示顺时针方向旋转,s(α_x, β_x)=1表示逆时针方向旋转.

表1 QACA旋转角调整策略

Tab.1 Rotation angle selection strategy of QACA

x_x	c_x	F(x)> F(c)	Δθ_x	s(α_x, β_x)
x_x	c_x	F(x)> F(c)	Δθ_x	α_xβ_x>0	α_xβ_x<0	α_x=0	β_x=0
0	0	否	0	-1	+1	±1	±1
0	0	是	0	-1	+1	±1	±1
0	1	否	0.06π	-1	+1	±1	±1
0	1	是	0.06π	+1	-1	±1	±1
1	0	否	0.06π	+1	-1	±1	±1
1	0	是	0.06π	-1	+1	±1	±1
1	1	否	0	+1	-1	±1	±1
1	1	是	0	+1	-1	±1	±1

新窗口打开| 下载CSV

旋转角大小和方向的选择由当前解和当代最优解决定,当代最优解对本次迭代得到的其他解起到引导作用,引导蚁群向当代最优解得到的路径散发信息素,体现QACA的正反馈性;且信息素使用量子比特编码体现了量子计算的并行性.因此,理论层面上QACA比蚁群算法具有更好的寻优能力.

2.2 QACA的改进技术研究

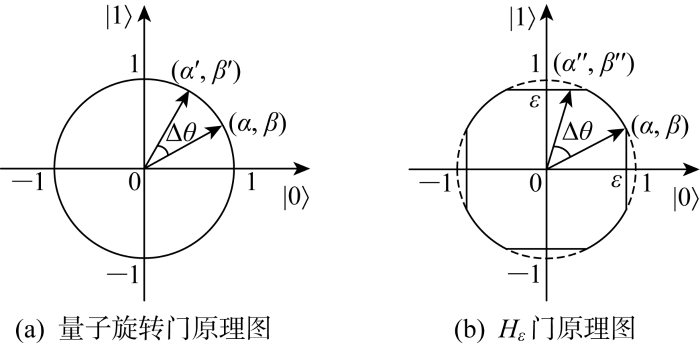
为了扩大种群多样性,加快算法收敛速度,提高解的质量,参考文献[23-24]的改进思想,将以下3点改进技术应用到基于QACA的配电网故障定位问题中.

(1) 使用H_ε门替换技术.传统量子旋转门操作的概率幅更趋近于0或1,算法易陷入局部最优.使用H_ε门替换量子旋转门,改变概率幅的趋近值,避免算法陷入局部最优.

具体更新规则为

(13)

[\begin{array}{l} α ″_{x} \\ β ″_{x} \end{array}]

=H_ε(α_x, β _x, Δθ _x)

若 ${|α'_{x}|}^{2}$ ≤ε且 ${|β'_{x}|}^{2}$ ≥1-ε,其中ε为H_ε门中的参数,则

(14)

[\begin{array}{l} α ″_{x} \\ β ″_{x} \end{array}]

[\begin{array}{l} \sqrt{ε} \\ \sqrt{1 - ε} \end{array}]

若 ${|α'_{x}|}^{2}$ ≥1-ε且 ${|β'_{x}|}^{2}$ ≤ε,则

(15)

[\begin{array}{l} α ″_{x} \\ β ″_{x} \end{array}]

[\begin{array}{l} \sqrt{1 - ε} \\ \sqrt{ε} \end{array}]

其他:

(16)

[\begin{array}{l} α ″_{x} \\ β ″_{x} \end{array}]

[\begin{array}{l} α'_{x} \\ β'_{x} \end{array}]

式中: ${[\begin{array}{l} α'_{x} & β'_{x} \end{array}]}^{T}$ 为利用H_ε门更新之前的概率幅; ${[\begin{array}{l} α ″_{x} & β ″_{x} \end{array}]}^{T}$ 为利用H_ε门更新后的概率幅.可以用单位圆来表示量子位的位置,量子旋转门及H_ε门原理图如图3所示.由图可见,传统量子旋转门在迭代后期概率幅会收敛于0或1,限制算法的搜索空间;H_ε门使概率幅收敛到0、1之外的其他值:ε与1-ε(0<ε<1)有效地避免早熟收敛,有利于算法的全局搜索^[25].

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 量子旋转门与H_ε门原理图

Fig.3 Schematic diagram of quantum rotation gate and H_ε gate

(2) 旋转角自适应动态调整技术.旋转角的大小决定算法收敛速度,过大可能会使算法陷入局部最优解,过小会影响算法收敛速度^[26].QACA采用查表法使用固定数值的旋转角限制种群多样性,综合考虑算法的寻优能力和优化效率,根据函数控制的方式将旋转角大小表示为当前迭代次数和最大迭代次数有关的函数,其表达式为

(17)Δθ=0.06π-

\frac{0.015 π g}{G}

式中:g为当前迭代次数;G为最大迭代次数.迭代初期大的旋转角可以加速算法收敛速度;随着迭代次数上升,可以减小旋转角大小,提高算法的寻优能力.

(3) 精英蚂蚁策略融入技术.在蚁群算法中一次循环的最优解被称为当代最优解,找到最优解的蚂蚁被称为精英蚂蚁^[27].为了加快算法的收敛速度,将精英策略融入QACA中,一次循环后给予精英蚂蚁走过的路径以额外的信息素奖励,即给予额外的旋转角增量,使最优解路径在下一次循环中对蚂蚁更有吸引力,从而加快算法寻优速度.

2.3 配电网故障定位问题转换

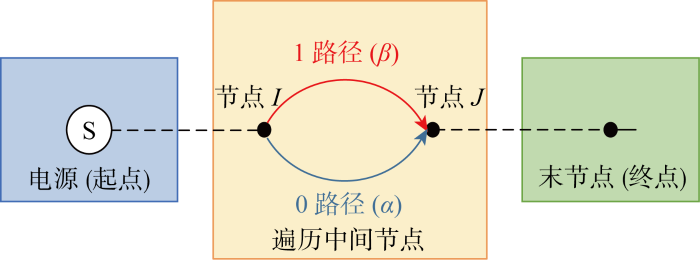
配电网故障定位问题是一个典型的0-1组合优化问题,可以将配电网故障定位问题转化成旅行商问题(Traveling Salesman Problem,TSP),以实现 QACA 的应用.

QACA故障定位模型如图4所示,电源相当于起点,配电网的末节点处为终点.每一个配电网节点相当于TSP问题中的不同城市,相邻节点间包含两条虚拟路径,分别为1路径和0路径,1路径代表区段故障,0路径代表区段非故障.图中的α、β分别与0号路径、1号路径对应,分别代表0号路径的概率幅和1号路径的概率幅.问题的二进制解可根据轮盘赌的方式由信息素概率幅决定,设计一个随机数b(b∈[0,1]),如果式(9)中的 ${|α_{t}|}^{2}$ >b,则个体r的第t个量子位的解状态为0,反之为1.因此a只蚂蚁会根据0、1路径上的不同信息素浓度大小选择相应的路径,当最后一只蚂蚁遍历完所有节点后,就能获得本次迭代得到的a个二进制解.经过多次迭代后,会得到使目标函数值的最小0、1集合,集合中取1的区段就是算法定位的故障区段.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 QACA故障定位模型

Fig.4 Fault location model of QACA

2.4 算法求解流程

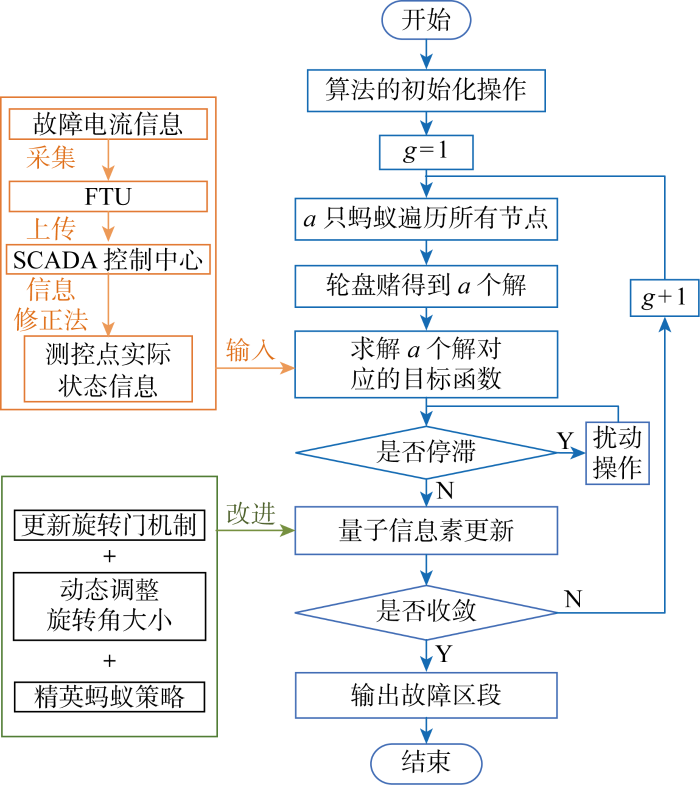
当配电网发生故障后FTU收集故障电流信息,经配电系统网络上传到SCADA控制中心并转换为节点状态信息,量子蚁群根据上传信息以及配电网拓扑进行故障区段定位^[28].QACA具体步骤如下:

步骤1 初始化量子蚁群.蚂蚁个数a、量子位数t;初始化参数:最大迭代次数G,初始信息素浓度设置借鉴文献[29]中的思想,满足α²+β²=1并且β/(α+β)=3/t.

步骤2a只蚂蚁开始遍历.

步骤3 轮盘赌法确定可行解.每只蚂蚁根据概率幅大小独立的构造一组二进制解,由此可以计算出蚂蚁r的目标函数值F(r).

步骤4 判断是否所有蚂蚁都走完所有节点,若是则转到步骤5,若不是则转到步骤2.

步骤5 统计每只蚂蚁生成解的目标函数值F,记录当代产生的最优解,记录最优解对应的蚂蚁个体和目标值,作为下一代信息素更新的依据.

步骤6 引入扰动规则.若算法的解连续三代稳定在一个值时,则在最优路径上选为故障线路的区段中随机选择一个区段,用0来取代该区段的状态,随机选择其他非故障区段,用1来取代该区段的状态以产生新路径.若该新路径比原最优路径的目标函数值更小,则将其更新为最优路径.引入扰动规则可减少信息素引导的盲目性,使算法更易跳出局部最优解.

步骤7 全局信息素浓度更新.根据历史全局最优解和当代最优解查表确定旋转角,用量子旋转门更新每个蚂蚁个体的信息素浓度.

步骤8 判断是否达到收敛要求,若是输出最优解,若不是则转入步骤2.

QACA进行配电网故障区段定位流程图如图5所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 QACA故障区段定位流程图

Fig.5 Flow chart of fault section location using QACA

3 仿真验证

仿真验证实验以平均迭代次数、准确率、容错率作为指标,在单极定位模型下将各算例运行50次取平均值作为实验结果.算法参数设置如下:蚂蚁个数40,最大迭代次数100,权重系数w=0.5.算法性能对比实验使用基本蚁群算法(Ant Colony Algorithm,ACA)、文献[29]的改进蚁群算法(Improved Ant Colony Algorithm,IACA)、文献[30]的免疫二进制粒子群优化算法(Immune Binary Particle Swarm Algorithm,IBPSO)、二进制粒子群优化算法(Binary Particle Swarm Algorithm,BPSO)、文献[31]的遗传算法(Genetic Algorithm,GA)、改进的遗传算法(Improved Genetic Algorithm,IGA)、天牛须搜索与改进遗传算法结合的算法(Beetle Antennae Search-Improved Genetic Algorithm,BAS-IGA)进行对比,从而验证所提算法的有效性、收敛性、准确性与容错性.

3.1 IEEE33节点配电网测试实验

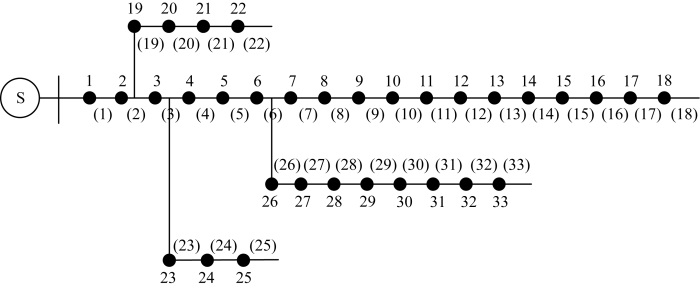
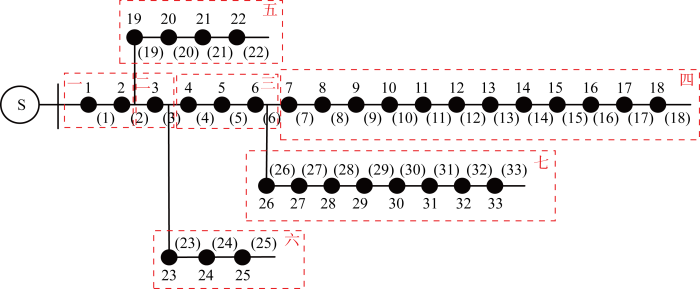
IEEE33节点配电网拓扑图如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 IEEE33节点配电网

Fig.6 IEEE 33-node distribution network

图6中:黑色圆点表示分段开关,编号1~33;圆点之间的线段表示馈线区段,编号(1)~(33).

3.1.1 算法参数选取与改进验证实验

使用H_ε门更新量子信息素使概率幅趋近于 $\sqrt{1 - ε}$ 与 $\sqrt{ε}$ 有效避免了算法陷入局部最优解,关键参数ε的大小直接影响算法的寻优能力与收敛性能.利用IEEE33节点配电网的单点故障、两点故障、三点故障算例验证关键参数 ε对算法的性能影响.6种不同ε值下实验结果如表2所示,其中加粗字体为最佳结果.

表2 参数ε对IQACA性能影响

Tab.2 Effect of parameter ε on IQACA performance

ε	单点故障		两点故障		三点故障
ε	平均迭代次数	准确率/%	平均迭代次数	准确率/%	平均迭代次数	准确率/%
0	8.67	98	23.68	96	35.57	80
0.01	4.64	100	14.41	92	18.55	94
0.02	3.20	100	8.20	100	13.24	100
0.04	3.46	100	8.84	100	13.28	100
0.08	5.80	100	16.32	100	17.86	100
0.12	14.60	96	26.48	98	37.93	98

新窗口打开| 下载CSV

表2中ε=0代表量子H_ε门不起作用,仍通过传统量子旋转门操作信息素更新.由表2可见:除ε=0.12外其余取值下平均迭代次数取值均小于ε=0,证明合适的ε取值可以加快算法收敛速度提高准确率;但是由量子H_ε门原理可知,ε取值过大会导致QACA的正反馈性下降,不利于算法尽快收敛.ε=0.02平均迭代次数最少,准确率保持在100%,因此选取ε=0.02,提高算法寻优能力.

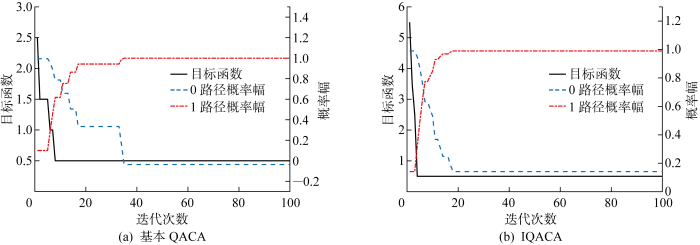
上文针对QACA进行了三方面的改进,并通过实验调参使IQACA性能达到最优状态.为了对比改进前后的算法性能,本文以IEEE33节点配电网22区段发生单点故障为例进行验证.图7为基本 QACA 与 IQACA 在同一故障情形下的算法收敛图以及某一蚂蚁在故障区段路径上的概率幅变化曲线.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 改进前后算法性能对比

Fig.7 Comparison of algorithm performance before and after improvement

最大迭代次数设置为100,基本QACA在第8代达到目标函数最小值,而IQACA仅用4代就达到收敛条件,且IQACA的概率幅值提前趋于稳定,说明IQACA不易陷入局部最优,收敛速度有所提升.在设置初始信息素浓度时0路径的信息素浓度大于1路径的信息素浓度,在算法正反馈性的作用下,0路径与1路径上的信息素浓度开始改变.由图7可以看出收敛结束后各路径的概率幅分布,使用传统量子旋转门的基本QACA最终的1路径与0路径上的概率幅分别为0.099与-0.037,使用量子H_ε门的IQACA最终的1路径与0路径上的概率幅分别为0.989与0.141,在迭代后期蚂蚁会更大概率选择走0路径,更利于算法跳出局部最优解,保证算法的全局寻优.

3.1.2 单点与多点故障

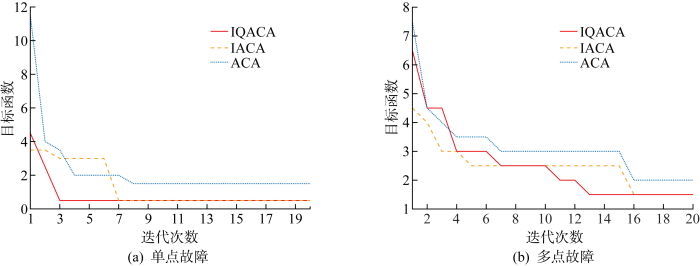
假设馈线区段发生无信息畸变情况下的单点故障及多点故障,算法迭代结束后将输出对故障区段的判定情况,并给出相应的最优适应度值,单点与多点故障定位的测试结果如表3所示.由表可见,无论是单点故障还是多点故障,IQACA对故障区段的判断结果均正确,验证了算法解决配电网故障定位问题的有效性;由平均迭代次数和准确率可以看出,IQACA准确率高,可快速收敛.

表3 基于IQACA的单点故障与多点故障测试结果

Tab.3 Test results of single-point fault and multi-point fault based on IQACA

故障类型	FTU上传的节点信息	目标函数	程序输出故障区段	平均迭代次数	准确率/%
单点故障	[111111100000000000 0000000000000000]	F=0.5	x7	2.72	100
两点故障	[111111111000000000 0000000111100000]	F=1	x9、x29	8.2	100
三点故障	[11111110000000000 0000011011000000]	F=1.5	x7、x24、x27	13.32	100

新窗口打开| 下载CSV

图8(a)和图8(b)分别为IQACA、IACA、ACA这3种算法定位单点故障、多点故障的收敛曲线.可以看出在20代以内,IQACA、IACA的收敛曲线均可达到最小目标函数值,ACA无法在20代以内得出正确的故障区段,且对比其他两种蚁群算法,IQACA可以更快找到最优解,不易陷入局部解.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 单点故障与多点故障下算法迭代曲线

Fig.8 Curves of algorithm iteration in single-point and multi-point faults

3.1.3 信息缺失与畸变

为了还原真实配电网故障电流信息,2.3节提出信息缺失自修正法,表4例证了信息缺失自修正法在单点故障、多点故障、含信息畸变情况中的可行性.由表可见,在不发生信息畸变情况下,故障信息自修正法可以成功补全信息.在发生信息畸变时会出现不成功的情况,如表4中红色字体所示,但是在真实情况下既发生信息畸变又发生信息缺失的情况很少,因此绝大部分缺失信息可以通过信息缺失自修正法得到正确修正;若没有成功修正可归类为故障信息畸变情况,利用算法本身良好的容错性,也可得到正确的故障区段.

表4 信息缺失自修正法验证

Tab.4 Validation of self-correction method for missing information

故障区段	信息缺失点	信息畸变点	补全前节点信息	补全后节点信息	是否成功
x6	k7	无	[111111x00000000000000000000000000]	[111111100000000000000000000000000]	是
x15、x30	k2	无	[1x111111111111100 00000000011111000]	[11111111111111100 00000000011111000]	是
x23、x4、x20	k3	无	[11x1000000000000 00110010000000000]	[1111000000000000 00110010000000000]	是
x20	k5	k7	[1100x01000000000 00110000000000000]	[1100101000000000 00110000000000000]	否
x12、x30	k11	k18	[1111111111x100000 1000000011111000]	[11111111111100000 1000000011111000]	是
x22、x5、x24	k9	k14	[11111000x00001000 0111111000000000]	[11111000100001000 0111111000000000]	否

新窗口打开| 下载CSV

为了验证IQACA的容错性,按表5列出的6种不同故障畸变算例进行实验验证,IQACA定位结果如图9所示.

表5 信息畸变实验算例

Tab.5 Case of information distortion experiment

故障序列	故障类型	FTU上传的节点信息	目标函数	程序输出结果
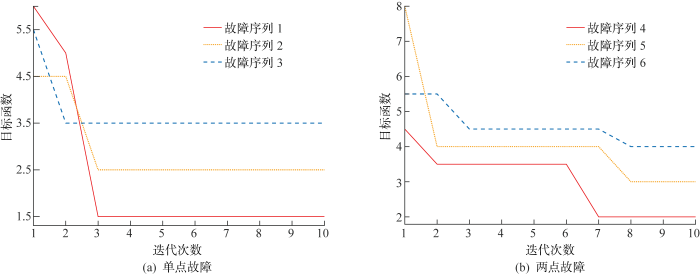
1	单点故障,一点畸变(k11)	[11000000001000000011100000000000]	F=1.5	x21
2	单点故障,两点畸变(k3、k30)	[11011111111111100000000000000100]	F=2.5	x15
3	单点故障,三点畸变(k8、k24、k5)	[11110111000000000000000101110000]	F=4.5	x28
4	两点故障,一点畸变(k8)	[11110001000000000011000000000000]	F=2	x4、x20
5	两点故障,两点畸变(k4、k11)	[11101111110111111100000001111100]	F=3	x18、x30
6	两点故障,三点畸变(k5、k12、k25)	[11110100000100000010000011100000]	F=4	x27、x19

新窗口打开| 下载CSV

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同缺失算例下的IQACA迭代图

Fig.9 Convergence diagram of IQACA in different distortion cases

图9(a)为单点故障情况下故障序列1、故障序列2、故障序列3的IQACA收敛图,图8(b)为两点故障情况下故障序列4、故障序列5、故障序列6的IQACA收敛图.由图9可以看出,IQACA可以在3代内定位含信息畸变的单点故障,可以在8代以内定位含信息畸变的两点故障,体现出IQACA具有快速收敛、容错性好的优点.

与IACA和ACA实验对比结果如表6所示.由表可见,IQACA收敛速度快、容错率高,准确率均达到100%,相较于ACA,IQACA在求解效率和容错率上都有显著优势.IQACA在平均迭代次数上优于IACA,可以快速准确地鉴别畸变信息得到故障区段.

表6 信息畸变实验各算法性能对比

Tab.6 Performance comparison of algorithms in information distortion experiment

故障序列	IQACA		IACA		ACA
故障序列	平均迭代次数	准确率/%	平均迭代次数	准确率/%	平均迭代次数	准确率/%
1	3.58	100	5.35	98	20.38	58
2	3.44	100	4.74	100	18.3	78
3	2.92	100	5.34	100	17.16	50
4	8.16	100	13.38	100	19.38	72
5	8.84	100	10.18	98	17.21	56
6	8.24	100	10.28	100	22.05	36

新窗口打开| 下载CSV

3.2 环网开环运行配电网测试实验

对于环网开环运行的配电网故障定位,可将配电网中联络开关作为分界线,基于区域划分思想,以断路器到联络开关为一组独立区域,将配电网划分为多个单电源辐射状配电网,根据单电源故障定位模型分别对各配电区域进行故障定位.图10所示为含3个电源(S1、S9、S14)的环网开环运行配电网,在该配电网上测试IQACA算法的有效性,实验算例及算法运行结果如表7所示.由表可见,在不同算例下,IQACA算法均能准确定位到故障区段所在位置,且不受信息缺失与畸变的影响,证明 IQACA 算法在环网开环运行配电网的定位有效性.

图10

新窗口打开| 下载原图ZIP| 生成PPT

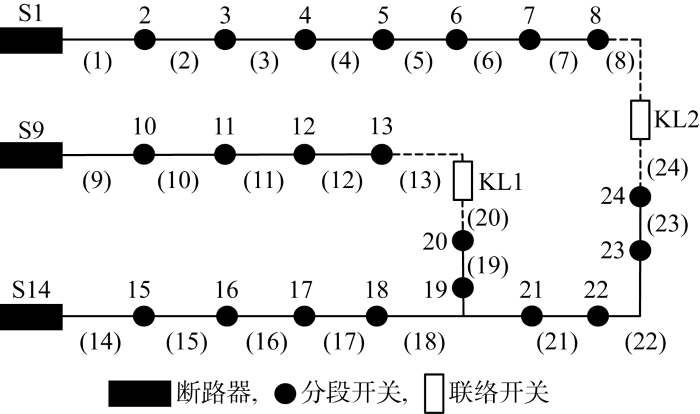
图10 3电源环网开环运行配电网

Fig.10 Open-loop operating distribution network with three power sources

表7 环网开环运行配电网算例下算法输出结果

Tab.7 Output results of the algorithm in open-loop operating distribution network

FTU上传的节点信息	缺失位置	畸变位置	程序输出故障区段	是否定位正确
[111110000000000000000000]	无	无	x5	是
[000000001111011100000000]	无	无	x12、x16	是
[0x0000000001011111001111]	k2	k12	x24	是
[000100001110011x11110000]	k16	k4	x20、x11	是

新窗口打开| 下载CSV

3.3 含分布式电源的69节点配电网测试实验

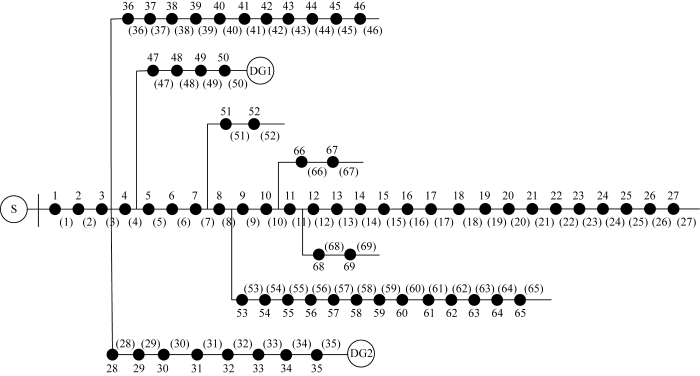
为了进一步证明算法的有效性和可扩展性,采用更大规模且含分布式电源的配电网进行算法有效性验证实验,配电网拓扑图如图11所示.该配电网包含69个节点、2个分布式电源(DG1~2),分布式电源状态为1代表接入,为0代表不接入.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 69节点含分布式电源的配电网

Fig.11 69-bus distribution network with distributed generation

如表8所示,考虑分布式电源投切、单点与多点故障以及信息缺失与畸变情况,在不同算例下统计IQACA算法运行结果.列举的6个算例中,算例1~3为不含信息缺失与畸变的单点故障与多点故障情况,算例4~6为含信息缺失与畸变的情况,缺失信息的节点采用信息缺失自修正法均成功修正.由表可得,故障区段位置与程序输出的故障区段均保持一致,体现出IQACA算法在含分布式电源的大规模配电网上定位的有效性.各算例下程序分别运行50次统计算法的正确次数,除算例3的正确次数为47次外,其余算例的正确次数均达50次,表明算法在分布式电源随意投切的大规模配电网上仍具备高准确率与容错率的定位能力.

表8 不同算例下算法输出结果

Tab.8 Algorithm output results of different cases

算例	故障区段	分布式电源投切情况	缺失位置	畸变位置	目标函数	程序输出故障区段
1	x7	[1, 0]	无	无	F=0.5	x7
2	x4、x31	[0, 1]	无	无	F=1	x4、x31
3	x11、x49、x56	[1, 1]	无	无	F=1.5	x11、x49、x56
4	x55	[1, 0]	k41	k22	F=1.5	x55
5	x29	[0, 1]	k14	k47	F=1.5	x29
6	x4	[1, 1]	k2	k49	F=2.5	x4

新窗口打开| 下载CSV

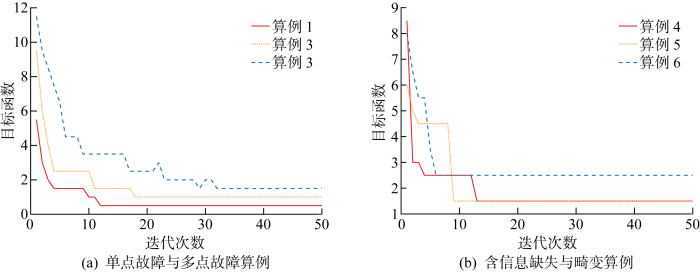
绘制IQACA算法在各算例的迭代曲线如图12所示.由图可见,在迭代后期IQACA算法均能收敛到各算例的最小目标函数位置,具备较快较稳定的收敛特性.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 不同算例下IQACA算法迭代曲线

Fig.12 Curve of IQACA algorithm iteration in different cases

3.4 与其他算法对比实验

为了更充分地证明QACA算法以及改进后的IQACA算法的优势所在,引用文献[30-31]中的数据,使用相同收敛判据及算例对QACA算法及IQACA算法进行实验测试.

文献[30]中在IEEE33节点配电网上进行仿真,在相同故障情形下仿真运行50次,统计算法QACA、IQACA的正确定位次数与平均迭代次数,实验结果如表9所示,各算例下各指标最优的数据加粗显示.

表9 与文献[30]中的算法比较结果

Tab.9 Comparison with the algorithm in Ref.[30]

故障区段	畸变点	平均迭代次数				正确次数
故障区段	畸变点	BPSO^[30]	IBPSO^[30]	QACA	IQACA	BPSO^[30]	IBPSO^[30]	QACA	IQACA
x22	无	13.1	7.6	4.16	3.44	31	44	50	50
x19、x33	无	13.44	7.94	10.74	8.40	24	39	50	50
x16	k29	12.38	7.82	3.69	3.00	32	43	48	50
x28	k4、k14、k25	13.28	7.56	5.98	3.20	29	37	49	50
x18、x32	k21、k29	13.28	8.5	11.93	8.46	25	41	45	50

新窗口打开| 下载CSV

BPSO算法与QACA算法实验数据对比可得,在相同算例下QACA算法收敛更快,能以更少的迭代次数得到目标解,且正确次数明显多于BPSO算法.IBPSO算法与IQACA算法实验数据对比可得,在单点故障情况下,IQACA使用的迭代次数更少,正确次数多于IBPSO算法,跳出局部最优解上的性能要优于IBPSO算法;两点故障情况下,虽然平均迭代次数与IBPSO算法不相上下,但是IQACA的准确率达到100%,明显高于IBPSO算法,体现出IQACA准确率高、容错率好的优势.

文献[31]中在含分布式电源IEEE33节点配电网上仿真测试.以区段5故障为例,在无信息畸变情况下,分布式电源投切情况为[1,0,0],将QACA算法和IQACA算法运行30次,数据如表10所示,各算例下各指标最优的数据加粗显示.

表10 与文献[31]中的算法比较结果

Tab.10 Comparison with the algorithm in Ref.[31]

算法	准确率/%	最小迭代次数	最大迭代次数	平均迭代次数
GA^[31]	95	27	59	34.00
IGA^[31]	100	13	18	14.40
BAS-IGA^[31]	100	9	12	10.85
QACA	100	1	21	4.97
IQACA	100	1	10	3.23

新窗口打开| 下载CSV

QACA算法的准确率达到100%,且平均4.97代得到最优解,相较于文献[30]中其他算法,QACA 算法的寻优效率更高.IQACA算法的各项指标相较于QACA算法有进一步突破,最少迭代次数仅为1代,最大迭代次数仅为10代,且使用的平均迭代次数最少,收敛性最优,可见IQACA算法在含分布式电源的配电网定位中拥有不俗的寻优性能.

3.5 分级定位模型有效性证明

根据对外等效原理,图6的配电网被划分为7个独立区域,如图13所示.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 IEEE33配电网分区后拓扑图

Fig.13 Topology of IEEE 33 distribution network after partitioning

在9个不同算例下对原模型即单级定位模型以及分级定位模型进行对比,使用定位时间、定位维度两个指标验证,实验结果如表11所示.

表11 分级定位模型有效性验证结果

Tab.11 Validation results of hierarchical positioning model

故障区段	畸变位置	分级定位模型定位维度	分级定位模型			原模型
故障区段	畸变位置	分级定位模型定位维度	第一级定位使用时间/ms	第二级定位使用时间/ms	总定位时间/ms	总定位时间/ms
x7	无	19	19.5	58.9	78.4	114.3
x9、x29	无	27	21.4	85.2	106.6	131.4
x7、x24、x27	无	30	19.7	101.7	121.4	176.6
x21	k11	11	22.3	19.5	41.8	100.0
x15	k3、k30	19	22.4	10.4	87.9	120.7
x28	k8、k24、k5	15	19.5	27.7	47.2	104.2
x20、x4	k8	14	19.7	35.2	54.9	151.5
x18、x30	k11、k4	27	21.4	89.6	111.0	138.6
x27、x19	k5、k12、k25	19	23.8	37.8	61.6	131.5

新窗口打开| 下载CSV

原模型定位维度均为33代表配电网节点数,分级定位模型的定位维度为配电网区域个数加故障区域包含的区段数,因此使用分级定位模型算法的定位维度有所减少;从算法定位时间指标分析,由于第一级为区域定位,维度固定为7,因此第一级定位时间差别不大,而第二级定位为具体区段定位,定位时间明显与区域个数和区域内包含区段数有关.在9个算例中,原模型下的算法总定位时间均多于分级定位模型,在分级定位模型下平均定位时间缩短39.15%.因此,可以证明分级定位模型降低定位维度、缩短定位时间的有效性.并且在9个算例下原模型与分级定位模型的定位准确率均为100%,说明分级定位模型不会降低算法的定位准确率.

4 结论

(1) 针对智能优化算法在解决配电网故障定位问题时会出现算法收敛速度慢、准确率不高的问题,使用QACA解决配电网故障区段定位问题,并对QACA进行针对性改进,进一步提高算法的全局寻优能力.

(2) 在原有单级定位模型的基础上,增加故障信息自修正环节,极大地避免因信息缺失产生的故障误判情况,并提出分级定位模型来减少定位维度缩短算法定位时间.

(3) 在IEEE33节点配电网、三电源环网开环运行配电网以及含分布式电源的69节点配电网上测试,验证了算法的定位有效性.IQACA无论在单点故障、多点故障、含信息畸变的情况下均具备较高的准确率与容错性,与其他算法在不同结构配电网上对比,体现了所提算法收敛速度快、寻优精度高的优势.

目前,配电网故障定位问题已有很多研究,本文提出的QACA为该领域问题提供了新思路,未来将考虑改进开关函数形式或使用合理的降维手段降低算法计算复杂度;并在建立计及节点信息缺失和畸变的非逻辑运算的配电网故障定位新模型或引入配电网其他信息进行多源故障定位等方向上进一步探索.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

谭嘉, 李知艺, 杨欢, 等.

基于分布式优化思想的配电网用电负荷多层协同预测方法

[J]. 上海交通大学学报, 2021, 55(12): 1544-1553.

DOI:10.16183/j.cnki.jsjtu.2021.296 [本文引用: 3]

当前,分布式新能源、电动汽车等新元素在配电网中涌现,改变了负荷的构成,丰富了负荷的内涵,给负荷预测带来了严峻挑战.事实上,用电负荷在配电网的多个电压层级以自下而上的方式聚合,但现有预测研究鲜少考虑此类层级化特征.为保障负荷自下而上的聚合一致性并且联合提升各层级的负荷预测性能,提出了一种基于分布式优化算法的用电负荷多层协同预测方法.首先,采用基于交替方向乘子法的分布式优化理念,构建了适配配电网层级特征、数据交互量少的多层协同预测框架.随后,提出了基于长短期记忆神经网络和联邦学习的具体预测方法,通过将底层负荷预测结果逐级聚合,能实现自下而上的配电网负荷一体化预测.算例结果表明,所提方法得到的用电负荷预测准确度高,应用前景好.

TAN

Jia

, LI

Zhiyi

, YANG

Huan

, et al.

A multi-level collaborative load forecasting method for distribution networks based on distributed optimization

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(12): 1544-1553.

[本文引用: 3]

[2]

王守相, 宋丽可, 舒欣.

分布式电源与多元负荷高渗透接入的主动配电网自适应过流保护方案

[J]. 高电压技术, 2019, 45(6): 1783-1794.