基于群体划分的冠状病毒群体免疫优化算法

doi:10.16183/j.cnki.jsjtu.2022.470

基于群体划分的冠状病毒群体免疫优化算法

李博群, 孙志锋^,

浙江大学电气工程学院,杭州 310027

A Coronavirus Herd Immunity Optimizer Based on Swarm Division

LI Boqun, SUN Zhifeng^,

College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China

通讯作者: 孙志锋,副教授;E-mail:eeszf@zju.edu.cn.

责任编辑: 王历历

收稿日期: 2022-11-25 修回日期: 2023-01-30 接受日期: 2023-03-3

基金资助:

国家自然科学基金重点项目(91647209)
浙江省自然科学基金项目(LGG18F030005)
宁波市重大专项(2022Z176)

Received: 2022-11-25 Revised: 2023-01-30 Accepted: 2023-03-3

作者简介 About authors

李博群(1997-),硕士生,从事智能控制算法研究.

摘要

针对冠状病毒群体免疫优化(CHIO)算法收敛速度慢、求解精度低的问题,提出一种基于群体划分的冠状病毒群体免疫优化(SD-CHIO)算法.基于适应度均匀原则将初始群体划分为两部分,即全局寻优个体与局部寻优个体.对于全局寻优个体,在其位置更新中加入差分变异与漫反射变异策略,分别用来增强全局寻优个体之间的交流与群体多样性,从而提高算法的全局搜索能力.对于局部寻优个体,在其位置更新中引入一种自适应快速收敛策略:基于增量法进行精英预测,并加入一种自适应收敛系数使局部寻优个体能快速收敛至精英解,以提升算法的局部搜索能力.数值实验表明:SD-CHIO能够有效提高原算法的收敛速度与精度,并表现出明显优于其他元启发式算法的全局与局部搜索能力以及一定的工程价值.

关键词： 冠状病毒群体免疫优化算法; 群体划分; 自适应快速收敛; 差分变异; 漫反射变异

Abstract

Aimed at the drawbacks of coronavirus herd immunity optimizer (CHIO), i.e., slow convergence speed and low optimization accuracy, a CHIO based on swarm division (SD-CHIO) is proposed. Based on the principle of uniform fitness, the initial swarm is divided into two parts, i.e., exploration individuals and exploitation individuals. For exploration individuals, differential mutation and diffuse reflection mutation are adopted in position update in order to enhance the communication among exploration individuals and swarm diversity respectively, so as to improve the exploration capability of the algorithm. For exploitation individuals, an adaptive fast convergence strategy is proposed in position update: elite prediction is conducted based on the incremental method, and an adaptive convergence coefficient is employed to ensure that exploitation individuals can quickly converge to the elite solution, which improves the exploitation capability of the algorithm. The numerical experiments demonstrate that SD-CHIO significantly improves the convergence speed and accuracy of the conventional algorithm, exhibiting better exploration and exploitation capabilities than other meta-heuristic algorithms do as well as certain value in engineering.

Keywords： coronavirus herd immunity optimizer (CHIO); swarm division; adaptive fast convergence; differential mutation; diffuse reflection mutation

PDF (1927KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李博群, 孙志锋. 基于群体划分的冠状病毒群体免疫优化算法[J]. 上海交通大学学报, 2024, 58(4): 555-564 doi:10.16183/j.cnki.jsjtu.2022.470

LI Boqun, SUN Zhifeng. A Coronavirus Herd Immunity Optimizer Based on Swarm Division[J]. Journal of Shanghai Jiaotong University, 2024, 58(4): 555-564 doi:10.16183/j.cnki.jsjtu.2022.470

元启发式算法(Meta-Heuristic Algorithm, MA)是一种模拟动植物群体行为或自然物理机制,通过迭代实现方案寻优的高鲁棒性智能算法,适用于多变量、非线性、多极值的复杂优化问题求解^[1-2].其中,粒子群优化^[3](Particle Swarm Optimization, PSO)算法、差分进化 (Differential Evolution, DE)算法^[4]与人工蜂群 (Artificial Bee Colony, ABC)算法^[5]为最常用的传统元启发式算法.近年来涌现出很多新型元启发式算法,如蜻蜓算法^[6]、正余弦算法^[7]、鲸鱼优化算法^[8](Whale Optimization Algorithm, WOA)、樽海鞘群算法^[9](Salp Swarm Algorithm, SSA)等.Al-Betar等^[10]受冠状病毒传播机制的启发,于2021年提出一种冠状病毒群体免疫优化 (Coronavirus Herd Immunity Optimizer, CHIO)算法.CHIO具有参数少、结构简单、易于实现等优点^[11-12],在车辆路径规划^[11]、电源配置^[13]、医学诊断^[14]、配电网重构^[15]等研究领域得到良好应用,具有重要的工程意义.但相对于很多元启发式算法,该算法的收敛速度与精度仍较低^[10].

为了提高CHIO的搜索性能,部分学者给出相应的改进方案.Dalbah等^[11]提出一种用于有能力约束车辆路径问题(Capacitated Vehicle Routing Problem, CVRP)的增强型CHIO,引入一种修复策略,即在CHIO初始化及进化过程中不断调整CVRP中的客户分布,有效维持优化过程中CVRP解的可行性;但该算法仅适用于CVRP问题,适用范围小,且在收敛速度与精度方面与很多元启发式算法相比无明显优势.Alweshah等^[14]在CHIO中引入一种贪婪交叉算子,即随机选择两个个体进行位置信息交叉变异来产生更优秀的子代,大大提高原算法的全局搜索性能;然而该算法在处理具有连续搜索空间的优化问题时,需要将待优化变量重新编码为整型数值,操作繁琐.Naderipour等^[15]提出一种改进CHIO(Improved Coronavirus Herd Immunity Optimizer, ICHIO)算法,采用一种非线性递减惯性权重调整位置更新方程,能有效提高原算法的收敛速度与求解精度.

基于上述研究,提出一种基于群体划分的CHIO(CHIO Based on Swarm Division, SD-CHIO)算法.基于适应度均匀原则,将初始群体划分为全局寻优个体与局部寻优个体.在原算法的“病毒休眠”阶段,利用全局寻优个体与局部寻优个体的作用分别提高算法的全局搜索能力与局部搜索能力.最后,基于数值实验验证了SD-CHIO的有效性.

1 冠状病毒群体免疫优化算法

医学界根据患者感染冠状病毒的时间段与症状轻重,将个体划分为3类:感染个体、易感个体与免疫个体.CHIO模仿冠状病毒在这3类个体间的传染机制,构建位置更新公式^[10]如下:

(1)

x_{i, j}^{(t + 1)} = \{\begin{array}{l} x_{i, j}^{(t)} \pm R_{D} (x_{i, j}^{(t)} - x_{S_{1} {M_{1}}, j}^{(t)}), & 0 \leq r < \frac{B_{r}}{3} \\ x_{i, j}^{(t)} \pm R_{D} (x_{i, j}^{(t)} - x_{S_{2} {M_{2}}, j}^{(t)}), & \frac{B_{r}}{3} \leq r < \frac{2 B_{r}}{3} \\ x_{i, j}^{(t)} \pm R_{D} (x_{i, j}^{(t)} - x_{S_{3} {M_{3}}, j}^{(t)}), & \frac{2 B_{r}}{3} \leq r < B_{r} \\ x_{i, j}^{(t)}, & B_{r} \leq r \leq 1 \end{array}

式中: $x_{i, j}^{(t)}$ (i=1, 2, …, N;j=1, 2, …, D;t=1, 2, …, T)为第t次迭代中,第i个个体在第j维的位置,N、D、T分别为群体规模、搜索空间维度与总迭代次数;感染个体、易感个体与免疫个体的编号分别组成集合S₁、S₂与S₃;M₁、M₂与M₃分别为随机选择的感染个体、随机选择的易感个体与最优免疫个体的编号在S₁、S₂与S₃中的序号;随机数r、R_D~U(0, 1);基本繁殖率B_r∈(0, 1).B_r为病毒传播与休眠阶段的分界线,当r<B_r时,为“病毒传播”阶段,此时病毒在感染个体、易感个体与免疫个体间扩散,个体位置会受 $x_{S_{1} {M_{1}}, j}^{(t)}$ 、 $x_{S_{2} {M_{2}}, j}^{(t)}$ 或 $x_{S_{3} {M_{3}}, j}^{(t)}$ 的扰动而发生变化;当r≥B_r时,为“病毒休眠”阶段,此时病毒停止扩散,个体位置将不受其他个体的影响而保持不变.每个个体的位置都将基于式(1)迭代T次,之后取N个个体中最优个体的位置作为优化结果.

CHIO中,3种个体可以相互转变.当易感个体的位置变差且低于平均水平时,将会转变为感染个体.同样,当感染个体的位置变好且高于平均水平时,将会转变为免疫个体.可以看出,较优个体一般都集中在易感个体与免疫个体中.

2 基于群体划分的冠状病毒群体免疫优化算法

在“病毒休眠”阶段,CHIO采用保持个体位置不变的策略.该策略在前期很难让个体跳出局部最优,后期不利于个体的局部收敛,会弱化CHIO的全局与局部搜索能力.为了克服这一缺陷,提出一种SD-CHIO算法,包含如下改进.

2.1 群体划分策略

引入群体划分策略,即将群体划分为全局寻优个体与局部寻优个体.在“病毒休眠”阶段,全局寻优个体与局部寻优个体采用不同的位置更新方式分别提高CHIO的全局与局部搜索能力.

基于适应度均匀原则进行群体划分.首先,基于初始群体的适应度对每个个体进行排序:

(2)${{O}_{0}}=\underset{i=1,2,\ldots,N}{\mathop{sort}}\,(\text{fobj}(x_{i,j}^{\left( 0 \right)}))$

式中:fobj(·)为适应度计算函数,适应度越小表示该个体的位置越优; $\underset{i = 1,2, \dots, N}{s o r t}$ (·)表示对N个个体的适应度进行升序排序,其输出O₀为排序后个体的编号集合.

然后,对全局寻优个体与局部寻优个体进行选择.定义全局寻优个体的编号集合I₁与局部寻优个体的编号集合I₂如下:

(3)${{I}_{1}}={{O}_{0}}\left\{ 2,4,6,\ldots,2N/2 \right\}$

(4)${{I}_{2}}={{O}_{0}}\left\{ 1,3,5,\ldots,2N/2-1 \right\}$

式中: $\left\lceil \bullet \right\rceil $与$\left\lfloor \bullet \right\rfloor $分别表示向上取整与向下取整.为了均衡全局与局部寻优个体的适应度,将O₀中序号为偶数与奇数的元素分别赋予I₁与I₂,以避免两种个体适应度差距较大对全局与局部搜索能力中一种能力的单方面不利影响.将最优个体编号O₀{1}赋予I₂,以降低算法在前期落入其他较差局部最优解的可能性.

2.2 全局寻优个体位置更新

为了增强个体之间的交流以提高算法的全局搜索能力,受差分进化算法的启发,引入“差分变异”策略^[4].定义全局寻优个体${{I}_{1}}\{{{i}_{G}}\}({{i}_{G}}=1,2,\ldots,\left\lfloor N/2 \right\rfloor )$的位置 $x_{I_{1} {i_{G}}, j}^{(t)}$ 对应的差分变异量为

(5)$\sigma _{{{I}_{1}}\left\{ {{i}_{G}} \right\},j}^{\left( t \right)}=x_{{{I}_{1}}\left\{ {{\zeta }_{1}} \right\},j}^{\left( t \right)}+{{R}_{D}}(x_{{{I}_{1}}\left\{ {{\zeta }_{2}} \right\},j}^{\left( t \right)}-x_{{{I}_{1}}\left\{ {{\zeta }_{3}} \right\},j}^{\left( t \right)})$

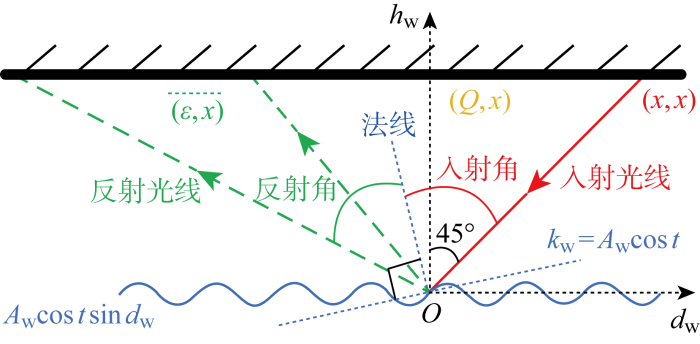
式中:ζ₁、ζ₂与ζ₃为$1\sim \left\lfloor N/2 \right\rfloor $中随机选取的3个互不相同且不为i_G的整数.将其他全局寻优个体I₁{ζ₁}的位置 $x_{I_{1} {ζ_{1}}, j}^{(t)}$ 赋值给差分变异量 $σ_{I_{1} {i_{G}}, j}^{(t)}$ ,并采用其他全局寻优个体I₁{ζ₂}与I₁{ζ₃}的位置差,即差分向量[ $x_{I_{1} {ζ_{2}}, j}^{(t)}$ - $x_{I_{1} {ζ_{3}}, j}^{(t)}$ ]对 $σ_{I_{1} {i_{G}}, j}^{(t)}$ 进行扰动,以达到增强个体之间交流的目的.

同时,当算法落入局部最优时,如果没有针对性的策略让其及时跳出局部最优,也会对算法的全局搜索能力造成负面影响.为了提高CHIO跳出局部最优的能力,模仿自然界中的漫反射现象,提出一种“漫反射变异”,其示意图如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 漫反射变异的示意图

Fig.1 Diagram of diffuse reflection mutation

图1中,为了便于分析,建立平面直角坐标系d_wOh_w.图中:ε、x、Q均为省略上、下标的简写.从点( $x_{I_{1} {i_{G}}, j}^{(t)}$ , $x_{I_{1} {i_{G}}, j}^{(t)}$ )向水面上的O点,即入射点( $Q_{j}^{(t)}$ , 0)射入光线,入射光线与h_w轴呈45°.水面波动会出现漫反射现象,即反射光线也存在波动,因此反射光线最终射向点( $ε_{I_{1} {i_{G}}, j}^{(t)}$ , $x_{I_{1} {i_{G}}, j}^{(t)}$ ), $ε_{I_{1} {i_{G}}}^{(t)}$ 即 $x_{I_{1} {i_{G}}}^{(t)}$ 对应的漫反射变异量.构造函数A_wcos tsin d_w来描述水面的形状,其中A_w为水面波动的最大幅值.由此可得O点处水面的斜率为

${{k}_{w}}=\frac{\text{d}{{A}_{w}}\text{cos }t\text{sin }{{d}_{w}}}{\text{d}{{d}_{w}}}\left| _{{{d}_{w}}=0} \right.={{A}_{w}}\cos t$

t为迭代次数.根据入射角等于反射角等几何关系可进一步得到:

(6)

\frac{- \frac{1}{k_{w}} - \frac{Q_{j}^{(t)} - x_{I_{1} {i_{G}}, j}^{(t)}}{Q_{j}^{(t)} - ε_{I_{1} {i_{G}}, j}^{(t)}}}{1 - \frac{Q_{j}^{(t)} - x_{I_{1} {i_{G}}, j}^{(t)}}{k_{w} (Q_{j}^{(t)} - ε_{I_{1} {i_{G}}, j}^{(t)})}} = \frac{1 + \frac{1}{k_{w}}}{1 - \frac{1}{k_{w}}}

为了使漫反射变异不存在过大偏差,定义入射点横坐标为所有全局寻优个体位置的平均值,即

Q_{j}^{(t)} = \frac{\sum_{i_{g} = 1}^{N / 2} x_{I_{1} {i_{g}}, j}^{(t)}}{N / 2}

基于式(6),可求得的表达式为

(7)$\begin{matrix} & \varepsilon _{{{I}_{1}}\left\{ {{i}_{G}} \right\},j}^{\left( t \right)}=\frac{1}{N/2}\overset{N/2}{\mathop{\underset{{{i}_{g}}=1}{\mathop \sum }\,}}\,x_{{{I}_{1}}\left\{ {{i}_{g}} \right\},j}^{\left( t \right)}+ \\ & \frac{1+2{{A}_{w}}\text{cos}t-A_{w}^{2}\text{co}{{\text{s}}^{2}}t}{1-2{{A}_{w}}\text{cos}t-A_{w}^{2}\text{co}{{\text{s}}^{2}}t}\times \\ & \left( \frac{1}{N/2}\overset{N/2}{\mathop{\underset{{{i}_{g}}=1}{\mathop \sum }\,}}\,x_{{{I}_{1}}\left\{ {{i}_{g}} \right\},j}^{\left( t \right)}-x_{{{I}_{1}}\left\{ {{i}_{G}} \right\},j}^{\left( t \right)} \right) \\ \end{matrix}$

采用漫反射变异策略,个体有更多机会探索未搜索过的领域,有利于提高群体的多样性,增强算法的全局搜索能力.

基于上述两种变异策略,构造全局寻优个体的位置更新公式如下:

(8)$x_{{{I}_{1}}\left\{ {{i}_{G}} \right\},j}^{\left( t+1 \right)}\left| _{{{_{j}}_{=1,2,\ldots,D}}} \right.=\left\{ \begin{array}{*{35}{l}} x_{{{I}_{1}}\left\{ {{i}_{G}} \right\},j}^{\left( t \right)}, & 0\le {{p}_{j}}<0.5 \\ \sigma _{{{I}_{1}}\left\{ {{i}_{G}} \right\},j}^{\left( t \right)}, & 0.5\le {{p}_{j}}<0.75 \\ \varepsilon _{{{I}_{1}}\left\{ {{i}_{G}} \right\},j}^{\left( t \right)}, & 0.75\le {{p}_{j}}\le 1 \\ \end{array} \right.$

式中:随机数p_j~U(0, 1),在每个维度j都会更新一次.p_j<0.5时,保持位置不变;p_j≥0.5时,加入差分变异与漫反射变异策略来增强个体之间的交流并提高群体的多样性.

2.3 局部寻优个体位置更新

为了提高算法收敛到最优解的速度与精度以加强算法的局部搜索能力,引入一种“自适应快速收敛”策略.基于该策略,构造局部寻优个体I₂{i_L}的位置更新公式如下:

(9)$x_{{{I}_{2}}\left\{ {{i}_{L}} \right\},j}^{\left( t+1 \right)}=(1\pm {{R}_{D}}\psi _{L}^{\left( t \right)})x_{{{I}_{2}}\left\{ {{i}_{L}} \right\},j}^{\left( t \right)}+\left[ 1\pm \left( {{R}_{D}}\pm {{B}_{s}} \right)\psi _{L}^{\left( t \right)} \right]~(\eta _{j}^{\left( t \right)}-x_{{{I}_{2}}\left\{ {{i}_{L}} \right\},j}^{\left( t \right)})$

式中:随机数B_s~U(0, 1); $ψ_{L}^{(t)}$ 为自适应收敛系数;个体的位置向精英解 $η_{j}^{(t)}$ 转移. $η_{j}^{(t)}$ 越优,个体就能更快收敛到较优位置,那么算法的收敛速度将会得到提升.

CHIO中,最优个体一般存在于易感个体或免疫个体中.为了保证精英解 $η_{j}^{(t)}$ 足够优秀以加快算法的收敛速度,基于易感与免疫个体中最优个体的位置 $λ_{j}^{(t)}$ 以及增量法构造精英解预测公式,即 $η_{j}^{(t)}$ 的表达式为

(10)$\eta _{j}^{\left( t \right)}=\lambda _{j}^{\left( t \right)}+{{R}_{D}}{{\gamma }_{\Delta }}\left( 1-\frac{t}{T} \right)(\lambda _{j}^{\left( t \right)}-\lambda _{j}^{\left( t-1 \right)})$

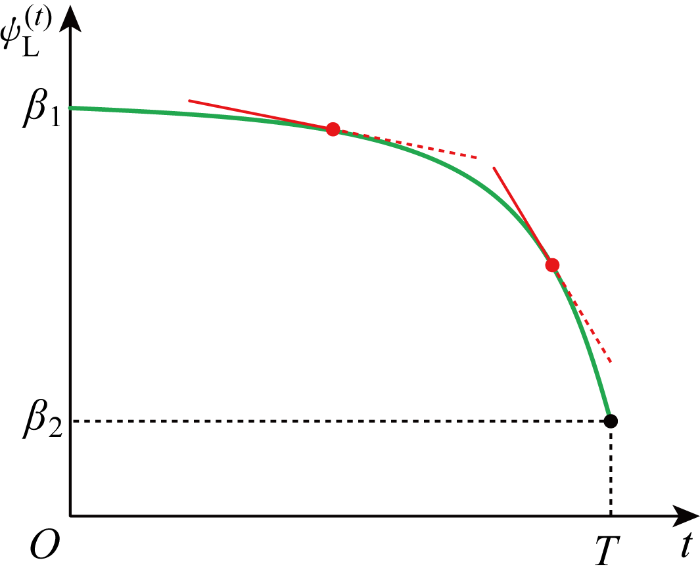
式中:引入易感与免疫个体中最优个体的位置增量 $(λ_{j}^{(t)} - λ_{j}^{(t - 1)})$ 对 $λ_{j}^{(t)}$ 进行补偿,来提前预测潜在最优解,即精英解 $η_{j}^{(t)}$ ;γ_Δ为预测步长,用来对位置增量的幅度进行调整.系数 $(1 - \frac{t}{T})$ 用来逐渐压缩位置增量的幅度,避免在后期产生过大预测误差从而对收敛精度产生不利影响.

为了提高算法的收敛精度,定义式(9)中的自适应收敛系数 $ψ_{L}^{(t)}$ 为一种单调递减的凸函数.基于反余切函数构造 $ψ_{L}^{(t)}$ 的表达式如下:

(11)$\psi _{L}^{\left( t \right)}=({{\beta }_{1}}-{{\beta }_{2}})\sqrt{\frac{4}{\pi }\text{arccot}\frac{t}{T}-1}+{{\beta }_{2}}~$

式中:β₁、β₂分别为 $ψ_{L}^{(t)}$ 的初值与终值.为了验证 $ψ_{L}^{(t)}$ 的凹凸性,求其二阶导数

(12)$\begin{matrix} & \frac{{{\text{d}}^{2}}\psi _{L}^{\left( t \right)}}{\text{d}{{t}^{2}}}=-\frac{4\left( {{\beta }_{1}}-{{\beta }_{2}} \right)}{{{\pi }^{2}}{{T}^{2}}}\frac{1+\frac{\pi t}{T}-\frac{4t}{T}\text{arccot}\frac{t}{T}}{{{\left[ 1+{{\left( \frac{t}{T} \right)}^{2}} \right]}^{2}}{{\left( \frac{4}{\pi }\text{arccot}\frac{t}{T}-1 \right)}^{\frac{3}{2}}}}\le \\ & -\frac{4\left( {{\beta }_{1}}-{{\beta }_{2}} \right)}{{{\pi }^{2}}{{T}^{2}}}\frac{1+\frac{\pi t}{T}-\frac{4t}{T}\frac{\pi }{2}\left( 1-\frac{t}{2T} \right)}{{{\left[ 1+{{\left( \frac{t}{T} \right)}^{2}} \right]}^{2}}{{\left( \frac{4}{\pi }\text{arccot}\frac{t}{T}-1 \right)}^{\frac{3}{2}}}}= \\ & -\frac{4\left( {{\beta }_{1}}-{{\beta }_{2}} \right)}{{{\pi }^{2}}{{T}^{2}}}\times \frac{\pi{{\left( \frac{t}{T}-\frac{1}{2} \right)}^{2}}+1-\frac{\pi }{4}}{{{\left[ 1+{{\left( \frac{t}{T} \right)}^{2}} \right]}^{2}}{{\left( \frac{4}{\pi }\text{arccot}\frac{t}{T}-1 \right)}^{\frac{3}{2}}}}<0 \\ \end{matrix}$

式中: $ψ_{L}^{(t)}$ 的二阶导数小于0,因此 $ψ_{L}^{(t)}$ 为凸函数.

根据式(11)可画出 $ψ_{L}^{(t)}$ 的图像,如图2所示.可以看出,随着迭代次数t的增加, $ψ_{L}^{(t)}$ 斜率的绝对值越来越大,表明 $ψ_{L}^{(t)}$ 在加速减小,有助于快速缩小局部寻优个体在 $η_{j}^{(t)}$ 周围的搜索区域,从而有效提高收敛精度,增强算法的局部搜索能力.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 自适应收敛系数 $ψ_{L}^{(t)}$ 的图像

Fig.2 Graph of adaptive convergence coefficient $ψ_{L}^{(t)}$

2.4 SD-CHIO的实现

对标准CHIO进行上述改进后,给出SD-CHIO的伪代码,其中行序号粗体的伪代码为改进步骤,具体如下.

SD-CHIO的复杂度主要由群体初始化、位置更新与适应度计算3个过程决定.其中,群体初始化的复杂度为O(N),位置更新的复杂度为O(DNT),适应度计算的复杂度为O(NT),因此SD-CHIO的总复杂度为O(N(1+DT+T)).因为SD-CHIO中的改进部分并不增加原算法CHIO的适应度计算次数,所以其复杂度与CHIO以及PSO、差分进化、WOA、SSA、ICHIO算法基本持平,且低于ABC算法.

3 数值实验及分析

为了验证SD-CHIO的有效性,采用基准测试函数以及工程问题对其进行性能测试.数值实验在AMD Ryzen 5 3500U with Radeon Vega Mobile Gfx 2.10 GHz 8 GB内存MATLAB2018b条件下实现.在SD-CHIO中,设定B_r=0.01,因为该情况下原算法CHIO的综合寻优性能最佳^[10];其他参数设置为A_w=0.1,γ_Δ=0.2,β₁=2,β₂=0.01.

3.1 函数测试

选取12个典型测试函数,如表1所示.其中F₁~F₄为单峰函数^[8,10],可用来检验算法的局部搜索能力;F₅~F₈为多峰函数^[10,16],可用来测试算法的全局搜索能力.F₉~F₁₂选自CEC’2008^[17]与CEC’2022^[18]函数优化竞赛,为带偏移量o与旋转量M的复杂函数,可测试算法在复杂优化问题中的性能.表中:random[0,1)表示[0,1)的随机数.

表1 基准测试函数

Tab.1 Function of benchmark test

函数名称	函数表达式	搜索范围
Sphere	F₁(x)= $\overset{D}{\sum_{j = 1}} x_{j}^{2}$	[-100, 100]
Schwefel P2.21	F₂(x)= $\underset{j = 1,2, \dots, D}{m a x} \|x_{j}\|$	[-100, 100]
Schwefel P2.22	F₃(x)= $\overset{D}{\sum_{j = 1}} \|x_{j}\|$ + $\overset{D}{\prod_{j = 1}} \|x_{j}\|$	[-10, 10]
Noise	F₄(x)= $\overset{D}{\sum_{j = 1}}$ j $x_{j}^{4}$ +random[0, 1)	[-100, 100]
Rastrigin	F₅(x)= $\overset{D}{\sum_{j = 1}} [x_{j}^{2} - 10 c o s (2 π x_{j}) + 10]$	[-5.12, 5.12]
Griewank	F₆(x)= $\frac{1}{4000} \overset{D}{\sum_{j = 1}} x_{j}^{2}$ - $\overset{D}{\prod_{j = 1}}$ cos $\frac{x_{j}}{\sqrt{j}}$ +1	[-600, 600]
Salomon	F₇(x)=-cos(2π $\sqrt{\overset{D}{\sum_{j = 1}} x_{j}^{2}}$ )+0.1 $\sqrt{\overset{D}{\sum_{j = 1}} x_{j}^{2}}$ +1	[-100, 100]
Ackley	F₈(x)=-20exp(-0.2 $\sqrt{\frac{1}{D} \overset{D}{\sum_{j = 1}} x_{j}^{2}}$ )-exp[ $\frac{1}{D} \overset{D}{\sum_{j = 1}}$ cos(2πx_j)]+20+e	[-32, 32]
Shifted Griewank	F₉(x)= $\frac{1}{4000} \overset{D}{\sum_{j = 1}}$ (x_j-o_j)²- $\overset{D}{\prod_{j = 1}}$ cos $\frac{x_{j} - o_{j}}{\sqrt{j}}$ +1	[-600, 600]
Shifted Ackley	F₁₀(x)=-20exp(-0.2 $\sqrt{\frac{1}{D} \overset{D}{\sum_{j = 1}} (x_{j} - o_{j})^{2}}$ )-exp[ $\frac{1}{D} \overset{D}{\sum_{j = 1}}$ cos 2π(x_j-o_j)]+20+e	[-32, 32]
Shifted+Rotated Rastrigin	F₁₁(x)= $\overset{D}{\sum_{j = 1}} [z_{j}^{2} - 10 c o s (2 π z_{j}) + 10]$ , z=M[0.051 2(x-o)]	[-100, 100]
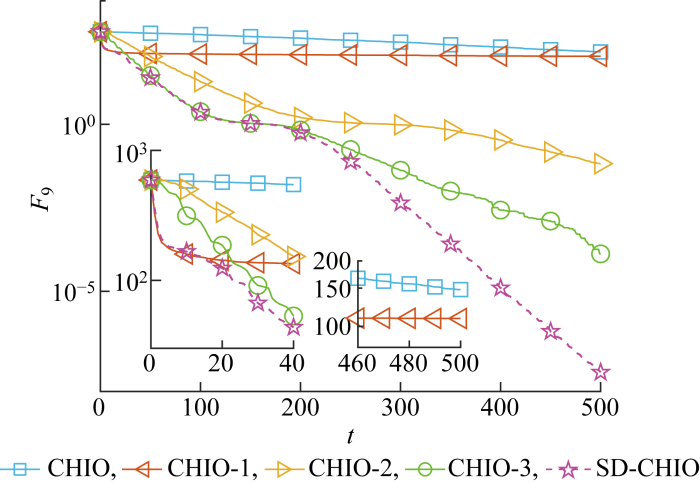
Shifted+Rotated Levy	F₁₂(x)=sin²(πw₁)+ $\overset{D - 1}{\sum_{j = 1}}$ (w_j-1)² $[1 + 10 s i n^{2} (π w_{j} - 1)]$ +(w_D-1)² $[1 + s i n^{2} (2 π w_{D})]$ , w_j=1+ $\frac{z_{j} - 1}{4}$ , z=M[0.051 2(x-o)]	[-100, 100]

新窗口打开| 下载CSV

为分别测试SD-CHIO中各改进策略的性能,基于各改进策略创建3种算法:CHIO-1、CHIO-2与CHIO-3.CHIO-1中只有局部寻优个体作用;CHIO-2中只有全局寻优个体作用且不采用漫反射变异,即在式(8)中0.75≤p_j≤1的位置更新部分也采用差分变异;CHIO-3中只有全局寻优个体作用,且差分变异与漫反射变异均被采用.基于函数F₉对CHIO、CHIO-1、CHIO-2、CHIO-3与SD-CHIO进行测试.为了公平对比,设置每种算法的初始解相同,且将每种算法的迭代参数均设为D=30,N=30,T=500.为了降低实验的偶然性,令每种算法独立运行30次,之后得出5种算法的平均收敛曲线,如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 基于不同改进策略的CHIO的平均收敛曲线

Fig.3 Average convergence curves of CHIOs based on different strategies for improvement

由图3可知,当只有局部寻优个体作用时,CHIO-1收敛曲线在前期(t=1~40)的下降速率远大于CHIO,因此CHIO-1的收敛速度在前期较CHIO有极大提升;但在后期(t=460~500),由于没有全局寻优个体作用,算法极易落入局部最优,所以CHIO-1的收敛精度较CHIO只有很小的提高.当只有全局寻优个体作用且只采用差分变异策略时,由于差分变异策略可以加强算法中个体之间的交流,从而提高算法的全局搜索能力,所以CHIO-2后期收敛精度较CHIO与CHIO-1有极大提升.当只有全局寻优个体作用且差分变异与漫反射变异策略均被采用时,由于漫反射变异策略可以提高算法跳出局部最优的能力,所以CHIO-3后期收敛精度较CHIO-2进一步提升.当全局寻优个体与局部寻优个体均作用时,相当于在CHIO-3跳出局部最优后加入局部寻优个体进行局部优化,使SD-CHIO的收敛速度与收敛精度较CHIO-3得到进一步提高,局部搜索能力增强.经验证,上述改进策略可以大大增强原算法的全局与局部搜索能力.

为了比较SD-CHIO与其他元启发式算法的搜索性能,基于F₁~F₁₂对SD-CHIO以及传统元启发式算法(DE、PSO、ABC)、新型元启发式算法(WOA、SSA)、CHIO及其改进算法ICHIO进行函数测试对比实验.实验中,以综合性能最优为导向设置每种元启发式算法的非共有参数.为了保证公平性,对于同一函数,设置每种元启发式算法的初始解相同,且将每个元启发式算法的迭代参数均设置为N=30;T=500;D=30(F₁~F₁₀),10(F₁₁~F₁₂).为了降低偶然性,对于同一函数,让每种元启发式算法独立运行30次,并记录最终求得的最优值的平均值(μ)与标准差(s)作为算法的评估指标,如表2所示.其中,最优数据加粗显示.

表2 不同元启发式算法的函数测试结果

Tab.2 Function test results of different MAs

函数	算法	μ/A	s/A	函数	算法	μ/A	s/A	函数	算法	μ/A	s/A
F₁	PSO	7.90×10^-3	1.15×10^-2	F₅	PSO	5.93×10¹	1.73×10¹	F₉	PSO	2.84×10^-2	2.04×10^-2
	DE	5.93×10^-4	3.42×10^-4		DE	1.54×10²	9.87×10⁰		DE	3.37×10^-2	6.18×10^-2
	ABC	2.43×10¹	1.52×10¹		ABC	2.38×10²	1.25×10¹		ABC	1.20×10⁰	9.48×10^-2
	WOA	1.48×10^-74	6.76×10^-74		WOA	3.79×10^-15	2.08×10^-14		WOA	1.12×10¹	3.58×10⁰
	SSA	2.45×10^-7	7.25×10^-7		SSA	5.16×10¹	1.68×10¹		SSA	1.71×10^-2	1.49×10^-2
	CHIO	1.21×10⁴	3.08×10³		CHIO	1.71×10²	1.75×10¹		CHIO	1.48×10²	3.48×10¹
	ICHIO	5.69×10^-43	1.62×10^-43		ICHIO	2.07×10²	7.68×10¹		ICHIO	1.28×10²	2.35×10¹
	SD-CHIO	0	0		SD-CHIO	0	0		SD-CHIO	3.76×10^-8	2.53×10^-8
F₂	PSO	7.58×10⁰	1.79×10⁰	F₆	PSO	2.49×10^-2	1.78×10^-2	F₁₀	PSO	2.19×10⁰	3.63×10⁰
	DE	9.34×10⁰	1.81×10⁰		DE	3.44×10^-2	6.30×10^-2		DE	5.98×10^-3	1.46×10^-3
	ABC	6.48×10¹	4.07×10⁰		ABC	1.22×10⁰	9.54×10^-2		ABC	4.15×10⁰	3.25×10^-1
	WOA	4.97×10¹	2.52×10¹		WOA	8.37×10^-3	4.59×10^-2		WOA	1.56×10¹	1.27×10⁰
	SSA	1.25×10¹	3.51×10⁰		SSA	1.64×10^-2	1.12×10^-2		SSA	2.71×10⁰	8.22×10^-1
	CHIO	7.37×10¹	3.41×10⁰		CHIO	1.13×10²	3.12×10¹		CHIO	1.73×10¹	7.18×10^-1
	ICHIO	4.25×10^-22	9.60×10^-23		ICHIO	0	0		ICHIO	1.63×10¹	3.05×10^-1
	SD-CHIO	9.51×10^-163	0		SD-CHIO	0	0		SD-CHIO	1.88×10^-5	5.49×10^-6
F₃	PSO	1.39×10⁰	3.45×10⁰	F₇	PSO	9.68×10^-1	1.99×10^-1	F₁₁	PSO	1.62×10¹	2.78×10⁰
	DE	4.89×10^-3	1.53×10^-3		DE	8.74×10^-1	1.03×10^-1		DE	3.72×10¹	2.25×10⁰
	ABC	2.96×10^-1	7.37×10^-2		ABC	3.17×10⁰	4.13×10^-1		ABC	3.66×10¹	5.15×10⁰
	WOA	3.84×10^-51	1.51×10^-50		WOA	1.43×10^-1	6.26×10^-2		WOA	3.14×10¹	2.17×10¹
	SSA	2.08×10⁰	1.49×10⁰		SSA	1.90×10⁰	4.60×10^-1		SSA	1.62×10¹	7.29×10⁰
	CHIO	8.19×10⁴	4.46×10⁵		CHIO	1.84×10¹	1.30×10⁰		CHIO	7.26×10¹	9.96×10⁰
	ICHIO	2.87×10^-22	4.10×10^-23		ICHIO	4.46×10^-1	5.71×10^-2		ICHIO	4.93×10¹	8.15×10⁰
	SD-CHIO	4.26×10^-164	0		SD-CHIO	0	0		SD-CHIO	1.02×10¹	2.81×10⁰
F₄	PSO	4.73×10^-2	1.34×10^-2	F₈	PSO	5.26×10^-1	7.42×10^-1	F₁₂	PSO	2.99×10^-3	1.63×10^-2
	DE	1.60×10^-1	3.11×10^-2		DE	7.47×10^-3	2.10×10^-3		DE	1.39×10^-12	7.12×10^-12
	ABC	3.09×10^-1	8.71×10^-2		ABC	4.17×10⁰	3.96×10^-1		ABC	3.07×10^-5	5.28×10^-5
	WOA	3.14×10^-3	2.68×10^-3		WOA	4.09×10^-15	3.00×10^-15		WOA	1.81×10⁰	1.60×10⁰
	SSA	2.38×10^-1	9.11×10^-2		SSA	2.53×10⁰	8.36×10^-1		SSA	3.77×10^-1	4.89×10^-1
	CHIO	1.36×10²	1.33×10²		CHIO	1.67×10¹	8.05×10^-1		CHIO	2.77×10⁰	6.26×10^-1
	ICHIO	1.65×10^-3	6.31×10^-4		ICHIO	1.13×10^-14	2.94×10^-15		ICHIO	1.36×10⁰	3.81×10^-1
	SD-CHIO	1.51×10^-4	8.50×10^-5		SD-CHIO	8.88×10^-16	0		SD-CHIO	4.90×10^-13	7.87×10^-13

新窗口打开| 下载CSV

由表2可见,在单峰函数F₁~F₄的测试中,SD-CHIO 不仅在F₁中收敛到μ的理论最优值0,而且在F₂~F₄中的收敛精度也优于其他元启发式算法,说明SD-CHIO大大提高了原算法CHIO的局部搜索能力,且其局部搜索能力优于改进算法ICHIO与其他元启发式算法.在多峰函数F₅~F₈的测试中, SD-CHIO在F₅~F₇中均取得μ的理论最优值0,且在F₈中的收敛精度也优于其他元启发式算法,表明SD-CHIO的全局搜索能力较原算法CHIO同样得到很大提升,且其全局搜索能力同样优于改进算法ICHIO与其他元启发式算法.在复杂函数F₉~F₁₂的测试中,SD-CHIO的收敛精度均优于其他元启发式算法,表明其在求解复杂优化问题时,相对于其他元启发式算法具有一定优势.除F₁₁外,SD-CHIO在所有函数测试中均能取得最小s值,且7次取得理论最优值0,说明SD-CHIO相比于其他元启发式算法具有较强鲁棒性.

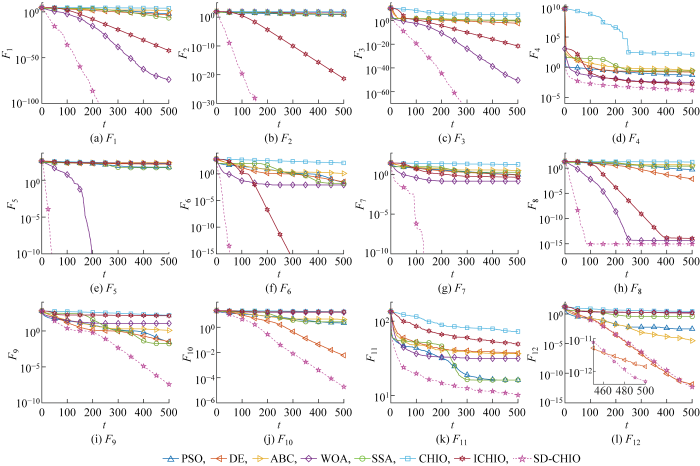
为了更加直观地比较各元启发式算法的收敛性能,给出8种元启发式算法的平均收敛曲线,如图4所示.由图4(a)~4(d)可知,对于单峰函数F₁~F₄,自适应快速收敛策略大大提高了原算法前期收敛速度与后期收敛精度,同时也让SD-CHIO拥有8类元启发式算法中最高的收敛速度与精度.由图4(e)~4(h)可知,对于多峰函数F₅~F₈,CHIO明显陷入局部最优,导致后期收敛精度很低;而差分变异与漫反射变异策略让SD-CHIO更容易跳出局部最优,有效提升原算法后期的收敛精度,同时也让SD-CHIO获得8类元启发式算法中最优的全局搜索能力.图4(i)~4(l)中,对于复杂函数F₉~F₁₂,SD-CHIO与原算法以及其他元启发式算法相比更易跳出局部最优,因此其后期收敛精度最高.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 函数测试中不同元启发式算法的平均收敛曲线

Fig.4 Average convergence curves of different MAs in function test

3.2 工程应用

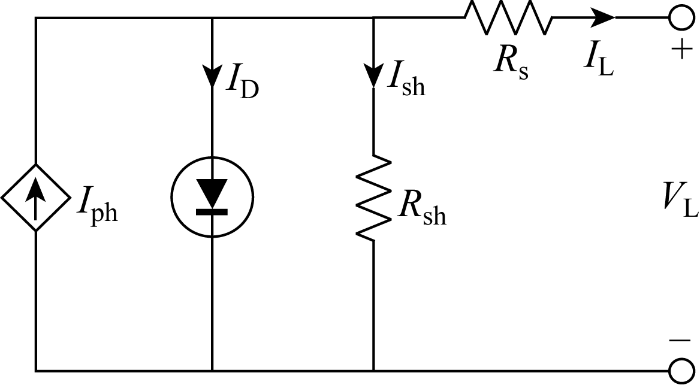
采用光伏电池参数辨识这一工程问题来测试SD-CHIO的实用性能.光伏电池的等效电路如图5所示^[19].图中:I_ph、I_D、I_sh分别为光生电流、二极管正向电流与二极管泄露电流;R_sh、R_s分别为并联电阻和串联电阻;V_L与I_L分别为光伏电池的输出电压与输出电流.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 光伏电池等效电路

Fig.5 Equivalent circuit of photovoltaic cell

根据图5可以推导出I_L的数学表达式为

(13)${{I}_{L}}={{I}_{ph}}-{{I}_{D}}-{{I}_{sh}}={{I}_{ph}}-{{I}_{sd}}\left\{ \text{exp}\left[ \frac{{{q}_{c}}\left( {{V}_{L}}+{{I}_{L}}{{R}_{s}} \right)}{{{A}_{c}}{{k}_{c}}{{T}_{c}}} \right]-1 \right\}-\frac{{{V}_{L}}+{{I}_{L}}{{R}_{s}}}{{{R}_{sh}}}$

式中:I_sd为二极管反向饱和电流;q_c、A_c、k_c、T_c分别为电子电荷量(1.602×10^-19 C)、二极管理想因子、玻耳兹曼常量(1.380×10^-23 J/K)与太阳电池工况下的绝对温度.

对一款直径为57 mm的商用(R.T.C France)硅太阳能电池进行参数辨识^[19].在温度为33 ℃、光强为1 000 W/m²的工况下,测得该电池的( $I_{L, n_{s}}$ , $V_{L, n_{s}}$ ) (n_s=1, 2, …, 26)数据点作为辨识数据集,对参数I_ph、I_sd、A_c、R_s、R_sh进行辨识,参数实测值为 $I_{p h}^{*}$ =0.760 8 A、 $I_{s d}^{*}$ =0.322 3 A、 $A_{c}^{*}$ =1.483 7、 $R_{s}^{*}$ =0.036 4 Ω、 $R_{s h}^{*}$ =53.763 4 Ω.为了衡量参数辨识的准确度,定义最终参数辨识值与实测值之间的差距即辨识误差如下:

(14)${{E}_{iden}}=\frac{1}{5}(\frac{\left| {{I}_{ph}}-I_{ph}^{\text{*}} \right|}{I_{ph}^{\text{*}}}+\frac{\left| {{I}_{sd}}-I_{sd}^{\text{*}} \right|}{I_{sd}^{\text{*}}}+\frac{\left| {{A}_{c}}-A_{c}^{\text{*}} \right|}{A_{c}^{\text{*}}}+\frac{\left| {{R}_{s}}-R_{s}^{\text{*}} \right|}{R_{s}^{\text{*}}}+\frac{\left| {{R}_{sh}}-R_{sh}^{\text{*}} \right|}{R_{sh}^{\text{*}}})$

在参数辨识中,基于式(13)构建模型误差F_pv,并以其作为目标函数,其表达式如下:

(15)$\left.\begin{array}{l} \min {{F}_{\text{pv}}}\text{=}\sqrt{\frac{\sum\limits_{{{n}_{s}}=1}^{26}{{{\left| {{I}_{\text{ph}}}-\frac{{{V}_{L,{{n}_{s}}}}+{{I}_{L,{{n}_{s}}}}{{R}_{s}}}{R}-{{I}_{L,{{n}_{s}}}}-{{I}_{\text{sd}}}\left\{ \exp \left[ \frac{{{q}_{c}}({{V}_{L,{{n}_{s}}}}+{{I}_{L,{{n}_{s}}}}{{R}_{s}})}{{{A}_{c}}{{k}_{c}}{{T}_{c}}} \right]-1 \right\} \right|}^{2}}}}{26}} \\ \text{s}\text{. t}\text{. }0 < {{I}_{\text{ph}}}\le \text{1 A, }0<{{I}_{\text{sd}}}\le \text{1 }\mu \text{A, }1\le {{A}_{c}}\le \text{2, }0<{{R}_{s}}\le \text{0}\text{.5 }\Omega \text{, }0<{{R}_{\text{sh}}}\le \text{100 }\Omega\end{array}\ \ \ \ \ \ \ \ \right\}$

设置SD-CHIO与其他元启发式算法的初始解相同,迭代参数为N=30、T=500,每种算法独立运行30次.图6为8种算法的平均收敛曲线,可以看出,SD-CHIO前期的收敛速度略低于DE与ABC,但明显高于CHIO与ICHIO;后期CHIO与ICHIO明显落入局部最优,而SD-CHIO成功跳出局部最优,且其求解结果在所有元启发式算法中具有最低的模型误差.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 光伏电池参数辨识中不同元启发式算法的平均收敛曲线

Fig.6 Average convergence curves of different MAs in parameter identification of photovoltaic cell

参数辨识结果如表3所示.可见,SD-CHIO得到最优μ与s值,表明其在参数辨识中较其他元启发式算法具有更强的全局与局部搜索能力以及鲁棒性.同时,还给出每种元启发式算法在30次运行中得到的最小F_pv值,即F_pv,min.SD-CHIO求得的F_pv,min值为 1.03×10^-3 A,分别降低至CHIO与ICHIO的22.25%与10.49%; 且该F_pv,min值对应的E_iden值在8种元启发式算法中最低,表明SD-CHIO辨识出的所有参数在整体上较其他元启发式算法更接近真实值.

表3 光伏电池参数辨识中不同元启发式算法的搜索结果

Tab.3 Searching results of different MAs in parameter identification of photovoltaic cell

算法	μ/A	s/A	F_{pv, min}/A	E_iden/%	I_ph/A	I_sd/μA	A_c	R_s/Ω	R_sh/Ω
PSO	4.27×10^-3	9.19×10^-3	1.55×10^-3	28.77	0.7604	0.5933	1.5455	0.0338	79.7655
DE	1.56×10^-3	1.11×10^-4	1.42×10^-3	23.33	0.7605	0.5466	1.5367	0.0341	73.7699
ABC	2.09×10^-3	2.65×10^-4	1.60×10^-3	27.32	0.7599	0.5812	1.5435	0.0337	77.7783
WOA	3.72×10^-2	2.91×10^-2	1.36×10^-3	9.10	0.7596	0.2638	1.4613	0.0373	66.2019
SSA	3.10×10^-3	3.34×10^-3	1.26×10^-3	19.23	0.7600	0.4574	1.5174	0.0351	79.7338
CHIO	6.21×10^-2	4.14×10^-2	4.63×10^-3	31.37	0.7646	0.5986	1.5466	0.0348	87.1315
ICHIO	7.42×10^-2	5.45×10^-2	9.82×10^-3	32.61	0.7574	0.0267	1.2671	0.0473	67.8832
SD-CHIO	1.27×10^-3	1.09×10^-4	1.03×10^-3	4.33	0.7607	0.3591	1.4924	0.0360	58.3065

新窗口打开| 下载CSV

4 结论

提出一种基于群体划分的冠状病毒群体免疫优化算法(SD-CHIO).将初始群体划分为全局寻优个体与局部寻优个体两部分,并通过这两部分的作用来分别提高算法的全局与局部搜索能力.通过基准函数与工程问题的测试得出如下结论:

(1) SD-CHIO在单峰函数测试中,相比于原算法以及其他元启发式算法有更高的收敛速度与精度,表明其局部搜索能力相比于原算法大大增强.

(2) SD-CHIO在多峰函数测试中,相比于原算法以及其他元启发式算法更易跳出局部最优解,在后期有更高求解精度,表明其全局搜索能力相比于原算法得到有效提高.

(3) 对于复杂函数的寻优,SD-CHIO在所有元启发式算法中有最高求解精度,表明其在求解复杂优化问题时具有一定优势.

(4) 在函数测试中,SD-CHIO求得的最优值标准差普遍小于其他元启发式算法,表明其具有较强鲁棒性.

(5) 在光伏电池参数辨识问题中,SD-CHIO能较快求得具有较高精度的电池参数,表明该算法具有一定的工程意义与实用价值.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

TAYARANI-N

M H

, YAO

, XU

H M

Meta-heuristic algorithms in car engine design: A literature survey

[J]. IEEE Transactions on Evolutionary Computation, 2015, 19(5): 609-629.

DOI:10.1109/TEVC.4235 URL [本文引用: 1]

[2]

杜晓昕, 王浩, 崔连和, 等.

基于聚类和探测精英引导的蜻蜓算法

[J]. 浙江大学学报: 工学版, 2022, 56(5): 977-986.

[本文引用: 1]

Xiaoxin

, WANG

Hao

, CUI

Lianhe

, et al.

Dragonfly algorithm based on clustering and detection elite guidance

[J]. Journal of Zhejiang University (Engineering Science), 2022, 56(5): 977-986.

[本文引用: 1]

[3]

BONYADI

M R

, MICHALEWICZ

Stability analysis of the particle swarm optimization without stagnation assumption

[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 814-819.

DOI:10.1109/TEVC.2015.2508101 URL [本文引用: 1]

[4]

HAMZA

N M

, ESSAM

D L

, SARKER

R A

Constraint consensus mutation-based differential evolution for constrained optimization

[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(3): 447-459.

DOI:10.1109/TEVC.2015.2477402 URL [本文引用: 2]

[5]

杜振鑫, 韩德志, 刘广钟, 等.

一种逐步加强开采的人工蜂群算法

[J]. 上海交通大学学报, 2018, 52(1): 96-102.

DOI:10.16183/j.cnki.jsjtu.2018.01.015 [本文引用: 1]

针对人工蜂群(ABC)算法开采能力差的问题，提出一种逐步加强开采能力的改进ABC算法.在雇佣蜂阶段，向局部最优解学习，并逐步增大局部最优解的比率；在观察蜂阶段，向局部最优解和全局最优解学习，并逐步增大全局最优解的比率，从而较好地平衡算法的勘探与开采能力.在CEC2014等36个函数上进行实验，结果表明，改进ABC算法的性能明显优于ABC-NS和CoDE等算法.

Zhenxin

, HAN

Dezhi

, LIU

Guangzhong

, et al.

Artificial bee colony algorithm with gradually enhanced exploitation

[J]. Journal of Shanghai Jiao Tong University, 2018, 52(1): 96-102.

[本文引用: 1]

[6]

MIRJALILI

Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems

[J]. Neural Computing & Applications, 2016, 27(4): 1053-1073.

[本文引用: 1]

[7]

MIRJALILI

SCA: A sine cosine algorithm for solving optimization problems

[J]. Knowledge-Based Systems, 2016, 96: 120-133.

DOI:10.1016/j.knosys.2015.12.022 URL [本文引用: 1]

[8]

MIRJALILI

, LEWIS

The whale optimization algorithm

[J]. Advances in Engineering Software, 2016, 95: 51-67.

DOI:10.1016/j.advengsoft.2016.01.008 URL [本文引用: 2]

[9]

MIRJALILI

, GANDOMI

A H

, MIRJALILI

S Z

, et al.

Salp swarm algorithm: A bio-inspired optimizer for engineering design problems

[J]. Advances in Engineering Software, 2017, 114: 163-191.

DOI:10.1016/j.advengsoft.2017.07.002 URL [本文引用: 1]

[10]

AL-BETAR

M A

, ALYASSERI

Z A A

, AWADALLAH

M A

, et al.

Coronavirus herd immunity optimizer (CHIO)

[J]. Neural Computing & Applications, 2021, 33(10): 5011-5042.

[本文引用: 6]

[11]

DALBAH

L M

, AL-BETAR

M A

, AWADALLAH

M A

, et al.

A modified coronavirus herd immunity optimizer for capacitated vehicle routing problem

[J]. Journal of King Saud University-Computer & Information Sciences, 2022, 34(8): 4782-4795.

[本文引用: 3]

[12]

DALBAH

L M

, AL-BETAR

M A

, AWADALLAH

M A

, et al.

A coronavirus herd immunity optimization (CHIO) for travelling salesman problem

[C]// International Conference on Innovative Computing & Communications. Singapore: Springer, 2022: 717-729.

[本文引用: 1]

[13]

ALQARNI

Sodium sulfur batteries allocation in high renewable penetration microgrids using coronavirus herd immunity optimization

[J]. Ain Shams Engineering Journal, 2021, 13(2): 1-14.

[本文引用: 1]

[14]

ALWESHAH

, ALKHALAILEH

, AL-BETAR

M A

, et al.

Coronavirus herd immunity optimizer with greedy crossover for feature selection in medical diagnosis

[J]. Knowledge-Based Systems, 2022, 235: 107629.

DOI:10.1016/j.knosys.2021.107629 URL [本文引用: 2]

[15]

NADERIPOUR

, ABDULLAH

, MARZBALI

M H

, et al.

An improved corona-virus herd immunity optimizer algorithm for network reconfiguration based on fuzzy multi-criteria approach

[J]. Expert Systems with Applications, 2022, 187: 115914.

DOI:10.1016/j.eswa.2021.115914 URL [本文引用: 2]

[16]

夏学文, 刘经南, 高柯夫, 等.

具备反向学习和局部学习能力的粒子群算法

[J]. 计算机学报, 2015, 38(7): 1397-1407.

[本文引用: 1]

XIA

Xuewen

, LIU

Jingnan

, GAO

Kefu

, et al.

Particle swarm optimization algorithm with reverse-learning and local-learning behavior

[J]. Chinese Journal of Computers, 2015, 38(7): 1397-1407.

[本文引用: 1]

[17]

TANG

, YAO

, SUGANTHAN

P N

, et al.

Benchmark functions for the CEC’2008 special session and competition on large scale global optimization

[R]. Taiwan: National Chiao Tung University, 2007.

[本文引用: 1]

[18]

KUMAR

, PRICE

K V

, MOHAMED

A W

, et al.

Problem definitions and evaluation criteria for the CEC 2022 special session and competition on single objective bound constrained numerical optimization

[R]. Singapore: Nanyang Technological University, 2021.

[本文引用: 1]

[19]

XIONG

G J

, ZHANG

, YUAN

X F

, et al.

Parameter extraction of solar photovoltaic models by means of a hybrid differential evolution with whale optimization algorithm

[J]. Solar Energy, 2018, 176: 742-761.

DOI:10.1016/j.solener.2018.10.050 URL [本文引用: 2]

Meta-heuristic algorithms in car engine design: A literature survey

2015

... 元启发式算法(Meta-Heuristic Algorithm, MA)是一种模拟动植物群体行为或自然物理机制,通过迭代实现方案寻优的高鲁棒性智能算法,适用于多变量、非线性、多极值的复杂优化问题求解^[1-2].其中,粒子群优化^[3](Particle Swarm Optimization, PSO)算法、差分进化 (Differential Evolution, DE)算法^[4]与人工蜂群 (Artificial Bee Colony, ABC)算法^[5]为最常用的传统元启发式算法.近年来涌现出很多新型元启发式算法,如蜻蜓算法^[6]、正余弦算法^[7]、鲸鱼优化算法^[8](Whale Optimization Algorithm, WOA)、樽海鞘群算法^[9](Salp Swarm Algorithm, SSA)等.Al-Betar等^[10]受冠状病毒传播机制的启发,于2021年提出一种冠状病毒群体免疫优化 (Coronavirus Herd Immunity Optimizer, CHIO)算法.CHIO具有参数少、结构简单、易于实现等优点^[11-12],在车辆路径规划^[11]、电源配置^[13]、医学诊断^[14]、配电网重构^[15]等研究领域得到良好应用,具有重要的工程意义.但相对于很多元启发式算法,该算法的收敛速度与精度仍较低^[10]. ...

基于聚类和探测精英引导的蜻蜓算法

2022

Dragonfly algorithm based on clustering and detection elite guidance

2022

Stability analysis of the particle swarm optimization without stagnation assumption

2016

Constraint consensus mutation-based differential evolution for constrained optimization

2016

... 为了增强个体之间的交流以提高算法的全局搜索能力,受差分进化算法的启发,引入“差分变异”策略^[4].定义全局寻优个体

${{I}_{1}}\{{{i}_{G}}\}({{i}_{G}}=1,2,\ldots,\left\lfloor N/2 \right\rfloor )$

的位置

x_{I_{1} {i_{G}}, j}^{(t)}

对应的差分变异量为 ...

一种逐步加强开采的人工蜂群算法

2018

Artificial bee colony algorithm with gradually enhanced exploitation

2018

Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems

2016

SCA: A sine cosine algorithm for solving optimization problems

2016

The whale optimization algorithm

2016

... 选取12个典型测试函数,如表1所示.其中F₁~F₄为单峰函数^[8,10],可用来检验算法的局部搜索能力;F₅~F₈为多峰函数^[10,16],可用来测试算法的全局搜索能力.F₉~F₁₂选自CEC’2008^[17]与CEC’2022^[18]函数优化竞赛,为带偏移量o与旋转量M的复杂函数,可测试算法在复杂优化问题中的性能.表中:random[0,1)表示[0,1)的随机数. ...

Salp swarm algorithm: A bio-inspired optimizer for engineering design problems

2017

Coronavirus herd immunity optimizer (CHIO)

2021

... [10]. ...

... 医学界根据患者感染冠状病毒的时间段与症状轻重,将个体划分为3类:感染个体、易感个体与免疫个体.CHIO模仿冠状病毒在这3类个体间的传染机制,构建位置更新公式^[10]如下: ...

... 为了验证SD-CHIO的有效性,采用基准测试函数以及工程问题对其进行性能测试.数值实验在AMD Ryzen 5 3500U with Radeon Vega Mobile Gfx 2.10 GHz 8 GB内存MATLAB2018b条件下实现.在SD-CHIO中,设定B_r=0.01,因为该情况下原算法CHIO的综合寻优性能最佳^[10];其他参数设置为A_w=0.1,γ_Δ=0.2,β₁=2,β₂=0.01. ...

... [10,16],可用来测试算法的全局搜索能力.F₉~F₁₂选自CEC’2008^[17]与CEC’2022^[18]函数优化竞赛,为带偏移量o与旋转量M的复杂函数,可测试算法在复杂优化问题中的性能.表中:random[0,1)表示[0,1)的随机数. ...

A modified coronavirus herd immunity optimizer for capacitated vehicle routing problem

2022

... [11]、电源配置^[13]、医学诊断^[14]、配电网重构^[15]等研究领域得到良好应用,具有重要的工程意义.但相对于很多元启发式算法,该算法的收敛速度与精度仍较低^[10]. ...

... 为了提高CHIO的搜索性能,部分学者给出相应的改进方案.Dalbah等^[11]提出一种用于有能力约束车辆路径问题(Capacitated Vehicle Routing Problem, CVRP)的增强型CHIO,引入一种修复策略,即在CHIO初始化及进化过程中不断调整CVRP中的客户分布,有效维持优化过程中CVRP解的可行性;但该算法仅适用于CVRP问题,适用范围小,且在收敛速度与精度方面与很多元启发式算法相比无明显优势.Alweshah等^[14]在CHIO中引入一种贪婪交叉算子,即随机选择两个个体进行位置信息交叉变异来产生更优秀的子代,大大提高原算法的全局搜索性能;然而该算法在处理具有连续搜索空间的优化问题时,需要将待优化变量重新编码为整型数值,操作繁琐.Naderipour等^[15]提出一种改进CHIO(Improved Coronavirus Herd Immunity Optimizer, ICHIO)算法,采用一种非线性递减惯性权重调整位置更新方程,能有效提高原算法的收敛速度与求解精度. ...

A coronavirus herd immunity optimization (CHIO) for travelling salesman problem

2022

Sodium sulfur batteries allocation in high renewable penetration microgrids using coronavirus herd immunity optimization

2021

Coronavirus herd immunity optimizer with greedy crossover for feature selection in medical diagnosis

2022

An improved corona-virus herd immunity optimizer algorithm for network reconfiguration based on fuzzy multi-criteria approach

2022

具备反向学习和局部学习能力的粒子群算法

2015

Particle swarm optimization algorithm with reverse-learning and local-learning behavior

2015

Benchmark functions for the CEC’2008 special session and competition on large scale global optimization

2007

Problem definitions and evaluation criteria for the CEC 2022 special session and competition on single objective bound constrained numerical optimization

2021

Parameter extraction of solar photovoltaic models by means of a hybrid differential evolution with whale optimization algorithm

2018

... 采用光伏电池参数辨识这一工程问题来测试SD-CHIO的实用性能.光伏电池的等效电路如图5所示^[19].图中:I_ph、I_D、I_sh分别为光生电流、二极管正向电流与二极管泄露电流;R_sh、R_s分别为并联电阻和串联电阻;V_L与I_L分别为光伏电池的输出电压与输出电流. ...

... 对一款直径为57 mm的商用(R.T.C France)硅太阳能电池进行参数辨识^[19].在温度为33 ℃、光强为1 000 W/m²的工况下,测得该电池的(

I_{L, n_{s}}

V_{L, n_{s}}

) (n_s=1, 2, …, 26)数据点作为辨识数据集,对参数I_ph、I_sd、A_c、R_s、R_sh进行辨识,参数实测值为

I_{p h}^{*}

=0.760 8 A、

I_{s d}^{*}

=0.322 3 A、

A_{c}^{*}

=1.483 7、

R_{s}^{*}

=0.036 4 Ω、

R_{s h}^{*}

=53.763 4 Ω.为了衡量参数辨识的准确度,定义最终参数辨识值与实测值之间的差距即辨识误差如下: ...

〈

〉