凝视成像模式下卫星姿态控制原理为根据卫星与地面目标的相对运动关系,通过对卫星滚动与俯仰轴姿态的实时调整,实现载荷对地面或空中动态目标的凝视观测.近年来,凝视观测技术广泛被用于对地观测卫星,观测载荷包括视频相机和面阵相机等.面阵相机不仅被广泛应用于高轨卫星领域[1 ⇓ -3 ] ,利用凝视观测技术,面阵相机同样可以被应用于低轨卫星成像和视频观测卫星领域[4 ] .
空中动态目标主要指各型飞机及其尾焰,高轨卫星在对动态目标进行跟踪时,始终让动态目标保持在卫星载荷的视场内即可.低轨卫星与空中动态目标相对运动角速度变化较快,在地面或其他卫星的引导下,可通过姿态调整,令动态目标出现在载荷视场内,在此基础上,需根据载荷处理得到的中心点像素信息[5 ] 即像面脱靶量信息,连续调整卫星姿态,始终让动态目标保持在卫星载荷的视场中心.由于探测器噪声等的影响,星载相机处理得到的目标中心点像素值存在噪声,该噪声将引起期望姿态和期望角速度噪声,进而影响卫星姿态控制稳定度,而姿态稳定度又会反过来影响面阵载荷积分成像[6 -7 ] .此外,通过连续多幅图像信息进行处理,才能获得准确的像面脱靶量信息,因此观测量存在明显延时,直接使用该信息进行控制,易引起凝视姿态振荡.如何在载荷脱靶量明显含有测量噪声和时延的情况下,实现卫星对空中动态目标高稳定度凝视姿态控制,是本文需要解决的问题.
现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] .
因此本文提出一种基于载荷脱靶量信息的卫星对空中动态目标凝视姿态规划方法,通过低轨单卫星对空中动态目标进行位置滤波估计,补偿观测延时对应的目标位置变化,规划凝视期望姿态和角速度,实现卫星对空中动态目标高稳定度凝视观测.
1 脱靶量噪声和延时对姿态稳定度的
影响 目标跟踪期间,为了保证面阵电荷耦合器件(Charge Coupled Device,CCD)高质量成像,一般应保证在曝光时间内的累积像移偏差不超过0.25~0.3像素[2 ] ,即要求:
(1) ω ≤ k Δ p τ
式中:k 为允许的像移偏差与像素之比;Δp 为像素对应的角分辨率;τ 为曝光时间.以某红外面阵相机为例,焦距0.386 m、CCD像素尺寸5.4×10-5 m,即像素角分辨率为1.4×10-4 rad,由跟踪过程稳定度引起的相机积分时间内像移分配指标为0.1个像素,相机通道最大积分时间为200 ms,则要求卫星姿态稳定度优于0.004 (°)/s (3σ ,σ 为正态分布标准差).因此,载荷相机要求对目标凝视跟踪期间,卫星姿态保持较高稳定度.
对空中动态目标凝视跟踪,常用的对目标凝视期望姿态计算方法为
(2) A r i = i x i y i z T
(3) i z = R s t i R s t i i x = A i o 0 1 0 T × R s t i A i o 0 1 0 T × R s t i i y = i z × i x
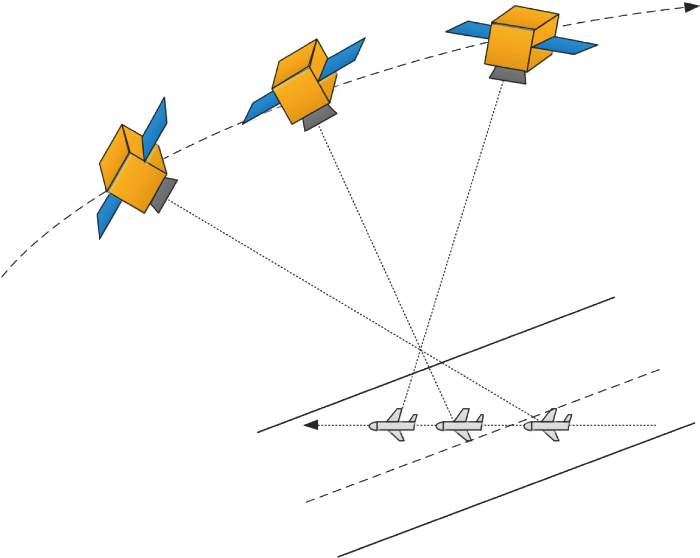
式中:R s t i A io 为卫星轨道坐标系至惯性坐标系转换矩阵;A ri 为惯性坐标系至凝视期望坐标系的转换矩阵.可以看出,卫星期望姿态的计算直接依赖目标方向信息.图1 给出了卫星凝视空中目标过程示意图,也体现了单星对目标定位观测过程.图2 给出了目标方向与像面脱靶量之间的映射关系.图中:x p 、y p 为目标中心点像素值,也即像面脱靶量;f 为相机焦距;h t 为目标与星下点方向距离.
图1
图1
卫星凝视空中动态目标示意图
Fig.1
Sketch of a satellite gazing at an aerial dynamic target
图2
图2
成像示意图
Fig.2
Diagram of imaging
以相机视轴平行卫星+z b 轴为例,目标相对卫星的方位角φ 和高低角θ 表征目标方向信息.凝视跟踪过程,目标近似位于像面中心,方位角和高低角均为小量,因此:
(4) φ = a r c t a n ( y p d / f ) ≈ y p d / f θ = a r c t a n ( x p d / f ) ≈ x p d / f
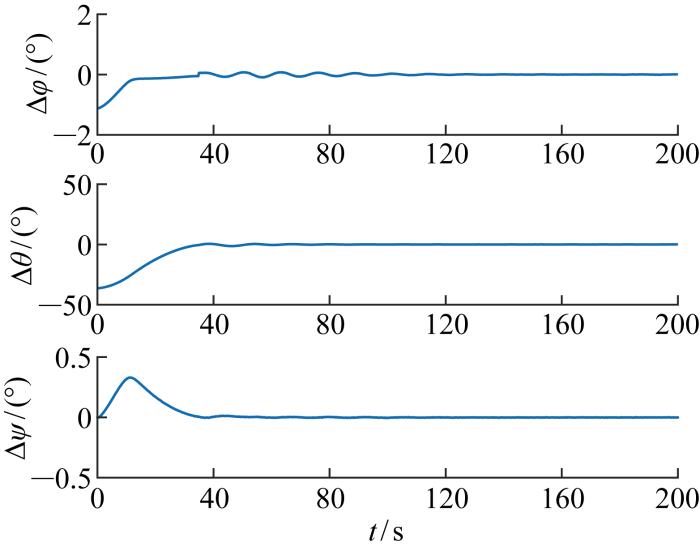
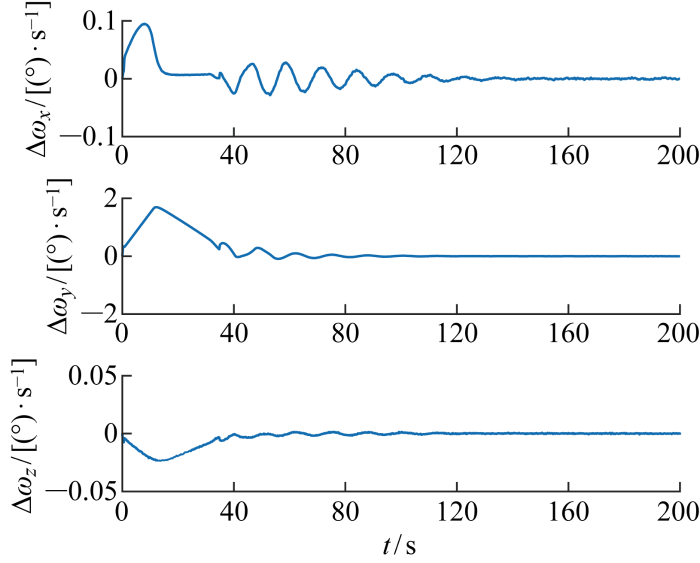
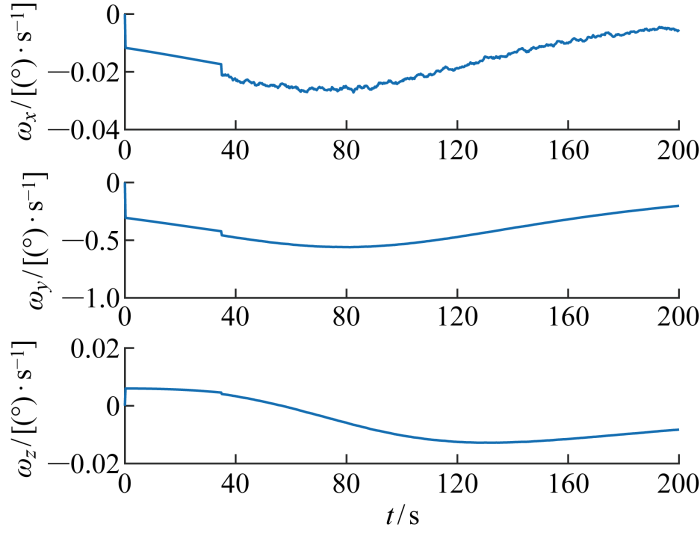
对于上述某型号红外相机参数,星上处理软件可保证脱靶量噪声0.5个像素(1σ ),根据上述公式,脱靶量噪声将引起目标方向角度噪声0.012°(3σ ),若直接采用该信息计算期望姿态和期望角速度,无法满足载荷对卫星平台的稳定度要求.对此,以脱靶量解算的方位角φ 和高低角θ 为观测量,以[φ θ φ · θ · φ ¨ θ ¨ 图3 和图4 所示.图中:t 为时间;Δφ 、Δθ 、Δψ 分别为x 轴、y 轴、z 轴姿态控制误差;Δωx 、Δωy 、Δωz 分别为x 轴、y 轴、z 轴角速度控制误差.
图3
图3
脱靶量延时和噪声引起的姿态误差
Fig.3
Attitude error caused by miss time delay and noise
图4
图4
脱靶量延时和噪声引起的角速度误差
Fig.4
Angular velocity error caused by miss time delay and noise
本文提出根据载荷观测信息对空中动态目标的位置或方向信息进行平滑估计和预报方法,在此基础上采用式(3)进行目标凝视姿态计算,以实现凝视过程卫星高稳定度姿态控制.通过对目标位置的滤波估计,避免直接使用脱靶量计算目标方向信息,可以降低脱靶量噪声对姿态稳定度的影响;通过滤波状态方程对目标位置进行预报,平稳且准确地获取当前时刻目标方向信息,可以避免脱靶量测量延时引起的姿态和角速度振荡问题.
2 基于卡尔曼滤波的目标位置估计
星载相机图像只能提供目标的方向信息,无法提供距离信息,因此单颗卫星难以获取目标的完整位置信息.对于飞机等类型的空中动态目标,巡航飞行高度范围已知,且飞行方向和飞行速度变化缓慢,因此可将目标在地球固联坐标系中的高度作为已知量,将目标所处的地理经度、地理纬度作为被估计量,则动态目标将是可观测的.
选取当前工程中常用的处理非线性问题的扩展卡尔曼滤波(EKF)[18 ] 来设计目标状态估计滤波器.以x p 、y p 为观测量,以目标在地固系经度λ t 、纬度γ t 、经度变化率λ · t γ · t
(5) X = λ t γ t λ · t γ · t
(6) Z = x p y p = K x K x y K y x K y f R s t c ( 1 ) R s t c ( 3 ) f R s t c ( 2 ) R s t c ( 3 )
式中:R s t c A cg (r t g - r s g ) ,R s t c r t g r s g A cg 为地球固联坐标系至相机坐标系转换矩阵;Kx 、Ky 、Kxy 、Kyx 为毫米到像素的转换参数.
在状态方程和观测方程基础上,需要根据状态方程求出状态转移矩阵,根据观测方程求出观测矩阵.由导航系统状态方程,可得状态转移矩阵应有如下形式:
(7) Φ = 1 0 T 0 0 1 0 T 0 0 1 0 0 0 0 1
对于观测矩阵H ,卫星速度在地球固联坐标系投影为已知量,其计算过程为
(8) H = ∂ ( x p , y p ) ∂ ( λ t , γ t , λ · t , γ · t ) = ∂ ( x p , y p ) ∂ R s t c ∂ R s t c ∂ R s t g ∂ R s t g ∂ ( λ t , γ t , λ · t , γ · t )
(9) ∂ ( x p , y p ) ∂ R s t c = f R s t c ( 3 ) K x K x y K y x K y × 1 0 - R s t c ( 1 ) R s t c ( 3 ) 0 1 - R s t c ( 2 ) R s t c ( 3 )
(10) ∂ R s t c ∂ R s t g = A c g
(11) ∂ ( R s t g ) ∂ ( λ t , γ t , λ · t , γ · t ) = 0 3 × 2 ( R e + h ) - c o s γ t s i n λ t - s i n γ t c o s λ t c o s γ t c o s λ t - s i n γ t s i n λ t 0 c o s γ t
式中:R s t g R e 为地球半径;h 为空中动态目标标称飞行高度.最终,观测矩阵为
(12) H = f R s t c ( 3 ) K x K x y K y x K y 1 0 - R s t c ( 1 ) R s t c ( 3 ) 0 1 - R s t c ( 2 ) R s t c ( 3 ) A c g × 0 3 × 2 ( R e + h ) - c o s γ t s i n λ t - s i n γ t c o s λ t c o s γ t c o s λ t - s i n γ t s i n λ t 0 c o s γ t
由于目标位置估计实时性要求高,所以采用EKF进行状态估计,其递推方程如下:
(13) X ^ k / k - 1 = Φ k / k - 1 X ^ k - 1 + B k - 1 u k - 1 P k / k - 1 = Φ k , k - 1 s P k - 1 Φ T k , k - 1 + Q k - 1 K k = P k / k - 1 H T k ( H k P k / k - 1 H T k + R k ) - 1 δ X ^ k = K k [ Z k - H k X ^ k / k - 1 ] X ^ k = X ^ k / k - 1 + δ X ^ k P k = ( I - K k H k ) P k / k - 1 ( I - K k H k ) T + K k R k K T k
式中:Bk -1 为控制输入矩阵;uk -1 为控制输入向量;Pk 为误差协方差矩阵;s 为滤波衰减因子;Kk 为滤波增益矩阵;Qk 和Rk 为系统噪声和量测噪声的协方差阵;Hk 为观测阵.
在卡尔曼滤波器开始工作前,首先要对各模型和参数初始化,例如相机的模型和参数、引导信息给出的目标经纬度初值、姿态和轨道模块给出的卫星在地球固联坐标系位置分量r s g A cg ,以及初始位置的误差协方差P 0 等.至此,以相机给出的x p 、y p 作为观测量,可通过滤波器实时计算目标经纬度信息.
需要注意的是,由于脱靶量信息存在延时,所以需记录脱靶量时间戳对应的r s g A cg 等信息,进行滤波计算.通过滤波估计的目标经度和纬度信息同样对应脱靶量处理时刻,因此需根据滤波状态递推获得当前时刻目标经度和纬度信息:
(14) λ t = λ t 0 + Δ t λ · t 0 γ t = γ t 0 + Δ t γ · t 0
式中:Δt 为脱靶量信息延时量;λt 0 、γt 0 、λ · t 0 γ · t 0
3 凝视期望姿态和期望角速度计算
通过卡尔曼滤波得到目标地理经度、地理纬度、经度变化率、纬度变化率的平滑估计值后,结合卫星轨道、相机安装矩阵等信息,可以得到卫星与目标相对矢量和矢量变化率.进而由相对位置矢量计算成像期望姿态,由相对位置矢量变化率计算成像期望角速度,以避免对角度差分放大噪声信号.
仍按式(2)方法计算凝视过程卫星本体坐标系相对惯性坐标系转换矩阵A ri ,并转化为期望姿态四元数q ir .进行期望角速度ω ir 推导:
(15) ω i r × = - A · r i A r i T
(16) i · z = ( I - ρ s t ρ s t T ) r · s t i r s t i i · x = ( I - i x i T x ) A i o 0 1 0 T × r · s t i A i o 0 1 0 T × r s t i i · y = i · z × i x + i z × i · x
式中:ρ st 为卫星至目标位置的单位矢量.卫星至目标位置矢量变化率:
(17) r · s t i = r · t i - r · s i
式中:r · s i
(18) r · t i = - ( ω i g ) i × A i g r t g + A i g r · t g
A ig 为地球固联坐标系至惯性坐标系转换矩阵,可由轨道计算模块得到.
由r t g = ( r t + h t ) c o s γ t c o s λ t ( r t + h t ) c o s γ t s i n λ t [ r t ( 1 - f e ) 2 + h t ] s i n γ t
(19) r · t g = ( r t + h t ) ( - s i n γ t c o s λ t γ · t - c o s γ t s i n λ t λ · t ) + h · t ( c o s γ t c o s λ t ) ( r t + h t ) ( - s i n γ t s i n λ t γ · t + c o s γ t c o s λ t λ · t ) + h · t ( c o s γ t s i n λ t ) [ r t ( 1 - f e ) 2 + h t ] c o s γ t γ · t + h · t s i n γ t
根据上述公式,可计算得到卫星期望角速度ω ir .至此,在期望姿态和期望角速度计算的基础上,调用基于四元数的卫星大角度任意姿态机动控制方法[19 ] ,即可实现基于图像的卫星对空中动态目标高稳定度凝视跟踪.完整的姿态规划与控制过程如图5 所示.图中:q ib 、ω ib 分别为卫星姿态四元数和角速度;T c 为姿态控制指令力矩.
图5
图5
姿态规划与控制流程
Fig.5
Attitude planning and control process
由姿态规划与控制流程可以看出,本方法相比常规目标凝视姿态控制方法,主要增加目标经纬度和经纬度变化率滤波估计模块,滤波状态量为4维,常规星敏陀螺联合滤波算法状态量一般为6维,即本方法所需增加运算量低于常规星敏陀螺滤波算法,可以由星载计算机在轨运行.
4 仿真校验
仿真参数设置如表1 所示.仿真开始时,卫星姿态处于对地定向模式,根据导引信息提供的目标初始地理经纬度,进行固定目标凝视姿态控制,在运动目标出现在相机视场内后,调用卡尔曼滤波器对目标经纬度进行实时估计,并进行动态目标跟踪凝视控制.
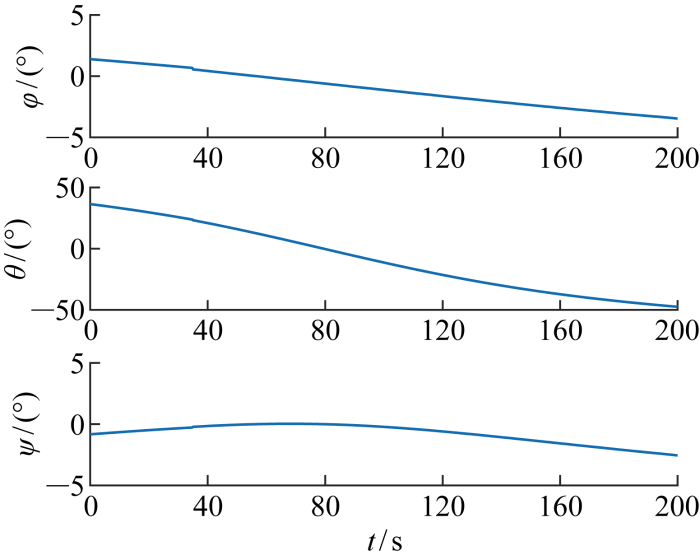
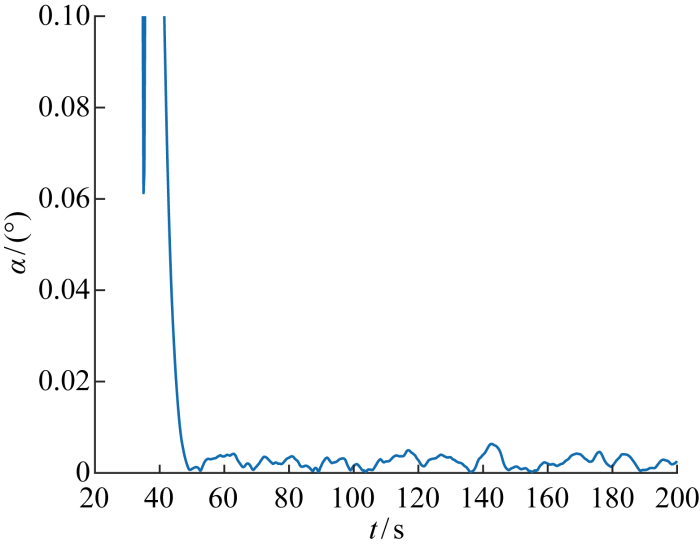
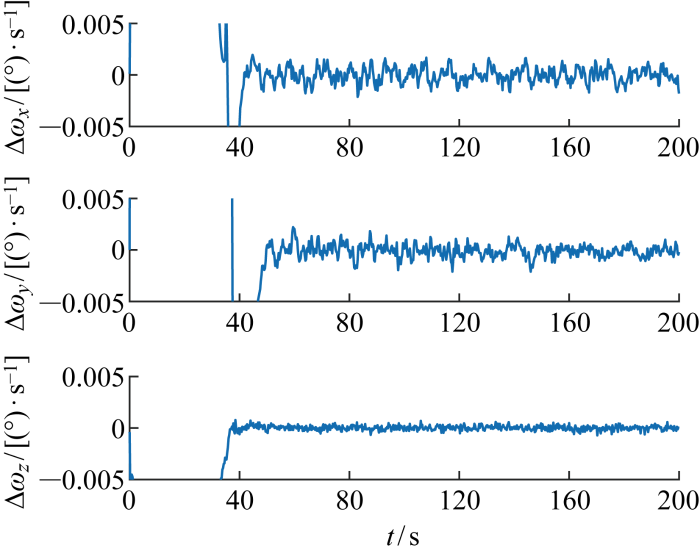
图6 和图7 分别为卫星本体坐标系相对轨道坐标系的规划姿态角和角速度曲线,体现了卫星平台对空中动态目标凝视过程期望姿态和期望角速度的变化规律.约在仿真开始33 s后,目标进入相机视场,由固定导引信息切换至像面脱靶量跟踪控制.可以看出, 在引入目标标称飞行高度误差 1 km、脱靶量噪声0.5 像素(1σ )和1 s延时、敏感器测量噪声3″(3σ )的情况下, 本文方法能够在10 s内完成基于脱靶量的目标经纬度及其变化率估计,并通过姿态凝视控制,保证目标维持在像面中心位置,如图8 所示;相机视轴与目标方向夹角α <0.01°,如图9 所示;图10 和图11 分别为目标经纬度和经纬度变化率估计误差,目标经度和纬度估计误差小于0.01° (3σ ), 经度和纬度变化率误差小于 0.000 1 (°)/s (3σ );图12 和图13 分别为凝视跟踪过程卫星姿态控制误差和角速度控制误差,姿态控制误差小于0.01°(3σ ), 姿态角速度误差小于0.003 (°)/s(3σ ),因此所提出方法相比图3 和图4 所示的常规方法具有明显优势.
图6
图6
卫星规划姿态角(本体系相对轨道系)
Fig.6
Planned attitude angle of satellite body-fixed frame relative to orbit frame
图7
图7
卫星规划角速度(本体系相对轨道系)
Fig.7
Planned angular velocity of satellite body-fixed frame relative to orbit frame
图8
图8
目标中心像素值(像面脱靶量)
Fig.8
Target center pixel value (image plane miss-distance)
图9
图9
相机视轴与目标方向夹角
Fig.9
Angle between viewing axis and target direction of camera
图10
图10
目标经度和纬度估计误差
Fig.10
Dstimation error of target latitude and longitude
图11
图11
目标经度和纬度变化率估计误差
Fig.11
Estimation error of target longitude and latitude change rate
图12
图12
三轴姿态控制误差
Fig.12
Control error of triaxial attitude
图13
图13
三轴角速度控制误差
Fig.13
Control error of triaxial angular velocity
5 结语
本文以面阵相机目标中心像素值即像面脱靶量为观测量,提出了目标地理经纬度及其变化率的精确平滑估计和预报方法.在此基础上,规划凝视期望姿态和角速度,避免了脱靶量噪声和延时对姿态稳定度的影响,并实现了单星对目标定位.数学仿真显示,所提出方法相比常规方法能够避免脱靶量延时引起的姿态振荡,目标状态估计快速收敛,凝视过程姿态稳定度满足载荷工作要求.
参考文献
View Option
[1]
XU J LIANG Y H LIU J , et al Multi-frame super-resolution of gaofen-4 remote sensing images
[J]. Sensors 2017 , 17 (2142 ): 1 -15 .
DOI:10.3390/s17010001
URL
[本文引用: 1]
[2]
刘刚 , 于淼 . 静止轨道光学成像卫星研究现状及建议
[J]. 飞控与探测 2020 , 3 (5 ): 21 -26 .
[本文引用: 2]
LIU Gang YU Miao . Status and development trends of high-resolution geostationary optical imaging satellite
[J]. Flight Control & Detection 2020 , 3 (5 ): 21 -26 .
[本文引用: 2]
[3]
黄丽霞 , 彭鑫 , 刘书豪 , 等 . 高轨光学成像卫星动目标跟踪策略设计与仿真
[J]. 航天器工程 2018 , 27 (4 ): 10 -16 .
[本文引用: 2]
HUANG Lixia PENG Xin LIU Shuhao , et al Design and simulation for moving target tracking strategy of high orbit optical imaging satellite
[J]. Spacecraft Engineering 2018 , 27 (4 ): 10 -16 .
[本文引用: 2]
[4]
ZHANG R ZHANG X Y XIAO L L , et al Recognition of aircraft activities at airports on video micro-satellites: Methodology and experimental validation
[J]. Aerospace 2022 , 9 (414 ): 1 -19 .
DOI:10.3390/aerospace9010001
URL
[本文引用: 1]
An understanding of the scalability of hybrid rocket regression models is critical for the enlargement and commercialization of small-scale engines developed within universities and similar research institutions. This paper investigates the fuel regression rates of recent 40 kN thrust-class motor experiments, which were designed based on fuel regression rate correlations of 2.5 kN thrust-class motors from previous research. The results show that fuel regression rates of the 40 kN experiments were within 26% of predictions made using correlations based on 2.5 kN experiments.
[5]
ZHANG X Y XIANG J H . Tracking imaging feedback attitude control of video satellite
[C]// 2016 Proceedings of the International Conference on Electrical Engineering and Automation Hong Kong, China : Electrical Engineering and Automation , 2017 : 729 -737 .
[本文引用: 1]
[6]
PEI W J . Staring imaging attitude tracking control laws for video satellites based on image Information by hyperbolic tangent fuzzy sliding mode control
[J]. Computational Intelligence and Neuroscience 2022 , 2022 : 8289934 -1 -13.
[本文引用: 2]
[7]
黄家明 , 陈寰 , 史庆杰 , 等 . 基于FPGA的红外目标识别神经网络加速器设计
[J]. 飞控与探测 2020 , 3 (6 ): 66 -75 .
[本文引用: 1]
HUANG Jiaming CHEN Huan SHI Qingjie , et al An infrared object detection neural network accelerator based on FPGA
[J]. Flight Control& Detection 2020 , 3 (6 ): 66 -75 .
[本文引用: 1]
[8]
JIANG L YANG X B . Study on enlarging the searching scope of staring area and tracking imaging of dynamic targets by optical satellites
[J]. IEEE Sensors Journal 2021 , 21 (4 ): 5349 -5358 .
DOI:10.1109/JSEN.7361
URL
[本文引用: 1]
[9]
YANG Y HOU Q Y ZHANG J X , et al Mission scheduling optimization of multi-optical satellites for multi-aerial targets staring surveillance
[J]. Journal of the Franklin Institute 2020 , 357 : 8657 -8677 .
DOI:10.1016/j.jfranklin.2020.06.023
URL
[本文引用: 1]
[10]
LIAN Y J GAO Y D ZENG G Q . Staring imaging attitude control of small satellites
[J]. Journal of Guidance Control and Dynamics 2017 , 40 (5 ): 1275 -1282 .
[本文引用: 1]
[11]
LI P Y DONG Y F LI H J . Staring imaging real-time optimal control based on neural network
[J]. International Journal of Aerospace Engineering Volume 2020 , 2020 : 8822223 -1 -14.
[本文引用: 1]
[13]
WU Y H HAN F ZHENG M H , et al Attitude tracking control for a space moving target with high dynamic performance using hybrid actuator
[J]. Aerospace Science and Technology 2018 , 78 : 102 -117 .
DOI:10.1016/j.ast.2018.03.041
URL
[本文引用: 1]
[14]
张宇 , 夏鲁瑞 , 蔡博宇 . 基于无迹卡尔曼滤波的空间目标双星定位方法
[J]. 上海航天 2020 , 37 (1 ): 38 -43 .
[本文引用: 1]
ZHANG Yu XIA Lurui CAI Boyu . A novel bi-satellite positioning method for spatial targets based on the unscented Kalman filter
[J]. Aerospace Shanghai (Chinese & English) 2020 , 37 (1 ): 38 -43 .
[本文引用: 1]
[15]
WANG C J WANG W H CHEN Z P . Single-satellite positioning algorithm based on direction-finding
[C]// 2017 Progress In Electromagnetics Research Symposium—Spring St Petersburg, Russia : IEEE , 2017 : 2533 -2538 .
[本文引用: 1]
[16]
于大腾 , 王华 , 尤岳 , 等 . 基于单星观测的弹道导弹参数估计方法综述
[J]. 现代防御技术 2014 , 42 (2 ): 62 -68 .
[本文引用: 1]
YU Dateng WANG Hua YOU Yue , et al Review for the method of single satellite early warning ballistic missile parameter estimation
[J]. Modern Defence Technology 2014 , 42 (2 ): 62 -68 .
[本文引用: 1]
[17]
KYUJIN M HOJUN K CHANG K R . Trajectory estimation for a ballistic missile in ballistic phase using IR images
[C]// 2018 9th International Conference on Mechanical and Aerospace Engineering Budapest, Hungary : IEEE , 2018 : 173 -177 .
[本文引用: 1]
[18]
SHYAM B JOSEPH E F STEPHEN P S . Autonomous nucleus tracking for comet/asteroid encounters: The STARDUST example
[C]// 1998 IEEE Aerospace Conference Proceedings Snowmass, CO, USA : IEEE , 1998 : 353 -365 .
[本文引用: 1]
[19]
BONG W . Rapid multitarget acquisition and pointing control of agile spacecraft
[J]. Journal of Guidance Control and Dynamics 2002 , 25 (1 ): 96 -104 .
DOI:10.2514/2.4854
URL
[本文引用: 1]
Multi-frame super-resolution of gaofen-4 remote sensing images
1
2017
... 凝视成像模式下卫星姿态控制原理为根据卫星与地面目标的相对运动关系,通过对卫星滚动与俯仰轴姿态的实时调整,实现载荷对地面或空中动态目标的凝视观测.近年来,凝视观测技术广泛被用于对地观测卫星,观测载荷包括视频相机和面阵相机等.面阵相机不仅被广泛应用于高轨卫星领域[1 ⇓ -3 ] ,利用凝视观测技术,面阵相机同样可以被应用于低轨卫星成像和视频观测卫星领域[4 ] . ...
静止轨道光学成像卫星研究现状及建议
2
2020
... 凝视成像模式下卫星姿态控制原理为根据卫星与地面目标的相对运动关系,通过对卫星滚动与俯仰轴姿态的实时调整,实现载荷对地面或空中动态目标的凝视观测.近年来,凝视观测技术广泛被用于对地观测卫星,观测载荷包括视频相机和面阵相机等.面阵相机不仅被广泛应用于高轨卫星领域[1 ⇓ -3 ] ,利用凝视观测技术,面阵相机同样可以被应用于低轨卫星成像和视频观测卫星领域[4 ] . ...
... 影响 目标跟踪期间,为了保证面阵电荷耦合器件(Charge Coupled Device,CCD)高质量成像,一般应保证在曝光时间内的累积像移偏差不超过0.25~0.3像素[2 ] ,即要求: ...
Status and development trends of high-resolution geostationary optical imaging satellite
2
2020
... 凝视成像模式下卫星姿态控制原理为根据卫星与地面目标的相对运动关系,通过对卫星滚动与俯仰轴姿态的实时调整,实现载荷对地面或空中动态目标的凝视观测.近年来,凝视观测技术广泛被用于对地观测卫星,观测载荷包括视频相机和面阵相机等.面阵相机不仅被广泛应用于高轨卫星领域[1 ⇓ -3 ] ,利用凝视观测技术,面阵相机同样可以被应用于低轨卫星成像和视频观测卫星领域[4 ] . ...
... 影响 目标跟踪期间,为了保证面阵电荷耦合器件(Charge Coupled Device,CCD)高质量成像,一般应保证在曝光时间内的累积像移偏差不超过0.25~0.3像素[2 ] ,即要求: ...
高轨光学成像卫星动目标跟踪策略设计与仿真
2
2018
... 凝视成像模式下卫星姿态控制原理为根据卫星与地面目标的相对运动关系,通过对卫星滚动与俯仰轴姿态的实时调整,实现载荷对地面或空中动态目标的凝视观测.近年来,凝视观测技术广泛被用于对地观测卫星,观测载荷包括视频相机和面阵相机等.面阵相机不仅被广泛应用于高轨卫星领域[1 ⇓ -3 ] ,利用凝视观测技术,面阵相机同样可以被应用于低轨卫星成像和视频观测卫星领域[4 ] . ...
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
Design and simulation for moving target tracking strategy of high orbit optical imaging satellite
2
2018
... 凝视成像模式下卫星姿态控制原理为根据卫星与地面目标的相对运动关系,通过对卫星滚动与俯仰轴姿态的实时调整,实现载荷对地面或空中动态目标的凝视观测.近年来,凝视观测技术广泛被用于对地观测卫星,观测载荷包括视频相机和面阵相机等.面阵相机不仅被广泛应用于高轨卫星领域[1 ⇓ -3 ] ,利用凝视观测技术,面阵相机同样可以被应用于低轨卫星成像和视频观测卫星领域[4 ] . ...
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
Recognition of aircraft activities at airports on video micro-satellites: Methodology and experimental validation
1
2022
... 凝视成像模式下卫星姿态控制原理为根据卫星与地面目标的相对运动关系,通过对卫星滚动与俯仰轴姿态的实时调整,实现载荷对地面或空中动态目标的凝视观测.近年来,凝视观测技术广泛被用于对地观测卫星,观测载荷包括视频相机和面阵相机等.面阵相机不仅被广泛应用于高轨卫星领域[1 ⇓ -3 ] ,利用凝视观测技术,面阵相机同样可以被应用于低轨卫星成像和视频观测卫星领域[4 ] . ...
Tracking imaging feedback attitude control of video satellite
1
2017
... 空中动态目标主要指各型飞机及其尾焰,高轨卫星在对动态目标进行跟踪时,始终让动态目标保持在卫星载荷的视场内即可.低轨卫星与空中动态目标相对运动角速度变化较快,在地面或其他卫星的引导下,可通过姿态调整,令动态目标出现在载荷视场内,在此基础上,需根据载荷处理得到的中心点像素信息[5 ] 即像面脱靶量信息,连续调整卫星姿态,始终让动态目标保持在卫星载荷的视场中心.由于探测器噪声等的影响,星载相机处理得到的目标中心点像素值存在噪声,该噪声将引起期望姿态和期望角速度噪声,进而影响卫星姿态控制稳定度,而姿态稳定度又会反过来影响面阵载荷积分成像[6 -7 ] .此外,通过连续多幅图像信息进行处理,才能获得准确的像面脱靶量信息,因此观测量存在明显延时,直接使用该信息进行控制,易引起凝视姿态振荡.如何在载荷脱靶量明显含有测量噪声和时延的情况下,实现卫星对空中动态目标高稳定度凝视姿态控制,是本文需要解决的问题. ...
Staring imaging attitude tracking control laws for video satellites based on image Information by hyperbolic tangent fuzzy sliding mode control
2
2022
... 空中动态目标主要指各型飞机及其尾焰,高轨卫星在对动态目标进行跟踪时,始终让动态目标保持在卫星载荷的视场内即可.低轨卫星与空中动态目标相对运动角速度变化较快,在地面或其他卫星的引导下,可通过姿态调整,令动态目标出现在载荷视场内,在此基础上,需根据载荷处理得到的中心点像素信息[5 ] 即像面脱靶量信息,连续调整卫星姿态,始终让动态目标保持在卫星载荷的视场中心.由于探测器噪声等的影响,星载相机处理得到的目标中心点像素值存在噪声,该噪声将引起期望姿态和期望角速度噪声,进而影响卫星姿态控制稳定度,而姿态稳定度又会反过来影响面阵载荷积分成像[6 -7 ] .此外,通过连续多幅图像信息进行处理,才能获得准确的像面脱靶量信息,因此观测量存在明显延时,直接使用该信息进行控制,易引起凝视姿态振荡.如何在载荷脱靶量明显含有测量噪声和时延的情况下,实现卫星对空中动态目标高稳定度凝视姿态控制,是本文需要解决的问题. ...
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
基于FPGA的红外目标识别神经网络加速器设计
1
2020
... 空中动态目标主要指各型飞机及其尾焰,高轨卫星在对动态目标进行跟踪时,始终让动态目标保持在卫星载荷的视场内即可.低轨卫星与空中动态目标相对运动角速度变化较快,在地面或其他卫星的引导下,可通过姿态调整,令动态目标出现在载荷视场内,在此基础上,需根据载荷处理得到的中心点像素信息[5 ] 即像面脱靶量信息,连续调整卫星姿态,始终让动态目标保持在卫星载荷的视场中心.由于探测器噪声等的影响,星载相机处理得到的目标中心点像素值存在噪声,该噪声将引起期望姿态和期望角速度噪声,进而影响卫星姿态控制稳定度,而姿态稳定度又会反过来影响面阵载荷积分成像[6 -7 ] .此外,通过连续多幅图像信息进行处理,才能获得准确的像面脱靶量信息,因此观测量存在明显延时,直接使用该信息进行控制,易引起凝视姿态振荡.如何在载荷脱靶量明显含有测量噪声和时延的情况下,实现卫星对空中动态目标高稳定度凝视姿态控制,是本文需要解决的问题. ...
An infrared object detection neural network accelerator based on FPGA
1
2020
... 空中动态目标主要指各型飞机及其尾焰,高轨卫星在对动态目标进行跟踪时,始终让动态目标保持在卫星载荷的视场内即可.低轨卫星与空中动态目标相对运动角速度变化较快,在地面或其他卫星的引导下,可通过姿态调整,令动态目标出现在载荷视场内,在此基础上,需根据载荷处理得到的中心点像素信息[5 ] 即像面脱靶量信息,连续调整卫星姿态,始终让动态目标保持在卫星载荷的视场中心.由于探测器噪声等的影响,星载相机处理得到的目标中心点像素值存在噪声,该噪声将引起期望姿态和期望角速度噪声,进而影响卫星姿态控制稳定度,而姿态稳定度又会反过来影响面阵载荷积分成像[6 -7 ] .此外,通过连续多幅图像信息进行处理,才能获得准确的像面脱靶量信息,因此观测量存在明显延时,直接使用该信息进行控制,易引起凝视姿态振荡.如何在载荷脱靶量明显含有测量噪声和时延的情况下,实现卫星对空中动态目标高稳定度凝视姿态控制,是本文需要解决的问题. ...
Study on enlarging the searching scope of staring area and tracking imaging of dynamic targets by optical satellites
1
2021
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
Mission scheduling optimization of multi-optical satellites for multi-aerial targets staring surveillance
1
2020
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
Staring imaging attitude control of small satellites
1
2017
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
Staring imaging real-time optimal control based on neural network
1
2020
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
Image-based attitude maneuvers for space debris tracking
1
2018
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
Attitude tracking control for a space moving target with high dynamic performance using hybrid actuator
1
2018
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
基于无迹卡尔曼滤波的空间目标双星定位方法
1
2020
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
A novel bi-satellite positioning method for spatial targets based on the unscented Kalman filter
1
2020
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
Single-satellite positioning algorithm based on direction-finding
1
2017
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
基于单星观测的弹道导弹参数估计方法综述
1
2014
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
Review for the method of single satellite early warning ballistic missile parameter estimation
1
2014
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
Trajectory estimation for a ballistic missile in ballistic phase using IR images
1
2018
... 现有参考文献中,对基于载荷脱靶量信息的空中动态目标凝视姿态控制问题研究较少.对目标凝视姿态控制问题的研究,主要集中在扩大观测范围的任务调度方法[8 -9 ] 和已知地面目标固定位置情况下的动态跟踪控制方法[3 ,10 -11 ] ,对基于图像信息的目标凝视跟踪问题,仅适用于空间符合轨道动力学特性的目标,或未考虑图像处理噪声对跟踪稳定度的影响[6 ,12 -13 ] .在目标定位方面,主要基于两颗卫星对同一目标进行观测,且适用于符合空间弹道动力学特性的目标[14 ⇓ ⇓ -17 ] . ...
Autonomous nucleus tracking for comet/asteroid encounters: The STARDUST example
1
1998
... 选取当前工程中常用的处理非线性问题的扩展卡尔曼滤波(EKF)[18 ] 来设计目标状态估计滤波器.以x p 、y p 为观测量,以目标在地固系经度λ t 、纬度γ t 、经度变化率 λ · t γ · t
Rapid multitarget acquisition and pointing control of agile spacecraft
1
2002
... 根据上述公式,可计算得到卫星期望角速度ω ir .至此,在期望姿态和期望角速度计算的基础上,调用基于四元数的卫星大角度任意姿态机动控制方法[19 ] ,即可实现基于图像的卫星对空中动态目标高稳定度凝视跟踪.完整的姿态规划与控制过程如图5 所示.图中:q ib 、ω ib 分别为卫星姿态四元数和角速度;T c 为姿态控制指令力矩. ...