空冷式多级热电制冷器性能综合分析

doi:10.16183/j.cnki.jsjtu.2022.451

空冷式多级热电制冷器性能综合分析

孙悦桐, 孟凡凯^,, 周林, 徐辰欣

海军工程大学动力工程学院,武汉 430033

Comprehensive Analysis of Performance of Air Cooled Multistage Thermoelectric Cooler

SUN Yuetong, MENG Fankai^,, ZHOU Lin, XU Chenxin

College of Power Engineering, Naval University of Engineering, Wuhan 430033, China

通讯作者: 孟凡凯,副教授;E-mail:mfk927@qq.com.

责任编辑: 王一凡

收稿日期: 2022-11-7 修回日期: 2023-01-7 接受日期: 2023-02-10

基金资助:

国家自然科学基金(11974429)
海军工程大学自主研发计划(425317T01C)

Received: 2022-11-7 Revised: 2023-01-7 Accepted: 2023-02-10

作者简介 About authors

孙悦桐(2000-),硕士生,从事多级热电制冷技术研究.

摘要

多级热电制冷器可提供更大的制冷温差,但制冷经济性能随级数增大而迅速降低.综合考虑热电材料各种内部效应与外部传热不可逆性,建立了空冷式多级热电制冷器的有限时间热力学模型,给出了制冷量和制冷系数的计算方法.为全面描述和分析多级热电制冷器性能,引入热力学完善度指标,并提出协调性能系数性能评价指标,分析了制冷器工作电流、热电臂横截面积与制冷温差对制冷量、制冷系数、热力学完善度和协调性能系数的影响.结果表明:当制冷温差为87 ℃时,电流分别为2.55 A和1.30 A时,热电臂横截面积分别为2.2 mm²和3.0 mm²时,制冷量和制冷系数分别达到最大值.综合考虑制冷能力与经济性,当电流为1.75 A时,可获得制冷量、耗功与制冷系数的最佳协调性能.

关键词： 多级热电制冷; 有限时间热力学; 热力学完善度; 协调性能; 性能优化

Abstract

The multistage thermoelectric cooler can provide a larger temperature difference, but its refrigeration and economic performance decreases rapidly with the increase of stages. Considering all kinds of internal effects of thermoelectric materials and the irreversibility of external heat transfer, a finite time thermodynamic model of air cooling multistage thermoelectric cooler is established. The calculation method for cooling capacity and coefficient of performance are given. In order to describe and analyze the performance of multistage thermoelectric cooler comprehensively, the index thermodynamic perfectibility is introduced, and the performance evaluation index of coordinated performance coefficient is proposed. The effects of working current, cross-sectional area of thermoelectric leg and temperature difference on cooling capacity, coefficient of performance, thermodynamic perfectibility and coordination performance coefficient are analyzed. With the cooling temperature difference of 87 ℃, when the current is 2.55 A and 1.30 A respectively, and the cross-sectional area of the thermoelectric arm is 2.2 mm² and 3.0 mm² respectively, the cooling capacity and coefficient of performance reach the maximum respectively. Considering the refrigeration and economic performance, when the current is 1.75 A, the best coordination performance of cooling capacity, power consumption, and refrigeration coefficient can be obtained.

Keywords： multistage thermoelectric cooling; finite time thermodynamics; thermodynamic perfectibility; coordination performance; performance optimization

PDF (2314KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

孙悦桐, 孟凡凯, 周林, 徐辰欣. 空冷式多级热电制冷器性能综合分析[J]. 上海交通大学学报, 2024, 58(3): 371-381 doi:10.16183/j.cnki.jsjtu.2022.451

SUN Yuetong, MENG Fankai, ZHOU Lin, XU Chenxin. Comprehensive Analysis of Performance of Air Cooled Multistage Thermoelectric Cooler[J]. Journal of Shanghai Jiaotong University, 2024, 58(3): 371-381 doi:10.16183/j.cnki.jsjtu.2022.451

热电制冷又称温差电制冷或半导体制冷,可通过帕尔贴效应将电能直接转化为温差^[1].与传统的压缩制冷相比,热电制冷无运动部件,可靠性高,寿命长、易维护;模块化特点使其在制冷量增大时没有显著的性能损失;无工作流体,可避免泄漏危害环境^[2⇓-4].随着热电材料技术的迅速发展,热电制冷技术成为制冷与低温领域的研究热点,在微电子系统、激光通信、医疗等领域得到了广泛应用^[5⇓-7].

一些特殊领域的设备需要在低温环境中维持运行.如基于异质结势垒型结构的中波红外探测器工作温度在150~195 K的范围内^[8];各油库和油站使用的测定仪器需要满足300~200 K逐点降温的要求;X射线太空望远镜需要在低温的状态下工作,制冷温度需达到170 K左右^[9],进而实现降低噪声、减弱灵敏度的效果.单级热电制冷器最大制冷温差只能达到60 K左右^[10],对于更大温差、更大温度跨度的场合,单级热电制冷器无法满足需求,此时需要采用多级制冷,通过增加级数获得更大的制冷温差.

多级热电制冷即采用垂直级联(金字塔状)排列方式,低一级冷端为高一级热端散热,由高温端至低温端,制冷温度逐渐降低,低温级模块可达到最低制冷温度^[11].随着温度跨度的增加,多级热电制冷器的性能会迅速降低^[12],对多热热电制冷器性能的分析与优化具有重要意义.Karimi等^[13]讨论了金字塔型多级制冷器的热流密度和性能系数最大值,数值模拟结果表明,热端散热器的热阻是决定多级热电制冷器整体性能的关键因素.Parashchuk等^[14]开发了一种多级热电制冷器,利用四级商用模块和两级超低温模块设计并制作了冷却样机,工作温度可达140 K.Phong和Shih^[15]在建模结果与性能尺寸权衡的基础上构建了多级热电制冷器的实验模型,实验结果显示,在热负荷为10 mW的情况下,六级热电制冷器可达到的温度差为137 K.Sofradir公司运用四级热电制冷器生产的处于非常温运行的面阵规格为320×256的MCT浅制冷型焦平面红外探测器,该类探测器可在200 K和250 K两个定点温度下工作^[16].

综合有关多级热电制冷的研究可见,一是研究模型中大多未考虑制冷器两端换热器件的影响,而外部热阻有限温差传热引起的不可逆性对制冷性能有很大影响;二是性能指标多为制冷量和制冷系数,缺少协调制冷能力和经济性能的综合指标.有限时间热力学是现代热力学理论的一个重要分支,实现了热力学、传热学、流体力学和化学反应动力学等多个基础学科理论的交叉融合,着重研究在有限时间、有限尺寸、有限面积、有限速率传热等约束下的各类过程、循环和装置的最优性能,是分析能量转换装置的重要理论与有力工具^{[17⇓⇓-20]},已广泛应用于化学热机^[21]、燃料电池^[22]、布朗热机^[23]、热电装置^[24]等能量转换装置的分析中,得到了一系列不同于传统分析结果的新结论和一系列更接近实际、更具普适意义的新成果.本文基于有限时间热力学理论,充分考虑外部热源与热电制冷器之间的不可逆性,建立空冷式多级热电制冷器有限时间热力学模型,提出协调性能系数评价指标,分析工作电流、热电臂横截面积和制冷温差对装置性能的影响,可为多级热电制冷器的结构设计与性能优化提供参考.

1 多级热电制冷器模型

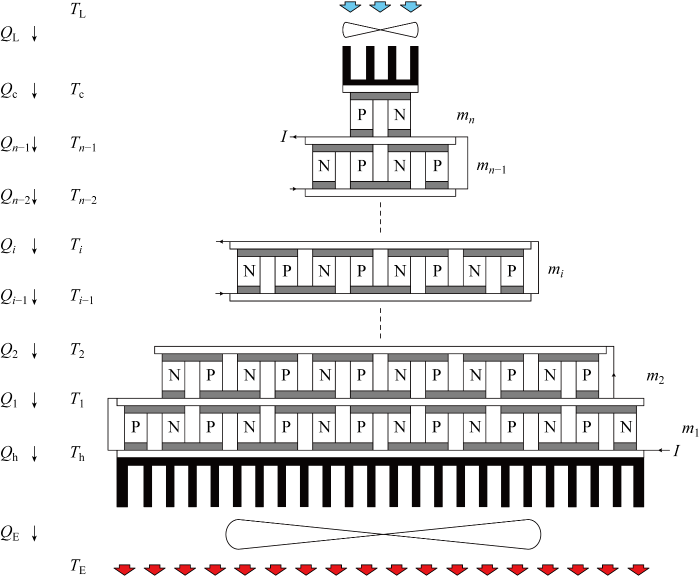
图1给出了多级热电制冷器有限时间热力学模型.图中:I为电流.区别于非平衡热力学模型,本模型考虑了热电模块端面与热源之间的换热器热阻,体现出外部有限传热面积下的有限速率传热不可逆性对装置性能的影响.装置主要分为两个部分:热电制冷模块和热沉.热电制冷模块与环境空气之间的热量交换通过热沉完成,并安装风扇加强换热.装置热电偶总数为M,每个热电偶由一个P型和一个N型热电偶臂组成.由高温端向低温端各级热电偶数分别为m_i (1≤i≤n).T_E为高温热源温度,T_L为低温热源温度,热电制冷器第1级热端温度(放热温度)和第n级冷端温度(吸热温度)分别为T_h和T_c,由第1级冷端至第n级热端各级间温度分别为T_i (1≤i≤n-1).高低温热源吸放热量为Q_E和Q_L,制冷模块放、吸热量分别为Q_h和Q_c,各节点热流量分别为Q_i (1 ≤ i ≤ n-1).

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 多级热电制冷器有限时间热力学模型

Fig.1 Finite time thermodynamic model of multistage thermoelectric cooler

忽略级间热漏损失,两级间热流量等于高一级热端的散热量,同时等于低一级冷端的吸热量.由非平衡热力学理论,可得由高温端至低温端的各节点的热流量,分别为

(1) \begin{aligned} Q_{\mathrm{h}}= & m_{1}\left[\alpha I T_{\mathrm{h}}-K\left(T_{\mathrm{h}}-T_{1}\right)+\right. \\ & \left.0.5 I^{2} R-0.5 \mu I\left(T_{\mathrm{h}}-T_{1}\right)\right] \end{aligned}

(2) \begin{aligned} Q_{1}= & m_{1}\left[\alpha I T_{1}-K\left(T_{\mathrm{h}}-T_{1}\right)-\right. \\ & \left.0.5 I^{2} R+0.5 \mu I\left(T_{\mathrm{h}}-T_{1}\right)\right]= \\ & m_{2}\left[\alpha I T_{1}-K\left(T_{1}-T_{2}\right)+\right. \\ & \left.0.5 I^{2} R-0.5 \mu I\left(T_{1}-T_{2}\right)\right] \end{aligned}

(3) \begin{aligned} Q_{i}= & m_{i}\left[\alpha I T_{i}-K\left(T_{i-1}-T_{i}\right)-\right. \\ & \left.0.5 I^{2} R+0.5 \mu I\left(T_{i-1}-T_{i}\right)\right]= \\ & m_{i+1}\left[\alpha I T_{i}-K\left(T_{i}-T_{i+1}\right)+\right. \\ & \left.0.5 I^{2} R-0.5 \mu I\left(T_{i}-T_{i+1}\right)\right] \\ & (2 \leqslant i \leqslant n-2) \end{aligned}

(4) \begin{aligned} Q_{n-1}= & m_{n-1}\left[\alpha I T_{n-1}-K\left(T_{n-2}-T_{n-1}\right)-\right. \\ & \left.0.5 I^{2} R+0.5 \mu I\left(T_{n-2}-T_{n-1}\right)\right]= \\ & m_{n}\left[\alpha I T_{n-1}-K\left(T_{n-1}-T_{c}\right)+\right. \\ & \left.0.5 I^{2} R-0.5 \mu I\left(T_{n-1}-T_{c}\right)\right] \end{aligned}

(5) \begin{aligned} Q_{\mathrm{c}}= & m_{n}\left[\alpha I T_{\mathrm{c}}-K\left(T_{n-1}-T_{\mathrm{c}}\right)-\right. \\ & \left.0.5 I^{2} R+0.5 \mu I\left(T_{n-1}-T_{\mathrm{c}}\right)\right] \end{aligned}

式中:α=α_P-α_N,α_P、α_N分别为P、N型热电偶臂的Seebeck系数,定义为热电材料单位温度梯度下产生的热电势,即α= $\frac{d U}{d T}$ ,U、T分别为温差电动势和热力学温度;R为两热电偶臂总热阻;K为两热电偶臂的总热导;μ为汤姆逊系数.

式(2)~(4)可整理成关于未知节点温度T_i (1≤i≤n-1)的由n-1个方程组成的方程组:

(6)$ \begin{array}{l} {\left[\left(m_{1}-m_{2}\right)(\alpha I-0.5 \mu I)+\left(m_{1}+m_{2}\right) K\right] \times} \\ \quad T_{1}-m_{2}(K+0.5 \mu I) T_{2}= \\ \quad m_{1}(K-0.5 \mu I) T_{\mathrm{h}}+\left(m_{1}+m_{2}\right) 0.5 I^{2} R \end{array}$

(7)$ \begin{array}{l} m_{i}(0.5 \mu I-K) T_{i-1}+\left[\left(m_{i}-m_{i+1}\right)(\alpha I-\right. \\ \left.\quad 0.5 \mu I)+\left(m_{i}+m_{i+1}\right) K\right] T_{i}-m_{i+1}(K+ \\ \quad 0.5 \mu I) T_{i+1}=\left(m_{i}+m_{i+1}\right) 0.5 I^{2} R \end{array}$

(8)$ \begin{array}{l} m_{n-1}(0.5 \mu I-K) T_{n-2}+\left[\left(m_{n-1}-m_{n}\right)(\alpha I-\right. \\ \left.\quad 0.5 \mu I)+\left(m_{n-1}+m_{n}\right) K\right] T_{n-1}= \\ \quad m_{n}(K+0.5 \mu I) T_{c}+\left(m_{n-1}+m_{n}\right) 0.5 I^{2} R \end{array}$

由式(6)~(8)联立解得中间连接层温度T_i (1≤i≤n-1)为

(9)T₁=

\frac{(m_{1} + m_{2}) 0.5 I^{2} R + m_{1} (K - 0.5 μ I) T_{h} + m_{2} (K + 0.5 μ I) T_{2}}{(m_{1} - m_{2}) (α I - 0.5 μ I) + (m_{1} + m_{2}) K}

(10)T_i=

\frac{(m_{i} + m_{i + 1}) 0.5 I^{2} R + m_{i} (K - 0.5 μ I) T_{i - 1} + m_{i + 1} (K + 0.5 μ I) T_{i + 1}}{(m_{i} - m_{i + 1}) (α I - 0.5 μ I) + (m_{i} + m_{i + 1}) K}

(2≤i≤n-2)

(11)T_n_-1=

\frac{(m_{n - 1} + m_{n}) 0.5 I^{2} R + m_{n - 1} (K - 0.5 μ I) T_{n - 2} + m_{n} (K + 0.5 μ I) T_{c}}{(m_{n - 1} - m_{n}) (α I - 0.5 μ I) + (m_{n - 1} + m_{n}) K}

考虑热电模块两端与热源不可逆传热的影响,根据有限时间热力学理论,热端和冷端的热流量可分别表示为

(12)Q_E=

\frac{T_{h} - T_{E}}{R_{E}}

, Q_L=

\frac{T_{L} - T_{c}}{R_{L}}

式中:R_E和R_L分别为热、冷端的传热热阻.

由能量守恒方程式可得:

(13)Q_h=Q_E, Q_c=Q_L

联立式(1)~(5)、(9)~(13),得到热电制冷器热、冷端温度.把T_i (1 ≤ i ≤ n-1)、T_h、T_c代入式(1)~(5)得流过各节点的热流量,可得各级功率为

(14)P₁=Q_h-Q₁

(15)P_i=Q_i_-1-Q_i (2≤i≤n-1)

(16)P_n=Q_n_-1-Q_c

各级制冷系数为

(17)ε₁=

\frac{Q_{1}}{P_{1}}

(18)ε_i=Q_i/P_i (2≤i≤n-1)

(19)ε_n=Q_c/P_n

装置整体的输入功率和制冷系数分别为

(20)P=

\overset{n}{\sum_{i = 1}}

P_i=Q_E-Q_L

(21)ε=

\frac{Q_{L}}{P}

2 热阻分析

冷热两端的热阻包括4个部分:陶瓷基板导热热阻R_cp、接触热阻R_c、热沉基板热阻R_ex和热沉对流换热热阻R_cv.式(12)中的R_E和R_L可表示为上述4个热阻之和.图2所示为相应的热阻网络图.图中:R_P和R_N分别为P型和N型热电偶的热阻.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 热阻网络

Fig.2 Thermal resistance network

模块的陶瓷基板热阻、接触热阻和热沉基板热阻分别为

(22)R_cp=

\frac{δ_{c p}}{A_{c p} λ_{c p}}

, R_c=

\frac{δ_{c}}{A_{c} λ_{c}}

, R_ex=

\frac{δ_{e x}}{A_{e x} λ_{e x}}

式中:δ_cp、δ_c和δ_ex分别为陶瓷基板、导热硅脂和热沉基板的厚度;A_cp、A_c和A_ex分别为陶瓷基板、导热硅脂和热沉基板的面积;λ_cp、λ_c和λ_ex分别为陶瓷、导热硅脂和热沉基板的导热率.

热电制冷器两侧通过气体与固体壁面对流换热,造成热阻较大,需要采用热沉和风扇组合强化换热.本文模型中采用等截面直肋热沉,其结构如图3所示.图中:δ_r为肋片厚度;b_r为肋片间距;H为肋片高度;W为肋片长度.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 热沉结构

Fig.3 Structure of heat sink

装置冷热两侧空气为肋壁的强迫风冷,对流换热热阻R_cv为^[25]

(23) $\begin{array}{c} R_{\mathrm{cv}}=\sqrt{2}\left(b_{\mathrm{r}}+\delta_{\mathrm{r}}\right)\left(H+\delta_{\mathrm{r}}\right) \sqrt{\frac{h_{1}}{\lambda_{\mathrm{r}} \delta_{\mathrm{r}}}} \operatorname{coth}[\sqrt{2}(H+ \\ \left.\left.\delta_{\mathrm{r}}\right) \sqrt{\frac{h_{1}}{\lambda_{\mathrm{r}} \delta_{\mathrm{r}}}}\right] /\left[h_{1}\left(b_{\mathrm{r}}+2 H+\delta_{\mathrm{r}}\right)\right] \end{array}$

式中:h₁为对流换热系数;λ_r为肋片热导率.

图4给出了一定工况下,制冷量与制冷系数随热端散热热阻的变化趋势.图中:t_E和t_L分别为高温热源温度和低温热源温度.当其他参数设定,随着冷热两端散热热阻的增大,装置的制冷量和制冷系数逐渐降低,热阻大小对制冷性能有着较大影响.因此,本文在热力学模型中考虑了冷热源与热电模块之间的有限速率传热,弥补了现有研究中未考虑制冷器两端换热器件外部热阻有限温差传热引起的不可逆性对制冷性能影响的不足.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 制冷量、制冷系数与热端热阻的关系

Fig.4 Relationship between cooling capacity, coefficient of performance and thermal resistance at hot end

3 评价指标

3.1 热力学完善度

制冷系数由设备运行的环境温度和制冷温度决定,其数值无法反映出装置的不可逆程度,在不同环境和制冷温度条件下也没有可比性.为了更好地对比反映装置的性能,马一太等^[26]首次提出热力学完善度η_re这一评价指标,并将其应用于压缩式制冷的计算中.热力学完善度定义为装置实际的制冷系数ε与同一温限下逆向卡诺循环制冷系数ε_c之比,即

(24)η_re=

\frac{ε}{ε_{c}}

热力学完善度反映了设备实际状况与理想循环之间的差距以及不可逆性,可以将不同制冷温差下的同一制冷装置或者具有相同运行模式的制冷装置在相同的基础上对比研究制冷特性,有助于更全面地反映装置的制冷特性和不可逆程度.

3.2 协调性能系数

由热电制冷的性能曲线可知,最大制冷量和最大制冷系数对应不同的最佳电流,制冷能力与制冷的经济性无法同时达到最优.为了寻求制冷性能的协调,文献[27]中提出了将制冷量和制冷系数两个性能指标与各自最大值的比值再线性加权,作为目标函数的双目标优化数学模型,即

(25)G=x

\frac{Q_{L}}{Q_{L m a x}}

+(1-x)

\frac{ε}{ε_{m a x}}

式中:Q_Lmax为所能达到的最大制冷量;ε_max为所能达到的最大制冷系数;x为0~1的比例系数.

系数G体现了制冷量与制冷系数的协调,x的取值大小反映了对这两个性能指标的偏好.当性能系数G达到最大时,表示一定偏好下制冷量与制冷系数协调达到最佳.

为了体现制冷量与耗功协调性能,定义协调性能系数F:

(26)F=

\frac{Q_{L}}{Q_{L m a x}}

\frac{P}{P_{m a x}}

式中:P_max为最大制冷量对应的耗功.

系数F体现了制冷量与耗功的协调,当其取最大值时,意味着取得了两者的最佳折衷.耗功在一定程度上反映了经济性能的高低,系数F越大,说明制冷量越接近最大制冷量、同时耗功相对较小,表明了制冷性能和经济性能越理想.工程应用中,当追求装置制冷量与经济性能的统一时,推荐协调性能系数F作为衡量标准;当装置对制冷量或制冷系数有所偏好,推荐采用协调性能系数G,可对x进行不同的取值.

4 影响参数分析

热电制冷器选用热电材料碲化铋(Bi₂Te₃),热电臂横截面积为A=1.4 mm×1.4 mm,单元长度为 L=2 mm.选取热电五级结构制冷器进行分析,第1级对数为m₁=300,随着级数的增加,热带单元对数逐级减半,总的热电偶对数为582对.材料的物性参数会随温度的变化而变化,参数拟合公式^[28]如下:

(27) \begin{aligned} \alpha_{\mathrm{P}}= & -\alpha_{\mathrm{N}}=(22224.0+930.6 T- \\ & \left.0.9905 T^{2}\right) \times 10^{-9} \end{aligned}

(28) \begin{aligned} \rho_{\mathrm{P}}= & \rho_{\mathrm{N}}=(5112.0+163.4 T+ \\ & \left.0.6279 T^{2}\right) \times 10^{-10} \end{aligned}

(29) \begin{aligned} \lambda_{\mathrm{P}}= & \lambda_{\mathrm{N}}=(62605.0-277.7 \mathrm{~T}+ \\ & \left.0.4131 T^{2}\right) \times 10^{-4} \end{aligned}

(30)$\mu_{\mathrm{P}}=-\mu_{\mathrm{N}}=\left(930.6 T-1.981 T^{2}\right) \times 10^{-9}$

式中:α_j、ρ_j、λ_j和μ_j (j=P, N)分别表示材料的塞贝克系数、电阻率、热导率和汤姆逊系数.冷热两端换热器一般为铝制,文中讨论温度范围内热导率变化较小,取为定值λ_ex=222 W/(m·K);空气比热容、热导率等物性参数取相应热源温度下的取值.

数值计算中,热电材料物性中的定性温度采用热端与冷端的平均温度.热端为300 K、冷端为213 K时,热电材料物性参数计算结果分别为:塞贝克系数为 1.957 6 V/K;电阻率为 8.833 5 Ω/m;热导率为 1.855 4 W/(m·K);汤姆逊系数为 1.083 6 V/K.

4.1 工作电流的影响

图5和图6分别给出了不同低温热源温度下装置的制冷量Q_L和制冷系数ε随工作电流的变化趋势.由图可见,当电流在0.8~2.8 A的范围内,随着电流的增大,制冷量和制冷系数都呈现先增大后减小的趋势,存在最佳电流,但是两者的变化情况有所不同.当低温热源温度为-60 ℃ 时,制冷量最大为2.245 W,对应的最佳工作电流为2.55 A;电流为1.3 A时对应最大的ε为0.059.最大的Q_L和ε对应的最佳电流相差较大,说明制冷能力与经济性能无法同时达到最优.随着制冷温度的降低,Q_L和ε均减小.相较于低温热源温度为-50 ℃ 来说,温度降低10 ℃,对应的最大Q_L和ε分别降低了19.18%和29.37%,温度降低20 ℃,对应的最大Q_L和ε分别降低了38.21%和52.21%.小电流时,焦耳热效应的影响很小可忽略不计,但由于热量与电流的平方呈正比,随着电流的增加,对制冷量和制冷效率的影响逐渐凸显,导致Q_L和ε存在最大值而后开始降低.随着低温热源温度的降低,Q_L取最大值所对应的最佳工作电流基本保持不变,ε取最大值所对应的最佳工作电流随之增大.由图6可以发现,相同的ε对应两个不同的工作电流,考虑到制冷量可知,当ε相同时选择大电流可以获得更好的制冷能力.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同制冷温度下制冷量与工作电流关系

Fig.5 Relationship between cooling capacity and working current at different cooling temperatures

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同制冷温度下制冷系数与工作电流关系

Fig.6 Relationship between coefficient of performance and working current at different cooling temperatures

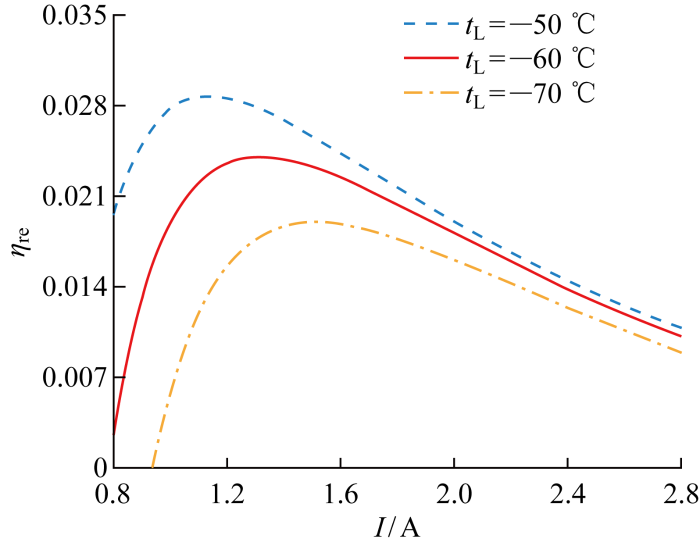
图7给出了不同低温热源温度下热力学完善度η_re与工作电流I的关系.热力学完善度随电流的变化趋势与ε相同,其值反映了装置的不可逆程度,可以排除其他的影响因素直接进行比较.当低温热源温度为-50 ℃ 时,热力学完善度随电流的增加先增大后减小,在I=1.15 A时取最大值为 0.028 8,对应的工作电流称为最佳工作电流.当t_L=-60 ℃时,热力学完善度在I=1.3 A时取最大值为 0.024 1,相较t_L=-50 ℃ 降低了16.44%;当t_L=-70 ℃ 时,热力学完善度在I=1.5 A时取最大值为0.019 0,相较t_L=-50 ℃ 降低了33.86%.随着低温热源温度的降低,η_re取最大值所对应的最佳工作电流也随之增大.与图6的结果对比表明,不同制冷温差下,ε_max的变化相较η_remax的变化更大,因为η_re是个相对值,可以更直观地反映出不同制冷温差下装置的性能,能够直接进行比较的优点使得引入热力学完善度这一评价指标有着重要意义.图8给出了最大制冷温差与电流的关系.由图可知,最大制冷温差随着工作电流的增大呈现先增大后减小的趋势,存在最佳电流使得制冷温差达到最大.当电流为2.35 A时,制冷温差取最大值为129 ℃.结果表明,采用多级热电制冷可以获得较低的制冷温度,实现大温差制冷,在需要低温工作环境的设备中具有广泛应用前景.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 不同制冷温度下热力学完善度与工作电流关系

Fig.7 Relationship between thermodynamic perfection and working current at different cooling temperatures

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 最大制冷温差与工作电流的关系

Fig.8 Relationship between maximum cooling temperature difference and working current

图9所示为不同低温热源温度下协调性能系数与工作电流的关系.图9(a)体现了制冷量与耗功的协调,当系数达到最大时表示一定工作条件下获得最佳折衷.系数F随着工作电流的增加呈现先增大后减小的趋势,结果表明存在最佳工作电流使得F取最大值.当t_L=-50 ℃ 时,在I=1.6 A时F取最大值为0.371,相较于t_L=-60 ℃和t_L=-70 ℃ 时的最大值分别增加了12.21%和31.64%.随着低温热源温度的降低,系数F取最大值所对应的最佳工作电流也随之增大.图9(b)表示通过权衡寻找制冷量和制冷系数的全局最优,本文取x=0.5进行计算.系数G随着工作电流的增加呈现先迅速增大后缓慢减小的趋势,存在最佳工作电流使得G取最大值.当t_L=-70 ℃时,在I=1.9 A时G取最大值为0.885,相较于t_L=-60 ℃ 和t_L=-50 ℃ 时的最大值分别增加了4.37%和9.38%,结果表明低温热源温度对系数G的影响较小,且当电流到达一定大小后对系数的影响效果较小.通过与图5和图6对比可以看出,G取得最大值的工作电流位于Q_Lmax和ε_max对应工作电流的中间,此时制冷量与制冷系数获得最佳折衷,可以实现综合效益最大化,充分体现了协调性能系数对双目标的协调意义,为热电装置运行工况的选择提供理论参考.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同制冷温度下协调性能系数与工作电流关系

Fig.9 Relationship between coordination performance coefficient and working current at different cooling temperatures

4.2 热电臂横截面积的影响

图10和图11分别给出了不同工作电流下装置的制冷量Q_L和制冷系数ε随热电臂横截面积的变化趋势.工况设置为低温热源温度为-60 ℃.由图可知,当横截面积在1.2~4.2 mm²的范围内逐渐增大,制冷量和制冷系数均呈现先增大后减小的趋势,存在最佳横截面积.横截面积的增大可以提高热流量,从而带来更大的制冷量和制冷系数,但是随着进一步增大,Q_L和ε存在极值而后开始下降,这是因为热电臂横截面积越大,填充系数越大,制冷模块电阻减小,系统散热率增加,从而影响制冷性能.随着工作电流的增加,最大制冷量以及对应的最优横截面积都增大,最大制冷系数基本保持不变,对应的最优横截面积增大.工作电流I=1.5 A时,横截面积A=1.7 mm²时制冷量Q_L取最大值为1.59 W;横截面积A=2.3 mm²时制冷系数ε取最大值为0.059.工作电流取2 A和2.5 A时的最大制冷量分别为2.12 W和2.65 W,相较于I=1.5 A的最大制冷量分别提高了33.24%和66.59%.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同工作电流下制冷量与横截面积关系

Fig.10 Relationship between cooling capacity and cross-sectional area at different working currents

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 不同工作电流下制冷系数与横截面积关系

Fig.11 Relationship between coefficient of performance and cross-sectional area at different working currents

图12所示为不同工作电流下热力学完善度η_re与横截面积A的关系.热力学完善度随横截面积的变化趋势与制冷系数相同,但是在数值上相差较大,结果表明热电装置的不可逆程度较大.随着工作电流的增大,最大η_re对应的最佳横截面积增大.工作电流I=1.5 A时,横截面积A=2.2 mm²时热力学完善度η_re取最大值为0.024;当I取2 A和2.5 A时,最大热力学完善度η_re对应的最佳横截面积分别为3.0 mm²和3.7 mm².

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 不同工作电流下热力学完善度与横截面积关系

Fig.12 Relationship between thermodynamic perfection and cross-sectional area at different working currents

图13所示为不同工作电流下协调性能系数与横截面积的关系.图13(a)中系数F随着横截面积的增加呈现先迅速增大后较为缓慢减小的趋势.工作电流I=1.5 A时,横截面积A=1.8 mm²时系数F取最大值为0.330.结果表明,通过协调存在最佳横截面积使得制冷量与装置耗功获得最佳折衷.图13(b)中系数G随着横截面积的增加呈现先增大后减小的趋势,存在最佳横截面积使G取最大值.工作电流I=1.5 A,横截面积A=1.7 mm²时系数G取最大值为0.848;当I取2 A和2.5 A时,F和G的最大值对应的最佳横截面积分别为2.2 mm²和2.8 mm².结果表明,通过赋予权重可以使制冷量与制冷系数之间有一个很好的权衡,有效协调两者之间因为横截面积变化而出现此消彼长的矛盾.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 不同工作电流下协调性能系数与横截面积关系

Fig.13 Relationship between coordination performance coefficient and cross-sectional area at different working currents

4.3 制冷温差的影响

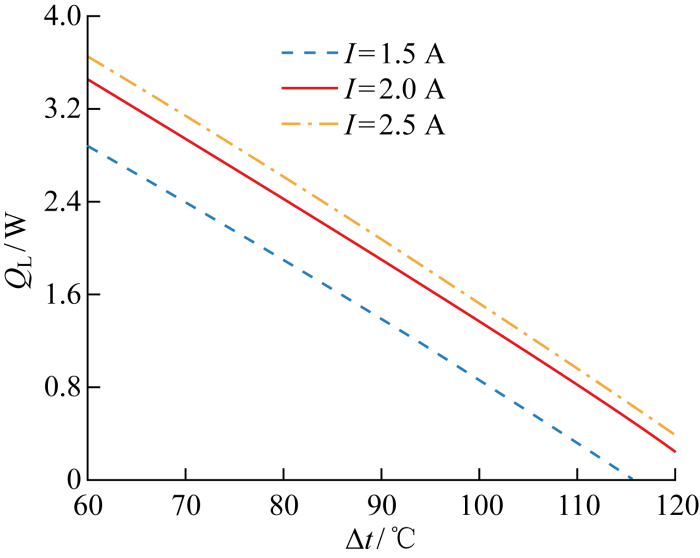
图14和图15分别给出了不同工作电流下装置的制冷量Q_L和制冷系数ε随制冷温差Δt的变化趋势.由图可以发现,当制冷温差在60~120 ℃的范围内,当I一定时,制冷量和制冷系数随着Δt的增大呈现单调减小的趋势.由于温差的不断增大,平均温度降低,热电模块的物性参数发生改变,造成制冷量的不断下降.图16所示为不同工作电流下热力学完善度η_re与制冷温差Δt的关系.工作电流I=2.5 A时,制冷温差Δt=78 ℃时热力学完善度η_re取最大值为0.013;当I取2 A和1.5 A时,制冷温差分别为78 ℃和70 ℃时对应η_re的最大值,分别为0.019和0.026,相比I=2.5 A条件下的最大η_re分别增大了42.2%和96.6%.结果表明,热力学完善度随制冷温差的增大呈现先缓慢增大后减小的趋势,与制冷量和制冷系数的变化趋势有所不同,存在最佳制冷温差使得热力学完善度最大,即不可逆程度达到最小.这是由于对于给定的环境温度,逆卡诺循环制冷系数ε_c=T_E/Δt-1与温差呈反比关系,热电制冷器制冷系数与温差呈类抛物线关系,导致存在最佳温差使得热电制冷器制冷系数最接近逆卡诺循环制冷系数,即热力学完善度最大.这个指标独立于制冷量和制冷系数,为系统的评价与优化提供了更全面的理论基础.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 不同工作电流下制冷量与制冷温差关系

Fig.14 Relationship between cooling capacity and temperature difference at different working currents

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 不同工作电流下制冷系数与制冷温差关系

Fig.15 Relationship between coefficient of performance and temperature difference at different working currents

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 不同工作电流下热力学完善度与制冷温差关系

Fig.16 Relationship between thermodynamic perfection and temperature difference at different working currents

5 结论

基于有限时间热力学理论,建立了空冷式多级热电制冷器热力学模型,提出了新的性能评价指标,分析了工作电流、热电臂横截面积和制冷温差对装置性能的影响,主要结论有:

(1) 当制冷温差为87 ℃时,工作电流分别为2.55 A和1.30 A,制冷量和制冷系数可分别达到最大值2.245 W和0.059;协调性能系数能够将制冷量、制冷系数和耗功进行协调后得到综合性能的最佳折衷,获得最佳运行参数.电流分别为1.70 A 和1.75 A时,协调性能系数F和G分别取得最大值,获得制冷量、耗功与制冷系数的最佳折衷.

(2) 一定工况下存在最佳热电臂横截面积对应最优的评价指标,超过最佳值后,由于模块电阻和热阻减小、模块产热量和热漏量增大,制冷性能降低.综合考虑制冷能力和经济性能的协调,当工作电流为2 A时,最佳横截面积为2~3 mm².

(3) 制冷量和制冷系数随制冷温差增大逐渐减小;热力学完善度随制冷温差增大呈现先增大后减小的趋势,即存在最佳制冷温差使得热力学完善度最大,系统不可逆程度最小.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

YANG

, ZHAO

, XIA

Performance analysis of multi thermoelectric cooling modules

[J]. Journal of Physics: Conference Series, 2021, 2030(1): 12015.

DOI:10.1088/1742-6596/2030/1/012015 [本文引用: 1]

[2]

CHEN

L G

, MENG

F K

, GE

Y L

, et al.

Performance optimization for a multielement thermoelectric refrigerator with linear phenomenological heat transfer law

[J]. Journal of Non-Equilibrium Thermodynamics, 2021, 46(2): 149-162.

DOI:10.1515/jnet-2020-0050 URL [本文引用: 1]

A model of a multielement thermoelectric refrigerator with another linear heat transfer law, the linear phenomenological heat transfer law \n \n \n \n Q\n ∝\n Δ\n (\n 1\n /\n T\n )\n \n Q\\propto \\Delta (1/T)\n \n, is established. The refrigerating capacity and coefficient of performance (COP) are analyzed and optimized. The junction temperature solution equations are derived. The optimum electrical currents and thermal conductance allocation are discussed. The influences of thermoelectric element quantity and refrigerating temperature difference on the optimum performances and optimum electrical currents are analyzed. The results show that different optimization objectives have different requirements for the distribution of electrical current and thermal conductance. The refrigeration capacity is not proportional to the number of thermoelectric elements. It is found that the refrigerating capacity can be achieved only when the number of thermoelectric elements is matched for fixed external heat exchangers. The input electrical current and the allocation of the thermal conductance between the two heat exchangers can be optimized synchronously to achieve maximum refrigerating capacity or maximum COP. Performance is compared with that with a Newtonian heat transfer law. The influences of the Thomson effect are also examined. Performance of the refrigerator with Newtonian heat transfer law is higher than that of the refrigerator with linear phenomenological heat transfer law. The Thomson effect can improve the performance of the refrigerator.

[3]

聂山钧, 王明富, 高晓东, 等.

热电制冷器温度依赖的材料参数的提取

[J]. 哈尔滨工业大学学报, 2019, 51(11): 68-74.