退化系统的质量控制、状态维修与备件订购联合策略优化

doi:10.16183/j.cnki.jsjtu.2022.356

退化系统的质量控制、状态维修与备件订购联合策略优化

韩梦莹¹, 马书刚^,¹, 杨建华²^,³, 李伟¹, 马志超⁴

1.河北经贸大学商学院,石家庄 050061

2.北京科技大学经济管理学院,北京 100083

3.北京企业低碳运营战略研究基地,北京 100083

4.河北工程大学管理工程与商学院,河北邯郸 056038

Joint Policy Optimization of Quality Control, Condition-Based Maintenance and Spare Ordering for a Degradation System

HAN Mengying¹, MA Shugang^,¹, YANG Jianhua²^,³, LI Wei¹, MA Zhichao⁴

1. School of Business, Hebei University of Economics and Business, Shijiazhuang 050061, China

2. School of Economics and Management, University of Science and Technology Beijing, Beijing 100083, China

3. Beijing Institute of Low Carbon Operations Strategy for Enterprises, Beijing 100083, China

4. School of Management Engineering and Business, Hebei University of Engineering, Handan 056038, Hebei, China

通讯作者: 马书刚,副教授,电话(Tel.):0311-87655622;E-mail:mashugang@126.com.

责任编辑: 王一凡

收稿日期: 2022-09-13 修回日期: 2022-11-21 接受日期: 2022-12-21

基金资助:

河北省自然科学基金(G2022207003)
河北省社会科学基金(HB21GL025)
河北省高等学校人文社会科学研究(BJS2023029)
河北省高等学校人文社会科学研究(BJ2021070)

Received: 2022-09-13 Revised: 2022-11-21 Accepted: 2022-12-21

作者简介 About authors

韩梦莹(1990-),讲师,现主要从事维修决策与优化、预测与健康管理研究.

摘要

针对关键生产系统退化过程中出现3种状态的问题,提出基于延迟时间理论的质量控制、状态维修与备件订购联合策略.首先,考虑系统退化状态与产品质量之间的函数关系,设计了在系统退化初期检查系统状态,而在退化后期检查产品质量的两阶段检测策略.其次,根据状态检测信息、产品质量信息及故障信息选择应采取的维修活动,结合系统更新时备件所处的状态确定检测周期内各种可能的事件,构建有限时域内的平均费用率模型.然后,基于离散事件仿真和响应曲面法设计优化算法以快速近似求解模型.最后,通过算例分析部分将所提联合策略与对比模型策略进行比较,验证了所提联合策略的有效性与可行性.

关键词： 质量控制; 状态维修; 备件订购; 延迟时间; 仿真优化

Abstract

A joint policy of quality control, condition-based maintenance and spare ordering is proposed for a degradation system subject to the delay time concept. First, considering the fact that product quality is largely dependent on system state, a two-stage inspection policy is proposed, in which the system state is detected during the initial deterioration process, but the product quality is checked after the defective state is found by an inspection. Then, based on the condition inspection information, quality information and failure information, the corresponding maintenance activity is chosen. Combining the state of the spare part when the system replacement is required, all possible events during an inspection interval are discussed and then a mathematical model of average cost rate is established. Afterwards, a simulation-based optimization approach coupling discrete event simulation and response surface methodology is devised to obtain a near optimal joint policy. Finally, a numerical example is provided to demonstrate the effectiveness and applicability of the proposed policy by comparing it with the comparative policy.

Keywords： quality control; condition-based maintenance; spare ordering; delay time; simulation-based optimization

PDF (5697KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

韩梦莹, 马书刚, 杨建华, 李伟, 马志超. 退化系统的质量控制、状态维修与备件订购联合策略优化[J]. 上海交通大学学报, 2024, 58(3): 361-370 doi:10.16183/j.cnki.jsjtu.2022.356

HAN Mengying, MA Shugang, YANG Jianhua, LI Wei, MA Zhichao. Joint Policy Optimization of Quality Control, Condition-Based Maintenance and Spare Ordering for a Degradation System[J]. Journal of Shanghai Jiaotong University, 2024, 58(3): 361-370 doi:10.16183/j.cnki.jsjtu.2022.356

基于状态的维修策略可以根据状态检测或监测收集到的信息建议维修活动,常被应用于实践中^[1].维修活动导致备件需求,备件是维修活动能够顺利执行的重要保障,二者相互影响与制约.对于关键生产系统(单部件系统)而言,系统的功能退化不仅是引发维修需求的根源,而且是导致产品质量下降的最主要原因^[2].因此,根据关键生产系统的功能退化过程,确定质量控制、状态维修及与之匹配的备件订购策略,对于提升产品质量、提高设备可靠性、降低运营成本有积极意义.

延迟时间模型(Delay-Time Model, DTM)由于能够建立系统状态与维修活动之间的关系,已被广泛应用于离散劣化系统的状态维修策略模型中^[3-4].如,刘勤明等^[5]建立了基于周期检测的单位时间费用模型,优化检测周期和预防性维修阈值;Yang等^[6]将基于状态的不完美维修策略与基于时间的预防更换策略相结合,优化检测周期、检测次数和预防性更换周期;Zhang等^[7]则构建了优化两阶段检测周期和次数的预防性维修模型.将设备维修与备件管理策略进行联合优化,确保维修时刻备件的可得率已被国内外许多学者提出并研究^[8⇓-10],近年来,利用DTM对状态维修与备件订购策略进行联合优化的研究也逐渐增多.如,赵斐等^[11]与韩梦莹等^[12]构建了基于时间的备件订购与状态维修联合策略模型;Zhao等^[13-14]则提出了基于系统状态的备件订购策略,建立了非周期检测与备件订购联合策略优化模型.

对生产企业而言,质量控制和设备维护这两项运营策略必须相互协作以确保生产过程的产出率^[15].上述研究虽然为设备维护以及设备维护与备件订购联合策略优化分析提供了基本框架,但并未考虑系统劣化对产品质量的影响.鉴于此,Wu等^[16]利用统计过程控制图监控产品质量,以确定最优的检测策略;Azimpoor等^[2]以产品质量评估系统状态,认为次品率为某一固定常数时,系统处于正常状态,而当次品率超出该固定值时,说明系统已进入缺陷状态,应立即进行预防性更换,据此优化检测周期和产品质量;Han等^[17]基于DTM构建了考虑缺陷品损失的状态维修与备件订购联合策略优化模型,但并未考虑产品质量的控制问题.

综上,现有基于DTM的质量控制、设备维护和备件订购联合决策研究,在理论与实际应用层面尚存在以下3个方面的局限性:① 产品质量、系统维修与备件管理3个要素之间存在密切联系,但鲜有文献同时考虑质量控制、状态维修与备件订购,对三者进行整合研究;② 在系统状态与产品质量相关时,一旦次品率超出前期固定水平就进行预防性更换^[2],易导致过度维修;③ 备件订购提前期假定为固定常数,实际上由于受多种因素的影响,备件订购之后的交付期具有随机性特征^[18].针对这些不足,本文将状态检测信息和质量检验信息作为互补,进行预防性维修决策,针对退化过程服从延迟时间理论的关键生产系统,提出质量控制、状态维修与备件订购联合策略.

1 问题描述与模型符号

1.1 问题描述

(1) 系统退化过程及系统状态与次品率关系说明.

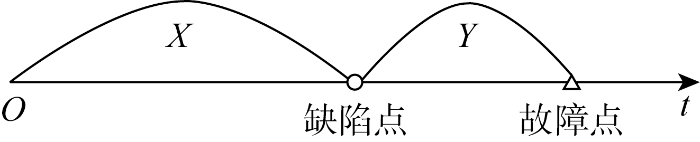
系统退化过程服从延迟时间理论,即系统由初始新状态退化到故障状态要经历正常阶段和缺陷阶段,其中X和Y分别表示正常阶段和缺陷阶段持续时间的随机变量,如图1所示.系统的状态空间也因此被划分为:正常、缺陷和故障.系统退化的两个阶段由Weibull分布来描述^{[11⇓⇓⇓-15]},Weibull分布的故障率函数为h(t)=απ(αt)^π^-1(α>0,π>0,t≥0),其中α为尺度参数,π为形状参数,t为时间随机变量.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 延迟时间理论

Fig.1 Concept of delay time

系统的运行状态与产品的加工质量密切相关.系统处于正常状态时,次品率固定在β₁水平;一旦系统进入缺陷状态,次品率则是关于缺陷状态实际持续时间,即缺陷点到达时刻与系统更换(预防更换或故障更换)需求发生时刻之间的时间间隔t₁的单调递增函数,可用β₂(t₁)表示,其公式如下:

(1)β₂(t₁)=β₁+λ[1-exp(-κ

t_{1}^{ε}

)]

式中:β₁为系统刚进入缺陷状态时的次品率;λ为产品质量退化的边界值;κ和ε为正常数.

(2) 两阶段检测的质量控制及状态维修策略说明.

①在系统退化初期以周期T(决策变量)检查系统状态,而在退化后期以周期T检查产品质量,退化初期的检测视为第一阶段检测,退化后期的检测视为第二阶段检测.系统退化的前后期以检测初次识别系统缺陷的时间点为基准进行划分,并在该时间点进行质量检测.

②对产品采用100%的质量检测方法,一旦质检结果表明产品次品率超出阈值R_P(决策变量),则需对系统进行预防性更换,该活动记为基于质量的更新;若第M(M≥1,为决策变量)次进行质量检测,次品率仍未超出阈值R_P,为减少系统的故障发生率,需在第M+1次执行质量检测活动的时刻进行预防性更换(但该时刻不进行质量检测),记为基于状态的更新;若在检测期内系统突发故障,则需进行故障后更换,记为基于故障的更新.

③无论是状态检测还是质量检测,检测结果都是完全可靠的.

(3) 质量控制、状态维修及备件订购联合策略优化.

在检测第1次识别系统缺陷状态时,进行备件订购,备件订购时刻与备件交付时刻之间的时间间隔随机,随机订购提前期L_R服从参数为ν和σ的正态分布,即L_R~N(ν,σ).由上文描述可知,系统存在3种更新方式:基于质量的更新、基于状态的更新和基于故障的更新.系统预防性更换或故障更换需求发生时,需要考虑备件的可得性:若备件已入库,则立即更新系统;若备件订购已下达但未交付,需等待备件进行交付;若备件未订购则立即订货,并在备件到达后更新系统.

1.2 模型符号

对模型构建过程中涉及的其他符号进行说明,如表1所示.

表1 主要模型符号及说明

Tab.1 Main notations and illustration for the model

符号	符号说明	符号	符号说明
P	产品生产率	Γ	时间阈值
C_IC	单位状态检测费用	C_IQ	单位质量检测费用(C_IQ > C_IC)
C_P	单位预防更换费用	C_F	单位故障更换费用
C_D	单位次品损失	C_S	等待备件的单位时间惩罚费用
C_R	备件订购费用	C_H	单位时间库存持有费用

新窗口打开| 下载CSV

2 模型建立

将系统寿命周期内的第n个检测期定义为从第n-1次检测结束时刻到第n次检测结束时刻之间的时间间隔,若在检测期内需对系统进行更换,则此时的检测期定义为从上一次检测结束时刻到系统更换完成时刻之间的时间间隔.令C_T_,n表示第n个检测期产生的总费用,L_T_,n表示第n个检测期期长.由系统退化过程的随机性、预防性更换和故障更换策略的描述可知,第n个检测期可能发生的事件如下.

事件1 第n次检测时,识别系统处于正常状态,无需进行维修活动.

事件2 第n次检测时,初次识别系统缺陷状态,且次品率未超出阈值R_P,无需进行维修活动.

事件3 第n次检测时,非初次识别系统缺陷状态,次品率未超出阈值R_P且质量检测次数未超出阈值M,无需进行维修活动.

事件4 第n次检测时,质量检测次数未超出阈值M,但次品率超出阈值R_P,需进行基于质量的更新.

事件5 第n次检测时刻,质量检测次数超出阈值M,需进行基于状态的更新.

事件6 系统在第n个检测期内突发故障,需进行基于故障的更新.

事件4~6需根据备件的状态,考虑不同的情形.令 $C_{T, n}^{k}$ 表示事件k(k=1,2,…,6)下第n个检测期消耗的总费用, $L_{T, n}^{k}$ 表示事件k下第n个检测期期长,分别求解每种事件下的总费用和总期长.

2.1 第n次检测时,识别系统处于正常状态,无需进行维修活动

事件1下第n个检测期消耗的总费用 $C_{T, n}^{1}$ 由C_IC和次品损失 $C_{D, n}^{1}$ 组成,即

(2)

C_{T, n}^{1}

=C_IC+

C_{D, n}^{1}

式中: $C_{D, n}^{1}$ =C_DPβ₁T.该事件下第n个检测期期长 $L_{T, n}^{1}$ 即为检测间隔期长T.

2.2 第n次检测时,初次识别系统缺陷状态,无需进行维修活动

令T_D为第n-1次检测结束至系统缺陷点的时间间隔, $N_{D}^{2}$ 表示事件2下本检测期内生产的次品总数.该事件下有 $\frac{N_{D}^{2}}{P T}$ <R_P成立,此时总费用 $C_{T, n}^{2}$ 由C_IC、C_IQ、C_R和次品损失 $C_{D, n}^{2}$ 构成,即

(3)

C_{T, n}^{2}

=C_IC+C_IQ+C_R+

C_{D, n}^{2}

式中: $C_{D, n}^{2}$ =C_D $N_{D}^{2}$ =C_D(Pβ₁T_D+P $\int_{0}^{T - T_{D}}$ β₂(t₁)dt₁).该事件下第n个检测期期长 $L_{T, n}^{2}$ 也为检测间隔期长T.

2.3 第n次检测时,非初次识别系统缺陷状态,无需进行维修活动

令 $N_{D}^{3}$ 表示事件3下本检测期内生产的次品总数,K(K≥1)表示在第K次检测时初次识别系统的缺陷状态.该事件下有 $\frac{N_{D}^{3}}{P T}$ <R_P和n-K<M成立,此时的总费用 $C_{T, n}^{3}$ 由C_IQ和次品损失 $C_{D, n}^{3}$ 构成,即

(4)

C_{T, n}^{3}

=C_IQ+

C_{D, n}^{3}

式中: $C_{D, n}^{3}$ =C_D $N_{D}^{3}$ =C_DP $\int_{(n - K) T - T_{D}}^{(n - K + 1) T - T_{D}}$ β₂(t₁)dt₁.该事件下第n个检测期期长 $L_{T, n}^{3}$ 等于检测间隔期长T.

2.4 第n次检测需进行基于质量的更新

事件4下,有n-K<M成立.根据系统更新时备件可能存在的3种状态,需要考虑3种更新场景.令 $N_{D}^{4,1}$ 、 $N_{D}^{4,2}$ 和 $N_{D}^{4,3}$ 分别表示事件4场景1、2和3下本检测期内生产的次品总数.

场景1 系统更新时备件已入库,说明L_R≤(n-K)T,n-K≥1,且 $\frac{N_{D}^{4,1}}{P T}$ ≥R_P,此时的总费用 $C_{T, n}^{4,1}$ 由C_IQ、C_P、次品损失 $C_{D, n}^{4,1}$ 和备件库存持有费用 $C_{I, n}^{4,1}$ 构成,即

(5)

C_{T, n}^{4,1}

=C_IQ+C_P+

C_{D, n}^{4,1}

C_{I, n}^{4,1}

式中: $C_{D, n}^{4,1}$ =C_D $N_{D}^{4,1}$ =C_D $N_{D}^{3}$ = $C_{D, n}^{3}$ ; $C_{I, n}^{4,1}$ =C_H×[(n-K)T-L_R].事件4场景1下第n个检测期期长 $L_{T, n}^{4,1}$ 为检测间隔期长T.

场景2 系统更新时备件已订货但未交付,有L_R>(n-K)T,n-K≥1且 $\frac{N_{D}^{4,2}}{P T}$ ≥R_P成立,此时的总费用 $C_{T, n}^{4,2}$ 由C_IQ、C_P、次品损失 $C_{D, n}^{4,2}$ 和等待备件的惩罚费用 $C_{S, n}^{4,2}$ 构成,即

(6)

C_{T, n}^{4,2}

=C_IQ+C_P+

C_{D, n}^{4,2}

C_{S, n}^{4,2}

式中: $C_{D, n}^{4,2}$ = $C_{D, n}^{4,1}$ ; $C_{S, n}^{4,2}$ =C_S[L_R-(n-K)T].事件4场景2下第n个检测期期长 $L_{T, n}^{4,2}$ 为检测间隔期长与备件等待时间之和,有 $L_{T, n}^{4,2}$ =T+L_R-(n-K)T.

场景3 系统更新时尚未订购备件,说明初次识别系统缺陷时,次品率就超出了阈值R_P,此时有 $N_{D}^{4,3}$ = $N_{D}^{2}$ 且 $\frac{N_{D}^{4,3}}{P T}$ ≥R_P,总费用 $C_{T, n}^{4,3}$ 由C_IC、C_IQ、C_R、C_P、次品损失 $C_{D, n}^{4,3}$ 和等待备件的惩罚费用 $C_{S, n}^{4,3}$ 构成,即

(7)

C_{T, n}^{4,3}

=C_IC+C_IQ+C_R+C_P+

C_{D, n}^{4,3}

C_{S, n}^{4,3}

式中: $C_{D, n}^{4,3}$ = $C_{D, n}^{2}$ ; $C_{S, n}^{4,3}$ =C_SL_R.事件4场景3下第n个检测期期长 $L_{T, n}^{4,3}$ 为检测间隔期长与备件等待时间之和,有 $L_{T, n}^{4,3}$ =T+L_R.

2.5 第n次检测时刻需进行基于状态的更新

因该事件下备件已进行订购,则必然存在M≥1,同时存在2种更新场景.

场景1 系统更新时备件已入库,说明L_R≤MT,此时的总费用 $C_{T, n}^{5,1}$ 由C_P、次品损失 $C_{D, n}^{5,1}$ 和备件库存持有费用 $C_{I, n}^{5,1}$ 组成,即

(8)

C_{T, n}^{5,1}

=C_P+

C_{D, n}^{5,1}

C_{I, n}^{5,1}

式中: $C_{D, n}^{5,1}$ =C_DP $\int_{M T - T_{D}}^{(M + 1) T - T_{D}}$ β₂(t₁)dt₁; $C_{I, n}^{5,1}$ =C_H(MT-L_R).令 $L_{T, n}^{5,1}$ 表示事件5场景1下第n个检测期期长,有 $L_{T, n}^{5,1}$ =T.

场景2 系统更新时备件尚未交付,说明L_R>MT,此时的总费用 $C_{T, n}^{5,2}$ 由C_P、次品损失 $C_{D, n}^{5,2}$ 和等待备件的惩罚费用 $C_{S, n}^{5,2}$ 组成,即

(9)

C_{T, n}^{5,2}

=C_P+

C_{D, n}^{5,2}

C_{S, n}^{5,2}

式中: $C_{D, n}^{5,2}$ = $C_{D, n}^{5,1}$ ; $C_{S, n}^{5,2}$ =C_S(L_R-MT).令 $L_{T, n}^{5,2}$ 为事件5场景2下第n个检测期期长,则有 $L_{T, n}^{5,2}$ =T+L_R-MT.

2.6 系统在第 n 个检测期内突发故障, 需进行基于故障的更新

令T_F为第n-1次检测结束至系统故障点的时间段,该事件下,有n-K≤M成立.考虑系统故障时备件的状态,存在3种更新场景.

场景1 系统故障时备件为在库状态,说明系统故障发生前已识别出缺陷状态,有L_R≤(n-1-K)T+T_F和n-K≥1成立,此时的总费用 $C_{T, n}^{6,1}$ 由C_F、次品损失 $C_{D, n}^{6,1}$ 和备件库存持有费用 $C_{I, n}^{6,1}$ 组成,即

(10)

C_{T, n}^{6,1}

=C_F+

C_{D, n}^{6,1}

C_{I, n}^{6,1}

式中: $C_{D, n}^{6,1}$ =C_DP $\int_{(n - K) T - T_{D}}^{(n - K) T + T_{F} - T_{D}}$ β₂(t₁)dt₁; $C_{I, n}^{6,1}$ =C_H[(n-1-K)T+T_F-L_R].令 $L_{T, n}^{6,1}$ 表示事件6场景1下第n个检测期期长,有 $L_{T, n}^{6,1}$ =T_F.

场景2 系统故障时备件已订货但未交付,说明L_R>(n-1-K)T+T_F,n-K≥1,此时的总费用 $C_{T, n}^{6,2}$ 由C_F、次品损失 $C_{D, n}^{6,2}$ 和等待备件的惩罚费用 $C_{S, n}^{6,2}$ 组成,即

(11)

C_{T, n}^{6,2}

=C_F+

C_{D, n}^{6,2}

C_{S, n}^{6,2}

式中: $C_{D, n}^{6,2}$ = $C_{D, n}^{6,1}$ ; $C_{S, n}^{6,2}$ =C_S[L_R-(n-1-K)T-T_F].令 $L_{T, n}^{6,2}$ 表示事件6场景2下第n个检测期期长,有 $L_{T, n}^{6,2}$ =L_R-(n-1-K)T.

场景3 系统故障时尚未订购备件,说明系统发生故障前并未识别系统的缺陷状态,即系统缺陷点和故障点发生在同一检测区间,此时的总费用 $C_{T, n}^{6,3}$ 由C_R、C_F、次品损失 $C_{D, n}^{6,3}$ 和等待备件的惩罚费用 $C_{S, n}^{6,3}$ 组成,即

(12)

C_{T, n}^{6,3}

=C_R+C_F+

C_{D, n}^{6,3}

C_{S, n}^{6,3}

式中: $C_{D, n}^{6,3}$ =C_D(Pβ₁T_D+P $\int_{0}^{T_{F} - T_{D}}$ β₂(t₁)dt₁); $C_{S, n}^{6,3}$ = $C_{S, n}^{4,3}$ .令 $L_{T, n}^{6,3}$ 表示事件6场景3下第n个检测期期长,有 $L_{T, n}^{6,3}$ =T_F+L_R.

2.7 联合策略优化模型

由上述分析可得,第n个检测期产生的总成本为

(13)C_T_,n=

\overset{3}{\sum_{k = 1}} C_{T, n}^{k}

χ(k)+

\overset{6}{\sum_{k = 4}} \overset{3}{\sum_{j = 1}} C_{T, n}^{k, j}

χ(k, j)

式中:χ(k)为示性函数,若事件k发生则值为1,否则值为0;χ(k,j)也为示性函数,若事件k下的场景j发生则值为1,否则值为0.

同样可得,第n个检测期的期长为

(14)L_T_,n=

\overset{3}{\sum_{k = 1}} L_{T, n}^{k}

χ(k)+

\overset{6}{\sum_{k = 4}} \overset{3}{\sum_{j = 1}} L_{T, n}^{k, j}

χ(k, j)

若N为[0, Γ]时间段内总的检测期数,则该时间段内的平均费用率C(T, M, R_P)可表示为

(15)C(T, M, R_P)=

\overset{N}{\sum_{n = 1}}

C_T_,n/

\overset{N}{\sum_{n = 1}}

L_T_,n

该联合策略模型可概括为以下非线性、混合整数、随机优化问题:

(16)$ \begin{aligned} \min & C\left(T, M, R_{\mathrm{P}}\right) \\ \text { s.t. } & \beta_{1} \leqslant R_{\mathrm{P}}<1 \\ & T, M \in \mathbf{N}^{*} \end{aligned}$

3 对比模型及优化算法

3.1 对比模型

将本文所建的质量控制、状态维修与备件订购联合策略模型记为模型1.仅考虑质量控制的预防性维修^[2]策略模型中,假定一旦次品率超出阈值β₁就进行预防性更换,决策变量仅为检测周期.为与模型1进行比较,将文献[2]中基于产品质量的维修策略进行扩展,假定在次品率超出阈值R_P(决策变量)时,进行预防性更换,在此基础上,提出对比模型2.模型2与模型1的不同之处在于:前者未考虑基于状态的更新策略.因此,模型2中不会出现事件5,将模型1中的 $C_{T, n}^{5, h}$ 和 $L_{T, n}^{5, h}$ (h=1, 2)设为0,其余公式保持不变,便可得到模型2的目标函数与约束条件,如下式所示:

(17)$ \begin{array}{ll} \min & C\left(T, R_{\mathrm{P}}\right)=\sum_{n=1}^{N} C_{\mathrm{T}, n} / \sum_{n=1}^{N} L_{\mathrm{T}, n} \\ \text { s.t. } & \beta_{1} \leqslant R_{P}<1 \\ & T \in \mathbf{N}^{*} \end{array}$

3.2 离散事件仿真算法

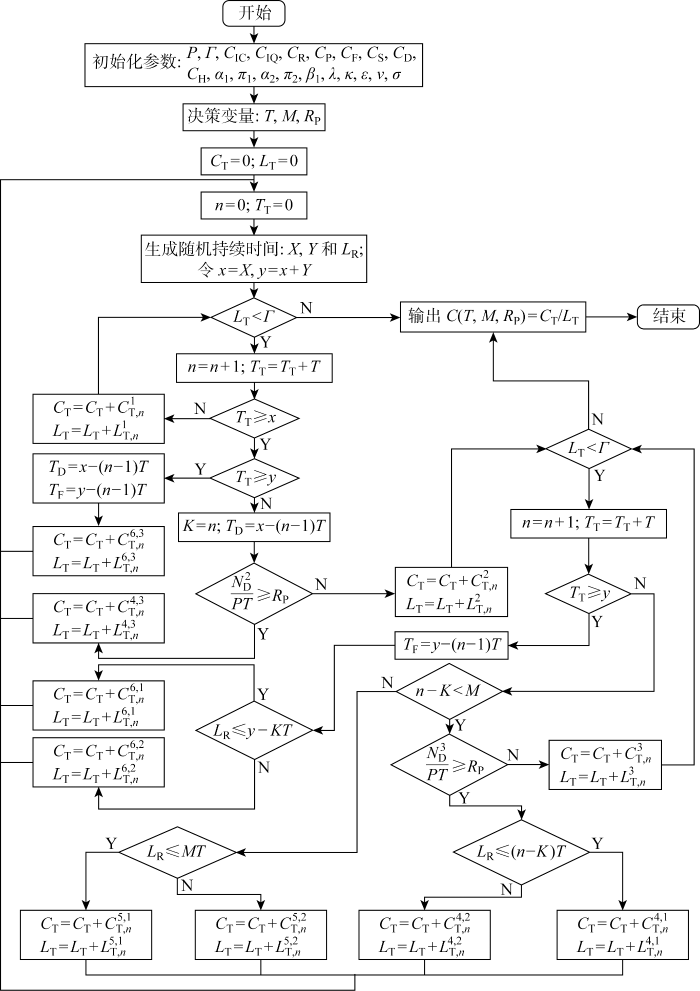
因模型1和2的目标函数中存在大量不确定性因素,如系统状态、备件状态及[0, Γ]时间段内的检测期总数等,故通过离散事件仿真算法模拟系统的更新过程,实现对式(16)~(17)的近似求解.模型1的离散事件仿真算法流程图如图2所示,主要步骤如下.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 离散事件仿真算法流程图

Fig.2 Flow chart of discrete-event simulation algorithm

步骤1 设置模型初始参数,包括时间阈值Γ、P、C_IC、C_IQ、C_R、C_P、C_F、C_S、C_D、C_H、系统两阶段故障率退化参数和次品率参数.

步骤2 设置决策变量T、M和R_P.

步骤3 设置[0,Γ]时间段内的总费用C_T=0,总的时间长度L_T=0.

步骤4 设置更新周期内的当前检测期数n=0,更新周期内的当前检测时刻T_T=0.

步骤5 根据相关分布及参数生成随机持续时间X和 Y及L_R.并令x表示缺陷点,y表示故障点,有x=X和y=x+Y成立.

步骤6 若L_T<Γ,系统更新周期内的检测期数n=n+1和检测时刻T_T=T_T+T逐渐累加;否则,输出目标函数值C(T, M, R_P).

步骤7 若当前检测时刻小于缺陷点到达时刻,则表明系统在检测时刻处于正常状态.因此,若T_T<x,事件1发生,计算C_T和L_T,并返回步骤6;否则,转到步骤8.

步骤8 若当前检测时刻T_T≥y则表明系统在第n个检测期内发生故障,且故障时刻并未订购备件,即事件6中的场景3发生,在求得T_D和T_F的基础上,计算C_T和L_T,并返回步骤4.反之,若T_T≥y不成立则意味着T_T时刻检测时初次识别系统的缺陷状态,此时有K=n成立并可求得T_D,转到步骤9.

步骤9 若 $\frac{N_{D}^{2}}{P T}$ ≥R_P,需进行基于质量的更新,由于备件未订购,事件4中的场景3发生,计算C_T和L_T,返回步骤4;否则,事件2发生,计算C_T和L_T,转到步骤10.

步骤10 若L_T<Γ,则系统更新周期内的检测期数按n=n+1逐渐累加,而检测时刻按T_T=T_T+T逐渐累加,并转到步骤11;否则,输出目标函数值C(T, M, R_P).

步骤11 若T_T≥y,首先应计算T_F,然后进一步判断故障时刻备件所处的状态.此时若L_R≤y-KT,则备件已入库,事件6中的场景1发生,计算C_T和L_T,并返回步骤4;若L_R>y-KT,则备件已订购但未交付,事件6中的场景2发生,计算C_T和L_T,并返回步骤4.若T_T<y,则转到步骤12.

步骤12 通过n-K<M判断是否达到了基于状态的更新条件.若n-K<M,则转到步骤13;否则,进行基于状态的更新,并判断状态更新需求时刻备件的状态,如果L_R≤MT,则备件已入库,事件5中的场景1发生,计算C_T和L_T,并返回步骤4,如果L_R>MT,则备件已订购但未交付,事件5中的场景2发生,计算C_T和L_T,并返回步骤4.

步骤13 若 $\frac{N_{D}^{3}}{P T}$ <R_P,事件3发生,计算C_T和L_T,并返回步骤10;否则,需进行基于质量的更新,转到步骤14.

步骤14 若L_R≤(n-K)T,则表明质量更新需求时刻备件已入库,事件4中的场景1发生,计算C_T和L_T,并返回步骤4;否则,说明质量更新需求时刻备件已订购但未交付,事件4中的场景2发生,计算C_T和L_T,并返回步骤4.

值得注意的是,将图2中n-K<M的判断及n-K<M不成立的流程取消,其余流程保持不变便可得到模型2的离散事件仿真流程图.就主要步骤而言,模型1步骤11中,在T_T<y成立的条件下,直接转到步骤13,并保持其余步骤不变,就可得到模型2的仿真过程.

3.3 目标函数的估计与优化

对于两个模型给定的决策变量(T, M, R_P)和(T, R_P),根据3.2节中离散事件仿真算法分别求得平均费用率数据.通过响应曲面法,利用Design Expert软件分别拟合模型1和2的二次平均费用率回归方程.拟合所得二次平均费用率函数连同约束条件构成非线性约束问题,进而借助MATLAB软件求解模型.多次重复以上过程,以获得全局近似最优解.

4 实验分析

4.1 参数设置

系统正常阶段和缺陷阶段故障率的退化参数分别为:α₁=0.019,π₁=1.5;α₂=0.031,π₂=1.5.模型次品率参数为:β₁=0.005,λ=0.25,κ=0.008,ε=1.2.L_R服从正态分布的参数为:ν=25,σ=3.其余参数设定为P=10 t/d, Γ=10 000 d, C_IC=50元/次, C_IQ=150元/次,C_R=600元/次,C_P=2 500 元/次, C_F=4 300元/次, C_S=250元/ (t·d^-1), C_D=80元/t,C_H=15元/d.

4.2 模型1结果分析

采用三因素、三水平的Box-Behnken实验方案来拟合模型1的费用率函数C(T, M, R_P).首先,利用离散仿真算法进行17组实验,每组实验重复200次,得出相应(T, M, R_P)组合下的平均费用率.其次,借助Design Expert软件拟合二次费用率函数c(T, M, R_P),得到的二次回归方程如下:

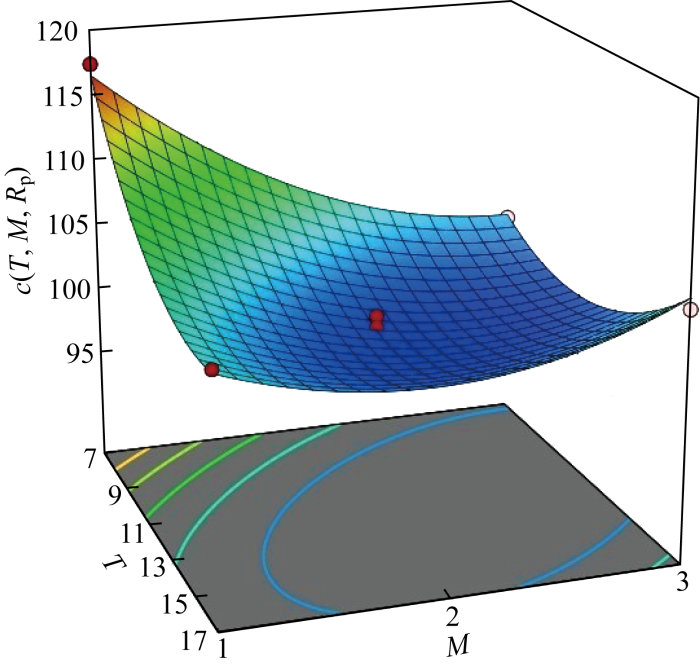
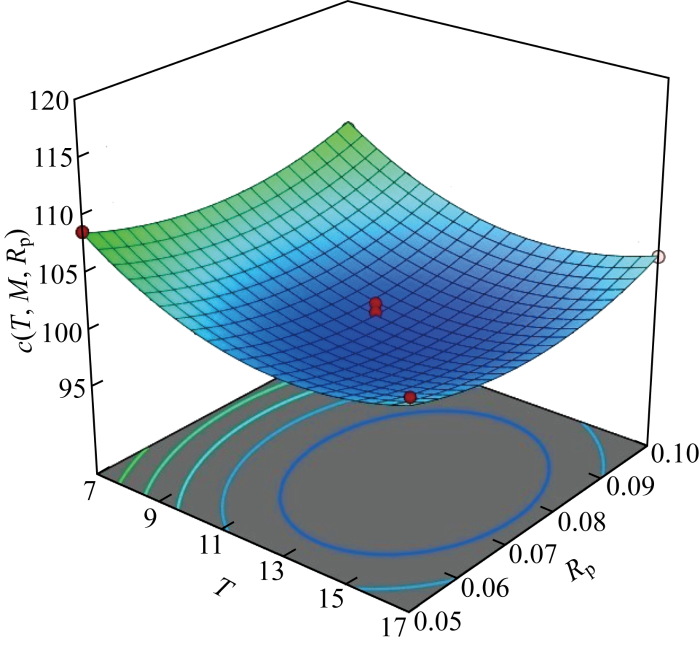
(18)$ \begin{array}{l} c\left(T, M, R_{\mathrm{P}}\right)=192.70258-5.70703 T- \\ 28.40024 M-645.646 R_{\mathrm{P}}+0.76685 T M+ \\ 0.8926 T R_{\mathrm{P}}+30.901 M R_{\mathrm{P}}+0.153253 T^{2}+ \\ 3.45012 M^{2}+3838.232 R_{\mathrm{P}}^{2} \end{array}$

图3和图4给出了c(T, M, R_P)随两参数变化的曲面.方差分析结果如表2所示.表中:SS表示离均差平方和;d.f表示自由度;MS表示均方差;F-value表示F值;p-value表示p值;Model表示模型;Lack of Fit表示失拟项;Pure Error表示纯误差;Cor Total 表示总计;R²-adjusted表示调整后的R².由表2可知,模型1的显著性检验值p<0.05说明该模型具有统计学意义;R²-adjusted为 0.956 9、失拟项为0.164 8>0.05,这表明利用二次回归方程来拟合模型1的目标函数是有效的且拟合程度高,无失拟因素存在,故可以利用拟合的二次费用率函数c(T, M, R_P)对结果进行分析.然后,借助MATLAB软件对c(T, M, R_P)求最小值,得优化结果 c(13, 2, 0.075)=100.021 1元/d.最后, 利用离散仿真算法求解最优策略下的费用率为C(13, 2, 0.075)=100.518 2元/d,两者的相对误差为 $\frac{100.518 2 元 / d - 100.021 1 元 / d}{100.518 2 元 / d}$ <0.5%.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 c(T, M, R_P) 随T和M变化曲面

Fig.3 Surface of c(T, M, R_P) with variation of T and M

图4

新窗口打开| 下载原图ZIP| 生成PPT

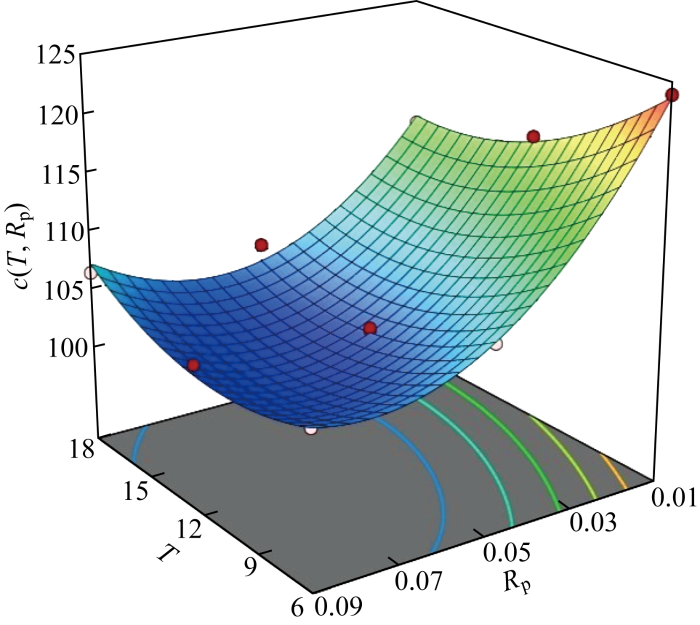
图4 c(T, M, R_P) 随T和R_P变化的曲面

Fig.4 Surface of c(T, M, R_P) with variation of T and R_P

表2 模型1方差分析(ANOVA)相关结果

Tab.2 Correlation results of ANOVA for Model 1

因素	SS	d.f	MS	F-value	p-value
Model 1	325.26	9	36.14	40.51	< 0.000 1
T	36.69	1	36.69	41.13	0.000 4
M	75.89	1	75.89	85.08	< 0.000 1
R_P	0.033 9	1	0.033 9	0.038	0.851 1
TM	58.81	1	58.81	65.92	< 0.000 1
TR_P	0.049 8	1	0.049 8	0.055 8	0.82
MR_P	2.39	1	2.39	2.68	0.145 9
T²	61.81	1	61.81	69.29	< 0.000 1
M²	50.12	1	50.12	56.19	0.000 1
$R_{P}^{2}$	24.23	1	24.23	27.16	0.001 2
Lack of Fit	4.28	3	1.43	2.9	0.164 8
Pure Error	1.96	4	0.491 2
Cor Total	331.5	16

注:“空白”表示无数值.

新窗口打开| 下载CSV

4.3 模型2结果分析

因模型2具有两个决策变量,故选用两因素、两水平的Central Composite实验方案进行13组实验,每组实验重复200次,以拟合模型2的费用率函数C(T, R_P),得到的二次回归方程如下:

(19)$ \begin{array}{c} c\left(T, R_{\mathrm{P}}\right)=144.38399-2.88613 T- \\ 733.56761 R_{\mathrm{P}}+12.34708 T R_{\mathrm{P}}+ \\ 0.082667 T^{2}+4219.56358 R_{\mathrm{P}}^{2} \end{array}$

图5为c(T, R_P)随T和R_P变化的曲面图.对拟合结果作统计学分析,如表3所示,R²-adjusted为 0.980 9.结果表明拟合的二次费用率函数能代替试验真实点对结果进行分析.利用MATLAB求解c(T, R_P),得最优解为(T^*, $R_{P}^{*}$ )=(12, 0.069),最优平均费用率为c(12, 0.069)=101.351元/d.在此最优策略下,利用离散仿真算法求解费用率为C(12, 0.069)=101.962 3元/d,两者的相对误差为 $\frac{101.962 3 元 / d - 101.351 元 / d}{101.962 3 元 / d}$ <0.6%.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 c(T, R_P)随T和R_P变化曲面

Fig.5 Surface of c(T, R_P) with variation of T and R_P

表3 模型2方差分析(ANOVA)相关结果

Tab.3 Correlation results of ANOVA for Model 2

因素	SS	d.f	MS	F-value	p-value
Model 2	534.43	5	106.89	123.49	< 0.000 1
T	17.52	1	17.52	20.24	0.002 8
R_P	256.46	1	256.46	296.29	< 0.000 1
TR_P	35.12	1	35.12	40.58	0.000 4
T²	24.46	1	24.46	28.26	0.001 1
$R_{P}^{2}$	125.89	1	125.89	145.44	< 0.000 1
Lack of Fit	4.47	3	1.49	3.75	0.117 3
Pure Error	1.59	4	0.397 7
Cor Total	540.49	12

注:“空白”表示无数值.

新窗口打开| 下载CSV

将两个模型的最优结果进行比较,可知:模型1的最优结果小于模型2的最优结果.这说明与仅考虑质量控制的预防性维修和备件订购联合策略相比,同时考虑质量控制和系统状态的预防性维修与备件订购联合策略,能够有效降低系统的平均费用率.

4.4 敏感性分析

由4.1节可知,影响模型最优解的参数有很多,此处以C_F为例进行敏感性分析,这是因为与其他情况相比,设备故障后的维修费用更高,给企业带来的经济损失更大,选取其进行敏感性分析具有一定的代表性.表4给出了不同C_F取值下,模型的最优结果.

表4 C_F敏感性分析结果

Tab.4 Sensitivity analysis results of C_F

C_F	(T^, M^, $R_{P}^{*}$ )	c(T^, M^, $R_{P}^{*}$ )	C(T^, M^, $R_{P}^{*}$ )	(T^, $R_{P}^{}$ )	c(T^, $R_{P}^{}$ )	C(T^, $R_{P}^{}$ )
3 100	(14, 2, 0.078)	90.381 0	91.257 6	(13, 0.076)	91.370 8	92.072 8
3 700	(14, 2, 0.076)	95.407 6	96.175 2	(13, 0.072)	96.708 8	97.084 8
4 300	(13, 2, 0.075)	100.021 1	100.518 2	(12, 0.069)	101.351 0	101.962 3
4 900	(13, 2, 0.065)	105.338 9	105.760 6	(12, 0.066)	106.364 0	106.226 3
5 500	(11, 3, 0.058)	109.960 4	110.274 5	(12, 0.06)	110.598 0	110.331 6

新窗口打开| 下载CSV

由1.1节可知,当质量检验次数超出阈值M时进行基于状态的更新,因此可将模型1中M与T的乘积视为时间维度上的延迟更新阈值,此时基于状态的更新可描述为:一旦初次识别系统缺陷状态后的运行时间达到MT就进行预防更新.由表4可知,随着C_F取值的增加,两个模型得到的最优检测周期T^*随C_F的增加阶梯型下降,最优质量控制阈值 $R_{P}^{*}$ 随C_F的增加逐渐减小,这说明 $R_{P}^{*}$ 对C_F的敏感程度强于T^*对C_F的敏感程度;随着C_F的增大,逐渐缩短检测周期,降低质量控制阈值,以减少故障的发生,这与实际情况相符.除此之外,C_F增加时,模型1中最优状态维修阈值M^*呈现出阶梯型上升的趋势,以使时间维度上的延迟更新阈值M^*T^*能够保持在一定水平,进而减少过度维修现象的发生.

同时由表4可以看出,最优解下两个模型的拟合值c(T^*, M^*, $R_{P}^{*}$ )、c(T^*, $R_{P}^{*}$ )与实际值C(T^*, M^*, $R_{P}^{*}$ )、C(T^*, $R_{P}^{*}$ )相差很小,证明了采用响应曲面法拟合、求解模型的有效性与正确性;相同C_F值下,模型1的最优平均费用率始终低于模型2的最优平均费用率,进一步验证了所提联合策略的有效性和可行性.

5 结语

对关键生产系统的质量控制、状态维修与备件订购进行了联合建模与优化.利用两阶段延迟时间故障过程刻画系统的退化过程,并认为系统状态与产品质量相关:系统处于正常状态时,次品率保持不变;系统处于缺陷状态时,次品率是关于缺陷状态持续时间的单调递增函数.以检测初次识别系统缺陷的时间点为基准划分系统退化的前后期,设计了在系统退化初期检查系统状态,而在退化后期检查产品质量的两阶段检测策略.为了降低系统故障率、避免系统过度维修,提出将系统状态检测信息和产品质量检验信息同时作为预防性维修决策的依据.以检测周期、状态维修阈值和质量控制阈值为决策变量,建立了有限时域内的平均费用率模型,并设计离散仿真算法对模型快速近似求解.通过与传统的仅考虑质量控制的预防性维修与备件订购联合策略对比,实验分析结果表明,在既定参数下本文所提的质量控制、状态维修与备件订购联合策略能够有效降低运营成本.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

ALASWAD

, XIANG

A review on condition-based maintenance optimization models for stochastically deteriorating system

[J]. Reliability Engineering & System Safety, 2017, 157: 54-63.

DOI:10.1016/j.ress.2016.08.009 URL [本文引用: 1]

[2]

AZIMPOOR

, TAGHIPOUR

Joint inspection and product quality optimization for a system with delayed failure

[J]. Reliability Engineering & System Safety, 2021, 215: 107793.

DOI:10.1016/j.ress.2021.107793 URL [本文引用: 5]

[3]

WANG

H Y

, WANG

W B

, PENG

A two-phase inspection model for a single component system with three-stage degradation

[J]. Reliability Engineering & System Safety, 2017, 158(2): 31-40.

DOI:10.1016/j.ress.2016.10.005 URL [本文引用: 1]

[4]

ALBERTI

A R

, FERREIRA

NETO W A

, CAVALCANTE

C A V

, et al.

Modelling a flexible two-phase inspection-maintenance policy for safety-critical systems considering revised and non-revised inspections

[J]. Reliability Engineering & System Safety, 2022, 221: 108309.

DOI:10.1016/j.ress.2021.108309 URL [本文引用: 1]

[5]

刘勤明, 李永朋, 叶春明.

基于三阶段时间延迟模型的设备预防维修策略

[J]. 控制与决策, 2020, 35(7): 1780-1786.

[本文引用: 1]

LIU

Qinming

, LI

Yongpeng

, YE

Chunming

Preventive maintenance plan of equipment based on three-stage time delay model

[J]. Control and Decision, 2020, 35(7): 1780-1786.

[本文引用: 1]

[6]

YANG

, YE

Z S

, LEE

C G

, et al.

A two-phase preventive maintenance policy considering imperfect repair and postponed replacement

[J]. European Journal of Operational Research, 2019, 274(3): 966-977.

DOI:10.1016/j.ejor.2018.10.049 URL [本文引用: 1]

[7]

ZHANG

F X

, SHEN

J Y

, LIAO

H T

, et al.

Optimal preventive maintenance policy for a system subject to two-phase imperfect inspections

[J]. Reliability Engineering & System Safety, 2021, 205: 107254.

DOI:10.1016/j.ress.2020.107254 URL [本文引用: 1]

[8]

杨志远, 赵建民, 程中华, 等.

多元退化系统维修与备件订购策略优化模型

[J]. 上海交通大学学报, 2021, 55(7): 858-867.

DOI:10.16183/j.cnki.jsjtu.2019.221 [本文引用: 1]

针对具有多个相关退化过程系统的状态维修及备件订购决策问题,在连续监测条件下,建立系统维修与备件订购决策优化模型.首先,采用Gamma过程和Copula函数建立系统多元退化模型,然后提出基于控制限策略的系统维修与备件订购策略.在此基础上,考虑系统退化量对维修费用的影响,获得系统长期运行条件下的期望维修费用率解析表达式.同时为简化模型计算,提出系统期望维修费用率近似表达式.利用人工蜂群算法在费用准则下获得系统最优预防性更换阈值和备件订购阈值.案例分析结果说明了在维修决策中考虑退化相关的必要性.与已有策略相比,综合优化预防性更换和备件订购阈值能够有效降低系统维修费用.

YANG

Zhiyuan

, ZHAO

Jianmin

, CHENG

Zhonghua

, et al.

Optimization model of maintenance and spare parts ordering policy in multivariate degradation system

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(7): 858-867.

[本文引用: 1]

[9]

YAN

, LEI

Y G

, WANG

, et al.

Joint maintenance and spare parts inventory optimization for multi-unit systems considering imperfect maintenance actions

[J]. Reliability Engineering & System Safety, 2020, 202: 106994.

DOI:10.1016/j.ress.2020.106994 URL [本文引用: 1]

[10]

PATER

I D

, MITICI

Predictive maintenance for multi-component systems of repairables with Remaining-Useful-Life prognostics and a limited stock of spare components

[J]. Reliability Engineering & System Safety, 2021, 214: 107761.

DOI:10.1016/j.ress.2021.107761 URL [本文引用: 1]

[11]

赵斐, 刘学娟.

考虑不完美维修的定期检测与备件策略联合优化

[J]. 系统工程理论与实践, 2017, 37(12): 3201-3214.

DOI:10.12011/1000-6788(2017)12-3201-14 [本文引用: 2]

针对退化过程服从三阶段故障过程的单部件系统提出了定期检测与备件订购策略联合优化.该策略下，根据检测时系统的状态执行不同的维修活动：当系统处于正常状态，不执行任何维修活动；若识别轻缺陷进行不完美维修并采用比例役龄回退模型描述不完美维修效果；若识别严重缺陷则更换系统.当更换系统时需考虑备件状态：若处于存货状态则立即更换，若正处于途中则到货时更换，若未订货需立即订货并在到货时刻更换.考虑所有更新事件采用更新报酬理论建立以最小化单位时间内期望成本为目标的模型，同时优化检测周期和订货点.最后，设计枚举优化算法和离散仿真算法求解模型，并在算例分析中验证模型的有效性和适用性.

ZHAO

Fei

, LIU

Xuejuan

Joint optimization of periodical inspection and spare parts policies considering imperfect maintenance

[J]. Systems Engineering-Theory & Practice, 2017, 37(12): 3201-3214.

[本文引用: 2]

[12]

韩梦莹, 杨建华.

考虑不完美检测的两阶段点检与备件订购策略联合优化

[J]. 运筹与管理, 2021, 30(3): 27-34.

DOI:10.12005/orms.2021.0071 [本文引用: 2]

针对设备维修与备件管理相互影响与制约的问题, 在基于延迟时间理论的基础上, 提出了两阶段点检与备件订购策略联合优化。点检是不完美的, 当点检识别设备的缺陷状态时, 进行预防更新; 设备故障时, 进行故障更新。结合设备更新时备件的状态, 采用更新报酬理论建立了以第一阶段点检时间、第二阶段点检周期和备件订购时间为决策变量, 以最小化单位时间期望成本为目标的模型。最后, 通过人工蜂群算法对模型求解, 并在数值分析中将两阶段点检策略与定期点检策略进行比较, 结果表明:两阶段点检策略始终优于定期点检策略, 验证了所建模型的有效性。

HAN

Mengying

, YANG

Jianhua

Joint optimization of two-phase inspection and spare parts ordering policies considering imperfect inspection

[J]. Operations Research and Management Science, 2021, 30(3): 27-34.

DOI:10.12005/orms.2021.0071 [本文引用: 2]

In line with the fact that equipment maintenance and spare parts management affect and restrict each other, this paper proposes a joint optimization model of two-phase inspection and spare parts ordering policy considering imperfect inspections based on the delay time theory. The inspection is imperfect, and preventive renewal needs to be carried out once a defect is detected; failure renewal should be performed when the equipment is at fault. With the consideration of the states of the spare parts when the equipment is required to be renewed, the joint optimization model is established based on the renewal reward theory, in which the minimal long-run expected cost per unit time is taken as objective function to optimize the first phase inspection time, the second phase inspection interval and the spare parts ordering time. Finally, an artificial bee colony algorithm is developed to find the optimal solution. The two-phase inspection policy is compared with the periodical inspection policy in the numerical analysis and the results show that the two-phase inspection policy is always superior to the periodical inspection policy; and the effectiveness of the proposed model is verified.

[13]

ZHAO

, XIE

F F

, SHI

C H

, et al.

A joint inspection-based preventive maintenance and spare ordering optimization policy using a three-stage failure process

[J]. Complexity, 2017, 2017: 1-19.

[本文引用: 2]

[14]

ZHAO

. LIU

X J

. PENG

, et al.

Joint optimization of inspection and spare ordering policy with multi-level defect information

[J]. Computers and Industrial Engineering, 2020, 139: 106205.

DOI:10.1016/j.cie.2019.106205 URL [本文引用: 2]

[15]

ZHAO

Y X

, HE

Y H

, ZHOU

, et al.

Functional risk-oriented integrated preventive maintenance considering product quality loss for multistate manufacturing systems

[J]. International Journal of Production Research, 2021, 59(4): 1003-1020.

DOI:10.1080/00207543.2020.1713416 URL [本文引用: 2]

[16]

S M

, WANG

W B

Optimal inspection policy for three-state systems monitored by control charts

[J]. Applied Mathematics and Computation, 2011, 217(23): 9810-9819.

DOI:10.1016/j.amc.2011.04.075 URL [本文引用: 1]

[17]

HAN

M Y

, YANG

J H

, ZHAO

Joint optimization of inspection, maintenance, and spare ordering policy considering defective products loss

[J]. Journal of Systems Engineering and Electronics, 2021, 32(5): 1167-1179.

DOI:10.23919/JSEE.2021.000100 [本文引用: 1]

This paper proposes a joint inspection-based maintenance and spare ordering optimization policy that considers the problem of integrated inspection, preventive maintenance, spare ordering, and quality control for a four-state single-unit manufacturing system. When an inspection detects a minor defect, a second phase inspection is initiated and a regular order is placed. Product quality begins to deteriorate when the system undergoes a severe defect. To counter this, an advanced replacement of the minor defective system is carried out at the $J{\rm{th}}$ second phase inspection. If a severe defect is recognized prior to the $J{\rm{th}}$ inspection, or if system failure occurs, preventive or corrective replacement is executed. The timeliness of replacement depends on the availability of spare. We adopt two modes of ordering: a regular order and an emergency order. Meanwhile, a threshold level is introduced to determine whether an emergency order is preferred even when the regular order is already ordered but has not yet arrived. The optimal joint inspection-based maintenance and spare ordering policy is formulated by minimizing the expected cost per unit time. A simulation algorithm is proposed to obtain the optimal two-phase inspection interval, threshold level and advanced replacement interval. Results from several numerical examples demonstrate that, in terms of the expected cost per unit time, our proposed model is superior to some existing models.

[18]

赵斐, 康建设, 王雷震, 等.

考虑非周期检测的视情维修与备件订购联合策略优化

[J]. 运筹与管理, 2021, 30(9): 31-37.

DOI:10.12005/orms.2021.0276 [本文引用: 1]

针对单部件系统/关键部件提出视情维修与备件订购联合策略,其中系统退化服从两阶段延迟时间过程且采用非周期检测策略,退化初期以检测间隔T1检查系统状态,而在第一次识别缺陷状态时,缩短检测周期为T2、订购备件且进行不完美维修;若系统在随后的退化中被识别处于缺陷状态,执行不完美维修直至超过阈值次数Nmax并采取预防性更换,但若在检测周期内发生故障则进行更换。根据系统状态和备件状态分析各种可能更新事件及相应的联合决策,利用更新报酬理论构建最小化单位时间内期望成本的目标函数,优化T1,T2, Nmax。与对比模型策略相比,算例结果表明所提出的联合策略能有效降低单位时间内的期望成本。

ZHAO

Fei

, KANG

Jianshe

, WANG

Leizhen

, et al.

Joint policy optimization of condition-based maintenance and spare ordering considering non-periodic inspection

[J]. Operations Research and Management Science, 2021, 30(9): 31-37.

DOI:10.12005/orms.2021.0276 [本文引用: 1]

A jointly policy of condition-based maintenance (CBM) and spare ordering is proposed for a single-unit system/critical component subject to a two-stage delay-time process. A non-periodic inspection policy with various intervals is presented, in which the system is detected with the relatively longer interval T1 during the initial deterioration process, but with a shorted interval T2 after the defective state is firstly found by an inspection. While, the spare is ordered and imperfect maintenance (IPM) is carried out. In the subsequent deterioration process, IPM is required and performed once the defective state is revealed until the number of IPM exceeds the threshold Nmax; then, a preventive replacement is needed. If a failure occurs within the inspection interval, a corrective replacement arises. According to the system's state and the spare's availability, all possible renewal events and the corresponding joint decisions are discussed and then the objective function to minimize the expected cost per unit time is established using the renewal award theorem for optimizing T1,T2, Nmax. The results fromthe numerical example indicate that the proposed policy decreases the expected cost per unit time compared to the comparative models.

A review on condition-based maintenance optimization models for stochastically deteriorating system

2017

... 基于状态的维修策略可以根据状态检测或监测收集到的信息建议维修活动,常被应用于实践中^[1].维修活动导致备件需求,备件是维修活动能够顺利执行的重要保障,二者相互影响与制约.对于关键生产系统(单部件系统)而言,系统的功能退化不仅是引发维修需求的根源,而且是导致产品质量下降的最主要原因^[2].因此,根据关键生产系统的功能退化过程,确定质量控制、状态维修及与之匹配的备件订购策略,对于提升产品质量、提高设备可靠性、降低运营成本有积极意义. ...

Joint inspection and product quality optimization for a system with delayed failure

2021

... 对生产企业而言,质量控制和设备维护这两项运营策略必须相互协作以确保生产过程的产出率^[15].上述研究虽然为设备维护以及设备维护与备件订购联合策略优化分析提供了基本框架,但并未考虑系统劣化对产品质量的影响.鉴于此,Wu等^[16]利用统计过程控制图监控产品质量,以确定最优的检测策略;Azimpoor等^[2]以产品质量评估系统状态,认为次品率为某一固定常数时,系统处于正常状态,而当次品率超出该固定值时,说明系统已进入缺陷状态,应立即进行预防性更换,据此优化检测周期和产品质量;Han等^[17]基于DTM构建了考虑缺陷品损失的状态维修与备件订购联合策略优化模型,但并未考虑产品质量的控制问题. ...

... 综上,现有基于DTM的质量控制、设备维护和备件订购联合决策研究,在理论与实际应用层面尚存在以下3个方面的局限性:① 产品质量、系统维修与备件管理3个要素之间存在密切联系,但鲜有文献同时考虑质量控制、状态维修与备件订购,对三者进行整合研究;② 在系统状态与产品质量相关时,一旦次品率超出前期固定水平就进行预防性更换^[2],易导致过度维修;③ 备件订购提前期假定为固定常数,实际上由于受多种因素的影响,备件订购之后的交付期具有随机性特征^[18].针对这些不足,本文将状态检测信息和质量检验信息作为互补,进行预防性维修决策,针对退化过程服从延迟时间理论的关键生产系统,提出质量控制、状态维修与备件订购联合策略. ...

... 将本文所建的质量控制、状态维修与备件订购联合策略模型记为模型1.仅考虑质量控制的预防性维修^[2]策略模型中,假定一旦次品率超出阈值β₁就进行预防性更换,决策变量仅为检测周期.为与模型1进行比较,将文献[2]中基于产品质量的维修策略进行扩展,假定在次品率超出阈值R_P(决策变量)时,进行预防性更换,在此基础上,提出对比模型2.模型2与模型1的不同之处在于:前者未考虑基于状态的更新策略.因此,模型2中不会出现事件5,将模型1中的

C_{T, n}^{5, h}

和

L_{T, n}^{5, h}

(h=1, 2)设为0,其余公式保持不变,便可得到模型2的目标函数与约束条件,如下式所示: ...

... 就进行预防性更换,决策变量仅为检测周期.为与模型1进行比较,将文献[2]中基于产品质量的维修策略进行扩展,假定在次品率超出阈值R_P(决策变量)时,进行预防性更换,在此基础上,提出对比模型2.模型2与模型1的不同之处在于:前者未考虑基于状态的更新策略.因此,模型2中不会出现事件5,将模型1中的

C_{T, n}^{5, h}

和

L_{T, n}^{5, h}

(h=1, 2)设为0,其余公式保持不变,便可得到模型2的目标函数与约束条件,如下式所示: ...

A two-phase inspection model for a single component system with three-stage degradation

2017

... 延迟时间模型(Delay-Time Model, DTM)由于能够建立系统状态与维修活动之间的关系,已被广泛应用于离散劣化系统的状态维修策略模型中^[3-4].如,刘勤明等^[5]建立了基于周期检测的单位时间费用模型,优化检测周期和预防性维修阈值;Yang等^[6]将基于状态的不完美维修策略与基于时间的预防更换策略相结合,优化检测周期、检测次数和预防性更换周期;Zhang等^[7]则构建了优化两阶段检测周期和次数的预防性维修模型.将设备维修与备件管理策略进行联合优化,确保维修时刻备件的可得率已被国内外许多学者提出并研究^[8⇓-10],近年来,利用DTM对状态维修与备件订购策略进行联合优化的研究也逐渐增多.如,赵斐等^[11]与韩梦莹等^[12]构建了基于时间的备件订购与状态维修联合策略模型;Zhao等^[13-14]则提出了基于系统状态的备件订购策略,建立了非周期检测与备件订购联合策略优化模型. ...

Modelling a flexible two-phase inspection-maintenance policy for safety-critical systems considering revised and non-revised inspections

2022

基于三阶段时间延迟模型的设备预防维修策略

2020

Preventive maintenance plan of equipment based on three-stage time delay model

2020

A two-phase preventive maintenance policy considering imperfect repair and postponed replacement

2019

Optimal preventive maintenance policy for a system subject to two-phase imperfect inspections

2021

多元退化系统维修与备件订购策略优化模型

2021

Optimization model of maintenance and spare parts ordering policy in multivariate degradation system

2021

Joint maintenance and spare parts inventory optimization for multi-unit systems considering imperfect maintenance actions

2020

Predictive maintenance for multi-component systems of repairables with Remaining-Useful-Life prognostics and a limited stock of spare components

2021

考虑不完美维修的定期检测与备件策略联合优化

2017

... 系统退化过程服从延迟时间理论,即系统由初始新状态退化到故障状态要经历正常阶段和缺陷阶段,其中X和Y分别表示正常阶段和缺陷阶段持续时间的随机变量,如图1所示.系统的状态空间也因此被划分为:正常、缺陷和故障.系统退化的两个阶段由Weibull分布来描述^{[11⇓⇓⇓-15]},Weibull分布的故障率函数为h(t)=απ(αt)^π^-1(α>0,π>0,t≥0),其中α为尺度参数,π为形状参数,t为时间随机变量. ...

Joint optimization of periodical inspection and spare parts policies considering imperfect maintenance

2017

考虑不完美检测的两阶段点检与备件订购策略联合优化

2021

Joint optimization of two-phase inspection and spare parts ordering policies considering imperfect inspection

2021

A joint inspection-based preventive maintenance and spare ordering optimization policy using a three-stage failure process

2017

Joint optimization of inspection and spare ordering policy with multi-level defect information

2020

Functional risk-oriented integrated preventive maintenance considering product quality loss for multistate manufacturing systems

2021

Optimal inspection policy for three-state systems monitored by control charts

2011

Joint optimization of inspection, maintenance, and spare ordering policy considering defective products loss

2021

考虑非周期检测的视情维修与备件订购联合策略优化

2021

Joint policy optimization of condition-based maintenance and spare ordering considering non-periodic inspection

2021

〈

〉