上海交通大学学报

上海交通大学学报, 2024, 58(2): 156-165 doi: 10.16183/j.cnki.jsjtu.2022.316

船舶海洋与建筑工程

基于人工神经网络的极地船舶冰阻力预报方法

孙乾洋1, 周利,2, 丁仕风1, 刘仁伟1, 丁一1

1.江苏科技大学 船舶与海洋工程学院,江苏 镇江 212100

2.上海交通大学 船舶海洋与建筑工程学院,上海 200240

An Artificial Neural Network-Based Method for Prediction of Ice Resistance of Polar Ships

SUN Qianyang1, ZHOU Li,2, DING Shifeng1, LIU Renwei1, DING Yi1

1. School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212100, Jiangsu, China

2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 周 利,教授,博士生导师;E-mail:zhouli209@hotmail.com.

责任编辑: 王一凡

收稿日期: 2022-08-19   修回日期: 2023-02-17   接受日期: 2023-02-20  

基金资助: 国家重点研发计划(2022YFE0107000)
国家自然科学基金面上项目(52171259)
工信部高技术船舶科研项目(工信部重装函[2021]342号)

Received: 2022-08-19   Revised: 2023-02-17   Accepted: 2023-02-20  

作者简介 About authors

孙乾洋(1995-),博士生,主要从事冰载荷方面的研究.

摘要

极地船舶冰区航行时,冰阻力的准确预报在保障船舶航行安全方面起着重要作用.近年来,机器学习在船舶方面的应用越来越广泛,其中,人工神经网络(ANN)是机器学习领域中一种常用的方法.本文的重点是设计一个用于预报极地船舶冰阻力的ANN模型.参考传统的经验和半经验公式,选择合适的输入特征参数,通过大量的船舶模型试验数据来训练神经网络,搭建径向基(RBF)神经网络模型,并选用遗传算法(GA)进行模型优化.研究表明,基于7个特征参数输入的遗传算法优化径向基(RBF-GA)神经网络模型具有良好的泛化效果,与模型试验和实船试验数据对比,平均误差在8%左右,具有较高的精度,可作为冰阻力预报工具.

关键词： 冰阻力; 机器学习; 径向基函数神经网络; 遗传算法; 船舶试验

Abstract

Accurate prediction of ice resistance plays an important role in ensuring the safety of ship sailing in polar navigation in ice areas. In recent years, machine learning has been widely used in the field of ships, among which artificial neural network (ANN) is a common method. The focus of this paper is to design an ANN model for predicting the ice resistance of polar ships. According to the traditional empirical and semi-empirical formula, appropriate input characteristic parameters are selected. The radial basis function (RBF) neural network model is built based on a large number of ship model test data, and the genetic algorithm (GA) is used to optimize the model. The research shows that the radial basis function neural network model optimized by genetic algorithm (RBF-GA) based on seven characteristic parameters input has good generalization effect. Compared with the model test and full-scale test data, the average error is about 8%, which shows that the RBF-GA model has a high accuracy, and can be used as a tool for ice resistance prediction.

Keywords： ice resistance; machine learning; radial basis function (RBF) neural network; genetic algorithm (GA); ship test

PDF (1823KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

孙乾洋, 周利, 丁仕风, 刘仁伟, 丁一. 基于人工神经网络的极地船舶冰阻力预报方法[J]. 上海交通大学学报, 2024, 58(2): 156-165 doi:10.16183/j.cnki.jsjtu.2022.316

SUN Qianyang, ZHOU Li, DING Shifeng, LIU Renwei, DING Yi. An Artificial Neural Network-Based Method for Prediction of Ice Resistance of Polar Ships[J]. Journal of Shanghai Jiaotong University, 2024, 58(2): 156-165 doi:10.16183/j.cnki.jsjtu.2022.316

随着全球气候变化和冰川融化,北极航线的开放时间更长,极地航运和资源开发已成为国际上关注的焦点问题,吸引了越来越多的关于极地船舶冰区航行的研究工作.其中,准确预报冰阻力是科学评价船舶极地航行能力的重要指标,能够有效提高航行安全.由于船舶破冰是一种复杂的非线性动态响应过程,以及海冰本构模型的复杂性,所以国内外还没有一种准确且被广泛使用的冰阻力预报方法.

在冰阻力研究中,需要深刻地理解冰况、船体几何形状和船-冰作用过程.目前冰阻力计算方法主要有经验和半经验公式方法、冰池模型试验、全尺度试验方法、数值分析方法,其中最可靠的是冰池模型试验和全尺度试验,但它们既昂贵又耗时.数值分析是计算冰阻力的一种很好的替代方法,但它依赖于对船-冰相互作用机理的理解[1],往往会对一些条件进行简化和假设,从而对分析结果产生影响.常用的方法是经验半经验公式方法,但每种经验半经验公式都有其各自的适用范围、应用背景和基本假定,因此,在某些情况下,与模型试验对比,其计算误差高达40%[2].此外,大多数经验半经验公式将总阻力划分为不同的分量来预测平整冰作用下的阻力,关于冰道中有碎冰的阻力研究较少,因此,需要一种新的具有较高精度的模型来进行冰阻力预报.

近年来,机器学习方法被广泛应用于海洋工程领域中,其中,人工神经网络(ANN)方法在许多领域中得到了应用,相较于回归模型和其他统计方法,ANN具有更好的灵活性和泛化效果,能更好地处理复杂非线性问题.本文参考传统经验半经验公式,选取合适的输入特征量,以船舶模型试验数据为ANN模型的训练数据,对训练数据进行数据预处理和皮尔逊相关性分析,构建径向基(RBF)模型并用遗传算法(GA)进行网络优化.将实船试验和模型试验作为验证对象,与RBF和遗传算法优化径向基(RBF-GA)神经网络模型预报结果进行对比分析.

1 冰阻力预报方法

1.1 人工神经网络

自动分析建模的机器学习方法可用于处理复杂非线性问题,例如函数近似、分类和回归,ANN是机器学习领域中一种常用的方法.ANN是模仿人类思维的一种方式,是以工程技术手段模拟人脑神经网络结构和功能特征的系统,从本质上讲,它是一个大规模并行的非线性动态系统[3].虽然单个神经元结构简单,功能有限,但由多个神经元组成的网络系统具有良好的泛化能力.ANN由一组算法组成,这些算法通过输入数据集进行训练,以找出目标问题的最优假设函数,它已被证实是解决高维度非线性问题的一种可行和实用的方法.输入特征量(如船长和冰厚等)的数量对输出结果的可靠性有着重要影响,其数量越多,代表着训练模型的稳定性越好,但在选择特征量时,重点是要在方差和偏差之间建立良好的平衡,以便为预测提供良好的泛化效果.

ANN方法近年来得到了快速发展,已成功应用于许多工程领域,在海洋工程领域的应用相对新颖,研究人员正在探索将其应用于解决不同问题.Koushan[4]应用ANN方法预测船舶阻力和湿表面积,并使用多个拖曳试验结果验证了该模型.Couser等[5]成功地使用ANN预测双体船的船体阻力.Cui等[6]开发了一种基于机器学习的船舶设计优化方法.Yang等[7]提出了一种基于RBF算法的集装箱船阻力预报模型,用于预测集装箱船在不同吃水下的阻力.陈爱国等[8]以60艘船舶模型试验为数据集,提出了一种基于ANN方法的船舶阻力预报模型.张乔宇等[9]提出了一种基于经典机器学习回归预测模型,以预报船舶阻力.Kim等[10]介绍了一种基于ANN的冰阻力预报方法,用于预测船舶在平整冰中的航行阻力.Islam[11]提出了一种机器学习技术,用于船舶在敞水和冰上性能预测.Zhang等[12]提出了一种可解释的ANN冰阻力预报模型,在此基础上开展了冰厚和船速分布的统计分析工作,将冰阻力预报ANN模型应用于评估船舶在冰雪覆盖水域的运行情况.目前,基于ANN方法的冰阻力预报研究相对较少,在已有的研究中,冰阻力预报精度在一定范围内都比较准确.然而,要获得一个更先进、预测误差更低的模型,还有很多需要研究的内容.

要建立一个可靠的极地船舶冰阻力预报模型,必须具有良好的非线性映射能力、泛化能力和高效的计算能力.RBF神经网络是一种三层前向神经网络[13-14],其学习收敛速度快,能够快速逼近任意非线性函数,因此RBF神经网络已被广泛应用于函数逼近、模式识别和非线性控制等领域.

1.2 冰阻力经验公式

为了建立一个可靠的冰阻力预报模型,选择合适的神经网络输入参数至关重要,目前6种常用的半经验公式可以为模型的输入特征选择提供重要依据.为了选择合适的神经网络输入特征,研究了半经验公式中使用的参数.根据6种常用的半经验公式,讨论了一些影响冰阻力的主要参数:

(1) Lewis等[15]总结了“风”级破冰船在冰海中航行的实船试验、 “风”级破冰船的模型试验、M-5和M-9船舶在淡水冰中的模型试验以及在盐水冰中的试验的冰阻力数据.根据这些数据,提出了冰阻力预报公式,假定为船速、冰厚度、冰密度和冰弯曲强度的函数.

(2) Vance[16]根据USCG Katmai Bay的全尺度试验,开发了一套与船舶长度和宽度相关的最佳回归方程,以预测破冰船航行阻力.

(3) Zahn等[17]通过USCG Mobile Bay全尺度试验,提出了冰阻力公式.阻力是船舶主尺度和冰厚的函数.

(4) Lindqvist[18]根据在波的尼亚海湾进行的实船试验开发了冰阻力预报公式,冰阻力分力主要分为破碎、弯曲和浸没,公式表示为船舶主尺度、船体形状系数、冰厚、冰摩擦系数和冰弯曲强度的函数.

(5) Riska等[19]通过更新Ionov[20]和Lindqvist[18]的方程,提出了平整冰的阻力预测公式.这些方程式基于一组经验系数,这些系数来自波罗的海多艘船舶的全尺寸试验.该公式显示了冰阻力与船速之间的线性关系.

(6) 考虑到5艘破冰船,Keinonen等[21]也进行了冰阻力预测研究.这些公式与船舶尺寸、船型、冰弯曲强度和环境温度等条件有关.

上述6个公式很好地说明了影响冰阻力的主要因素,主要参数如表1所示.

表1   经验和半经验公式主要参数

Tab.1  Main parameters of empirical and semi-empirical formula

类别参数Lewis等[15]Vance[16]Zahn等[17]Lindqvist[18]Riska等[19]Keinonen等[21]
船舶参数船长/m√√√√√
船宽/m√√√√√√
吃水/m√√√
首柱倾角/(°)√√
水线角/(°)√
船速/(m·s-1)√√√√√√
冰参数冰厚/m√√√√√√
弯曲强度/kPa√√√√√
弹性模量/kPa√
雪厚/m√

新窗口打开| 下载CSV


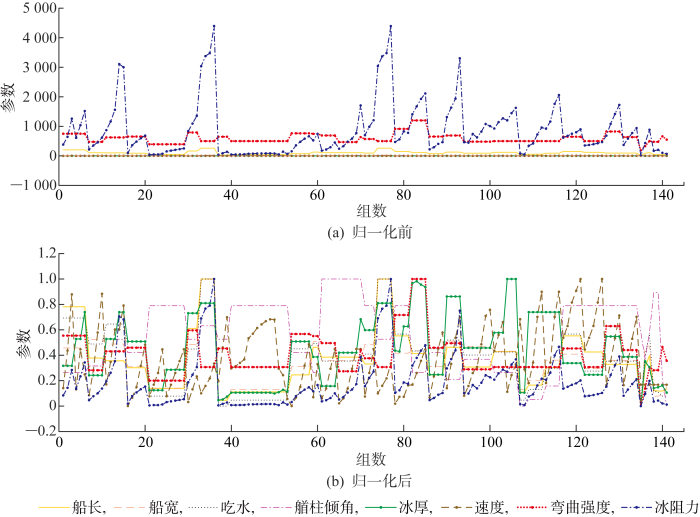
从表中可以看出,船长、船宽、船速、冰厚和弯曲强度被各经验半经验公式广泛采用,而水线角、弹性模量和雪厚采用较少.结合参数在模型试验和实船试验中出现的频次,且ANN本身不受输入特征物理特性的影响,本研究选取7个特征参数输入,分别为:船长、船宽、吃水、首柱倾角、船速、冰厚和弯曲强度,输出为冰阻力.对特征输入和冰阻力之间进行皮尔逊相关系数分析,并对数据集进行归一化处理.

2 神经网络训练的数据库和特征

2.1 数据集准备

在搭建可靠的ANN模型时,数据集尤为重要.为确保模型的预报质量,充分和全面的数据准备是前提.由于全尺度试验数据较少,本研究选取来自18个不同的模型试验中140余组数据作为数据集,其中数据集分为训练集和验证集,分割比例为 8∶2,相关论文研究和船舶[1-2,22⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]如表2所示.所有训练数据根据给定的比例因子λ放大到全尺度,模型试验数据换算到全尺度的相似关系,如表3所示[35].

表2   冰阻力预报模型数据集来源

Tab.2  Source of data set of ice resistance prediction model

船名来源冰况
Ferry NB550文献[22]平整冰
CCGS (Terry Fox)文献[23]平整冰
USCGC (Healy)平整冰
Korean RV (Araon)平整冰
ICE BREAKER PSV(KS1654)文献[24]平整冰
MV Arctic文献[25]平整冰
Polar Star平整冰
Japanese Model Ship平整冰
Terry Fox平整冰
PM Teshio平整冰
R-Class平整冰
Healy平整冰
SA-15平整冰
Korean RV (Araon)文献[26]碎冰
Terry Fox文献[27]碎冰
An artic tanker文献[28]平整冰
Icebreaking cargo vessel文献[29]碎冰
Korean RV (Araon)文献[30]碎冰
MT Uikku文献[31]平整冰
MT Uikku文献[1]平整冰
MT Uikku文献[2]平整冰
Korean RV Araon文献[32]平整冰
Arctic PSV平整冰
Icebreaking cargo vessel文献[33]碎冰
A new icebreaker of China文献[34]平整冰

新窗口打开| 下载CSV


表3   冰区船舶建模的相似性关系[35]

Tab.3  Similarity relations for modeling vessels in ice areas[35]

参数比例系数
船长λ
船宽λ
吃水λ
首柱倾角1
船速λ1/2
水线角1
冰厚λ
弯曲强度λ
冰密度1
摩擦系数1
冰阻力λ

新窗口打开| 下载CSV


理想情况下,船舶全尺度试验是确定船舶冰阻力的最准确、可靠的方法.但由于其昂贵性、耗时性以及不可重复性,所以,大多数情况下通过船舶模型试验进行替代.由于尺度效应,将模型试验数据转换为全尺度试验数据时会存在一定的误差性.Schwarz[36]比较了破冰船CCGS FRANKLIN号模型试验和全尺度试验的冰阻力,结果表明,误差在8%以内,模型试验可用于船舶初步设计.因此,本文选用船舶模型试验数据作为ANN数据集.

2.2 数据预处理

为了提高神经网络模型的收敛速度和预报精度,需要对特征量进行缩放,使维数保持在可比范围内,本研究使用归一化方法进行特征量缩放,使训练后得到的每个特征量权重处于同一尺度上.归一化公式如下,缩放后的特征量范围在[0,1]之间,数据集归一化前后对比如图1所示.从图1中可以看出,归一化前的输入输出特征值不在可比范围内,各特征量之间几乎互不影响,归一化后的各特征量之间是相互影响的.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   数据集归一化前后对比

Fig.1   Comparison of data sets before and after normalization


z'=z-zminzmax-zmin

式中:zmax和zmin分别为一个特征量的最大值和最小值;z和z'分别为归一化前后的数据.

为了量化输入特征量和输出之间的线性关系,引入皮尔逊相关系数ρx,y[37]:

　ρx,y=cov(x,y)σxσy=E((x-μx)(y-μy))σxσy=E(xy)-E(x)E(y)E(x2)-E2(x)E(y2)-E2(y)

式中: cov(x,y) 为变量x和y的协方差;μ为变量x和y的均值,其中x和y都是经过归一化的; σx和σy为x和y的标准偏差; E为数学期望.

表4给出了7个输入特征量和冰阻力之间的线性相关性.从表中可以看出,船宽、船长、吃水和冰厚与冰阻力之间高度相关,而首柱倾角和弯曲强度对冰阻力的依赖性相对较小,船速和冰阻力之间几乎没有相关性.

表4   特征选择和皮尔逊相关系数

Tab.4  Feature selection and Pearson correlation coefficient

类别特征取值ρx,y
船舶相关参数船速,v/kn0~110.056
船长,L/m26.155~259.20.630
船宽,B/m7.5~440.774
船舶吃水,T/m2.3~150.645
首柱倾角,ϕ/(°)19~35-0.178
冰相关参数冰厚,hi/m0.2~1.60.628
冰弯曲强度,σf/kPa392~1 2000.122

新窗口打开| 下载CSV


在船舶模型试验时,数据和参数的选择记录受试验本身环境的影响,一些因素可能会被理想化或忽略.例如,Lindqvist公式没有考虑破碎强度对冰阻力的影响,这对于破碎强度较低的波罗的海的冰况来说可能是合理的,但在其他海域的船舶全尺度试验中,当冰的破碎强度非常大时,总冰阻力可能会被低估.由于皮尔逊相关系数仅依赖于数据库,从表4中可以看出,船速和冰阻力之间的皮尔逊相关系数最小,这并不代表船速对冰阻力的影响最小,皮尔逊相关系数仅度量线性关系,即使相关系数为0,也可能存在有意义的关系.

3 神经网络模型训练

3.1 RBF神经网络

RBF神经网络属于前向神经网络[38],网络的输出是由输入和神经元参数组成的RBF函数的线性组合,其结构如图2所示.图中: ui和wij分别为输入到隐藏层、隐藏层到输出的权值; c1~cj为隐藏层神经元; ‖xp-ci‖为欧氏范数; xp为第p个输入样本; ci为高斯函数的中心;σ为高斯函数的方差.

图2

新窗口打开| 下载原图ZIP| 生成PPT

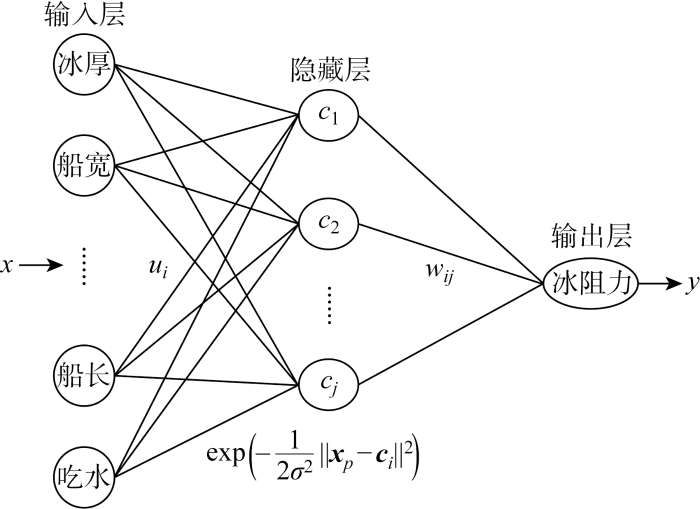
图2   RBF神经网络结构

Fig.2   Structure of RBF neural network


RBF神经网络的激活函数可以表示为

R(xp-ci)=exp-12σ2‖xp-ci‖2

式中: i=1,2,…,n, n为网络输出节点数.

输出层的表达函数为

yj=∑i=1hwijR(xp-cj),　j=1,2,…,n

式中: cj为网络隐含层结点的中心; wij为隐含层到输出层的连接权值; h为隐含层结点数;yj为输入样本对应的网络输出结点的实际输出.

RBF和RBF-GA模型的函数关系分别表示为

y1=W1exp-12σ12‖X-b1‖
σ1=1.403
W1=-0.0245-0.0248-0.0246-0.0248-0.0245-0.0247-0.0248-0.0253-0.0244-0.0248…,　b1=0.41730.04970.90270.94480.49090.48930.33770.90010.36920.1112

式中: W1是一组146×1的矩阵; b1是一组10×1的矩阵.

3.2 GA

GA是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法,其本质是一种高效、并行、全局搜索的方法,能在搜索过程中自动获取和积累有关搜索空间的信息,并自适应地控制搜索过程以求得最佳解.

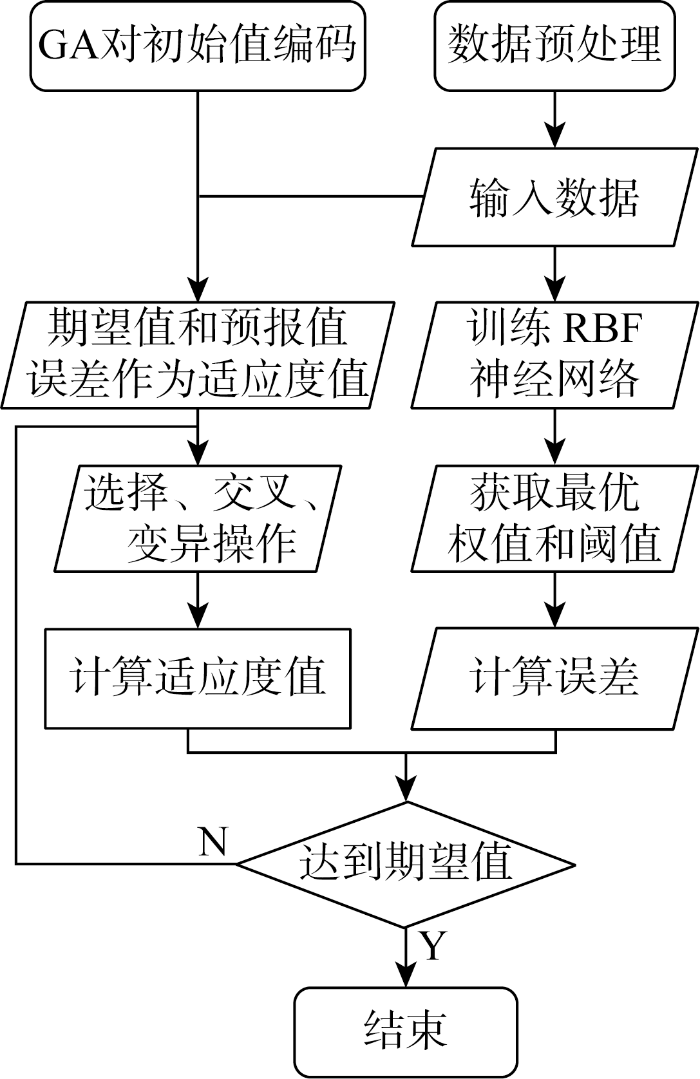
RBF-GA神经网络是用GA来优化RBF神经网络的初始权值和阈值,使优化后的RBF神经网络能更好地预测函数输出.RBF-GA神经网络包括种群初始化、适应度函数、选择操作、交叉操作和变异操作.在GA中,将问题的候选解用染色体表示,实现解空间向编码空间的映射,然后用随机数初始化一个种群,种群里的个体即为编码,根据个体得到RBF神经网络的初始权值和阈值,把网络预测输出和期望输出之间的误差绝对值和E作为个体适应度值F.用选择函数择优选择,让个体基因变异,产生子代,重复上述步骤,直到新种群的产生,其流程如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   GA流程图

Fig.3   Flow chart of GA


其中,适应度函数为

F=k∑i=1n|yi-oi|

式中: yi为RBF神经网络第i个节点的期望输出; oi为第i个节点的预报值;k为系数.

图4为GA优化过程汇总的最佳个体适应度值和GA优化RBF网络的预测误差.从图4(a)中可以看出,GA优化过程中,适应度值随着迭代次数的增加而快速减小,在迭代次数40以后趋于平缓,并在迭代次数为100时寻得最佳个体适应度值,其最大迭代次数为100.在图4(b)中,预测样本为从训练集中选取的30余组数据,其中,蓝色为实验值,橙色为预报值.可以看出,经过GA优化后的模型预报值与实验值较为接近,其预报值呈现出较高的准确性和可靠性.表5为RBF-GA的超参数值.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   GA优化过程

Fig.4   Optimization process of GA


表5   RBF-GA的超参数值

Tab.5  Hyperparametric value of RBF-GA

名称数值
激活函数Sigmoid
初始化粒子数100
最大迭代次数100
种群规模50
交叉概率0.1
变异概率0.2
个体长度10
最佳个体适应度0.7
学习率0.01
损失函数MSE

新窗口打开| 下载CSV


RBF-GA的函数关系如下:

y2=W2exp-12σ22‖X-b2‖
σ2=0.2
W2=0.79480.52050.74000.58820.3750…0.79480.52050.74000.58820.3750…0.79480.52050.74000.58820.3750…0.79480.52050.74000.58820.5620…0.79480.52050.74000.58820.5620…0.79480.52050.74000.58820.5620…0.79480.52050.74000.58820.7500…0.79480.52050.74000.58820.7500…0.79480.52050.74000.58820.7500…0.41400.57950.56670.61760.3087………………b2=0.32550.32550.32550.32550.32550.32550.32550.32550.32550.3255

式中: W2是一组146×7的矩阵; b2是一组10×1的矩阵.

4 试验数据验证

4.1 某极地破冰船(模型试验)

本节以一艘标准破冰船[39]为研究对象,该船的模型试验是在两种给定的冰厚条件下进行的,其冰厚分别为0.97 m和1.57 m.图5为按比例放大的冰阻力测量值和RBF、RBF-GA模型预测的冰阻力Rice.

图5

新窗口打开| 下载原图ZIP| 生成PPT

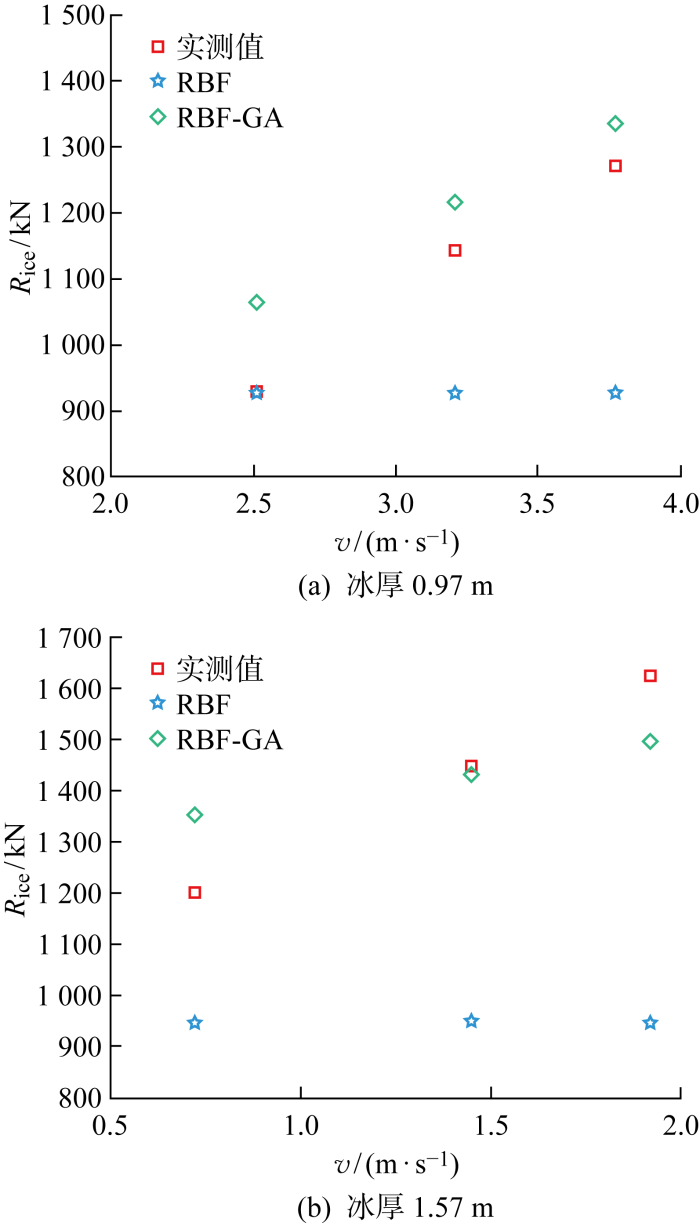
图5   在不同冰厚下的冰阻力模型预报

Fig.5   Ice resistance model prediction at different ice thicknesses


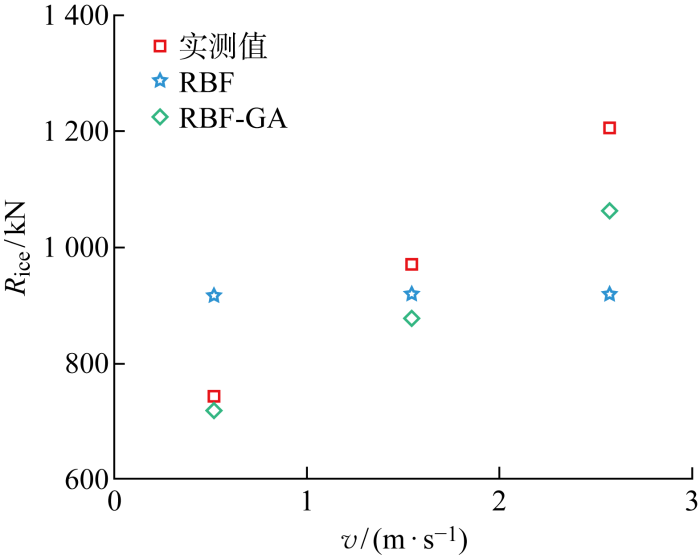
从图5中可以看出,RBF模型预报的冰阻力没有显著变化,RBF-GA模型预报结果随着船速的增加而增加.当冰厚为0.97 m时,RBF模型的预报值比测量值低得多,其平均误差为15.5%,RBF-GA模型的预报值比测量值偏高,其平均误差为8.6%.当冰厚为1.57 m时,RBF模型的预报值基本稳定在950 kN,其平均误差为32.5%,RBF-GA模型的预报值与实测值趋势一致,其平均误差为7.2%.可观察到,在不同的冰厚下,随着船速增加,RBF-GA 模型的预报误差约在8%,其与RBF模型相比,精度得到了明显的提高.

4.2 破冰船PSV(模型试验)

选用破冰船PSV的模型实验[40]数据进行预报分析,数据按比例放大到全尺度,预报结果如图6所示.从图6中可以看出,RBF-GA模型预报值与实测值最为接近,随着船速的增加,其预报值和实测值趋势一致,与实测值相比,平均误差为8.2%,当v=0.5 m/s时,两者结果基本一致.RBF模型在进行阻力预报时,随着船速的增加,其预报值基本不变,与实测值相比,平均误差为17.5%.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   基于ANN模型的破冰船PSV冰阻力预报

Fig.6   Ice resistance prediction of ice breaker PSV based on ANN model


4.3 Tor Viking II(实船试验)

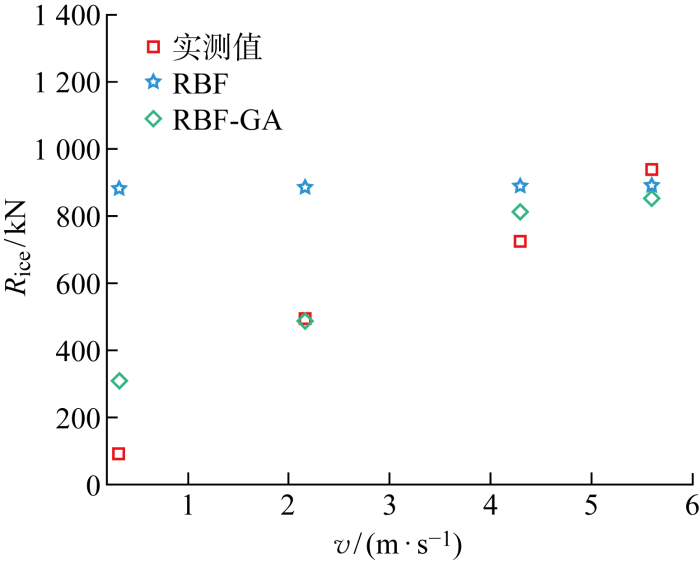
Tor Viking II是一艘多用途破冰船,以该船在波罗的海北部的试验[1]为例,将RBF、RBF-GA模型预报结果与测量值进行比较分析,如图7所示.从图7中可以看出,当v<0.5 m/s时,RBF和RBF-GA预报值是实测值的几倍之多,其原因可能在于训练样本集中,当v=0~0.5 m/s时,冰阻力数据过少,从而导致模型在预测船舶低速航行下的冰阻力时,产生了较大的偏差.随着船速的增加,两个模型预报值与实测值误差也随之减小,当v=2~6 m/s时,RBF模型预报值与实测值之间的平均误差为11.9%,RBF-GA模型预报值与实测值更为接近,平均误差为7.4%.随着船速的增加,RBF模型预报值几乎不变;而RBF-GA模型预报值与实测值趋势一致,在一定程度上说明了经过GA优化后的RBF模型对船速的敏感性优于未被优化的RBF模型.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   基于ANN模型的Tor Viking II 冰阻力预报

Fig.7   Ice resistance prediction of Tor Viking II based on ANN model


5 结论

提出一种基于ANN的极地船舶冰阻力预报模型,介绍两种神经网络预测方法:RBF和RBF-GA,将两种预报模型与船舶模型试验和全尺度试验进行对比分析,考虑了在不同冰厚和船速下的模型预报结果,得出的主要结论如下:

(1) RBF-GA模型具有良好的泛化效果,对冰厚和船速的敏感性优于RBF模型,能够准确预报冰阻力,其平均误差在8%左右.

(2) 在高质量且充足的数据前提下,特征量归一化是保持每个特征权重在可比范围内的关键,可以有效确保预测结果的稳定性和准确性.

(3) 在数据库中,平整冰条件下的船舶试验数据较多,这使得神经网络模型在平整冰条件下的预报结果更加准确.低速航行时,预报误差较大,这可能由于训练样本缺少船舶低速试验数据.

(4) 船速和冰阻力之间的皮尔逊相关系数最小,这并不代表船速对冰阻力的影响最小.皮尔逊相关系数仅衡量线性关系,即使系数为0,也不代表着没有相关性.

参考文献

ZHOU L, SU B, RISKA K, et al.

Numerical simulation of moored structure station keeping in level ice

[J]. Cold Regions Science and Technology, 2012, 71: 54-66.

DOI:10.1016/j.coldregions.2011.10.008      URL     [本文引用: 4]

HU J, ZHOU L.

Further study on level ice resistance and channel resistance for an icebreaking vessel

[J]. International Journal of Naval Architecture and Ocean Engineering, 2016, 8: 169-176.

DOI:10.1016/j.ijnaoe.2016.01.004      URL     [本文引用: 3]

MARKOPOULOS A P, GEORGIOPOULOS S, MANOLAKOS D E.

On the use of back propagation and radial basis function neural networks in surface roughness prediction

[J]. Journal of Industrial Engineering International, 2016, 12: 389-400.

DOI:10.1007/s40092-016-0146-x      URL     [本文引用: 1]

KOUSHAN K.

Empirical prediction of ship resistance and wetted surface area using artificial neural networks

[J]. Practical Design of Ships & Other Floating Structures, 2001, 1: 501-507.

[本文引用: 1]

COUSER P, MASON A, MASON G, et al.

Artificial neural networks for hull resistance prediction

[C]// 3rd International Conference on Computer and IT Applications in the Maritime Industries. Siguenza, Spain:Compit, 2004: 391-402.

[本文引用: 1]

CUI H, TURAN O, SAYER P.

Learning-based ship design optimization approach

[J]. Computer-Aided Design, 2012, 44: 186-195.

DOI:10.1016/j.cad.2011.06.011      URL     [本文引用: 1]

YANG Y, TU H, SONG L, et al.

Research on accurate prediction of the container ship resistance by RBFNN and other machine learning algorithms

[J]. Journal of Marine Science and Engineering, 2021, 9(4): 376-393.

DOI:10.3390/jmse9040376      URL     [本文引用: 1]

Resistance is one of the important performance indicators of ships. In this paper, a prediction method based on the Radial Basis Function neural network (RBFNN) is proposed to predict the resistance of a 13500 transmission extension unit (13500TEU) container ship at different drafts. The predicted draft state in the known range is called interpolation prediction; otherwise, it is extrapolation prediction. First, ship features are extracted to make the resistance Rt prediction. The resistance prediction results show that the performance of the RBFNN is significantly better than the other four machine learning models, backpropagation neural network (BPNN), support vector machine (SVM), random forest (RF), and extreme gradient boosting (XGBoost). Then, the ship data is processed in a dimensionless manner, and the models mentioned above are used to predict the total resistance coefficient Ct of the container ship. The prediction results show that the RBFNN prediction model still performs well. Good results can be obtained by RBFNN in interpolation prediction, even when using part of dimensionless features. Finally, the accuracy of the prediction method based on RBFNN is greatly improved compared with the modified admiralty coefficient.

陈爱国, 叶家玮.

基于神经网络的船舶阻力计算数值实验研究

[J]. 中国造船, 2010, 51(2): 21-27.

[本文引用: 1]

CHEN Aiguo, YE Jiawei.

Numerical experimental study of ship resistance calculation based on neural network

[J]. Shipbuilding of China, 2010, 51(2): 21-27.

[本文引用: 1]

张乔宇, 黄国富, 金建海.

基于机器学习的船舶阻力预报模型研究

[J]. 舰船科学技术, 2019, 41(23): 6-10.

[本文引用: 1]

ZHANG Qiaoyu, HUANG Guofu, JIN Jianhai.

Research on ship resistance prediction model based on machine learning

[J]. Ship Science and Technology, 2019, 41(23): 6-10.

[本文引用: 1]

KIM J H, KIM Y, LU W.

Prediction of ice resistance for ice-going ships in level ice using artificial neural network technique

[J]. Ocean Engineering, 2020, 9(6): 613-623.

[本文引用: 1]

ISLAM M.

Machine learning techniques for ship performance predictions in open water and ice

[C]// The 31st International Ocean and Polar Engineering Conference. Rhodes, Greece: OnePetro, 2021: ISOPE-I-21-1296.

[本文引用: 1]

ZHANG M, SUN Q, GARME K, et al.

Analysis of inland waterway ship performance in ice: Operation Time Window

[J]. Ocean Engineering, 2022, 263: 112409.

DOI:10.1016/j.oceaneng.2022.112409      URL     [本文引用: 1]

BROOMHEAD D, LOWE D.

Multivariable functional interpolation and adaptive networks

[J]. Complex Systems, 1988, 2: 321-355.

[本文引用: 1]

GAN M, PENG H, DONG X P.

A hybrid algorithm to optimize RBF network architecture and parameters for nonlinear time series prediction

[J]. Applied Mathematical Modelling, 2012, 36: 2911-2919.

DOI:10.1016/j.apm.2011.09.066      URL     [本文引用: 1]

LEWIS J W, EDWARDS R Y.

Methods for predicting icebreaking and ice resistance characteristics of icebreakers

[J]. SNAME Transactions, 1970, 78: 213-249.

[本文引用: 2]

VANCE G. Analysis of the performance of a 140-foot great lakes icebreaker:USCGC Katmai Bay. Report No.80-8[R]. Hanover, USA: U.S. ACRREL, 1980.

[本文引用: 2]

ZAHN P, PHILLIPS L. Towed resistance trials in ice of the USCGC Mobile Bay (WTGB103)[M]. Montreal, Canada: Transportation Development Centre, 1987.

[本文引用: 2]

LINDQVIST G.

A straightforward method for calculation of ice resistance of ships

[C]// Proceedings of 10th International Conference on Port and Ocean Engineering under Arctic Conditions. Lulea, Sweden: POAC, 1989: 722-735.

[本文引用: 3]

RISKA K, WILHELMSON M, ENGLUND K, et al. Performance of merchant vessels in ice in the Baltic. Research Report No. 52[R]. Helsinki, Finland: Winter Navigation Research Board, 1998.

[本文引用: 2]

IONOV B. Ice resistance and its composition[R]. Moscow, Russia: Arctic and Antarctic Research Institute, 1988.

[本文引用: 1]

KEINONEN A, BROWNE R P, REVILL C R, et al.

Icebreaker performance prediction

[J]. Transactions-Society of Naval Architects and Marine Engineers, 1991, 99: 221-248.

[本文引用: 2]

ZHANG M, GARME K, BURMAN M, et al.

A numerical ice load prediction model based on ice-hull collision mechanism

[J]. Applied Sciences, 2020, 10: 692-713.

DOI:10.3390/app10020692      URL     [本文引用: 2]

A simplified numerical model is introduced to predict ice impact force acting on the ship hull in level ice condition. The model is based on ice-hull collision mechanisms and the essential ice breaking characteristics. The two critical ice failure modes, localized crushing and bending breaking, are addressed. An energy method is used to estimate the crushing force and the indentation displacement for different geometry schemes of ice-ship interaction. Ice bending breaking scenario is taken as a semi-infinite plate under a distributed load resting on an elastic foundation. An integrated complete ice-hull impact event is introduced with ice failure modes and breaking patterns. Impact location randomness and number of broken ice wedges are considered in order to establish a stochastic model. The analysis is validated by comparison with the model ice test of a shuttle passenger ferry performed in May 2017 for SSPA Sweden AB at Aker Arctic Technology Inc. Good agreement is achieved with appropriate parameter selection assumed from the model test and when ice bending failure is dominant. This model can be used to predict the ice impact load and creates a bridge between design parameters (ice properties and ship geometry) and structure loads.

CHO S R, LEE S.

A prediction method of ice breaking resistance using a multiple regression analysis

[J]. International Journal of Naval Architecture and Ocean Engineering, 2015, 7: 708-719.

DOI:10.1515/ijnaoe-2015-0050      URL     [本文引用: 2]

YUM J G, KANG K J, JANG J H, et al.

A Study on the Hull form design and ice resistance & propulsion performance of a platform support vessel (PSV) operated in the Arctic Ocean

[J]. Journal of the Society of Naval Architects of Korea, 2018, 55: 497-504.

DOI:10.3744/SNAK.2018.55.6.497      URL     [本文引用: 2]

JEONG S Y, CHOI K.

A review on ice resistance prediction formula for icebreaking vessels

[C]// Proceedings of the International Offshore and Polar Engineering Conference. Osaka, Japan: ISOPE, 2009: 513-522.

[本文引用: 2]

JEONG S Y, JANG J, KIM C H, et al.

A study of ship resistance characteristics for ice-strengthened vessel by broken ice channel width and size of broken ice pieces

[J]. Journal of the Society of Naval Architects of Korea, 2018, 55: 22-27.

DOI:10.3744/SNAK.2018.55.1.22      URL     [本文引用: 2]

SONG Y Y, KIM M C, CHUN H H.

A study on resistance test of icebreaker with synthetic ice

[J]. Journal of the Society of Naval Architects of Korea, 2007, 44: 389-397.

DOI:10.3744/SNAK.2007.44.4.389      URL     [本文引用: 2]

ZHOU L, DIAO F, SONG M, et al.

Calculation methods of icebreaking capability for a double-acting polar ship

[J]. Journal of Marine Science and Engineering, 2020, 8(3): 179-200.

DOI:10.3390/jmse8030179      URL     [本文引用: 2]

As a key parameter, icebreaking capability is often used to judge whether a polar ship could navigate in level ice at a certain speed. This paper presents two methods to calculate icebreaking capability. The first one is a static method based on the estimation of ice resistance under different ice thicknesses and ship speeds. The second is a dynamic method that involves solving the equation of motion. A series of model tests with a double-acting icebreaking tanker were also carried out in the ice basin of the Krylov State Research Center to measure ice resistances. The simulated ice resistances were compared with model tests results for both ahead and astern running operations. The calculated icebreaking capability based on static and dynamic methods was validated with the model test result. A good agreement was achieved between measurement and simulation. The discrepancy between the model test result and the result simulated by the static or dynamic method was minor.

KIM M C, LEE W J, SHIN Y J.

Comparative study on the resistance performance of an icebreaking cargo vessel according to the variation of waterline angles in pack ice conditions

[J]. International Journal of Naval Architecture and Ocean Engineering, 2014, 6: 876-893.

DOI:10.2478/IJNAOE-2013-0219      URL     [本文引用: 2]

CHO S R, JEONG S Y, LEE S.

Development of effective model test in pack ice conditions of square-type ice model basin

[J]. Ocean Engineering, 2013, 67: 35-44.

DOI:10.1016/j.oceaneng.2013.04.011      URL     [本文引用: 2]

HU J, ZHOU L.

Experimental and numerical study on ice resistance for icebreaking vessels

[J]. International Journal of Naval Architecture and Ocean Engineering, 2015, 7: 626-639.

DOI:10.1515/ijnaoe-2015-0044      URL     [本文引用: 2]

JEONG S. Ice resistance prediction method based on icebreaking pattern and ice-hull contact conditions[D]. Republic of Korea: Korea Maritime and Ocean University, 2016.

[本文引用: 2]

KIM M C, LEE S K, LEE W J, et al.

Numerical and experimental investigation of the resistance performance of an icebreaking cargo vessel in pack ice conditions

[J]. International Journal of Naval Architecture and Ocean Engineering, 2013, 5: 116-131.

DOI:10.2478/IJNAOE-2013-0121      URL     [本文引用: 2]

HUANG Y, HUANG S, SUN J.

Experiments on navigating resistance of an icebreaker in snow covered level ice

[J]. Cold Regions Science and Technology, 2018, 152: 1-14.

DOI:10.1016/j.coldregions.2018.04.007      URL     [本文引用: 2]

CHAKRABARTI S K. Offshore structure modeling[M]. Chicago, USA: World Scientific, 1994.

[本文引用: 3]

SCHWARZ J.

Some latest developments in icebreaker technology

[J]. Journal of Energy Resources Technology, 1986, 108: 161-167.

DOI:10.1115/1.3231256      URL     [本文引用: 1]

Icebreaking technology has been improved over the last 10–15 yr so that the installed power of icebreaking ships could be drastically reduced. The improvement is demonstrated on four examples of icebreaking ships, one conventional and three advanced concepts, which have shown their icebreaking ability already in full scale. The icebreaking capability of ships is suggested to be evaluated through model tests, theoretical approach and by full-scale measurements. The evaluation should be carried out for various ice conditions by resistance and self-propulsion tests. Finally, some thoughts are presented on features of an advanced icebreaker.

BENESTY J, CHEN J, HUANG Y, et al. Pearson correlation coefficient[M]. Berlin & Heidelberg, Germany: Springer-Verlag, 2009.

[本文引用: 1]

RUDER S.

An overview of gradient descent optimization algorithms

[DB/OL]. (2016-09-15) [2022-08-18]. https://doi.org/10.48550/arXiv.1609.04747.

[本文引用: 1]

于晨芳, 吕烈彪, 柳卫东.

破冰船冰阻力估算方法研究

[J]. 船舶标准化工程师, 2018, 51(4): 74-81.

[本文引用: 1]

YU Chenfang, LV Liebiao, LIU Weidong.

Research on ice resistance estimation method for icebreakers

[J]. Ship Standardization Engineer, 2018, 51(4): 74-81.

[本文引用: 1]

RISKA K, LEIVISKÄ T, NYMAN T, et al.

Ice performance of the Swedish multi-purpose icebreaker Tor Viking II

[C]// Proceedings of the International Conference on Port and Ocean Engineering under Arctic Conditions. Ottawa, Canada: POAC, 2001: 849-866.

[本文引用: 1]

/

〈 〉