含抽水蓄能电站的高比例新能源发电系统多时间尺度调度模型

doi:10.16183/j.cnki.jsjtu.2023.123

含抽水蓄能电站的高比例新能源发电系统多时间尺度调度模型

顾慧杰¹, 周华锋¹, 彭超逸¹, 胡亚平¹, 赵心怡², 谢俊^,², 施雄华³

1.中国南方电网电力调度控制中心,广州 510623

2.河海大学能源与电气学院,南京 211100

3.南京南瑞继保电气有限公司,南京 211102

A Multi-Time Scale Scheduling Model for Power Generation Systems with a High Proportion of New Energy Including Pumped Storage Power Stations

GU Huijie¹, ZHOU Huafeng¹, PENG Chaoyi¹, HU Yaping¹, ZHAO Xinyi², XIE Jun^,², SHI Xionghua³

1. Dispatching and Control Center, China Southern Power Grid, Guangzhou 510623, China

2. College of Energy and Electrical Engineering, Hohai University, Nanjing 211100, China

3. NR Electric Co., Ltd., Nanjing 211102, China

通讯作者: 谢俊,教授,博士生导师,电话(Tel.):025-85099097;E-mail:eejxie@163.com.

责任编辑: 王历历

收稿日期: 2023-04-7 修回日期: 2023-06-14 接受日期: 2023-06-16

基金资助:

国家重点研发计划(2019YFE0105200)

Received: 2023-04-7 Revised: 2023-06-14 Accepted: 2023-06-16

作者简介 About authors

顾慧杰(1985—),高级工程师,主要研究方向为电力市场.

摘要

针对高比例新能源接入电网的消纳问题,提出一种含抽水蓄能电站的高比例新能源发电系统多时间尺度协调调度模型.依据风电、光伏、负荷功率预测精度随时间尺度缩短逐级提高的特点,以系统总运行成本最小为目标构建日前24 h、日内1 h、实时15 min三阶段协调调度模型.通过多时间尺度的协调配合,逐级修正发电计划,实现抽蓄、风电、光伏、火电出力良好跟踪负荷.基于CPLEX商业优化软件,利用混合整数线性规划法对含6台抽蓄机组的风光火抽蓄互补发电系统展开仿真分析.结果表明:抽水蓄能机组可发挥其负荷响应时间短、功率调节速度快的优势,减轻火电机组调节负担,有效缓解火电机组调节压力.通过多时间尺度的协调配合,可减少弃风弃光,提高新能源消纳水平.

关键词： 抽水蓄能电站; 高比例新能源发电系统; 多时间尺度协调调度; 新能源消纳; 预测精度; 混合整数线性规划

Abstract

Aimed at the accommodation problem of a high proportion of new energy connected to the power grid, a multi-time scale coordinated scheduling model for power generation systems with a high proportion of new energy including pumped storage power stations is proposed. Based on the characteristics that the prediction accuracy of wind, photovoltaic (PV) and load power improves step by step with the shortening of time scales, a three-phase coordinated scheduling model is constructed with the goal of minimizing the total operating cost of the system, which includes a 24-hour day-ahead plan, a 1-hour intraday plan and a 15-minute real-time plan. Through the coordination of multiple time scales, the power generation plan is revised step by step, which ensures that the pumped storage power, the wind power, the PV power, and the thermal power output track the load well. Based on the CPLEX commercial optimization software, a mixed integer linear programming method is used to simulate and analyze the wind-PV-thermal-pumped storage complementary power generation system with six pumped storage units. The results show that the pumped storage units can take advantage of short load response time and fast power regulation speed to reduce the regulatory burden of thermal power units and relieve their regulatory pressure effectively. The coordination and cooperation on multiple time scales reduces wind and PV power curtailment and improves new energy accommodation level.

Keywords： pumped storage power station; power generation system with a high proportion of new energy; multi-time scale coordinated scheduling; new energy accommodation; prediction accuracy; mixed integer linear programming

PDF (2568KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

顾慧杰, 周华锋, 彭超逸, 胡亚平, 赵心怡, 谢俊, 施雄华. 含抽水蓄能电站的高比例新能源发电系统多时间尺度调度模型[J]. 上海交通大学学报, 2024, 58(12): 1957-1967 doi:10.16183/j.cnki.jsjtu.2023.123

GU Huijie, ZHOU Huafeng, PENG Chaoyi, HU Yaping, ZHAO Xinyi, XIE Jun, SHI Xionghua. A Multi-Time Scale Scheduling Model for Power Generation Systems with a High Proportion of New Energy Including Pumped Storage Power Stations[J]. Journal of Shanghai Jiaotong University, 2024, 58(12): 1957-1967 doi:10.16183/j.cnki.jsjtu.2023.123

能源是人类赖以生存和发展的基础,随着能源需求不断提升和环境问题日益恶化,发展清洁低碳、安全高效的能源体系已经成为我国能源发展的战略方向^[1-2].截至2022年底,我国可再生能源装机突破12亿kW,占全国发电总装机的47.3%.其中,风电3.65亿kW、太阳能发电3.93亿kW、常规水电3.68亿kW、抽水蓄能0.45亿kW^[3].为实现“双碳”目标,促进能源清洁发展,大规模开发利用水电、风电、光电等可再生清洁能源是我国能源变革的战略方向.

现有电网难以满足可再生能源大规模并网消纳的要求,部分地区可再生能源弃电问题严重.为克服新能源并网引起的不稳定性并实现清洁能源高效利用,新能源与常规电源互补发电系统应运而生.夏芹芹等^[4]对风光水火常规能源互补发电系统展开研究,验证了利用互补特性能够有效降低风光输出功率波动,提高系统运行的经济性与安全性.

然而,依靠水电、火电与风光之间的互补特性,仅能够平抑风光的出力波动性,并不能完全解决风光消纳问题.储能技术是解决电网调度问题、保证电网稳定和降低新能源并网弃电率的有效手段,在提升电力系统灵活性方面显示出日益重要的作用^[5].其中,抽水蓄能电站凭借快速便捷的机组启停和灵活的运行方式以及良好的调峰性能,成为目前最经济、最成熟、最理想的优质调节电源,在促进可再生能源消纳方面发挥着不可或缺的作用^[6].夏沛等^[7]建立风电和抽水蓄能联合运行优化模型, 表明抽水蓄能电站的接入能够有效提高风电的消纳水平.车泉辉等^[8]提出用抽水蓄能和电池储能调节光伏电站出力波动以促进大规模光伏并网消纳的方法,提升了系统低碳化经济运行水平.梁子鹏等^[9]针对旋转备用优化问题,建立风、水、火、气、核、抽水蓄能多类型电源协同调度模型,能有效兼顾风电不确定性带来的风险成本和系统综合效益.

以上文献均聚焦日前时间尺度,未利用风电、光伏、负荷功率预测精度随时间尺度缩短逐级提高的特点来研究多时间尺度协调调度.风光等间歇性能源大规模接入电网后,需要通过多个时间尺度调度的协调优化,逐级消除其功率预测偏差对系统运行的影响,提升系统消纳新能源的能力.鉴于此,黄杨等^[10]通过日前和日内时间尺度的配合对波动性风电出力进行平抑与消纳.蒋万枭等^[11]提出两阶段的短时间尺度水电、光伏、抽蓄多能互补发电系统备用容量确定策略.Ding等^[12]聚焦日前-日内风电场与抽蓄储能系统的滚动优化,利用不断更新的预测信息和抽蓄调节能力提升联合运行收益.

上述研究主要仅考虑抽蓄与新能源互补,而同时考虑火电与抽水蓄能以及对高比例新能源并网系统进行多时间尺度联合优化调度的研究较少.为解决大规模风光并网消纳问题,若仅依靠火电机组进行调节,势必造成火电机组频繁启停,威胁电网运行安全性与经济性;若仅依靠抽蓄机组进行调节,虽然其具备灵活的调节性能,但是其容量占系统总装机的比例较小.因此,以火电机组作为基础电源,配置一定容量的抽水蓄能机组与火电机组配合,能为系统提供更多的新能源消纳空间^[13].

针对上述问题,在现有研究基础上提出一种含抽蓄电站的高比例新能源互补发电系统多时间尺度协调调度模型.利用风电、光伏、负荷功率不断更新的预测信息建立日前24 h、日内1 h、实时15 min三阶段协调调度模型,将火电和抽蓄运行成本中复杂的非线性因素转化为混合整数线性模型进行求解.基于修改的IEEE-10机系统进行算例仿真,深入探索抽蓄机组的快速调节能力,验证所提多时间尺度协调调度模型能够有效缓解火电机组调峰、备用压力,同时减少弃风弃光,提高可再生能源消纳水平.

1 多时间尺度调度的基本架构

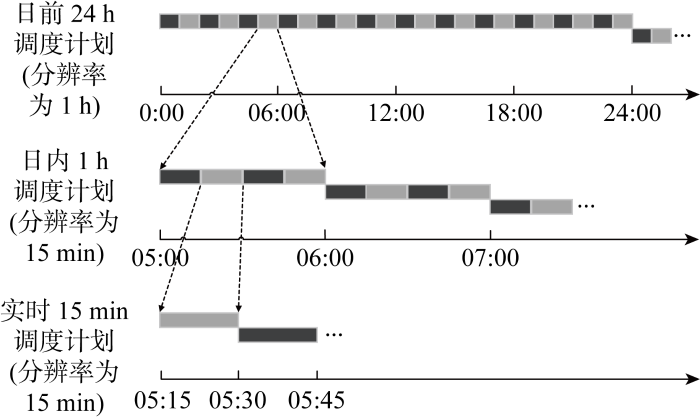
基于风电、光伏、负荷预测精度随时间尺度的缩小而逐级提高的特点,利用不断更新的预测信息,兼顾系统运行的经济性与清洁能源的高效利用性,以综合运行成本最小为目标建立含日前24 h调度、日内1 h调度、实时15 min调度的含抽蓄电站的高比例新能源发电系统多时间尺度协调调度模型.日前-日内-实时协调调度关系示意图如图1所示,图中黑、灰色块代表当前调度周期的分辨率.多时间尺度调度的基本架构具体说明如下.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 日前-日内-实时协调调度关系示意图

Fig.1 Relationship between day-ahead dispatch, in-day dispatch, and real-time dispatch

(1) 日前调度模型:每24 h执行一次,一天执行1次,分辨率为1 h.采用风、光、负荷提前24 h预测数据,优化得出未来24 h风、光、火、抽蓄的出力计划.将火电机组启停计划作为已知量代入日内调度和实时调度模型中.

(2) 日内1 h调度模型:每1 h执行一次,一天执行24次,分辨率为15 min.采用风、光、负荷提前1 h预测数据和日前调度确定的火电机组启停计划,以日前火电机组出力计划作为参考,优化得出未来1 h风、光出力计划,抽蓄机组启停、出力计划和火电机组出力日内修正计划.将日内抽蓄机组启停、出力计划以及火电机组出力修正计划作为已知量代入实时调度模型.

(3) 实时15 min调度模型:每15 min执行一次,一天执行96次,分辨率为15 min.采用风、光、负荷提前15 min预测数据、日前调度确定的火电机组启停计划和日内调度确定的抽蓄机组启停计划,以日内火电机组出力修正计划和日内抽蓄机组出力计划作为参考,优化得出未来15 min风、光出力计划,火电机组出力实时修正计划和抽蓄机组出力实时修正计划.

2 多时间尺度调度模型

2.1 日前调度模型

2.1.1 目标函数

日前调度模型以系统总运行成本最小为目标,包括火电机组发电成本即火电机组煤耗成本和启停成本之和、抽蓄机组启停损耗成本^[14]和弃风、弃光惩罚成本,具体表示为

(1)

f_{1} = m i n (C_{H} + C_{q} + C_{p s} + C_{A})

(2)

\begin{array}{l} C_{H} = \overset{T}{\sum_{t = 1}} \overset{G}{\sum_{g = 1}} U_{g, t} (a_{g} P_{g, t}^{2} + b_{g} P_{g, t} + c_{g}) \\ C_{q} = \overset{T}{\sum_{t = 1}} \overset{G}{\sum_{g = 1}} S_{g} [U_{g, t - 1} (1 - U_{g, t}) + \\ U_{g, t} (1 - U_{g, t - 1})] \\ C_{p s} = \overset{T}{\sum_{t = 1}} \overset{J}{\sum_{j = 1}} {S_{o n} [{I^{g}}_{j, t} (1 - {I^{g}}_{j, t - 1}) + \\ {I^{p}}_{j, t} (1 - {I^{p}}_{j, t - 1})] + \\ S_{o f f} [{I^{g}}_{j, t - 1} (1 - {I^{g}}_{j, t}) + \\ {I^{p}}_{j, t - 1} (1 - {I^{p}}_{j, t})]} \\ C_{A} = \overset{T}{\sum_{t = 1}} (λ_{w} A_{w, t} + λ_{v} A_{v, t}) \end{array}\}

式中:$f_1$ 为日前调度模型总运行成本; $C_H$ 为火电机组煤耗成本; $C_q$ 为火电机组启停成本; $C_{ps}$ 为抽蓄机组运行成本; $C_A$ 为弃风弃光惩罚成本; $T$为调度周期内的总时段数; $G$为火电机组总数; $J$为抽蓄机组总数; $a_g$ 、$b_g$ 、$c_g$ 分别为火电机组$g$的煤耗成本系数; $P_{(g,t)} $ 为日前调度模型中$t$时段火电机组$g$的有功功率; $U_{(g,t)} $ 为表征$t$时段火电机组$g$运行状态的二进制变量, $U_{(g,t)}=0$表示停机, $U_{(g,t)}=1$表示运行; $S_g$ 为火电机组$g$的启停成本; $S_{on}$ 、$S_{off}$ 分别为抽蓄机组的启动成本系数和关停成本系数;$ I_{j, t}^{\mathrm{g}}, ~ I_{j, t}^{\mathrm{p}}$ 分别为表征抽蓄机组$j$在$t$时段是否处于发电工况或抽水工况的0-1状态变量,1为是,0为否; $λ_w $为弃风惩罚成本系数;$A_{(w,t)}$ 为$t$时段风电场的弃风电量; $λ_v $为弃光惩罚成本系数; $A_{(v,t)} $ 为$t$时段光伏电站的弃光电量.

2.1.2 约束条件

(1) 风光出力约束.在含风电的多能互补系统随机优化调度模型中,通常以置信区间^[15]的形式描述风电出力不确定性.因此,风电出力建模如下:

(3)

0 \leq P_{w, t} \leq P_{w, N}

(4)

P_{w, m i n, t} \leq P_{w, t} \leq P_{w, m a x, t}

(5)

\begin{array}{l} P_{w, t}^{u p} = μ_{w, t} + 1.96 σ_{w, t} \\ P_{w, t}^{d n} = μ_{w, t} - 1.96 σ_{w, t} \end{array}\}

(6)

\begin{array}{l} P_{w, m a x, t} = m i n {P_{w, t}^{u p}, P_{w, N}} \\ P_{w, m i n, t} = m a x {0, P_{w, t}^{d n}} \end{array}\}

(7)

A_{w, t} = P_{w, m a x, t} - P_{w, t}

式中:P_w_{, N}为风电场的装机容量;P_w_{, t}为t时段风电调度出力;P_w_,_max_{, t}、P_w_,_min_{, t}分别为t时段风电场可用功率上下限; $P_{w, t}^{u p}$ 、 $P_{w, t}^{d n}$ 分别为t时段风电场预测出力上下限;μ_w_{, t}、σ_w_{, t}分别为t时段风电场预测出力概率分布的均值和标准差.若风电输出功率区间过大,则会降低系统优化调度的经济性,甚至使得调度模型无解.因此,设定风电以及光伏发电的出力区间为[μ_w_{, t}-1.96σ_w_{, t}, μ_w_{, t}+1.96σ_w_{, t}]以保证至少95%的风光出力得以利用.光伏发电出力建模与上述风电出力一致,不再赘述.

(2) 火电机组运行约束.火电机组出力约束为

(8)

\begin{matrix} U_{g, t} P_{g, m i n} \leq P_{g, t} \leq U_{g, t} P_{g, m a x} \end{matrix}

式中: $P_{g, m a x} 、 P_{g, m i n} 分别为火电机组 g$ 出力上下限.

火电机组出力爬坡约束为

(9)

\begin{matrix} \begin{array}{l} P_{g, t} - P_{g, t - 1} \leq {R^{U}}_{g} U_{g, t - 1} \\ P_{g, t - 1} - P_{g, t} \leq {R^{D}}_{g} U_{g, t} \end{array}\} \end{matrix}

式中: ${R^{U}}_{g} 、 {R^{D}}_{g} 分别为火电机组 g$ 的小时级上、下爬坡速率.

火电机组最小启停时间约束为

(10)

\begin{matrix} \begin{array}{l} (U_{g, t - 1} - U_{g, t}) (T_{g, t - 1}^{o n} - T_{g, m i n}^{o n}) \geq 0 \\ (U_{g, t} - U_{g, t - 1}) (T_{g, t - 1}^{o f f} - T_{g, m i n}^{o f f}) \geq 0 \end{array}\} \end{matrix}

式中: $T_{g, t - 1}^{o n}$ 、 $T_{g, t - 1}^{o f f}$ 分别为火电机组g至t-1时段已经连续开机与关停的时间; $T_{g, m i n}^{o n}$ 、 $T_{g, m i n}^{o f f}$ 分别为火电机组g的最小连续开机与停机时间.

火电机组备用容量约束^[16]为

(11)

\begin{matrix} \begin{array}{l} P_{g, t} + R_{g, t}^{u p} \leq P_{g, m a x} U_{g, t} \\ P_{g, t} - R_{g, t}^{d n} \geq P_{g, m i n} U_{g, t} \end{array}\} \end{matrix}

式中: $R_{g, t}^{u p} 、 R_{g, t}^{d n} 分别为 t 时段火电机组 g$ 为应对风光出力不确定性而预留的上调备用容量和下调备用容量.

(3) 抽蓄电站运行约束.抽蓄机组出力约束为

(12)

\begin{matrix} \begin{array}{l} {I^{g}}_{j, t} {P^{g}}_{j, m i n} \leq {P^{g}}_{j, t} \leq {I^{g}}_{j, t} {P^{g}}_{j, m a x} \\ {I^{p}}_{j, t} {P^{p}}_{j, m i n} \leq {P^{p}}_{j, t} \leq {I^{p}}_{j, t} {P^{p}}_{j, m a x} \end{array}\} \end{matrix}

式中: ${P^{g}}_{j, t}$ 、 ${P^{p}}_{j, t}$ 分别为t时段抽蓄机组j的发电功率和抽水功率; ${P^{g}}_{j, m a x}$ 、 ${P^{g}}_{j, m i n}$ 分别为抽蓄机组j的最大、最小发电功率; ${P^{p}}_{j, m a x}$ 、 ${P^{p}}_{j, m i n}$ 分别为抽蓄机组j的最大、最小抽水功率.

抽蓄机组运行工况约束为

(13)

{I^{g}}_{j, t} + {I^{p}}_{j, t} \leq 1

(14)

\begin{array}{l} \overset{J}{\sum_{j = 1, j \neq j'}} {I^{g}}_{j, t} \leq (J - 1) - (J - 1) {I^{p}}_{j', t} \\ \overset{J}{\sum_{j = 1, j \neq j'}} {I^{p}}_{j, t} \leq (J - 1) - (J - 1) {I^{g}}_{j', t} \end{array}\}

式中:j'为不同于j的某个机组.式(13)保证单台抽蓄机组不能同时在发电和抽水模式下运行.此外,抽水蓄能电站的上水库和水泵水轮机之间通常包括一段压力水管,因此无论抽蓄机组数量如何,都不能同时在发电和抽水模式下运行.换言之,如果至少一台抽蓄机组在发电模式下运行,那么同一时刻其他任何机组都不能在抽水模式下运行,反之亦然.式(14)即为同一时刻下抽蓄机组群的抽发互斥运行条件.

抽蓄电站水量约束为

(15)

X_{t} = X_{t - 1} + \overset{J}{\sum_{j = 1}} ({η^{p}}_{j} {P^{p}}_{j, t} - {η^{g}}_{j} {P^{g}}_{j, t})

(16)

X_{m i n} \leq X_{t} \leq X_{m a x}

(17)

X_{T} = X_{0}

式中:X_t为t时段抽蓄电站上水库的库容; ${η^{g}}_{j}$ 、 ${η^{p}}_{j}$ 分别为抽蓄机组j发电和抽水时的平均水量/电量转换系数;X_max、X_min分别为抽蓄电站上水库的最大、最小蓄水量;X₀为上水库的初始库容;X_T为调度期末上水库的库容.式(17)保证抽蓄电站上水库日运行能量平衡.

抽蓄机组备用容量约束^[16]为

(18)

\begin{array}{l} {P^{g}}_{j, t} + R_{j, t}^{g u} \leq {P^{g}}_{j, m a x} {I^{g}}_{j, t} \\ {P^{g}}_{j, t} - R_{j, t}^{g d} \geq {P^{g}}_{j, m i n} {I^{g}}_{j, t} \end{array}\}

(19)

\begin{array}{l} {P^{p}}_{j, t} + R_{j, t}^{p u} \leq {P^{p}}_{j, m a x} {I^{p}}_{j, t} \\ {P^{p}}_{j, t} - R_{j, t}^{p d} \geq {P^{p}}_{j, m i n} {I^{p}}_{j, t} \end{array}\}

式中: $R_{j, t}^{g u}$ 、 $R_{j, t}^{g d}$ 分别为发电工况下t时段抽蓄机组j提供的上、下备用容量; $R_{j, t}^{p u}$ 、 $R_{j, t}^{p d}$ 分别表示抽水工况下t时段抽蓄机组j提供的上、下备用容量.

(4) 系统约束.功率平衡约束为

(20)

\begin{array}{l} P_{w, t}^{d a y} + P_{v, t}^{d a y} + \overset{G}{\sum_{g = 1}} P_{g, t}^{d a y} + \\ \overset{J}{\sum_{j = 1}} (P_{j, t}^{g, d a y} - P_{j, t}^{p, d a y}) = P_{L, t}^{d a y} \end{array}

式中: $P_{w, t}^{d a y}$ 为日前模型中风电场在t时段的调度出力; $P_{v, t}^{d a y}$ 为日前模型中光伏电站在t时段的调度出力; $P_{g, t}^{d a y}$ 为日前模型中火电机组g在t时段的调度出力; $P_{j, t}^{g, d a y}$ 、 $P_{j, t}^{p, d a y}$ 分别为抽蓄机组在日前调度模型下的发电功率和抽水功率; $P_{L, t}^{d a y}$ 为t时段提前一天预测的负荷.

旋转备用需求约束为

(21)

\begin{array}{l} \overset{G}{\sum_{g = 1}} R_{g, t}^{u p} + \overset{J}{\sum_{j = 1}} (R_{j, t}^{g u} + R_{j, t}^{p d}) \geq \\ α_{1} (P_{w, t} - P_{w, m i n, t}) + β_{1} (P_{v, t} - P_{v, m i n, t}) \\ \overset{G}{\sum_{g = 1}} R_{g, t}^{d n} + \overset{J}{\sum_{j = 1}} (R_{j, t}^{g d} + R_{j, t}^{p u}) \geq \\ α_{1} (P_{w, m a x, t} - P_{w, t}) + β_{1} (P_{v, m a x, t} - P_{v, t}) \end{array}\}

式中:α₁、β₁分别为考虑日前风电、光伏出力不确定性的备用需求系数,约为15%~25%^[17]; $P_{v, t} 为光伏在 t 时段的出力; P_{v, m i n, t} 、 P_{v, m a x, t} 分别为光伏在 t$ 时段的最小、最大出力.

传输线容量约束为

(22)

\begin{matrix} - L_{l, m a x} \leq \overset{M}{\sum_{m = 1}} G_{l, m} P_{m, t} \leq L_{l, m a x} \end{matrix}

式中:m为节点编号;M为节点总数;G_l_,_m为节点m到线路l的转移分布因子;P_m_,_t为t时段节点m的有功注入功率;L_l,_max为线路l的最大传输功率.

2.2 日内调度模型

2.2.1 目标函数

由于日前调度模型已经优化得出未来24 h的火电机组启停计划,所以日内调度模型不考虑火电机组的开停机情况.通过调整火电机组出力平抑日前到日内风光负荷预测的偏差量.日内调度模型以调度周期内系统总运行成本最小为目标,包括火电机组煤耗成本、火电机组出力调整成本、抽蓄机组启停损耗成本和弃风、弃光惩罚成本,具体表示为

(23)

f_{2} = m i n (C_{H} + C_{Δ p g} + C_{p s} + C_{A})

(24)

\begin{array}{l} C_{H} = \overset{t_{0} + N_{T} - 1}{\sum_{t = t_{0}}} \overset{G}{\sum_{g = 1}} U_{g, t} (a_{g} P_{g, t}^{2} + b_{g} P_{g, t} + c_{g}) \\ C_{Δ p g} = \overset{t_{0} + N_{T} - 1}{\sum_{t = t_{0}}} \overset{G}{\sum_{g = 1}} S_{p g} Δ P_{g, t}^{h o u r} \\ C_{p s} = \overset{t_{0} + N_{T} - 1}{\sum_{t = t_{0}}} \overset{J}{\sum_{j = 1}} {S_{o n} [{I^{g}}_{j, t} (1 - {I^{g}}_{j, t - 1}) + \\ {I^{p}}_{j, t} (1 - {I^{p}}_{j, t - 1})] + \\ S_{o f f} [{I^{g}}_{j, t - 1} (1 - {I^{g}}_{j, t}) + \\ {I^{p}}_{j, t - 1} (1 - {I^{p}}_{j, t})]} \\ C_{A} = \overset{t_{0} + N_{T} - 1}{\sum_{t = t_{0}}} (λ_{w} A_{w, t} + λ_{v} A_{v, t}) \end{array}\}

式中:f₂为日内调度模型总运行成本;t₀为当前调度周期的初始时段;N_T为日内调度周期内的总时段数,日内1 h调度周期包含4个15 min时段;C_Δpg为1个调度周期内火电机组出力调整成本;S_pg为火电机组单位出力调整成本系数;Δ $P_{g, t}^{h o u r}$ 为火电机组g在t时段相较于日前的出力调整量,可表达为 Δ $P_{g, t}^{h o u r}$ = $|P_{g, t}^{h o u r} - P_{g, t}^{d a y}|$ ,其中 $P_{g, t}^{h o u r}$ 为日内小时级调度计划下火电机组g在t时段的发电功率.

2.2.2 约束条件

(1) 风光出力约束.随着时间尺度的推进,风光出力日内预测水平进一步提高,因此该约束中预测出力概率分布的均值和标准差根据风光出力预测更新,但形式仍然同日前.

(2) 火电机组运行约束.日内调度由于采用日前火电机组启停计划,所以不考虑火电机组最小启停时间约束.机组出力爬坡约束参数由于时间尺度的改变需进行相应的调整.火电机组出力约束和备用容量约束同日前.

火电机组出力爬坡约束^[10]为

(25)

\begin{matrix} \begin{array}{l} P_{g, t}^{h o u r} - P_{g, t - 1}^{h o u r} \leq \frac{{R^{U}}_{g}}{4} U_{g, t - 1} \\ P_{g, t - 1}^{h o u r} - P_{g, t}^{h o u r} \leq \frac{{R^{D}}_{g}}{4} U_{g, t} \end{array}\} \end{matrix}

式中: $P_{g, t}^{h o u r} 为日内模型中火电机组 g 在 t$ 时段的调度出力.

(3) 抽蓄电站运行约束.经日内小时级滚动调度后的抽水蓄能电站依然遵循水库日运行水量平衡约束^[18]:

(26)

\begin{matrix} X_{24}^{h o u r} = X_{0} \end{matrix}

式中: $X_{24}^{h o u r}$ 为日末第24个周期经过小时级滚动调度后的上水库储存水量.其余抽蓄电站约束条件同日前.

(4) 系统约束.旋转备用需求约束中的风光备用需求系数均有更新,但形式同日前.传输线容量约束同日前.

系统功率平衡约束为

(27)

\begin{array}{l} P_{w, t}^{h o u r} + P_{v, t}^{h o u r} + P_{g, t}^{h o u r} + \\ \overset{J}{\sum_{j = 1}} (P_{j, t}^{g, h o u r} - P_{j, t}^{p, h o u r}) = P_{L, t}^{h o u r} \end{array}

式中: $P_{w, t}^{h o u r}$ 为日内模型中风电场在t时段的调度出力; $P_{v, t}^{h o u r}$ 为日内模型中光伏电站在t时段的调度出力; $P_{j, t}^{g, h o u r}$ 、 $P_{j, t}^{p, h o u r}$ 分别为日内小时级调度计划下抽蓄机组j在t时段的发电功率和抽水功率; $P_{L, t}^{h o u r}$ 为t时段提前1 h预测的负荷.

2.3 实时调度模型

2.3.1 目标函数

实时调度中火电机组启停状态和出力计划保持不变,将日内调度结果中的抽蓄机组启停计划代入实时调度模型中,利用抽蓄机组快速调节能力消纳日内与实时时间尺度下风光负荷预测的偏差量.实时调度模型以系统实时运行成本最小为目标,包括抽蓄机组出力实时调整成本和弃风、弃光惩罚成本,具体表示为

(28)

f_{3} = m i n (C_{Δ p s} + C_{A})

(29)

\begin{array}{l} C_{Δ p s} = \overset{J}{\sum_{j = 1}} S_{p s} Δ P_{j, t}^{r e a l t} \\ C_{A} = λ_{w} A_{w, t} + λ_{v} A_{v, t} \end{array}\}

式中:f₃为系统实时运行成本;C_Δps为抽蓄机组出力实时调整成本;S_ps为抽蓄机组单位出力调整成本系数;Δ $P_{j, t}^{r e a l t}$ 为抽蓄机组j在t时段相较于日内调度计划的实时出力调整量,可细分为相同抽蓄机组启停状态下的发电功率调整量和抽水功率调整量,即Δ $P_{j, t}^{r e a l t}$ = $|P_{j, t}^{g, r e a l t} - P_{j, t}^{g, h o u r}|$ + $|P_{j, t}^{p, r e a l t} - P_{j, t}^{p, h o u r}|$ ,其中 $P_{j, t}^{g, r e a l t}$ 、 $P_{j, t}^{p, r e a l t}$ 分别为实时调度计划下抽蓄机组j在t时段的发电功率和抽水功率.

2.3.2 约束条件

(1) 风光出力约束.随着时间尺度的推进,风光出力实时预测水平进一步提高,因此该约束中预测出力概率分布的均值和标准差均根据风光出力预测更新,但形式仍然同日前.

(2) 火电机组运行约束.实时调度保持火电机组启停计划和出力计划不变,火电机组出力按照日内调度结果进行.因此,只考虑火电机组备用容量约束,同式(11).

(3) 抽蓄电站运行约束.经实时滚动调度后的抽水蓄能电站依然遵循水库日运行水量平衡约束^[18]:

(30)

\begin{matrix} X_{96}^{r e a l t} = X_{0} \end{matrix}

式中: $X_{96}^{r e a l t}$ 为日末第96个周期经过实时滚动调度后的上水库储存水量.

由于实时调度模型中的抽蓄机组启停状态保持与日内一致,所以不考虑抽蓄机组运行工况约束,其余抽蓄电站约束条件同日前.

(4) 系统约束.旋转备用需求约束中的风光备用需求系数均有更新,但形式同日前.传输线容量约束同日前.

系统功率平衡约束为

(31)

\begin{array}{l} P_{w, t}^{r e a l t} + P_{v, t}^{r e a l t} + P_{g, t}^{h o u r} + \\ \overset{J}{\sum_{j = 1}} (P_{j, t}^{g, r e a l t} - P_{j, t}^{p, r e a l t}) = P_{L, t}^{r e a l t} \end{array}

式中: $P_{w, t}^{r e a l t}$ 为实时模型中风电场在t时段的调度出力; $P_{v, t}^{r e a l t}$ 为实时模型中光伏电站在t时段的调度出力; $P_{L, t}^{r e a l t}$ 为t时段提前15 min预测的负荷.

3 算例分析

3.1 算例参数

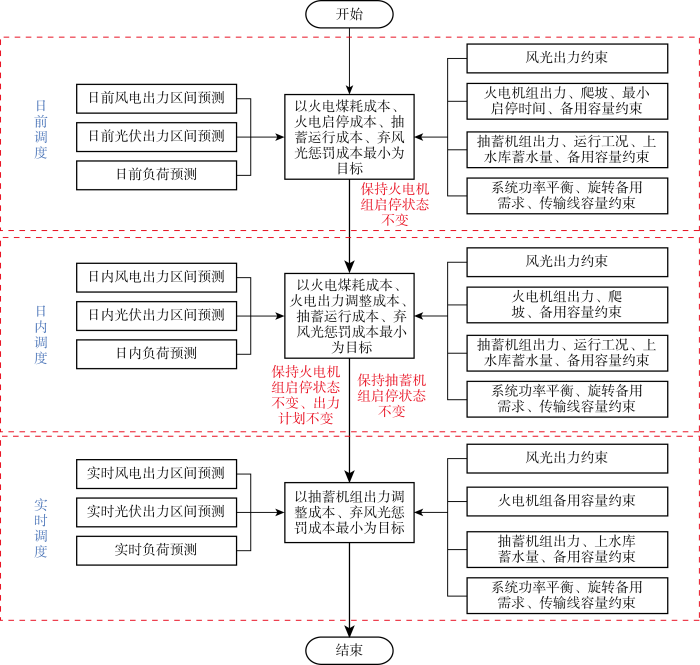
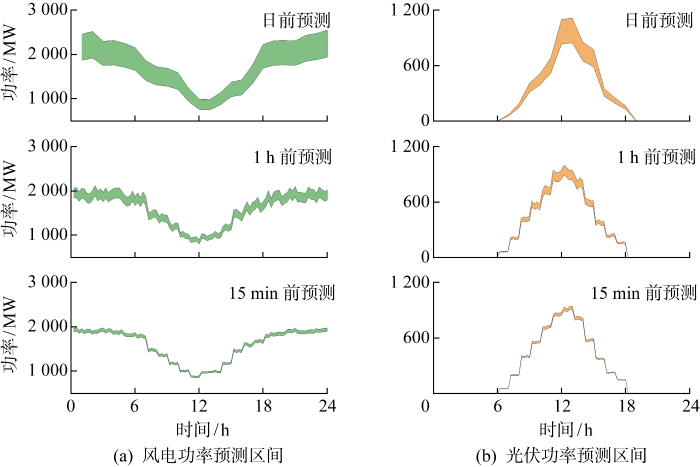
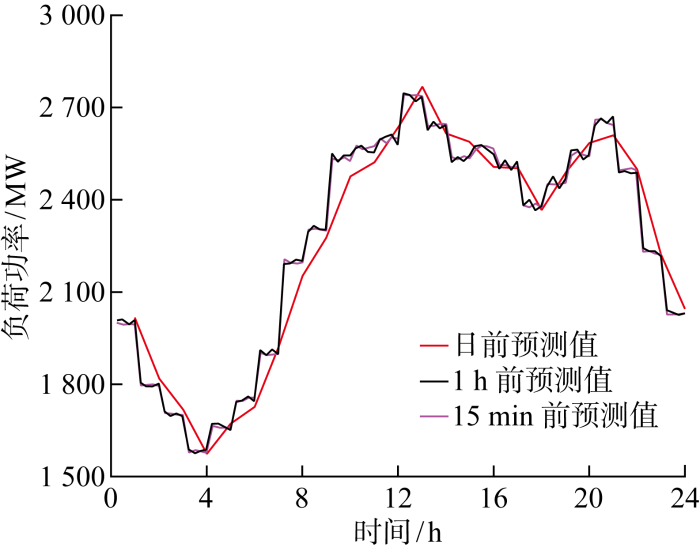
多时间尺度调度流程如图2所示.参照文献[19]配置风电场和光伏电站接入总装机容量为 3.3 GW,容量配比为2∶1.10台火电机组数据来自IEEE-10机标准算例.抽水蓄能电站包括6台单机额定容量为300 MW的变速恒频机组,总装机容量为 1.8 GW.参考美国巴斯康蒂抽蓄电站^[13]设置机组参数,抽水、发电功率连续可调,抽蓄机组参数如表1所示.弃风、弃光惩罚成本为300 美元/(MW·h),火电机组和抽蓄机组出力单位调整成本系数均为100 美元/MW.风电和光伏出力日前、日内、实时预测误差分别为20%、5%、2%,负荷日前、日内、实时预测误差分别为3%、1%、0.5%^[20].图3为不同时间尺度下风电和光伏的预测出力区间.图4为多时间尺度负荷预测曲线.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 多时间尺度调度流程图

Fig.2 Flow chart of multi-time scale dispatch

表1 抽蓄电站参数

Tab.1 Parameters of pumped storage station

参数	数值	参数	数值
$P_{j, m i n}^{g}$ /MW	15	$η_{j}^{p}$ /[m³·(MW·h)^-1]	780
$P_{j, m a x}^{g}$ /MW	300	X₀×10^-7/m³	2
$P_{j, m i n}^{p}$ /MW	30	X_min×10^-7/m³	1.06
$P_{j, m a x}^{p}$ /MW	300	X_max×10^-7/m³	4.38
$η_{j}^{g}$ /[m³·(MW·h)^-1]	999	J	6

新窗口打开| 下载CSV

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 多时间尺度风电、光伏功率预测区间

Fig.3 Predicted output range of wind power and photovoltaic in multi-time scales

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 多时间尺度负荷预测出力

Fig.4 Predicted output of load in multi-time scales

3.2 模型求解

机组组合问题在数学上是一个非凸和非线性的混合整数规划问题,含有大量离散变量和连续变量.火电机组煤耗成本C_H采用文献[21]中的方法进行分段线性转化.火电机组启停成本与抽水蓄能机组的运行成本表达方式类似,两者线性化原理相同. 此处以火电机组启停成本C_q为例展开线性转化说明,其中U_g_,_tU_g_,_t_-1为两个二元整型变量乘积组成的非线性项,可以通过引入新的变量和约束对其进行线性化转换^[22].引入新的二元整型变量U_G_{, t},并令U_G_,_t=U_g_,_tU_g_,_t_-1,则该式可等效为线性化约束:

(32)

\begin{matrix} \begin{array}{l} 0 \leq U_{G, t} \leq U_{g, t} \\ U_{G, t} \leq U_{g, t - 1} \\ U_{G, t} \geq U_{g, t} + U_{g, t - 1} - 1 \end{array}\} \end{matrix}

至此便消除了整个模型中所有非线性项,模型转化为求解混合整数线性规划问题.在Intel 2.6 GHz双核处理器和8 GB内存的个人计算机上使用CPLEX12.6商业软件进行各调度模型的求解.

3.3 调度结果分析

3.3.1 抽水蓄能对系统调度影响分析

为研究抽水蓄能电站对系统优化调度的影响,分别考虑以下两种方案:方案1为不考虑抽水蓄能,采用风-光-火多时间尺度协调调度模型^[23];方案2为考虑抽水蓄能,采用本章提出的风-光-火-抽蓄多时间尺度协调调度模型.

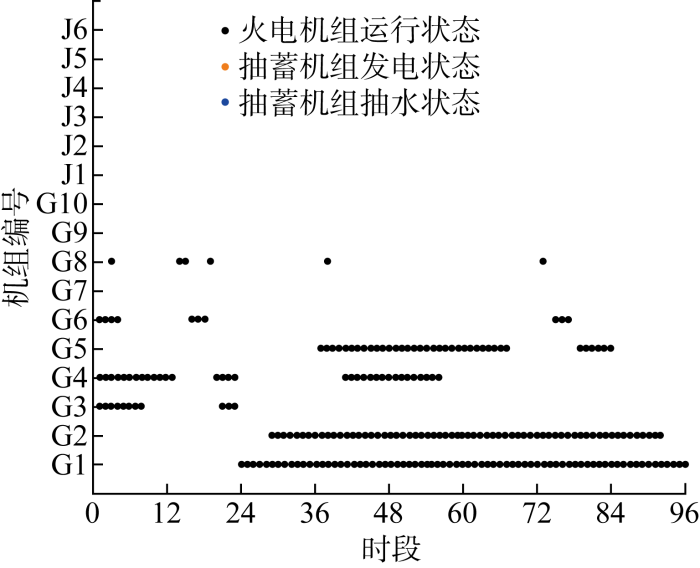
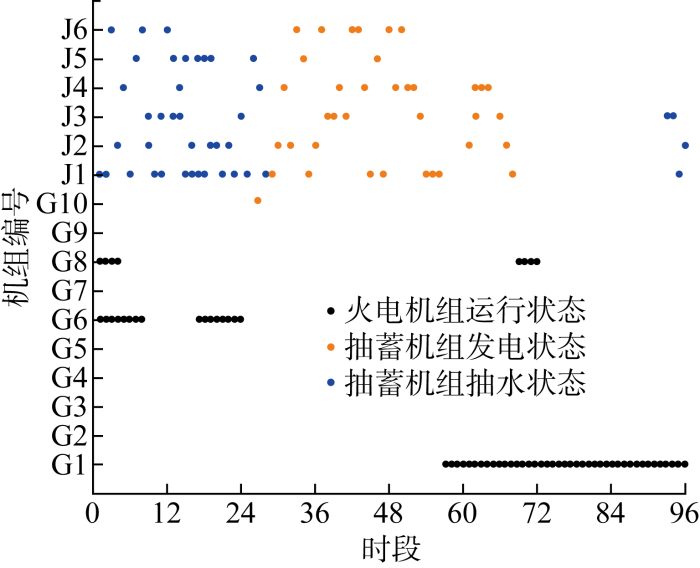
表2对比了两种方案的24 h优化结果.图5和图6分别为两种方案下96时段机组启停状态图,每个时段为15 min,火电机组编号为G1~G10,抽蓄机组编号为J1~J6.图中空白区域代表火电机组或抽蓄机组处于关停状态,带颜色的实心圆点表示开机运行状态.

表2 两种方案24 h优化调度结果

Tab.2 24-hour optimal scheduling results of two methods

方案	火力发电成本/万美元	弃风弃光惩罚成本/ 美元	火电提供的上备用容量/ MW	火电提供的下备用容量/ MW
方案1	128.42	3.507×10⁵	12165	40398
方案2	93.58	700	7460	22459

新窗口打开| 下载CSV

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 方案1不考虑抽水蓄能时机组启停情况

Fig.5 Unit commitment of Method 1 without pumped storage power

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 方案2考虑抽水蓄能时机组启停情况

Fig.6 Unit commitment of Method 2 with pumped storage power

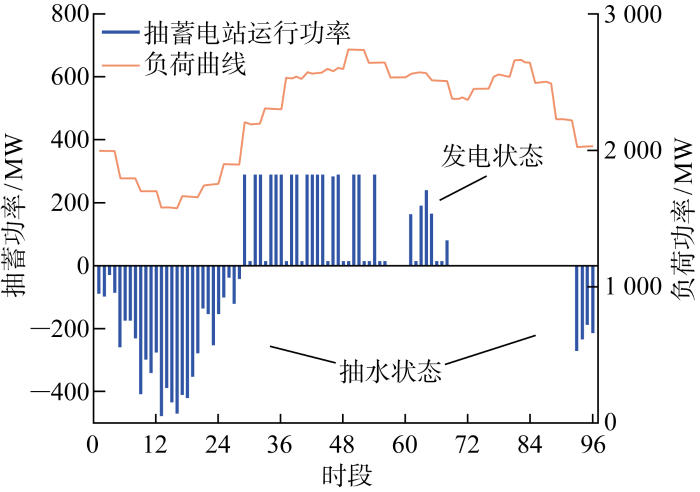
结合图6和图7可知,抽蓄机组呈现出在负荷需求较低时抽水、在负荷需求较高时发电的运行规律,发挥了削峰填谷的作用.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 方案2抽水蓄能电站运行情况

Fig.7 Operation of pumped storage power station in Method 2

对比图5和图6以及表2可知,方案1无抽蓄电站时,在时段28~70的负荷高峰时期,火电机组G1、G2、G4、G5开机时间较长,主要承担基荷发电部分;而且此时为应对风光出力的不确定性系统完全由火电机组提供备用容量.而方案2有抽蓄电站时,抽蓄机组可以承担部分备用.抽蓄机组的加入使得负荷高峰时火电机组开机数量明显减少,减轻火电机组的调峰压力,使火电机组避免大幅的出力调整,有效缓解风电、光伏波动造成的火电机组频繁启停.此外,抽蓄机组的参与使火电机组发电成本降低27%,有利于系统经济运行.

光伏电站昼发夜停,能够有效跟踪负荷,具有正调峰特性,故两种方案下均能全部消纳光伏发电功率,表2中弃光惩罚成本为0.风电具有典型的反调峰特性,方案1中存在大量弃风,大幅增加系统运行总成本.与此同时,由于方案2中抽蓄机组具备灵活的双向调节能力,可以在负荷低谷时耗能抽水,将弃风电量转化为水的重力势能存储起来以便负荷高峰时向系统发电,所以方案2中弃风惩罚成本远低于方案1,表明抽水蓄能参与电力系统调度有利于提高新能源消纳水平.

综上所述,抽水蓄能的加入能够有效改善火电机组运行情况,并获得良好的经济效益,促进风电光伏的利用与消纳.

3.3.2 时间尺度对系统调度影响分析

为研究不同时间尺度对系统调度的影响,设置方案3与方案2进行对比分析.方案3为只考虑单一时间尺度,采用所提风-光-火-抽蓄日前调度模型.

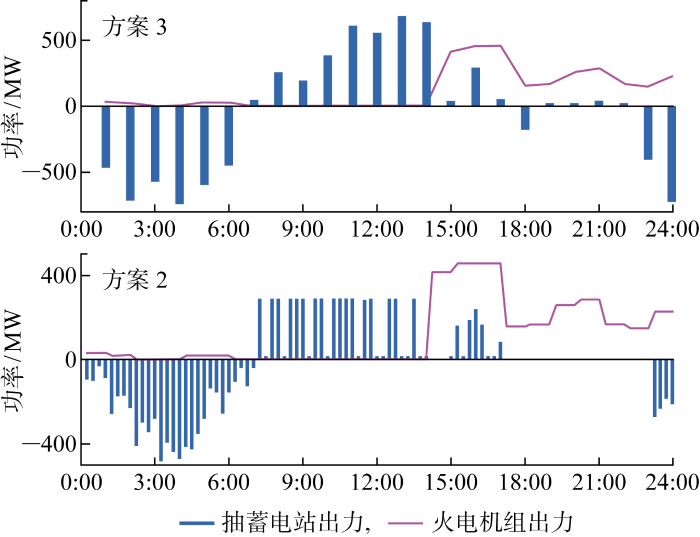
图8为方案2多时间尺度调度与方案3单一日前尺度调度的结果对比图.方案3仅涉及日前调度,故横轴为24数据点,方案2的调度策略精确至实时15 min尺度,故横轴为96数据点.结合图7中全天负荷曲线,可将24 h负荷情况简单划分为“两峰两谷”.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 方案2与方案3调度结果对比

Fig.8 Comparison of scheduling results between Methods 2 and 3

0:00—6:00为全天的负荷最低谷时期,此时光伏出力较弱,风电出力较强,抽蓄机组发挥自身调节性能从电网充电,开始抽水蓄能,抬高负荷曲线.8:00—14:00迎来一天中负荷最高的时期,抽蓄机组向系统中大量发电以缓解负荷高峰.这一阶段由于火电机组调节成本较高,故主要由抽蓄机组承担负荷.16:00左右处于一天中的负荷低谷,由于抽蓄电站需保证一天内水位平衡与能量平衡,无法再大规模抽水调节,所以火电机组调峰填谷.20:00—21:00 处于晚间负荷高峰,火电机组持续发力维持系统功率平衡,直至23:00负荷水平整体回落.无论是单一日前调度还是本章提出的多时间尺度协调调度,抽蓄机组和火电机组互相配合、共同完成电力系统调峰填谷任务.

由图8方案2的调度结果图可以看出,在最终的实时调度阶段,抽水蓄能机组可以充分发挥其快速调节能力来平衡风光荷日内1 h预测和未来15 min 内预测数据的偏差,以此缓解短期甚至超短时间尺度下火电机组的功率调整压力,提高电源侧功率调整的灵活性.这表明所提含抽蓄电站的高比例新能源发电系统多时间尺度协调调度模型能够充分挖掘抽水蓄能机组快速调节功率的能力.

3.3.3 风光渗透率对系统调度影响分析

表3给出不同风光渗透率下,所提风光火抽蓄多时间尺度协调调度模型96时段优化调度结果.设定固定火电机组总装机容量 1 662 MW,抽蓄电站装机容量 1 800 MW,当风电厂和光伏电站总装机容量增加时,风光渗透率随之提高.由于风光大量接入,系统总运行成本逐渐下降,火电机组出力降低,火电发电成本也随之降低.在风光渗透率上升的过程中,抽蓄电站始终发挥其灵活的功率调节能力应对风光波动和负荷变化,因此系统能够较好地消纳风光,当风光渗透率升至48.8%时才会产生少量弃电惩罚成本.此外,随着风光渗透率增加,风光出力不确定性影响进一步扩大,火电需提供更多备用容量以确保高比例新能源发电系统的安全经济运行.

表3 不同风光渗透率下优化调度结果

Tab.3 Optimal scheduling results at different wind and solar penetration rates

风光总装机容量/GW	风光渗透率/%	系统总运行成本/ 万美元	火电发电成本/ 万美元	抽蓄运行成本/ 万美元	弃风弃光惩罚成本/ 美元	火电提供的备用容量总和/GW
3.96	53.4	66.99	45.77	20.97	2500	116.883
3.30	48.8	114.73	93.58	21.08	700	91.639
2.75	44.3	144.90	123.11	21.79	0	65.903
2.20	38.8	208.19	186.64	21.55	0	39.903
1.65	32.3	279.59	258.90	20.69	0	22.029
1.10	24.1	387.64	367.55	20.09	0	15.487

新窗口打开| 下载CSV

4 结论

高比例新能源发电系统是新型电力系统的重要内容,抽水蓄能电站是新能源消纳的重要手段.提出一种含抽水蓄能电站的高比例新能源发电系统多时间尺度协调调度模型,利用风电、光伏、负荷功率预测精度随时间尺度缩短逐级提高的特点,建立日前24 h、日内1 h、实时15 min三阶段协调调度模型.

(1) 抽蓄机组参与电网调度可以有效缓解火电机组调峰、备用压力,减少火电机组频繁启停.两者协调调度兼顾电网运行安全性与经济性,并且能有效减少绿色弃电,有利于提高新能源的消纳水平.

(2) 抽水蓄能电站为应对风光负荷波动充分发挥其双向调节、削峰填谷的作用,灵活跟踪负荷变化,维持系统功率平衡.

(3) 在多时间尺度调度模式下,抽蓄机组能缓解短期甚至超短期时间尺度下火电机组出力调整压力,提高电源侧灵活性.

未来将考虑在需求侧加入灵活响应资源进行协调调度,进一步探索电网消纳大规模风光的途径.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

舒印彪, 薛禹胜, 蔡斌, 等.

关于能源转型分析的评述 (一)转型要素及研究范式

[J]. 电力系统自动化, 2018, 42(9): 1-15.