基于高斯混合聚类的综合物探方法及其在岩溶勘探中的应用

doi:10.16183/j.cnki.jsjtu.2023.020

基于高斯混合聚类的综合物探方法及其在岩溶勘探中的应用

何文¹, 高斌¹, 王强强², 冯少孔¹, 叶冠林^,¹

1.上海交通大学船舶海洋与建筑工程学院,上海 200240

2.国网浙江省电力有限公司衢州供电公司,浙江衢州 324000

A Comprehensive Geophysical Prospection Method Based on Gaussian Mixture Clustering and its Application in Karst Exploration

HE Wen¹, GAO Bin¹, WANG Qiangqiang², FENG Shaokong¹, YE Guanlin^,¹

1. School of Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. Quzhou Electric Power Company, Zhejiang Eelectric Power Corporation, Quzhou 324000, Zhejiang, China

通讯作者: 叶冠林,教授,博士生导师;E-mail:ygl@sjtu.edu.cn.

责任编辑: 李博文

收稿日期: 2023-01-18 修回日期: 2023-03-11 接受日期: 2023-03-14

基金资助:

国网浙江省电力有限公司科技项目(5211QZ2000U6)

Received: 2023-01-18 Revised: 2023-03-11 Accepted: 2023-03-14

作者简介 About authors

何文(1998—),硕士生,从事岩溶勘探物探研究.

摘要

综合物探是一种有效的岩溶勘探技术,但其预测结果中存在人为影响大、溶洞边界模糊等缺点.首先,基于机器学习技术,采用高斯混合模型,分别对高密度电法和面波法勘探数据做分类处理;然后,提出Category-boundary算法,进一步细分上述分类得到的边界,提高高斯混合模型分类精度;最后,根据专家经验与地勘资料制定分类融合规则,在勘察数据驱动和工程地质知识引导的有机结合下,形成一套综合物探的高精度分类融合新方法.将新方法应用于浙南某岩溶勘探工程,获得了边界清晰的溶洞探测结果,与实际钻孔信息对比高度吻合,验证了新方法的有效性.

关键词： 综合物探技术; 高斯混合聚类; 分类融合; 岩溶勘探; 机器学习

Abstract

Comprehensive geophysical prospection is an effective technique for karst exploration, but its prediction results usually suffer from significant artificial influence and fuzzy boundaries of karst caves. Based on the machine learning technology, a Gaussian mixture model is used to classify the exploration data of high-density electrical method and data of surface wave method respectively. Then, a Category-boundary algorithm is proposed to further subdivide the classification results, which improves the accuracy of Gaussian mixture model classification. Finally, the classification fusion rules are formulated based on expert experience and geological exploration data. Under the organic combination of survey data-driven and engineering geological knowledge guidance, a new set of high-precision classification and fusion methods is proposed for comprehensive geophysical exploration. By applying this new method to the karst exploration project in southern Zhejiang, a karst cave prediction is made with clearer boundaries. Compared with the actual drilling information, cave prediction and drilling information are highly consistent, which verifies the effectiveness of the method proposed.

Keywords： comprehensive geophysical prospection; Gaussian mixture clustering; classification fusion; karst exploration; machine learning

PDF (12182KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

何文, 高斌, 王强强, 冯少孔, 叶冠林. 基于高斯混合聚类的综合物探方法及其在岩溶勘探中的应用[J]. 上海交通大学学报, 2024, 58(11): 1724-1734 doi:10.16183/j.cnki.jsjtu.2023.020

HE Wen, GAO Bin, WANG Qiangqiang, FENG Shaokong, YE Guanlin. A Comprehensive Geophysical Prospection Method Based on Gaussian Mixture Clustering and its Application in Karst Exploration[J]. Journal of Shanghai Jiaotong University, 2024, 58(11): 1724-1734 doi:10.16183/j.cnki.jsjtu.2023.020

岩溶(喀斯特)是一种可溶性岩石受水侵蚀而形成的地貌,岩溶的存在通常会导致地基承载力不足,进而造成地基坍塌、路面沉降等一系列工程问题^[1].岩溶地貌在我国分布广泛,岩溶坍塌问题更是困扰我国基础建设实践的主要难题之一.因此,如何提高对岩溶地区可能存在的溶洞位置、大小和类型等信息探测的精度与准度,是当前物探研究领域的重点.目前常见的岩溶勘探方法包括地质钻探法、高密度面波法、高密度电法、地质雷达法、弹性波CT法和冲击映像法等^[2⇓-4],工程上常采用两种或几种方法结合的综合物探技术^[2],以此提高溶洞预测结果的可靠性.综合物探技术在岩溶勘探工程中应用广泛,技术方案相对成熟,但综合物探的解释往往因人而异,因此,利用机器学习方法从优化综合物探试验数据处理方式角度出发,统一解译综合物探结果.

近年来,随着机器学习方法的不断发展,机器学习在数据分类、数据挖掘上表现突出,越来越多的学者将机器学习方法引入土木工程相关领域中,并将机器学习作为一种数据处理手段,取得了一些成果.柴明锐等^[5]将机器学习应用于凝灰岩岩屑成分分析中,预测误差为17.17%,证明该方法用于预测岩屑成分可行;Liu等^[6]在独立变量分析基础上,提出C-EFastICA 算法,基于该算法提取来自混合泄漏声信号中的原始泄漏声信号,提高了水管系统的漏点定位的准确性;干磊等^[7]利用线性判别分析、支持向量机、多层感知机神经网络,建立油气田储层分类模型,对区分有效储层和非有效储层效果明显;Chou等^[8]利用机器学习的集成思想,针对高性能混凝土的抗压强度开展综合研究,借助机器学习集成技术获得有效模拟混凝土抗压强度.此外,在土木工程结构检测领域中,机器学习应用广泛^[9⇓-11],包括结构无损伤检测、结构健康监测等方面,均优于传统土木检测数据处理方法.

综合物探分析方法可以简单描述为,通过不同的岩溶勘探方法采集地层信息的试验数据,简单分类试验数据,形成勘探断面云图,综合对比不同试验方法,获得勘探断面结果,再预测在溶洞的合理性.受限于地下介质构造及物性分布特征的复杂性,传统综合物探方法的预测结果具有不确定性,预测结果的精度受解译专家经验的主观影响较大^[12].传统的综合物探分析方法存在以下问题:① 试验数据量庞大,试验数据根据数值大小被赋予不同的颜色标签,但未作系统划分,导致数据利用率不高;② 断面云图反映的预测结果地层类别划分粗糙,溶洞边界模糊;③ 综合分析不同试验方法的预测结果时,关注点为云图而非数据本身,预测结果较为主观.

在物探领域中,机器学习的一个重要应用是划分不同地质单元数据并做出客观分析.一方面,可以将各种勘探方法采集的数据作为特征数据,应用机器学习方法进行系统科学分类,进一步划分不同地质单元;另一方面,基于机器学习的边缘检测技术,可以辅助判断不同地质单元的位置信息,综合上述两方面技术可提高地层分类精度^{[13⇓⇓-16]}.

李希元等^[17]基于多源地球物理数据,采用支持向量机方法,将密度、磁化率、电阻率作为特征数据,开展地质体岩性识别和分类研究,开辟了将机器学习用于地质解释的新道路;Abubakar^[18]把油气行业勘探作业作为支撑,利用机器学习方法一方面能快速从复杂数据集中提取有用信息,另一方面减少处理数据集的人力成本,系统地阐明机器学习在物探领域的发展潜力;Fowler等^[19]提出将机器学习应用于测井解释,研究表明由机器学习支持开发的工作流做出的解译结果质量好、解译工时短,证明应用人工智能可高效快捷地对测井进行解释.

如何解决传统物探分析方法存在的问题,提升物探结果精度,关键在于是否能精确划分地球物理信号数据^[20],即数据的精准分类.近年来,机器学习在数据分类、数据处理、数据挖掘等领域表现突出^{[21⇓⇓⇓⇓-26]},学者们通过建立数学模型将试验数据加以训练,在学习到一个能满足项目需求的模型后,借助训练好的模型,进一步实现对数据的有效分类、预测和聚类等.将机器学习方法应用在综合物探技术的数据处理部分,从改进试验数据处理的角度出发,有望进一步提升溶洞预测结果的可靠性.

将岩溶勘探工程中由高密度电法获取的电阻率以及高密度面波法获取的剪切波速度作为底层数据,借助高斯混合模型(GMM)分别对电阻率数据集合剪切波速数据集进行分类处理,提出Category-boundary 算法优化精度,并将该方法的溶洞预测结果和实际钻孔信息进行对比验证.研究成果可为类似综合物探技术的改进与提升提供参考.

1 基于GMM的高精度分类融合方法

GMM属于机器学习中“无监督学习”分析方法,其训练样本的标签,即训练样本的物理含义是未知的,通过建立GMM对无标签训练样本学习,揭示数据的内在规律,以此达成对一系列无标签样本数据的分类处理.在GMM基础上,提出Category-boundary算法,用于找出不同类别数据之间的分类界限,同时提高分类精度以满足工程需求.

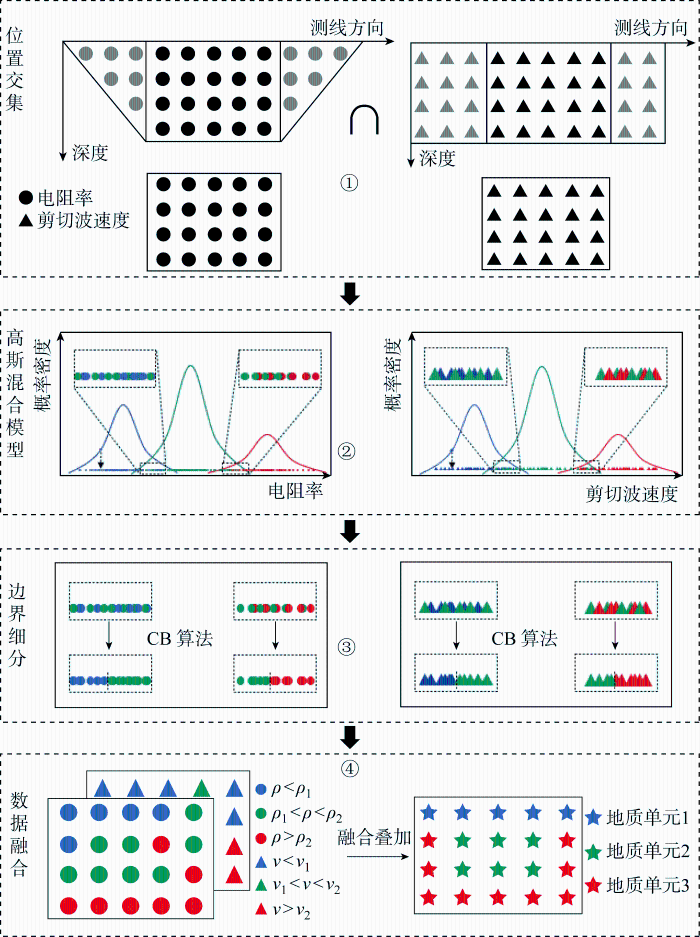
基于GMM的高精度分类融合方法实现流程如图1所示.① 数据预处理,对不同物探试验数据添加位置信息,取位置交集中的试验数据作为有效数据;② 借助GMM将物探数据集A 划分为k类,其中图1以电阻率数据集表示为数据集A,不同类别数据点原则上会服从不同的高斯分布,若不加处理,会普遍存在数据点同时服从不同高斯分布曲线的情况,这些数据点组成的点集文中称为混合数据集;③ 提出Category-boundary算法,对混合数据集进一步划分,从而得到改进GMM的细分结果;④ 同理,对其他数据集B、C 做分类处理后,引入专家经验,对不同物探试验数据的分类结果叠加融合,可得到融合多种物探方法的溶洞预测结果.其中,图1以剪切波速度数据集表示为数据集B,数据集C并未在图中表示出来,它可以是其他物探方法采集的数据集.图中:ρ和v分别为电阻率和剪切波速度.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 基于改进高斯混合模型的分类融合方法流程

Fig.1 Process of classification fusion method based on improved Gaussian mixture model

在整套分类融合方法中,只需依据地勘信息人为指定类别数即GMM中的k值和分类规则,其余过程可依据GMM和Category-boundary算法自动实现,较传统综合物探分析方法,提出的分类融合方法在获得边界清晰的溶洞预测结果同时,人工干预部分相对减少,能有效解决综合物探的解释因人而异和精度不足的问题.

1.1 数据预处理

综合物探技术指采用两种或两种以上的岩溶勘探方法进行分析.由于不同的方法有不同的精度和适用范围,对于同一条测线所能获取的数据集在深度范围也有所差异.为保障分类融合结果的正确性,需对数据进行预处理,即加入数据点的位置信息,选择不同试验的位置交集中的试验数据作为有效数据点,整套方法基于有效数据点进行.以电阻率数据集和剪切波速度数据集为例,数据预处理过程如图2所示.图中:d为断面沿测线方向的距离;下标1、2分别表示剪切波速度断面和电阻率断面在空间位置上重合部分沿测线方向的起点和终点.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 试验数据预处理

Fig.2 Preprocessing of experimental data

1.2 高斯混合模型

GMM函数是一个参数概率密度函数,表示为高斯密度分量的加权和.假设有随机变量x,可表示高斯混合分布

(1)$p(x)=\sum_{i=1} \alpha_{i} p\left(x \mid \mu_{i}, \sigma_{i}\right)$

式中:α_i为混合系数且满足 $\overset{k}{\sum_{i = 1}}$ α_i=1;α_i、 μ_i、 σ_i统称为模型参数;p(x|μ_i, σ_i)表示第i个高斯分布的概率密度函数;μ_i、 σ_i表示第i个高斯混合成分的参数;混合分布共由k个高斯分布组成.且有

(2)$p\left(x \mid \mu_{i}, \sigma_{i}\right)=\frac{1}{\sqrt{2 \pi \sigma_{i}^{2}}} \exp \left(-\frac{\left(x-\mu_{i}\right)^{2}}{2 \sigma_{i}^{2}}\right)$

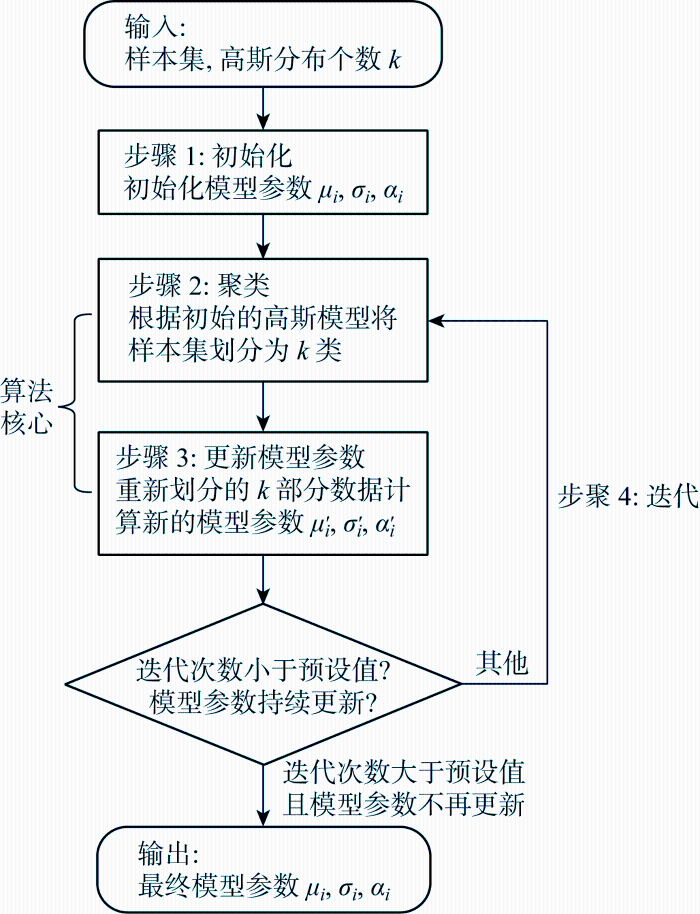
高斯混合聚类模型训练过程为迭代的过程,其流程如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 高斯混合聚类流程

Fig.3 Process of Gaussian mixture clustering

步骤1 初始化模型参数.已知训练集D={x₁, x₂, …, x_m},根据初始混合系数α₁, α₂, …, α_k定义的先验分布选择高斯混合成分,其中初始混合系数可自定义,一般初始值取1/k.根据各个混合成分α_i中的数据计算对应的均值μ_i和标准差σ_i,建立各混合成分的高斯分布概率密度函数,进而建立初始GMM,即高斯混合模型

p(x)=

\overset{k}{\sum_{i = 1}}

α_ip(x|μ_i, σ_i)

步骤2 聚类.令随机变量z_j∈{1, 2, …, k},其中j∈{1, 2, …, m},表示生成样本x_j的高斯混合成分,即第j个数据点所属的数据类别.显然,有z_j的先验概率p(z_j=i)=α_i. 其中z_j根据贝叶斯定理,可以求出z_j的后验概率:

(3)$\begin{aligned} \gamma_{j i}= & p\left(z_j=i \mid x_j\right)= \\ & \frac{p\left(z_j=i\right) p\left(x_j \mid z_j=i\right)}{p\left(x_j\right)}= \\ & \frac{\alpha_i p\left(x_j \mid \mu_i, \sigma_i\right)}{\sum_{l=1} \alpha_l p\left(x_j \mid \mu_l, \sigma_l\right)}\end{aligned}$

当高斯模型建立起来后,把样本集D划分为k个类别,每个样本x_j的类标签λ_j=arg max γ_ji,其中i∈{1, 2, …, k},对每个样本数据做标签标记,以实现聚类目的.

步骤3 更新模型参数.经过聚类处理后,所有样本数据被重新划分为k类,模型参数亦随之发生改变,对模型参数作对应更新处理,即:

(4)$\begin{aligned}\mu_{i}^{\prime} & =\frac{\sum_{j=1}^{m} \gamma_{j i} x_{j}}{\sum_{j=1}^{m} \gamma_{j i}} \end{aligned}$

(5)$\begin{aligned}\sigma_{i}^{2^{\prime}} & =\frac{\sum_{j=1}^{m} \gamma_{j i}\left(x_{j}-\mu_{i}^{\prime}\right)^{2}}{\sum_{j=1}^{m} \gamma_{j i}} \end{aligned}$

(6)$\begin{aligned}\sigma_{i}^{\prime} & =\frac{1}{m} \sum_{j=1}^{m} \gamma_{j i}\end{aligned}$

式中:模型参数由{μ_i, σ_i, α_i}更新为{μ'_i, σ'_i, α'_i}.

步骤4 迭代.基于更新后的模型参数进一步做聚类操作,返回至步骤2,重复步骤2、3,经历n轮迭代,当模型参数不再更新或者认为迭代次数足够大后,停止迭代过程.

步骤5 输出.输出最后一次更新的模型参数,算法终止,最终完成高斯混合聚类.

1.3 Category-boundary算法

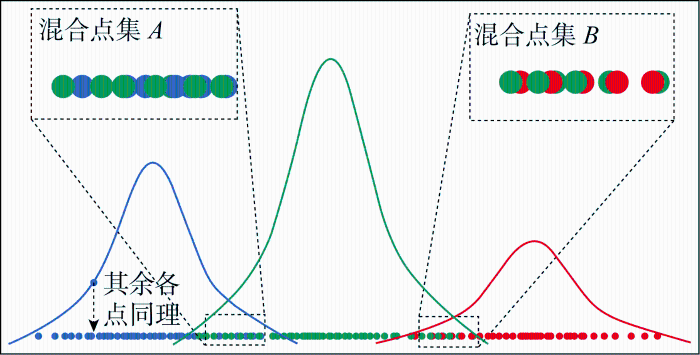
将高斯混合聚类模型应用到岩溶勘探领域时,存在两个问题:①表征不同地质构造的地球物理信号数据,在实际情况中是连续数据集,借助高斯混合聚类针对的只有物探方法采集到的数据集,即散点数据集,不同地质单元之间的类别界限未知;②在不同高斯曲线的交集部分存在多个混合数据点集,如图4所示的混合点集A、B,其中数据点可以被解释为同时服从两个高斯分布,换言之,处于这个区间的数据点所表征的物理含义存在争议,这在岩溶勘探中需尽量避免.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 高斯混合聚类结果示例

Fig.4 Example of Gaussian mixture clustering results

在机器学习领域,常取相邻高斯曲线的交点作为不同类别数据集的分类界限,基于“使高斯曲线混合区间中数据点被误判的概率最小”的原则提出Category-boundary算法,在GMM的分类结果上进一步细分,以提升分类精度.

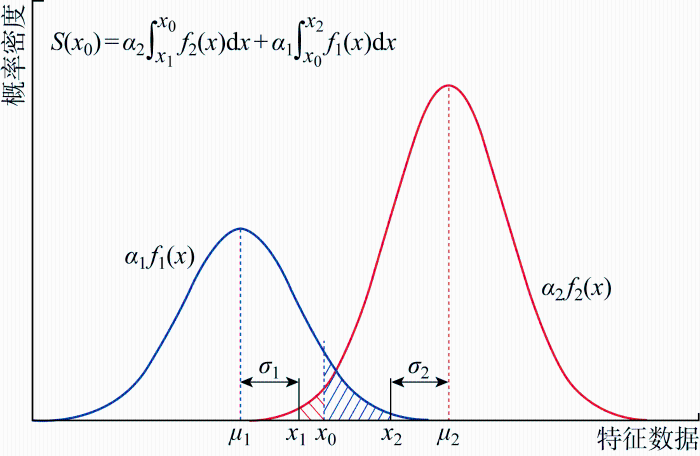
Category-boundary算法的原理如图5所示,假设类别界限为x₀,认为高斯曲线混合区间为[x₁, x₂],建立如下数学模型,表示为在选定分类界限为x₀的情况下,高斯曲线混合区间[x₁, x₂]中数据点被误判的概率为

(7)$S\left(x_{0}\right)=\alpha_{2} \int_{x_{1}}^{x_{0}} f_{2}(x) \mathrm{d} x+\alpha_{1} \int_{x_{0}}^{x_{2}} f_{1}(x) \mathrm{d} x$

式中:x₁=μ₁+σ₁作为混合区间起点;x₂=μ₂-σ₂作为混合区间终点;α₁、α₂为高斯混合模型最终输出的混合系数;f₁(x)、f₂(x)为对应高斯分布的概率密度函数.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 Category-boundary算法原理

Fig.5 Principle of Category-boundary algorithm

通过区间遍历,求出使高斯曲线混合区间中数据点被误判的概率最小的分类界限作为高斯拟合曲线,相邻类别间的最优分类界线

x₀=arg min

S_{(x_{0})}

, x₀∈[x₁, x₂]

即保证在类别界线确定后被误分的数据点最少.通过分类界限,可以对混合数据点集的数据做进一步系统的划分,从而得到更加精确的k个不同类别的数据子集,实现对高斯混合聚类结果的改进.

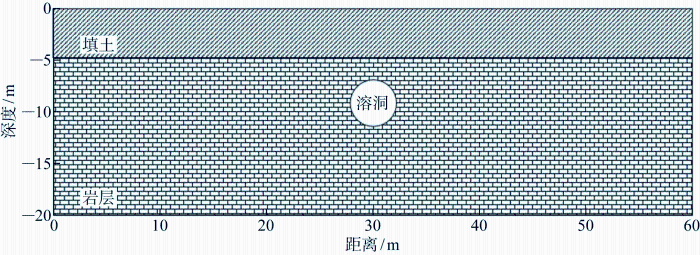
为进一步验证引入Category-boundary算法后的“改进高斯模型”的有效性,借助数值模拟的方法模拟了高密度面波法试验^[27],建立正演模型如图6所示.模型由三部分地质单元组成,分别为填土、溶洞和岩层,其中填土部分位于模型纵向4 m深度范围内,岩层部分位于4 m以下,溶洞位于岩层.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 正演模型

Fig.6 Forward modeling

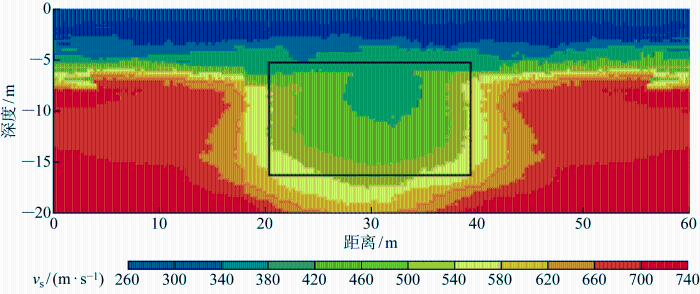
借助数值模拟获得的数据,利用传统物探反演手段计算出整个模型区间的各点剪切波速度,对不同区间的剪切波速度赋予不同颜色,其反演模型云图如图7所示.图中,黑框区域内同一深度的剪切波速度呈现出中间小周围大的现象,与实际地质构造中岩层中形成充填溶洞时,即溶洞剪切波速度小于岩层剪切波速度时,所表现的情况近似,因此判断黑色方框标记的区域存在溶洞的可能性较大,但溶洞的具体位置及大小等信息依旧无法准确判断.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 反演模型

Fig.7 Inverse modeling

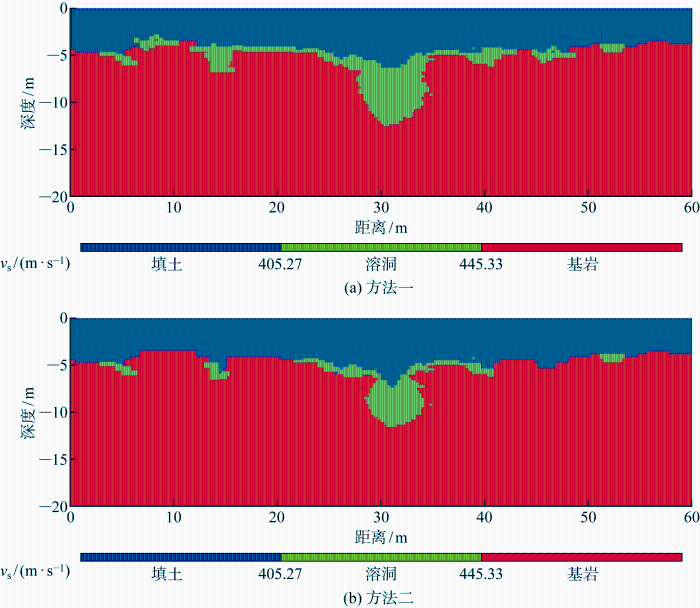
引入高斯混合聚类模型对剪切波速度数据集进行分类后,赋予不同类别不同的颜色标签,得出最终岩溶预测模型如图8所示.其中,方法一为取相邻高斯曲线的交点作为不同类别数据集分类界限所做出的岩溶预测模型见图8(a);方法二为利用 Category-boundary算法选取类别界限后所做出的岩溶预测模型见图8(b),将两图与正演模型对比,溶洞形状、大小、位置基本吻合.将预测模型中各个位置的标签信息与正演模型中对应位置的标签信息一一对比,从而计算预测模型与正演模型的整体模型吻合度.结果发现“未改进高斯混合模型”所得出的预测模型,即图8(a)模型吻合度为83.72%;引入 Category-boundary算法后的“改进高斯模型”,即图 8(b) 模型吻合度达91.06%,整体提升了约8百分点.通过对比研究结果,验证了提出Category-boundary算法对于提升整套方法预测精度的有效性.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 预测模型

Fig.8 Prediction modeling

不同物探方法具有局限性与适用性,使其分类结果不能完全对应.因此,利用高斯混合聚类模型和Category-boundary算法对不同物探试验数据划分后,重新添加位置信息,可得到多个不同的分类断面.为实现综合物探分析的目的,需对包括高密度电法和高密度面波法在内的不同物探方法所得的分类断面进行叠加融合.将地区的地质信息、相关学者研究和专家评判意见综合统一为专家经验进行融合叠加指导,从而得出最终满足工程需求的分类结果.

2 工程应用

2.1 工程背景

依托浙南某岩溶勘探工程,主要采取高密度面波法与高密度电法两种试验方法,试验现场如图9所示.根据地勘资料可以整体将该地区的地层划分为土层、溶洞、岩层三部分,因此对单个物探试验的分类均预设类别个数k_o=3.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 现场试验

Fig.9 Field test

2.2 改进的GMM分类结果

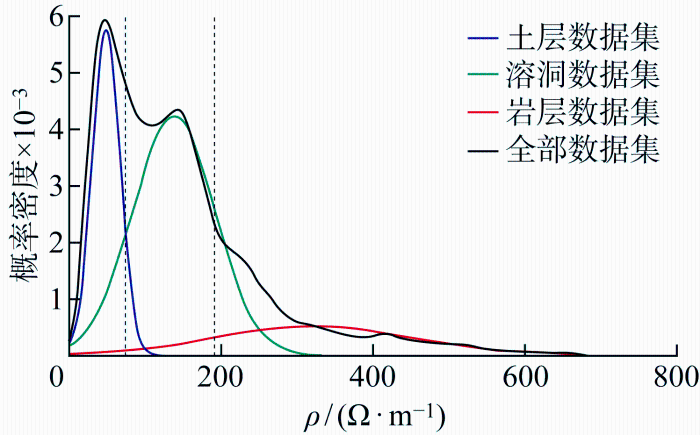
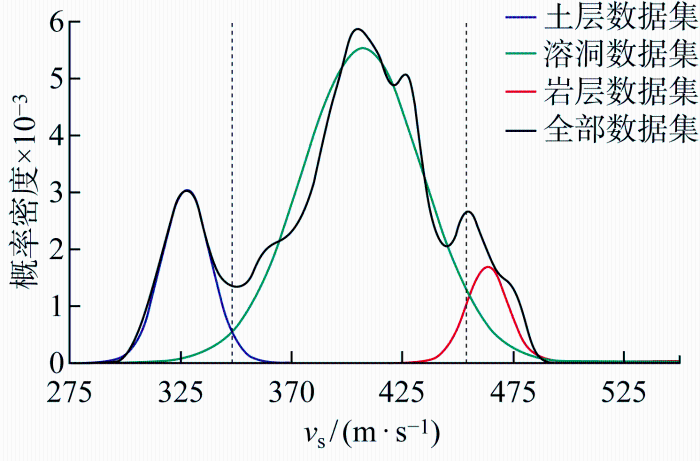
将改进的GMM分别应用于两种物探方法获得的数据集中.高密度电法数据(电阻率)的分类结果如图10所示,图中蓝色曲线表示土层数据点集服从高斯分布,绿色曲线表示溶洞数据点集服从高斯分布,红色曲线表示岩层数据点集服从高斯分布,黑色曲线表示全部电阻率数据点的概率分布曲线.不难看出3条高斯曲线近似拟合整条概率分布曲线.两条黑色虚线表示由Category boudary算法所确定的不同地质单元间的分类边界.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 高密度电法分类结果

Fig.10 Results of high-density electrical classification

高密度面波法(剪切波速度)数据的分类结果如图11所示,表示剪切波速度的高斯拟合结果,各条曲线含义与图10所代表的意义基本一致.最终确定电阻率的分类界限为75和 190 Ω·m,剪切波速度的分类界线为340和455 m/s.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 高密度面波法分类结果

Fig.11 Results of high-density surface wave method classification

2.3 分类融合

结合该工程项目的地勘报告,对剪切波速度和电阻率总结出以下分类依据.

(1) 由物理探测知识可知,岩层的剪切波速度和电阻率都大于土层 ^[28⇓-30].

(2) 该工程地勘资料显示溶洞类型为全充填,充填物主要为粗砾、砂砾和黏土,填充物的剪切波速度和电阻率均介于岩层与土层之间.

(3) 根据2.2节中改进GMM做出的分类界限确定土层与溶洞的剪切波速分类界限为 340 m/s,ρ分类界限为75 Ω·m;溶洞与岩层剪切波速的分类界限为455 m/s,ρ分类界限为190 Ω·m.

(4) 进一步综合专家意见与钻孔资料,制定分类融合叠加规则如表1所示.① 当面波法和电法分类结果表现为同一类别时,分类融合结果一致;② 面波法和电法的分类结果为“土层”和“溶洞”的组合时,分类融合的结果为“杂填土”;③ 面波法和电法的分类结果为“岩层”和“溶洞”的组合时,分类融合的结果为“粗砾~砂砾”;④ 面波法和电法的分类结果为“土层”和“岩层”的组合时,分类结果差异大,可将其定义为“未知”,以待今后进一步研究.

表1 分类融合叠加规则

Tab.1 Classification fusion superposition rule

电法分类	面波法分类
电法分类	土层 v_s≤ 340 m/s	溶洞(h>5 m) 340<v_s≤455	岩层(h>5 m) v_s>455 m/s
土层 ρ≤75 Ω·m	砂土~黏土	杂填土	未知
溶洞(h>5 m) 75<ρ≤ 190	杂填土	溶洞	粗砾~砂砾
岩层(h>5 m) ρ>190 Ω·m	未知	粗砾~砂砾	基岩

注:土层包括杂填土表层填土和黏土砂土等溶洞填充物等;岩层包括粗砾砂砾等溶洞充填物和基岩等.

新窗口打开| 下载CSV

需指出,分类融合叠加规则满足以下两个前提条件:① 溶洞和基岩只存在于5 m以下;② 两种物探试验对结果的影响程度不同,面波法由地质构造决定力学参数,受其他因素干扰小,而电法反映的是物质的电学性质,其往往容易受含水率等因素影响.因此,在二者表现为不同类别时,需更多参考面波法的分类结果,电法结果则作为补充.

2.4 分类融合结果分析

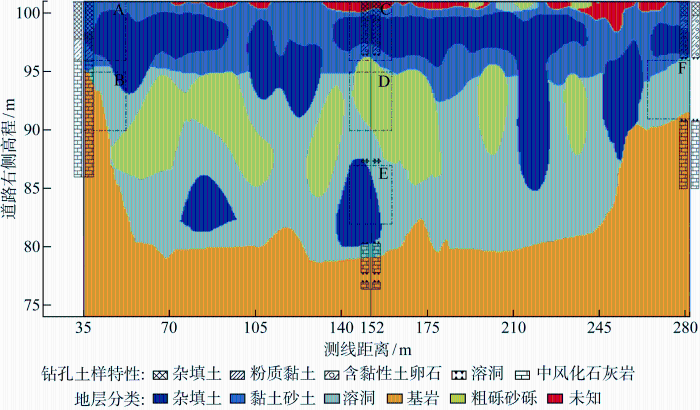
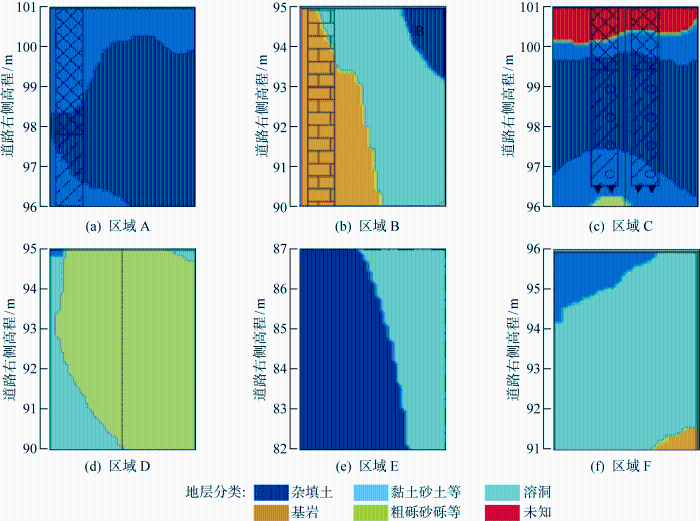
将分类融合的断面结果与实际断面钻孔信息结合,得到分类融合结果与钻孔信息对比如图12所示,其中D、E、F这3个区域钻孔取不上土样,地勘判断为溶洞.分类融合得到的“未知”区域基本位于表层,原因是表层填土所表征的地球物理信号由多种物质成分叠加而来,导致两种物探所得结果差异较大.在深度5 m范围内,分类融合结果为杂填土、黏土砂土等,在深度22 m以下范围内为基岩,与钻孔信息相吻合;在深度5~22 m范围内,分类融合所得结果丰富多样,截取含钻孔信息的6个区域,即图12中黑框A~F进行详细分析,6个区域放大图如图13所示.对截取的代表区域放大图做出如下解读.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 融合分类与钻孔信息

Fig.12 Results of integration classification and Drilling information

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 代表区域

注:DEF三个区域取不上土样,地勘判断为溶洞

Fig.13 Representative area

(1) 区域A.钻孔信息深度0~3 m为杂填土、深度3~5 m为粉质黏土,对应融合分类结果分别为杂填土和砂土~黏土,钻孔信息与分类结果基本吻合.

(2) 区域B.钻孔信息为中风化石灰岩,对应融合分类结果为基岩,钻孔信息与分类结果完全吻合.

(3) 区域C.钻孔信息深度0~2 m为杂填土,深度2~4 m为含黏性土卵石混合填土,对应融合分类的结果分别为杂填土和砂土~黏土,钻孔信息与分类结果完全吻合.

(4) 区域D.钻孔信息为全充填溶洞,充填物为灰黄色松散状粗砂,局部混少量卵石、圆砾等,对应融合分类结果为粗砾~砂砾等,钻孔信息表示为溶洞与融合分类结果存在差异,但溶洞充填物性质与融合分类结果完全吻合.

(5) 区域E.钻孔信息为全充填溶洞, 充填物为软塑状粉质黏土,混合有中粗砂等,对应融合分类的

结果为砂土~黏土,钻孔信息表示为溶洞与融合分类结果存在差异,但充填物性质与融合分类结果高度吻合.

(6) 区域F.钻孔信息为溶洞,对应融合分类结果为溶洞,钻孔信息与分类结果高度吻合.

综上所述,基于GMM的精确分类融合方法的预测结果和钻孔信息的吻合度高,可解释性强,且溶洞、土层、岩层等不同地层单元之间边界明确,溶洞轮廓清晰,能对溶洞做出精准评判.

3 结论

将机器学习方法引入传统综合物探,改进数据解释人为影响大、溶洞边界模糊等不足,通过系统研究得到以下结论:

(1) 基于GMM,提出进一步细化分类结果的Category-boundary算法,实现了对面波法和电法试验数据的自动划分,给出了土层、溶洞、岩层3种介质的电阻率和剪切波速度的分类界限,且分类结果与实际试验数据高度吻合.

(2) 实现了勘察数据驱动和工程地质知识引导的有机结合,在精细化分类数据的基础上,加入基于专家经验和勘察数据的分类规则,获得与钻孔信息吻合的溶洞预测结果,有效解决了综合物探技术预测结果人工因素影响大、边界模糊等缺点.

(3) 所建立的分类融合规则仍部分依赖专家经验和地勘资料,今后需进一步研究如何建立更加有效、准确、客观的分类融合规则.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

FORD

, WILLIAMS

P W

Karst hydrogeology and geomorphology[M]. Chichester, England: John Wiley & Sons, 2007.