泵喷推进器间隙流场尺度效应数值研究

doi:10.16183/j.cnki.jsjtu.2023.147

泵喷推进器间隙流场尺度效应数值研究

杨春¹, 郭春雨², 孙聪^,¹, 王超¹, 岳启辉¹

1.哈尔滨工程大学船舶工程学院,哈尔滨 150001

2.哈尔滨工程大学青岛创新发展中心,山东青岛 266000

Numerical Study of Scale Effects of Tip Clearance Flow Field of Pump-Jet Propulsor

YANG Chun¹, GUO Chunyu², SUN Cong^,¹, WANG Chao¹, YUE Qihui¹

1. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China

2. Qingdao Innovation and Development Center of Harbin Engineering University, Qingdao 266000, Shandong, China

通讯作者: 孙聪,副教授;E-mail:suncong@hrbeu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-04-20 修回日期: 2023-07-13 接受日期: 2023-08-7

基金资助:

黑龙江省自然科学基金(LH2021E042)

Received: 2023-04-20 Revised: 2023-07-13 Accepted: 2023-08-7

作者简介 About authors

杨春(1994—),博士生,从事泵喷推进器水动力性能数值研究.

摘要

由于泵喷推进器转子与导管之间有间隙的存在,内流场特性较复杂.为了探究尺度效应对泵喷推进器间隙流场的影响,采用非定常雷诺平均Navier-Stokes(URANS)方程和SST k-ω 湍流模型,利用全结构化网格对计算域进行离散处理,滑移网格用于处理转子和其他部件之间的相对运动.首先通过网格不确定分析来验证本文数值方法的可行性,数值计算结果与模型试验数据进行了比较,两者吻合良好;然后对3种尺度泵喷推进器模型的敞水性能进行了数值计算,从涡量场和压力场的角度进行了分析.结果表明,全进速系数下,实尺度模型的效率会提高;实尺度模型的叶梢泄漏涡(TLV)涡量溃灭提前,涡量强度更低,并且TLV涡核中心压力系数更小,间隙间的脉动压力幅值更低.

关键词： 泵喷推进器; 间隙流场; 敞水性能; 尺度效应; 滑移网格

Abstract

Due to the tip clearance of the pump-jet propulsor (PJP), the flow field characteristics in the PJP are more complicated. To explore the influence of scale effects on the tip clearance flow field of PJP, the unsteady Reynolds-averaged Navier-Stokes (URANS) equation and the SST k-ω turbulence model are used. The computational domain is discretized by structured grid, and the sliding grid is used to deal with the relative motion between the rotor and stationary components. The feasibility of the numerical method is verified by grid uncertainty analysis, and the numerical results are in good agreement with the model-scale PJP experimental data. The open water performance of the three scale PJP models is numerically calculated and analyzed from the perspective of vorticity field and pressure field. The results show that the efficiency of the full-scale PJP model will be improved under all the advance coefficients, the vorticity collapse of the full-scale PJP is earlier, the intensity is lower, the pressure coefficient of the TLV vortex core center is smaller, and the fluctuating pressure amplitude between the tip clearance is lower.

Keywords： pump-jet propulsor (PJP); tip clearance flow field; open water performance; scale effects; sliding grid

PDF (54428KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨春, 郭春雨, 孙聪, 王超, 岳启辉. 泵喷推进器间隙流场尺度效应数值研究[J]. 上海交通大学学报, 2024, 58(11): 1674-1686 doi:10.16183/j.cnki.jsjtu.2023.147

YANG Chun, GUO Chunyu, SUN Cong, WANG Chao, YUE Qihui. Numerical Study of Scale Effects of Tip Clearance Flow Field of Pump-Jet Propulsor[J]. Journal of Shanghai Jiaotong University, 2024, 58(11): 1674-1686 doi:10.16183/j.cnki.jsjtu.2023.147

泵喷推进器(pump-jet propulsor,PJP)作为一种新型推进器,相比7叶大侧斜螺旋桨,具有低噪声、效率高等特点,泵喷推进器中的导管可以有效地屏蔽一部分辐射噪声,不同形式的导管还可改善泵喷推进器的空泡性能;定子分为前置定子和后置定子,其中前置定子可以为后方转子的进流进行预旋,从而改善转子进流的条件;后置定子可以回收转子周向旋转尾流,有效提高泵喷推进器的推进效率,因此泵喷推进器被广泛应用于船舶工业.

目前国内外大多通过计算流体力学(CFD)来研究泵喷推进器的水动力性能^[1⇓-3].潘中永等^[4]基于SIMPLE算法,对不同工况下斜流式泵喷推进器水动力性能进行了数值研究.分析了其内部流场流动与不稳定性之间的关系及转子叶片表面的压力分布规律.徐顺等^[5]采用分离涡模拟(DES)方法和Zwart-Gerber-Belamri(ZGB)空化模型对喷水推进器的空化性能进行了数值模拟,研究发现斜压矩项和膨胀项主要集中在气液交界面处,会引起涡量场的重新分布,并且膨胀项的量级要大于斜压矩项;在间隙处,黏性耗散性量级较大,黏性耗散项的作用不可忽略.并且还分析了不同来流工况下泵喷推进器的外流场流动特性^[6].张明宇等^[7]利用三维反问题设计方法及计算流体力学方法对泵喷推进器进行了优化设计,通过从尺寸选型、毂径比、叶片负载分布和入流角4个方面进行优化设计,使得泵喷推进器的抗空化性能明显提高.张凯等^[8]借鉴航空发动机“处理机匣”技术,在泵喷推进器的导管内壁开设凹槽结构,达到了降低间隙梢涡强度和抑制梢涡空化的目的.李福正等^[9-10]基于雷诺平均N-S(RANS)方程和SST k-ω湍流模型,对不同转速和不同的定子参数下前置定子泵喷推进器进行了水动力性能对比.Ji等^[11]提出了一种减小泵喷推进器叶尖间隙流动的方法,即增大转子叶片的截面厚度和前倾度(95%叶尖半径),并采用SST k-ω湍流模型求解RANS方程,通过数值模拟研究了所提出的尖端修正方法的影响.潘光等^[12]采用雷诺时均方法和切应力输运湍流模型,并基于有限体积法,进行了定常水动力性能的数值模拟,建立了内外流场的一体化数值计算模型.随后还进行了非定常空化性能的数值模拟^[13].施瑶等^[14]基于Rayleigh-Plesset方程均质多相模型和滑移网格技术对泵喷推进器的空化性能进行了数值分析,考虑了转子转速、空泡数和来流速度3个因素,较为系统地分析其对泵喷推进器空化性能的影响.Wang等^[15]利用势流的方法,分析了间隙流动模型对泵喷水动力性能的影响.

对于尺度效应的研究,以往都大量集中在常规螺旋桨和导管桨.Abdel-Maksoud等^[16]和Bhattacharyya等^[17]数值对比了导管桨的尺度效应,发现实尺度下导管推力增加,而转子推力会减小.Choi等^[18]进行了吊舱螺旋桨性能的尺度效应研究,实尺度下吊舱推进器阻力比较小.Yao等^[19]研究了缩尺螺旋桨和实尺度螺旋桨的尺度效应.结果表明,螺旋桨性能的尺度效应主要是由不同的边界层流动引起的.Yang等^[20]数值研究了3种几何相似的7叶大侧斜螺旋桨的空化流体动力学和空化低频噪声谱.随着几何尺度的增大,螺旋桨推力系数增大,转矩系数减小.

泵喷推进器是导管螺旋桨模型的一种延伸,目前关于泵喷推进器尺度效应的研究还较少.Li等^[21]通过系统的计算,发现转子在高进速系数下,表现出来的尺度效应影响更大.导管的流动分离减弱,叶尖泄漏涡涡量增强,但受高进速系数的限制更显著.Yang等^[22-23]通过内部CFD进行了泵喷推进器的尺度效应研究,发现总推力和转矩系数的变化主要由转子贡献.Shirazi等^[24]通过数值和实验研究了实尺度泵喷推进器水动力性能,表明定子也会产生一定的推力,因此使泵喷推进器整体性能高达82%.孙明宇等^[25]通过求解RANS方程, 对模型尺度和实尺度的泵喷推进器敞水性能进行数值仿真, 分析尺度效应引起的水动力差异.

综上,采用数值模拟对泵喷推进器水动力性能已经进行了诸多研究,但泵喷推进器结构复杂,它的尺度效应机理还尚未完全揭开,因此本文以前置定子式泵喷推进器为研究对象,求解非定常RANS(URANS)方程,采用滑移网格技术和SST k-ω湍流模型对泵喷推进器进行数值研究,分析间隙处的涡量场和压力场差异,得到了尺度效应对泵喷推进器间隙流场的影响,为后续的试验研究和数值模拟提供一定的参考.

1 数值理论方法

1.1 控制方程

本研究采用商用CFD软件STAR-CCM+作为黏性求解器进行数值模拟.对于泵喷推进器周围的三维黏性流体流动,假设流体是不可压缩的,采用URANS方程,压力-速度耦合基于 SIMPLE 算法进行求解.控制方程如下:

(1)$\boldsymbol{\nabla} \cdot \boldsymbol{u}=0$

(2)$\rho \frac{\boldsymbol{u}}{t}+\rho \boldsymbol{u} \cdot \boldsymbol{\nabla}(\boldsymbol{u})=-\boldsymbol{\nabla} p+\boldsymbol{F}+\mu \boldsymbol{\nabla}^{2} \boldsymbol{u}$

式中:u为3个方向上的流动速度,分别为u_x、u_y和u_z;ρ为流体密度(997.561 kg/m³);p为流场压力;μ为流体的动力黏性系数(8.888 71×10^-4 Pa·s),μ=ρν,ν为流体的运动黏性系数(1.0×10^-6m²/s); F为体积力.

将连续性方程式(1)代入动量方程式(2)中的最后一项,得到:

(3)$\rho \frac{\boldsymbol{u}}{t}+\rho \boldsymbol{u} \cdot \boldsymbol{\nabla}(\boldsymbol{u})=-\boldsymbol{\nabla} p+\boldsymbol{F}+\boldsymbol{\nabla} \cdot \boldsymbol{T}$

式中:T为与黏性相关的张量,其分量可由下式进行计算:

(4)$\tau_{i j}=\mu\left(\frac{u_{i}}{x_{j}}+\frac{u_{j}}{x_{i}}\right)$

式中:x_i和x_j为空间坐标分量,i, j=1, 2, 3.

雷诺时均化是将瞬时物理量写为时间平均值和瞬时脉动值之和.对控制方程中的速度和压力进行雷诺时均化,得到时均连续性方程及RANS方程,其分量形式如下:

(5)

\frac{\partial {\bar{u}}_{i}}{\partial x_{i}}

(6)$\begin{aligned}\rho \frac{\partial \bar{u}_{i}}{\partial t} & +\rho \frac{\partial\left(\bar{u}_{j} \bar{u}_{i}\right)}{\partial x_{j}}= \\& -\frac{\partial \bar{p}}{\partial x_{i}}+f_{i}+\mu \frac{\partial}{\partial x_{j}}\left(\frac{\partial \bar{u}_{i}}{\partial x_{j}}-\rho \overline{u_{i}^{\prime}} \overline{u_{j}^{\prime}}\right)\end{aligned}$

式中:顶标“-”为各项的时均值;上标“'”为各项的脉动值.可以看出在雷诺时均化后的式(6)中引入了一个未知项-ρ $\bar{u'_{i}} \bar{u'_{j}}$ ,该未知量主要代表湍流中的雷诺应力项,其物理意义为湍流中的脉动现象对平均流动的影响.由于式(6)中的未知数增加了9个,所以方程组为不封闭的.为了使方程组有解,需要对雷诺应力项-ρ $\bar{u'_{i}} \bar{u'_{j}}$ 进行合理的假设,建立相对应的方程式或者加入其他的湍流方程,进而建立起脉动值和时均值之间的转化关系.

1.2 湍流模型

对雷诺应力项有许多种假设与计算方法,主要分为两大类,一类为雷诺应力模型,另一类为涡黏模型,其中涡黏模型的应用更具有广泛性.因为在采用涡黏模型处理湍流时,对雷诺应力项不做直接的计算,而是通过加入湍动黏度,将湍流应力表示为湍动黏度的函数.根据Boussinesq假设,不可压缩流动的雷诺应力表示为

(7)$\begin{aligned}-\rho \overline{u_{i}^{\prime}} \overline{u_{j}^{\prime}}= & \mu_{\mathrm{t}}\left(\frac{u_{i}}{x_{j}}+\frac{u_{j}}{x_{i}}\right)- \\& \frac{2}{3}\left(\rho k+\mu_{\mathrm{t}} \frac{u_{i}}{x_{i}}\right) \delta_{i j}\end{aligned}$

式中:μ_t为湍动黏度或者涡黏系数;δ_ij为Kronecker符号.湍流模型根据μ_t中微分方程的个数可以分为零方程模型、一方程模型和两方程模型.应用最为广泛的是两方程,包括标准k-ε模型、标准k-ω以及两种模型的改进模型.

本文将采用最为常见的SST k-ω模型来对方程组进行封闭.该模型是1994年由Menter^[26]提出来的一种混合模型,它结合了k-ω模型和k-ε模型各自的优点.在近壁面使用稳定的k-ω模型,而在计算域的远场使用k-ε模型.其改进后的湍流模型的湍流强度k方程和湍流频率ω分别为

(8)$\begin{array}{l}\frac{\partial}{\partial t}(\rho k)+\frac{\partial}{\partial x_{i}}\left(\rho k u_{i}\right)= \\\frac{\partial}{\partial x_{j}}\left(\Gamma_{k} \frac{\partial k}{\partial x_{j}}\right)+G_{k}-Y_{k}+S_{k} \\\end{array}$

(9)$\begin{array}{l}\frac{\partial}{\partial t}(\rho k)+\frac{\partial}{\partial x_{i}}\left(\rho \omega u_{i}\right)= \\\frac{\partial}{\partial x_{j}}\left(\Gamma_{\omega} \frac{\partial \omega}{\partial x_{j}}\right)+G_{\omega}-Y_{\omega}+S_{\omega}\end{array}$

式中:G_k和G_ω为湍流动能产生项;Γ_k和Γ_ω分别为k和ω的扩散速率;Y_k和Y_ω为湍流耗散项;S_k和S_ω为源项.

转子的旋转采用滑移网格技术进行处理,为了保证计算精度,时间步长为转子所旋转1° 所需要的时间,时间瞬态项为一阶离散,每个时间步设置5次内迭代;对流项为二阶迎风离散,扩散项目为中心差分格式.

2 数值方法与验证

2.1 几何模型

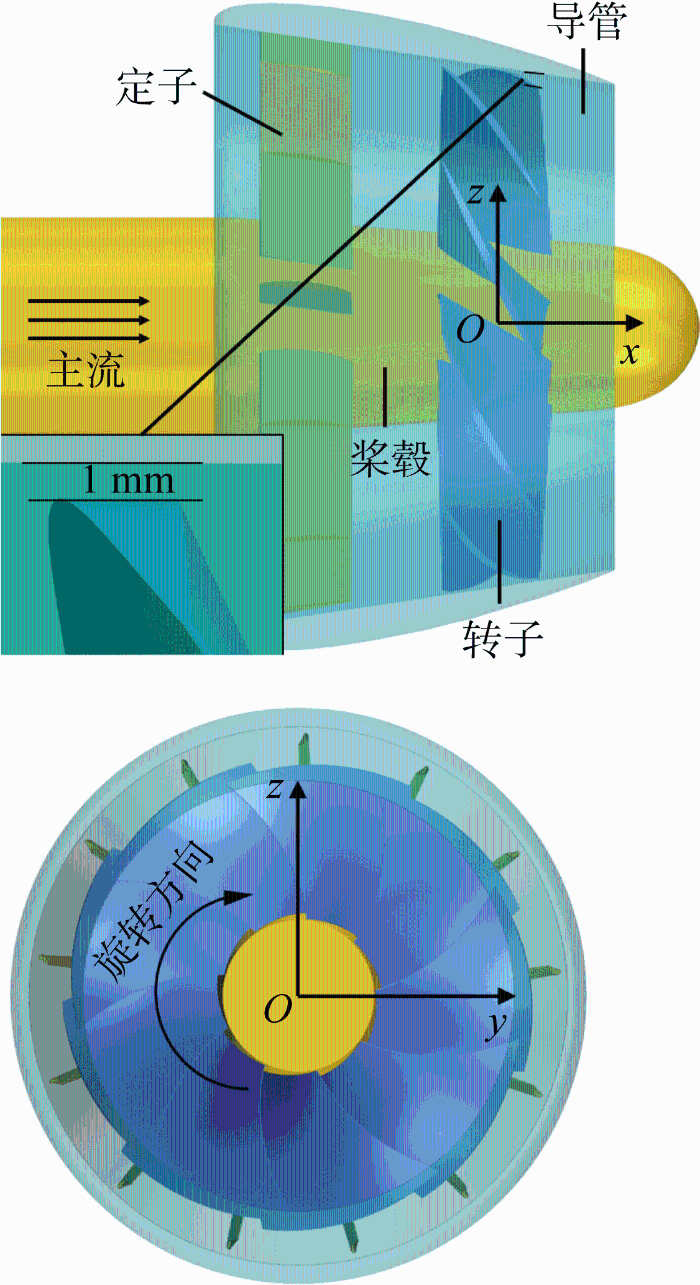
本文将选取3种尺度比例的泵喷推进器进行数值模拟,缩尺比分别为1∶3.5和1∶7.0,由13叶前置定子、9叶转子、1个导管和1个桨毂组成,三维缩尺λ=7.0数值模型和坐标系如图1所示,缩尺λ=7.0模型转子直径D=0.204 85 m,定子直径为0.229 m,导管进口直径为0.24 m,出口直径为0.192 m,导管轴向长度为0.158 m,转子与导管之间的间隙为1 mm.缩尺λ=7.0模型的转子转速为16 r/s,根据弗劳德数和进速系数相等,λ=3.5和λ=1.0模型转子转速分别为8.55 r/s和6.05 r/s.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 数值模型

Fig.1 Numerical model

为了方便对比和讨论,对泵喷推进器水动力系数进行无量纲化.进速系数J、转子推力系数K_T_r、转子转矩系数K_Q_r、定子推力系数K_T_s、导管推力系数K_T_d、泵喷推进器整体推力系数K_T、泵喷推进器整体效率η₀以及压力系数C_p定义如下:

\frac{U}{n D}

, K_T_r=

\frac{T_{r}}{ρ n^{2} D^{4}}

, K_Q_r=

\frac{Q_{r}}{ρ n^{2} D^{5}}

,
K_T_s=

\frac{T_{s}}{ρ n^{2} D^{4}}

, K_T_d=

\frac{T_{d}}{ρ n^{2} D^{4}}

, η₀=

\frac{J K_{T}}{2 π K_{Q r}}

K_T=K_T_r+K_T_s+K_T_d, C_p=

\frac{p}{0.5 ρ U^{2}}

其中:T_r和Q_r为转子的推力和转矩;T_s为定子的推力;T_d为导管的推力;n为转子转速.

2.2 计算域及网格划分

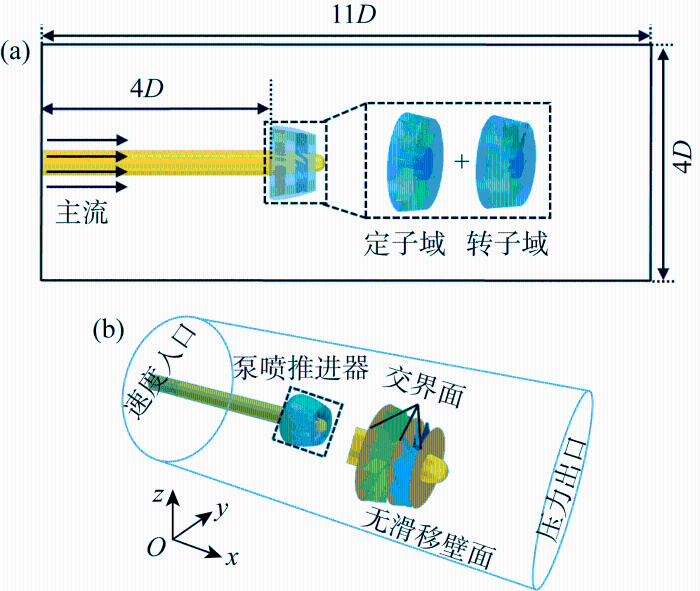
在数值模拟时,将整个计算域分为3个域,分别为包含转子叶片的转子域、包含定子叶片的定子域以及静止域.如图2所示,静止域为一个大圆柱,根据Baltazar等^[27]进行了计算域大小对螺旋桨水动力性能影响的研究,研究表明其影响很小,小于1%,因此在本文中计算域圆柱直径为4D,边界条件为无滑移壁面;入口设置在距离泵喷推进器前方4D处, 边界条件为速度入口,入口速度根据进速系数来改变;出口设置在距离泵喷推进器后方7D处,边界条件为压力出口,利用滑移网格技术来处理3套网格之间的数据交互.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 计算域及边界条件设置

Fig.2 Calculation domain and settings of boundary condition

在数值计算过程中,为了更好地得到间隙处的流场信息,全局网格采用ANSYS ICEM软件进行全结构化网格划分.为了满足缩尺模型的y⁺值控制在0~3之间,桨叶第1层网格高度应设置为8.0 μm,导管边界层网格第1层厚度为19 μm,延伸率均为1.2.为了使缩尺模型和实尺度模型的网格拓扑完全一致,只需将缩尺模型的网格放大得到实尺度模型的网格,再根据y⁺值要求调整实尺度模型下边界层网格数量.若实尺度模型y⁺值控制在1左右,将大幅增加网格数量,因此实尺度模型下调用壁面函数对边界层进行求解,实尺度模型y⁺值控制在30~350之间,桨叶第1层网格高度应设置为1.5 mm,延伸率为1.2.为了捕捉间隙处的流场细节,在间隙处布置20个网格节点,网格的详细细节如图3和图4所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 PJP网格拓扑

Fig.3 Grid topology of PJP

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 中纵剖面网格视图

Fig.4 Grid view of longitudinal section

2.3 网格不确定度分析

为了考虑网格尺寸对泵喷推进器水动力性能数值结果的影响,在进速系数J=1.1工况下对缩尺模型进行网格不确定性分析.网格生成按照 $\sqrt{2}$ 的比例进行生成3套不同数量级的网格方案,3套网格的网格拓扑完全一致.在细、中和粗3套网格下,桨叶边界层第1层厚度分别为8、11和16 μm,导管边界层网格第1层厚度分别为19、27和38 μm,间隙之间的网格节点数分别为20、14和10.不同网格具体数量如表1所示,网格如图5所示.

表1 3套不同数量的网格

Tab.1 Three different sets of grids

方案	网格	转子域	定子域	静止域	总网格数
1	细	1.06×10⁷	1.11×10⁷	8.04×10⁶	3.01×10⁷
2	中	4.86×10⁶	3.85×10⁶	2.99×10⁶	1.17×10⁷
3	粗	1.45×10⁶	1.35×10⁶	0.99×10⁶	3.79×10⁶

新窗口打开| 下载CSV

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同量级的表面网格

Fig.5 Surface meshes with different resolutions

其中Celik等^[28]在进行网格不确定度分析过程中,S₁、S₂和S₃分别为细、中和粗网格对应的数值结果,根据数值结果可以得出收敛率R_G.网格细化因子r₂₁和r₃₂分别为 1.369 97 和 1.456 98.

不确定度分析结果如表2所示.表中:P为准确度阶数精度; $φ_{e x t}^{21}$ 为外推值; $e_{a}^{21}$ 为近似相对误差; $e_{e x t}^{21}$ 为外推相对误差; $G_{f i n e}^{21}$ 为精细网格收敛指数.根据收敛率进行判断,可得出转子的推力系数K_T_r和转矩系数K_Q_r的收敛率均小于1,因此判断为单调收敛,推力系数的 $G_{f i n e}^{21}$ 最大为1.49%, 转矩系数的 $G_{f i n e}^{21}$ 最大为0.68%, $G_{f i n e}^{21}$ 的值表明增加网格数量对泵喷推进器水动力系数不会有太大的改善.表明本文网格划分是比较合理的,在后续计算中为提高流场的品质,将选择细网格进行计算.

表2 数值计算结果

Tab.2 Numerical simulation results

J=1.1	K_Tr	K_Qr
S₁	0.570 6	1.356 9
S₂	0.567 0	1.347 1
S₃	0.562 6	1.329 8
R_G	0.82	0.57
P	1.347	2.674
	0.577	1.364
/%	0.63	0.72
/%	1.18	0.54
/%	1.49	0.68

新窗口打开| 下载CSV

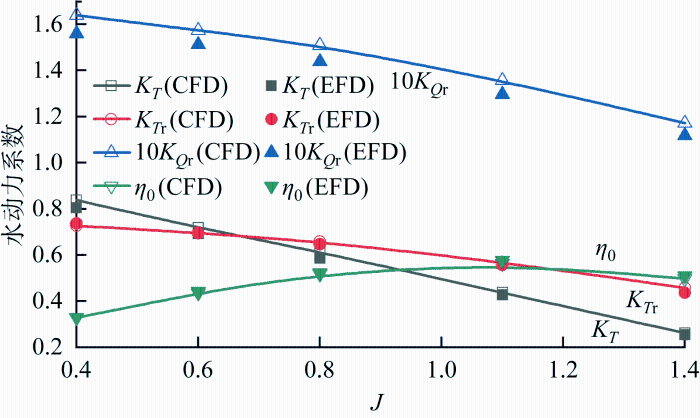
2.4 缩尺模型敞水验证

选取5个工况点,将数值结果与实验值(EFD)进行对比,如图6所示.可以看出泵喷推进器的敞水曲线与常规螺旋桨的敞水曲线变化趋势一致,转子的推力系数K_T_r和转矩系数K_Q_r均随着进速系数的增大而下降.效率呈先增大后减小的趋势,进速系数J=1.1为最佳效率点.转子推力系数K_T_r和整体推力系数K_T误差均在4.5%以下,转子转矩系数K_Q_r均在5%以下,而整体效率η₀误差在-2.5%以下,这是由转子转矩系数偏大导致.整体来说,数值计算结果与实验值吻合较好,即本文采用的数值方法和网格划分方法是合理的,可以进行后续的计算.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 缩尺模型敞水计算结果

Fig.6 Open-water calculation results for model-scale

3 数值结果及讨论

3.1 水动力系数对比

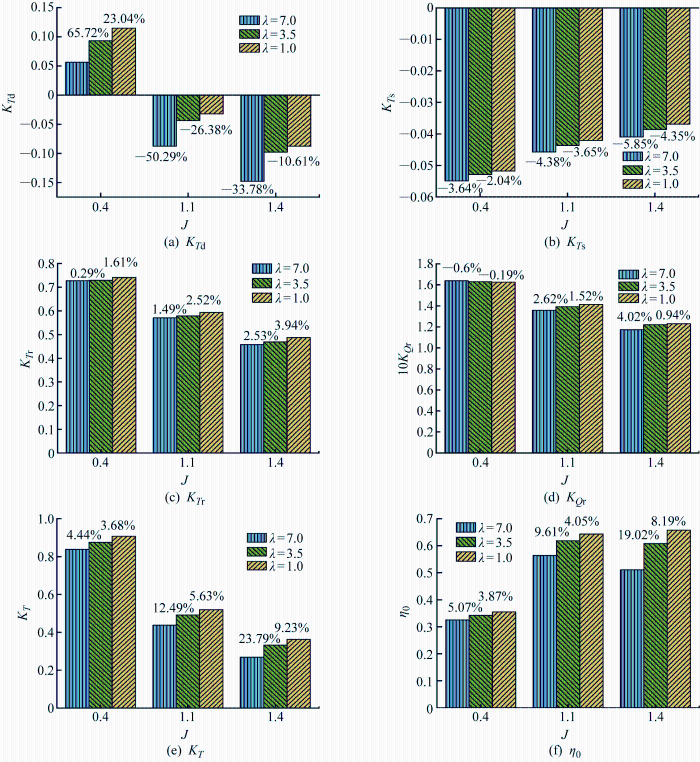
选取重载工况(J=0.4)、设计工况点(J=1.1)和轻载工况(J=1.4)对3种尺度模型(λ=1.0,3.5,7.0)的水动力系数进行分析.为了更加方便地对比相邻两种模型之间各项力系数的差异,通过公式Δ=(K_s-K_m)/K_m求得,K_s和K_m分别代表实尺度和缩尺模型的水动力系数,各系数对比结果显示在图7中.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 3种模型水动力系数对比差异

Fig.7 Differences in hydrodynamic coefficients of three models

在J=0.4下,导管力为推力,随着尺度的增大,导管推力系数也在增大;但随着进速系数的增大,导管力逐渐变为阻力,并且随着尺度的增大,导管阻力系数在减小,这是由于导管前缘和后缘边界层分离程度不同造成的.在3种尺度模型下定子的力均为阻力,随着尺度和进速系数的增大,阻力系数逐渐变小,对于转子来说,随着尺度的变大,转子推力系数逐渐增大;而转子转矩系数在重载工况J=0.4下,随着尺度的变大而减小,在J=1.1和J=1.4下,随着尺度的增大,转矩系数也在增大.对于整体效率而言,整体推力的增大使得整体效率随着尺度的增大而增大.

另外可以看出在不同进速下,各水动力系数之间的差异明显不同,导管的力系数K_T_d、K_T_r和η₀的差异变化较大;随着泵喷尺度的增大,各个水动力系数的差异明显下降.此外,导管力系数K_T_d随着进速系数的增大,差异逐渐减小,而K_T_s、K_T_r、K_T、10K_Q_r和η₀的差异均随着进速系数的增大而增大.

3.2 间隙涡量场对比

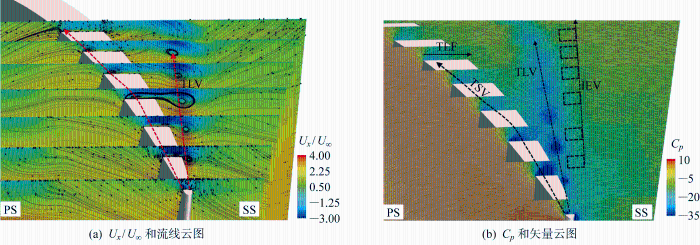
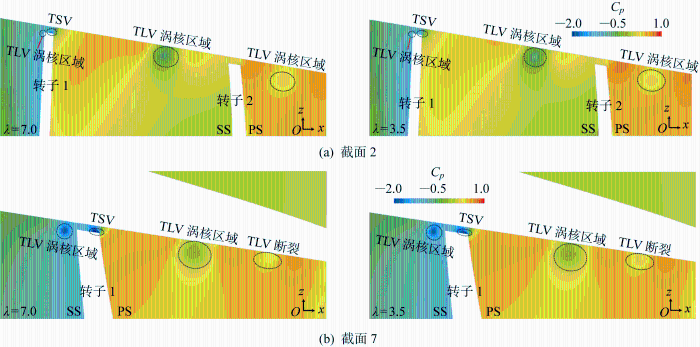
待流场计算稳定后,取转子旋转10圈后的瞬时流场进行分析.图8为缩尺λ=7.0模型泵喷推进器在J=0.4下的间隙流场云图.图中:U_x/U_∞为无因次轴向速度.可以看出转子在高速旋转过程中,泵喷的流场涡结构复杂.间隙的存在使得部分间隙流体(TLF)会从压力面(PS)回流到吸力面(SS),形成叶梢泄漏涡(TLV);在叶梢顶端也有一部分流体向着叶片顶端后方发展,形成叶尖分离涡(TSV);此外,TLV往下游发展过程中,与导管内壁上的涡相互作用形成诱导端壁涡(IEV).

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 J=0.4泵喷推进器间隙流场

Fig.8 Gap flow field of PJP at J=0.4

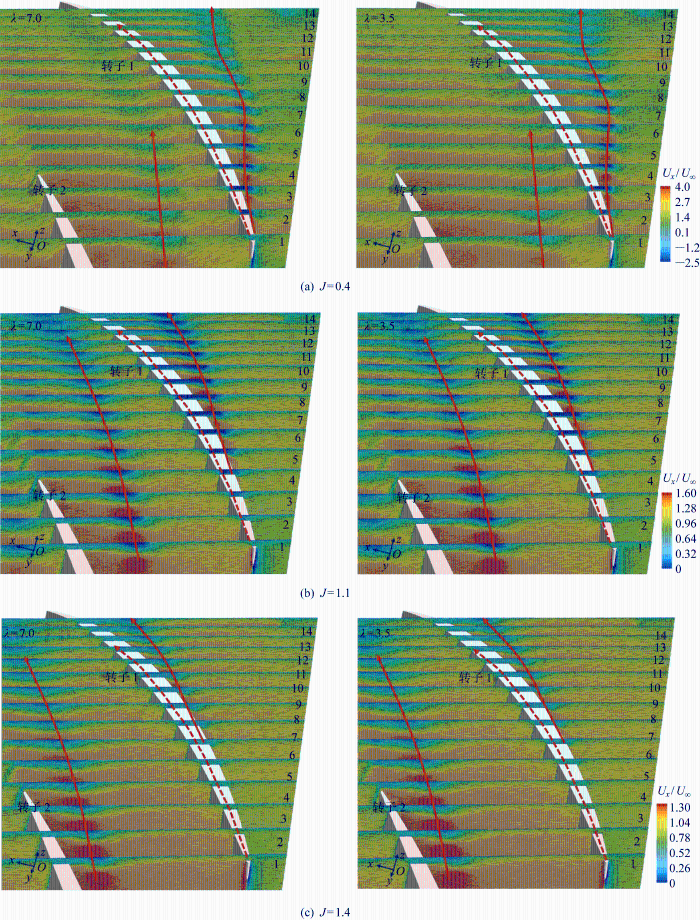
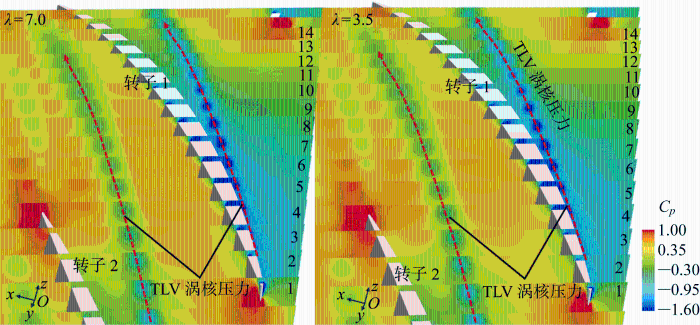
以缩尺比为λ=3.5和λ=7.0为例,图9为两种尺度模型在不同进速系数下间隙流场涡的演化路径.为了方便观察间隙处涡的运动规律,在两种尺度下从导边开始截面,一直到随边结束,截取14个截面,编号从1到14.结合图8,可以看出两种尺度模型在重载工况(J=0.4)下,泵喷主流速度较小,转子1的压力面泄涡低压中心在截面2处明显脱落,并且逐渐向转子通道后方发展,TLV与转子通道主流混合后,发生相互作用,使TLV的涡核中心压力逐渐降低,涡核强度下降.另外,转子2的TLV在向下游发展过程中,泄涡尾端会发展到转子1的压力面上,有可能会影响转子1的水动力.随着进速系数的增大,TLV的涡核低压中心脱落位置逐渐延后,在J=1.4时,低压中心在截面7开始脱落.主流速度提高后,TLV与主流的相互作用变小,TLV的整体发展路径与转子叶片的夹角变小,逐渐向下游延伸.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 两种尺度模型在不同进速系数下间隙涡的轴向速度U_x/U_∞分布

Fig.9 Distribution of axial velocity U_x/U_∞ of the gap vortex for two scale models at different advance coefficients

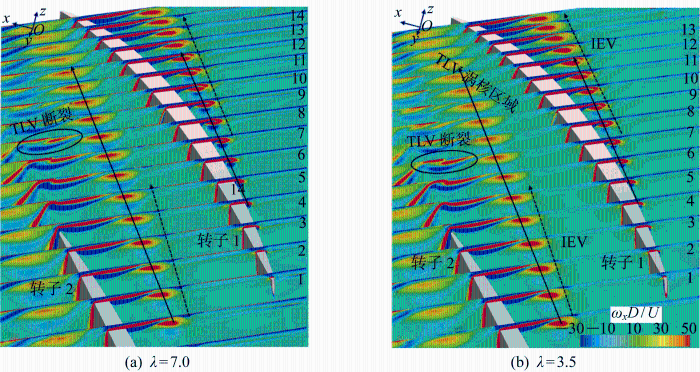
为分析尺度效应对间隙流场的影响,以缩尺比为λ=3.5和λ=7.0为例,对两种尺度模型下xOz平面下间隙涡量进行分析,如图10所示.图中:ω_xD/U为无因次间隙涡量的x分量.整体来看,两种尺度模型下涡的演化路径是一致的,TLV从压力面泄出,正涡量和负涡量在吸力侧往下游发展.λ=7.0模型的TLV涡量强度较大,TLV向下游发展过程中涡强度不断耗散,在截面8处出现断裂现象,使得涡核中心强度迅速下降;而λ=3.5模型的TLV涡量强度较小,在截面7处就出现断裂现象.此外,由于λ=3.5模型的TLV的涡核强度较小,与导管内壁涡相互作用减弱,这意味着λ=3.5模型下IEV的涡量强度也比λ=7.0模型小.图11所示为J=1.1时两种尺度模型不同截面处的涡量x分量轮廓.可以看出在截面2处TLV开始泄出,λ=7.0模型转子2的泄涡与导管内壁涡发生相互作用更强,使得IEV涡量强度更大.当TLV向下游发展到截面7时,可看出λ=3.5模型下TLV的断裂,能量快速耗散,使涡核附近的正涡和负涡强度更小,IEV甚至消失.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 J=1.1时两种尺度模型xOz平面下无因次间隙涡量x分量ω_xD/U的分布

Fig.10 The distribution of x component of gap vorticity for two scale model xOz plane at J=1.1

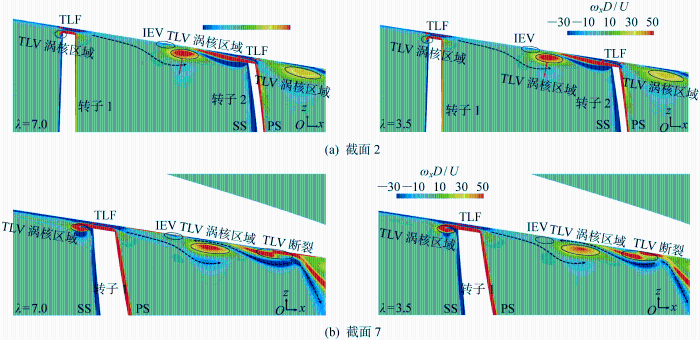
图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 J=1.1时两种尺度模型不同截面处的涡量x分量轮廓

Fig.11 Comparison of vorticity x component profile and pressure coefficient at different sections for two scale models at J=1.1

3.3 间隙压力场对比

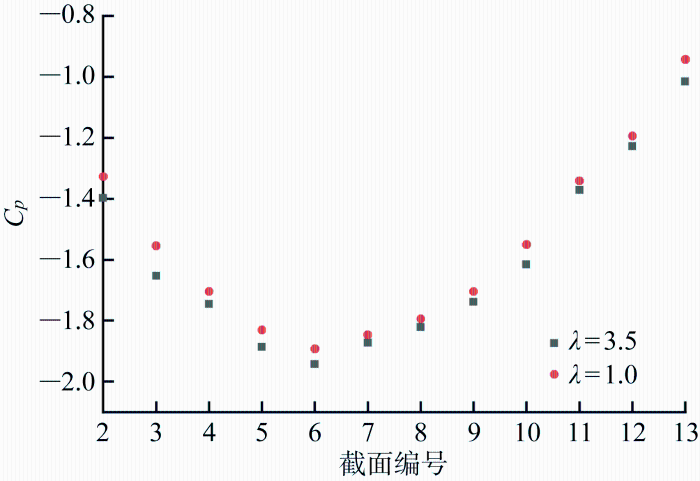
图12为J=1.1下间隙流场压力系数的对比云图.可以清晰地看出TLV从截面2处泄出,沿着吸力侧往下游发展,随着涡量强度的耗散,TLV的压力系数逐渐降低.对TLV涡核中心的压力系数进行提取,如图13所示,从曲线整体来看,两种尺度模型下TLV涡核中心压力系数的变化趋势是一致的,在截面2处泄出,压力系数绝对值逐渐增大,在截面6处压力系数绝对值达到最大值,然后继续往下游发展过程中,压力系数绝对值逐渐降低.另外,由于λ=3.5模型的TLV涡量强度更低,这也使得λ=3.5模型的涡核中心压力系数更低.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 J=1.1时两种尺度模型xOz平面下TLV涡核压力系数云图

Fig.12 Pressure coefficient of TLV vortex core at xOz plane of two scale models at J=1.1

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 TLV涡核中心压力系数曲线

Fig.13 Pressure coefficient curve of TLV vortex core center

对截面2和截面7的压力系数进行对比,如图14所示.λ=7.0除了TLV的压力系数比λ=3.5模型大之外,还可以看出λ=7.0模型在叶尖处TSV的压力系数比λ=3.5模型的大.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 J=1.1时两种尺度模型不同截面的压力系数分布

Fig.14 Pressure coefficient of TLV vortex core of two scale models at J=1.1

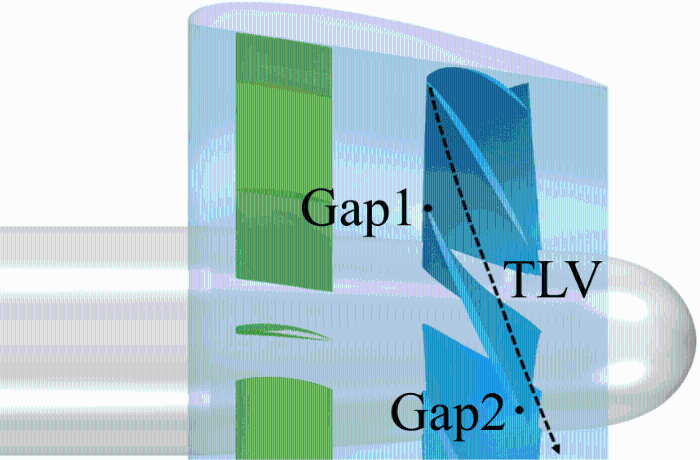
为分析间隙处的脉动压力,以J=1.1为例,在间隙之间布置两个脉动压力监测点Gap1和Gap2,如图15所示.Gap1位于转子导边,Gap2位于转子随边,图中虚线为间隙TLV的发展路径,Gap1距离TLV最远,Gap2距离TLV最近.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 脉动压力监测点设置

Fig.15 Setting of monitoring point of pulse pressure

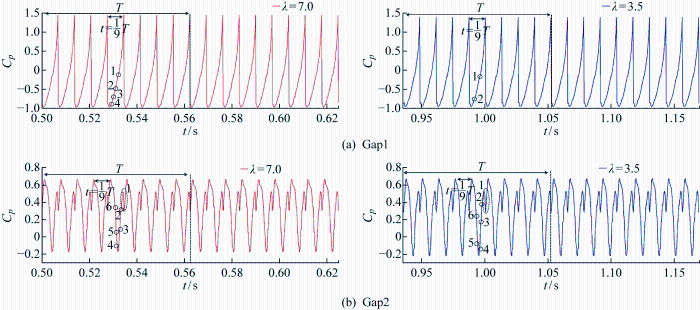
待流场数值计算稳定后,取最后2个周期T内的压力系数进行分析,图16和17分别为两种尺度模型(λ=7.0和λ=3.5)下Gap1和Gap2的脉动压力系数的时域和频域曲线,图16为两种尺度模型下各阶脉动峰值对比.从时域曲线可知,两种尺度模型下曲线均成周期性变化,由于转子叶片为9叶,意味着转子旋转一个周期内会出现9个峰值和9个谷值,相邻两个峰值之间为1/9个周期;并且两种模型下时域曲线整个周期内均有不同程度的振荡(图中黑色小圆圈),由于Gap1距离上一桨叶的TLV的发展路径较远,所以其压力系数曲线受影响较小;但λ=7.0模型的Gap1监测点压力系数在T/9内出现了4次振荡,而随着尺度的增大,λ=3.5模型只出现了两次,这可能是由于λ=3.5模型的TLV涡量强度较低.当TLV的涡量强度逐渐耗散后,在Gap2处两种尺度模型下压力系数曲线无明显差异.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 两种尺度模型下Gap1和Gap2监测点压力系数时域曲线

Fig.16 Time domain of pressure coefficients of Gap1 and Gap2 monitoring points of two scale models

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 两种尺度模型下Gap1和Gap2监测点压力系数频域曲线

Fig.17 Frequency domain of pressure coefficients of Gap1 and Gap2 monitoring points of two scale models

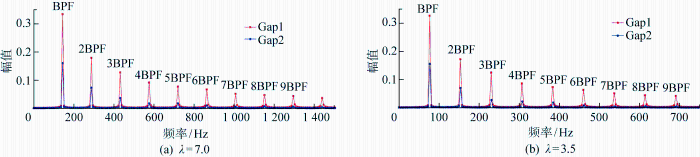
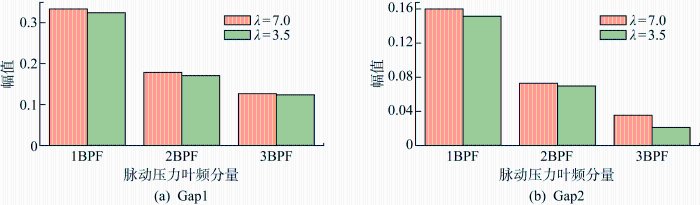
从频域曲线看出,两个监测点位于泵喷推进器的间隙处,距离桨叶最近,间隙流场复杂,因此两种尺度模型Gap1和Gap2监测点在频域上出现较多的脉动峰值,这里只比较前3个脉动峰值.其中λ=7.0模型在倍叶频(BPF)144 Hz处峰值是最大的、其次是2BPF(288 Hz)和3BPF(432 Hz)处出现峰值;同样,λ=3.5模型的监测点在BPF(76.95 Hz)、2BPF(153.9 Hz)和3BPF(231 Hz)处出现峰值.由图17和18可知,两种尺度模型下Gap1的脉动峰值均大于Gap2,而λ=7.0模型在Gap1和Gap2处各阶的脉动峰值均要大于λ=3.5模型.

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 两种尺度模型下Gap1和Gap2监测点压力系数频域峰值对比

Fig.18 Comparison of peak values of pressure coefficients in frequency domain between Gap1 and Gap2 monitoring points of two scale models

4 结论

本文基于URANS方法和SST k-ω湍流模型,首先对网格不确定度和泵喷推进器的敞水性能进行了数值验证,在结构网格上进行数值模拟,证明了结构网格的合理性.然后研究了3种尺度模型下尺度效应对泵喷推进器水动力性能的影响,重点研究了尺度效应对间隙流场涡量和脉动压力的影响,结论如下:

(1) 3种尺度模型在重载工况J=0.4下,导管力为推力,随着尺度的增大,导管推力系数K_T_d也增大;随着进速系数的增大,导管力逐渐变为阻力,但是随着尺度的增大,导管阻力系数K_T_d减小.定子阻力系数K_T_s随着尺度和进速系数的增大而逐渐变小;转子推力系数K_T_r随着尺度的变大而逐渐增大;而转子转矩系数10K_Q_r在重载工况J=0.4下,随着尺度的变大而减小,在J=1.1和J=1.4下,随着尺度的增大,转矩系数也在增大.整体效率η₀随着尺度的增大而增大.此外,K_T_s、K_T_r、K_T、10K_Q_r和η₀的差异均随着进速系数的增大而增大,效率差异最高为19.02%.

(2) 泵喷推进器间隙的存在,使得间隙处涡系统由TLF、TLV、TSV和IEV组成.由压力面泄出的TLV,在吸力侧继续往下游发展.随着进速系数的增大,主流速度增大,TLV在桨叶顶端泄出位置逐渐延后,并且TLV与对应的桨叶之间的夹角逐渐变小.随着泵喷尺度的增大,实尺度模型下转子叶尖处泄出的TLV涡量强度逐渐变低,泄涡溃灭提前,TLV与导管壁涡相互作用减弱,使得IEV涡量强度也逐渐降低.此外,随着泵喷尺度的增大,转子叶顶处TSV负压系数更小,TLV涡核中心压力系数更小,间隙流场的脉动压力频域峰值更小.

本文分析了尺度效应对间隙流场的影响,可为泵喷的设计和优化提供一定的参考.为了更详细地揭示泵喷推进器间隙流场的机理,下一步工作将基于DES或大涡模拟(LES)方法对泵喷推进器水动力性能进行数值模拟.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

QIU

, PAN

, HUANG

et al.

Numerical analysis of unsteady hydrodynamic performance of pump-jet propulsor in oblique flow

[J]. International Journal of Naval Architecture and Ocean Engineering, 2020, 12: 102-115.