考虑多重不确定性因素的可靠性指标计算与备用容量优化

doi:10.16183/j.cnki.jsjtu.2022.366

考虑多重不确定性因素的可靠性指标计算与备用容量优化

叶伦¹, 欧阳旭¹, 姚建刚^,¹, 杨胜杰², 尹骏刚¹

1.湖南大学电气与信息工程学院,长沙 410082

2.湖南工商大学计算机学院,长沙 410205

Reliability Index Calculation and Reserve Capacity Optimization Considering Multiple Uncertainties

YE Lun¹, OUYANG Xu¹, YAO Jiangang^,¹, YANG Shengjie², YIN Jungang¹

1. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China

2. School of Computer Science, Hunan University of Technology and Business, Changsha 410205, China

通讯作者: 姚建刚,教授,博士生导师,电话(Tel.):0731-88821872;E-mail:yaojiangang@126.com.

责任编辑: 王一凡

收稿日期: 2022-09-19 修回日期: 2022-10-7 接受日期: 2022-11-10

基金资助:

湖南省教育厅重点项目(21A0385)
湖南省自然科学基金面上项目(2022JJ30214)

Received: 2022-09-19 Revised: 2022-10-7 Accepted: 2022-11-10

作者简介 About authors

叶伦(1992-),博士生,从事电力系统优化、辅助服务市场研究.

摘要

在含高比例可再生能源的电力系统中,考虑多重不确定性因素并实现源荷协调的优化调度是电力系统运行的重要问题.为此,构建了基于多场景的概率性旋转备用优化模型,该模型综合考虑了风电和光伏出力预测误差、负荷预测误差及发电机非计划停运等多重不确定性因素对旋转备用容量的影响,将可再生能源弃电、系统切负荷分别作为特殊的备用资源融入发电日前调度计划,以提高电力系统的经济运行效率.改进了系统可再生能源削减期望和电量不足期望值两个可靠性指标的计算方法,减少了与该指标相关的不等式约束条件,用于提升模型的计算性能.该备用优化模型在兼顾场景多样性的同时,实现了多场景下系统的总成本最优.以改进的IEEE-RTS系统作为算例,验证了所提模型的有效性.算例结果表明,改进的可靠性指标计算方法能够有效降低备用优化模型的求解时间;建立的最优旋转备用优化方法能够实现系统日前旋转备用容量的动态配置,提升系统经济运行水平.

关键词： 可再生能源; 旋转备用; 可靠性指标; 安全约束机组组合; 成本效益分析

Abstract

In power systems with a high proportion of renewable energy, to achieve coordinated optimal scheduling of source and load considering multiple uncertainties is an important issue in power system operation. Therefore, a probabilistic spinning reserve optimization model based on multiple scenarios is constructed. Multiple uncertain factors are considered in the model, such as wind power and solar power forecast errors, load forecast error and unscheduled generator outage. Renewable energy curtailment and load shedding are used as special reserve resources in the day-ahead security-constrained unit commitment (SCUC) to improve the economic operation efficiency. The calculations of reliability indexes, expected energy not served and expected energy curtailment, are simplified, and the inequality constraints related to these two indexes are reduced, which improves the computational performance of the model. The model optimizes the total expected cost considering multiple uncertainties. Case studies based on the IEEE-RTS demonstrate the effectiveness of the proposed model. The numerical results show that the improved calculation method of reliability indexes can effectively reduce the solution time of the SCUC model. The reserve optimization model can realize the dynamic allocation of the spinning reserve capacity of the system and improve economic operation of the system.

Keywords： renewable energy; spinning reserve; reliability index; security-constrained unit commitment; cost-benefit analysis

PDF (1413KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

叶伦, 欧阳旭, 姚建刚, 杨胜杰, 尹骏刚. 考虑多重不确定性因素的可靠性指标计算与备用容量优化[J]. 上海交通大学学报, 2024, 58(1): 30-39 doi:10.16183/j.cnki.jsjtu.2022.366

YE Lun, OUYANG Xu, YAO Jiangang, YANG Shengjie, YIN Jungang. Reliability Index Calculation and Reserve Capacity Optimization Considering Multiple Uncertainties[J]. Journal of Shanghai Jiaotong University, 2024, 58(1): 30-39 doi:10.16183/j.cnki.jsjtu.2022.366

大力发展风电、光伏等可再生能源是应对能源安全、环境污染,实现“碳达峰”“碳中和”目标的重大需求^[1-2].截至2021年底,我国风电装机328 GW,光伏发电装机306 GW,二者已分别占全国总发电装机容量的16.5%和12.9%.预计到2030年,我国风电、太阳能发电总装机容量将达到120 GW以上.风电、光伏等可再生能源出力具有波动性、间歇性和不确定性等特点,大规模可再生能源并网运行需要电力系统安排额外的备用容量以确保系统的可靠性,对系统的灵活调节能力提出了新的要求.现行的电网运行规则中一般采用确定性的方式确定系统的备用容量配置,如最大在线机组容量或者负荷的一定比例等,这种近似“一刀切”的确定性方式过于粗放,容易造成备用资源的浪费,已难以适应高比例可再生能源的并网运行需求.因此,需要综合考虑各种不确定性因素,采用更合理的方式实现备用容量的优化配置,提高电力系统的经济运行效率.

目前,针对可再生能源并网系统备用容量的优化问题,已有了广泛的研究.文献[3-4] 中采用正态分布模型描述净负荷的预测误差,结合机组停运容量概率表(Capacity Outage Probability Table,COPT)和净负荷预测误差评估系统电量不足期望值(Expected Energy Not Served,EENS),采用成本效益方法确定最优旋转备用容量.文献[5]中提出一种概率性安全约束机组组合(Security-Constrained Unit Commitment, SCUC)模型,模型中考虑了机组故障、负荷和风电出力的不确定性,建立了考虑常规机组运行状态的EENS计算方法.文献[6]中考虑将需求侧响应和储能作为备用资源,将EENS和失负荷概率(Loss of Load Probability, LOLP)作为系统的可靠性约束,计及可靠性约束进行发电和备用协调优化.然而,考虑机组故障和净负荷预测误差时,可靠性指标EENS和LOLP通常为非线性表达式,大幅增加了SCUC模型的复杂性.文献[7]中在文献[5]的基础上改进了可靠性指标EENS的计算方法,优化了EENS表达式中的0-1变量,大幅提高了SCUC的计算效率.文献[8]中考虑机组故障、负荷的随机波动、风电和光伏出力的不确定性,建立了可靠性约束的机组组合模型.

随着可再生能源并网比例的增加,系统需要安排足够的负备用容量以应对可再生能源的波动性和不确定性^[9].文献[10]中综合考虑风电预测误差、负荷波动及发电机非计划停运不确定性因素对旋转备用的需求,将弃风、可中断负荷分别作为部分负、正旋转备用融入发电日前调度计划,建立了基于多场景的概率性日前机组组合优化模型,同时优化了正负备用容量.文献[11]中将负荷和风电预测误差建模为等效的机组停运容量,改进了机组停运容量概率表,建立了备用互济的分散协调调度模型.文献[12]中分析了负备用对电力系统运行和可靠性的影响.文献[13]中结合碳交易机制和风电、火电的运行特征,建立了碳交易环境下含风电电力系统短期生产模拟模型.文献[14]中构建了基于光热电站出力灵活调度的多源电力系统随机机组组合优化调度模型,该模型在各场景中考虑了风电、光伏的弃电惩罚.文献[15]中分析了风电的调度模式,建立了考虑风电降载的电力系统鲁棒备用调度模型.然而,以上文献研究大多考虑单一或几种不确定性因素,未充分考虑风电和光伏出力预测误差、负荷预测误差及发电机非计划停运等多重不确定性因素对系统可靠性的影响.同时,采用场景分析法计算系统的EENS和弃风、弃光量等指标时,通常需要采样大量的场景以获得较高的精度,进而大幅增加备用优化问题的求解难度.因此,需要对大量场景进行合理地简化,优化系统可靠性指标的计算方法,进而提升备用优化问题的求解速度.

基于以上研究现状,本文构建了基于多场景的源荷协调备用优化模型.该模型综合考虑了风电和光伏出力预测误差、负荷预测误差及发电机非计划停运等多重不确定性因素对旋转备用容量配置的影响,将可再生能源弃电、系统切负荷分别作为特殊的备用资源融入日前发电调度计划.将该模型建立为混合整数线性规划问题,并通过线性松弛的方式简化了系统EENS和能源削减期望值(Expected Energy Curtailment,EEC)两个可靠性指标的计算方法,减少了与该指标相关的不等式约束条件,提升了模型的计算性能.所提备用优化模型兼顾了场景多样性,使能源削减和负荷削减在应对系统预测误差很大的小概率、高风险场景下发挥重要作用,实现了多个场景集下的综合成本最优和系统正、负旋转备用容量的优化配置.算例表明,建立的可靠性指标计算方法能够加快SCUC模型的求解速度;最优旋转备用优化模型能够实现系统日前旋转备用容量的动态配置,提升系统经济运行水平.

1 电力系统不确定性因素建模

1.1 负荷不确定性模型

负荷是电力系统中主要的不确定性因素之一.虽然负荷需求是随机变化的,但其具有较强的周期性和规律性,目前,在负荷预测的研究和应用方面均已经取得了比较高的预测准确度.在日前辅助服务市场的相关应用中,负荷预测误差通常被认为服从零均值的正态分布^[3-4]:

${D^{A}}_{t}$ =D_t+

${e^{D}}_{t}$

(1)

σ_D,_t=

$\frac{e_{L F}}{100}$ D_t

(2)

式中: ${D^{A}}_{t}$ 和D_t分别表示t时段系统负荷的实际值和预测值; ${e^{D}}_{t}$ 表示负荷预测误差;σ_D,_t表示负荷预测误差的标准差;e_LF为表征预测工具精度的比例系数.

1.2 风电出力不确定性模型

受自然来风等因素的影响,风电出力呈波动性和不确定性等特点.对于风电出力的预测误差分布,目前尚没有一个统一的模型来描述,常用的预测误差分布模型包括正态分布^[3]和贝塔分布^[16].然而,在大规模风电并网的电力系统中,由于风电场在地理位置上的广泛分布,根据中心极限定理,总的风电出力预测误差可以被认为服从零均值的正态分布^[5].文献[3]中给出了日前市场中风电出力预测误差与预测值的关系式如下:

${P^{A}}_{W, t}$

${P^{F}}_{W, t}$

${e^{W}}_{t}$

(3)

σ_W,_t=

$\frac{1}{5} P_{W, t}^{F}$ +

$\frac{1}{50} P_{W}^{c a p}$

(4)

式中: $P_{W, t}^{A}$ 和 $P_{W, t}^{F}$ 分别表示t时段风电出力的实际值和预测值; ${e^{W}}_{t}$ 表示风电出力预测误差;σ_W,_t表示风电出力预测误差的标准差; $P_{W}^{c a p}$ 表示风电场总装机容量.

1.3 光伏出力不确定性模型

光伏发电与风力发电类似,具有波动性和不确定性的特点.光伏出力受太阳辐射的影响还具有昼发夜停的特性,并且光伏大发与负荷高峰的时段具有一定的匹配度^[14].光伏出力预测误差可以用零均值的正态分布来描述,光伏出力预测误差与预测值的关系式如下^[14,17]:

$P_{P V, t}^{A}$

$P_{P V, t}^{F}$

$e_{t}^{P V}$

(5)

σ_PV,_t=

$\frac{1}{5} P_{P V, t}^{F}$

(6)

式中: $P_{P V, t}^{A}$ 和 $P_{P V, t}^{F}$ 分别表示t时段光伏出力的实际值和预测值;σ_PV,_t表示光伏出力预测误差的标准差.

1.4 净负荷不确定性模型

系统净负荷定义为系统负荷减去风电和光伏的出力值,即需要由系统中的其他发电源进行平衡的负荷值^[5].假设负荷、风电出力和光伏出力的预测误差不相关,则系统净负荷预测误差也服从均值为零的正态分布^[8].系统净负荷预测误差与预测值的关系式如下:

$D_{t}^{N L, A}$ =D_t-

$P_{W, t}^{F}$ -

$P_{P V, t}^{F}$ =

$D_{t}^{N L}$ +

$e_{t}^{N L}$

(7)

σ_NL,_t=

$\sqrt{(σ_{D, t})^{2} + (σ_{W, t})^{2} + (σ_{P V, t})^{2}}$

(8)

式中: $D_{t}^{N L, A}$ 和 $D_{t}^{N L}$ 分别表示t时段系统净负荷的实际值和预测值; $e_{t}^{N L}$ 表示净负荷预测误差;σ_NL,_t表示净负荷预测误差的标准差.

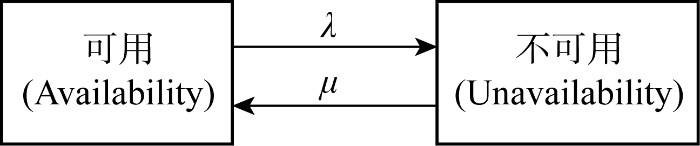
1.5 发电机不确定性模型

常规机组的短期发电模型可以用两状态马尔可夫模型来表示^[18],如图1所示.发电机的故障率和修复率分别用λ和μ表示,假设发电机平均无故障工作时间与平均修复时间均为指数分布,如果已知机组在t=0时刻是正常运行状态,则在投运前导时间(Lead Time)T^L内机组i不可用的概率U_i(T^L)和处于可用状态的概率A_i(T^L)分别为^[6]

U_i(T^L)≈λ_iT^L=

$O_{i}^{R R}$

(9)

A_i(T^L)=1-

$O_{i}^{R R}$

(10)

式中: $O_{i}^{R R}$ 表示机组i的停运替代率.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 发电机两状态模型

Fig.1 Two-state model of generator

2 可靠性指标建模

2.1 EENS

当系统净负荷的实际值大于预测值,且系统中可用的正旋转备用容量不足时,需要削减部分负荷以使系统的供需达到平衡.EENS衡量了负荷电量供应不足的期望值,可在计算系统全部运行场景下的切负荷量以及对应场景概率的基础上,通过概率加权得到.由于多机组同时发生故障的概率很低,且会增加计算负担,因此本文的研究中,只考虑单一机组的故障,然而,在规划计算中应考虑多机组故障事件.

系统中仅机组i发生故障而所有剩余发电机组均处于正常运行状态的概率为^[19]

p_i_,_t=u_i_,_tU_i

$\prod_{i' \in G_{C}, i' \neq i}$ (1-u_i'_,_tU_i')

(11)

式中:u_i_,_t为表示机组运行状态的0-1变量,1表示机组i在时段t处于开机状态;G_C表示常规机组的集合.通过将式(11)中乘积展开中的高阶项替换为上界,单一机组故障的概率可以进一步近似为^[5]

p_i_,_t≈u_i_,_tU_i

(12)

根据场景中发电机组的实际运行情况,可计算该场景下系统可用正旋备用容量 $R_{s, t}^{A U}$ 的冗余或不足:

$R_{s, t}^{A U}$ =

$\sum_{i \in {G^{A}}_{s, t}} {R^{U}}_{i, t}$ -

$\sum_{i' \in {G^{U}}_{s, t}}$ P_i'_,_t

(13)

式中: ${G^{A}}_{s, t}$ 和 ${G^{U}}_{s, t}$ 分别表示在时段t和场景s中可用机组和不可用机组的集合; ${R^{U}}_{i, t}$ 表示机组i在时段t提供的正旋转备用容量;P_i'_,_t表示不可用机组i'在时段t的出力.需要注意的是,当s=0时, ${G^{U}}_{s, t}$ 为空集,即所有发电机均处于正常运行状态.

式(7)中的净负荷预测误差 $e_{t}^{N L}$ 为连续的随机变量,不利用于优化计算,可以考虑将该连续变量近似为一组离散变量^[3].本文将净负荷预测误差离散为N_K个奇数分段,每个分段的宽度为预测误差的标准差σ_NL,_t,以每个分段的中间值作为该分段的预测误差,则第k个预测误差分段值为

$e_{t, k}^{N L}$ =

$(k - \frac{N_{K} + 1}{2})$ σ_NL,_t

(14)

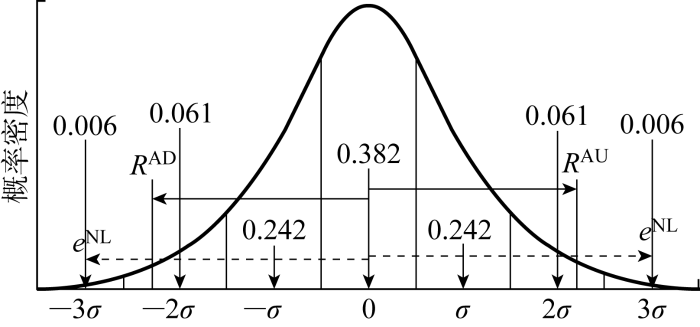
N_K值越大,计算结果的准确性越高,但需要的计算资源也就更多.图2显示了净负荷预测误差正态分布的7分段示意图.图中:R^AD为可用的负旋转备用.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 净负荷预测误差的7分段示意图

Fig.2 Seven-interval approximation of the Gaussian distribution for the net load

将发电机组故障停运和净负荷预测误差两方面的不确定性结合,获得系统全部场景下的功率不平衡量:

$P_{s, t, k}^{I m b}$ =

$(k - \frac{N_{K} + 1}{2})$ σ_NL,_t+

$\sum_{i' \in {G^{U}}_{s, t}}$ P_i'_,_t

(15)

系统功率不平衡场景中存在以下两种风险:① 功率不平衡量大于0,即系统出现功率缺额,若此时系统可用的正旋转备用不足,则可能发生失负荷事件;② 功率不平衡量小于0,即系统出现功率盈余,若此时系统可用的负旋转备用不足,则可能发生弃风、弃光等事件.正旋转备用不足容量Δ $P_{s, t, k}^{L C}$ 可由下式表示:

$P_{s, t, k}^{L C}$ =max

$\{e_{t, k}^{N L} - R_{s, t}^{A U}, 0\}$

(16)

若Δ $P_{s, t, k}^{L C}$ =0,说明该场景中,系统预留的正旋转备用容量能够应对系统中的不确定性因素;若Δ $P_{s, t, k}^{L C}$ >0,说明该场景中,系统预留的正旋转备用容量不足以应对系统中的不确定性因素,需要削减部分负荷以达到平衡,此时,Δ $P_{s, t, k}^{L C}$ 即为负荷削减量.

最后,将每个场景中负荷的削减量用相应场景的概率加权并求和,即可得到系统在每个时段的电量不足期望值^[5]:

$E_{t}^{E N S}$ =

$\overset{N_{S}}{\sum_{s = 0}} E_{s, t}^{E N S}$ p_s_,_t

(17)

$E_{s, t}^{E N S}$ p_s_,_t=

$\overset{N_{K}}{\sum_{k = 1}}$ π_k(

$e_{t, k}^{N L}$ -

$R_{s, t}^{A U}$ )b_s_,_t_,_ku_s_,_tU_s

(18)

b_s_,_t_,_k=

$\{\begin{array}{l} 1, e_{t, k}^{N L} - R_{s, t}^{A U} \geq 0 \\ 0, e_{t, k}^{N L} - R_{s, t}^{A U} < 0 \end{array}$

(19)

式中:N_S为机组故障的场景数,本章考虑的是单一机组故障,因此N_S等于机组数量加1; $E_{s, t}^{E N S}$ 为时段t和场景s中的EENS;π_k为净负荷预测误差第k分段的概率;b_s_,_t_,_k为0-1辅助变量,当在场景s和净负荷预测误差的第k分段产生了负荷削减时,该变量为1,否则为0. $E_{s, t}^{E N S}$ p_s_,_t为两个0-1变量(b_s_,_t_,_k, u_s_,_t)和一个连续变量( $e_{t, k}^{N L}$ - $R_{s, t}^{A U}$ )乘积的非线性项,可以通过以下3种方法进行等价线性变换.

2.2 EENS的线性化

2.2.1 传统方法

文献[5]中基于大M法,通过引入一个0-1变量a_s_,_t_,_k,一个连续变量L_s_,_t_,_k和若干不

等式约束,给出了式(18)的线性化表达:

$E_{s, t}^{E N S}$ p_s_,_t=

$\overset{N_{K}}{\sum_{k = 1}}$ π_kL_s_,_t_,_kU_s

(20)

-M(1-a_s_,_t_,_k)+

$e_{t, k}^{N L}$ -

$R_{s, t}^{A U}$ ≤L_s_,_t_,_k≤

$e_{t, k}^{N L}$ -

$R_{s, t}^{A U}$ +M(1-a_s_,_t_,_k)

(21)

-Ma_s_,_t_,_k≤L_s_,_t_,_k≤Ma_s_,_t_,_k

(22)

$\begin{array}{l} a_{s, t, k} \leqslant b_{s, t, k}, \quad a_{s, t, k} \leqslant u_{s, t} \\ a_{s, t, k} \geqslant b_{s, t, k}+u_{s, t}-1 \end{array}$

(23)

b_s_,_t_,_k≤b_s_,_t_,_k₊₁

(24)

$\frac{N_{K} + 1}{2}$ +

$\frac{e_{t, k}^{N L}}{σ_{N L, t}}$ ≥

$\overset{N_{K}}{\sum_{k = 1}}$ b_s_,_t_,_k≥(N_K-1)/2+

$e_{t, k}^{N L}$ /σ_NL,_t

(25)

式(21)~(22)为0-1变量和连续变量乘积的线性变换;式(23)为0-1变量乘积的线性变换;式(24)~(25)表示净负荷预测误差的第k分段出现负荷削减时,位于k右侧的净负荷预测误差分段均会出现负荷削减.

2.2.2 改进方法

(1) 改进方法1.文献[7]中结合式(18)中不同变量之间的联系,通过引入绝对值运算,将式(18)改写为如下表达式:

$E_{s, t}^{E N S}$ p_s_,_t=

$\overset{N_{K}}{\sum_{k = 1}}$ (

$e_{t, k}^{N L}$ -

$R_{i, t}^{A U}$ )π_kb_s_,_t_,_ku_s_,_tU_s=

$\overset{N_{K}}{\sum_{k = 1}} \frac{|e_{t, k}^{N L} u_{s, t} - R_{i, t}^{A U}| + e_{t, k}^{N L} u_{s, t} - R_{i, t}^{A U}}{2}$ π_kU_s

(26)

在最小化问题中,绝对值运算可以进行如下等价变换:

r=|x|⇔

$\{\begin{array}{l} r \geq x \\ r \geq - x \end{array}$

(27)

因此,式(26)可以进一步改写为如下表达式:

$E_{s, t}^{E N S}$ p_s_,_t=

$\overset{N_{K}}{\sum_{k = 1}} \frac{r_{s, t, k} + e_{t, k}^{N L} u_{s, t} - R_{i, t}^{A U}}{2}$ π_kU_s

(28)

-r_s_,_t_,_k≤

$e_{t, k}^{N L}$ u_s_,_t-

$R_{s, t}^{A U}$ ≤r_s_,_t_,_k, r_s_,_t_,_k≥0

(29)

式中:r_s_,_t_,_k为引入的辅助变量.

针对式(18)中非线性项 $E_{s, t}^{E N S}$ p_s_,_t的线性化,传统方法需要引入两个0-1变量a_s_,_t_,_k和b_s_,_t_,_k,一个连续变量L_s_,_t_,_k,以及若干与这3个变量相关的不等式约束;而改进方法1仅需要引入一个连续变量r_s_,_t_,_k.因此,相对于传统方法,改进方法1减少了2×N_S×N_T×N_K (N_T为调度时段数)个0-1变量,以及与这些0-1变量相关的不等式约束.采用改进方法1后,优化计算的效率可以得到大幅提高.

(2) 改进方法2,即本文所提方法.在改进方法1的基础上,采用线性松弛的方式,对式(28)~(29)进一步简化:

$E_{s, t}^{E N S}$ p_s_,_t=

$\overset{N_{K}}{\sum_{k = 1}} r_{s, t, k}^{a u}$ π_kU_s

(30)

$r_{s, t, k}^{a u}$ ≥

$e_{t, k}^{N L}$ u_s_,_t-

$R_{s, t}^{A U}$ ,

$r_{s, t, k}^{a u}$ ≥0

(31)

式中: $r_{s, t, k}^{a u}$ 为引入的辅助变量.

式(30)~(31)减少了式(26)中的绝对值运算,可以证明式(30)~(31)和式(28)~(29)是等效的.u_s_,_t为0-1变量,因此考虑以下两种可能的条件:

(a) u_s_,_t=0.u_s_,_t=0表示与场景s对应的机组处于停机状态,其出力P_s_,_t=0,在此条件下系统预测误差为

$e_{t, k}^{N L}$ u_s_,_t-

$R_{s, t}^{A U}$ =-

$\sum_{i \in G_{C}, i \neq s} {R^{U}}_{i, t}$ ≤0

(32)

由于EENS在本文目标函数中是最小化的,在目标函数达到最优值时可以得到r_s_,_t_,_k= $R_{s, t}^{A U}$ , $r_{s, t, k}^{a u}$ =0,式(28)~(29)和式(30)~(31)均得到 $E_{s, t}^{E N S}$ p_s_,_t=0.

(b) u_s_,_t=1.在目标函数达到最优值时,r_s_,_t_,_k和 $r_{s, t, k}^{a u}$ 的优化结果将取决于 $e_{t, k}^{N L}$ - $R_{s, t}^{A U}$ 的大小:

若 $e_{t, k}^{N L}$ - $R_{s, t}^{A U}$ ≥0,可以得到r_s_,_t_,_k= $r_{s, t, k}^{a u}$ = $e_{t, k}^{N L}$ - $R_{s, t}^{A U}$ ,由式(28)~(29)和式(30)~(31)均得到 $E_{s, t}^{E N S}$ p_s_,_t= $\overset{N_{K}}{\sum_{k = 1}}$ ( $e_{t, k}^{N L}$ - $R_{s, t}^{A U}$ )π_kU_s.

若 $e_{t, k}^{N L}$ - $R_{s, t}^{A U}$ <0,可以得到r_s_,_t_,_k=-( $e_{t, k}^{N L}$ - $R_{s, t}^{A U}$ ), $r_{s, t, k}^{a u}$ =0,式(28)~(29)和式(30)~(31)均得到 $E_{s, t}^{E N S}$ p_s_,_t=0.

结合以上分析可知,式(28)~(29)和式(30)~(31)在以上所有条件下均得到相同的优化结果,因此,式(28)~(29)和式(30)~(31)是等效的.

相对于改进方法1,本文方法有两点进一步提升之处:① 减少了式(26)中的绝对值运算,由此减少了与辅助变量相关的运算量,本文方法在优化计算中仅需计算一个变量项 $r_{s, t, k}^{a u}$ ,而式(28)需要同时计算3个变量项r_s_,_t_,_k, $e_{t, k}^{N L}$ u_s_,_t和 $R_{i, t}^{A U}$ ;② 减少了N_S×N_T×N_K 个与辅助变量相关的不等式约束.最终,相对于改进方法1,本文方法在EENS指标等价变换的同时,进一步简化了计算.

2.3 EEC

电力系统中存在的另一种可能的损失是可再生能源无法得到充分利用.如果可再生能源出力的实际值大于预测值,且系统可用的负旋转备用不足,则多余的可再生能源将被削减以使系统的供需达到平衡^[10,14].在时段t和场景s中系统可用的负旋转备用 $R_{s, t}^{A D}$ 计算如下^[10]:

$R_{s, t}^{A D}$

$\sum_{i \in {G^{A}}_{s, t}} {R^{D}}_{i, t}$

(33)

式中: ${R^{D}}_{i, t}$ 为机组i在时段t提供的负旋转备用容量.

当系统出现功率盈余且可用的负旋转备用不足时,负旋转备用不足容量计算:

$P_{s, t, k}^{E C}$ =max

$\{- e_{t, k}^{N L} - R_{s, t}^{A U} - \sum_{i' \in {G^{U}}_{s, t}} P_{i', t}, 0\}$

(34)

若Δ $P_{s, t, k}^{E C}$ =0,说明该场景中,系统预留的负旋转备用容量能够应对系统中的不确定性因素;若Δ $P_{s, t, k}^{E C}$ >0,说明该场景中,系统预留的负旋转备用容量不足以应对系统中的不确定性因素,需要削减部分可再生能源以达到供需平衡,此时,Δ $P_{s, t, k}^{E C}$ 即为能源削减量.

将每个场景中的能量削减量用相应场景的概率加权求和,即可得到系统在每个时段的能源削减期望值 $E_{t}^{E C}$ . $E_{t}^{E C}$ 的计算涉及到0-1变量和连续变量乘积,同样可以采用前文提出的线性松弛方法进行计算.引入辅助变量 $r_{s, t, k}^{a d}$ , $E_{t}^{E C}$ 的计算公式如下:

$E_{t}^{E C}$ =

$\overset{N_{S}}{\sum_{s = 0}} \overset{N_{K}}{\sum_{k = 1}} r_{s, t, k}^{a d}$ π_kU_s

(35)

$r_{s, t, k}^{a d}$ ≥-

$e_{t, k}^{N L} u_{s, t}^{R D}$ -

$R_{s, t}^{A D}$ -

$\sum_{i' \in {G^{U}}_{s, t}}$ P_i'_,_t

(36)

式中: $u_{s, t}^{R D}$ 为0-1变量,表示与场景s对应的机组是否提供了负旋转备用,如果提供负旋转备用,则 $u_{s, t}^{R D}$ 为1,否则为0.

3 安全约束机组组合

3.1 目标函数

高比例风电和光伏并网增加了系统备用容量需求.预留充足的备用容量可以有效应对机组非计划停运和负荷、可再生能源随机波动造成的功率不平衡,减少系统失负荷和能源削减的风险.但另一方面,过多的旋转备用容量将增加系统的运行成本,降低系统的经济效率.因此,本文将失负荷和能源削减纳入目标函数,并采用失负荷价值(VOLL)和单位能源削减成本(VOAC)分别作为EENS和EEC指标的惩罚参数.基于成本效益分析,通过联合优化电量和备用服务市场,使系统的运行成本和损失成本之间达到最优均衡^[5].目标是在满足系统约束和元件约束的前提下,使调度时段内系统总期望成本(Expected Cost, EC)最小,EC由电能生产成本、启动成本、停机成本、正负旋转备用成本、失负荷成本和能源削减成本等组成,表达式如下:

$\begin{aligned} E^{\mathrm{C}}= & \sum_{t \in T} \sum_{i \in G_{\mathrm{C}}}\left(\sum_{m \in N_{\mathrm{M}}} \lambda_{i, m}^{\mathrm{e}} P_{i, m, t}+\lambda_{i}^{\mathrm{ru}} R_{i, t}^{\mathrm{U}}+\right. \\ & \left.\lambda_{i}^{\mathrm{rd}} R_{i, t}^{\mathrm{D}}+y_{i, t} C_{i, t}^{\mathrm{SU}}+z_{i, t} C_{i, t}^{\mathrm{SD}}\right)+ \\ & \sum_{t \in T}\left(V_{t}^{\mathrm{OLL}} E_{t}^{\mathrm{ENS}}+V_{t}^{\mathrm{OAE}} E_{t}^{\mathrm{EC}}\right) \end{aligned}$

(37)

式中:T表示调度时段的集合;N_M表示机组出力区间的集合;机组的成本函数采用了分段线性的形式, ${λ^{e}}_{i, m}$ 表示机组i的第m个出力区间对应的能量价格;P_i_,_m_,_t表示机组i在时段t的第m个出力区间的中标电量; $λ_{i}^{r u}$ 和 $λ_{i}^{r d}$ 分别表示机组i的正、负旋转备用价格;y_i_,_t为0-1变量,表示机组i在时段t的启动状态; $C_{i, t}^{S U}$ 表示机组i在时段t的启动成本;z_i_,_t为0-1变量,表示机组i在时段t的关停状态; $C_{i, t}^{S D}$ 表示机组i在时段t的停机成本; $V_{t}^{O L L}$ 和 $V_{t}^{O A E}$ 分别表示系统在时段t的失负荷价值和单位能源削减成本.

3.2 约束条件

SCUC问题需要满足功率平衡约束、机组出力约束、正负旋转备用约束、机组爬坡约束、机组最小起停时间约束、整数变量约束、潮流约束等.

(1) 系统功率平衡约束:

$\sum_{i \in G_{C}}$ P_i_,_t+

$\sum_{w \in G_{W}}$ P_w_,_t+

$\sum_{g_{p v} \in G_{P V}}$ P_pv,_t=

$\sum_{j \in J}$ D_j_,_t

(38)

式中:P_w_,_t和P_pv,_t分别表示风电场w和光伏电站g_pv在时段t的出力;D_j_,_t为节点j在时段t的负荷需求;G_W、G_PV和J分别表示风电场、光伏电站和负荷节点的集合.

(2) 机组出力约束:

P_i_,_t=

$\sum_{m \in N_{M}}$ P_i_,_m_,_t

(39)

0≤P_i_,_m_,_t≤

$P_{i, m}^{m, m a x}$

(40)

式中: $P_{i, m}^{m, m a x}$ 表示机组i第m个出力区间的容量.

(3) 旋转备用约束:

0≤

${R^{U}}_{i, t}$ ≤

$P_{i}^{m a x}$ -P_i_,_t

(41)

0≤

${R^{D}}_{i, t}$ ≤P_i_,_t-

$P_{i}^{m i n}$

(42)

${R^{U}}_{i, t}$ ≤v_ramp_iT^S

(43)

${R^{D}}_{i, t}$ ≤v_ramp_iT^S

(44)

式中: $P_{i}^{m a x}$ 和 $P_{i}^{m i n}$ 分别表示机组i的最大、最小出力;v_ramp_i表示机组i的爬坡速率;T^S表示旋转备用响应时间.

(4) 机组爬坡约束:

P_i_,_t-P_i_,_t_-1≤Δ

${P^{U}}_{i}$ +(1-u_i_,_t_-1)

$P_{i}^{m a x}$

(45)

P_i_,_t_-1-P_i_,_t≤Δ

${P^{D}}_{i}$ +(1-u_i_,_t)

$P_{i}^{m a x}$

(46)

式中:Δ ${P^{U}}_{i}$ 和Δ ${P^{D}}_{i}$ 分别表示机组i的最大向上和最大向下爬坡速率.

(5) 机组最小起停时间约束:

$\overset{t + T_{i}^{o n} - 1}{\sum_{τ = t}}$ u_i_,_τ≥

$T_{i}^{o n}$ y_i_,_t

(47)

$\overset{t + T_{i}^{o f f} - 1}{\sum_{τ = t}}$ (1-u_i_,_τ)≥

$T_{i}^{o f f}$ z_i_,_t

(48)

式中: $T_{i}^{o n}$ 和 $T_{i}^{o f f}$ 分别表示机组i的最小连续运行时间和最小连续停机时间.

(6) 整数变量约束:

y_i_,_t-z_i_,_t=u_i_,_t-u_i_,_t_-1

(49)

y_i_,_t+z_i_,_t≤1

(50)

(7) 潮流约束:

$\begin{array}{l} \mid \sum_{i \in G_{\mathrm{C}}} X_{l-i} P_{i, t}+\sum_{w \in G_{\mathrm{W}}} X_{l-w} P_{w, t}+ \\ \quad \sum_{g_{\mathrm{pv}} \in G_{\mathrm{PV}}} X_{l-g_{\mathrm{pv}}} P_{\mathrm{pv}, t}-\sum_{j \in J} X_{l-j} D_{j, t} \mid \leqslant P_{l}^{\max } \end{array}$

(51)

式中:X_l_-_i、X_l_-_w、 $X_{l - g_{p v}}$ 、X_l_-_j分别为i、w、g_pv、j所在节点对线路l的功率转移分布因子; $P_{l}^{m a x}$ 表示线路l的额定传输容量.

4 算例分析

4.1 算例参数设定

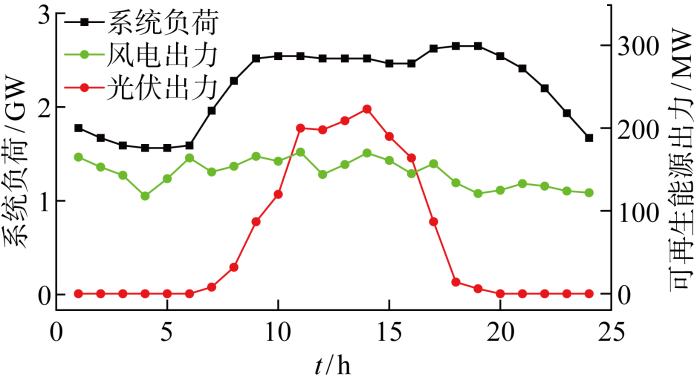
在改进的IEEE-RTS系统中进行算例分析,系统的详细参数包括网络拓扑图、机组参数和平均故障时间、负荷分布等信息,见文献[20].该系统由26个机组组成,未考虑水电机组,机组的燃料成本见文献[19],每个机组提供正负备用的价格均为其最高电能生产边际成本的10%^[5].以1 h为一个调度时段,共24个调度时段.并网的两个风电场装机容量均为150 MW,分别位于母线1和母线2上;并网的光伏电站一个,装机容量为300 MW,位于母线13上.系统负荷、风电和光伏出力的预测曲线如图3所示.负荷预测误差的标准差为负荷预测值的3%^[5],净负荷预测误差离散为如图2所示的7个分段.V^OLL和V^OAE分别设置为 4 000 美元/(MW·h)和100美元/(MW·h).

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 系统负荷、风电和光伏出力预测

Fig.3 Forecast of system load, wind and solar power

所用计算机采用Windows 10专业版64位操作系统,运行环境为CPU AMD R5 3600,主频 3.60 GHz,内存16 GB.建立的SCUC模型为MILP问题,在GAMS 24.4环境下编程并通过Cplex求解器求解,求解精度设置为10^-3.

4.2 算法表现分析

比较了采用文献[5,7]和本文提出的3种可靠性指标线性化方法求解SCUC的性能表现,为方便对比,将这3种方法依次用I、II、III 表示.表1列出了采用这3种方法在求解精度为10^-3和10^-6(精确到个位数),以及不同净负荷预测误差分段数时,SCUC的最优计算结果和计算时间.表1显示,随着净负荷预测误差分段数N_K的增加,3种方法的计算时间均有所增加,方法I计算时间的增加尤为明显,在求解精度为10^-6,N_K为7时,方法I的计算时间超过 1 000 s.其主要原因是,在方法I中,与N_K相关的0-1变量有1 248×N_K个,计算这些0-1变量和相关的约束条件需要大量的运算资源.而方法 II 和 III 不需要计算这些与N_K相关的0-1变量,因此方法 II 和 III 相对于方法I的计算时间大幅缩短.结合2.2.2小节中的分析可知,方法 III 相对于方法 II 减少了与辅助变量相关的运算量.算例中,方法 III 相对于方法 II 还减少了624×N_K个不等式约束,因此方法 III 的计算时间相对于方法 II 进一步减少.N_K为7时,方法 III 的计算时间仅为1.35 s,分别为方法I和方法 II 计算时间(94.21 s和4.68 s)的1.43%和28.85%,计算时间分别下降98.57%和71.15%,计算效率提升明显.当求解精度为10^-6时,方法 III 的计算时间仍明显少于其他两种方法的计算时间.对比表1中的结果可知,本文提出的可靠性指标线性化方法在净负荷误差多场景和高精度求解要求下,对SCUC模型的求解有一定优势.

表1 3种方法求解SCUC的性能对比

Tab.1 Performance comparison of three methods for solving SCUC

求解精度	N_K	I		II		III
求解精度	N_K	E^C /美元	计算时间/s	E^C /美元	计算时间/s	E^C /美元	计算时间/s
10^-3	3	689 421	7.28	689 426	2.30	689 370	1.16
	5	695 448	51.12	695 226	2.81	695 234	1.06
	7	697 071	94.21	697 008	4.68	697 058	1.35
	9	697 487	181.11	697 380	7.05	697 398	1.86
10^-6	3	689 231	23.39	689 231	10.17	689 231	2.38
	5	695 167	181.33	695 167	48.98	695 167	4.21
	7	—	>1 000	696 910	60.94	696 910	5.43
	9	—	>1 000	697 342	80.11	697 342	5.46

新窗口打开| 下载CSV

由表1还可知,当求解精度为10^-6,N_K分别为7和9两种条件下期望成本E_C的差值仅为432 美元,该差值仅占N_K为9时期望成本的0.06%,这说明净负荷预测误差划分为7个分段已能取得很高的计算准确性.

4.3 旋转备用容量配置方式的比较

不同的旋转备用容量设置对系统的运行成本和可靠性有很着大影响,对比分析了以下3种旋转备用容量配置方式的运行效果.

方式1 采用传统的N-1备用准则,取最大在线机组容量(400 MW)作为系统正旋转备用容量配置标准.

方式2 考虑负荷和可再生能源的预测偏差,采用“3.5σ”经验方法^[3],系统正、负旋转备用容量配置标准为净负荷预测误差标准差的3.5倍.

方式3 同时考虑机组故障、负荷和可再生能源的预测偏差,采用本章建立的SCUC确定最优正、负旋转备用容量配置.

由于传统的N-1备用准则仅给出了正旋转备用容量配置标准,方式1中负旋转备用容量配置需求与方式2中的相同,设为净负荷预测误差标准差的3.5倍,因此,这两种方式下负旋转备用容量配置处于同一水平.

表2列出了3种备用容量配置方式下的期望成本及其组成成分.表中,方式1中预留的正旋转备用容量最多,对应的正旋转备用成本也最多,但失负荷成本最少;方式2中预留的正旋转备用容量最少,对应的正旋转备用成本也最少,但失负荷成本最多;方式1和2同样预留了充裕的负旋转备用容量,保证了可再生能源的消纳,对应的负旋转备用成本也最多;方式3预留的正旋转备用容量则处于方式1和2之间.虽然方式3中失负荷成本和可再生能源削减成本均不是3种方法中最小的,但其期望成本达到了最小,分别相对于方式1和2中的期望成本下降了2.07%和1.59%.这说明,在测试系统中,方式1中以最大在线机组的容量作为正旋转备用容量配置标准是相对粗放且偏保守的;综合考虑系统中的各种不确定性因素以及备用的成本因素,适当的降低一定的备用容量配置有利于电力系统实现更高的经济运行效率.对比3种方法的启停成本可知,允许小概率条件下削减部分负荷,可减少机组的频繁启停,进而减少启停成本.

表2 3种备用配置方式的成本对比

Tab.2 Cost comparison of three modes

备用配置方式	期望成本/ 美元	电能成本/ 美元	启动成本/ 美元	正旋转备用成本/美元	负旋转备用成本/美元	失负荷成本/美元	能源削减成本/美元
方式1	711 785	662 544	9 551	25 446	8 303	5 942	0
方式2	708 351	646 677	7 830	19 202	8 303	26 339	0
方式3	697 058	647 101	7 092	22 889	4 325	14 563	1 088

新窗口打开| 下载CSV

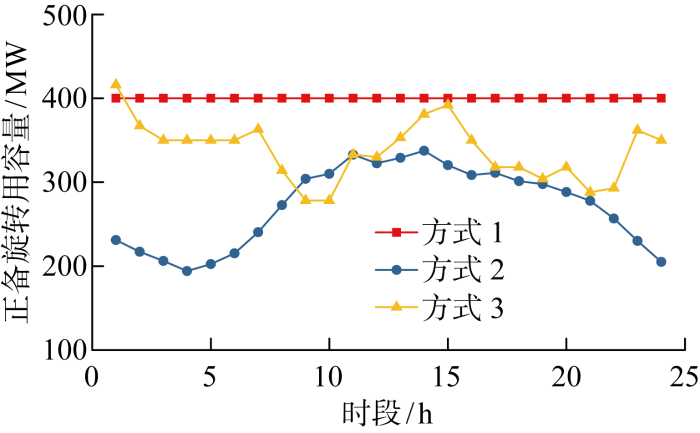
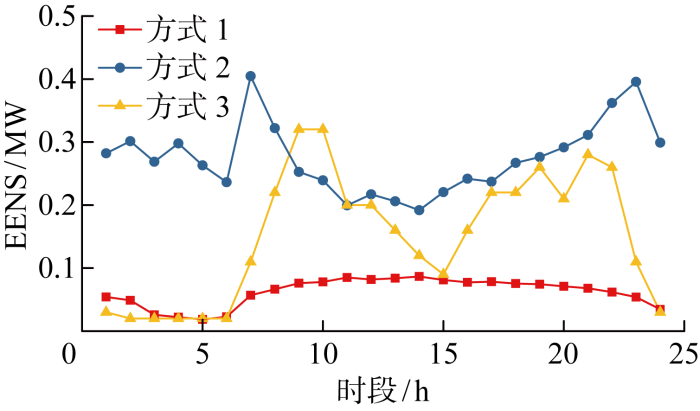
图4展示了不同备用配置方式下的正旋转备用容量配置结果.方式1中仅给出了当前普遍关注的正旋转备用容量配置需求,方式2、3中考虑到高比例可再生能源的消纳需求,同时给出了系统运行过程中的正、负旋转备用容量需求.对比图4中不同备用容量配置方式下的正旋转备用容量曲线可知,方式1以最大在线机组容量400 MW作为系统正旋转备用配置标准,在不同时段内均保持恒定,这种方式能够有效应对单一机组故障导致的功率缺额,但无法同时应对不同时段负荷和可再生能出力的不确定性对系统备用容量的动态需求.方式2以净负荷预测误差的3.5倍作为正、负旋转备用的配置标准,由于本文考虑的净负荷预测误差最大值为标准差的3倍,因此,这种方式能够有效应对负荷波动和可再生能源出力的不确定性,但该方法无法兼顾机组故障对系统正旋转备用的影响.方式3同时考虑到机组故障、负荷和可再生能源出力的不确定性,最优正旋转备用容量配置在不同时段根据系统运行成本和损失成本的最佳均衡点动态调整.图5展示了不同方式下的失负荷期望值.对比图4和5可知,预留的正备用容量越多时,电量不足期望值EENS越小,系统的供电可靠性越高.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 3种备用容量配置方式的正旋转备用容量

Fig.4 Up reserve capacities of three modes

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 3种备用容量配置方式的EENS

Fig.5 EENS of three modes

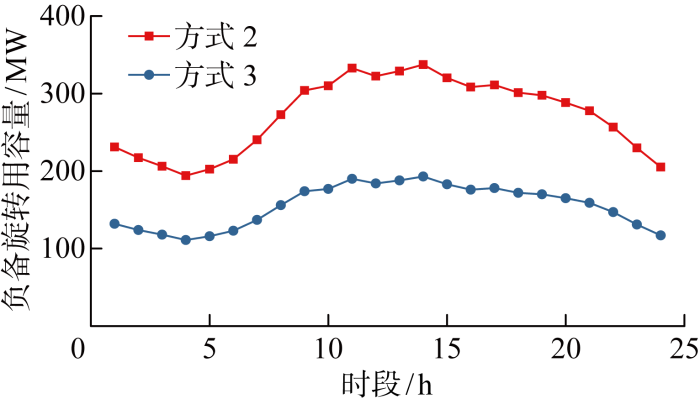
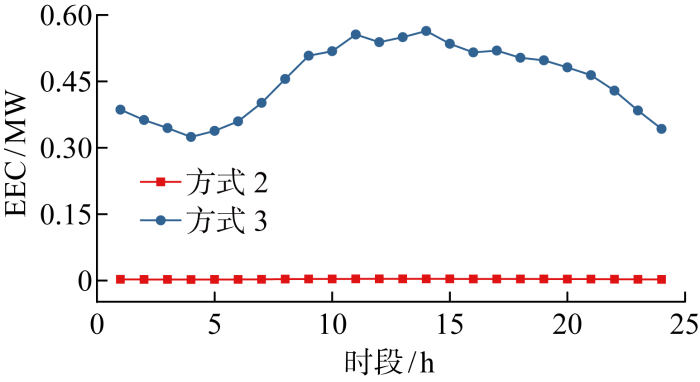
图6和7分别展示了方式2和3中系统负旋转备用容量配置和可再生能源削减期望值.对比图6和7可知,预留的负旋转备用容量越多,系统向下调节的能力越强,能源削减的风险越低.由于方式1采用了方式2中的负旋转备用容量配置方式,这两种方式下负旋转备用容量处于同一水平,所以图6仅显示了方式2中的负旋转备用容量曲线.方式2以净负荷预测误差的3.5倍作为负旋转备用的配置标准,本文考虑的净负荷预测误差最大值为标准差的3倍,因此可以应对所有场景对负旋转备用的需求,确保可再生能源的全额消纳,此时可再生能源削减期望为0.方式3基于成本效益分析,在系统最优运行成本和损失成本之间达到均衡时,系统预留的负旋转备用容量为净负荷预测误差标准差的2倍,因此在净负荷预测偏差达到最大值(3倍标准差)时,将会在以很小的概率(0.006)削减部分可再生能源出力以达到供需平衡.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 方式2和3的负旋转备用容量

Fig.6 Down reserve capacities for modes 2 and 3

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 方式2和3的EEC

Fig.7 EEC of modes 2 and 3

综上所述,本节建立的最优旋转备用配置方式有别于电网现行备用准则及“3.5σ”经验方法,能够结合机组故障、负荷和可再生能源出力预测偏差等不确定性因素,实现系统日前旋转备用容量的动态配置.同时,所提方法能够提升系统经济运行水平,促进风电和光伏安全、经济的消纳.

5 结语

本文结合高比例可再生能源并网运行对发电资源优化配置的需求,研究了综合考虑非计划停运障、负荷和可再生能源出力随机波动等多种不缺定性因素的备用容量优化模型.该模型能够在系统运行成本和损失成本达到最优均衡时,同时实现正负备用容量的最优配置.提出了可靠性指标EENS和EEC的改进计算方法,用于加快SCUC模型的求解速度.仿真结果表明,与其他两种EENS线性化方法相比,提出的改进方法能够有效降低SCUC模型的求解时间,并且随着预测误差场景数的增加和求解精度的提高,计算优势更为明显;建立的最优旋转备用配置方式有别于电网现行备用准则及“3.5σ”经验方法,能够实现系统日前旋转备用容量的动态配置,提升系统经济运行水平.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

黄强, 郭怿, 江建华, 等.

“双碳”目标下中国清洁电力发展路径

[J]. 上海交通大学学报, 2021, 55(12): 1499-1509.

[本文引用: 1]

HUANG

Qiang

, GUO

, JIANG

Jianhua

, et al.

Development pathway of China’s clean electricity under carbon peaking and carbon neutrality goals

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(12): 1499-1509.

[本文引用: 1]

[2]

康重庆, 姚良忠.

高比例可再生能源电力系统的关键科学问题与理论研究框架

[J]. 电力系统自动化, 2017, 41(9): 2-11.

[本文引用: 1]

KANG

Chongqing

, YAO

Liangzhong

Key scientific issues and theoretical research framework for power systems with high proportion of renewable energy

[J]. Automation of Electric Power Systems, 2017, 41(9): 2-11.

[本文引用: 1]

[3]

ORTEGA-VAZQUEZ

M A

, KIRSCHEN

D S

Estimating the spinning reserve requirements in systems with significant wind power generation penetration

[J]. IEEE Transactions on Power System, 2009, 24(1):114-124.

DOI:10.1109/TPWRS.2008.2004745 URL [本文引用: 6]

[4]

苏鹏, 刘天琪, 李兴源.

含风电的系统最优旋转备用的确定

[J]. 电网技术, 2010, 34(12): 158-162.

[本文引用: 2]

Peng

, LIU

Tianqi

, LI

Xingyuan

Determination of optimal spinning reserve of power grid containing wind

[J]. Power System Technology, 2010, 34(12): 158-162.

[本文引用: 2]

[5]

LIU

, TOMSOVIV

Quantifying spinning reserve in systems with significant wind power penetration

[J]. IEEE Transactions on Power System, 2012, 27(4): 2385-2393.

DOI:10.1109/TPWRS.2012.2207465 URL [本文引用: 11]

[6]

KHAZALI

, KALANTAR

Spinning reserve quantification by a stochastic-probabilistic scheme for smart power systems with high wind penetration

[J]. Energy Conversion and Management, 2015, 96: 242-257.

DOI:10.1016/j.enconman.2015.02.070 URL [本文引用: 2]

[7]

, DING

, BIE

, et al.

A novel linearization variant of reliability costs in the optimal scheduling model

[J]. IEEE Transactions on Power System, 2017, 32(5): 4140-4142.

DOI:10.1109/TPWRS.2017.2650783 URL [本文引用: 3]

[8]

LIU

, JIANG

, SHEN

, et al.

Cost allocation of spinning reserve based on risk contribution

[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2015, 10: 664-673.

DOI:10.1002/tee.2015.10.issue-6 URL [本文引用: 2]

[9]

ELA

, MILLIGAN

, KIRBY

Operating reserves and variable generation[R]. Golden, USA: National Renewable Energy Laboratory, 2011.

[本文引用: 1]

[10]

陈厚合, 王杨, 张儒峰, 等.

考虑源荷协调的风电并网系统旋转备用容量优化

[J]. 电力自动化设备, 2017, 37(8): 185-192.

[本文引用: 3]

CHEN

Houhe

, WANG

Yang

, ZHANG

Rufeng

, et al.

Spinning reserve capacity optimization considering coordination between source and load for power system with wind power

[J]. Electric Power Automation Equipment, 2017, 37(8): 185-192.

[本文引用: 3]

[11]

黄瀚燕, 周明, 李庚银.

考虑多重不确定性和备用互济的含风电互联电力系统分散协调调度方法

[J]. 电网技术, 2019, 42(2): 381-389.

[本文引用: 1]

HUANG

Hanyan

, ZHOU

Ming

, LI

Gengyin

Coordinated decentralized dispatch of wind-power-integrated multi-area interconnected power systems considering multiple uncertainties and mutual reserve support

[J]. Power System Technology, 2019, 42(2): 381-389.

[本文引用: 1]

[12]

YANG

, BAO

, DING

, et al.

Impact of down spinning reserve on operation reliability of power systems

[J]. Journal of Modern Power System and Clean Energy, 2020, 8(4): 709-718.

DOI:10.35833/MPCE.2019.000110 URL [本文引用: 1]

[13]

刘明涛, 谢俊, 张秋艳, 等.

碳交易环境下含风电电力系统短期生产模拟

[J]. 上海交通大学学报, 2021, 55(12): 1598-1607.

[本文引用: 1]

LIU

Mingtao

, XIE

Jun

, ZHANG

Qiuyan

, et al.

Short-term production simulation of power system containing wind power under carbon trading environment

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(12): 1598-1607.

[本文引用: 1]

[14]

崔杨, 张汇泉, 仲悟之, 等.

考虑需求响应的含光热电站可再生能源高渗透率电力系统多源优化调度

[J]. 高电压技术, 2020, 26(5): 1499-1509.

[本文引用: 4]

CUI

Yang

, ZHANG

Huiquan

, ZHONG

Wuzhi

, et al.

Multi-source optimal scheduling of renewable energy high-permeability power system with CSP plants considering demand response

[J]. High Voltage Engineering, 2020, 26(5): 1499-1509.

[本文引用: 4]

[15]

林峰, 汪震, 王冠中, 等.

考虑风电降载的电力系统鲁棒备用调度模型

[J]. 电力系统自动化, 2018, 42(19): 64-70.

[本文引用: 1]

LIN

Feng

, WANG

Zhen

, WANG

Guanzhong

, et al.

Robust reserve scheduling model of electric power system considering WTG de-loading capability

[J]. Automation of Electric Power Systems, 2018, 42(19): 64-70.

[本文引用: 1]

[16]

FABBRI

, ROMAN

T G

, ABBAD

J R

, et al.

Assessment of the cost associated with wind generation prediction errors in a liberalized electricity market

[J]. IEEE Transactions on Power System, 2005, 20(3): 1440-1446.

DOI:10.1109/TPWRS.2005.852148 URL [本文引用: 1]

[17]

ZHAO

, FANG

, WEI

Stochastic optimal dispatch of integrating concentrating solar power plants with wind farms

[J]. International Journal of Electrical Power and Energy Systems, 2019, 109: 575-583.

DOI:10.1016/j.ijepes.2019.01.043 URL [本文引用: 1]

[18]

BILLINTON

, ALLAN

R N

Reliability evaluation of power systems[M]. 2nd ed. New York, USA: Plenum Press, 1996.

[本文引用: 1]

[19]

BOUFFARD

, GALIANA

F D

An electricity market with a probabilistic spinning reserve criterion

[J]. IEEE Transactions on Power System, 2004, 19(1): 300-307.

DOI:10.1109/TPWRS.2003.818587 URL [本文引用: 2]

[20]

GRIGG

, WONG

, ALBRECHT

, et al.

The IEEE reliability test system — 1996

[J]. IEEE Transactions on Power System, 1999, 14(3): 1010-1018.

DOI:10.1109/59.780914 URL [本文引用: 1]

“双碳”目标下中国清洁电力发展路径

2021

... 大力发展风电、光伏等可再生能源是应对能源安全、环境污染,实现“碳达峰”“碳中和”目标的重大需求^[1-2].截至2021年底,我国风电装机328 GW,光伏发电装机306 GW,二者已分别占全国总发电装机容量的16.5%和12.9%.预计到2030年,我国风电、太阳能发电总装机容量将达到120 GW以上.风电、光伏等可再生能源出力具有波动性、间歇性和不确定性等特点,大规模可再生能源并网运行需要电力系统安排额外的备用容量以确保系统的可靠性,对系统的灵活调节能力提出了新的要求.现行的电网运行规则中一般采用确定性的方式确定系统的备用容量配置,如最大在线机组容量或者负荷的一定比例等,这种近似“一刀切”的确定性方式过于粗放,容易造成备用资源的浪费,已难以适应高比例可再生能源的并网运行需求.因此,需要综合考虑各种不确定性因素,采用更合理的方式实现备用容量的优化配置,提高电力系统的经济运行效率. ...

“双碳”目标下中国清洁电力发展路径

2021

高比例可再生能源电力系统的关键科学问题与理论研究框架

2017

高比例可再生能源电力系统的关键科学问题与理论研究框架

2017

Estimating the spinning reserve requirements in systems with significant wind power generation penetration

2009

... 目前,针对可再生能源并网系统备用容量的优化问题,已有了广泛的研究.文献[3-4] 中采用正态分布模型描述净负荷的预测误差,结合机组停运容量概率表(Capacity Outage Probability Table,COPT)和净负荷预测误差评估系统电量不足期望值(Expected Energy Not Served,EENS),采用成本效益方法确定最优旋转备用容量.文献[5]中提出一种概率性安全约束机组组合(Security-Constrained Unit Commitment, SCUC)模型,模型中考虑了机组故障、负荷和风电出力的不确定性,建立了考虑常规机组运行状态的EENS计算方法.文献[6]中考虑将需求侧响应和储能作为备用资源,将EENS和失负荷概率(Loss of Load Probability, LOLP)作为系统的可靠性约束,计及可靠性约束进行发电和备用协调优化.然而,考虑机组故障和净负荷预测误差时,可靠性指标EENS和LOLP通常为非线性表达式,大幅增加了SCUC模型的复杂性.文献[7]中在文献[5]的基础上改进了可靠性指标EENS的计算方法,优化了EENS表达式中的0-1变量,大幅提高了SCUC的计算效率.文献[8]中考虑机组故障、负荷的随机波动、风电和光伏出力的不确定性,建立了可靠性约束的机组组合模型. ...

... 负荷是电力系统中主要的不确定性因素之一.虽然负荷需求是随机变化的,但其具有较强的周期性和规律性,目前,在负荷预测的研究和应用方面均已经取得了比较高的预测准确度.在日前辅助服务市场的相关应用中,负荷预测误差通常被认为服从零均值的正态分布^[3-4]: ...

... 受自然来风等因素的影响,风电出力呈波动性和不确定性等特点.对于风电出力的预测误差分布,目前尚没有一个统一的模型来描述,常用的预测误差分布模型包括正态分布^[3]和贝塔分布^[16].然而,在大规模风电并网的电力系统中,由于风电场在地理位置上的广泛分布,根据中心极限定理,总的风电出力预测误差可以被认为服从零均值的正态分布^[5].文献[3]中给出了日前市场中风电出力预测误差与预测值的关系式如下: ...

... .文献[3]中给出了日前市场中风电出力预测误差与预测值的关系式如下: ...

... 式(7)中的净负荷预测误差

$e_{t}^{N L}$

为连续的随机变量,不利用于优化计算,可以考虑将该连续变量近似为一组离散变量^[3].本文将净负荷预测误差离散为N_K个奇数分段,每个分段的宽度为预测误差的标准差σ_NL,_t,以每个分段的中间值作为该分段的预测误差,则第k个预测误差分段值为 ...

... 方式2 考虑负荷和可再生能源的预测偏差,采用“3.5σ”经验方法^[3],系统正、负旋转备用容量配置标准为净负荷预测误差标准差的3.5倍. ...

含风电的系统最优旋转备用的确定

2010

含风电的系统最优旋转备用的确定

2010

Quantifying spinning reserve in systems with significant wind power penetration

2012

... ]中在文献[5]的基础上改进了可靠性指标EENS的计算方法,优化了EENS表达式中的0-1变量,大幅提高了SCUC的计算效率.文献[8]中考虑机组故障、负荷的随机波动、风电和光伏出力的不确定性,建立了可靠性约束的机组组合模型. ...

... 系统净负荷定义为系统负荷减去风电和光伏的出力值,即需要由系统中的其他发电源进行平衡的负荷值^[5].假设负荷、风电出力和光伏出力的预测误差不相关,则系统净负荷预测误差也服从均值为零的正态分布^[8].系统净负荷预测误差与预测值的关系式如下: ...

... 式中:u_i_,_t为表示机组运行状态的0-1变量,1表示机组i在时段t处于开机状态;G_C表示常规机组的集合.通过将式(11)中乘积展开中的高阶项替换为上界,单一机组故障的概率可以进一步近似为^[5] ...

... 最后,将每个场景中负荷的削减量用相应场景的概率加权并求和,即可得到系统在每个时段的电量不足期望值^[5]: ...

... 文献[5]中基于大M法,通过引入一个0-1变量a_s_,_t_,_k,一个连续变量L_s_,_t_,_k和若干不 ...

... 高比例风电和光伏并网增加了系统备用容量需求.预留充足的备用容量可以有效应对机组非计划停运和负荷、可再生能源随机波动造成的功率不平衡,减少系统失负荷和能源削减的风险.但另一方面,过多的旋转备用容量将增加系统的运行成本,降低系统的经济效率.因此,本文将失负荷和能源削减纳入目标函数,并采用失负荷价值(VOLL)和单位能源削减成本(VOAC)分别作为EENS和EEC指标的惩罚参数.基于成本效益分析,通过联合优化电量和备用服务市场,使系统的运行成本和损失成本之间达到最优均衡^[5].目标是在满足系统约束和元件约束的前提下,使调度时段内系统总期望成本(Expected Cost, EC)最小,EC由电能生产成本、启动成本、停机成本、正负旋转备用成本、失负荷成本和能源削减成本等组成,表达式如下: ...

... 在改进的IEEE-RTS系统中进行算例分析,系统的详细参数包括网络拓扑图、机组参数和平均故障时间、负荷分布等信息,见文献[20].该系统由26个机组组成,未考虑水电机组,机组的燃料成本见文献[19],每个机组提供正负备用的价格均为其最高电能生产边际成本的10%^[5].以1 h为一个调度时段,共24个调度时段.并网的两个风电场装机容量均为150 MW,分别位于母线1和母线2上;并网的光伏电站一个,装机容量为300 MW,位于母线13上.系统负荷、风电和光伏出力的预测曲线如图3所示.负荷预测误差的标准差为负荷预测值的3%^[5],净负荷预测误差离散为如图2所示的7个分段.V^OLL和V^OAE分别设置为 4 000 美元/(MW·h)和100美元/(MW·h). ...

... [5],净负荷预测误差离散为如图2所示的7个分段.V^OLL和V^OAE分别设置为 4 000 美元/(MW·h)和100美元/(MW·h). ...

... 比较了采用文献[5,7]和本文提出的3种可靠性指标线性化方法求解SCUC的性能表现,为方便对比,将这3种方法依次用I、II、III 表示.表1列出了采用这3种方法在求解精度为10^-3和10^-6(精确到个位数),以及不同净负荷预测误差分段数时,SCUC的最优计算结果和计算时间.表1显示,随着净负荷预测误差分段数N_K的增加,3种方法的计算时间均有所增加,方法I计算时间的增加尤为明显,在求解精度为10^-6,N_K为7时,方法I的计算时间超过 1 000 s.其主要原因是,在方法I中,与N_K相关的0-1变量有1 248×N_K个,计算这些0-1变量和相关的约束条件需要大量的运算资源.而方法 II 和 III 不需要计算这些与N_K相关的0-1变量,因此方法 II 和 III 相对于方法I的计算时间大幅缩短.结合2.2.2小节中的分析可知,方法 III 相对于方法 II 减少了与辅助变量相关的运算量.算例中,方法 III 相对于方法 II 还减少了624×N_K个不等式约束,因此方法 III 的计算时间相对于方法 II 进一步减少.N_K为7时,方法 III 的计算时间仅为1.35 s,分别为方法I和方法 II 计算时间(94.21 s和4.68 s)的1.43%和28.85%,计算时间分别下降98.57%和71.15%,计算效率提升明显.当求解精度为10^-6时,方法 III 的计算时间仍明显少于其他两种方法的计算时间.对比表1中的结果可知,本文提出的可靠性指标线性化方法在净负荷误差多场景和高精度求解要求下,对SCUC模型的求解有一定优势. ...

Spinning reserve quantification by a stochastic-probabilistic scheme for smart power systems with high wind penetration

2015

... 常规机组的短期发电模型可以用两状态马尔可夫模型来表示^[18],如图1所示.发电机的故障率和修复率分别用λ和μ表示,假设发电机平均无故障工作时间与平均修复时间均为指数分布,如果已知机组在t=0时刻是正常运行状态,则在投运前导时间(Lead Time)T^L内机组i不可用的概率U_i(T^L)和处于可用状态的概率A_i(T^L)分别为^[6] ...

A novel linearization variant of reliability costs in the optimal scheduling model

2017

... (1) 改进方法1.文献[7]中结合式(18)中不同变量之间的联系,通过引入绝对值运算,将式(18)改写为如下表达式: ...

Cost allocation of spinning reserve based on risk contribution

2015

2011

... 随着可再生能源并网比例的增加,系统需要安排足够的负备用容量以应对可再生能源的波动性和不确定性^[9].文献[10]中综合考虑风电预测误差、负荷波动及发电机非计划停运不确定性因素对旋转备用的需求,将弃风、可中断负荷分别作为部分负、正旋转备用融入发电日前调度计划,建立了基于多场景的概率性日前机组组合优化模型,同时优化了正负备用容量.文献[11]中将负荷和风电预测误差建模为等效的机组停运容量,改进了机组停运容量概率表,建立了备用互济的分散协调调度模型.文献[12]中分析了负备用对电力系统运行和可靠性的影响.文献[13]中结合碳交易机制和风电、火电的运行特征,建立了碳交易环境下含风电电力系统短期生产模拟模型.文献[14]中构建了基于光热电站出力灵活调度的多源电力系统随机机组组合优化调度模型,该模型在各场景中考虑了风电、光伏的弃电惩罚.文献[15]中分析了风电的调度模式,建立了考虑风电降载的电力系统鲁棒备用调度模型.然而,以上文献研究大多考虑单一或几种不确定性因素,未充分考虑风电和光伏出力预测误差、负荷预测误差及发电机非计划停运等多重不确定性因素对系统可靠性的影响.同时,采用场景分析法计算系统的EENS和弃风、弃光量等指标时,通常需要采样大量的场景以获得较高的精度,进而大幅增加备用优化问题的求解难度.因此,需要对大量场景进行合理地简化,优化系统可靠性指标的计算方法,进而提升备用优化问题的求解速度. ...

考虑源荷协调的风电并网系统旋转备用容量优化

2017

... 电力系统中存在的另一种可能的损失是可再生能源无法得到充分利用.如果可再生能源出力的实际值大于预测值,且系统可用的负旋转备用不足,则多余的可再生能源将被削减以使系统的供需达到平衡^[10,14].在时段t和场景s中系统可用的负旋转备用

$R_{s, t}^{A D}$

计算如下^[10]: ...

... [10]: ...

考虑源荷协调的风电并网系统旋转备用容量优化

2017

$R_{s, t}^{A D}$

计算如下^[10]: ...

... [10]: ...

考虑多重不确定性和备用互济的含风电互联电力系统分散协调调度方法

2019

考虑多重不确定性和备用互济的含风电互联电力系统分散协调调度方法

2019

Impact of down spinning reserve on operation reliability of power systems

2020

碳交易环境下含风电电力系统短期生产模拟

2021

碳交易环境下含风电电力系统短期生产模拟

2021

考虑需求响应的含光热电站可再生能源高渗透率电力系统多源优化调度

2020

... 光伏发电与风力发电类似,具有波动性和不确定性的特点.光伏出力受太阳辐射的影响还具有昼发夜停的特性,并且光伏大发与负荷高峰的时段具有一定的匹配度^[14].光伏出力预测误差可以用零均值的正态分布来描述,光伏出力预测误差与预测值的关系式如下^[14,17]: ...

... [14,17]: ...

$R_{s, t}^{A D}$

计算如下^[10]: ...

考虑需求响应的含光热电站可再生能源高渗透率电力系统多源优化调度

2020

... [14,17]: ...

$R_{s, t}^{A D}$

计算如下^[10]: ...

考虑风电降载的电力系统鲁棒备用调度模型

2018

考虑风电降载的电力系统鲁棒备用调度模型

2018

Assessment of the cost associated with wind generation prediction errors in a liberalized electricity market

2005

Stochastic optimal dispatch of integrating concentrating solar power plants with wind farms

2019

1996

An electricity market with a probabilistic spinning reserve criterion

2004

... 系统中仅机组i发生故障而所有剩余发电机组均处于正常运行状态的概率为^[19] ...

The IEEE reliability test system — 1996

1999

〈

〉