世界能源消费始终以煤炭、石油以及天然气等化石能源为中心.然而,传统化石能源正面临储量危机和环境污染的双重难题.因此,世界各国纷纷推进能源结构改革,开发清洁可再生的新能源以逐步取代化石能源在能源市场的地位,同时研究提高总能源利用效率的新技术,如太阳能、风能、潮汐能和生物质能等.然而目前新能源利用率低,在能源转换过程中还会产生大量废热,大量能源未得到高效利用.温差发电(Thermoelectric Generation, TEG)技术可以很好地解决这一问题.这是一种利用塞贝克效应的发电技术,其原理是当半导体或导体两端处在不同温度下,回路中将产生温差电动势.如今,TEG技术应用方式包括利用汽车排气中的废热[1]、利用太阳能驱动半导体TEG[2],甚至是利用人体运动中产生的热能来发电[3].
为了使得TEG技术能够在温度变化等复杂场景中正常工作,需要设计合适且高效的最大功率点跟踪(Maximum Power Point Tracking, MPPT)算法.在TEG阵列的MPPT中常用的方式有扰动观察法、增量电导法、开路电压法和短路电流法[4-5].文献[6]中提出一种适用于半导体温差发电系统的改进变步长扰动观察法,在TEG阵列冷热两端的温度发生变化时,能够快速地确定最大功率点.文献[7]中提出一种基于开路电压法的MPPT方法,保证TEG阵列能够在大温差范围下仍然能够快速地确定最佳电气操作点.文献[8]中提出一种新的TEG短路电流最大功率点跟踪控制算法,这种方法可靠性高,只需一组电流传感器就能实现最大功率点跟踪.需要注意的是,TEG系统的应用环境较为复杂,TEG阵列温度分布不均时有发生,其功率-电压(P-V)曲线存在多个峰值.采用扰动观察法、增量电导法等传统方法难以实现MPPT,极易陷入局部最优.针对增量电导法步长固定存在跟踪速度慢和稳态误差大的问题,文献[9]中提出一种恒定电压法和双曲正切函数自适应变步长算法相结合的MPPT控制策略,提升了光伏/温差联合发电系统最大功率跟踪的速度和精度.文献[10]中采用启发式算法和增量电导法的混合控制算法,利用粒子群优化算法能够快速寻优的特点以及电导增量法能够精细搜索的能力,使得跟踪MPPT变得快速、准确;但是无论如何提高MPPT的精度,在温度不均匀的环境下,TEG阵列的P-V输出曲线仍然会出现多个峰值,即MPPT仍存在陷入局部最优的可能性.在光伏系统中,许多学者提出光伏重构技术来解决P-V曲线多峰问题,并取得理想的效果.例如,文献[11]中采用改进的蜉蝣算法对光伏阵列进行动态重构,使P-V曲线趋于呈现单个峰值,与数独方法等算法相比,该算法能够快速、稳定地获得重构结果.文献[12]中采用基于海洋捕食者算法对3种不同规模的光伏阵列进行重构,结果表明,该算法能有效地使P-V曲线呈现单峰特征.
文献[13]中采用一种基于简单冒泡排序的方法来分散光伏阵列上方的阴影,以确定光伏重构方案,但是该方法的程序过于复杂,不能在短时间内得到最优重构方案.重构问题是一种离散化且有约束的优化问题,采用传统优化方式很难快速获取最优解决方案.相比传统数学方式,启发式算法不依赖特定数学模型,寻优能力强、速度快且不易陷入局部最优,具备极高的灵活性和泛化能力,被广泛用于各种重构问题[14-15].因此,本文提出一种基于人工蜂群(Artificial Bee Colony, ABC)算法[16]的TEG阵列最优重构方法,并将其与遗传算法(Genetic Algorithm, GA)、粒子群优化(Particle Swarm Optimization, PSO)算法和秃鹰搜索(Bald Eagle Search, BES)优化算法进行对比.结果表明:ABC的稳定性好、全局搜索能力强,能有效地提高TEG阵列的输出功率.
1 TEG阵列建模
1.1 TEG模块建模
1.1.1 TEG模块物理模型
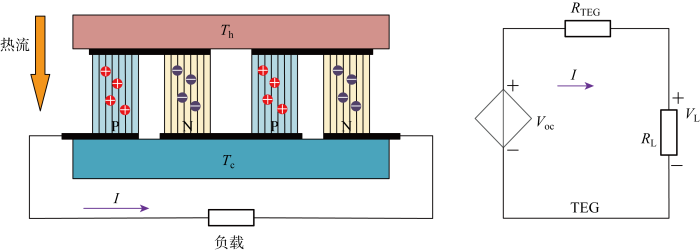
图1
1.1.2 TEG模块数学模型
从图1可以看出,TEG模块可以看作是与内部电阻串联的电压源.电压源电压和电阻的值随温度变化而变化,电压源电压和温度之间的数学关系可以表示为
式中:ΔT为热端和冷端温度差;as为塞贝克系数,它反映出材料的塞贝克效应.as与温度的关系可表示为
式中:a0为塞贝克系数的基本部分;a1为塞贝克系数变化率;T、T0分别为平均温度和参考温度[20].
当TEG模块连接负载Rload时,流过电路的电流和产生相应的输出功率分别表示为
式中:RT为TEG模块的等效内阻.
由式(4)可见,输出功率P是一个凸二次函数.设P对Rload的导数为0,可知当Rload=RT时输出功率最大,即
1.2 TEG阵列模型
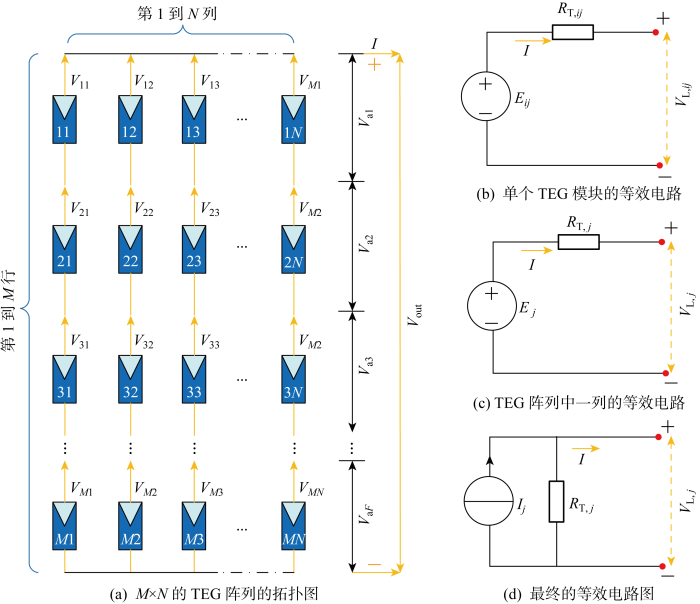
图2
第i行、第j列TEG模块的开路电压和内阻分别表示为Eij和RT,ij(i=1, 2, …, M; j=1, 2, …, N);同样,TEG阵列第j列的开路电压和内阻分别表示为Ej和
每个TEG模块的等效电路与TEG阵列中某一列的等效电路之间的关系可表示为
需要注意的是,TEG阵列的输出功率很大程度上依赖于负载电压.特别是当TEG阵列中一列的输出电压与负载电压一致时,才能输出电能.因此,各TEG模块的等效内阻应表示为
式中:Vj为TEG阵列中第j列输出电压.
此外,根据戴维南定理,TEG阵列的每一列都可以等效为与其对应内阻并联的电流源,如图2(d)所示.当前电流源电流可以表示为
因此,TEG阵列的总内阻和电流源电流可以分别表示为
根据戴维南定理将等效电路简化为一个总电压源,该总电压源的值可以表示为
在TEG阵列的最大功率点处,总内阻Rs,T与负载电阻相等,两者平均地分配总电压,即VL=
功率提升率是评估重构方法的重要参数,可表示为经过重构和未经过重构的最大功率之差占后者的比例,即
式中:Penh为功率提升率.
2 基于ABC的TEG阵列重构方法
2.1 TEG阵列重构设计
(1) 目标函数.对TEG阵列重构的目的在于提升系统最大功率,因此,目标函数可设计为
式中:Ij(xr)和Vj(xr)分别为TEG阵列中第j列的电流和电压;xr为优化变量,即TEG阵列的布局策略,以3×3的TEG阵列为例,TEG各模块的初始布局和第r个个体所对应的布局分别为
(2) 约束条件.在TEG阵列中,同一列的TEG模块的电压相同,交换TEG阵列同一列中的不同TEG模块,无法改变这TEG阵列的输出功率.因此可以将约束条件设计为
式(18)表示M行的列变换,其中,
2.2 ABC人工蜂群算法
2.2.1 算法原理
ABC算法模拟蜜蜂寻找食物并且吸引蜂群中的蜜蜂跟随首批蜜蜂采蜜,或者在旧蜜源附近寻找新蜜源的过程.该算法引入蜜源作为优化问题中的解,并且解的质量由适应度衡量.此算法对蜂群的模拟主要由3种类型的蜜蜂进行:
(1) 侦查蜂.在每次迭代过程中只存在一只,侦查蜂随机定位一个新蜜源的位置,蜂群会前往该蜜源采蜜.
(2) 工蜂.一只工蜂只对应一个蜜源的位置,工蜂在采集该蜜源之后返回蜂巢分享该蜜源的信息.
(3) 观察蜂.观察蜂从工蜂处得到蜜源的信息,再根据工蜂提供的蜜源信息选择跟随工蜂进行区域搜索.
2.2.2 算法实现步骤
(1) 蜜源初始化.在最初阶段,在解空间中工蜂全局随机搜索蜜源位置,并随机生成一批蜜源Xed的位置
式中:e=1, 2, …, N',N'为蜜源的数量;d=1, 2, …, D,D为解空间的维度;rand()为区间[0,1]上的一个随机数;Ud和Ld分别为解空间的上下界.
(2) 新蜜源更新.工蜂会在蜜源附近根据下式在限定的范围内搜索新蜜源
式中:X'ed为新蜜源的位置;Xgd为N'个蜜源中任意一个不等于Xed的蜜源;φ为区间[-1, 1]上的一个随机数,决定扰动程度.当新蜜源的适应度优于原先蜜源的适应度,旧蜜源将会被新蜜源代替.
(3) 蜜源选择.使用贪婪准则对新的蜜源位置进行记忆,观察蜂会对新蜜源的信息进行估计,并且通过以下概率公式选择一个蜜源:
式中:Pe为选取新蜜源的概率;Fe为第e个解对应的适应度值.
(4) 产生侦查蜂.在搜索蜜源的过程中,如果经过klim次迭代仍没有更好的蜜源出现,工蜂和观察蜂将舍弃该蜜源,并转变为侦查蜂,寻找新蜜源
式中:Xkd为仍处于优化过程的蜜源.
2.2.3 离散ABC算法
在离散ABC算法中,初始蜜源位置同连续ABC一样由式(19)生成.此时,蜜源的位置由1和0表示,1表示蜂群会对该蜜源采蜜,0表示不会对该蜜源进行采蜜,如下式所示:
式中:sig(Xkd)为Sigmoid函数,即
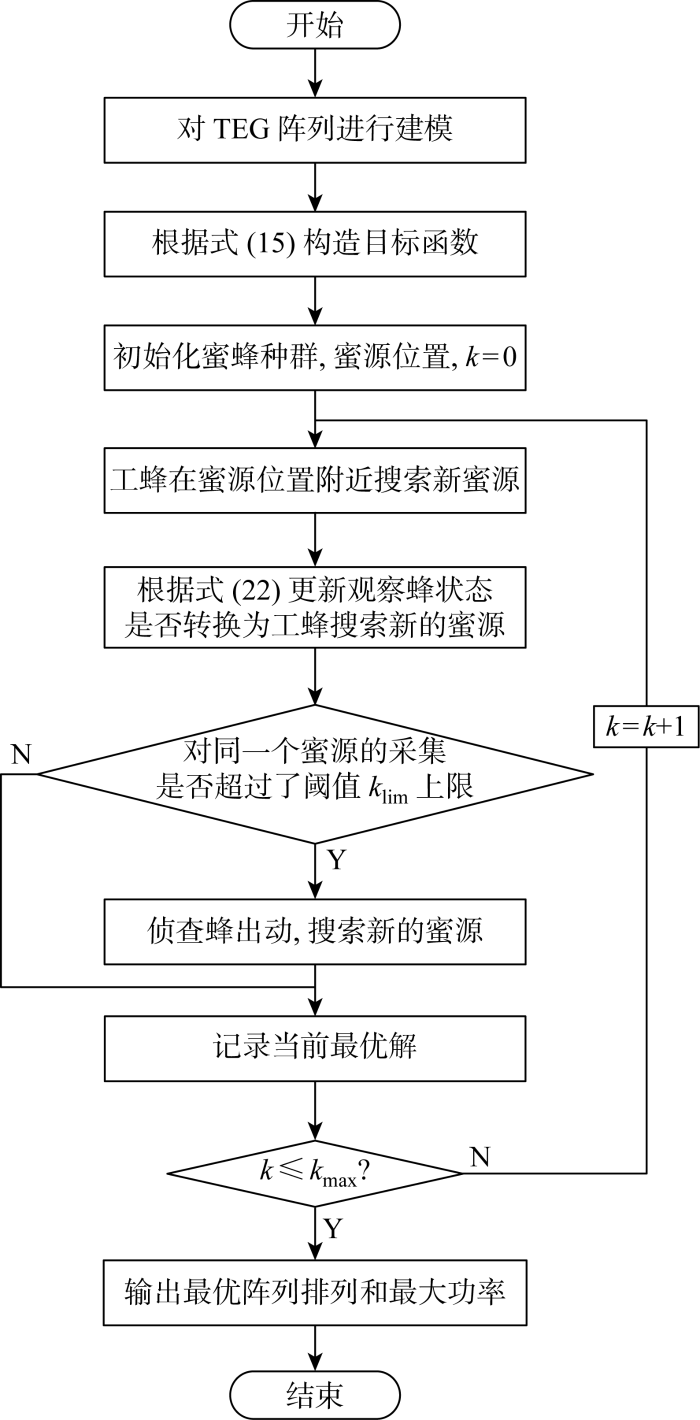
综上,基于ABC的TEG阵列重构的流程图如图3所示.图中:kmax为最大迭代次数.
图3
3 仿真算例分析
设置3种常见温度条件以评估ABC算法在对称9×9 TEG阵列和不对称10×15 TEG阵列下的重构性能,即对角线、外部和内部[23].同时,GA[24]、PSO[25]和BES[26]作为对比算法验证ABC算法的先进性和有效性.需要注意的是,种群数量和最大迭代次数的值越大,算法运行所需的时间越长.为了在合理的时间内得到较为理想的优化结果,同时保证算法对比的公平性,将所有算法的最大迭代次数设置为500、种群数量设置为50,独立运行次数均为30次.此外,所有仿真试验均通过主频为2.90 GHz的Intel(R) Core(TM) i5-10400F CPU,内存为32.0 GB的计算机在MATLAB 2020a环境下实施.
3.1 对称9×9 TEG阵列
图4
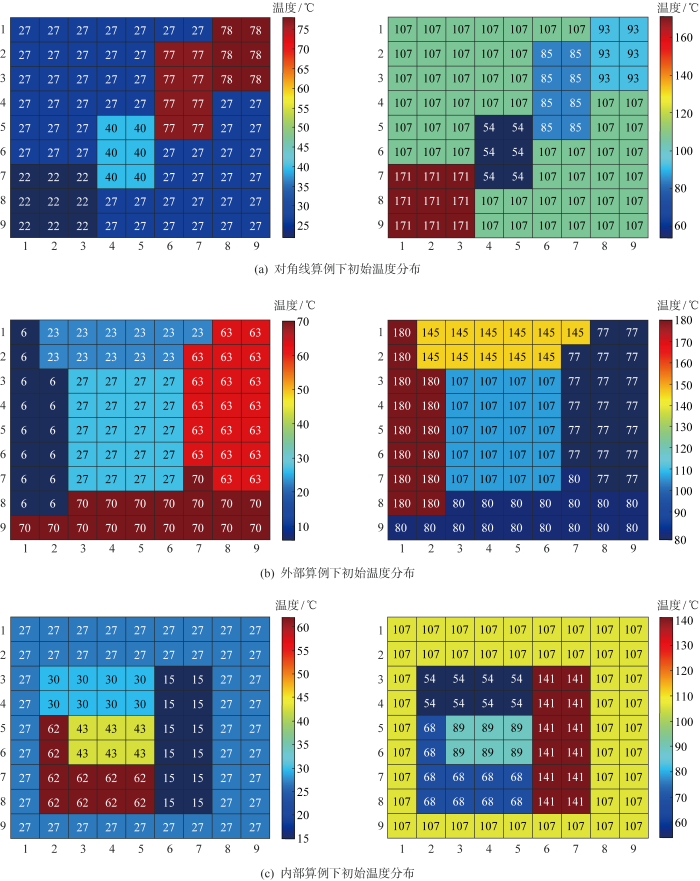
图4
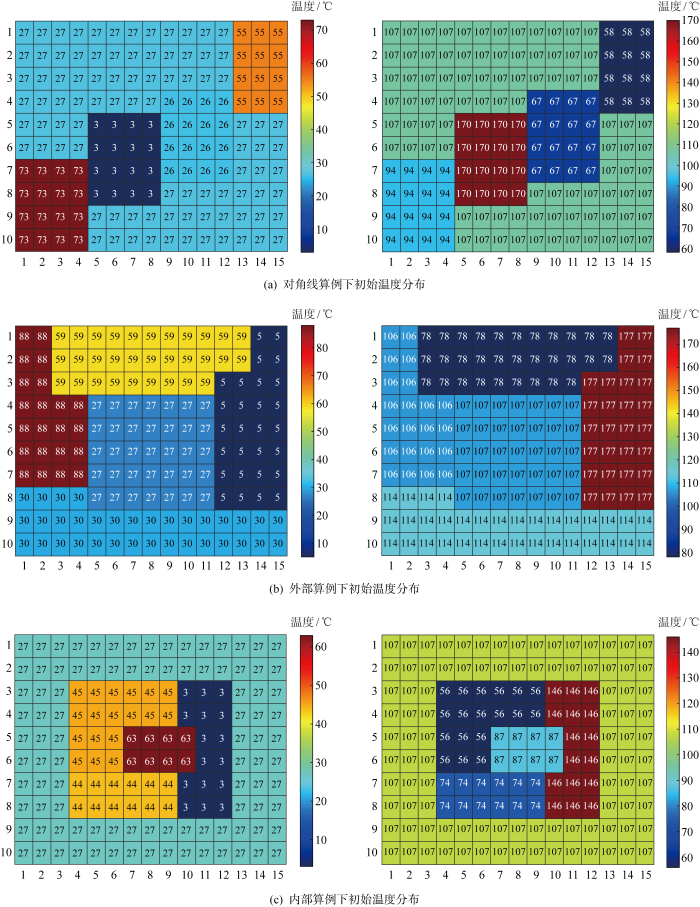
对称9×9 TEG阵列3种不同情况下的初始温度分布
Fig.4
Initial temperature distribution of three different scenarios for symmetric 9×9 TEG array
图5
图5
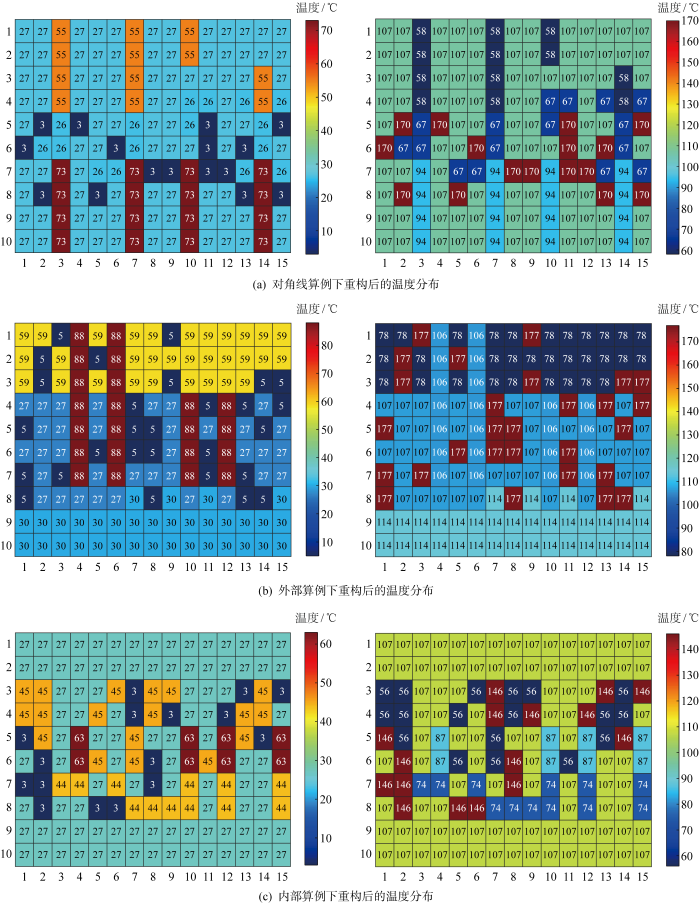
经过ABC重构后的对称9×9 TEG阵列的温度分布
Fig.5
Temperature distribution of symmetric 9×9 TEG array optimized by ABC
图6
图6
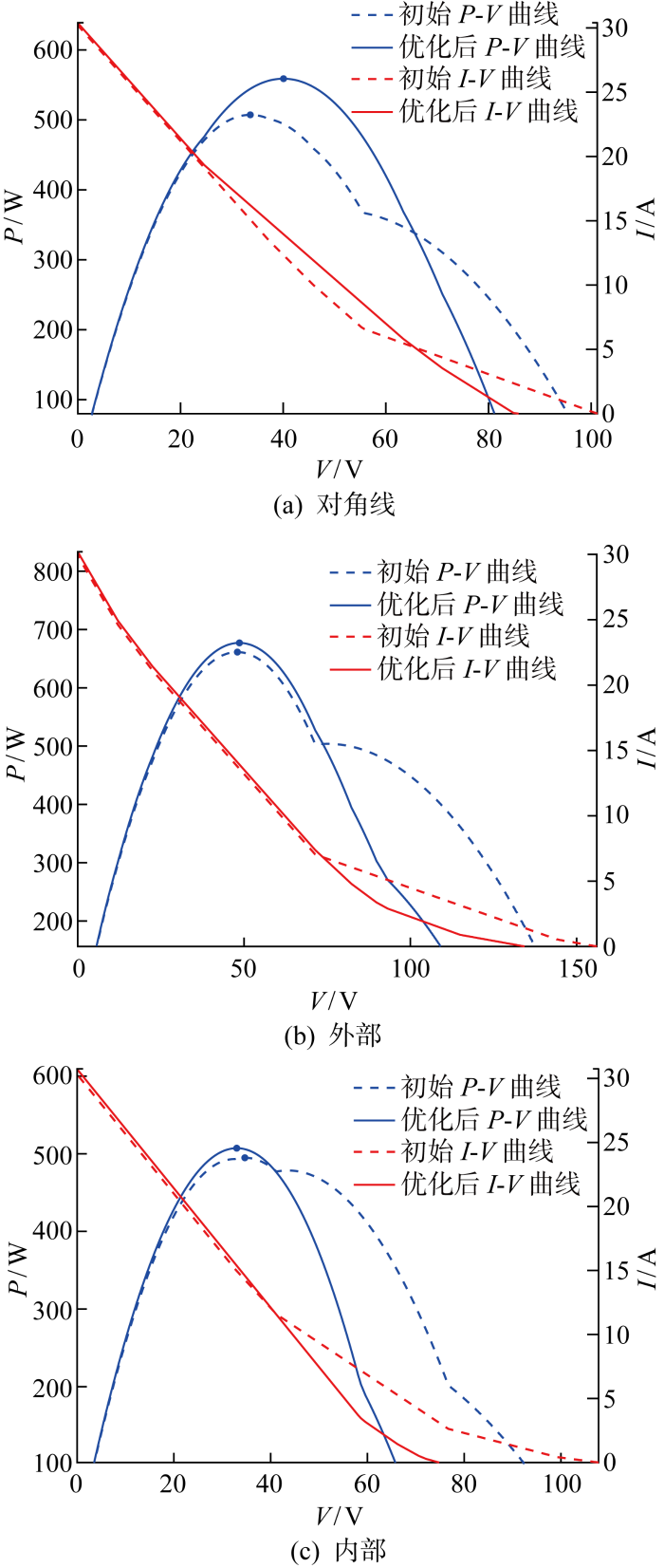
对称9×9 TEG阵列在3种不同温度分布下经过ABC优化前后的输出特性曲线
Fig.6
Output characteristic of symmetric 9×9 TEG array before and after ABC optimization in three different temperature distributions
表1给出对称9×9 TEG阵列下各算法输出功率的统计结果,其中Pave为平均输出功率.与优化前相比,经过ABC算法优化后,TEG阵列在对角线、外部、内部3个算例下的最大输出功率分别提高10.0%、3.5%、2.6%. 由表1可见,ABC仅在外部算例中平均输出功率低于GA,其余结果为4种算法中最好.在相同计算机硬件、迭代次数和种群数目的条件下, ABC、BES、GA和PSO独立运行1次的平均时间如表2所示.此外,基于不同算法30次独立运行所得到的统计结果绘制盒须图,如图7所示.由图可见, 除外部算例外,ABC的最大输出功率最高、离群值数量最少,表现为4种算法中最优.4种算法的收敛曲线如图8所示.其中,在对角线算例中ABC算法的求解时间短于GA算法,在外部和内部算例中ABC算法求解时间略长于GA算法0.1 s左右,但ABC算法在对角线算例和内部算例中有着比GA算法更快的收敛速度.同时,与其他算法相比,ABC算法在各种算例下均可获得最大输出功率.在对角线算例和内部算例下,BES算法收敛时所需迭代次数最少,ABC算法次之;但BES算法所获输出功率远低于ABC算法,这表明BES算法并未搜寻到最佳重构策略,陷入了局部最优,而ABC算法通过更多迭代找到了最佳重构策略,有效验证了ABC算法较强的全局搜索能力.
表1 对称9×9 TEG阵列各算法的输出功率的统计结果
Tab.1
| 算法 | 算例结果 | 不均匀温度分布类型 | ||
|---|---|---|---|---|
| 对角线 | 外部 | 内部 | ||
| 未优化状态 | Pmax/W | 532.4 | 670.9 | 519.8 |
| ABC | Pmax/W | 585.8 | 694.4 | 533.2 |
| Pave/W | 579.0 | 693.7 | 533.1 | |
| GA | Pmax/W | 585.8 | 694.4 | 533.2 |
| Pave/W | 565.5 | 694.4 | 532.8 | |
| PSO | Pmax/W | 585.8 | 686.9 | 533.2 |
| Pave/W | 570.4 | 675.1 | 532.8 | |
| BES | Pmax/W | 565.0 | 647.0 | 532.6 |
| Pave/W | 558.7 | 623.3 | 532.4 | |
表2 对称9×9 TEG阵列各算法的运行时间统计
Tab.2
| 算法 | 运行时间/s | ||
|---|---|---|---|
| 对角线 | 外部 | 内部 | |
| ABC | 6.26 | 6.36 | 6.39 |
| GA | 6.39 | 6.28 | 6.26 |
| PSO | 12.41 | 12.35 | 12.97 |
| BES | 15.96 | 15.66 | 15.00 |
图7
图7
对称9×9 TEG阵列不均匀温度分布下重构所得最大输出功率盒须图
Fig.7
Boxplots of the maximum output power obtained from the reconfiguration of symmetric 9×9 TEG array in heterogeneous temperature distribution
图8
图8
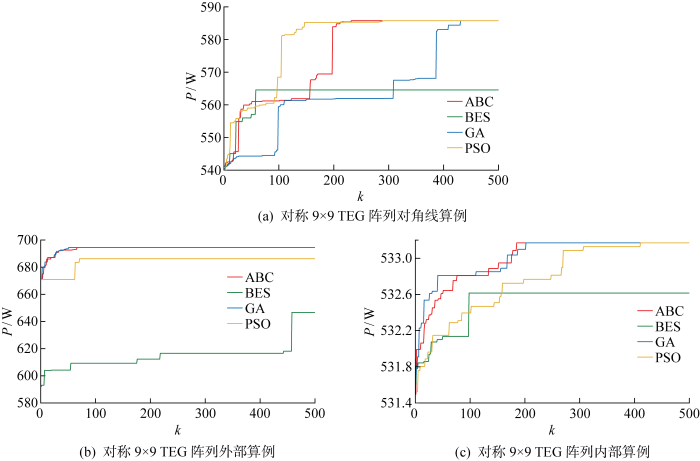
对称9×9 TEG阵列在3种不同温度分布下4种算法的收敛曲线
Fig.8
Convergence curves of four algorithms for symmetric 9×9 TEG array in three different temperature distributions
3.2 不对称10×15 TEG阵列
图9
图9
不对称10×15 TEG阵列3种不同情况下的初始温度分布
Fig.9
Initial temperature distribution of three different scenarios for unsymmetric 10×15 TEG array
图10
图10
经过ABC重构后的不对称10×15 TEG阵列的温度分布
Fig.10
Temperature distribution of unsymmetric 10×15 TEG array optimized by ABC
图11
图11
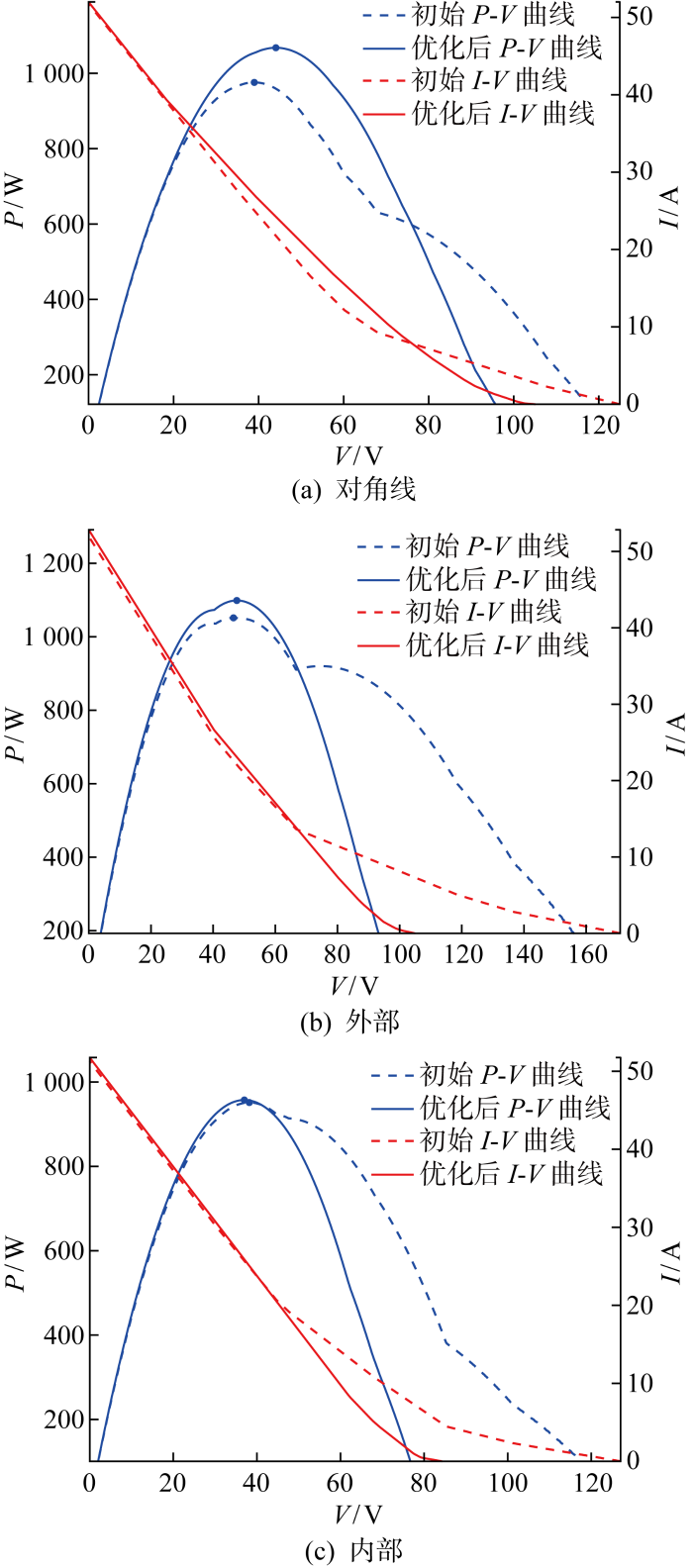
不对称10×15 TEG阵列在3种不同温度分布下经过ABC优化前后的输出特性曲线
Fig.11
Output characteristic of unsymmetric 10×15 TEG array before and after ABC optimization in four different temperature distributions
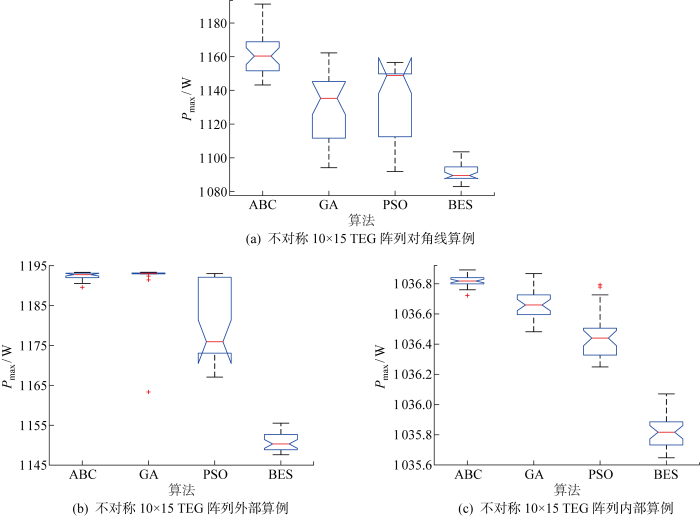
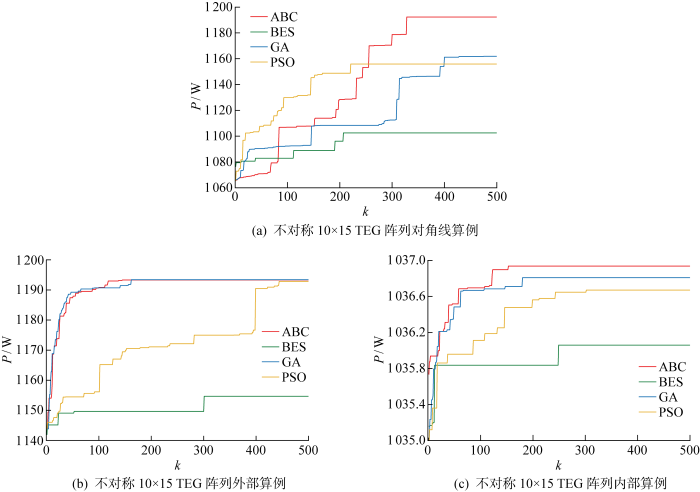
表3为不对称10×15 TEG阵列算例中各算法输出功率的统计结果.经过ABC算法优化后对角线、外部、内部算例的最大输出功率相比于未优化之前分别提高13.6%、4.3%、1.9%.由表3可见,在外部算例中,GA的最大输出功率最高,与ABC算法仅相差0.1 W, 但GA平均输出功率比ABC低0.4 W.在其余算例中ABC的结果相比其他3种算法更为优秀.表4给出各算法的运行时间统计.此外,基于不同算法30次独立运行所得到的统计结果绘制盒须图,如图12所示.由图可见,在外部算例中,虽然GA的最大输出功率高于ABC,但GA的离群值数目多于ABC.图13给出4种算法的收敛曲线.由表4中可见,在内部算例中,ABC算法的运行时间与GA算法相比仅差0.4 s.但是ABC算法比GA算法的收敛速度更快,并且在对角线和内部算例中ABC能够得到更高的输出功率.在对角线算例中,ABC算法虽然不是最快收敛的,但是相比BES算法和PSO算法,ABC算法运行速度更快,能够得到更高的输出功率,这表明ABC算法全局搜索能力更好.因此,在3种算例中,ABC的表现最好.
表3 不对称10×15 TEG阵列各算法的输出功率的统计结果
Tab.3
| 算法 | 算例结果 | 不均匀温度分布类型 | ||
|---|---|---|---|---|
| 对角线 | 外部 | 内部 | ||
| 未优化状态 | Pmax/W | 1048.5 | 1143.8 | 1017.5 |
| ABC | Pmax/W | 1191.2 | 1193.3 | 1036.9 |
| Pave/W | 1161.4 | 1192.4 | 1036.8 | |
| GA | Pmax/W | 1162.3 | 1193.4 | 1036.9 |
| Pave/W | 1130.1 | 1192.0 | 1036.7 | |
| PSO | Pmax/W | 1156.6 | 1193.0 | 1036.8 |
| Pave/W | 1133.0 | 1180.3 | 1036.5 | |
| BES | Pmax/W | 1103.5 | 1155.5 | 1036.1 |
| Pave/W | 1091.2 | 1150.9 | 1035.8 | |
表4 不对称10×15 TEG阵列各算法的运行时间统计
Tab.4
| 算法 | 运行时间/s | ||
|---|---|---|---|
| 对角线 | 外部 | 内部 | |
| ABC | 7.82 | 7.79 | 7.82 |
| GA | 7.59 | 7.20 | 7.42 |
| PSO | 18.48 | 18.45 | 18.47 |
| BES | 16.41 | 16.67 | 16.78 |
图12
图12
不对称10×15 TEG阵列不均匀温度分布下重构所得最大输出功率盒须图
Fig.12
Boxplots of the maximum output power obtained from the reconfiguration of unsymmetric 10×15 TEG array in heterogeneous temperature distribution
图13
图13
不对称10×15 TEG阵列在3种不同温度分布下4种算法的收敛曲线
Fig.13
Convergence curves of four algorithms for unsymmetric 10×15 TEG array in three different temperature distributions
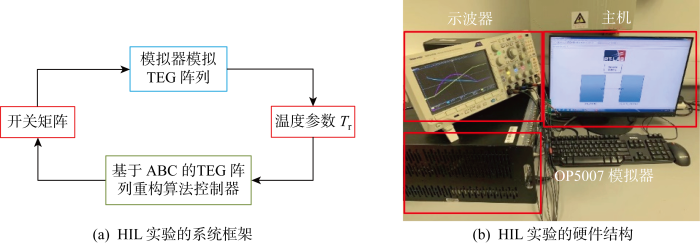
4 RTLAB硬件在环实验
图14
图15
图15
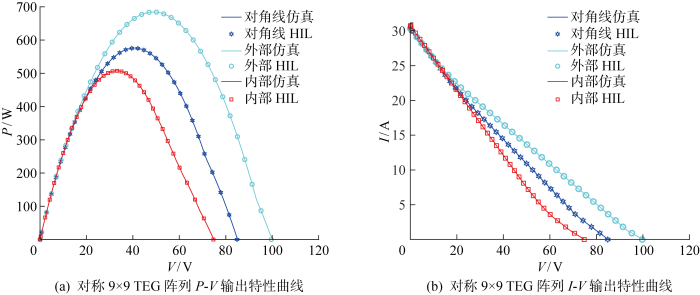
对称9×9 TEG阵列下仿真实验与HIL实验结果对比
Fig.15
Comparison of the simulation results and HIL test results of symmetric 9×9 TEG array
图16
图16
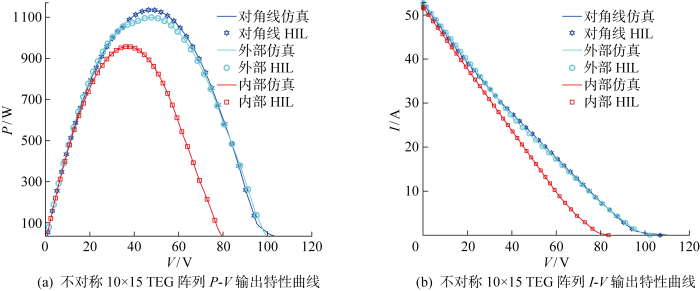
不对称10×15 TEG阵列下仿真实验与HIL实验结果对比
Fig.16
Comparison of the simulation results and HIL test results of unsymmetric 10×15 TEG array
5 讨论
由于算法内部的寻优机制不同,全局搜索能力有强弱,对同一算例下进行重构得到的最优解有差异,所以不同算法在TEG阵列重构问题中得到的最大输出功率不同.由式(1)~(5)可知,TEG阵列所处的温度环境影响其输出电压,进而影响TEG阵列潜在的输出功率.因此,在采用ABC对TEG阵列进行重构时,不同算例下最大输出功率提升率不同.优化算法虽无法从根本上改变TEG阵列所处环境的固有温度条件,但可以通过优化算法动态重构改变其温度分布,尽可能挖掘TEG阵列的发电潜能,提升其发电效率.
此外,部分研究采用数独算法和奇偶排序算法的数学方法解决重构问题.数独算法将TEG阵列分为n个3×3的子阵列,在子阵列中填入1~9的模块序号,该方法要求TEG阵列的规模为3的倍数的方阵.奇偶排序算法在保持TEG模块电气连接方式不变的情况下,改变TEG模块的位置.上述方法在求解非对称、大规模TEG阵列重构问题时存在求解时间长的问题,数独算法还会受到TEG阵列形状的约束.本文所提基于启发式算法的TEG阵列重构方法能够快速求解大规模阵列的重构问题,且不受阵列形状的限制,具有更强的适应性[23].
6 结论
提出基于人工蜂群算法的TEG阵列最优重构方法,主要贡献如下:
(1) 建立TEG阵列的模型,提出TEG阵列的动态重构方法.旨在高效利用新能源发电中的余热和废热,保证能源能够得到充分的利用.
(2) 在9×9 TEG阵列、10×15 TEG阵列的3种算例中ABC优化算法能够使得TEG阵列输出功率提升1.9%~13.6%,且相比于GA、PSO以及BES的优化能力好.
(3) 基于RTLAB的HIL实验验证了ABC的硬件可行性.
在未来的研究中,将把ABC应用到TEG阵列与光伏系统的混合动态重构,使其能够应用于电力工程行业的多个方面.
参考文献
太阳能驱动半导体温差发电器性能参数的优化设计
[J].
Optimum design of the performance parameters of a solar-driven semiconductor thermoelectric generator
[J].
Realization of a wearable miniaturized thermoelectric generator for human body applications
[J].
Thermoelectric automotive waste heat energy recovery using maximum power point tracking
[J].
Comparative study of MPPT algorithms for thermoelectric generators
[C]//
半导体温差发电特性分析及MPPT控制算法研究
[C]//
Semiconductor thermoelectric generation characteristics analysis and MPPT control algorithm research
[C]//
Maximum power point tracking converter based on the open-circuit voltage method for thermoelectric generators
[J].DOI:10.1109/TPEL.63 URL [本文引用: 1]
基于短路电流法的温差发电最大功率点跟踪控制
[J].
Maximum power point tracking scheme for thermoelectric generators based on short-circuit current method
[J].
基于双曲正切函数的光伏/温差自适应MPPT控制策略研究
[J].
Self-adaptive photovoltaic/temperature difference MPPT control strategy based on hyperbolic tangent function
[J].
基于电导增量法与改进粒子群算法混合控制的最大功率点跟踪策略
[J].
The hybrid control maximum power point tracking(MPPT) strategy based on incremental conductance method and improved particle swarm optimization algorithm
[J].
基于改进蜉蝣算法的光伏阵列最优重构方法
[J].
Optimal reconfiguration method for photovoltaic arrays based on improved mayfly algorithm
[J].
A robust strategy based on marine predators algorithm for large scale photovoltaic array reconfiguration to mitigate the partial shading effect on the performance of PV system
[J].DOI:10.1109/Access.6287639 URL [本文引用: 1]
An adaptive utility interactive photovoltaic system based on a flexible switch matrix to optimize performance in real-time
[J].DOI:10.1016/j.solener.2011.12.028 URL [本文引用: 1]
基于秃鹰搜索算法的部分遮蔽条件下光伏阵列重构方法
[J].
DOI:10.12204/j.issn.1000-7229.2022.03.003
[本文引用: 1]

部分遮蔽(partial shading, PS)是影响光伏发电效率最主要的因素之一,它通常会引起失配损耗并降低光伏阵列的输出功率。为了解决这个问题,光伏重构技术被广泛应用于光伏发电系统。文章提出了一种基于秃鹰搜索算法(bald eagle search, BES)的光伏阵列重构方法,它可以有效地减少功率损失,提高发电效率。基于BES的重构方法旨在重新配置光伏阵列的电气连接,以减轻部分遮蔽带来的不利影响,并获得更高质量的输出特性。为了验证BES的有效性,模拟了缓慢移动的云在10 min内造成的阴影,基于此对3个典型的启发式算法进行了全面的比较。仿真结果表明,与网状连接(total cross tied, TCT)相比,BES在缓慢移动的云层阴影下能提高15.10%的输出功率,减小57.90%的失配损耗,并将填充因子由0.625 4提高到0.714 3;与蚁群算法(ant colony optimization, ACO)和禁忌搜索算法(tabu search, TS)相比,BES也能够获得更低的失配损耗、更高的功率提升百分比和更高的填充因子。
Bald eagle search based PV array reconfiguration technique under partial shading condition
[J].
DOI:10.12204/j.issn.1000-7229.2022.03.003
[本文引用: 1]

Partial shading (PS) is one of the most severe factors affecting the efficiency of photovoltaic (PV) generation, which usually causes mismatch losses and reduces the output power of PV arrays. To solve this problem, PV reconfiguration technology is widely used in PV systems. This paper proposes a PV array reconfiguration method based on bald eagle search (BES) algorithm, which can effectively reduce power losses and improve power generation efficiency. To mitigate the malignant effect of PS and obtain satisfactory output characteristics, BES is designed to reconfigure the electrical connection of PV arrays. To verify the effectiveness of BES, shadows of slowly moving clouds in ten minutes are simulated, upon which a comprehensive comparison of three typical metaheuristic algorithms is undertaken. Simulation results show that compared with total cross tied (TCT), BES can increase the output power by 15.10%, reduce the mismatch loss by 57.90%, and increase the filling factor from 0.6254 to 0.7143 under shadow of slowly moving clouds. Compared with ant colony optimization (ACO) and tabu search (TS), BES also obtains lower mismatch loss, higher power enhancement, and higher filling factor.
优化的GA算法在大型配电网络重构中的应用
[J].
Application of optimized GA algorithm in large distribution network reconfiguration
[J].
人工蜂群算法研究综述
[J].
Artificial colony algorithm research were reviewed
[J].
Novel model and maximum power tracking algorithm for thermoelectric generators operated under constant heat flux
[J].DOI:10.1016/j.apenergy.2019.113930 URL [本文引用: 1]
Combined solar concentration and carbon nanotube absorber for high performance solar thermoelectric generators
[J].
High step-up DC/DC topology and MPPT algorithm for use with a thermoelectric generator
[J].DOI:10.1109/TPEL.2012.2219393 URL [本文引用: 1]
A novel maximum power point tracker for thermoelectric generation system
[J].DOI:10.1016/j.renene.2016.05.001 URL [本文引用: 1]
AI-based global MPPT for partial shaded grid connected PV plant via MFO approach
[J].DOI:10.1016/j.solener.2018.06.109 URL [本文引用: 1]
Energy management for thermoelectric generators based on maximum power point and load power tracking
[J].
PV arrays reconfiguration for partial shading mitigation: Recent advances, challenges and perspectives
[J].
Solar PV array reconfiguration using the concept of standard deviation and genetic algorithm
[J].DOI:10.1016/j.egypro.2017.05.229 URL [本文引用: 1]
Particle swarm optimization based solar PV array reconfiguration of the maximum power extraction under partial shading conditions
[J].DOI:10.1109/TSTE.2017.2714905 URL [本文引用: 1]
Novel meta-heuristic bald eagle search optimisation algorithm
[J].DOI:10.1007/s10462-019-09732-5 [本文引用: 1]