竖向小曲率半径曲线顶管掘进管节-土体相互作用

doi:10.16183/j.cnki.jsjtu.2023.S1.02

竖向小曲率半径曲线顶管掘进管节-土体相互作用

李登¹, 庄欠伟³, 黄昕^,¹^,², 周东荣⁴, 朱小东⁴, 张弛³, 魏良孟⁴

1.同济大学地下建筑与工程系,上海 200092

2.新疆大学建筑工程学院,乌鲁木齐 830047

3.上海隧道工程有限公司,上海 200032

4.交通运输部上海打捞局,上海 200090

Pipe-Ground Interaction During Curved Pipe Jacking Process with a Small Radius of Vertical Curvature

LI Deng¹, ZHUANG Qianwei³, HUANG Xin^,¹^,², ZHOU Dongrong⁴, ZHU Xiaodong⁴, ZHANG Chi³, WEI Liangmeng⁴

1. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China

2. College of Civil Engineering and Architecture, Xinjiang University, Urumuchi 830047, China

3. Shanghai Tunnel Engineering Co., Ltd., Shanghai 200032, China

4. Shanghai Salvage Ministry of Transport, Shanghai 200090, China

通讯作者: 黄昕,副教授,博士生导师,电话(Tel.):021-65982986;E-mail:xhuang@tongji.edu.cn.

收稿日期: 2022-07-7 修回日期: 2022-07-25 接受日期: 2022-08-22

基金资助:

上海市科委社发领域重大项目(21DZ1201103)
国家自然科学基金(52278407)

Received: 2022-07-7 Revised: 2022-07-25 Accepted: 2022-08-22

作者简介 About authors

李登(1998-),硕士生,从事隧道及地下工程方面的研究.

摘要

“长江口二号”古沉船采用国际首创的曲线顶管底幕法进行打捞,其顶管机的机械设计及管节的结构设计需明确顶管管节与地层的相互作用并建立合理的顶推力计算模型.在厘清顶管掘进过程中管节-地层相互作用因素的基础上,基于极限平衡理论,推导竖向小曲率半径曲线顶管掘进顶推力计算方法.采用耦合欧拉-拉格朗日(CEL)方法对单根管节的动态掘进过程进行数值模拟分析,获得小曲率半径矩形曲线顶管掘进过程中地层应力和地表变形的动态变化规律,并通过与模型试验、现场施工监测数据和理论计算结果的对比分析,明确竖向小曲率半径曲线顶管动态掘进过程中顶推力的动态变化特征及控制因素.研究成果可为类似“长江口二号”打捞工程的实施提供重要的理论依据和技术指导.

关键词： 曲线顶管底幕法; 沉船打捞; 顶推力; 耦合欧拉-拉格朗日方法; 地层变形

Abstract

The salvage of “Yangtze River Estuary II” ancient wreck adopted the world’s first curved pipe based method. The mechanical design of the pipe jacking machine and the structure design of curved pipe relied on the understanding of the pipe-ground interaction mechanism and establishment of a reasonable model for calculating the driving force. Based on the understanding of the major factors contributing to the pipe-ground interaction, a theoretical model for calculating the driving force of curved pipe jacking machine with a small radius of vertical curvature was derived through equilibrium analysis. The dynamic jacking process of a single pipe was simulated using the coupled Eulerian Lagrangian (CEL) method, from which the evolution processes of ground stress and ground surface settlement during the curved pipe jacking process with a small radius of vertical curvature were obtained. The simulation results were compared with model test data, on-site monitoring data, and theoretical calculation results, whereby the characteristics of driven force evolution and its controlling factors were obtained. The research outcome can provide theoretical basis and technical support for future wreck salvage project similar to “Yangtze River Estuary II”.

Keywords： curved pipe based method; wreck salvage; driving force; coupled Eulerian Lagrangian (CEL) method; ground settlement

PDF (19245KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李登, 庄欠伟, 黄昕, 周东荣, 朱小东, 张弛, 魏良孟. 竖向小曲率半径曲线顶管掘进管节-土体相互作用[J]. 上海交通大学学报, 2023, 57(S1): 69-79 doi:10.16183/j.cnki.jsjtu.2023.S1.02

LI Deng, ZHUANG Qianwei, HUANG Xin, ZHOU Dongrong, ZHU Xiaodong, ZHANG Chi, WEI Liangmeng. Pipe-Ground Interaction During Curved Pipe Jacking Process with a Small Radius of Vertical Curvature[J]. Journal of Shanghai Jiaotong University, 2023, 57(S1): 69-79 doi:10.16183/j.cnki.jsjtu.2023.S1.02

2022年11月21日,目前我国水下考古发现的体量最大、保存最为完整的木质沉船“长江口二号”在上海长江口横沙岛附近顺利打捞出水,标志着我国水下打捞技术取得了里程碑式的突破.“长江口二号”采用国际首创的矩形曲线顶管底幕法进行整体打捞和搬迁,其基本思想来源于隧道及地下工程中的管幕法^[1],采用“无缝”连接的矩形曲线顶管顺次通过竖向小曲率推进在土体中形成弧形底部托盘,对内部空间进行保护.由于没有先例可循,打捞工程的实施需要解决顶管机设计、施工顺序优化、沉船扰动控制等一系列难题.其中,明确顶管管节与地层的相互作用、建立合理的顶推力计算模型是该技术应用中顶管机机械设计和管节结构设计需要重点关注的问题.

目前,管幕法以短距离、小直径的直线管幕居多,且曲线顶管工艺主要考虑水平面曲率的变化,极小曲率半径竖向曲线顶管的工程案例还未见报道^[2].管节推进时,需要克服多种阻力,部分学者对管节-地层的相互作用进行了研究.Sofianos等^[3]通过对比顶管摩阻力实测值、管土全接触模型预测值和管土部分接触模型预测值,发现管土全接触模型摩阻力预测值大于实测值,而基于Hertz弹性接触理论的管土部分接触摩阻力预测值略小于实测值;张鹏^[4]依托拱北隧道曲线顶管管幕工程,对顶管施工过程中的应力应变进行现场实时监测,获得管节的受力变形规律;雷晗等^[5]研究了施工过程中管土接触压力的变化及顶管覆土厚度对管道外土压力的影响;刘翔等^[6]通过实测分析软土中大直径顶管在顶进过程中的受力特性,发现顶管在良好泥浆套中顶进时,管壁接触压力整体分布较均匀,管道两侧土压力大于顶部土压;由广明等^[7]通过建立三维有限元模型,研究曲线顶管施工过程中地表的变形规律;邴风举等^[8]通过三维数值模型对顶管隧道不同土质条件下的适用性进行了探讨;王贺敏等^[9]通过刚度迁移方法对顶管顶进过程进行了多步仿真模拟.这些学者采用数值方法研究顶管施工环境效应时,大都采用静态分析方法,通过施加顶力来模拟顶管的顶进,顶管仅有较小位移,难以反映实际施工情况.故也有学者尝试模拟顶管顶进的动态效应,黄吉龙^[10]采用考虑管土接触界面大变形滑动的数值方法,动态模拟玻璃钢夹砂顶管的施工过程.

国内外绝大多数顶管规范中对于曲线顶管顶推力的计算尚无明确规定,仅有一些简单的经验公式可供参考.张斌梁等^[11]开展拱北隧道管幕曲线顶管顶进模拟实验,研究管节应力与顶推力大小的变化规律;史培新等^[12]总结曲线顶管顶推力的主要组成及影响因素,比较和分析了中国和日本顶管规范的预测顶力和现场实测顶力的差异;丁传松^[13]对传统曲线顶管法和单元曲线顶管法稳定性进行分析,在得出管侧土体抗力计算公式基础上,同时考虑管周静止土压力的影响,推导出曲线顶管顶进力递推公式;陈忠杰^[14]通过静力平衡原理分析曲线顶管周围土压力分布规律,考虑了由于曲线顶进引起的管周附加土压力以及静止土压力引起的侧摩阻力,但其计算结果偏大;Shou等^[15]在此基础上,参考日本微型隧道掘进协会(JMTA)的曲线顶管顶进力公式建立了一种修正的顶推力计算公式.

总体而言,目前缺乏竖向小曲率半径曲线顶管顶进的工程实例及顶推力计算模型.顶管顶进及隧道开挖的模拟通常是多步仿真模拟,管节受到的荷载主要通过计算或实测数据手动添加,这样的模拟方式难以有效且直接地反映管土相互作用.故本文首先梳理顶管管节-地层相互作用的主要机制,基于极限平衡理论,建立竖向矩形曲线顶管顶推力计算模型;接着,以“长江口二号”沉船打捞工程为背景,采用CEL法模拟单根矩形曲线顶管顶进的全过程,与现场实测数据结果进行对比验证;最后,获得顶管顶进过程中地层的应力和变形特征.

1 矩形曲线顶管底幕法简介

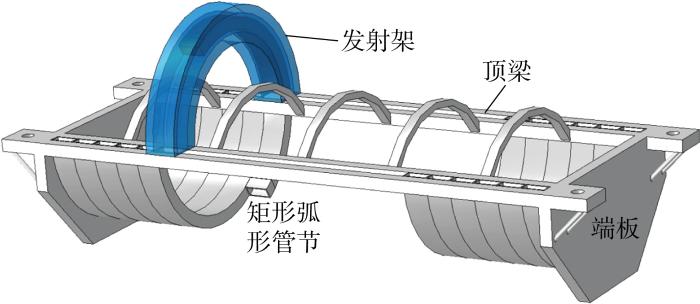
“长江口二号”矩形曲线顶管底幕法打捞概念图如图1 所示.打捞装置主要部件包括端板及端板间的顶梁、导向架和矩形弧形顶管管节.通过两侧端板进行侧向定位,由相互密合的弧形管节形成底部托盘承载沉船及船上文物,端板和管节形成封闭的空间防止托盘内的水土流失,避免对沉船和船载文物造成损伤.顶梁为管节始发及接收的支座,同时也是最终整体起吊的受力点.通过自主研发的行星式顶管机驱动管节通过导向架顶入地层,在导向架顶部、底部和两侧设置滚珠的方式,降低顶推力的摩擦损失.为了避免顶梁产生较大形变,兼顾现场施工条件,采用一定的顺序依次顶进管节,直至形成完整的底部托盘.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 矩形曲线顶管底幕法示意图

Fig.1 Schematic illustration of rectangular curved pipe based method

2 “长江口二号”打捞工程实施过程

第1根管节于2022年9月28日开始推进,最后1根管节,即第22根,于2022年11月15日完成推进.管节推进前,需要完成两侧端板的沉放以实现侧向定位,每根管节通过工程船吊机调入甲板上的滑轨,在处理后沿滑轨推入发射架中.管节沿滑轨进入发射架后,需要进行机头、推进装置、插销油缸调试,安装吊点防护及标识,潜水泵加装,发射架管路调整,管路保护等准备工作.完成准备工作后,将发射架起吊并移动至预定位置,然后下放至水中.发射架于水下的固定及管节推进完成后与端板的绑定需要专业潜水人员配合插入插销来完成.每根管节完成推进后,将发射架调回,并对机头进行清理,随后开始下一根管节作业,实际打捞作业流程如图2所示.正常情况下,每根管节推进完成需要4 h;遇到如水流因素、装置故障等特殊情况,管节的推进时间会延长至8~12 h不等;如遇大风天气,则停止施工.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 现场打捞施工作业流程

Fig.2 Process of on-site salvage operation

3 基于极限平衡的竖向小曲率半径顶管-地层相互作用模型

顶管在推进过程中,其端面、入土部分的侧面和上下表面均会与土体产生接触,分析管节-地层相互作用需要对不同的接触机制分别进行考虑.

3.1 基本假设

(1) 土体初始主应力沿竖直和水平方向.

(2) 管节为刚体,即不计其变形的影响.

(3) 考虑发射架的限位作用,假设管节始终沿着既定轨迹运动,顶推力始终沿着顶进轨迹的切线方向作用.

(4) 假设轴向力的传递是连续的,管节与导向架的摩擦阻力可忽略不计.

(5) 土体的剪切塑性特性服从摩尔库伦准则.

(6) 管节顶进过程中,邻近土体处于临界剪切屈服状态.

3.2 管节受力模型

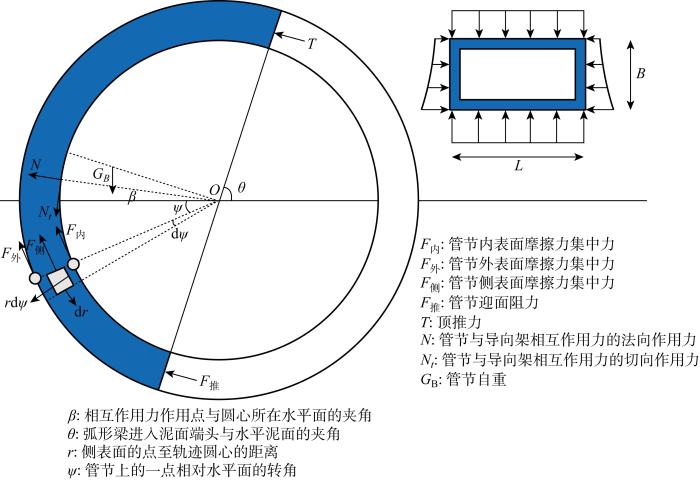
基于上述假设,进一步考虑管节宽度方向的对称性,只考虑内弧面摩阻力F_内、外弧面摩阻力F_外、两侧摩阻力的切向力F_侧及迎面阻力F_推相对侧平面圆心的力矩.其正交平面的力矩因为对称性形成平衡,侧平面法向力因为对称性形成平衡.将各力积分后,可以将三维受力模型转换为二维受力模型.李登等^[16]推导了多层地层条件下极小曲率半径矩形曲线顶管管节受力计算模型,本文针对“长江口二号”沉船实际穿越的地层条件简化计算模型如图3所示,图中B为管节高度;L为管节宽度;T为顶推力.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 极小曲率半径矩形曲线顶管弧形管节受力示意图

Fig.3 Schematic illustration of forces experienced by rectangular curved beam with an extremely small curvature

3.3 管节-地层相互作用组成

3.3.1 内弧面分量

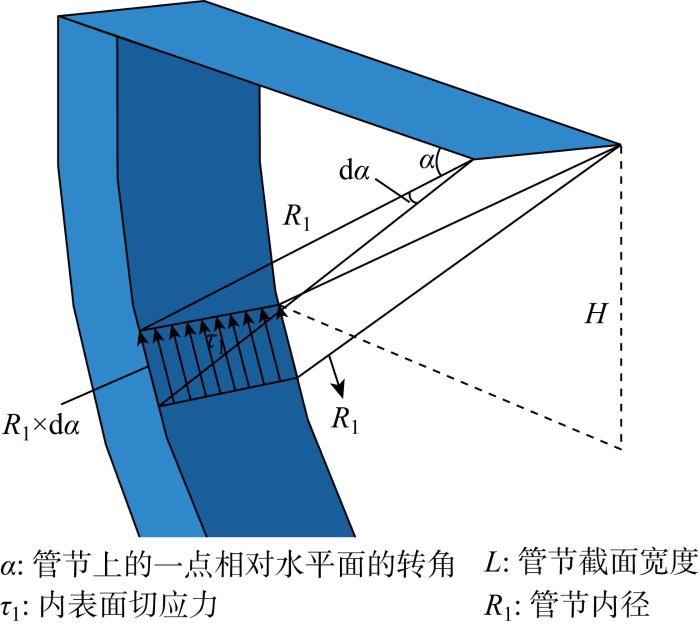
对于内弧面摩阻力,考虑其对称性,将内弧面的力进行积分,从而使其从三维中内弧面转换于与之正交的运动轨迹平面中,便于最终力学平衡方程的建立.内弧面摩阻力计算模型简图如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 内弧面摩阻力计算模型简图

Fig.4 Simplified calculation model of frictional resistance on inner surface

土体作用于管节内弧面的正应力和切应力分别为

$\begin{array}{l} σ_{1} = γ R_{1} s i n α \end{array}$

(1)

$τ_{1} = c + σ_{1} t a n φ$

(2)

式中: $γ$ 为土体重度,在水中时考虑为浮重度; $R_{1}$ 为内弧面半径; $c$ 为土体黏聚力; $φ$ 为内摩擦角.为方便平衡方程建立,通过对内弧面摩阻力产生的法向应力与切向应力分解并积分,得到内弧面摩阻力分解后的水平分量 $X_{1}$ 与竖向分量 $Y_{1}$ 分别为:

$\begin{array}{l} M_{1} = L R_{1}^{2} \int_{0}^{θ} τ_{1} d α α < θ, θ < π \\ X_{1} = L R_{1} \int_{0}^{θ} (- σ_{1} \cdot c o s α - τ_{1} \cdot s i n α) d α \\ α < θ, θ < π \\ Y_{1} = L R_{1} \int_{0}^{θ} (- σ_{1} \cdot s i n α + τ_{1} \cdot c o s α) d α \\ α < θ, θ < π \end{array}\}$

(3)

式中,M₁为内弧面摩阻力引起的力矩.

3.3.2 外弧面分量

外弧面摩阻力计算模型简图如图5所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

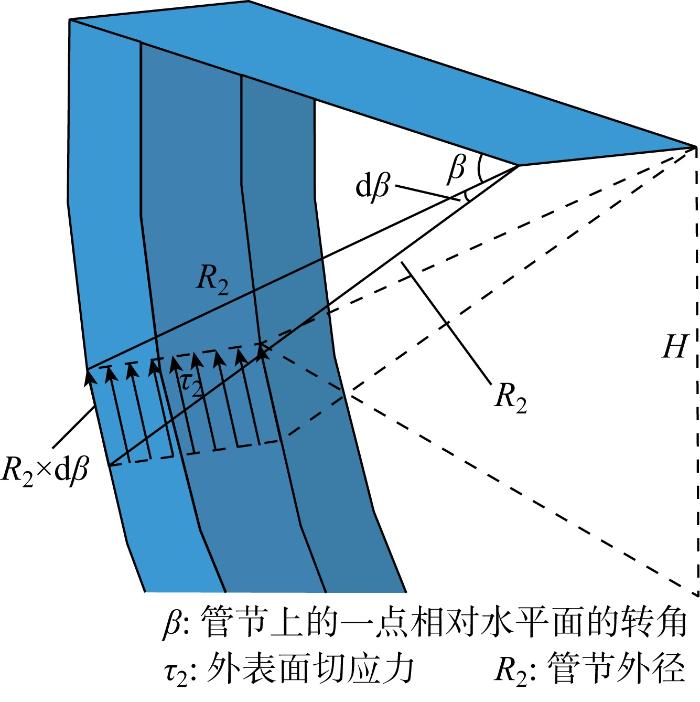
图5 外弧面摩阻力计算模型简图

Fig.5 Simplified calculation model for frictional resistance on external surface

外弧面摩阻力推导与内弧面摩阻力类似,土体作用于管节外弧面的正应力和切应力分别为:

$\begin{matrix} σ_{2} = γ R_{2} s i n β \end{matrix}$

(4)

$τ_{2} = c + σ_{2} t a n φ$

(5)

外弧面摩阻力引起的力矩M₂及其分解后的水平分量X₂和竖向分量Y₂分别为:

$\begin{array}{l} M_{2} = L R_{2}^{2} \int_{0}^{θ} τ_{2} d β β < θ, θ < π \\ X_{2} = L R_{2} \int_{0}^{θ} (σ_{2} \cdot c o s β - τ_{2} \cdot s i n β) d β \\ β < θ, θ < π \\ Y_{2} = L R_{2} \int_{0}^{θ} (σ_{2} \cdot s i n β + τ_{2} \cdot c o s β) d β \\ β < θ, θ < π \end{array}\}$

(6)

式中,R₂为外弧面半径,其他参数含义同前.

3.3.3 侧面分量

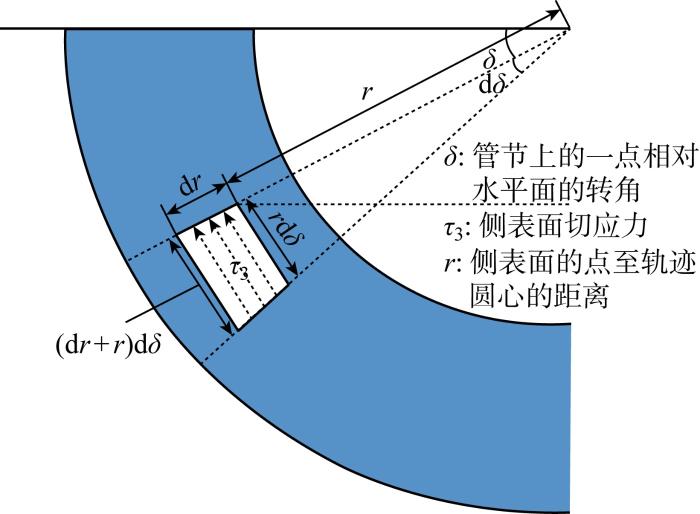
如图6所示,由对称性,两侧表面的法向力形成平衡,因此不考虑其产生的侧平面力矩.土体作用于管节侧表面的切向应力为

$\begin{matrix} τ_{3} = c + K γ r s i n θ \end{matrix}$

(7)

式中,K为摩擦因数.其引起的力矩 $M_{3}, 水平集中力分量 X_{3}, 竖向集中力分量 Y_{3}$ 分别为:

$\begin{array}{l} M_{3} = \int_{0}^{θ} τ_{3} r^{2} d r d δ & δ < θ, θ < π \\ X_{3} = (- s i n δ) \int_{0}^{θ} τ_{3} r d r d δ & δ < θ, θ < π \\ Y_{3} = c o s δ \int_{0}^{δ} τ_{3} r d r d δ & δ < θ, θ < π \end{array}\}$

(8)

当两个侧面同时考虑时,需要将上述公式乘以2代入平衡方程中.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 侧摩阻力计算模型

Fig.6 Simplified calculation model for side frictional resistance

3.3.4 迎面分量

因迎面阻力与运动路径无关,故迎面阻力无需进行分类讨论.迎面阻力力矩、水平集中力分量、竖向集中力分量分别为:

$\begin{array}{l} \begin{array}{l} M_{4} = γ \cdot L \frac{R_{2}^{3} - R_{1}^{3}}{3} s i n θ \cdot (c o s^{2} θ + K s i n^{2} θ) \\ X_{4} = - s i n θ \cdot γ \cdot L \frac{R_{2}^{2} - R_{1}^{2}}{3} \times \\ s i n θ \cdot (c o s^{2} θ + K s i n^{2} θ) \\ Y_{4} = c o s θ \cdot γ \cdot L \frac{R_{2}^{2} - R_{1}^{2}}{3} \times \\ s i n θ \cdot (c o s^{2} θ + K s i n^{2} θ) \end{array}\} \end{array}$

(9)

3.4 顶推力计算模型

获得管节-地层相互作用的受力模型后,即可利用受力平衡条件推导顶推力计算模型.

3.4.1 管节自重

由半圆形形心与圆心的距离公式可得圆环的形心与圆心距离为

$\begin{matrix} h_{c} = \frac{S_{2} h_{2} - S_{1} h_{1}}{S_{1} - S_{2}} = \frac{4}{3 π} \frac{R_{2}^{3} - R_{1}^{3}}{R_{2}^{2} - R_{1}^{2}} \end{matrix}$

(10)

式中: $S_{1} 、 S_{2} 分别为内半圆弧和外半圆弧的面积; R_{1} 、 R_{2}$ 分别为管节内、外半径.管节自重引起的力矩、其水平集中力分量、竖向集中力分量分别为:

$\begin{matrix} \begin{array}{l} M_{5} = G_{B} h_{c} s i n θ \\ X_{5} = 0 \\ Y_{5} = - G_{B} \end{array}\} \end{matrix}$

(11)

式中: $G_{B} 为管节的自重; θ$ 为管节进入泥面端头与水平泥面的夹角.自重为竖向力,不存在水平分力.

3.4.2 管节与导向架相互作用力

假设管节与导向架的相互作用力为作用位置未知的集中力,相互作用力方向为运行轨迹的切向和法向.由此可得管节与导向架的相互作用力对轨迹形心的力矩、水平集中力分量、竖向集中力分量分别为:

$\begin{array}{l} \begin{array}{l} M_{6} = N_{t} R_{1} \\ X_{6} = N_{t} s i n (β) - N c o s (β) \\ Y_{6} = N_{t} c o s (β) + N s i n (β) \end{array}\} \end{array}$

(12)

$N_{t} = |K_{t} N|$

(13)

式中,N_t为相互作用力中的切向分量,取绝对值代表其方向始终不变,与管节运动方向相反.

3.4.3 顶推力

将顶推力设置为未知力T,推导顶推力对轨迹形心的力矩、水平集中力分量、竖向集中力分量分别为:

$\begin{matrix} \begin{array}{l} M_{7} = - T (R_{1} + R_{2}) / 2 \\ X_{7} = - T s i n θ \\ Y_{7} = T c o s θ \end{array}\} \end{matrix}$

(14)

3.4.4 平衡方程

基于3.3节和本节内容可建立管节的力矩平衡方程、水平集中力平衡方程和竖向集中力平衡方程:

$\begin{array}{l} 0 = M_{1} + M_{2} + M_{3} + M_{4} + M_{5} + M_{6} + M_{7} \\ 0 = X_{1} + X_{2} + X_{3} + X_{4} + X_{5} + X_{6} + X_{7} \\ 0 = Y_{1} + Y_{2} + Y_{3} + Y_{4} + Y_{5} + Y_{6} + Y_{7} \end{array}\}$

(15)

求解该方程组即可得不同推进角度时对应的顶推力、管节与导向架相互作用力中的法向力,管节与导向架相互作用力中的作用位置.

4 考虑大变形的CEL有限元方法

4.1 CEL方法简介

拉格朗日方法中有限元网格会随材料一起变形;欧拉方法中,介质材料可以在欧拉域中自由移动,但网格始终保持不变.耦合欧拉-拉格朗日(CEL)分析方法最早由Noh^[17]提出,结合拉格朗日网格与欧拉网格的优点,可以有效地解决有关大变形和材料破坏等诸多问题^[18].在拉格朗日分析中,网格与材料绑定,在受力时两者会一起变形,若变形较大,计算容易出现不收敛情况;在欧拉分析中,网格与材料分离,欧拉域中的网格不会与材料一同发生变形,因此不会出现计算不收敛情况,而材料会像“流体”一样,受力后通过在欧拉域网格中流动来模拟变形.CEL方法在分析岩土大变形问题时的适用性和相对拉格朗日方法的优越性在Qiu等^[19]和Tho等^[20]的研究中已经被广泛证明.

4.2 基于CEL方法的顶推模型构建

4.2.1 模型建立

土体采用欧拉体建模,管节推进过程中土体材料在欧拉域中流动.翟一欣^[21]发现管节在推进过程中前方土体表面会出现明显的隆起现象,即土体材料会流出初始设定的范围.在欧拉分析方法中,欧拉网格在空间位置固定不变,欧拉材料将会根据受力情况在欧拉网格中运动.根据欧拉分析方法的这一特点,在土体上方设置一定尺寸的空穴^[22],即不包含任何材料的空单元,使得管节入土与出土时一定范围内的土体材料可以向上运动进入空穴,给予土体隆起的空间.

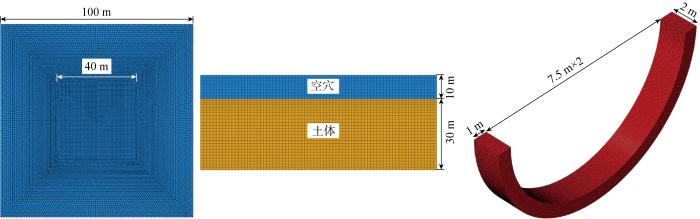
地基土设为欧拉体,根据“长江口二号”打捞区域现场地勘报告,土体密度为 1 830 kg /m³,弹性模量为6.8 MPa,黏聚力为10 kPa,有效内摩擦角为28°.因为管节模型较大,为减小边界效应对模拟结果的影响,代表土体的欧拉域范围需足够大^[23],故将欧拉域范围设置为高度40 m,水平面积为100 m×100 m,其中欧拉域下部30 m为土体,欧拉域上部10 m为空穴.对包含空穴及土体在内的欧拉体设置预应力场,并在管节推进的分析步前设置地应力平衡分析步,以在管节推进模拟前得到合理的地应力场.

考虑到管节刚度远大于土体刚度,故管节采用拉格朗日体建模.管节模型内径为7.5 m,外径为8.5 m,截面大小为1 m×2 m.因管节与欧拉体划分网格后网格数量巨大,为提高计算效率,考虑到管节刚度远大于土体刚度,对管节施加荷载时将管节与转动中心绑定为刚体,采用“位移控制法”实现管节的旋转推进过程.根据测试,该模型结果在分析步时长达300 s后结果趋于稳定,因此在荷载模块中选用 10.5 mrad 的贯入速率来完成管节的推进过程.管节、空穴和土体的位置关系如图7所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 弧形管节-空穴-土体的空间位置关系

Fig.7 Spatial relation of curved beam-air-soil system

设置欧拉法向速度固定边界^[24],在欧拉域四周与底面施加垂直于该面的速度约束,设置为0,即材料流动速度为0.并且设置欧拉吸收边界(Eulerian boundary),以消除由于计算模型尺寸选取导致的边界效应,减小计算结果的振荡.欧拉材料与拉格朗日体之间的接触采用“通用接触” (General contact)的接触算法.

网格划分时,需要考虑网格对模拟结果准确性以及计算速率的影响. 管节周围及管节推进面接触的土体为相互作用主要区域,采用细密网格,远离管节运动区域的土体受力相对较小,采用稀疏网格,即采用细至粗的放射性网格划分模型, 如图8所示.将以管节旋转中心为中心的边长为40 m的正方形区域与土体表面向下10 m范围的欧拉域设为细密网格,由此区域向外逐渐增大网格尺寸.为避免计算结果中土体材料渗入管节网格中影响对结果的分析,应保证管节网格尺寸小于土体网格尺寸,土体采用欧拉单元 EC3D8R模拟.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 CEL模型网格划分

Fig.8 Mesh of CEL model

土体网格全局尺寸为1.2 m,水平面中心 40 m×40 m区域的网格尺寸为0.6 m,中心区域与边界对应的角的连线尺寸从0.6 m渐变至1.6 m.竖向部分,土体表面以下10 m内的网格使用0.8 m至 1.6 m 的渐变尺寸,空穴及土体表面以下10~30 m 部分使用全局尺寸.管节网格全局尺寸0.1 m.

4.2.2 示踪粒子设置

为研究管节顶进过程对周围土体沉降造成的影响,需要实现对欧拉体材料点位移的提取,因此在计算前定义示踪粒子对欧拉体中的材料点进行跟踪,计算完后可通过示踪粒子记录的位移变量输出位移^[23].

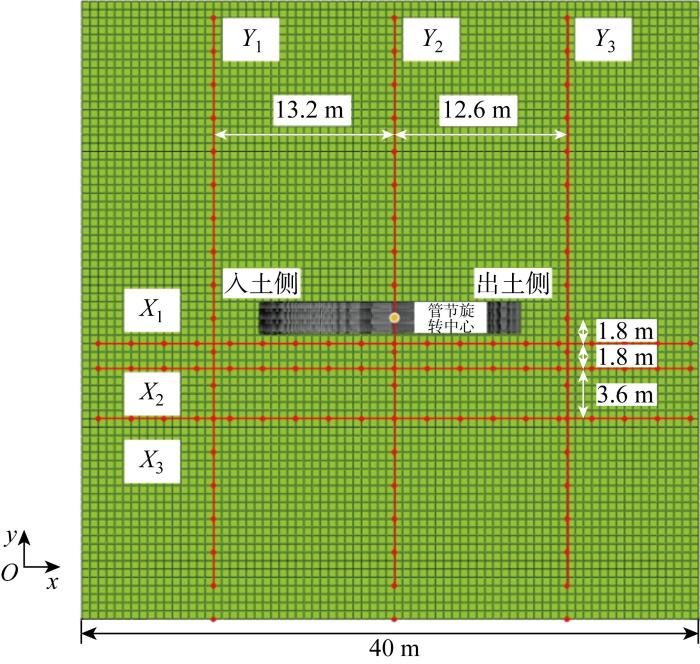
示踪粒子布置位置与管节的相对关系如图9所示,示踪粒子均布置于欧拉域中心区域土体表面.每条布置线由18个示踪粒子组成,每条线中示踪粒子距离2 m.在x向和y向各布置3排示踪粒子. $x$ 向测线编号分别为 $X_{1} 、 X_{2} 、 X_{3} . y$ 向测线编号分别为 $Y_{1} 、 Y_{2} 、 Y_{3} .$

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 示踪粒子位置示意图

Fig.9 Schematic graph of locations of tracing particles

5 结果分析

5.1 地层应力分析

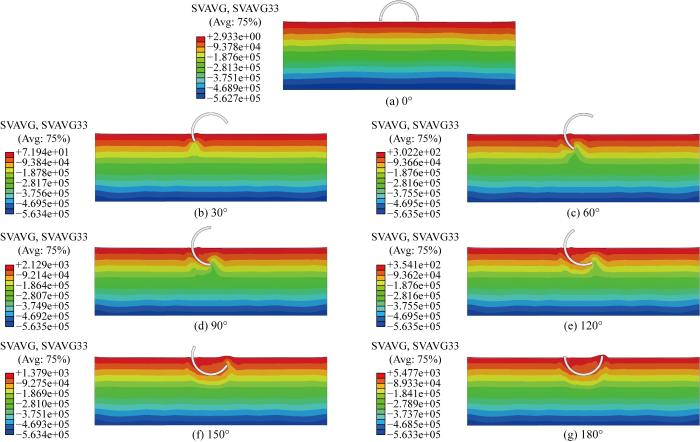
管节在不同推进角度时,土体的竖向应力(SVAVG33)云图如图10所示.0工况为地应力平衡结果.顶进过程中,管节推进面处有明显的应力集中现象,管节入土侧出现了明显的塌陷,推进150°时出土侧地表土体隆起明显.管节穿越过的区域,除入土侧与出土侧土体正下方土体外,竖向应力均出现了明显下降, 这可能是由于一部分土体随管节运动导致局部脱空使得竖向应力降低.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 管节推进过程中地层竖向应力场

Fig.10 Stress contour of strata in advancement of curved beam

5.2 地层变形分析

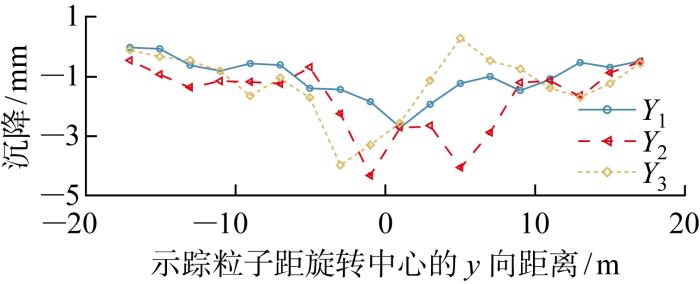
示踪粒子横向测线 $Y_{1} 、 Y_{2} 、 Y_{3}$ 与管节的相对位置及土体的最终沉降曲线如图11所示.图中: $Y_{1}$ 在管节入土处外侧, $Y_{2}$ 位于管节入土与出土处中间, $Y_{3}$ 在管节出土处外侧.3条测线均在管节顶进区域出现了明显的沉槽,但沉降槽为非对称. $Y_{1} 和 Y_{3}$ 土体沉降曲线最大沉降量位于管节推进位置一侧而非管节的正上方. $Y_{2}$ 土体沉降曲线则呈现两个波谷在管节处有轻微抬升,这可能是由管节推进过程中土体向一侧的流动大于向另一侧的流动导致的.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 y向最终土体沉降

Fig.11 y-direction soil settlement at the end of construction

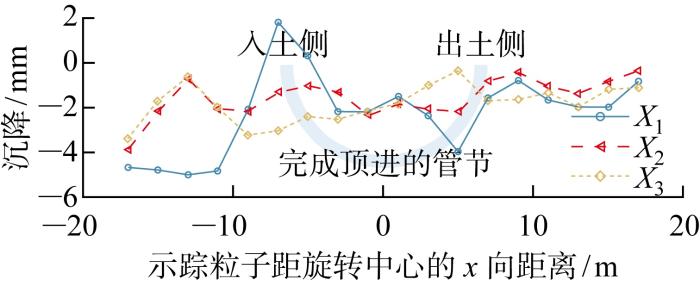
$Y_{3}$ 测线在距离管节5 m处有轻微的隆起,这是因为管节进出入土时周围土体被挤开,管节入土处周围土体相较于外侧土体呈隆起状,这一点与图10(g)一致.

示踪粒子纵向测线X₁、X₂、X₃上土体沉降曲线及其与管节的相对位置如图12所示, 3条测线与管节推进轨迹面平行.总体而言,沿着纵向地层呈沉降的趋势,最终沉降量沿纵向差别不大,出土侧的沉降量略小于入土侧.X₁测线由于最靠近管节,在靠近入土侧出现了一定的隆起,与图11一致.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 x向最终土体沉降

Fig.12 x-direction soil settlement at the end of construction

5.3 顶推力结果对比分析

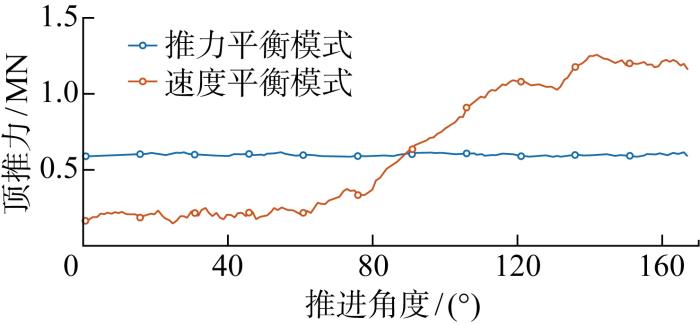
施工过程中采用了推进力平衡和推进速度平衡两种模式,代表性顶推力时程曲线如图13所示.管节采用推进力平衡的推进模式时,管节推进中顶推力均匀保持在约600 kN.管节采用推进速度平衡模式时,顶推力会随着推进角度增加而增大,在推进角度在140° 左右时达到峰值约 1.2 MN,随后开始缓慢降低.在理论计算与数值模拟中,管节均为匀速运动状态,因此对比分析中实测顶推力数据选择速度平衡模式.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 不同推进模式下管节顶推力变化

Fig.13 Thrust force evolution in different advancement modes

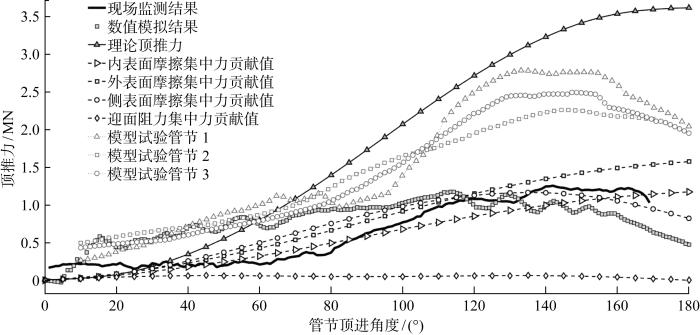
基于施工现场条件的理论计算结果、推进速度平衡模式的实测数据、CEL方法模拟结果及李登等^[16]的1∶10缩尺试验结果的顶推力随推进角度变化的对比如图14所示,同时还给出了3.3节理论模型计算得到的各类管节-地层相互作用分量随推进角度变化情况.理论计算中假设管节和导向架间的摩擦因数K取0.01,使用参数如表1所示.理论计算结果、监测结果、数值模拟结果和缩尺试验结果的变化趋势均较为接近,除理论计算结果外,均存在明显的峰值,峰值位于在顶进角度120°~140° 附近.顶进结束时,总顶进力仍较大.此时,管节已经出土,残余的顶推力为摩阻力主导.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 顶推力随推进角度变化曲线

Fig.14 Evolution of driving force with advancement angle

表1 地层主要物理力学参数

Tab.1 Major physical and mechanical properties of stratum

地层	γ/(kN·m^-3)	c/kPa	φ/(°)	泊松比	E/GPa
铁板砂	18.4	10	28	0.2	6.8

新窗口打开| 下载CSV

在所有类型的力中,管-土摩阻力的贡献最大,迎面阻力在顶进初期有一定的影响而后可忽略不计,由于滚轮的存在管节与框架间的摩擦阻力较小,管节自重产生的力矩对顶推有利,故其贡献为负值.在顶进角度小于 90°时,管节自重的贡献逐渐增加,管节和土体之间的摩擦力因接触面积的增大而增大,且此时由于法向应力随埋深的增加而增大,初始阶段顶推力需要克服的阻力随顶进角度增大而增大;当顶进角度大于 90°后,自重产生的力矩逐渐减小至 0,同时顶进面开始从最底层往上运动,迎面阻力、管节前端摩阻力等都因埋深的减小而降低,因此,在顶推力需要克服的阻力中,管节自重分量的贡献逐渐减小,摩阻力的贡献逐渐增大但增大趋势放缓,因此在 90°之后顶推力在某个时刻达到峰值是合理的.管节在推进过程中除受到上下及两侧的摩阻力外,还受到端头面板阻力的作用.理论上前者在推进过程中随管节与土体接触面积的增大而增大,而后者在顶进角度小于90°时随入土深度的增加而增加,而后逐渐减小至0.由矩形顶管底幕法1∶10模型试验及顶推力计算方法分析可知^[16],当弧形梁顶进超过一定角度时,地表发生隆起,这意味着弧形梁端头前方土体发生了劈裂破坏,此时作用在端头面板上的法向力要远大于土体自重在端头处的法向分量,存在一个临界角度,使得侧部摩阻力和端头面板阻力产生的力矩达到最大.

数值上,模拟结果和施工监测结果较为接近,缩尺试验结果和理论计算结果较大.顶推力随推进角度变化曲线如图14所示,由图可知推进全程摩擦阻力占主导地位.

缩尺试验结果较大的原因在于试验采用无刀盘“闷顶”模式,使土体产生劈裂破坏,导致顶推力增大.理论计算时考虑土体和管节完整贴合,二者接触达到剪切破坏极限.事实上,无论是模拟、试验还是施工,随着管节推进,土体均会出现明显的开裂、松动与塌陷,并不会与管节完整贴合,这是导致理论计算结果大于其他结果的主要原因.在施工中为保证管节顺利推进,会使用刀盘切割,刀盘尺寸略大于管节截面尺寸,产生超挖现象,进一步减弱了管节与土体间的相互作用.此外,潜水人员作业与泵机出泥出水也会对土体造成一定程度的扰动,再则,管节推进时,至少有一侧是管节或端板,而管节侧边存在滑槽,顶进前也会填充减摩材料降低摩擦力,因此实测的顶推力较小.

6 结论

以“长江口二号”古沉船打捞项目为研究对象,介绍矩形曲线顶管底幕法沉船打捞工法,推导矩形竖曲线顶管管节-地层相互作用模型及顶推力理论计算公式,并基于CEL数值模拟结果分析了矩形曲线顶管动态掘进顶推力变化趋势及地层的力学响应.主要结论如下:

(1) 管节端面土体出现了明显的应力集中,由于一部分土体随管节运动导致局部脱空使管节所受竖向应力降低,这可能是导致实测及数值模拟顶推力小于理论计算结果的主要原因.

(2) 入土侧、管节上方和出土侧的横向沉降呈现不同规律,但沿纵向的沉降变化不大,出土侧略小于入土侧.

(3) 土由于管节自重、摩阻力和管节-框架相互作用力的联合作用,竖向曲线顶管顶推力随顶进角度的增加先增大后减小,在推进至约120°~140°时达到峰值,剪切滑移为顶管管节-地层相互作用的控制因素.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

沈桂平, 曹文宏, 杨俊龙, 等.

管幕法综述

[J]. 岩土工程界, 2006(2): 27-29.