上海交通大学学报

上海交通大学学报, 2023, 57(S1): 60-68 doi: 10.16183/j.cnki.jsjtu.2023.S1.01

曲线顶管底幕法施工对沉船扰动的CEL数值模拟

周东荣1, 张家铭,2, 庄欠伟4, 黄昕2,3, 翟一欣4, 朱小东1, 张弛4, 张子新2

1.交通运输部上海打捞局, 上海 200090

2.同济大学 地下建筑与工程系, 上海 200092

3.新疆大学 建筑工程学院, 乌鲁木齐 830047

4.上海隧道工程有限公司, 上海 200032

CEL Numerical Analysis of Disturbance of Constructing Curved Beam Based on “Yangtze River Estuary II” Ancient Wreck

ZHOU Dongrong1, ZHANG Jiaming,2, ZHUANG Qianwei4, HUANG Xin2,3, ZHAI Yixin4, ZHU Xiaodong1, ZHANG Chi4, ZHANG Zixin2

1. Shanghai Salvage Ministry of Transport, Shanghai 200090, China

2. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China

3. College of Civil Engineering and Architecture, Xinjiang University, Urumchi 830047, China

4. Shanghai Tunnel Engineering Co., Ltd., Shanghai 200032, China

通讯作者: 张家铭,工程师,主要从事隧道施工安全控制方面的研究;E-mail:2032641@tongji.edu.cn.

收稿日期: 2022-07-7   修回日期: 2022-07-24   接受日期: 2022-08-19  

基金资助: 上海市科委社会发展领域重大项目(21DZ1201103)
国家自然科学基金(52278407)

Received: 2022-07-7   Revised: 2022-07-24   Accepted: 2022-08-19  

作者简介 About authors

周东荣(1978-),教授级高级工程师,主要从事船舶与海洋工程的研究.

摘要

依托“长江口二号”沉船打捞工程,采用耦合欧拉-拉格朗日法对极小曲率半径矩形曲线顶管底幕法沉船打捞工程进行数值模拟分析,获得底幕施工过程中顶推力以及船体竖向位移的动态变化,并与模型试验结果进行了对比验证.结果表明:所提的数值模型模拟结果和模型试验结果吻合较好,能较精确地预测沉船的变位和顶管的顶推力变化;最后一根管节推进为最危险工况,需要加强施工控制;采用左右对称推进而非顺序推进能够有效降低施工对沉船和土体的扰动.

关键词： 曲线顶管; 沉船打捞; 数值模拟; 耦合欧拉-拉格朗日法

Abstract

Based on the salvage project of “Yangtze River Estuary II” ancient wreck, a coupled Eluer-Lagrangian (CEL) numerical analysis was conducted for the wreck salvage project adopting the curved beam based method using rectangular curved pipe jacking with an extremely small radius of vertical curvature. The dynamic evolutions of the driving force and the vertical displacement of the wreck were obtained and compared with the results of model test. The results show that the simulation results of the established numerical model agree well with the experimental data, which could predict the variation laws of movement and the driving force of the wreck. Pipe jacking of the last beam is the most dangerous, which requires a strengthened construction control. In comparison with sequential jacking from one side to the other, the left-to-right symmetric jacking can effectively reduce the disturbance to the wreck and its surrounding ground.

Keywords： curved pipe jacking; wreck salvage; numerical analysis; coupled Eluer-Lagrangian (CEL) method

PDF (16674KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

周东荣, 张家铭, 庄欠伟, 黄昕, 翟一欣, 朱小东, 张弛, 张子新. 曲线顶管底幕法施工对沉船扰动的CEL数值模拟[J]. 上海交通大学学报, 2023, 57(S1): 60-68 doi:10.16183/j.cnki.jsjtu.2023.S1.01

ZHOU Dongrong, ZHANG Jiaming, ZHUANG Qianwei, HUANG Xin, ZHAI Yixin, ZHU Xiaodong, ZHANG Chi, ZHANG Zixin. CEL Numerical Analysis of Disturbance of Constructing Curved Beam Based on “Yangtze River Estuary II” Ancient Wreck[J]. Journal of Shanghai Jiaotong University, 2023, 57(S1): 60-68 doi:10.16183/j.cnki.jsjtu.2023.S1.01

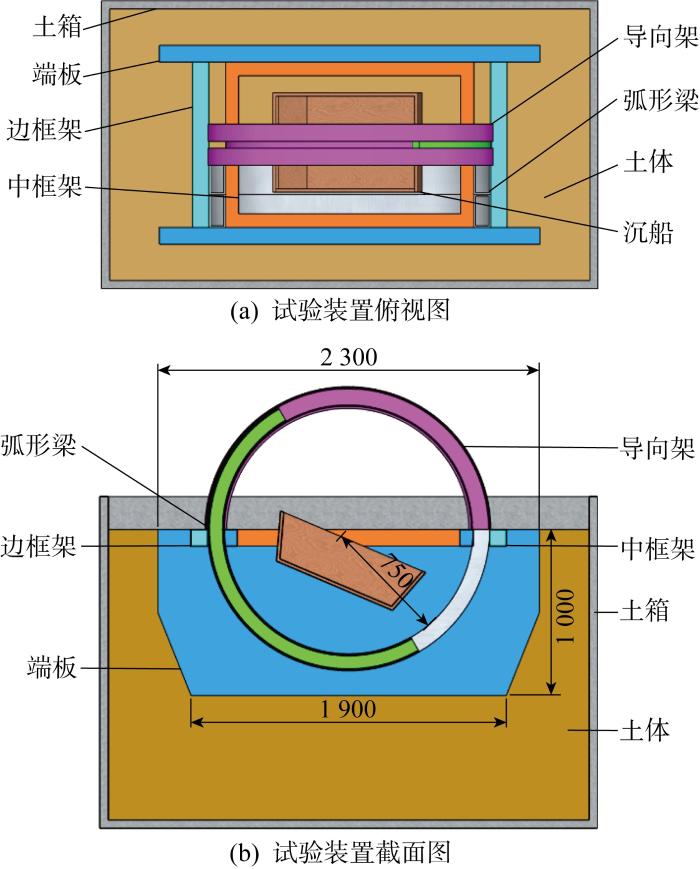
2015 年 9 月在长江口横沙岛附近发现的“长江口二号”古沉船是目前我国水下考古发现的体量最大、保存最完整、船载文物数量巨大的木质沉船.该船已于2022年11月整体打捞出水,目前正在进行后期的考古发掘工作[1].在整体打捞工程实践过程中,经实地调研和多方论证,最终确定采用国际首创的曲线顶管底幕法进行整体打捞和搬迁,以保障沉船遗址及文物的原生性、完整性和安全性.该方法采用曲线小顶管依次牵引管节沿半圆形轨迹从“长江口二号”下方穿越地层形成弧形的托盘结构,并与上部框架通过销钉连接,最后再整体抬浮打捞.本次打捞实施是国际上首次在水下进行极小曲率半径矩形曲线顶管群施工,尚无先例可循,在施工安全控制和对沉船扰动评估等方面面临着诸多技术风险及挑战.

在曲线顶管底幕法的施工过程中,需要重点关注顶管所需顶推力和推进过程对邻近土体和沉船的扰动,前者是顶管机设计的关键参数,后者是评价沉船船体及船载文物安全性的重要指标.对于此类问题,可以借鉴曲线顶管管幕法的相关研究[2].Shou等[3]基于静力平衡条件对曲线顶管的受力进行理论研究,并推导了顶推力的理论计算公式;Zhang等[4]提出一种Terzaghi土拱计算模型,用于预测深埋顶管的土压力,并通过试验研究分析了几个关键参数的取值;王宁等[5]推导了适用于矩形顶管的顶推力计算公式,总结了顶管推进对后背土体扰动的规律;刘永辉等[6]依托实际工程对浅覆粉土中大断面矩形顶管施工引起的地面沉降分布特征及变化规律进行了总结分析,指出矩形顶管施工扰动对横断面地面沉降影响的最大范围约1.4D,其中D为矩形断面等效圆形直径,且地面累计沉降槽的最大值在隧道轴线上方附近.由此可见,顶管推进过程中将不可避免地对邻近地层及沉船产生扰动.张家铭等[7]针对“长江口二号”沉船打捞工程开展了5根管节的1∶10缩尺模型试验,获得曲线顶管底幕法打捞顶管顶推力及沉船的旋转变位.但受试验条件所限,模型试验采集的地层变形及沉船位移信息较小,无法全面反映底幕法施工对地层及沉船的扰动效应.

目前,对于顶管推进或沉桩贯入土体过程的数值模拟大多数采用静态方法或传统任意拉格朗日-欧拉(ALE)方法.汤渊[8]结合轨道交通10 号线华山路站,对曲线顶管暗挖法施工地铁车站的技术进行数值模拟,分析开挖方案可能引起的地层响应;Qi等[9]通过建立数值模型,分析流砂地层中顶管施工时产生的地表沉降模式,验证了顶管法施工过程中所采用沉降控制措施的有效性;Ma等[10]通过数值模拟研究了顶管推进引起的附加应力在沿顶管轴线方向和垂直方向上的分布,提出越靠近管道轴线,附加应力越大,衰减速度越快,影响范围越小;Li等[11]通过三维有限元模型,对超长距离岩石微顶管施工过程进行模拟,揭示顶管与围岩之间摩擦阻力的变化规律,并通过现场监测,验证顶推力预测结果;Cheng等[12]在有限元模型中通过向隧道边界施加位移来模拟隧道开挖,并利用该模型提出基于现场观测和离心试验结果确定隧道周边位移大小和方向的方法;Wang等[13]结合土壤软化模型,使用大变形有限元方法研究了海底管道贯入过程中的侧向位移.

然而,对于所涉及的曲线顶管底幕法打捞连续推进情况,传统的静态方法或基于ALE的显式动力学分析[14]在分析此类大变形问题时,可能会出现网格畸变导致结果不收敛或误差过大的致命缺陷.对于此类问题, Benson[15]提出了耦合欧拉-拉格朗日(CEL)方法;孟振等[16]利用CEL方法模拟不排水条件下软黏土中沉桩施工对桩周土体的影响.对计算得到的桩周土体流动、水平位移、超孔压、水平应力进行分析,验证了CEL在土体沉桩过程模拟中的有效性;Qiu等[17]使用CEL方法模拟岩土工程中的大变形问题,包括沉桩、船舶搁浅等,证明了该方法的可靠性;Hamann等[18]研究了ALE和CEL方法在部分排水条件下完全饱和土体中顶桩问题的应用,并研究了施工过程及渗透性对周围土体的影响;Tho等[19]利用CEL法,模拟桩靴基础贯入海床的过程,讨论了网格密度、贯入速率对模拟时间的影响.综上可知,CEL方法在岩土工程大变形问题中已有成熟应用,但目前鲜有对顶管动态推进过程的分析.

以“长江口二号”曲线顶管底幕法沉船打捞为背景,通过建立与1∶10模型试验对应的CEL数值模型,对曲线顶管底幕施工过程中顶推力、沉船位移等关键参数与试验结果进行对比分析,并探讨施工工序对沉船变位的影响.

1 基于CEL的打捞过程数值模拟

1.1 CEL方法简介

使用拉格朗日网格来模拟曲线顶管顶入土体的过程,网格会产生较大的变形,导致计算结果不收敛或结果误差过大.因此在研究过程中,使用CEL方法来克服网格畸变问题.

在Eulerian方法中,材料在网格内的流动是通过计算单元的欧拉体积分数(EVF)确定的.EVF定义为Eulerian材料占据单元体积的百分比:EVF为0表示单元中没有材料,而EVF为1表示单元中充满材料.在CEL方法中,Lagrangian单元与Eulerian单元通过罚接触法相互作用,Lagrangian单元可以自由穿过EVF为0,即无材料填充的Eulerian单元,而在遇到一个EVF非0,即有材料填充的 Eulerian 单元时与其发生接触.由于网格并非与材料同步变形,可以有效避免接触位置附近土体发生大变形而导致网格的过度畸变,从而保证模拟过程的可靠性和准确性.

1.2 几何模型建立

张家铭等[7]进行了如图1所示的“长江口二号”沉船曲线顶管底幕法打捞的1∶10模型试验.该试验考虑5根管节顺序推进,采用梯形断面棱台来模拟实际沉船.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   模型试验装置示意图(mm)[7]

Fig.1   Illustration of model test setup (mm)[7]


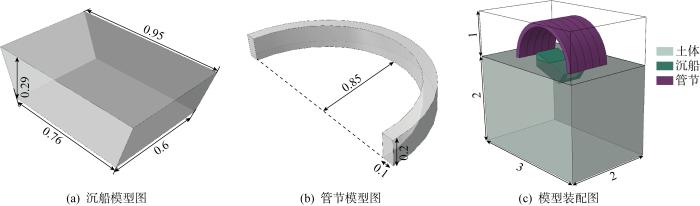
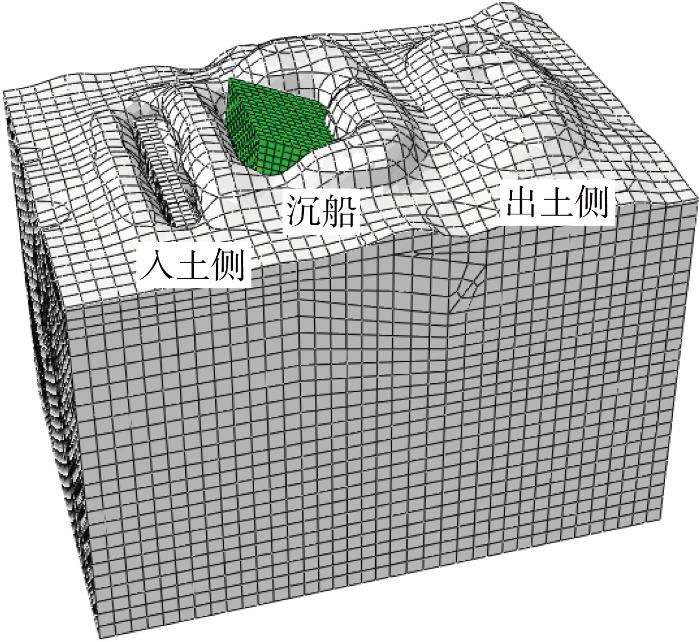
沉船模型在Abaqus软件中近似简化为梯形截面的等截面拉伸体,其上表面长0.95 m,宽0.6 m, 沉船高0.29 m,下表面长0.76 m,宽0.6 m. 土体范围与模型试验一致,为3 m×2 m×2 m的土箱.顶管共5节,其半径为0.85 m,顶进面长0.2 m,宽0.1 m.为实施欧拉分析,在土箱上方额外增加一个高度为1 m的空气层,通过在空气层赋予EVF=0,土层赋予EVF=1实现空气层和土层的效果.模型各部件及装配图如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   几何模型图(m)

Fig.2   Illustration of geometric model (m)


1.3 物理力学参数

模拟所用土层物理力学参数如表1所示,与模型试验一致,即表中②3土层与图2中土体部分一致.本构模型采取Drucker-Prager硬化模型.沉船和管节模型所用单元类型为C3D8R,即带沙漏控制的8节点立方体缩减积分单元;土体单元类型为EC3D8R,即用于欧拉分析的C3D8R单元.管节相对土体刚度非常大,模拟时作为刚体处理.

表1   沉船位置土体的物理力学参数

Tab.1  Physical and mechanical properties of soil at wreck location

层号土层名称E/MPa泊松比c/kPa内摩擦角,φ/(°)静止土压力系数,K0湿重度,g/(kN·m-3)
②3灰色砂质粉土150.410280.3718.4

新窗口打开| 下载CSV


1.4 边界条件施加和网格划分

在地应力平衡分析步中,对整个模型施加 9.8 m/s2的重力场;对于土体,在前后、左右、下边界分别施加x、y、z方向上位移为0的边界条件;在除空气层上表面的土体所有外表面施加欧拉边界条件,流入方向上为自由,流出方向上为无反射(Non-Reflecting)边界条件.

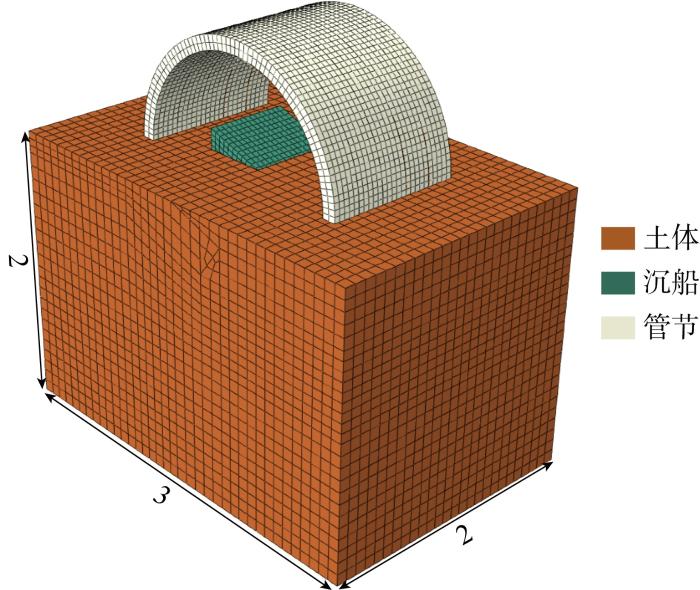
在进行网格划分时,为保证模拟时材料不流入管节和船体,需要保证管节和沉船的网格尺寸小于土体的网格尺寸,同时由于本模型尺寸小,计算速度偏慢,为保证计算速度和计算质量,最终选定管节和船体网格最小横向尺寸为0.04 m,土体为0.08 m,使用共 36 352 个EC3D8R单元对土体进行离散.网格划分后的模型图如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   模型网格划分示意图(m)

Fig.3   Illustration of model meshing (m)


1.5 模拟过程

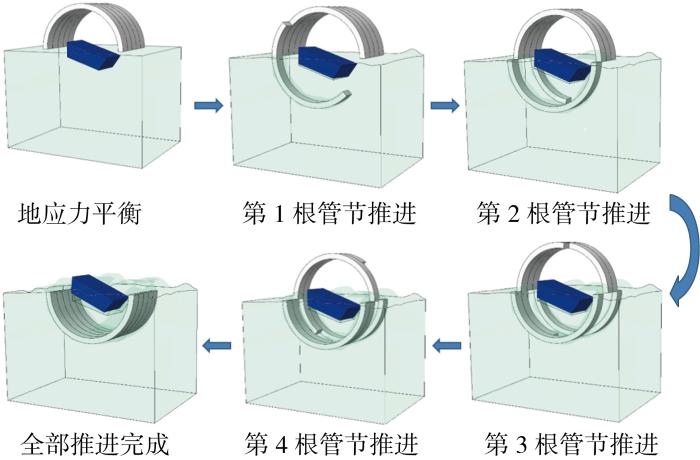
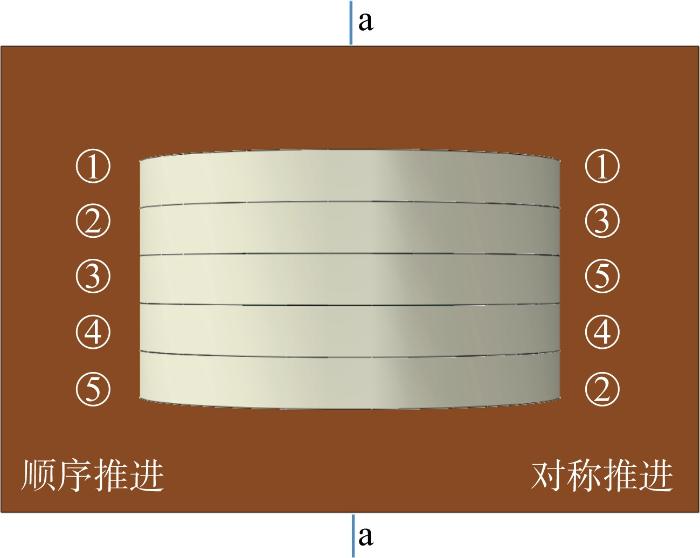
模拟过程分为6个分析步:①地应力平衡,在整个模型上施加z轴负方向大小为9.8 m/s2的重力加速度,平衡时长为0.2 s,以土体任一点竖向应力值等于自重应力,且土体表面位移小于10 μm为判断平衡完成的依据;②~⑥为分析步,分别对应5根管节的推进过程,在每个分析步起始时限制其他管节的运动,并对目标管节施加绕其圆心的角速度至分析步结束,以模拟管节的推进过程.在推进过程中,采用左右对称推进的推进方式,其推进全过程流程如图4所示.同时为了与模型试验进行对比验证并对不同推进顺序的结果进行对比分析,也开展了从左到右顺序推进的数值模拟.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   模拟过程流程图

Fig.4   Illustration of simulation procedure


对称推进时,推进完毕后的模型网格如图5所示,土体的凹陷和隆起趋势可由图上等高线判断.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   最终模拟状态网格变形图

Fig.5   Deformed mesh at the end of simulation


2 模型验证

2.1 顶推力结果与模型试验的对比验证

张家铭等[7]和李登等[20]在上海开展了“长江口二号”沉船打捞1∶10缩尺全过程模拟顶进试验,测量模型试验过程中的管节顶推力变化情况.其前3根管节顶推力结果与同为从左到右顺序推进的数值模拟结果的对比如图6所示,模型试验中管节4和管节5因管节有初始挠曲缺陷导致顶进力偏大,故未列入.

图6

新窗口打开| 下载原图ZIP| 生成PPT

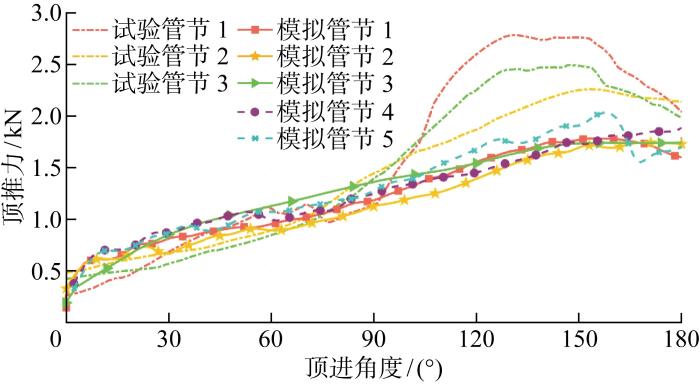
图6   模型试验和数值模拟顶推力结果对比

Fig.6   Comparison of driving force between model test and numerical model


模型试验和数值模拟中5根管节顶推力的变化趋势都较为接近,均大体呈现先逐渐增大至峰值后再减小的趋势,峰值顶推力发生在约 120°~160°之间.模型试验中始发管节,即图1(a)中靠近最下端端板的管节,因靠近端板导致顶推力较大,其他两根管节的顶推力较为接近,而数值模拟中5根管节的顶推力数值上较为接近,第5根管节的顶推力值比前4根稍大一些,可能与第5根管节推进时,两侧已完成推进的管节对其挤压产生摩擦阻力增大有关.事实上,在模型试验中也遇到了类似的问题,由于累积轴线偏移,最后1根管节推进较前序管节更为困难,管节本体甚至产生了较大的挠曲变形[20].数值模拟得到的顶推力计算结果小于模型试验.考虑到数值模拟过程中假定情况较为理想,将管节作为绕圆心匀速旋转的刚体处理,而试验中由于推进造成的管节变形对导向架造成的挤压、链条电动机润滑、泥浆泵的效率较低等因素都会造成额外的阻力,故在模型试验中得到的顶推力值更大.同时模型试验试验过程中,由于使用的刀盘电动机功率较小、切削效率较低,在试验过程中过热损坏,又因泥浆、水、土体等进入电动机内部造成刀盘的失效,导致在刀盘电动机失效损坏的情况下管节前部矩形端面直接贯入土体.此过程缺少了刀盘切削的辅助作用,即造成“闷顶”,显著增大了推进过程中的迎面阻力.此外,由图5可知,在管节顶推过程中有部分土体随管节一起移动,造成局部管节和地层的脱空降低了法向接触应力,进而导致剪切摩阻力下降.这些均有可能导致数值模拟所获得顶推力小于模型试验结果.

2.2 沉船形心竖向刚体位移的验证

在文献[7]中的试验过程中,使用视觉传感器获取了沉船在第1、3、5管节推进完毕后的沉船形心竖向刚体位移值,其与数值模拟结果的对比如图7所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

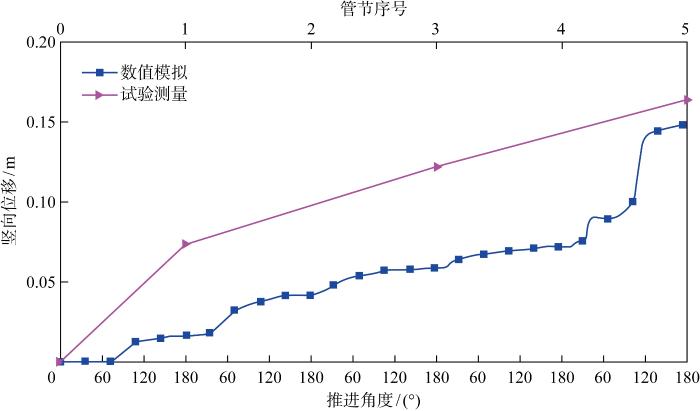
图7   沉船竖向位移结果对比

Fig.7   Comparison of vertical displacement of wreck between model test and numerical modeling


由图7可知,数值模拟和模型试验在竖向位移值的变化趋势上较为接近,随管节的推进呈不断上升趋势,最大值约为15 cm.视觉传感器测量复杂、受光线因素影响测量成功率低,数据点较少,因而能获得的信息较少.从数值模拟结果来看,在每根管节推进过程中位移的变化呈从快到慢的趋势,这与顶推力的变化趋势一致.在120°~160°处,顶推力达到最大值,此后管节对沉船和土体造成的影响变小,因此竖向位移趋于不变.第1根管节由于距离沉船较远,对沉船的扰动最小,随着管节顺序下穿船体,沉船累计位移值逐渐增大.最后1根管节推进时,沉船竖向变形出现了突变,表明最后1根管节推进为最危险工况,要注意控制推进速度加强对沉船的保护.

2.3 土体扰动

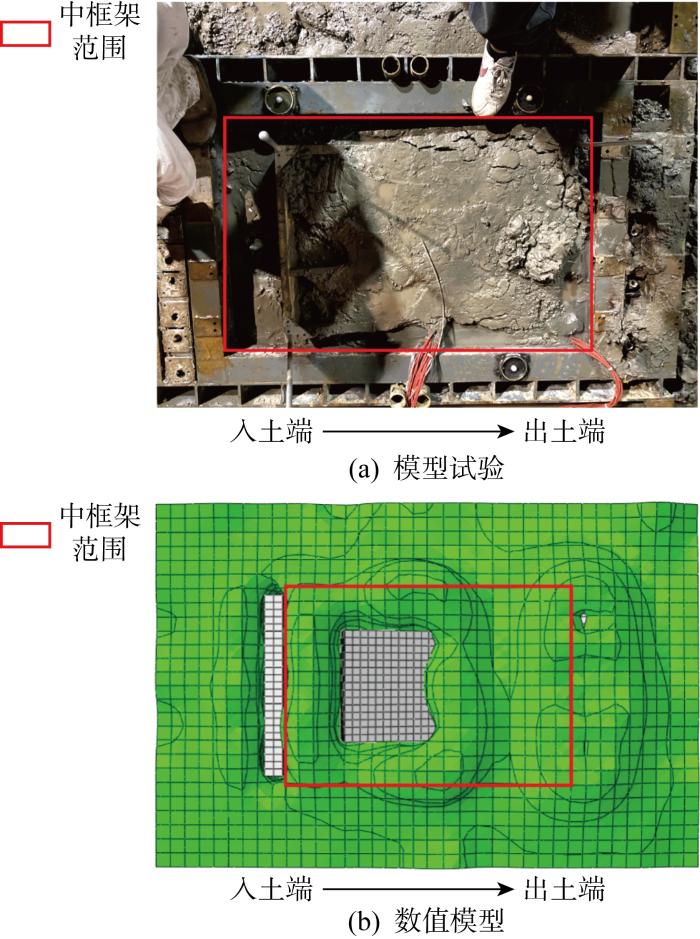
模型试验推进完成后、数值模拟推进结束后的土体俯视图如图8所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   推进结束后的地层变形俯视图

Fig.8   Top view of soil deformation after jacking process


模型试验中存在中框架及导向架,对管节出入端框架以外土体的变形有抑制作用.在中框架以内部分,可见模型试验中沉船周围土体拱起开裂,部分土体被挤压流向沉船方向,与数值模拟在推进过程中对土体造成的扰动模式相近.

综上可知,从顶推力变化和沉船及地层位移的对比来看,数值模型和模型试验结果吻合均较好.因此,可认为该数值模型较准确地反映了推进过程中管节-沉船-土体三者之间的相互作用机制和沉船变位、管节顶推力的变化情况.

3 顶推顺序影响分析

不同的管节施工顺序会对地层及沉船造成不同影响,在5根管节的推进过程中,管节的推进顺序如图9所示,主要有从一侧向另一侧的顺序推进和左右对称推进两种模式,图中,a-a为特征截面.为明确不同推进顺序对地层及沉船变位的影响,在ABAQUS中采用改变边界条件施加顺序的方式,分别对两种推进顺序进行模拟,所获得的沉船形心竖向位移的对比结果如图10所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   推进顺序示意图

Fig.9   Illustration of jacking order


图10

新窗口打开| 下载原图ZIP| 生成PPT

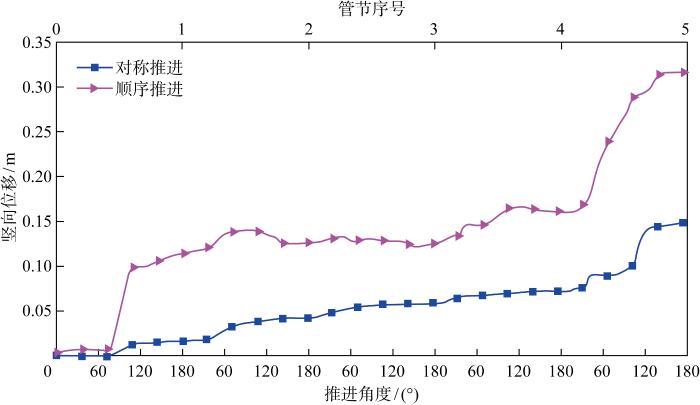
图10   采用两种推进顺序的沉船形心竖向位移结果对比

Fig.10   Comparison of vertical displacement at centroid of wreck subjected to two jacking orders


由图可知,顺序推进造成的沉船形心竖向位移较对称推进更大,最终位移值约为对称推进情况的2倍.推测是由于对称推进时,左右相对称的管节在推进时对土体和沉船的作用有一部分相互抵消,带来的对沉船、顶管的姿态变化抵消作用降低了土体-沉船-顶管三者之间的相互扰动,因此使得沉船的竖向位移相对顺序推进时显著降低.

在两种推进顺序下,每根管节引起的沉船形心竖向位移变化比较接近,呈先基本不变,随后快速增加,最后又趋于不变的趋势,这与顶推力先增大后不变的变化趋势相近.在两种推进顺序下,引起较大竖向位移的都是第1、5根管节,而中间3根管节的影响较小.推测其原因是每根管节在推进时,引起内部沉船的运动可以分解为竖向刚体位移作用和转动作用,而对称的两根管节间引起沉船的转动作用会相互抵消,两种作用共同组成了沉船的竖向刚体位移.因此在对称推进时,前4根管节的竖向位移相对较小,而第5根管节位于中心,其位置经过沉船重力作用线,对沉船几乎不引起转动作用,只引起竖向位移,且此时顶推力也较大,故其引起的竖向位移相对前序管节也较大.在这两根管节推进时,引起沉船绕短轴旋转的旋转中心位于最远端处,其力矩比中间3根要大,引起沉船的旋转变位也更大,引起沉船形心更大的总竖向位移.在顺序推进时,基于同样的分析,第1、5根管节推进时,沉船旋转中心位于最远端的另一侧底部,造成很大的旋转变位,从而造成较大的沉船竖向位移,中间3根管节, 相对造成的旋转变位较小,因此沉船形心竖向位移也较小.

取底幕中部如图9所示的a-a断面为特征截面,对这两种推进顺序下土体的变形和沉船变位进行分析,如图11所示.

图11

新窗口打开| 下载原图ZIP| 生成PPT

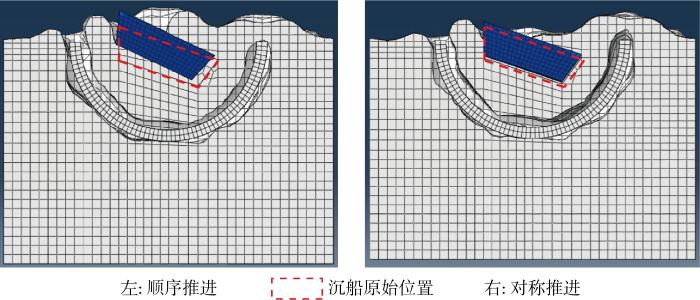
图11   采用两种推进顺序的土体扰动结果对比(a-a断面)

Fig.11   Comparison of disturbance on soil and wreck subjected to two jacking orders (a-a section)


由图可知,在顺序推进时,管节出土端拱起部分比对称推进时约高出2~4 cm,有较多土体流向沉船上方,对土体扰动较大;同时,顺序推进导致的沉船姿态变位也比对称推进时明显,导致沉船上方出现明显隆起.在对称推进时,沉船变位较小,沉船上方地层的变形也较小,表面左右对称推进有助于降低打捞施工对沉船和地层的扰动效应.

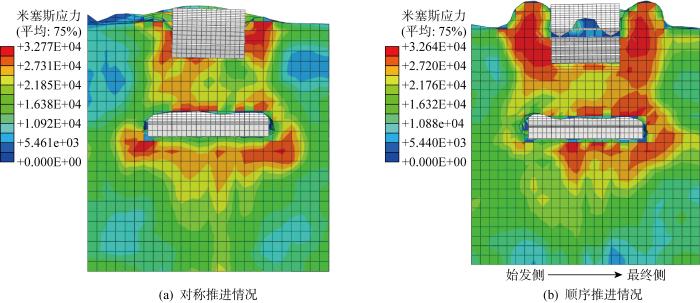
两种推进顺序在特征断面上的米塞斯(Mises)应力云图如图12所示.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   a-a截面Mises应力对比

Fig.12   Comparison of Mises stress on cross section a-a


由图12可知,顺序推进和对称推进产生的地层最大Mises应力较为接近.但相比顺序推进,对称推进对土体造成附加应力的主要影响范围更小,约为土体表面至1.5 m深处.对称推进时,地层应力也近似对称分布.顺序推进时,沉船位置应力呈不对称分布,由于前序管节的限位作用,最右侧第5根管节附近应力集中更加明显,对土体影响更大,这是导致最后1根管节推进时沉船变位发生突变的主要原因.

总体而言,模拟结果表明,采用对称推进的方式比从一侧到另一侧顺序推进对土体和沉船二者的扰动和影响都较小,是较理想的推进方式,且在实际打捞过程中可根据现场的施工条件合理安排施工顺序.

4 结论

以“长江口二号”古沉船打捞项目为研究对象,建立曲线顶管底幕法沉船打捞的CEL数值模拟方法,开展顶管-土体-沉船相互作用的数值模拟研究,主要结论如下:

(1) 针对顶管推进时的地层大变形问题建立CEL数值模型,其模拟结果和模型试验结果吻合较好,能较精确地预测沉船的变位和顶管的顶推力变化.

(2) 单根管节推进过程中沉船变位的演化规律和顶推力类似,初始随推进角度增大而逐渐增加,在推进角度120°~160° 处达到峰值后基本不变.

(3) 管节顺序推进过程中,沉船变位不断增加,最后1根管节推进为最不利工况,管节变位量出现了突变,需重点关注.

(4) 通过对比左右对称推进和顺序推进两种模式下沉船和土体的扰动情况,发现采用左右对称推进时能有效降低施工对沉船和土体的扰动,在实际工程中能有效保护古沉船遗址的完整性、安全性,对打捞工程实施有一定的指导作用.

参考文献

新华网.

“长江口二号”出水,打开近代上海的“时光宝盒”

[EB/OL]. (2022-11-26)[2023-02-27]. http:\\csj.news.cn/2022-11/26/c_1310679804.htm.

URL     [本文引用: 1]

XINHUA NET.

“Yangtze Estuary II” unearthed, launches the time machine of modern Shanghai

[EB/OL]. (2022-11-26)[2023-02-27]. http:\\csj.news.cn/2022-11/26/c_1310679804.htm.

URL     [本文引用: 1]

史培新, 俞蔡城, 潘建立, 等.

拱北隧道大直径曲线管幕顶管顶力研究

[J]. 岩石力学与工程学报, 2017, 36(9): 2251-2259.

[本文引用: 1]

SHI Peixin, YU Caicheng, PAN Jianli, et al.

Study on jacking force of large diameter curved pipe curtain pipe jacking in Gongbei tunnel

[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(9): 2251-2259.

[本文引用: 1]

SHOU K J, JIANG J M,

A study of jacking force for a curved pipejacking

[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2010, 2(4): 298-304.

[本文引用: 1]

ZHANG H F, ZHANG P, ZHOU W, et al.

A new model to predict soil pressure acting on deep burial jacked pipes

[J]. Tunnelling and Underground Space Technology, 2016, 60: 183-196.

DOI:10.1016/j.tust.2016.09.005      URL     [本文引用: 1]

王宁, 高毅, 于少辉, 等.

矩形顶管隧道群施工对后背土体扰动规律的初步研究

[J]. 隧道建设(中英文), 2019, 39(3):413-420.

[本文引用: 1]

WANG Ning, GAO Yi, YU Shaohui, et al.

Disturbance of rectangular pipe jacking tunnel group construction on soil behind working shaft

[J]. Tunnel Construction, 2019, 39(3): 413-420.

[本文引用: 1]

刘永辉, 李明宇, 吕聪, 等.

浅覆土矩形顶管施工中地面沉降变化规律及分布特征研究

[J]. 建筑技术, 2020, 51(2): 226-229.

[本文引用: 1]

LIU Yonghui, LI Mingyu, LYU Cong, et al.

Study on law and distribution characteristics of ground settlement aused by construction of shallow-overburden rectangular pipe jacking

[J]. Architecture Technology, 2020, 51(2): 226-229.

[本文引用: 1]

张家铭, 庄欠伟, 黄昕, 等.

“长江口二号”古沉船曲线顶管底幕法打捞缩尺模型试验研究

[J]. 现代隧道技术, 2022, 59(S1): 618-626.

[本文引用: 6]

ZHANG Jiaming, et al.

A reduced-scale model test of “Yangtze Estuary II” ancient shipwreck salvage

[J]. Modern Tunnelling Technology, 2022, 59(S1): 618-626.

[本文引用: 6]

汤渊.

地铁车站曲线顶管暗挖新方法数值模拟研究

[J]. 地下空间与工程学报, 2014, 10(3): 650-655.

[本文引用: 1]

TANG Yuan.

Investigation on a new curved pipe jacking tunneling method for subway station using numerical simulation

[J]. Chinese Journal of Underground Space and Engineering, 2014, 10(3): 650-655.

[本文引用: 1]

QI P, HUANG Y, CHENG L J, et al.

Influence of pipe jacking excavation in overlying quicksand layer on surface settlement and numerical analysis

[J]. Highlights in Science, Engineering and Technology, 2022, 18: 20-25.

DOI:10.54097/hset.v18i.2518      URL     [本文引用: 1]

MA W J, WANG B L, WANG X, et al.

Soil layer disturbance caused by pipe jacking: Measurement and simulation of a case study

[J]. KSCE Journal of Civil Engineering, 2021, 25(4): 1467-1478.

DOI:10.1007/s12205-021-2262-4      [本文引用: 1]

LI C, ZHONG Z L, LIU X R, et al.

Numerical simulation for an estimation of the jacking force of ultra-long-distance pipe jacking with frictional property testing at the rock mass-pipe interface

[J]. Tunnelling and Underground Space Technology, 2019, 89: 205-221.

DOI:10.1016/j.tust.2019.04.004      URL     [本文引用: 1]

CHENG C Y, DASARI G R, CHOW Y K, et al.

Finite element analysis of tunnel-soil-pile interaction using displacement controlled model

[J]. Tunnelling and Underground Space Technology, 2007, 22(4): 450-466.

DOI:10.1016/j.tust.2006.08.002      URL     [本文引用: 1]

WANG D, WHITE D J, RANDOLPH M F.

Large-deformation finite element analysis of pipe penetration and large-amplitude lateral displacement

[J]. Canadian Geotechnical Journal, 2010, 47(8): 842-856.

DOI:10.1139/T09-147      URL     [本文引用: 1]

NAZEM M, CARTER J P, AIREY D W.

Arbitrary Lagrangian-Eulerian method for dynamic analysis of geotechnical problems

[J]. Computers and Geotechnics, 2009, 36(4): 549-557.

DOI:10.1016/j.compgeo.2008.11.001      URL     [本文引用: 1]

BENSON D J.

Computational methods in Lagrangian and eulerian hydrocodes

[J]. Computer Methods in Applied Mechanics and Engineering, 1992, 99(2/3): 235-394.

DOI:10.1016/0045-7825(92)90042-I      URL     [本文引用: 1]

孟振, 陈锦剑, 王建华.

基于修正剑桥模型的软黏土中沉桩过程欧拉-拉格朗日耦合模拟分析

[J]. 上海交通大学学报, 2017, 51(3): 263-268.

[本文引用: 1]

MENG Zhen, CHEN Jinjian, WANG Jianhua.

The coupled eulerian-Lagrangian analysis of pile jacking process in saturated soft clay by using modified cam-clay model

[J]. Journal of Shanghai Jiao Tong University, 2017, 51(3): 263-268.

[本文引用: 1]

QIU G, HENKE S, GRABE J.

Application of a Coupled Eulerian-Lagrangian approach on geomechanical problems involving large deformations

[J]. Computers and Geotechnics, 2011, 38(1): 30-39.

DOI:10.1016/j.compgeo.2010.09.002      URL     [本文引用: 1]

HAMANN T, QIU G, GRABE J.

Application of a Coupled Eulerian-Lagrangian approach on pile installation problems under partially drained conditions

[J]. Computers and Geotechnics, 2015, 63: 279-290.

DOI:10.1016/j.compgeo.2014.10.006      URL     [本文引用: 1]

THO K K, LEUNG C F, CHOW Y K, et al.

Eulerian finite-element technique for analysis of jack-up spudcan penetration

[J]. International Journal of Geomechanics, 2012, 12(1): 64-73.

DOI:10.1061/(ASCE)GM.1943-5622.0000111      URL     [本文引用: 1]

李登, 庄欠伟, 黄昕, 等.

矩形曲线顶管底幕法顶管顶推力计算方法研究

[J]. 现代隧道技术, 2022, 59(S1): 461-470.

[本文引用: 2]

LI Deng, ZHUANG Qianwei, Huang Xin, et al.

Research on the calculation model of driving force for pipe jacking of rectangular curved pipe basing method

[J]. Modern Tunnelling Technology, 2022, 59(S1): 461-470.

[本文引用: 2]

/

〈 〉