随着人工智能技术的快速发展,通过机器学习算法建立代理模型[7]具备强大的非线性拟合能力和泛化能力,非常适合用于模拟复杂物理系统[8].海工结构物响应预报属于时间序列数据预测问题,响应前后之间存在紧密联系,循环神经网络(Recurrent Neural Network, RNN)非常适用于这一类问题.例如,郝立柱等[9]利用RNN网络预报船舶回转和Z形操纵运动;Zeng等[10]应用Elman神经网络对浮式结构物垂荡响应进行超前预测.然而,传统的RNN模型存在梯度爆炸或梯度消失问题,因而难以对长序列中距离较远的信息建立联系.研究者在基本RNN模型的基础上进行改进,提出了更加强大的长短期记忆(Long Short-Term Memory, LSTM)网络结构[11-12].例如,刘飞飞[13]利用LSTM、卷积神经网络等网络结构以波面升高和运动信号为输入预测船舶纵荡、纵摇、升沉运动响应;Qiao等[14]利用LSTM以六自由度运动信号为输入预测浮式生产储油船(FPSO)系泊系统响应,在多工况下训练和测试中证明了LSTM具备一定的泛化能力;Gao等[15]利用LSTM以速度、航向角、坐标序列为输入预测船舶短期轨迹,并通过与支持向量回归、卡尔曼滤波等方法的对比展示出LSTM方法的强大能力.Shi等[16] 针对5 MW无支撑平台在不同环境条件下的漂浮式风力发电机进行数值模拟,选取平台运动响应、波浪高程、系泊力数据作为输入变量.然后对数据进行后处理后建立训练组和测试组,并建立单输入LSTM(SI-LSTM)模型和多输入LSTM(MI-LSTM)模型来学习输入数据.比较结果的整体精度后发现,附加系泊力和波浪高程对平台响应预测结果有积极影响.
因此,以漂浮式风力发电机为研究对象,基于LSTM神经网络模型实现对其平台运动响应的超前智能预报.首先,设计基于LSTM网络模型的风力发电机运动响应预报方法,对预报方法中面临的网络结构设计、数据归一化方法、网络训练方法、网络超参数调整、预报结果评价指标等问题进行研究和讨论,确定了预报方法的总体流程.其次,利用漂浮式风力发电机的实测数据对平台纵荡(Surge)运动开展验证工作.最后,针对网络结构、输入信号特征、信号时间长度等因素开展敏感性分析.主要创新点在于,首次采用了LSTM网络结构对漂浮式风力发电机实测运动响应数据进行超前预报,并量化了该方法的不确定影响.
1 基于LSTM编解码器的极短期预报方法
1.1 LSTM网络模型
图1
LSTM对传统RNN的改进可概括为两个方面:一方面在隐含状态
(1) 首先利用当前时刻的输入向量
式中:
(2) 结合遗忘门、输入门和候选内部状态更新内部状态.先由遗忘门对上一时刻内部状态进行选取,再将由输入门选取后的候选内部状态加入到内部状态中:
(3) 最后利用输出门根据tanh函数激活后的内部状态向量计算当前时刻输出的隐含向量:
当前时刻的隐含向量
1.2 预报方法
1.2.1 网络结构
在网络结构方面初步选取“多对多”和“编解码器”两种模式,两种网络结构如图2所示,RNN的类型选取为LSTM并在输出端设置了全连接层.对于“编解码器”结构,编码向量C为编码器最后一个时间步的隐含层向量h_T 以及单元格状态向量c_T 通过全连接层表示的结果,分别作为解码器起始时间步隐含层向量
图2
图2
“多对多”(左)和“编解码器”(右)网络结构
Fig.2
Structures of many-to-many (left) and codec (right) network
采取将序列的时间尺度向序列的特征尺度折叠的方法来提高预报过程中输入的历史数据量,同时缩短网络在时间尺度上的深度,如图3所示.每一时间步的输入信号
图3
图3
预报模型输入输出序列示意图
Fig.3
Schematic diagram of input and output sequence of prediction model
1.2.2 数据预处理
在一般的问题中,分别取训练集总体的最小和最大值开展数据的归一化处理,但是对于漂浮式风力发电机运动响应数据,采用统一的最小值和最大值无法使不同运行工况下的数据集均匀地分布在(0, 1)区间.漂浮式风力发电机运动响应数据值的分布区间可能会随运行环境的改变而发生显著的变化,若以统一的最值归一化全部数据集,则会导致归一化后各工况数据分布区间较窄,增大网络学习数据变化趋势的难度.因此,本文采取了对每个工况下的数据集单独归一化的方法.对于测试集,为反映预估的最值与真实最值之间的差异,归一化所用的最值由下式计算得到:
式中:xmax和xmin为测试集上真实的最大、最小值;xmean为测试集平均值;C0为反映预估误差的裕度的系数.
1.2.3 评价指标
在神经网络训练中的损失函数选取均方误差函数(Mean Squared Error, MSE),用于反映序列预报值与真实值之间误差的期望.为了更好评估模型预报的精度,选取回归任务中常用的一些评价指标,如平均绝对百分比误差(Mean Absolute Percentage Error, MAPE),用于反映预报值与真实值之间相对误差的期望;拟合优度(R2),用于反映预测曲线对真实曲线的拟合程度.另外,为反映海工领域较为关心的极值预报精度,设计一种1/N最大值平均绝对百分比误差(One-Nth largest Error, ONE),该指标对一段时期内预报值与真实值序列中由大到小排序前1/N最大值的平均值计算平均绝对百分比误差.上述几种评价指标的计算公式如下所示:
式中: n为序列长度;y为真实值;
1.3 预报流程
图4
图4
基于循环神经网络的极短期运动响应预报流程
Fig.4
Flow chart of ultra-short-term motion response prediction based on recurrent neural network RNN network
表1 网络参数配置
Tab.1
| 参变量 | 取值 | 参变量 | 取值 |
|---|---|---|---|
| 窗口长度 | 20 | 批量大小 | 50 |
| 网络层数 | 2 | 网络节点数 | 64 |
| 最大训练轮数 | 1000 | 最小训练轮数 | 100 |
| 初始学习率 | 0.01 | C0 | 0.3 |
2 对比验证
表2 工况表
Tab.2
| 编号 | 时间周期 | Hs/m | Tp/s | 风速/(m·s-1) | 流速/(m·s-1) | 浪向/(°) | 风向/(°) | 流向/(°) |
|---|---|---|---|---|---|---|---|---|
| 1 | 2018-01-06T08:00 | 4.4 | 10.9 | 13.7 | 0.21 | 17 | 11 | 19 |
| 2 | 2018-01-09T09:40 | 3.2 | 9.3 | 13.9 | 0.09 | 131 | 146 | 303 |
| 3 | 2018-01-14T15:40 | 4.2 | 8.7 | 20.4 | 0.32 | 165 | 174 | 24 |
| 4 | 2018-02-13T01:20 | 2.1 | 6.5 | 15.5 | 0.27 | 201 | 174 | 187 |
| 5 | 2018-03-26T23:30 | 2.2 | 10.6 | 8.5 | 0.24 | 14 | 172 | 16 |
| 6 | 2018-04-14T00:40 | 2.1 | 10.5 | 5.2 | 0.32 | 107 | 171 | 195 |
| 7 | 2018-05-02T04:00 | 2.3 | 6.5 | 15.6 | 0.12 | 185 | 175 | 233 |
| 8 | 2018-07-29T04:00 | 3.0 | 7.9 | 16.6 | 0.33 | 161 | 179 | 44 |
| 9 | 2018-02-24T04:50 | 2.5 | 7.3 | 14.1 | 0.17 | 164 | 161 | 150 |
2.1 不同网络结构对比
针对“多对多”和“编解码器”两种网络结构的预报精度进行比较,以预报时刻前30 s的历史纵荡运动时历为输入,持续预报未来30 s的纵荡运动时历,输入和输出序列的窗口长度为2 s,时间步数为15步.针对每个工况进行5次独立试验,预报结果的评价指标、时历曲线以及时历曲线对应的箱型图见图5.图中,M2M指代多对多结构,EnDe指代编解码器结构,True为真实的实测数据统计结果.
图5
图5
“多对多”与“编解码”纵荡预报对比结果
Fig.5
Comparison of “many-to-many” and “encoder-decoder” surge prediction
根据图5(c),编解码器结构的预报精度总体上优于多对多结构.一方面编解码器网络结构复杂程度高于多对多结构,因此能够在输入与输出之间建立更为复杂的映射关系;另一方面,编解码器结构在前向传播过程中,编码器部分首先遍历完整的输入序列,将其中的有效信息转化为编码向量并传递给解码器,因此解码器部分产生输出信号时,每个时刻都能够获得整个输入序列的信息,从而增加了预报时的已知信息量.相比之下,多对多结构采取遍历输入信号和预报同时进行的策略,在每个序列的起始部分RNN的记忆单元从输入信号中积累的信息较少,此时预报时所依赖的已知信息只来源于输入序列的一部分,因此预报效果略差于编解码器结构.除预报精度更高外,编解码器网络结构的另一个优点是输入和输出序列的时间步数不必相等,这为输入信息的选择提供了更高的灵活性.因此,在后续的分析中均采用编解码器网络结构.
2.2 不同输入特征对比
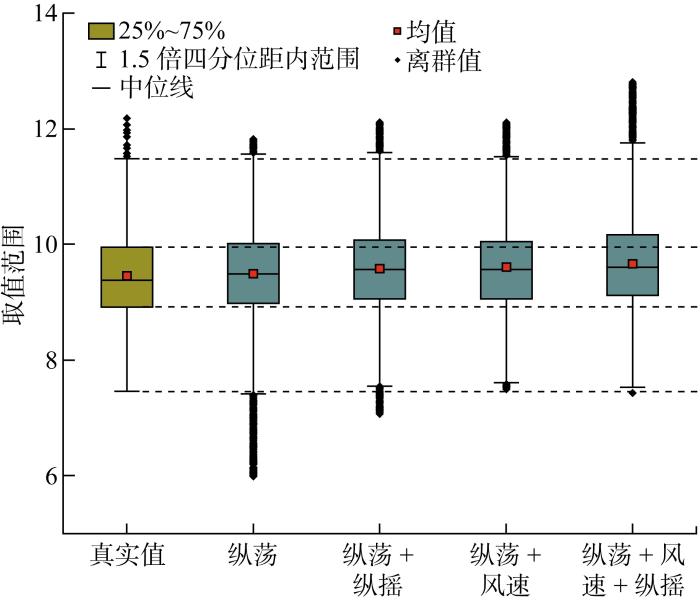
考虑漂浮式风力发电机的物理特性,在选取输入信号时,除了采用目标信号自身外,还尝试将可能与所预报自由度运动有较紧密关系的其他信号添加到输入信息中.例如,漂浮式风力发电机的纵荡运动和纵摇运动具有耦合关系,纵荡与纵荡运动时历之间可能存在较高的相关性;风载荷是风力发电机产生运动的重要外界激励,风速时历在一定程度上能够反映风载荷的变化情况,因此可能与风力发电机的运动信号之间有较为密切的关系.以预报纵荡运动为例,考虑4种输入信号组合方案,分别为纵荡、纵荡和纵摇、纵荡和风速、纵荡和纵摇以及风速,以预报时刻前30 s的历史信号为输入,预报未来30 s运动响应时历.每组参数进行5次独立试验,预报结果的评价指标、时历曲线和对应的箱型图如图6和图7所示.
图6
图6
四种输入信号下纵荡预报结果时历曲线
Fig.6
Comparison of surge prediction of four input signal plans
图7
根据图7,相比仅以纵荡运动本身作为输入信号,以风速和纵荡运动时历同时作为输入信号时预报精度略微提升,尤其是在工作状态下预报时历曲线的拟合程度有一定提高;以纵摇运动和纵荡运动时历同时作为输入信号时预报结果的极值误差显著增大,在多次预报结果中发现了剧烈的幅值变化,对预报精度产生不利影响;以风速、纵摇运动和纵荡运动时历为同时作为输入信号时,预报精度有一定的下降,且极值误差较大,其原因一方面可能是输入信号太多,网络结构过于简单而无法建立起有效的映射关系,另一方面可能是纵摇运动信号的变化频率远大于纵荡运动,快速变化的输入信号对网络的训练过程产生了干扰.而在停机状态下,添加其他信息后的预报精度均有一定程度下降.因此,在预报纵荡运动时,以纵荡运动本身或风速和纵荡运动的时历作为输入信号是较好的选择.
2.3 不同时长对比
2.3.1 不同预报时长
为讨论预报时间长度对精度的影响,设置预报时长选取为10、30和60 s.其中,输入时长与预报时长相等,输入信号为纵荡运动时历;两种方法下LSTM编解码器均为2层64节点.每组参数进行5次独立试验,预报结果的评价指标如表3所示.其中,60 s工作状态下的均方差误差仅有1%左右.
表3 网络参数配置
Tab.3
| 预报时长/s | 测试集 | eMSE×102 | eMAPE×102 | R2 ×102 | eONE×102 | ||||
|---|---|---|---|---|---|---|---|---|---|
| 10 | 工作 | 4.2± | 0.0006 | 5.59± | 0.0043 | 17.34± | 0.1200 | 3.30± | 0.0105 |
| 停机 | 8.6± | 0.0005 | 14.34± | 0.0055 | 53.20± | 0.0266 | 5.51± | 0.0155 | |
| 30 | 工作 | 5.7± | 0.0007 | 6.67± | 0.0044 | -15.69± | 0.1457 | 4.36± | 0.0079 |
| 停机 | 7.4± | 0.0014 | 12.32± | 0.0120 | 62.73± | 0.0849 | 5.47± | 0.0175 | |
| 60 | 工作 | 10.9± | 0.0022 | 9.25± | 0.0099 | -119.88± | 0.4546 | 7.19± | 0.0133 |
| 停机 | 16.6± | 0.0021 | 19.39± | 0.0114 | -0.846± | 0.1514 | 10.18± | 0.0120 | |
2.3.2 不同输入时长对比
为讨论输入序列时间长度的影响,调整输入序列的时间长度
图8
图8
不同预报时长和输入时长的统计值对比
Fig.8
Comparison of different prediction durations and input durations
根据图8,一方面随着预报时长
3 结论
提出一种创新的漂浮式风力发电机平台极短期运动的预报方法,详细阐述了预报方法的建立过程,包括网络结构选择、数据预处理、预报结果的评价指标等.并利用实测数据验证了该方法的准确性,对可能影响预报精度的3个不确定因素进行了敏感性分析,主要结论如下:
(1) 网络结构.“编解码器”结构相比“多对多”结构更适合进行多步超前预报.
(2) 输入特征.预报纵荡运动时以其本身或添加风速信号作为输入效果较好,添加纵摇运动信号可能会对极值预报精度造成不利的影响.
(3) 输入时长.就所选取的“编解码器”网络结构而言,取输入时长与预报时长相等较为合适,延长和缩短输入时长均不会带来有利的影响.
然而,本文的研究尚有很多不完善之处有待深入研究和改进,在未来的研究中可以设计一种更适合风力发电机运动时历的损失函数来更好地表征网络输出值和真实值之间的相似程度.同时,鉴于漂浮式风力发电机运动响应预报问题的复杂程度较高,未来需要对网络结构进行进一步优化.
参考文献
大型漂浮式风电装备耦合动力学研究: 历史、进展与挑战
[J].
Coupling dynamics of floating wind turbines: History, progress and challenges
[J].
A fully coupled method for numerical modeling and dynamic analysis of floating vertical axis wind turbines
[J].DOI:10.1016/j.renene.2017.02.028 URL [本文引用: 1]
A semi-analytical frequency domain model for efficient design evaluation of spar floating wind turbines
[J].DOI:10.1016/j.marstruc.2018.10.015 URL [本文引用: 1]
A numerical model for fully coupled aero-hydrodynamic analysis of floating offshore wind turbine
[J].DOI:10.1016/j.oceaneng.2018.12.021 URL [本文引用: 1]
海上浮式风力机及其动力学问题
[J].
Offshore floating wind turbines and related dynamic problems
[J].
基于小波-SVR模型的浮体极短期运动预报方法
[J].
A method for very short-term motion prediction of floaters based on Wavelet-SVR model
[J].
Forecasting with artificial neural networks:
[J].DOI:10.1016/S0169-2070(97)00044-7 URL [本文引用: 1]
循环神经网络方法预报船舶操纵运动研究
[C]
A study on predicting ship handling movements using recurrent neural network method
[C]
Multi-step predictions for generalized heave motion of wave compensating platform based on ELMAN neural network
[C]
Long short-term memory
[J].
DOI:10.1162/neco.1997.9.8.1735
PMID:9377276
[本文引用: 2]

Learning to store information over extended time intervals by recurrent backpropagation takes a very long time, mostly because of insufficient, decaying error backflow. We briefly review Hochreiter's (1991) analysis of this problem, then address it by introducing a novel, efficient, gradient-based method called long short-term memory (LSTM). Truncating the gradient where this does not do harm, LSTM can learn to bridge minimal time lags in excess of 1000 discrete-time steps by enforcing constant error flow through constant error carousels within special units. Multiplicative gate units learn to open and close access to the constant error flow. LSTM is local in space and time; its computational complexity per time step and weight is O(1). Our experiments with artificial data involve local, distributed, real-valued, and noisy pattern representations. In comparisons with real-time recurrent learning, back propagation through time, recurrent cascade correlation, Elman nets, and neural sequence chunking, LSTM leads to many more successful runs, and learns much faster. LSTM also solves complex, artificial long-time-lag tasks that have never been solved by previous recurrent network algorithms.
Learning phrase representations using RNN encoder-decoder for statistical machine translation
[C]
Realtime prediction of dynamic mooring lines responses with LSTM neural network model
[J].DOI:10.1016/j.oceaneng.2020.108368 URL [本文引用: 1]
A novel MP-LSTM method for ship trajectory prediction based on AIS data
[J].DOI:10.1016/j.oceaneng.2021.108956 URL [本文引用: 1]
Short-term motion prediction of floating offshore wind turbine based on muti-input LSTM neural network
[J].DOI:10.1016/j.oceaneng.2023.114558 URL [本文引用: 1]
Learning to forget: Continual prediction with LSTM
[J].Long short-term memory (LSTM; Hochreiter & Schmidhuber, 1997) can solve numerous tasks not solvable by previous learning algorithms for recurrent neural networks (RNNs). We identify a weakness of LSTM networks processing continual input streams that are not a priori segmented into subsequences with explicitly marked ends at which the network's internal state could be reset. Without resets, the state may grow indefinitely and eventually cause the network to break down. Our remedy is a novel, adaptive "forget gate" that enables an LSTM cell to learn to reset itself at appropriate times, thus releasing internal resources. We review illustrative benchmark problems on which standard LSTM outperforms other RNN algorithms. All algorithms (including LSTM) fail to solve continual versions of these problems. LSTM with forget gates, however, easily solves them, and in an elegant way.
Application of SADA method on full-scale measurement data for dynamic responses prediction of Hywind floating wind turbines
[J].DOI:10.1016/j.oceaneng.2021.109814 URL [本文引用: 1]