橡胶制品的生产工艺一般包括原料混炼、半成品部件挤出/压延、成型、硫化定型4个过程.硫化定型工艺中,橡胶内部高分子链与硫原子之间发生化学反应,形成硫化交联网络,橡胶的弹性水平提高,黏塑性降低,耐老化性能增强[1],因此硫化橡胶得到较为广泛的应用,对其力学性能的研究也受到广大学者的重视.相比于硫化橡胶,未硫化橡胶对产品性能的影响却常被忽视,目前对其力学行为的研究依然较少.然而,未硫化橡胶的力学性能在很大程度上决定了前期的挤出、压延及成型工艺效果.事实上,上述过程中工艺参数如果不能与未硫化橡胶性能相匹配,往往会严重降低产品最终使用性能,甚至导致生产缺陷[2-3].近年来,随着各国对橡胶工业制造工艺研究的愈加深入,未硫化橡胶的力学性能也受到越来越多的关注.
文献[4-5]中最早较为系统地测试了未硫化炭黑填充橡胶在常温环境中不同变形模式(拉伸、压缩、剪切)下的非线性力学行为.结果表明,未硫化橡胶的力学响应具有明显的应变率相关性,以及迟滞效应、Mullins损伤、残余变形等非线性黏弹塑性特征.根据实验结果,文献[4-5]中提出一个基于Yeoh模型和广义Maxwell模型的非线性黏弹性本构模型,但此模型无法较好刻画未硫化橡胶应变率相关的塑性力学行为以及损伤软化等变形特征.为了改善表征效果,文献[6⇓-8]中基于微球模型(Micro-sphere Model)提出一个新的内变量型黏塑性本构模型,此模型采用微球模型运动学框架对非弹性响应进行描述,无需对变形梯度进行乘法分解,但其表征效果并未得到明显提升.随后,上述研究基于黏弹性分数Zener模型[8]对未硫化橡胶的力学行为进行表征,该模型可以较好反映材料的弹性水平,但对黏塑性的表征效果仍较差.文献[9⇓-11]中将1个 Marlow 弹簧模型和3个Maxwell模型并联,获得了未硫化橡胶Prony级数形式的黏弹性本构模型.此模型与Kaliske等[4]的本构模型并无本质区别,模型对未硫化橡胶单一工况下的松弛实验取得了较好的表征效果,尚无法表征未硫化橡胶复杂变形下的非线性黏弹塑性力学行为.需要说明的是,以上研究获得的本构模型虽然都包含应变率效应,但在本构模型参数拟合过程中均未同时包含多种应变率工况,本构模型能否较好地描述未硫化橡胶不同应变率下的非线性黏弹塑性响应仍需进一步验证.Kim等[12]通过多种拉伸实验探究未硫化橡胶应变率相关的非线性拉伸力学行为,并采用一个基于广义Maxwell模型和修正Kelvin模型的黏弹-黏塑性本构模型对其非线性力学行为进行表征,但该模型在较高应变率下(0.1 s-1)的表征效果略差,也未能较好反映出未硫化橡胶应变率相关的塑性变形特征.文献[13-14]中对未硫化橡胶开展不同应变率和不同温度下的拉伸实验,并基于八链模型和Bergström-Boyce流动法则提出了等温黏弹塑性本构模型和温度相关的黏弹塑性本构模型,较好地表征了未硫化橡胶较为复杂的非线性力学行为特征,如应变率效应、迟滞效应、残余变形等.值得一提的是,上述表征未硫化橡胶力学性能的本构模型[4⇓⇓⇓⇓⇓⇓⇓⇓⇓-14]形式都较为复杂,参数众多,只有文献[6,12]中对提出的基于微球的本构模型给出了具体有限元实现过程,并进行了必要的数值验证,而其他本构模型能否用于未硫化橡胶复杂变形条件下的数值仿真仍有待研究.
本文对未硫化橡胶开展了不同应变率下的单调拉伸及循环拉伸加卸载实验,获得了未硫化橡胶较为复杂的非线性黏弹塑性力学行为.根据实验结果,提出了一个三网络黏弹塑性本构模型(TN模型)对未硫化橡胶的力学行为进行表征,模型充分考虑了胶料的超弹应力响应、非线性黏塑性流动、Mullins损伤软化等力学特征,能够较好表征未硫化橡胶非线性的黏弹塑性拉伸力学行为.最后,依托Abaqus有限元仿真软件用户材料子程序接口(UMAT),完成了上述TN模型的有限元实现,并对未硫化橡胶多步松弛加卸载和轮胎胎面胶压入模具的过程进行了有限元仿真,验证了TN模型的有效性和数值稳定性.
1 实验及结果讨论
1.1 实验材料及试件准备
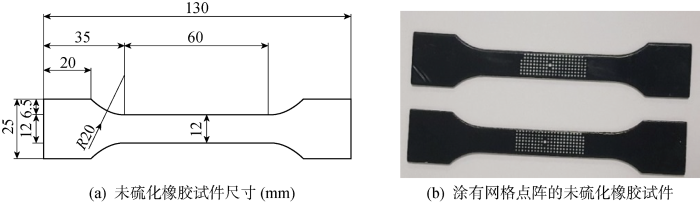
实验采用的胶料均来自安徽佳通轮胎有限公司,为避免试件制备过程中橡胶内部发生硫化反应,胶料均为不含硫化体系的母炼胶.
图1
1.2 橡胶实验及结果分析
实验均是在Instron E3000试验机上开展,包括单调拉伸和循环拉伸加卸载两种变形模式,通过单调拉伸实验,可以观察到未硫化橡胶的弹性水平和屈服特性,而循环拉伸加卸载实验则可综合反映出未硫化橡胶的超弹性、黏性、塑性等力学行为特征.作者对轮胎生产中压延、成型、定型等工艺过程进行了初步仿真(此部分工作还未整理发表),结果表明上述工艺过程中未硫化橡胶应变率最大不超过 0.1 s-1,故本文在每种变形模式下均开展4种不同应变率(
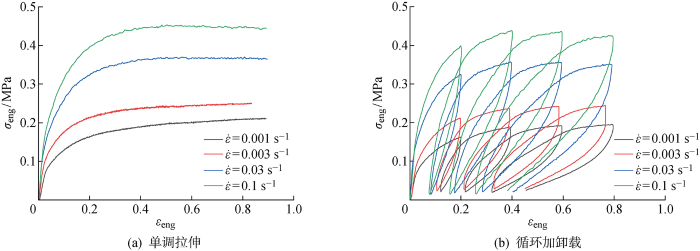
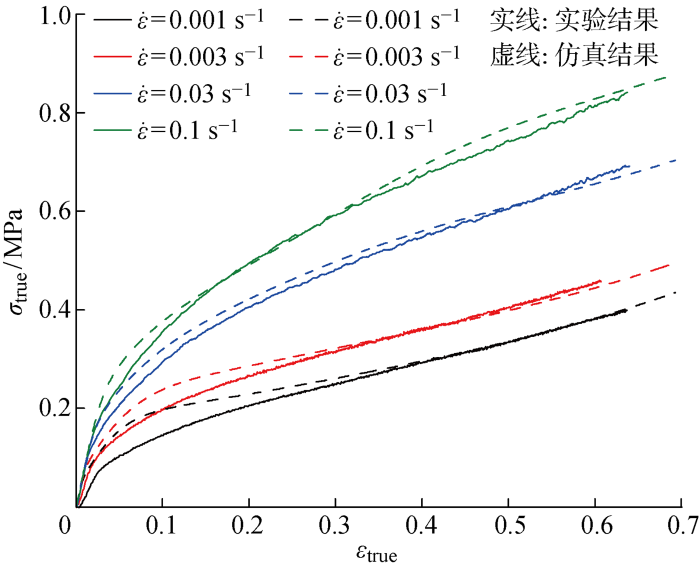
单调拉伸工况下未硫化橡胶的拉伸实验结果如图2(a)所示.图中:εeng为工程应变;σeng为工程应力.从图中可以看出,不同应变率下未硫化橡胶具有相似的非线性力学特征,在拉伸初始时具有很小的线性段,随后发生软化行为,最终应力趋于平缓.胶料拉伸应力水平表现出明显的应变率相关性,随着应变率增加,初始刚度显著增加,应力水平提高.相比于硫化橡胶,未硫化橡胶在100%的应变范围内未出现反“S”现象,可能由其内部未形成交联网络所致.
图2
图2
未硫化橡胶不同应变率下拉伸实验结果
Fig.2
Mechanical behaviors of uncured rubber at different strain rates
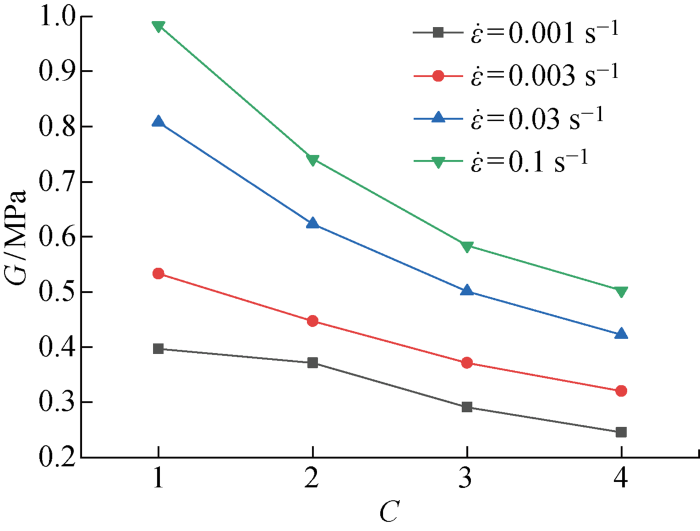
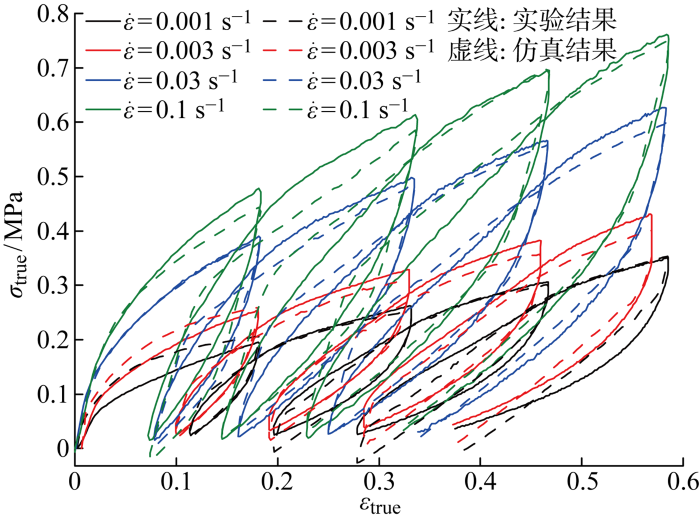
循环拉伸加卸载实验中,未硫化橡胶同样表现出明显的应变率相关性,且在加载段的应变率相关性略大于卸载段的应变率相关性,如图2(b)所示.此外,还可以看出,未硫化橡胶存在较为明显的Mullins软化现象,以及显著的迟滞效应和残余变形.Mullins软化效应反映了试件在首次拉伸时的损伤,为了更清晰地观察未硫化橡胶的软化现象,图3给出了其在不同应变率下随拉伸循环次数(C)增加,拉伸上升段在前20%应变范围内的切变模量(G).可见,随着循环次数增加,胶料切变模量明显降低,且在较高应变率时降低速度更快.迟滞效应反映了循环加卸载实验中的能量耗散,未硫化橡胶迟滞效应同样受到应变率的影响,随着应变率增加,迟滞效应有所增强.由于未硫化橡胶黏塑性较强,每次卸载后均存在一定的塑性残余变形,且残余变形量随着循环次数的增加而累计增加,随着应变率的增加有所降低.
图3
图3
不同应变率下4次上升段切变模量
Fig.3
Shear modulus in four loading steps at different strain rates
2 未硫化橡胶黏弹塑性本构模型
基于对未硫化橡胶实验结果的分析,提出了TN模型对未硫化橡胶的力学行为进行表征,模型的黏塑性响应基于对变形梯度的乘法分解,具体推导过程介绍如下.
2.1 变形梯度分解
对于不可压缩材料,变形梯度F通过乘法分解为形变分量(Distortional Part)与体积分量(Dilatational Part)[17]:
形变分量与体积分量分别具有以下形式[18]:
式中:
此时左Cauchy-Green变形张量可表示为
式中:B*为B的形变分量.
对于近似不可压缩橡胶类材料黏塑性变形,形变分量也可分解为弹性变形分量和黏塑性分量[19]:
式中:Fe为变形梯度的弹性分量;Fv为变形梯度的黏塑性分量.
此时可获得速度梯度Ldis:
式中:Le为速度梯度的弹性分量;
2.2 TN模型
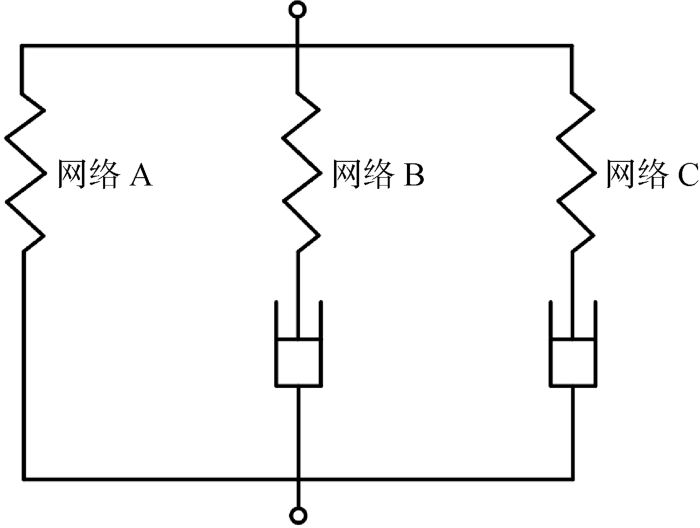
本文提出的TN模型包含3个并联网络,如图4所示.其中一个网络(网络A)为超弹性网络,用于表征未硫化橡胶的超弹性应力响应;另外两个网络为黏塑性网络(网络B、C),用于表征其黏塑性响应.不同于通常所采用的广义Maxwell模型,黏塑性网络B、C采用了基于高分子链微观运动学机制的Bergström-Boyce流动模型,能更好地表征未硫化橡胶的非线性黏塑性流动特征.同时,模型引入了基于分子链运动演化机制的损伤模型来表征未硫化橡胶的Mullins损伤软化效应.
图4
模型Cauchy应力σtol为3个网络Cauchy应力的和:
2.2.1 TN模型应力响应
式中: W为应变能密度;L为朗之万函数,L(x)=coth x-1/x;n为分子链密度(单位体积分子链的数量);N为分子链联接点(包括分子链的缠结点,分子链与填充颗粒的物理吸附点等)之间的分子链段数目; 为八链网络中的链伸长;
对于超弹性力学响应,Cauchy应力可用应变能密度函数[18]表示为
式中:C为右Cauchy-Green变形张量.将应变能密度函数表达式(10)和(11)代入上式,并将C以不变量的形式写入,即可获得八链模型的Cauchy应力表达式[25]:
式中:
对于本文中三网络框架,3个网络的Cauchy应力可通过八链模型分别表示为
超弹性网络(网络A)的Cauchy应力由整体变形梯度决定;黏塑性网络(网络B、C)的变形梯度可进行乘法分解为弹性分量和黏塑性分量:F=FeBFvB,F=FeCFvC,其Cauchy应力仅由弹性分量提供,即
式中:FeB和FeC分别为B、C网络的弹性变形梯度;FvB和FvC为B、C网络的黏塑性变形梯度.
2.2.2 黏塑性流动模型
要获得黏塑性网络B、C的弹性变形梯度,首先需要求解其黏塑性变形梯度,故需要合适的模型来对黏塑性流动进行表征.由1.2节实验结果可知,未硫化橡胶力学行为较为复杂,通常的Maxwell模型不足以较好地表征其非线性黏塑性,故本文采用了基于高分子链微观动力学机制的Bergström-Boyce流动模型.该流动模型认为橡胶类聚合物材料的黏塑性变形是分子链的布朗运动(Brownian Motion)和“爬行”运动(Reptation Motion)联合作用的结果[18],基于此假设,模型具有以下的表达形式:
式中:
黏塑性伸长率由
将式(22)和(23)代入黏塑性变形速度梯度表达式(8),即可获得黏塑性变形梯度的时间导数:
网络B、C中黏塑性变形梯度的时间导数分别为
对式(26)和(27)进行时间积分即可获得B、C网络的黏塑性变形梯度.
2.2.3 Mullins损伤效应
N的变化同样与λcha有关:
式中:C4~C9均为材料常数.
将式(28)和(29)代入Cauchy应力表达式(14),可得包含应力软化效应的炭黑填充分子链网络的Cauchy应力表达式:
化学共价键联接构成的自由链网络(网络B、C)对Mullins效应的影响主要来自于分子链的运动演化回复,并表现为胶料模量的增大.在此采用微观泡沫模型(MFM)[29]的形式来计及分子链运动的影响,并将原模型中的缩减密度改写为应力回复因子R(取值应大于1,本文取为1.2)以体现分子链的运动回复对应力的增强效果,从而获得了切变模量与体积模量的表达式:
式中:
将式(31)和(32)代入Cauchy应力表达式(15)和(16),可获得包含分子运动演化效应的B、C网络Cauchy应力表达式:
式中:G0B、G0C和K0B、K0C分别为B、C网络的初始切变模量和体积模量.
2.3 本构模型表征效果
曲线拟合即实验曲线与表征曲线之间误差最小化的过程,本文采用最小二乘法进行误差计算:
表1 三网络模型拟合参数
Tab.1
| 参数名称 | 参数符号 | 参数值 | 参数取值区间 |
|---|---|---|---|
| 切变模量 | G0B, G0C /MPa | 1.562 2, 0.403 87 | >0 |
| 链段密度 | NB, NC | 9.610 1 | (1, 10) |
| 体积模量 | K/MPa | 180.656 | >0 |
| 流动阻力 | 1.311 8, 5.810 4 | >0 | |
| 流动指数 | mB, mC | 2.340 1, 5.610 7 | (1, 20) |
| B、C网络模量缩放因子 | α, h | 1.254 2, 2.681 4 | (1, 10) |
| A网络模量因子 | C4, C5, C6 | 0.367 4, 17.185 9, 2.292 1 | — |
| A网络模量因子 | C7, C8, C9 | 1.048 1, 0.354 1,-0.052 4 | — |
图5
3 TN模型的有限元实现及验证
获得的本构模型若要应用于工程实践,则需要将其进行数值实现.本文依托于有限元软件Abaqus,完成了TN模型用户材料子程序(UMAT)的开发,并进行了仿真计算以验证模型的有效性和数值稳定性.
模型有限元实现过程中采用的应力更新算法为二阶精度的显式龙格库塔算法(Explicit Midpoint Rule)[32],该算法流程清晰,灵活性强,能够较好地平衡计算精度、数值稳定性以及易数值植入性.采用t代表前一个增量步,t+1代表后一个增量步,则该应力更新算法步骤如下.
(1) t时刻从Abaqus中读取各变形梯度张量:Ft、
(2) 由应力计算公式(14)~(16)和黏塑性流动法则式(22)、(23),计算t+1/2时刻黏塑性网络B、C的黏塑性变形梯度
(3) 对t时刻和t+1时刻总变形梯度平均获得t+1/2时刻总变形梯度
(4) 根据步骤(2)、(3)的计算结果,计算t+1/2时刻B、C网络的弹性变形梯度
(5) 根据应力公式(14)~(16)和式(22)、(23),以及Ft+1、
(6) 检验B、C网络的黏塑性变形梯度是否满足误差准则,若满足则进入第(7)步,否则更新时间步长后返回第(2)步.
(7) 计算t+1时刻B、C网络的弹性变形梯度并根据式(14)~(16)计算t+1时刻Cauchy应力.
(8) 储存自定义状态变量并计算一致切线刚度矩阵(Jacobian矩阵).
图6
图7
图7
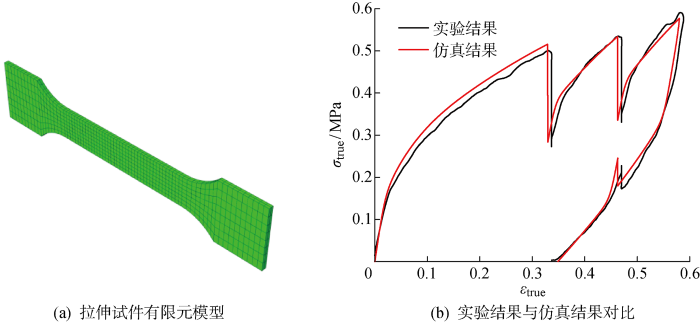
拉伸仿真结果与单调拉伸实验结果对比
Fig.7
Comparison of simulation results with experiments under uniaxial tensile conditions
为了进一步验证数值仿真精度,开展了未硫化橡胶在
图8
图8
多段松弛加卸载实验与仿真结果对比
Fig.8
Comparison of multistep tensile relaxation test and simulation result
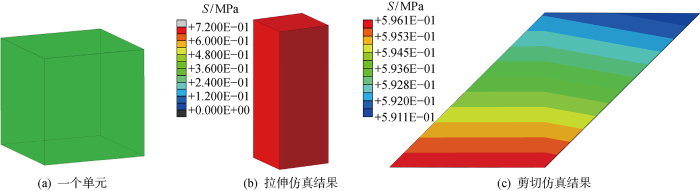
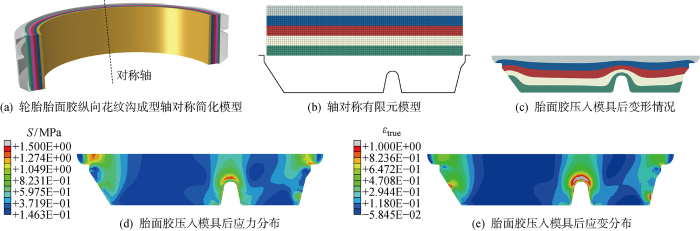
另一方面,未硫化橡胶多用于成型工艺,此过程中胶料需经历较为复杂的变形,故本构模型在复杂变形工况下的计算稳定性尤为重要.为了验证TN模型的数值稳定性,对轮胎胎面胶压入模具的成型过程进行了数值仿真,如图9所示.此模型实际上是对轮胎胎面胶纵向花纹沟成型工艺的简化,如图9(a)所示,模型轴对称分布,且仅包含一条花纹沟.采用轴对称有限元模型对此过程进行仿真,如图9(b)所示,将胎面胶分为5层以便于观察胶料流动,总厚度为20 mm,宽度为80 mm,采用的单元类型为CAX4H,节点数为 2 721 个,单元数为 2 594 个.模具采用离散刚体,深度为15 mm,中间的拱形突起高8.75 mm,宽7.5 mm.对胎面胶上层节点施加径向向下的位移边界条件,速度为0.5 mm/s,橡胶与模具之间的接触摩擦因数设为0.5.胎面胶压入模具后的各层胶料分布如图9(c)所示,由于未硫化橡胶具有近似不可压缩性,胶料充满模具后由两侧溢出.图9(d)和9(e)给出了此时刻胎面胶的应力和应变分布情况,可以看出,中间的拱形突起处胶料流动较为剧烈,存在一定的应力应变集中,靠近模具边缘处的应力应变分布高于底部平坦部位.胶料流动情况以及应力应变分布情况与文献[6,8]中实验及仿真结果基本一致.综上可见,TN模型在复杂变形工况下仍能给出合理的计算结果,表明TN模型具有良好的数值稳定性.
图9
4 结论
(1) 对未硫化橡胶开展了不同应变率下(
(2) 根据实验结果,提出一个用于表征未硫化橡胶黏弹塑性力学行为的TN本构模型,模型由一个超弹性网络和两个非线性黏塑性网络构成.3个网络的应力响应均基于超弹八链模型,同时在黏塑性网络中采用了Bergström-Boyce流动法则描述胶料的非线性黏塑性流动.此外,模型从橡胶高分子链的分子演化理论出发考虑了未硫化橡胶的 Mullins 损伤软化效应.采用TN模型对未硫化橡胶循环拉伸加卸载实验曲线进行表征,表征结果与实验结果吻合良好,胶料的各种拉伸力学特征均得到了较好的体现.
(3) 依托有限元仿真软件Abaqus,完成了TN模型用户材料子程序(UMAT)的开发,并对试件单调拉伸和多段松弛拉伸加卸载实验进行了仿真,仿真结果与实验结果吻合较好,验证了此TN模型的有效性.最后,采用TN模型对轮胎胎面胶压入模具的过程进行数值计算,进一步验证了模型在复杂变形工况下良好的数值稳定性.
参考文献
农业子午线轮胎成型胎坯质量缺陷原因分析与解决措施
[J].
Cause analysis and solutions of green tire quality defects of agricultural radial tire
[J].
Characteristics and investigation of selected manufacturing defects of passenger car tires
[J].DOI:10.1016/j.trpro.2019.07.020 URL [本文引用: 1]
Experimental characterization and constitutive modeling of the mechanical properties of uncured rubber
[J].
DOI:10.5254/1.3548264
URL
[本文引用: 4]

The properties of uncured rubber are characterized by a viscoelastic material formulation in order to develop a finite element method (FEM) to predict the deformation behavior of this material during processing. As material formulation, a viscoelastic material model is considered, which consists of a nonlinear Hooke spring connected in parallel to a finite number of Maxwell elements. To identify the material parameters, various tests have to be conducted. The chosen test procedure and data analysis strategy are presented. An evolutionary optimization procedure is used to fit the material parameters to the measurements by minimizing the mean square error of the approximation. At the end, the suitability of the chosen material model and the identified material parameters is shown. Finally, the result of a molding test is compared to the corresponding FEM simulation.
Research on nonlinear viscoelastic constitutive model for uncured rubber
[J].
Micro-sphere based viscoplastic constitutive model for uncured green rubber
[J].
Numerical characterisation of uncured elastomers by a neural network based approach
[J].DOI:10.1016/j.compstruc.2016.12.012 URL [本文引用: 2]
Comparison of approaches to model viscoelasticity based on fractional time derivatives
[J].DOI:10.1016/j.commatsci.2014.11.012 URL [本文引用: 4]
Radial tire construction design method based on finite element simulation
[J].
子午线轮胎二次法成型过程仿真
[J].
Simulation of the radial tire second-stage building process
[J].
Wide-base tire-building process and design optimization using finite element analysis
[J].
DOI:10.2346/tire.18.460405
URL
[本文引用: 2]

The wide-base tire is a relatively new design that originated to replace dual tires because of its potential for improved performance. However, during the construction process, the wide-base tire is more likely to experience tread deformation and uneven stress distribution. The goal of this study is to incorporate numeric techniques for the construction and design optimization of a wide-base, heavy vehicle, pneumatic tire. First, four conditions of the tire (385/55R22.5)–building process, including gluing of components on the main drum, gluing of components on the auxiliary drum, green tire, and finalizing the capsule vulcanizing machine, were simulated using finite element analysis. Second, to solve the difference in the tire's (435/50R19.5) material distribution between the real manufactured structure and the theoretical structure, the curved surface drum-building method and the parameters of the curved surface drum were determined by tire construction simulation. In this article, we present the method for collecting tire material, the measurement process, the analysis method, some general results, and statistics on the wide-base tire. Finally, validation of results of the simulation and measurement are given.
Strain rate-dependent behavior of uncured rubber: Experimental investigation and constitutive modeling
[DB/OL]. (
Experimental investigation and constitutive modeling of uncured carbon black filled rubber at different strain rates
[J].DOI:10.1016/j.polymertesting.2019.02.005 URL [本文引用: 3]
Effect of the temperature and strain rate on the tension response of uncured rubber: Experiments and modeling
[J].DOI:10.1016/j.mechmat.2020.103480 URL [本文引用: 2]
High-rate tensile behavior of silicone rubber at various temperatures
[J].
DOI:10.5254/rct.19.81562
URL
[本文引用: 1]

The effects of strain rate and temperature on the tensile behavior of silicone rubber were investigated. The quasi-static uniaxial tensile experiments were conducted using an electromechanical testing system, and the high-rate uniaxial tensile tests were performed employing a modified split Hopkinson tension bar technique for low-strength and low-impedance materials. The tensile responses were obtained at strain rates of 0.001–1400 s−1 and temperatures ranging from −50 to 50 °C. The experiments reveal that the tensile stress–strain behavior of silicone rubber is nonlinear and highly dependent on strain rate and temperature. The values of stiffness and nominal stress at a given elongation increase with increased strain rate and decrease with increasing temperature. It is appropriate to postulate that the tensile response at high strain rates arises from the combination of hyperelasticity and viscoelasticity. According to the incompressibility assumption, a phenomenologically inspired visco-hyperelastic model was proposed to describe the constitutive behavior of silicone rubber over wide ranges of strain rates and temperatures.
温度影响下炭黑增强橡胶复合材料的循环拉伸力学行为
[J].
Temperature effect on the mechanical behavior of carbon black reinforced rubber composites under cyclic tensile loadings
[J].
A thermo-viscoelastic-damage constitutive model for cyclically loaded rubbers. Part I: Model formulation and numerical examples
[J].DOI:10.1016/j.ijplas.2017.10.011 URL [本文引用: 1]
Nonlinear finite element modelling of thermo-visco-plastic styrene and polyurethane shape memory polymer foams
[J].
DOI:10.3390/act10030046
URL
[本文引用: 1]

This paper presents nonlinear finite element (FE) models to predict time- and temperature-dependent responses of shape memory polymer (SMP) foams in the large deformation regime. For the first time, an A SMP foam constitutive model is implemented in the ABAQUS FE package with the aid of a VUMAT subroutine to predict thermo-visco-plastic behaviors. A phenomenological constitutive model is reformulated adopting a multiplicative decomposition of the deformation gradient into thermal and mechanical parts considering visco-plastic SMP matrix and glass microsphere inclusions. The stress split scheme is considered by a Maxwell element in parallel with a hyper-elastic rubbery spring. The Eyring dashpot is used for modelling the isotropic resistance to the local molecular rearrangement such as chain rotation. A viscous flow rule is adopted to prescribe shear viscosity and stress. An evolution rule is also considered for the athermal shear strengths to simulate macroscopic post-yield strain-softening behavior. In order to validate the accuracy of the model as well as the solution procedure, the numerical results are compared to experimental responses of Styrene and Polyurethane SMP foams at different temperatures and under different strain rates. The results show that the introduced FE modelling procedure is capable of capturing the major phenomena observed in experiments such as elastic and elastic-plastic behaviors, softening plateau regime, and densification.
On the kinematics of finite strain plasticity
[J].DOI:10.1016/0022-5096(89)90033-1 URL [本文引用: 1]
Molecular chain networks and strain energy functions in rubber elasticity
[J].
A review on material models for isotropic hyperelasticity
[J].DOI:10.1002/msd2.v1.1 URL [本文引用: 1]
A review of physically based and thermodynamically based constitutive models for soft materials
[J].
DOI:10.1115/1.4047776
URL
[本文引用: 1]

In this paper, we review constitutive models for soft materials. We specifically focus on physically based models accounting for hyperelasticity, visco-hyperelasticity, and damage phenomena. For completeness, we include the thermodynamically based viscohyperelastic and damage models as well as the so-called mixed models. The models are put in the frame of statistical mechanics and thermodynamics. Based on the available experimental data, we provide a quantitative comparison of the hyperelastic models. This information can be used as guidance in the selection of suitable constitutive models. Next, we consider visco-hyperelasticity in the frame of the thermodynamic theory and molecular chain dynamics. We provide a concise summary of the viscohyperelastic models including specific strain energy density function, the evolution laws of internal variables, and applicable conditions. Finally, we review the models accounting for damage phenomenon in soft materials. Various proposed damage criteria are summarized and discussed in connection with the physical interpretations that can be drawn from physically based damage models. The discussed mechanisms include the breakage of polymer chains, debonding between polymer chains and fillers, disentanglement, and so on.
Comparison of hyperelastic models for rubber-like materials
[J].
DOI:10.5254/1.3547969
URL
[本文引用: 1]

The present paper proposes a thorough comparison of twenty hyperelastic models for rubber-like materials. The ability of these models to reproduce different types of loading conditions is analyzed thanks to two classical sets of experimental data. Both material parameters and the stretch range of validity of each model are determined by an efficient fitting procedure. Then, a ranking of these twenty models is established, highlighting new efficient constitutive equations that could advantageously replace well-known models, which are widely used by engineers for finite element simulation of rubber parts.
A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials
[J].DOI:10.1016/0022-5096(93)90013-6 URL [本文引用: 2]
A theory of network alteration for the Mullins effect
[J].DOI:10.1016/S0022-5096(01)00136-3 URL [本文引用: 2]
Development of a network alteration theory for the Mullins-softening of filled elastomers based on the morphology of filler-chain interactions
[J].DOI:10.1016/j.ijsolstr.2015.10.032 URL [本文引用: 3]
Isoconversional kinetic analysis of thermally stimulated processes in polymers
[J].DOI:10.1002/(ISSN)1521-3927 URL [本文引用: 1]
Elastic properties of model random three-dimensional open-cell solids
[J].DOI:10.1016/S0022-5096(01)00056-4 URL [本文引用: 1]
A library of advanced user materials: Version 5.0.0
[EB/OL]. (
Development of a flow evolution network model for the stress-strain behavior of poly(L-lactide)
[J].
DOI:10.1115/1.4037071
URL
[本文引用: 1]

Computational modeling is critical to medical device development and has grown in its utility for predicting device performance. Additionally, there is an increasing trend to use absorbable polymers for the manufacturing of medical devices. However, computational modeling of absorbable devices is hampered by a lack of appropriate constitutive models that capture their viscoelasticity and postyield behavior. The objective of this study was to develop a constitutive model that incorporated viscoplasticity for a common medical absorbable polymer. Microtensile bars of poly(L-lactide) (PLLA) were studied experimentally to evaluate their monotonic, cyclic, unloading, and relaxation behavior as well as rate dependencies under physiological conditions. The data were then fit to a viscoplastic flow evolution network (FEN) constitutive model. PLLA exhibited rate-dependent stress–strain behavior with significant postyield softening and stress relaxation. The FEN model was able to capture these relevant mechanical behaviors well with high accuracy. In addition, the suitability of the FEN model for predicting the stress–strain behavior of PLLA medical devices was investigated using finite element (FE) simulations of nonstandard geometries. The nonstandard geometries chosen were representative of generic PLLA cardiovascular stent subunits. These finite element simulations demonstrated that modeling PLLA using the FEN constitutive relationship accurately reproduced the specimen’s force–displacement curve, and therefore, is a suitable relationship to use when simulating stress distribution in PLLA medical devices. This study demonstrates the utility of an advanced constitutive model that incorporates viscoplasticity for simulating PLLA mechanical behavior.
Accurate, efficient and robust explicit and implicit integration schemes for the Arruda-Boyce viscoplastic model
[J].