基于核函数-Wiener过程的轧辊非线性退化建模与剩余寿命预测

doi:10.16183/j.cnki.jsjtu.2022.004

基于核函数-Wiener过程的轧辊非线性退化建模与剩余寿命预测

王汉禹, 陈震, 周笛, 陈兆祥, 潘尔顺^,

上海交通大学机械与动力工程学院,上海 200240

Nonlinear Degradation Modeling and Residual Life Prediction for Rollers Based on Kernel-based Wiener Process

WANG Hanyu, CHEN Zhen, ZHOU Di, CHEN Zhaoxiang, PAN Ershun^,

School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 潘尔顺,教授,博士生导师; E-mail:pes@sjtu.edu.cn.

责任编辑: 李博文

收稿日期: 2022-01-5 修回日期: 2022-01-31 接受日期: 2022-02-16

基金资助:

国家重点研发计划项目(2020YFB1711100)
国家自然科学基金(72001138)
国家自然科学基金(52005327)
国家自然科学基金(72071127)

Received: 2022-01-5 Revised: 2022-01-31 Accepted: 2022-02-16

作者简介 About authors

王汉禹(1997-),硕士生,从事设备退化建模与寿命预测研究.

摘要

在轧钢生产过程中,由于磨损等原因,长时间复杂工况运行下的轧辊工作性能会呈现逐步衰退的特征.考虑轧辊工作环境具有工况复杂、随机干扰强等特点,提出基于核函数-Wiener过程(KWP)退化模型,使用Wiener过程刻画轧辊退化趋势的强随机性特征,引入核函数捕捉轧辊的非线性退化路径,推导贝叶斯框架下参数估计的解析表达式,并构造轧辊可工作转动量的健康指标,进一步预测轧辊剩余寿命(RUL).结合某钢铁公司1580热轧生产线现场数据,所构建模型拟合优度达到0.989,剩余寿命预测误差低于4.7%,相较常见机器学习算法取得了更好效果,有助于提高设备运转效率与安全性并实现视情维护.

关键词： 轧辊; 性能退化; 非线性建模; 核函数; Wiener过程; 剩余寿命预测

Abstract

In the process of steel rolling, due to wear and other reasons, the working performance of the roll under long and complex working conditions has a gradual decline. Considering the characteristics of complex working conditions and strong random interference of the roll working environment, this paper proposed a kernel-based Wiener process (KWP) degradation model to characterize the strong randomness of the roll degradation trend by using the Wiener process, and to capture the nonlinear degradation path of the roll by using the kerna function. This paper derives the analytical expression of parameter estimation in the Bayesian framework, and constructs the health index of the roll working rotation, then predicts the remaining useful life (RUL) of the roll. In combination with the field data of 1580 hot rolling production line of an iron and steel company, the goodness of fit of the model built is 0.989, and the residual life prediction error is less than 4.7%. Compared with the common machine learning algorithm, it has achieved better results, which is helpful to improve the operating efficiency and safety of equipment and achieve maintenance as needed.

Keywords： roller; performance degradation; nonlinear modeling; kernel function; Wiener process; remaining useful life (RUL) prediction

PDF (1553KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王汉禹, 陈震, 周笛, 陈兆祥, 潘尔顺. 基于核函数-Wiener过程的轧辊非线性退化建模与剩余寿命预测[J]. 上海交通大学学报, 2023, 57(8): 1037-1045 doi:10.16183/j.cnki.jsjtu.2022.004

WANG Hanyu, CHEN Zhen, ZHOU Di, CHEN Zhaoxiang, PAN Ershun. Nonlinear Degradation Modeling and Residual Life Prediction for Rollers Based on Kernel-based Wiener Process[J]. Journal of Shanghai Jiaotong University, 2023, 57(8): 1037-1045 doi:10.16183/j.cnki.jsjtu.2022.004

我国钢铁产量已多年位居世界第一^[1],但作为典型的流程型制造行业,其生产效率和经济效益仍与世界先进水平存在较大差距.轧辊是轧钢生产线上的关键部件和大型耗材,表面磨损是其主要失效形式,并对带钢表面质量及板形产生不利影响.针对轧辊失效过程建立退化模型并实现剩余寿命(RUL)预测,对于提高轧辊使用寿命和产品质量尤为重要,也可为管理人员确定换辊周期与维修策略提供决策依据,最终达到节能减排、降低成本的目标,为推动绿色生产和碳中和做出贡献.但由于轧辊工况恶劣,通常是在高压、高温、高速等条件下工作,且轧辊与金属表面间存在氧化铁皮、冷却水等多种影响因素,导致轧辊退化过程具有随机性、非线性、强耦合等特征,所以对轧辊进行准确的退化建模与RUL预测是当前研究难点.

目前,针对轧辊的退化建模研究,常用方法可分为两类:物理解析模型和基于数据驱动的方法^[2].物理解析模型通过研究轧辊材料属性、失效机理、负载条件等影响退化的因素,构建轧辊退化数学模型并进行RUL预测.刘子英等^[3]和Cai等^[4]指出,轧辊退化过程涉及轧制力、带钢宽度、温度、速度、冷却水等众多影响因素,且这些因素具有耦合关系,并伴随机械磨损、热磨损、化学腐蚀等多种退化形式.多数研究通常基于轧制力、轧制长度、轧辊材质、磨损距离等主要影响因素构建经典模型^[5],也有研究在其基础上考虑轧辊表面温度^[6]、轧制速度^[7]、不均匀磨损^[8]等因素提出改进模型.考虑轧辊磨损是一个极其复杂的过程,涉及物理、化学及材料学等众多学科,这无疑限制了物理解析模型在轧辊退化建模领域中的发展.

基于历史大数据,通过构建输入和输出间的映射关系,数据驱动方法可以避免物理模型完全还原复杂因果关系的缺陷^[9].目前,面向轧辊退化领域的数据驱动方法研究相对较少,仅少数学者将神经网络应用于轧辊的退化建模和RUL预测.如吴进等^[10]采用反向传播(BP)神经网络与有限元分析软件,通过对摩擦因数进行预测得到了较高精度的轧制力预测结果.Jiao等^[11]提出了一种新的基于递归神经网络的深度学习网络结构,从批量数据中提取健康指标预测轧辊的RUL.神经网络方法在工程应用中需要大量轧辊历史数据来训练模型,否则难以较好地预测轧辊性能.此外,神经网络模型难以捕捉退化数据的随机性,一般只能给出相关特征量的点估计,不能表征退化过程的不确定性.

鉴于轧辊退化的影响因素众多,难以建立有效的物理解析模型,而神经网络方法所需数据量大且对随机数据处理能力有限.考虑随机过程能够较好表征设备退化量的随机性,可以给出RUL的概率分布,并能结合具有较强非线性映射能力的核函数,因此提出基于核函数-Wiener过程(KWP)退化模型,并在贝叶斯框架下推导参数估计的解析形式.同时基于轧辊磨损机理,提出基于轧辊可工作转动量的健康指标,构建基于KWP退化模型的健康状态估计和RUL预测流程.所提方法在某钢铁公司1580热轧生产线实测数据上取得了较好的建模效果和准确的RUL预测,有助于提高生产线作业计划的稳定性和连续性^[12].

1 问题描述

轧辊磨损是典型的逐步累积的非线性退化过程,其磨损速率随着轧制长度(km)增加逐渐加快,主要原因包括三方面:① 轧辊表面经过特殊热处理形成耐磨层,耐磨层磨损后进入快速磨损期;② 随着轧辊直径减小,导致轧制相同距离的轧辊表面所受冲击频率更高;③ 轧辊越细,单位轧辊表面所受压力更大,磨损更快.

受轧制压力、热冲击和热应力等多种因素耦合作用的影响,轧辊退化路径具有复杂的非线性和随机性特征.考虑随机过程能够较好地处理设备退化过程中的随机性特征^[13-14],并已在锂电池、数控机床、制动器、轴承等设备及部件上取得了较好的应用效果^[15],它在轧辊退化建模领域具有巨大潜力,因此本文使用随机过程对轧辊进行可靠性建模并预测其RUL.

退化建模中常用的随机过程模型包括Wiener过程、Gamma过程和Inverse Gaussian过程等^[16],由于Wiener过程更适用于非单调退化路径的建模且具备良好的数学可追溯性,目前已成为可靠性技术研究和应用的重要方法之一^[17].假设X(t)为t时刻的退化量,则满足以下性质的随机过程:{X(t),t≥0},定义为一元线性Wiener过程.

(1) 任意时刻的增量服从正态分布,即:

(1)

Δ X = X (t + Δ t) - X (t) ~ N (η Δ t, σ^{2} Δ t)

式中:η和σ分别表示漂移系数和扩散系数.

(2) 任意两个不相交时间段内的增量相互独立.相应的数学描述为:对于任意的 $0 < t_{1} < \dots < t_{n}$ ,则 $X (t_{1}) - X (t_{0}), X (t_{2}) - X (t_{1}), \dots, X (t_{n}) - X (t_{n - 1})$ 相互独立.

(3) X(0)=0.

线性Wiener过程难以描述非线性退化的动态特性,而轧辊历史数据表明其性能退化路径具有明显非线性特征,因此有必要进一步研究非线性Wiener过程模型.典型非线性Wiener过程退化模型可由下式给出:

(2)

\begin{matrix} X (t) = η Λ (t) + σ B (t) \end{matrix}

式中:Λ(t)为时间尺度转换函数;扩散系数可用于调整函数B(t)布朗运动的扩散程度.

非线性Wiener过程的研究大多是假设时间尺度转换函数满足指数形式^[18],即 $Λ (t) = t^{λ} .$ 然而轧辊的磨损是一个多因素相互耦合的复杂非线性过程,基于指数函数的Wiener过程只适用于小部分非线性退化问题,需研究形式更灵活的漂移函数以提高对复杂非线性问题的建模能力.

非线性建模可以通过核函数将低维数据映射到高维空间进行非线性变换,使其在高维空间中呈现线性特征^[19].本文基于此思想在Wiener过程中引入核函数来解决轧辊退化过程中的非线性表征问题.相较基于指数函数的Wiener过程,KWP具有如下优点:

(1) 针对轧辊退化趋势因工况复杂、随机干扰强造成的强随机性特征,将Wiener过程应用于轧辊的RUL预测中.相较神经网络等人工智能方法,Wiener过程可以表征样本差异、测量误差、环境干扰等不确定信息,且推导得到的失效分布蕴含首达时的概念,为制定合理的预防维护方案提供决策支持.

(2) 考虑现有随机过程模型对复杂非线性退化路径的刻画能力较弱,引入核函数构建基于KWP的退化模型.该模型能够有效描述轧辊退化过程的随机性和非线性,有助于实现轧钢生产线从当前定期维护策略到基于状态维护策略的转变^[20].

(3) 相较神经网络等常见数据驱动方法,基于KWP可以获取RUL预测的概率密度函数,度量退化的不确定性,并为其他类似领域的RUL预测和实时状态监测问题提供参考.

2 轧辊性能退化过程非线性建模

2.1 基于KWP的退化模型

引入核函数代替式(1)中非线性Wiener过程的漂移函数项 $η Λ (t),$ 构建基于KWP的退化模型如下:

(3)

\begin{matrix} X (t) = (\overset{m}{\sum_{i = 1}} w_{i} k (t, t_{i}) + w_{0}) + σ B (t) \end{matrix}

式中: 为核函数;$w_i $为权重系数; $w_0 $为截距; $t_i $为第i次测量的时间;m为测量总次数.定义.

式(3)中 $k (t, t_{i})$ 为核函数的一般形式,常用核函数的表达式如表1所示.

表1 常用核函数及其公式

Tab.1 Kernel functions and formulas

核函数	表达式	参数
线性核函数	$t t_{i}$	无特殊参数
高斯核函数	$e x p (- \frac{\|t - t_{i} \|^{2}}{2 v^{2}})$	v为高斯核函数的宽度
多项式核函数	$(t t_{i} {+ r)}^{d}, d = 1,2, \dots, n$	$r 为偏置系数; d$ 为多项式阶数
Laplace核函数	$e x p (- \frac{\|t - t_{i} \|}{o})$	o>0
Sigmoid核函数	$t a n h (ρ t t_{i} + θ)$	$ρ > 0, θ < 0$

新窗口打开| 下载CSV

核函数性能取决于其形式和参数,也决定了模型对非线性问题的处理能力,从而影响KWP模型对轧辊性能预测的准确性与有效性.为使核函数能够更好地刻画轧辊性能退化所特有的路径特征,在实际应用中可根据轧辊实测数据的预测效果,选取核函数嵌入到模型中的漂移函数项.

KWP模型的独立增量为 $x = [Δ x_{1} Δ x_{2} \dots Δ x_{n}]^{T},$ 其联合概率密度函数服从多元高斯分布:

(4)

\begin{array}{l} p (x | w, σ) = \frac{1}{\sqrt{{(2 π)}^{n} |E|}} \times \\ e x p [- \frac{1}{2} (x - [φ (Δ x_{1}) \dots φ (Δ x_{n} {)]}^{T} \times \\ {w)}^{T} E^{- 1} (x - [φ (Δ x_{1}) \dots φ (Δ x_{n} {)]}^{T} w)] \end{array}

式中: $φ (Δ x_{i}) = [1 k (Δ x_{i}, Δ x_{1}) \dots k (Δ x_{i}, Δ x_{n})]$ ;E为元素的先验协方差矩阵, $E (i, j) = σ^{2} m i n (t_{i}, t_{j})$ .

对于未知参数 $w 和 σ,$ 其取值需根据轧辊退化历史数据进行估计.

2.2 基于退化模型的贝叶斯参数估计

针对模型参数估计,首先基于贝叶斯理论推导参数 $w 和 σ$ 的后验分布,获得边际似然函数,再通过最大化边缘似然函数,便可得到参数 $w 和 σ$ 的最大似然估计值.

使用极大似然估计法估计参数易使模型出现过拟合情况,为避免模型出现过拟合现象,定义参数 $w$ 的先验分布为均值等于0的高斯分布,即:

(5)

\begin{matrix} p (w | α) = \overset{m}{\prod_{i = 0}} (\frac{α_{i}}{\sqrt{2 π}} e x p (\frac{- α_{i} w_{i}^{2}}{2})) \end{matrix}

式中: $α = [α_{0} α_{1} \dots α_{m}] 为 w$ 的超参数向量.

根据多层贝叶斯先验分布,定义α和β的超先验分布服从Gamma分布,即:

(6)

\begin{matrix} \begin{matrix} p (α) = \overset{m}{\prod_{i = 0}} G a m m a (α_{i} |a, b) \end{matrix} \end{matrix}

(7)

p (β) = G a m m a (β | c, d)

式中:

\begin{array}{r} β = σ^{- 2} \\ G a m m a (α_{i} |a, b) = Γ {(a)}^{- 1} b^{a} α^{a - 1} e^{- b a} \\ Γ (a) = \int_{0}^{\infty} t^{a - 1} e^{- t} d t \end{array}

在选取无信息先验作为α和$σ^2$ 的超先验分布时,参数a、b、c和d应足够小,如a=b=c=d=10^-4^[21].

基于贝叶斯公式,未知参数w、α和σ的后验分布可表示为

(8)

p (w, α, σ^{2} |x) = p (w | x, α, σ^{2}) p (α, σ^{2} |x)

由贝叶斯定理,可得w计算式如下:

(9)

\begin{array}{l} p (w | x, α, σ^{2}) = \\ \frac{p (x | w, σ^{2}) p (w | α)}{p (x | α, σ^{2})} = \\ {(2 π)}^{- (m + 1) / 2} |E |^{- 1 / 2} \times \\ e x p [- \frac{1}{2} {(w - μ)}^{T} E^{- 1} (w - μ)] \end{array}

参数α和σ的估计值可以通过最大化边际似然函数 $p (α, σ^{2} |x)$ 得到,即使 $p (x | α, σ^{2})$ 最大:

(10)

\begin{array}{l} p (x | α, σ^{2}) = \int p (x | w, σ^{2}) p (w | α) d w = \\ {(2 π)}^{- \frac{m}{2}} σ^{2} + Φ A^{- 1} Φ^{T} |^{- \frac{1}{2}} \times \\ e x p [- \frac{1}{2} x^{T} (σ^{2} Φ A^{- 1} Φ^{T})^{- 1} x] \end{array}

式中: $Φ = [φ (Δ x_{1}) φ (Δ x_{2}) \dots φ (Δ x_{n} {)]}^{T}$ ; $A = d i a g (a_{1}, \dots, a_{m}) .$ 式(10)的后验协方差和均值分别为

(11)

\begin{matrix} C = (σ^{- 2} Φ^{T} Φ + d i a g (α_{1}, \dots, α_{m} {))}^{- 1} \end{matrix}

(12)

μ = (d i a g (α_{1}, \dots, α_{m}) + Φ^{T} E^{- 1} {Φ)}^{- 1} Φ^{T} E^{- 1} x

设计迭代估计算法求得式(10)中超参数α和$σ^2$的近似解.按照Mackay^[22]的方法令式(9)等于0,整理得α和$σ^2$的迭代更新值为

(13)

\begin{matrix} \begin{matrix} α_{i}^{n e w} = γ_{i} / μ_{i}^{2} \end{matrix} \end{matrix}

(14)

(σ^{2})^{n e w} = \frac{{‖x - Φ μ‖}^{2}}{m} - E_{i i} γ_{i}

式中: 为式(12)的第i个后验平均权重;定义; 为式(11)后验方差矩阵的第i个对角元素,可由α和$σ^2$ 值计算得到.迭代中若$α_i$ 很大,且$w_i $被其先验概率严格约束时,则令, ;若$α_i $很小,且$w_i $适应数据时,令$γ_i≈1$.

针对单组轧辊退化向量样本 $x, 为了得到相应的预测值 x_{*},$ 基于概率论和贝叶斯定理可得:

(15)

\begin{array}{l} p (x_{*} | x) = \int p (x_{*} | w, σ^{2}) p (w, σ^{2} | x) d w d σ^{2} = \\ \int p (x_{*} | w, α, σ^{2}) p (w, α, σ^{2} |x) d w d α d σ^{2} \end{array}

将式(8)代入式(15)中可得预测值 $x_{*}$ 的条件概率为

(16)

\begin{matrix} p (x_{*} |x) = \int p (x_{*} |w, α, σ^{2}) p (w, α, σ^{2} |x) d w d α d σ^{2} \end{matrix}

因难以计算积分 $p (x) = \int p (x| w, α, σ^{2}) p (w, α, σ^{2}) d w d α d σ^{2}$ ,无法直接得到式(16)中的后验概率 $p (w, α, σ^{2} |x)$ ,所以依据贝叶斯定理将后验概率分解为

p (w, α, σ^{2} |x) = p (w | x, α, σ^{2}) p (α, σ^{2} |x)

即

(17)

\begin{matrix} p (x_{*} |x) = \int p (x_{*} |w, α, σ^{2}) p (w | x, α, σ^{2}) \times p (α, σ^{2} |x) d w d α d σ^{2} \end{matrix}

基于式(13)和(14)更新参数,同时计算式(11)和(12)更新后验统计 $C 和 μ,$ 直到达到最大循环次数或者输出结果的梯度小于收敛条件,即10^-3.由于在迭代过程中易发生部分α_i趋于无穷的现象,根据核函数性质^[23]删除迭代过程中所有 $α_{i} > α_{m a x} 的 α_{i} 所对应的权重和核函数, 并设 α_{m a x} = 10^{5},$ 通过此过程实现KWP退化模型的稀疏性,提升了工程分析效率以适用轧辊性能状态的在线监测.

记 $α_{M P} 和 σ_{M P}^{2}$ 为停止迭代后的最优值(MP),此时若给定一组新的轧辊退化数据x,其预测输出可由下式得到:

(18)

\begin{matrix} p (x_{*} |x, α_{M P}, σ_{M P}^{2}) = \end{matrix} \int p (x_{*} |w, σ_{M P}^{2}) p (w | x, α_{M P}, σ_{M P}^{2}) d w

由于等式右边的两个积分项均满足高斯分布,所以预测值 $x_{*}$ 满足分布如下:

(19)

p (x_{*} |x, α_{M P}, σ_{M P}^{2}) = N (x_{*} | y_{*}, σ_{*}^{2})

式中:预测输出$x_*$ 的均值$y_* $和方差$σ_*^2$分别为

(20)

\begin{array}{l} y_{*} = μ^{T} φ (x_{*}) \\ σ_{*}^{2} = σ_{M P}^{2} + φ (x_{*})^{T} E φ (x_{*}) \end{array}\}

由式(20)可知,本模型的预测误差由两部分组成:数据固有噪声和模型权重估计过程中的不确定性.在一般的机器学习算法中,使用极大似然估计法估计参数易出现过拟合现象,KWP模型通过约束参数w和调整扩散参数σB(t),可以较好地规避过拟合的情况.

针对轧辊性能指标退化曲线具有随机性和非线性的特征,构建了KWP退化模型,并基于贝叶斯推理给出模型参数的估计值以及预测值的概率分布.

3 基于KWP的轧辊健康状态预测

3.1 健康指标及可解释性

健康指标的构建是轧辊可靠性建模和寿命预测中不可缺少的一环,应满足以下条件:①直观显示轧辊的磨损速度,判断轧辊是否进入快速磨损期;② 为轧辊下机周期的确定提供参考,以减少总停机时间并保证产品质量,进而提高钢铁生产线的经济效益;③ 表征轧辊直径与工作距离间的耦合关系,为维修策略提供参考.若采用累积距离或轧辊直径作为健康指标,并不能反映轧辊磨损速度随着轧辊直径减少而加剧的特征,对确定轧辊更换、维修决策的参考价值有限.

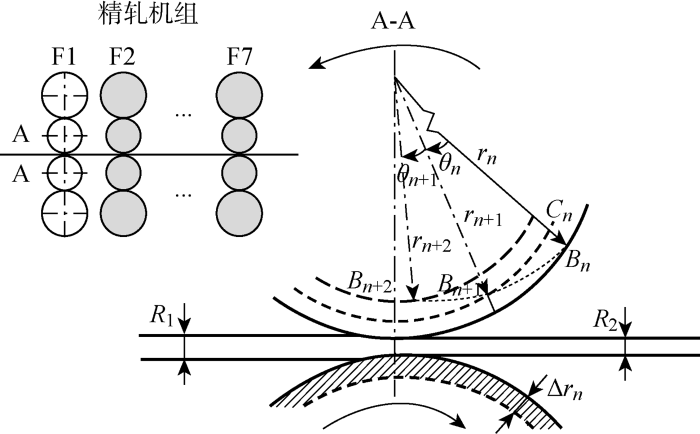
基于轧辊磨损机理,构建轧辊健康指标如下:轧辊的直径变化过程如图1所示,F1~F7代表产线中存在的7个精轧机组,$R_1$ 、$R_2$ 分别代表轧制前后的轧辊厚度,且轧辊的起始工作点$B_n$ 位于第n次工作周期开始前的表面$C_n$ 上,半径为$r_n$,终止工作点$B_{n+1} $位于轧辊工作周期结束后磨损的表面,半径为$r_{n+1}$,$Δr_n$ 为本次磨损半径.弧$B_n B_{n+1}$ 为轧辊实际工作里程, $θ_n$ 为第n次工作周期实际转过的角度.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 轧辊磨损示意图

Fig.1 Schematic diagram of roller wearing

考虑轧辊在单次工作周期前后直径变化十分微小,可近似为 $r_{n} - r_{n + 1} / r_{n} \approx 1$ ,从而合理认为轧辊实际工作的路程 $B_{n} B_{n + 1}$ 相当于 $C_{n} B_{n + 1}$ ,则第n次工作周期距离的计算式为

(21)

\begin{matrix} l_{n} = (π / 180) θ_{n} (r_{n} - Δ r_{n}) \end{matrix}

设轧辊在完整工作周期内的可工作总距离为l,则推导得轧辊在第n次工作周期下机后的剩余可工作距离 $l - l_{n} = (π / 180) (θ - θ_{n}) (r - r_{n})$ ,整理得:

(22)

\begin{matrix} l_{y} / r_{y} = (π / 180) θ_{y} \end{matrix}

式中:$l_y$为轧辊剩余可工作距离; $r_y$为轧辊剩余可磨削直径; $θ_y$为轧辊可工作转动量.考虑$l_y/r_y∝θ_y$,呈正相关关系,以轧辊可工作转动量作为健康指标,刻画轧机工作辊的可服役信息.因此所构建指标既考虑了轧辊工作距离与轧辊直径的耦合关系,又具备工程可解释性与健康状态的集成表征性,为后续寿命预测和动态维护提供理论与技术支持^[24].

3.2 轧辊RUL预测

将轧辊历史运行数据 $θ_{1 : n} = {θ_{1}, θ_{2}, \dots, θ_{n}}$ 作为输入序列,基于KWP退化模型,通过循环迭代计算得到轧辊未来时刻的健康状态.考虑轧辊的失效阈值 $ξ,$ 轧辊的可工作转动量退化轨迹由KWP退化模型描述,则轧辊寿命T为轧辊的性能退化量X(t)首次达到ξ的时间(FPT):

(23)

\begin{matrix} T = i n f {T | X (t) \geq ξ, t > 0} \end{matrix}

式中:inf{·}表示函数的下确界,则轧辊在任意时间t_k的RUL被定义为

(24)

H_{k} = i n f {h_{k} : X (t_{k} + h_{k}) \geq ξ | X (t_{k}) < ξ}

Wiener过程的首达时间服从逆高斯分布,为估计轧辊FPT的概率密度,基于式(4)、(24),推导得轧辊RUL的概率密度函数:

(25)

\begin{matrix} f_{2} (t | w) = \frac{ξ}{\sqrt{2 π σ^{2} t^{3}}} e x p [- \frac{(ξ - y {(t | w))}^{2}}{2 σ^{2} t}] \frac{d y (t | w)}{d t} \end{matrix}

基于式(25)获得轧辊在任意时刻的RUL预测值,可为确定轧辊更换周期和磨削量提供技术支撑和决策依据,进而提高产品质量和轧辊使用寿命,降低停机损失.

3.3 退化建模与健康预测流程

基于KWP的模型构建和寿命预测流程如图2所示.输入轧辊历史数据并清洗、正则化,结合轧制距离与轧辊直径构建可工作转动量健康指标.在模型训练过程中,首先初始化KWP退化模型的扩散参数$σ^2 $和核函数参数$α$.根据式(11)~(14)计算权重的后验协方差C和均值μ,并更新参数$α_i$ 和$σ^2$,直至模型收敛得到参数最优值.并剔除超参数中α_i>α_max的所对应的权重和核函数,以实现KWP退化模型的稀疏性,即可获得完整预测模型.最终结合轧制时间和失效阈值,给出RUL估计值及其概率分布函数,从而实现对轧辊可工作转动量的预测.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 KWP退化模型的轧辊健康状态估计方法

Fig.2 Roller health state estimation based on KWP degradation model

4 基于某钢铁公司 1580 热轧生产线的实验分析

4.1 实验数据

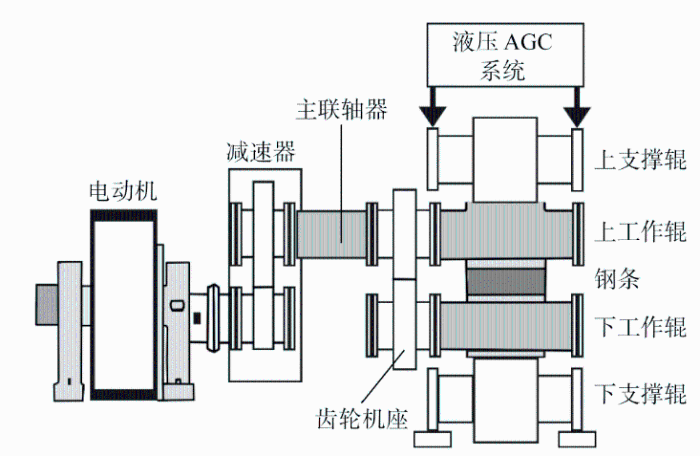
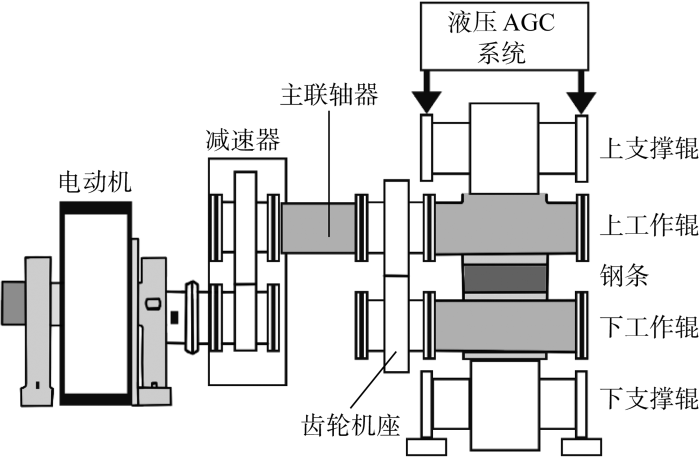
轧辊实验数据来自某钢铁公司1580热轧生产线精轧机组,该精轧机组的基本结构如图3所示.实地调研获得的部分数据如表2所示.基于轧辊可工作转动量健康指标,对数据进行整理、清洗,考虑数据完整性等因素后,以1580热轧生产线F1精轧机组C14S91460072号轧辊的工作周期数据为例进行实验.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 精轧机组结构示意图

Fig.3 Finishing mill structure

表2 轧辊部分原始数据展示

Tab.2 Raw data of rollers

轧辊编号	上机时间	下机时间	生产量/t	轧制距离/km	轧辊直径/mm
1580I1	2017-12-27T15:04	2017-12-27T17:36	1016	4.863	825.92
1580I2	2017-12-27T20:27	2017-12-27T22:42	739	4.803	825.92
1580I2	2017-12-28T1:04	2017-12-28T4:34	1427	6.588	825.83
1580I2	2017-12-28T12:26	2017-12-28T17:48	2570	14.504	825.83
1580I2	2017-12-29T10:32	2017-12-29T17:25	2360	14.013	825. 83

新窗口打开| 下载CSV

4.2 实验结果与分析

4.2.1 评价指标

使用均方根误差(RMSE)、平均绝对误差(MAE)、拟合优度(CD)评价算法的性能.RMSE和MAE两者的值越小则表明算法预测精度越高,其公式分别为

(26)

\begin{matrix} \begin{matrix} α_{R M S E} = \sqrt{\frac{1}{n'} \overset{n'}{\sum_{t = 1}} (x (t) - \hat{x} {(t))}^{2}} \end{matrix} \end{matrix}

(27)

α_{M A E} = \frac{1}{n'} \overset{n'}{\sum_{t = 1}} | x (t) - \hat{x} (t) |

CD值越接近1,说明模型预测性能越好,其公式为

(28)

\begin{matrix} η_{C D} = \frac{\overset{n'}{\sum_{t = 1}} (\hat{x} {(t) - \bar{x})}^{2}}{\overset{n'}{\sum_{t = 1}} (x {(t) - \bar{x})}^{2}} \end{matrix}

式中:n'表示时间序列总数;x(t)表示时刻t的健康状态实际值; $\hat{x} (t)$ 为算法预测值; $\bar{x}$ 为真实值均值.由此,可通过计算绝对值和相对值全方位评估模型的建模效果与预测性能.

4.2.2 核函数选择

核函数的选择直接影响KWP退化模型的预测精度,也同样影响模型稀疏性及训练时间.基于C14S91460072号轧辊的退化数据,根据核函数不同,实验共分5组进行比较,计算各模型的RMSE、CD、MAE进行评估,如表3所示.

表3 核函数选择

Tab.3 Kernel function selection

核函数类型	RMSE	CD	MAE
高斯核函数	1109.8	0.9893	865.1
多项式核函数	7713.1	0.4781	5916.9
线性核函数	10717.1	0.0000	7589.3
Laplace核函数	2046.5	0.8664	1475.4
Sigmoid核函数	10717.0	0.0000	7589.3

新窗口打开| 下载CSV

根据表3可知,高斯核函数的RMSE、CD和MSE均优其他核函数,说明原数据在通过高斯核函数映射到高维特征空间后线性特征更好,也证明了不同的核函数特性并不相同,不同的应用场景下性能差别很大.在迭代过程中,基于高斯核函数的Wiener过程退化模型仅使用了6个相关向量(RVs),具有较好的稀疏性,从而测试时间更短,便于实时在线监测.根据实验结果,轧辊性能的退化预测将高斯核函数嵌入Wiener过程中作为漂移函数.

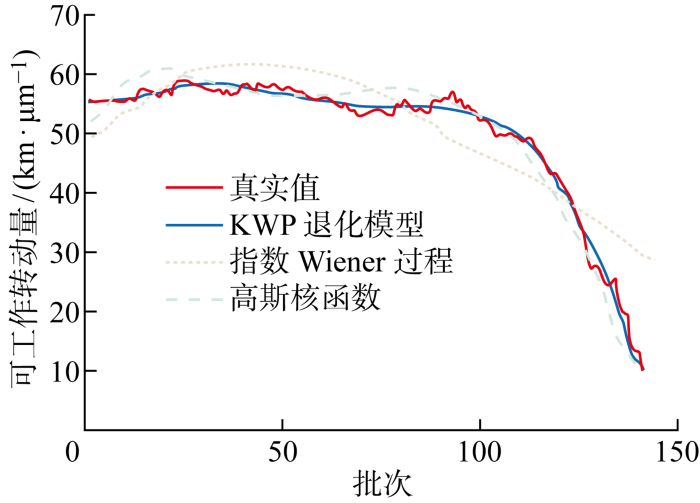
为验证KWP退化模型相较其他常用算法的优越性,使用基于指数函数的Wiener过程算法和基于高斯核函数的相关向量机算法,对C14S91460072号轧辊的非线性时间序列进行回归建模,3种模型建模效果如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 KWP模型建模效果对比

Fig.4 Modeling results of KWP

基于指数函数的Wiener过程见图4,其预测值与真实值偏差较大,说明基于指数函数的Wiener过程算法在轧辊退化建模上的适应性较差.其原因主要是指数函数构造过于简单,所能刻画的非线性数据较为有限,无法表征轧辊实际退化路径的复杂非线性特征.基于高斯核函数的相关向量机算法预测效果见图4.高斯核函数相较指数函数能够捕捉更复杂非线性退化路径,获得更好的预测效果.但是,基于高斯核函数的相关向量机算法在其退化建模上的鲁棒性较差.考虑钢铁热轧生产线关键设备结构极端复杂、随机干扰强,轧辊性能退化过程需要有效地描述设备性能演化的随机特征.因此,基于高斯核函数的相关向量机方法无法较好地处理退化路径中的随机性特征,难以描述真实的轧辊退化路径.

基于高斯核函数的Wiener退化过程的预测效果见图4,可以看出模型可以较好地预测轧辊的退化趋势,使得预测值基本落在规定的误差范围内,预测效果大大优于基于指数函数的Wiener过程,并较基于高斯核函数的相关向量机算法有明显改善.

为了更好地说明本模型的优越性,统计3个模型的RMSE、CD、MAE以进行量化分析,结果如表4所示.

表4 模型预测误差

Tab.4 Prediction error of models

模型	RMSE	CD	MAE
基于高斯核函数的Wiener过程模型	1109.7	0.9893	865.1
指数Wiener过程模型	8059.8	0.4726	6369.4
基于高斯核函数的相关向量机模型	1992.7	0.8719	1591.2

新窗口打开| 下载CSV

由表4可知,基于高斯核函数的Wiener过程模型,在拟合优度上较指数Wiener过程模型提高了109%,较相关向量机模型提高了14%,证明了KWP退化模型的优越性.在计算过程中,相较相关向量机算法的85个RVs,基于高斯核函数的Wiener退化过程只需要6个RVs,说明本模型的稀疏性远小于一般的相关向量机算法.这证明KWP退化模型不仅对非线性和随机性强的数据具有较好的处理能力,并且有助于模型快速收敛,适用于轧辊性能状态的在线监测.

基于C14S91460072号轧辊数据,采用KWP退化模型预测80、100、120批次的RUL,通过计算预测值与实际值之间的误差评价算法的性能,结果如表5所示.

表5 轧辊可工作转动量预测平均误差统计

Tab.5 Average error of roller working rotation prediction

时间序列	RUL预测值	RUL实际值	误差/%
No.80	53790.5	56537.7	4.9
No.100	52630.2	52021.6	1.2
No.120	40764.1	37671.3	8.2

新窗口打开| 下载CSV

基于KWP退化模型的RUL预测值比较接近真实值,平均误差为4.7%,且随着时间推移误差不存在明显的扩散现象,所构建Wiener过程与核函数相结合可以有效地预测轧辊的RUL.

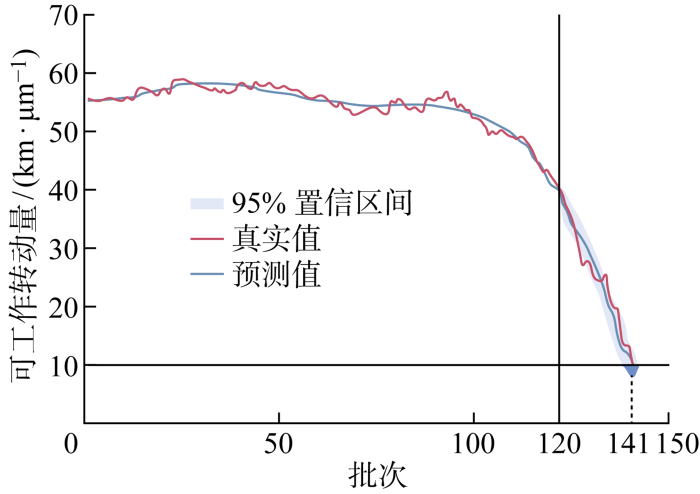
以120批次时预测的RUL为例,由式(25)推导RUL的概率分布如图5蓝色区间所示.预计下线批次为141批次,包含了可能失效的概率分布范围,推导得RUL在5%、50%和95%置信区间的取值分别为16、21和26,可为制定轧辊维修和备件计划提供更具体的决策依据.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 基于120批次的RUL概率分布函数

Fig.5 Estimated RUL at 120 batches

基于轧辊可工作转动量健康指标,通过轧辊退化建模与寿命预测研究,可以有效区分轧辊磨损的平稳退化阶段和快速磨损阶段,表征退化过程慢变与快变过程,体现轧辊RUL的不同变化规律.结合某钢铁公司1580热轧线工程数据,基于KWP退化模型,捕捉到轧辊退化路径的非线性和随机性特征,刻画了轧辊退化的动态规律与不确定性范围,进一步预测轧辊服役过程的RUL值.所构建方法通过数据驱动轧辊退化的特征参数,以机理模型刻画轧辊寿命的变化规律,融合两者表征精轧机组健康状态的退化过程和服役寿命特征.

5 结语

针对轧辊退化路径中存在的随机性和非线性问题,提出了KWP退化模型.一方面,Wiener过程充分刻画了轧辊工作中因工况复杂、随机干扰强而造成的退化趋势上的强随机性;另一方面,引入核函数将非线性数据映射到高维空间作时间变换,以解决复杂非线性问题并使模型稀疏化,两者结合使算法能够在更广泛的数据集上取得良好效果.

本文基于某钢铁公司1580热轧生产线轧辊退化数据,相较非线性Wiener过程和相关向量机算法,所提方法在拟合优度上分别提高109%和14%,RUL预测误差仅有4.7%,具有较优秀的建模能力与预测效果.该结果充分表明所提模型具有较好适用性,可对轧辊运行状况进行分析、预测与决策,有助于轧钢生产线从当前的定期维护过渡到基于条件的维护,亦可为其他类似领域的RUL预测和实时状态监测问题提供参考.由于轧钢生产线的产品种类具有多样性,KWP退化模型并未考虑轧钢排产、轧辊材质等具体信息,后续将融合轧辊生产批次信息构建基于多核函数的Wiener过程退化模型,开展预测性维护的相关研究.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

郑国栋, 陈其慎, 邢佳韵, 等.

典型国家钢铁产业发展路径与启示

[J]. 中国国土资源经济, 2021, 34(8): 51-56.