内角钝度对微重力下液体推进剂毛细流动特性的影响

doi:10.16183/j.cnki.jsjtu.2021.504

内角钝度对微重力下液体推进剂毛细流动特性的影响

杨恩博¹, 金宇鹏¹, 杨光^,¹, 黄永华¹, 王天祥², 雷刚², 吴静怡¹

1.上海交通大学机械与动力工程学院,上海 200240

2.航天低温推进剂技术国家重点实验室,北京 100028

Effect of Corner Roundedness on Capillary Flow of Liquid Propellants in Microgravity

YANG Enbo¹, JIN Yupeng¹, YANG Guang^,¹, HUANG Yonghua¹, WANG Tianxiang², LEI Gang², WU Jingyi¹

1. School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. State Key Laboratory of Technologies in Space Cryogenic Propellants, Beijing 100028, China

通讯作者: 杨光,副教授,博士生导师,电话(Tel. ):021-34206814; E-mail:y_g@sjtu.edu.cn.

责任编辑: 王历历

收稿日期: 2021-12-10 修回日期: 2022-01-19 接受日期: 2022-02-7

基金资助:

国家自然科学基金重点项目(51936006)
航天低温推进剂技术国家重点实验室开放课题资助项目(SKLTSCP202005)

Received: 2021-12-10 Revised: 2022-01-19 Accepted: 2022-02-7

作者简介 About authors

杨恩博(2001-),本科生,现从事微重力流体力学研究.

摘要

表面张力驱动下的内角流动理论为空间液体管理装置的设计提供重要支撑,其动态流动过程中的液体流量、流速、液面位置等参数是决定液体管理性能的关键因素.在实际应用中,受到加工条件的限制或为了提高机械承载能力,内角尖端通常存在一定的钝度.采用理论分析与实验验证相结合的方法,定量分析了钝度对内角流动特性的影响规律.结果表明,在钝度一定的条件下,液面运动距离与时间的1/2次方始终保持近似正比关系,且钝度越大毛细流动的速度越低.通过基于磁补偿原理的微重力模拟流动实验,初步验证理论模型的正确性.并将理论模型应用于以液氢和液氧为代表的低温推进剂的表面张力输运过程,发现不同条件下的流量变化规律,为低温推进剂表面张力式液体管理装置的设计提供重要基础数据.

关键词： 表面张力; 内角; 毛细驱动流; 钝度; 磁补偿; 低温推进剂

Abstract

The theory of interior corner flow driven by surface tension provides an important support for design of liquid management devices in space. The flow rate, velocity, and liquid position are important factors to determine liquid management efficiency. In practice, due to machining precision or aiming to enhance the mechanical strength, the interior corner is often imperfect with a certain degree of roundedness. In this paper, the influence of corner roundedness on liquid flow characteristics is quantitatively analyzed by combining theoretical and experimental analysis. The results show that with a fixed corner roundedness, the height of liquid is always proportional to the square root of time. The velocity of capillary flow also decreases with the increase of corner roundedness. The present theoretical model is validated by the microgravity experiments based on magnetic compensation. Furthermore, the model is applied to simulate the capillary flow of liquid hydrogen and liquid oxygen. The variations of flow rate under different conditions are obtained, which provides important basic data for the design of liquid management devices for cryogenic propellant.

Keywords： surface tension; interior corners; capillary driven flow; roundedness; magnetic compensation; cryogenic propellant

PDF (3571KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨恩博, 金宇鹏, 杨光, 黄永华, 王天祥, 雷刚, 吴静怡. 内角钝度对微重力下液体推进剂毛细流动特性的影响[J]. 上海交通大学学报, 2023, 57(6): 739-746 doi:10.16183/j.cnki.jsjtu.2021.504

YANG Enbo, JIN Yupeng, YANG Guang, HUANG Yonghua, WANG Tianxiang, LEI Gang, WU Jingyi. Effect of Corner Roundedness on Capillary Flow of Liquid Propellants in Microgravity[J]. Journal of Shanghai Jiaotong University, 2023, 57(6): 739-746 doi:10.16183/j.cnki.jsjtu.2021.504

随着载人航天技术的发展以及空间探索的日趋长期化,空间推进剂的在轨管理成为一个重要课题,从而带动微重力流体科学的进一步发展.在微重力环境下,重力的影响可以忽略,此时表/界面张力成为主导流体行为的最主要因素.板式表面张力贮箱正是根据表面张力驱动下的内角自流现象而设计的推进剂空间管理装置.

作为微重力流体力学下的一个重要模型,内角流动是研究在表面张力主导下,液体沿固体二面角爬升的理论.有关内角流动的研究可以追溯到20世纪60年代,Concus等^[1]提出微重力条件下内角流动液体前缘稳定性的临界条件,即Concus-Finn条件; Weislogel 等^[2]对内角流动的Navier-Stokes方程进行简化,将三维问题简化为一维问题,利用滑移假设进行求解,提出流阻的理论近似解,并推广到复杂几何形状的计算^[3-4]; Wang等^[5]研究了微重力条件下不同初始液体体积对内角毛细流动的影响; 李京浩等^[6]针对不对称内角情形,给出扇形内角情形下的计算公式; 沈逸等^[7]利用磁补偿原理在地面实现微重力环境,并分析了重力水平、内角材质等因素对液面位置的影响.

尽管有关内角流动的理论与实验分析已经比较成熟,但现有理论模型大多仅适用于理想情况下的完全尖锐内角.而实际加工制造得到的内角通常不可避免地存在一定钝度; 此外,内角尖端采用圆角过渡也能够增强装置的机械承载能力.理想内角的流动模型无法直接推广到含钝度的毛细流动.有关内角钝度对液体内角流动的影响,Ransohoff等^[8-9]对内角流动过程的流阻进行了数值计算,并研究了有关内角圆率对内角自流现象影响的一系列问题; Chen等^[10]对内角存在一定钝度的情况进行分析,并研究了极限情况下薄层流动的问题; Zhou等^[11]得出薄层流动的计算方法,并将其推广到一般情形; 魏月兴等^[12]利用Ransohoff提出的方法对存在钝度的情形进行了理论分析.然而,由于微重力环境实验复杂且成本高,钝度对内角毛细流动的影响机理仍未完全解析并缺少实验验证.

建立含钝度的微重力内角毛细驱动流动模型,并首次开展基于磁补偿的微重力模拟实验以验证理论模型的准确性,定量获得钝度对毛细流动特性的影响特性.同时,将理论模型推广到以液氢和液氧为代表的低温推进剂的空间应用,为面向未来深空探测任务的推进剂管理装置的设计提供重要基础数据.

1 钝度内角中的毛细力驱动流动模型

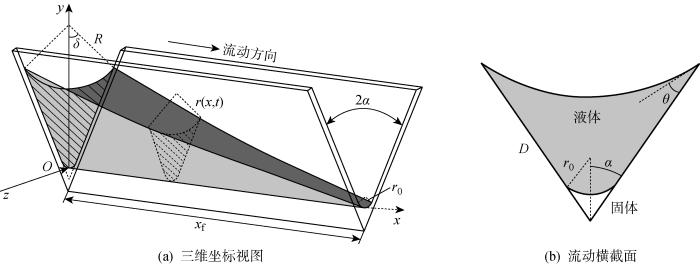
内角指两个固体壁面形成的二面角结构.初始状态下,流体集中在内角的一端,而内角自流则是流体在表面张力作用下由内角的一端流向另外一端的物理现象.尖端存在钝度的内角自流模型如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 钝度内角中的毛细力驱动流动示意图

Fig.1 Schematics of capillary flowing in rounded corners

内角毛细流动模型中,假定流体的流动方向为x轴方向,内角开口为2α,流体与壁面的接触角为θ,固体夹角处形成的圆弧曲率半径为r₀,流体的毛细流动距离为x_f,液体润湿内角的边长为D.液面在x处沿y-z平面的曲率半径记为r(x, t),其中x=0处的曲率半径记为R,t为时间,弯曲液面的圆心角为2δ,且在该截面上有δ=π/2-θ-α.实验表明,在内角流体爬升过程中,R始终为定值^[2],从而定义 τ=r₀/R,表征决定钝度大小的相对曲率半径.微重力条件下,针对图1所示的流动过程,液体主要受到表面张力、外界压力以及流动阻力的共同作用.在气液交界面处,由Young-Laplace方程可得气液交界面的压强差为

(1)p_c=σ

(\frac{1}{r_{1}} + \frac{1}{r_{2}})

式中:σ为液体的表面张力系数;r₁和r₂分别为y-z平面和x-y平面的曲率半径.在流动假设中,认为流动的长度远远大于截面尺度,此时r₂趋于无穷大,因此只考虑r₁对流动的影响.

当液体从一端进入内角时,在表面张力作用下沿x方向的曲率半径逐渐减小,从而在液体内部形成压强梯度.在流动的任意位置x,气液交界面的压强差^[12]可以表示为

(2)p_c=σ

\frac{1}{r (x, t)}

根据Weislogel等^[2]对内角流动模型的简化,连续性方程有如下微分形式:

(3)

\frac{\partial (ρ S)}{\partial t}

+Δ(ρvS)=0

式中:ρ为液体密度; v为流动速度;液体在某x处截面的截面积设为S.

假设液体的密度为常数,可得

(4)

\frac{\partial q}{\partial x}

\frac{\partial S}{\partial t}

式中:q为液体的体积流量.

在图1中任意位置x处取y-z平面的横截面,可以得到该处曲率半径r(x, t)和S的关系为

(5)S=

(\frac{s i n δ c o s θ}{s i n α} - δ)

r²-

(c o t α + α - \frac{π}{2}) r_{0}^{2}

采用平均流速 $\bar{u}$ 代替流速v,并引入无量纲化流阻β_v,可得^[9]:

(6)

\bar{u}

\frac{r^{2}}{μ β_{v}} \frac{\partial p_{c}}{\partial x}

式中:μ为流体的动力黏度.

体积流量可以写成如下的微分形式:

(7)q(x, t)=-S

\frac{r^{2}}{μ β_{v}} \frac{\partial p_{c}}{\partial x}

将式 (7) 代入式(4)可得在二维流动假设条件下关于S的控制方程:

(8)

\frac{\partial S}{\partial t}

\frac{σ}{μ β_{v}} \frac{\partial}{\partial x} (S \frac{\partial r}{\partial x})

求解式(8)可得^[13]:

(9)S=S₀

{[1 - \frac{a x}{x_{0} \sqrt{1 + 2 ε t}} + \frac{(a - 1) x^{2}}{x_{0}^{2} (1 + 2 ε t)}]}^{2}

式中:S₀为初始状态的截面积,S₀=CR²,其中C= $\frac{s i n δ c o s θ}{s i n α}$ -δ- $(c o t α + α - \frac{π}{2})$ τ²;ε为时间常数,ε=K $\frac{σ}{μ β_{v}} \frac{R}{x_{0}^{2}}$ ,a和K为求解过程中出现的参数^[4,12].x₀取决于初始状态^[12].通常时间项2εt ≫1,由此得到毛细驱动下液体前缘流动距离的表达式^[4,14]为

(10)x_f=

\sqrt{2 K \frac{σ}{μ β_{v}} R t}

并由此得到流量的表达式:

(11)q=aC

\sqrt{\frac{1}{2 K} \frac{σ}{μ β_{v}} \frac{R^{5}}{t}}

其中,根据薄层流动理论可得β_v的取值^[11,15]如下:

β_v=

\frac{12 s i n^{2} α {(1 - B)}^{2}}{{(1 - s i n α)}^{2} B^{2}}

(12) $\begin{aligned} \beta_{\mathrm{v}}= & \frac{12 \sin ^2 \alpha(1-B)^2}{(1-\sin \alpha)^2 B^2} \times \\ & \frac{\left(\varphi_1-B \varphi_2\right)\left[\varphi_3+B \varphi_2-(1-B) \tau\right]}{\left[\varphi_1-B \varphi_2-(1-B) \tau^2\right]^3} \\ B= & \left(\frac{\pi}{2}-\alpha\right) \tan \alpha \\ \varphi_1= & \cos ^2(\alpha+\theta)+\sin (\alpha+\theta) \cos (\alpha+\theta) \tan \alpha \\ \varphi_2= & 1-\theta /\left(\frac{\pi}{2}-\alpha\right), \quad \varphi_3=\frac{\cos (\alpha+\theta)}{\cos \alpha}\end{aligned}$

将式(12)代入式(10),即可得到钝度内角中爬升距离以及流量的动态表达式:

(13)x_f=

\sqrt{\frac{K σ}{μ} \frac{B^{2} {(1 - s i n α)}^{2} [φ_{1} - B φ_{2} - (1 - B) τ^{2}]^{3}}{6 s i n^{2} α {(1 - B)}^{2} (φ_{1} - B φ_{2}) [φ_{3} + B φ_{2} - {(1 - B) τ]}^{2}} R t}

(14)q=aC

\sqrt{\frac{σ B^{2} R^{5} {(1 - s i n α)}^{2} [φ_{1} - B φ_{2} - (1 - B) τ^{2}]^{3}}{24 K μ s i n^{2} α {(1 - B)}^{2} (φ_{1} - B φ_{2}) [φ_{3} + B φ_{2} - {(1 - B) τ]}^{2}} \frac{1}{t}}

当钝度τ=0时,可得到理想尖锐内角下毛细驱动距离以及流量的动态表达式:

(15)x_f=

\sqrt{\frac{K σ}{μ} \frac{B^{2} {(1 - s i n α)}^{2} (φ_{1} - B φ_{2})^{2}}{6 s i n^{2} α {(1 - B)}^{2} (φ_{3} + B φ_{2})^{2}} R t}

(16)q=aC

\sqrt{\frac{σ B^{2} R^{5} {(1 - s i n α)}^{2} (φ_{1} - B φ_{2})^{2}}{24 K μ s i n^{2} α {(1 - B)}^{2} (φ_{3} + B φ_{2})^{2}} \frac{1}{t}}

2 基于磁补偿原理的微重力地面模拟实验

在前期已建立的磁流体微重力模拟实验台^[7]中开展实验,其原理是利用磁流体作为实验工质,利用梯度磁场产生的磁场力抵消重力从而获得等效微重力环境.实验中利用亥姆霍兹-麦克斯韦线圈作为梯度磁场发生装置,可实现优于±2.5%的磁场梯度纵向非均匀度,具有成本低、重复性好、重力水平可控等显著优点.

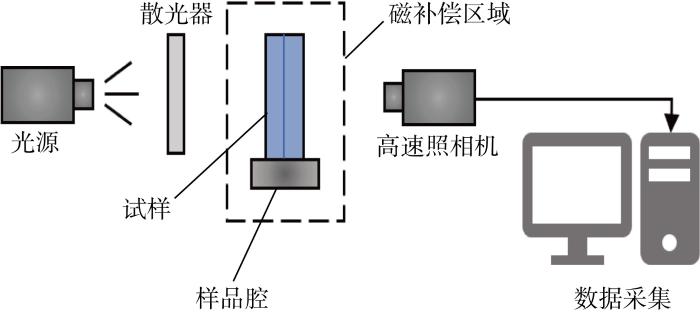
图2为实验装置示意图.利用高精度三轴定位装置对样品位置进行调节定位,从而将样品腔置于线圈的中心位置,并保证整个样品处于磁流体的重力被磁场力完全补偿的区域内.利用高速照相机捕捉磁流体在内角整个流动过程中液面位置的动态变化,并利用光源进行辅助照明.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 基于磁补偿原理的微重力地面模拟实验系统

Fig.2 Microgravity simulation experimental system with magnetic fluid

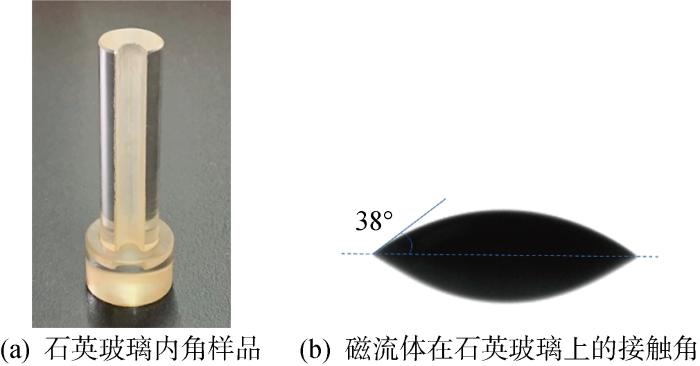
内角样品材料为光学透明的石英玻璃,肋板直径d = 10.0 mm,D=7.80 mm,2α=45°, 并设置不同的内角钝度值.实验所采用磁流体的物理性质如下: σ=36.2×10^-3 N/m,μ= 29.0×10^-3 Pa·s,ρ=1 163.33 kg/m³,其在石英玻璃上的接触角测量值为38° (见图3).

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 实验样品及表面接触角

Fig.3 Experimental sample and contact angle

初始状态下,内角样品在磁流体中的浸没高度为3 mm.待液面稳定后,开启线圈的电流开关.利用高速照相机记录磁流体的液面高度变化,待磁流体达到最大爬升距离且液面稳定后关闭线圈电流开关,完成一次实验记录.所得图像的位置分辨率为0.2 mm/像素,照相机的采样帧率为870帧/s.因此,实验数据中的液面位置测量误差为 ±0.2 mm,时间误差为1.1 ms.实验过程中,内角样品中液面的升高会导致样品腔中液位下降,根据体积守恒可计算得其对毛细爬升距离测量结果的影响小于4%.每个工况的实验至少独立测试3次,以保证数据结果的可重复性.

3 结果与讨论

3.1 内角流动实验及其与计算结果的对比

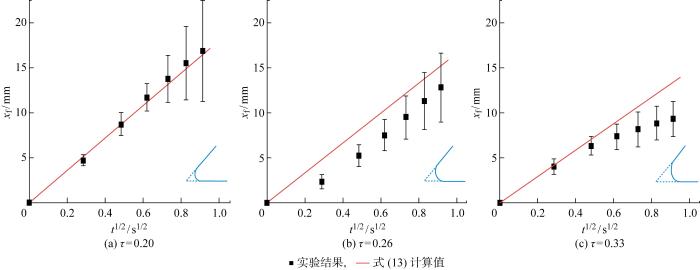
图4为在内角钝度τ=0.26恒定的条件下,磁流体在表面张力驱动下沿内角爬升的位置动态变化情况.其中t=0时刻为在磁场开启之前,液体在地面常重力时的状态.当开启磁场后,液面位置随时间逐渐升高.通过改变样品内角钝度的大小, 即可通过实验定量获得钝度对动态内角毛细流动特性的影响.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同时刻下磁流体的内角爬升图像(τ=0.26)

Fig.4 Movement of magnetic fluid along interior corner at different moments (τ=0.26)

为进一步验证基于磁补偿原理的微重力模拟实验的准确性,首先开展存在微小钝度τ = 0.13时的内角流动实验,并与理想内角流动模型式(15)和钝度内角流动模型式(13)进行对比.由图5可见,实验过程中磁流体的毛细驱动距离x_f与时间的1/2次方(t^1/2)近似呈正比例关系,该结论与文献[3,12,16]中结果一致.此外, 图5中实验结果、式(13)和式(15) 之间的平均相对误差在15%以内,误差线为3次独立重复实验的标准差,下同.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 τ = 0.13时磁流体的毛细爬升曲线

Fig.5 Movement of magnetic fluid at τ =0.13

图6为在不同钝度条件下液体爬升距离动态变化的实验与计算结果.由图可见,当钝度一定时,x_f与t^1/2始终近似符合线性关系,且钝度值越小线性度越高.在本文所研究的钝度范围内,液体在内角中的爬升速度随着钝度值的增大而减小,该规律与Zhou等^[11]的分析结果一致.对比实验结果与计算模型可知,两者的偏差随着钝度的增加而增大,其原因可能在于实验加工的圆角仍不可避免地存在粗糙度的影响,因此会导致流速降低.然而,多种不同钝度下实验与计算的平均相对偏差仍在20%以内.因此考虑到实验误差,可以认为式(13)能够定量反映在不同钝度条件下液体毛细爬升距离的动态变化特性.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同钝度下的内角爬升曲线

Fig.6 Fluid motion for different roundedness of interior corners

3.2 钝度对内角毛细流动流量的影响

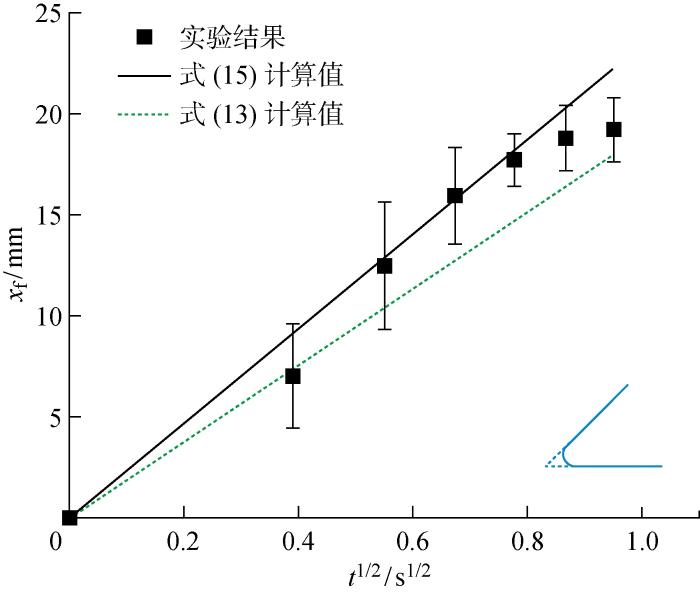
从前面的分析得出,在理想内角以及含钝度内角的毛细流动中,x_f与t^1/2始终保持线性关系.为了定量描述液体的毛细流动速度,定义毛细爬升系数为

(17)k=x_f/t¹^/²

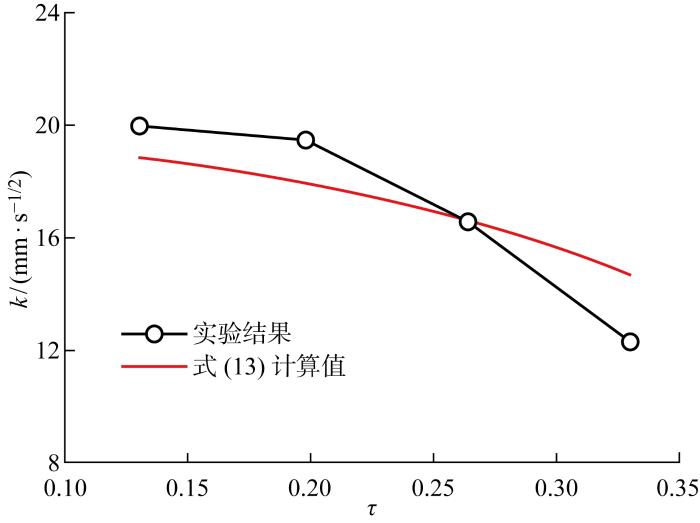
图7为在不同钝度条件下毛细爬升系数的实验值与计算值.从图中可以看出,实验与计算结果均表明毛细爬升速度随钝度的增加而单调减小.当内角钝度从0.13增加到0.33时,实验测得的毛细爬升系数从22.68 mm/s^1/2降低至12.69 mm/s^1/2,下降约44%,而该条件下通过计算模型获得的毛细爬升系数从18.85 mm/s^1/2降低至14.68 mm/s^1/2.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 不同钝度条件下的毛细爬升系数

Fig.7 Values of k of different corner roundednesses

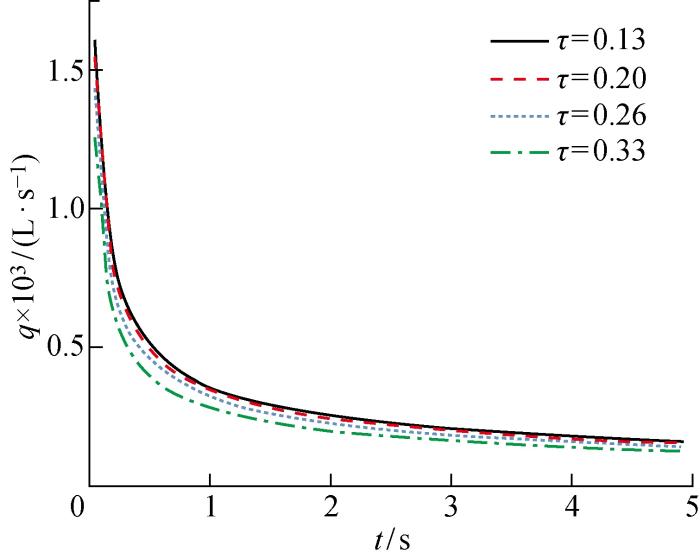
图8为在不同钝度条件下内角毛细流动流量的动态变化计算结果.在钝度一定时,液体的流量在初始阶段随时间推移迅速减小,后又逐渐趋于稳定.其原因在于随着液体前端位置不断向前发展,液体流动的截面积逐渐减小,且爬升速度在初始阶段迅速下降,两方面因素共同加剧了流量随时间的下降.此外,在同一时刻,钝度越大,液体流量越小.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同钝度条件下内角毛细流动流量的动态变化

Fig.8 Variation of capillary flow rate at different corner roundednesses

3.3 低温推进剂的内角流动特性

相较于常规推进剂,以液氢/液氧为代表的低温推进剂具有高比冲、无毒、无污染等诸多优势,是目前以及未来很长一段时间内空间工程的首选推进剂^[17].然而,低温推进剂沸点低、汽化潜热低等特殊物性,为其长期空间贮存和在轨管理技术带来巨大挑战^[18].因此,对于低温推进剂,采用表面张力式流体液体管理装置是解决其空间应用难题的关键突破点.基于前文的毛细流动模型,对液氢、液氧两种流体的内角流动情况进行计算分析.液氢和液氧的物理性质参数如表1所示.为了与空间贮箱中的应用一致,采用低温流体在不锈钢表面上的接触角(近似为0°)^{[19⇓⇓-22]}.

表1 液氢与液氧的物性参数(0.1 MPa)

Tab.1 Physical properties of liquid hydrogen and liquid oxygen (0.1 MPa)

流体	温度/K	ρ/(kg·m^-3)	μ/(μPa·s)	σ/(mN·m)
液氢	20	70.85	13.92	2.001
液氧	90	1 141	195.64	13.198

新窗口打开| 下载CSV

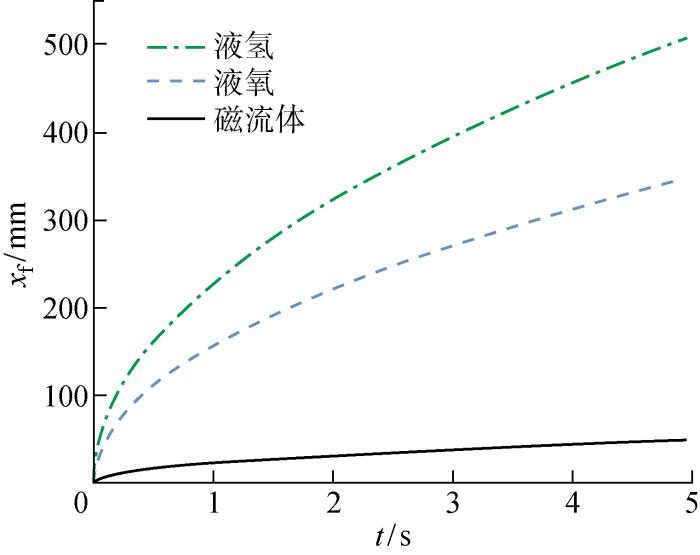
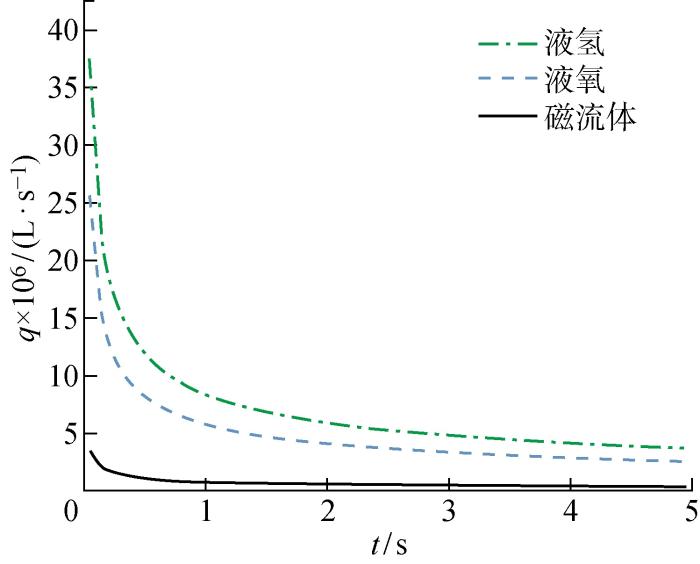
图9为在 τ = 0.1,R=6×10^-3 m,α=15° 的内角条件下,液氢、液氧以及磁流体的毛细爬升距离随时间的变化曲线.由图可见,液氢与液氧的流动速度均显著高于前文实验中的磁流体,且液氢的运动速度高于液氧.其原因在于尽管低温推进剂的表面张力较小,但由于其黏滞系数同样较小,导致式(13)中因子σ/μ反而增大; 且上述两种流体对不锈钢有很好的润湿效果,最终导致爬升能力的提高.此外,对于上述两种低温推进剂,液氢的表面张力以及黏度均小于液氧,但由于黏度对流动的作用更显著,所以液氢的运动速度始终高于液氧.图10为在与图9相同的工作条件下, 3种不同流体流量动态变化规律的计算结果. 在同一时刻, 液氢的内角流动流量高于液氧约40% 以上, 而两者流量均高出磁流体流量一个数量级.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同流体的动态毛细爬升特性对比

Fig.9 Movement of different fluids along the corner at microgravity

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同流体的动态流量大小对比

Fig.10 Comparison of flow rate of different fluids

图11(a)和11(b)分别为钝度对液氢和液氧内角毛细流动流量的影响.随着钝度的增大,两种推进剂的流量均减小.当钝度τ从0.1增大到0.5时,液氢和液氧流量均分别下降约 17.3%,由此可见减小内角钝度对提高推进剂流量的重要性.

图11

新窗口打开| 下载原图ZIP| 生成PPT

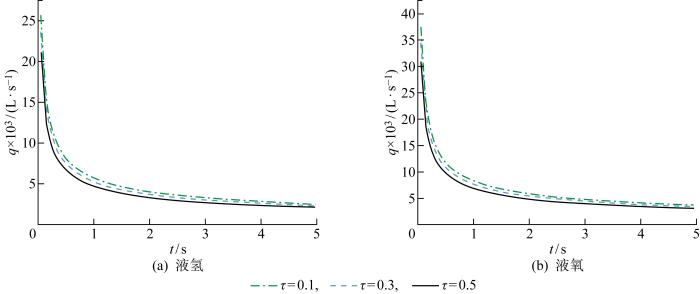
图11 液氢和液氧流量随钝度的变化曲线

Fig.11 Flow rates of liquid hydrogen and liquid oxygen versus roundedness of interior corners

4 结论

针对含钝度条件下内角毛细流动建立数学模型,通过引入流阻的概念,得出内角毛细流动液面前端位置和液体流量的计算表达式.搭建磁补偿微重力模拟装置,在地面上开展了基于磁流体的微重力流动实验,并将实验结果与数学模型进行比较.并在此基础上,针对低温推进剂的内角流动特性进行分析,主要结论如下:

(1) 获得微重力条件下流体沿内角爬升距离与流量的计算模型,通过与微重力模拟实验数据对比,验证了该计算模型的可行性,且平均相对误差在20%以内.理论与实验数据均表明,在内角毛细流动中,x_f与t^1/2始终近似保持线性关系.

(2) 在内角钝度τ∈[0.13,0.33]范围内,流体沿内角爬升的速度、流量均随着内角钝度的增大而单调减小.实验结果表明,当内角钝度从0.13增加到0.33时,磁流体的毛细爬升系数(h/t^1/2)下降约44%.在相同条件下,流量随着液面高度的增加而减小.

(3) 液氢、液氧等低温推进剂由于黏度小,其在内角毛细流动流量上高于磁流体一个数量级以上.尽管液氢的表面张力小,但其低黏度的特性在微重力流动中起主导性作用,导致其内角流动速度高于液氧和磁流体.

由于微重力流动机理的复杂性,所以计算模型的精度仍需要通过空间搭载等实验途径进一步验证.此外,低温推进剂具有低沸点等特殊物理性质,其在流动过程中的热学耦合特性还需进一步探索.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

CONCUS

, FINN

On the behavior of a capillary surface in a wedge

[J]. PNAS, 1969, 63(2): 292-299.

PMID:16591761 [本文引用: 1]

Estimates above and below are obtained for the height of the equilibrium-free surface of a liquid when the liquid partially fills a cylindrical container whose cross section contains a corner with interior angle 2alpha. The surface is characterized by the condition that its mean curvature be proportional to its height above a reference plane (or, in the case of zero gravity, that the mean curvature be constant), and by the requirement that it meet the container wall with prescribed contact angle gamma. It turns out that the qualitative behavior of such a surface near the vertex changes markedly, according as alpha + gamma < (1/2)pi, or alpha + gamma >/= (1/2)pi. In the former case, the surface is either unbounded or fails to exist, while in the latter case every such surface is bounded. Some experimental comparisons are indicated, and an application to the problem of describing the mechanism of water rise in trees is discussed.The above results describe a limiting case among corresponding properties that hold for surfaces defined over domains with smooth boundaries. This extension is indicated, as well as a formal extension to n-dimensional surfaces; here the interest centers on the fact that it is the mean curvature of an (n-1)-dimensional boundary element that controls the local behavior of the n-dimensional solution surface.

[2]

WEISLOGEL

M M

, LICHTER

Capillary flow in an interior corner

[J]. Journal of Fluid Mechanics, 1998, 373: 349-378.

DOI:10.1017/S0022112098002535 URL [本文引用: 3]

The design of fluids management processes in the low-gravity environment\n of space \nrequires an accurate description of capillarity-controlled flow in containers.\n Here we \nconsider the spontaneous redistribution of fluid along an interior corner\n of a container \ndue to capillary forces. The analytical portion of the work presents an\n asymptotic \nformulation in the limit of a slender fluid column, slight surface curvature\n along the flow \ndirection z, small inertia, and low gravity. The scaling introduced\n explicitly accounts \nfor much of the variation of flow resistance due to geometry and so the\n effects of \ncorner geometry can be distinguished from those of surface curvature. For\n the special \ncases of a constant height boundary condition and a constant flow condition,\n the \nsimilarity solutions yield that the length of the fluid column increases\n as \nt1/2 and t3/5, \nrespectively. In the experimental portion of the work, measurements from\n a 2.2 s drop \ntower are reported. An extensive data set, collected over a previously\n unexplored range \nof flow parameters, includes estimates of repeatability and accuracy, the\n role of inertia \nand column slenderness, and the effects of corner angle, container geometry,\n and fluid \nproperties. At short times, the fluid is governed by inertia \n(t[lsim ]tLc).\n Afterwards, an \nintermediate regime \n(tLc[lsim ]t[lsim ]\ntH) can be shown to be modelled by a constant-flow-like\n similarity \nsolution. For t[ges ]tH it is found\n \nthat there exists a location zH at which \nthe interface height remains constant at a value \nh(zH, t)=H which\n can be shown \nto be well predicted. Comprehensive comparison is made between the analysis\n and \nmeasurements using the constant height boundary condition. As time increases,\n it is \nfound that the constant height similarity solution describes the flow over\n a lengthening \ninterval which extends from the origin to the invariant tip solution. For\n \nt[Gt ]tH, the \nconstant height solution describes the entire flow domain. A formulation\n applicable \nthroughout the container (not just in corners) is presented in the limit\n of long times.

[3]

WEISLOGEL

M M

, COLLICOTT

Analysis of tank PMD rewetting following thrust resettling

[C]//40th AIAA Aerospace Sciences Meeting & Exhibit. Reno, NV, USA: AIAA, 2002: AIAA 2002-0757.

[本文引用: 2]

[4]

ENRIQUE

, WEISLOGEL

M M

Gravity effects on capillary flows in sharp corners

[J]. Physics of Fluids, 2009, 21(4): 1-12.

[本文引用: 3]

[5]

WANG

C X

, XU

S H

, SUN

Z W

et al.

A study of the influence of initial liquid volume on the capillary flow in an interior corner under microgravity

[J]. International Journal of Heat and Mass Transfer, 2010, 53(9/10): 1801-1807.

DOI:10.1016/j.ijheatmasstransfer.2010.01.009 URL [本文引用: 1]

[6]

李京浩, 陈小前, 黄奕勇,

等.

微重力环境下的不对称内角流动研究

[J]. 中国科学: 技术科学, 2012, 42(8): 957-962.

[本文引用: 1]

Jinghao

, CHEN

Xiaoqian

, HUANG

Yiyong

et al.

Study on asymmetric interior corner flow in microgravity condition

[J]. Scientia Sinica (Technologica), 2012, 42(8): 957-962.

[本文引用: 1]

[7]

沈逸, 张泽宇, 梁益涛,

等.

磁补偿微重力环境实现及磁流体微重力内角流动研究

[J]. 化工学报, 2020, 71(8): 3490-3499.

DOI:10.11949/0438-1157.20200291 [本文引用: 2]

由于表面张力的作用，流体在微重力环境中沿一定夹角的内角壁面爬升过程与常重力状态不同。为了对微重力内角流动的物理过程进行研究，利用磁补偿方法搭建了常温磁流体微重力补偿实验台，实现了目标区域内纵向小于5%非均匀度的磁补偿微重力环境。并对不同重力条件下水基磁流体沿若干材料内角爬升过程进行了可视化实验研究，探究了微重力环境下流体与材料间的接触角以及内角角度对液体导流性能的影响以及毛细流动规律。结果表明，在满足Concus-Finn条件时，液面爬升高度和重力加速度近似呈反比关系。接触角和内角角度越小，流体输运能力越强，且重力水平越低，越为明显。当不满足Concus-Finn条件时，液面爬升高度和重力加速度近似呈线性关系，接触角和内角角度对流体输运能力的影响并不明显。

SHEN

, ZHANG

Zeyu

, LIANG

Yitao

et al.

Realization of microgravity environment by magnetic compensation and study on interior corner flow of magnetic fluid in microgravity

[J]. CIESC Journal, 2020, 71(8): 3490-3499.

DOI:10.11949/0438-1157.20200291 [本文引用: 2]

Due to the effect of surface tension, the process of fluid climbing along the inner wall at a certain angle in the microgravity environment is different from that of normal gravity. To study the physical process of capillary flow in microgravity, this paper uses the magnetic compensation method to set up a normal temperature magnetic fluid microgravity compensation experimental platform, which achieves magnetic compensation of less than 5% non-uniformity longitudinally in the target area. Visualized experimental research on the climb process of water-based magnetic fluid along the interior corner of different materials under the condition of different gravity is performed to verify the influence of contact angle and interior corner angle on the fluid transport capacity in the microgravity environment and to reveal the capillary flow law of the magnetic fluid in the microgravity environment. The results show that when the Concus-Finn condition is satisfied, the liquid surface climbing height and the gravity acceleration are approximately inversely proportional. The smaller the contact angle and interior corner angle, the stronger the fluid transport capacity of the material, especially in a good microgravity environment. When the Concus-Finn condition is not satisfied, the liquid surface climbing height and the acceleration of gravity have a linear relationship, and the impact of changes in contact angle and interior corner angle on the fluid transport capacity is not obvious.

[8]

RANSOHOFF

T C

, GAUGLITZ

P A

, RADKE

C J

Snap-off of gas bubbles in smoothly constricted noncircular capillaries

[J]. AIChE Journal, 1987, 33(5): 753-765.

DOI:10.1002/(ISSN)1547-5905 URL [本文引用: 1]

[9]

RANSOHOFF

T C

, RADKE

C J

Laminar flow of a wetting liquid along the cormers of a predominantly gas-occupied noncircular pore

[J]. Journal of Colloid and Interface Science. 1988, 121(2): 392-401.

DOI:10.1016/0021-9797(88)90442-0 URL [本文引用: 2]

[10]

CHEN

Y K

, WEISLOGEL

M M

, NARDIN

C L

Capillary-driven flows along rounded interior corners

[J]. Journal of Fluid Mechanics, 2006, 566: 235-271.

DOI:10.1017/S0022112006001996 URL [本文引用: 1]

[11]

ZHOU

D G

, BLUNT

, ORR

F M

Hydrocarbon drainage along corners of noncircular capillaries

[J]. Journal of Colloid and Interface Science, 1997, 187(1): 11-21.

PMID:9245311 [本文引用: 3]

An approximate solution for liquid flow along corners of noncircular capillaries is proposed that relates the flow resistance to the geometry of a capillary and to the contact angle of the interfaces. The theory predicts liquid flow rates for both two-phase (hydrocarbon/air) and three-phase (hydrocarbon/air/water) drainage. This solution is found to be superior to other expressions in the literature. Drainage rates of two different hydrocarbons along corners of square capillaries are measured with both air and water as stationary phases. The new solution was used to predict the measured hydrocarbon drainage rates successfully. Comparison of the measured and predicted drainage rates indicates that a free boundary is appropriate for the air/hydrocarbon interface and a no-flow boundary condition is valid for the water/hydrocarbon interface. The effect of spreading coefficient on drainage rates is also demonstrated by the measurements and is compared with the proposed solution. A brief discussion of three-phase relative permeabilities is offered based on the measured drainage rates and proposed solution.

[12]

魏月兴, 陈小前, 黄奕勇.

内角流动及其在卫星贮箱设计中的应用

[J]. 中国科学: 技术科学, 2011, 41(9): 1218-1224.

[本文引用: 5]

WEI

Yuexing

, CHEN

Xiaoqian

, HUANG

Yiyong

Interior corner flow theory and its application to the satellite propellant management device design

[J]. Scientia Sinica (Technologica), 2011, 41(9): 1218-1224.

[本文引用: 5]

[13]

MAYER

F J

, MCGRATH

J F

, STEELE

J W

A class of similarity solutions for the nonlinear thermal conduction problem

[J]. Journal of Physics A: Mathematical and General, 1983, 16(14): 3393-3400.

DOI:10.1088/0305-4470/16/14/031 URL [本文引用: 1]

[14]

DONG

, CHATZIS

The imbibition and flow of a wetting liquid along the corners of a square capillary tube

[J]. Journal of Colloid and Interface Science, 1995, 172(2): 278-288.

DOI:10.1006/jcis.1995.1253 URL [本文引用: 1]

[15]

WEISLOGEL

, BUNNELL

, KURTA

et al.

Preliminary results from the capillary flow experiment aboard ISS: The moving contact line boundary condition

[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada: AIAA, 2005: AIAA 2005-1439.

[本文引用: 1]

[16]

CHEN

Y K

Review of spontaneous capillary driven flow along interior corners

[J]. Physics of Gases, 2017, 2(1): 21-29.

[本文引用: 1]

[17]

王磊, 厉彦忠, 张少华,

等.

低温推进剂空间管理技术研究进展与展望

[J]. 宇航学报, 2020, 41(7): 978-988.

[本文引用: 1]

WANG

Lei

, LI

Yanzhong

, ZHANG

Shaohua

et al.

Research progress and outlooks of cryogenic propellant space management technologies

[J]. Journal of Astronautics, 2020, 41(7): 978-988.

[本文引用: 1]

[18]

陈忠灿, 李鹏, 孙培杰,

等.

工作于室温温区的热力学排气模拟与增压测试

[J]. 上海交通大学学报, 2017, 51(8): 946-953.

[本文引用: 1]

CHEN

Zhongcan

, LI

Peng

, SUN

Peijie

et al.

Simulation of a thermodynamic vent system working at room temperature and its preliminary pressurization testing

[J]. Journal of Shanghai Jiao Tong University, 2017, 51(8): 946-953.

[本文引用: 1]

[19]

HARTWIG

, MANN

J A

Bubble point pressures of binary methanol/water mixtures in fine-mesh screens

[J]. AIChE Journal, 2014, 60(2): 730-739.

DOI:10.1002/aic.v60.2 URL [本文引用: 1]

[20]

HARTWIG

, DARR

Influential factors for liquid acquisition device screen selection for cryogenic propulsion systems

[J]. Applied Thermal Engineering, 2014, 66(1/2): 548-562.

DOI:10.1016/j.applthermaleng.2014.02.022 URL [本文引用: 1]

[21]

魏月兴.

微重力条件下航天器贮箱推进剂管理过程中的流动特性研究[D]. 长沙: 国防科学技术大学, 2013.

[本文引用: 1]

WEI

Yuexing

Research on the flow in the process of the propellant management in a spacecraft tank under microgravity[D]. Changsha: National University of Defense Technology, 2013.

[本文引用: 1]

[22]

张泽宇, 黄永华, 梁益涛,

等.

磁场力非均匀度对液氧磁补偿微重力自由界面的影响

[J]. 真空与低温, 2019, 25(6): 372-378.

[本文引用: 1]

ZHANG

Zeyu

, HUANG

Yonghua

, LIANG

Yitao

et al.

Impact of magnetic force inhomogeneity on free surface of liquid oxygen under magnetically compensated microgravity

[J]. Vacuum and Cryogenics, 2019, 25(6): 372-378.

[本文引用: 1]

On the behavior of a capillary surface in a wedge

1969

... 作为微重力流体力学下的一个重要模型,内角流动是研究在表面张力主导下,液体沿固体二面角爬升的理论.有关内角流动的研究可以追溯到20世纪60年代,Concus等^[1]提出微重力条件下内角流动液体前缘稳定性的临界条件,即Concus-Finn条件; Weislogel 等^[2]对内角流动的Navier-Stokes方程进行简化,将三维问题简化为一维问题,利用滑移假设进行求解,提出流阻的理论近似解,并推广到复杂几何形状的计算^[3-4]; Wang等^[5]研究了微重力条件下不同初始液体体积对内角毛细流动的影响; 李京浩等^[6]针对不对称内角情形,给出扇形内角情形下的计算公式; 沈逸等^[7]利用磁补偿原理在地面实现微重力环境,并分析了重力水平、内角材质等因素对液面位置的影响. ...

Capillary flow in an interior corner

1998

... 内角毛细流动模型中,假定流体的流动方向为x轴方向,内角开口为2α,流体与壁面的接触角为θ,固体夹角处形成的圆弧曲率半径为r₀,流体的毛细流动距离为x_f,液体润湿内角的边长为D.液面在x处沿y-z平面的曲率半径记为r(x, t),其中x=0处的曲率半径记为R,t为时间,弯曲液面的圆心角为2δ,且在该截面上有δ=π/2-θ-α.实验表明,在内角流体爬升过程中,R始终为定值^[2],从而定义 τ=r₀/R,表征决定钝度大小的相对曲率半径.微重力条件下,针对图1所示的流动过程,液体主要受到表面张力、外界压力以及流动阻力的共同作用.在气液交界面处,由Young-Laplace方程可得气液交界面的压强差为 ...

... 根据Weislogel等^[2]对内角流动模型的简化,连续性方程有如下微分形式: ...

Analysis of tank PMD rewetting following thrust resettling

2002

... 为进一步验证基于磁补偿原理的微重力模拟实验的准确性,首先开展存在微小钝度τ = 0.13时的内角流动实验,并与理想内角流动模型式(15)和钝度内角流动模型式(13)进行对比.由图5可见,实验过程中磁流体的毛细驱动距离x_f与时间的1/2次方(t^1/2)近似呈正比例关系,该结论与文献[3,12,16]中结果一致.此外, 图5中实验结果、式(13)和式(15) 之间的平均相对误差在15%以内,误差线为3次独立重复实验的标准差,下同. ...

Gravity effects on capillary flows in sharp corners

2009

... 式中:S₀为初始状态的截面积,S₀=CR²,其中C=

\frac{s i n δ c o s θ}{s i n α}

-δ-

(c o t α + α - \frac{π}{2})

τ²;ε为时间常数,ε=K

\frac{σ}{μ β_{v}} \frac{R}{x_{0}^{2}}

,a和K为求解过程中出现的参数^[4,12].x₀取决于初始状态^[12].通常时间项2εt ≫1,由此得到毛细驱动下液体前缘流动距离的表达式^[4,14]为 ...

... [4,14]为 ...

A study of the influence of initial liquid volume on the capillary flow in an interior corner under microgravity

2010

微重力环境下的不对称内角流动研究

2012

微重力环境下的不对称内角流动研究

2012

磁补偿微重力环境实现及磁流体微重力内角流动研究

2020

... 在前期已建立的磁流体微重力模拟实验台^[7]中开展实验,其原理是利用磁流体作为实验工质,利用梯度磁场产生的磁场力抵消重力从而获得等效微重力环境.实验中利用亥姆霍兹-麦克斯韦线圈作为梯度磁场发生装置,可实现优于±2.5%的磁场梯度纵向非均匀度,具有成本低、重复性好、重力水平可控等显著优点. ...

磁补偿微重力环境实现及磁流体微重力内角流动研究

2020

Snap-off of gas bubbles in smoothly constricted noncircular capillaries

1987

... 尽管有关内角流动的理论与实验分析已经比较成熟,但现有理论模型大多仅适用于理想情况下的完全尖锐内角.而实际加工制造得到的内角通常不可避免地存在一定钝度; 此外,内角尖端采用圆角过渡也能够增强装置的机械承载能力.理想内角的流动模型无法直接推广到含钝度的毛细流动.有关内角钝度对液体内角流动的影响,Ransohoff等^[8-9]对内角流动过程的流阻进行了数值计算,并研究了有关内角圆率对内角自流现象影响的一系列问题; Chen等^[10]对内角存在一定钝度的情况进行分析,并研究了极限情况下薄层流动的问题; Zhou等^[11]得出薄层流动的计算方法,并将其推广到一般情形; 魏月兴等^[12]利用Ransohoff提出的方法对存在钝度的情形进行了理论分析.然而,由于微重力环境实验复杂且成本高,钝度对内角毛细流动的影响机理仍未完全解析并缺少实验验证. ...

Laminar flow of a wetting liquid along the cormers of a predominantly gas-occupied noncircular pore

1988

... 采用平均流速

\bar{u}

代替流速v,并引入无量纲化流阻β_v,可得^[9]: ...

Capillary-driven flows along rounded interior corners

2006

Hydrocarbon drainage along corners of noncircular capillaries

1997

... 其中,根据薄层流动理论可得β_v的取值^[11,15]如下: ...

... 图6为在不同钝度条件下液体爬升距离动态变化的实验与计算结果.由图可见,当钝度一定时,x_f与t^1/2始终近似符合线性关系,且钝度值越小线性度越高.在本文所研究的钝度范围内,液体在内角中的爬升速度随着钝度值的增大而减小,该规律与Zhou等^[11]的分析结果一致.对比实验结果与计算模型可知,两者的偏差随着钝度的增加而增大,其原因可能在于实验加工的圆角仍不可避免地存在粗糙度的影响,因此会导致流速降低.然而,多种不同钝度下实验与计算的平均相对偏差仍在20%以内.因此考虑到实验误差,可以认为式(13)能够定量反映在不同钝度条件下液体毛细爬升距离的动态变化特性. ...

内角流动及其在卫星贮箱设计中的应用

2011

... 当液体从一端进入内角时,在表面张力作用下沿x方向的曲率半径逐渐减小,从而在液体内部形成压强梯度.在流动的任意位置x,气液交界面的压强差^[12]可以表示为 ...

... 式中:S₀为初始状态的截面积,S₀=CR²,其中C=

\frac{s i n δ c o s θ}{s i n α}

-δ-

(c o t α + α - \frac{π}{2})

τ²;ε为时间常数,ε=K

\frac{σ}{μ β_{v}} \frac{R}{x_{0}^{2}}

,a和K为求解过程中出现的参数^[4,12].x₀取决于初始状态^[12].通常时间项2εt ≫1,由此得到毛细驱动下液体前缘流动距离的表达式^[4,14]为 ...

... [12].通常时间项2εt ≫1,由此得到毛细驱动下液体前缘流动距离的表达式^[4,14]为 ...

内角流动及其在卫星贮箱设计中的应用

2011

... 式中:S₀为初始状态的截面积,S₀=CR²,其中C=

\frac{s i n δ c o s θ}{s i n α}

-δ-

(c o t α + α - \frac{π}{2})

τ²;ε为时间常数,ε=K

\frac{σ}{μ β_{v}} \frac{R}{x_{0}^{2}}

,a和K为求解过程中出现的参数^[4,12].x₀取决于初始状态^[12].通常时间项2εt ≫1,由此得到毛细驱动下液体前缘流动距离的表达式^[4,14]为 ...

... [12].通常时间项2εt ≫1,由此得到毛细驱动下液体前缘流动距离的表达式^[4,14]为 ...

A class of similarity solutions for the nonlinear thermal conduction problem

1983

... 求解式(8)可得^[13]: ...

The imbibition and flow of a wetting liquid along the corners of a square capillary tube

1995

... 式中:S₀为初始状态的截面积,S₀=CR²,其中C=

\frac{s i n δ c o s θ}{s i n α}

-δ-

(c o t α + α - \frac{π}{2})

τ²;ε为时间常数,ε=K

\frac{σ}{μ β_{v}} \frac{R}{x_{0}^{2}}

,a和K为求解过程中出现的参数^[4,12].x₀取决于初始状态^[12].通常时间项2εt ≫1,由此得到毛细驱动下液体前缘流动距离的表达式^[4,14]为 ...

Preliminary results from the capillary flow experiment aboard ISS: The moving contact line boundary condition

2005

... 其中,根据薄层流动理论可得β_v的取值^[11,15]如下: ...

Review of spontaneous capillary driven flow along interior corners

2017

低温推进剂空间管理技术研究进展与展望

2020

... 相较于常规推进剂,以液氢/液氧为代表的低温推进剂具有高比冲、无毒、无污染等诸多优势,是目前以及未来很长一段时间内空间工程的首选推进剂^[17].然而,低温推进剂沸点低、汽化潜热低等特殊物性,为其长期空间贮存和在轨管理技术带来巨大挑战^[18].因此,对于低温推进剂,采用表面张力式流体液体管理装置是解决其空间应用难题的关键突破点.基于前文的毛细流动模型,对液氢、液氧两种流体的内角流动情况进行计算分析.液氢和液氧的物理性质参数如表1所示.为了与空间贮箱中的应用一致,采用低温流体在不锈钢表面上的接触角(近似为0°)^{[19⇓⇓-22]}. ...

低温推进剂空间管理技术研究进展与展望

2020

工作于室温温区的热力学排气模拟与增压测试

2017

工作于室温温区的热力学排气模拟与增压测试

2017

Bubble point pressures of binary methanol/water mixtures in fine-mesh screens

2014

Influential factors for liquid acquisition device screen selection for cryogenic propulsion systems

2014

2013

磁场力非均匀度对液氧磁补偿微重力自由界面的影响

2019

磁场力非均匀度对液氧磁补偿微重力自由界面的影响

2019

〈

〉