浅海风-浪-流-海床耦合场非定常时空演化规律及评价指标

图1 南海东北部海域海床地貌及简化模型图

Fig.1 Seabed topography and simplified model map in northeastern South China Sea

1.1.2 黏性流体流动数学模型

通常假设浮体周围流域内的流体是不可压缩性的,不考虑流体的表面张力,可结合连续性方程和N-S方程来表达流体的黏性运动^[24]:

(1)Δ·u=0

(2)

\frac{\partial ρ u}{\partial t}

+Δ·(ρuu)=Δ(μΔu)-Δp+ρg+f_s

式中:u为三维流体x、y、z方向的速度矢量;ρ为密度;t为流体运动时间;μ为动力黏度系数与涡动黏度系数之和;p为压力;g为重力矢量;f_s为消波源项.

海床面的运动边界条件:

(3)

{\frac{\partial ϕ}{\partial z}|}_{z = - D}

式中:D为海水深度.

1.1.3 改进多层风-浪-流耦合模型

线性波浪波面高程方程为

(4)η=

\frac{H}{2}

cos(kx-ωt)

式中:η为波面高程;H为波高; k为波数;ω为圆频率.

以五阶Stokes波模拟周期性波浪,该波浪波面具有非对称余弦曲线函数状态,可直观观察到波峰与波谷形态,比线性波浪更接近实际海况.其波面高程方程为

(5)η=

\frac{1}{k} \overset{5}{\sum_{n = 1}}

λ_ncos[n(kx-ωt)]

x方向的速度表达式:

(6)u_x=c

\overset{5}{\sum_{n = 1}}

nλ_ncosh[nk(z+d)]cos[n(kx-ωt)]

z方向的速度表达式:

(7)u_z=c

\overset{5}{\sum_{n = 1}}

nλ_ncosh[nk(z+d)]sin[n(kx-ωt)]

式中:d为水深;c=cosh(kd);λ₁=λ,λ₂=λ²B₂₂+λ⁴B₂₄,λ₃=λ²B₃₃+λ⁴B₃₅,λ₄=λ²B₄₄,λ₅=λ²B₅₅;λ、B系列参数详见文献[25].

风场依据《建筑结构荷载规范》^[26]采用A类地貌风剖面系数,以指数率梯度风进行定义:

(8)u_w=u₁₀

{(\frac{z}{10})}^{α}

式中:u_w、u₁₀分别为高度z和高度10 m对应的平均风速;α为地面粗糙度指数,A类地貌取值0.12.

自由液面以下的海流流速以1/7定律的指数型分布表示:

(9)u_c=

\{\begin{array}{l} v_{c} {(\frac{l}{0.32 d})}^{1 / 7}, & 0 < l / d < 0.5 \\ 1.07 v_{c}, & 0.5 \leq l / d < 1 \end{array}

式中:u_c、v_c分别为海流的流速和平均流速;l为距海床底距离.

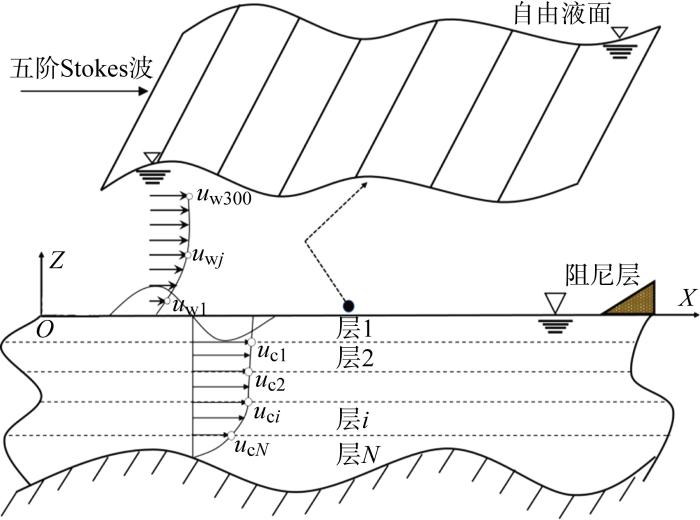
实际海域中水流速度在垂向上具有一定的分布差异,从而导致波浪沿不同水深发生变化;同时风在垂向上也呈现梯度分布,导致波面传播会产生变形现象.为研究近海风-浪-流演化问题,需要同时考虑风、流垂向分布的影响.以多层质点速度耦合方法应用于风浪流共存情况,如图2所示.图中:在多层风浪流耦合模型中建立笛卡尔坐标系OXYZ;原点O为海平面位置;Z坐标描述水深;Y坐标描述风-浪-流横向宽度;风-浪-流沿着X正方向传播.对计算域进行风波耦合区、波流耦合区、水深一半以上区和水深一半以下区的分层,不同层的风速、流速以风剖面、剪切流的速度进行分解输入,以此建立新型多层风-浪-流耦合模型.该模型的速度u_w_j、u_c_i分别为j、i层的风浪耦合速度和浪流耦合速度.风-浪-流在x方向上的速度:

(10)U_x=

\{\begin{array}{l} u_{10} {(\frac{z}{10})}^{0.12}, & \frac{H}{2} < z \\ u_{10} {(\frac{z}{10})}^{0.12} + u_{x}, & η < z \leq \frac{H}{2} \\ 1.07 v_{c} + u_{x} d, & - \frac{H}{2} < z \leq η \\ 1.07 v_{c}, & - 15 m < z \leq - \frac{H}{2} \\ v_{c} {(\frac{z + d}{0.32 d})}^{1 / 7}, & - 30 m < z \leq - 15 m \end{array}

图2

图2 多层风-浪-流耦合场模型示意图

Fig.2 Diagram of multilayer wind-wave-current coupling field model

1.2 CFD模拟参数设定

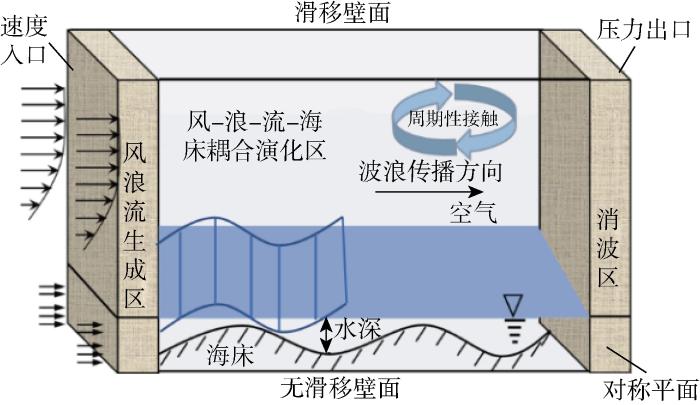
图3给出了风-浪-流-海床三维数值黏性水池模型示意图.计算域由风-浪-流生成区、阻尼消波区和风-浪-流-海床耦合演化区组成.为保证流体充分发展,计算流体域取400 m×200 m×330 m(流向x×展向y×纵向z),水深按照实际海深取值30 m,尾端设置尺寸为66 m×200 m×330 m的消波区.

图3

图3 多层风-浪-流-海床三维数值黏性水池模型示意图

Fig.3 3D numerical viscous pool model of multilayer wind-wave-current-seabed

计算域边界条件设置如下:左边界为风-浪-流速度入口,右边界设为压力出口,前后边界设为对称边界,顶部边界设为滑移壁面,底部边界设为无滑移壁面,其中为了流体得以更快地形成稳定场,速度入口和压力出口设置成周期性接触,形成充分发展性边界.雷诺平均N-S方程(RANS)非定常计算模型采用更适合于求解雷诺应力分量输运方程的SST k-ω湍流模型,使用流体体积方法对自由液面进行追踪处理.通过自定义场函数接口,将多层风浪流耦合场模型施加在入口边界上,初始化时停用第一波前设置,可生成对应的风浪流初始场.为防止出口风浪流反射,形成壁面效应,在水池尾部添加动量源阻尼项.根据DNV-RP-C205规范^[3]中统计的各海区风浪流长期分布参数,选择研究区域属于40号海区,选取海区作业海况作为输入条件,波高设置为2.1 m,周期为5.3 s,设10 m处风速为11.4 m/s,平均流速为0.68 m/s,通过波浪速度分解x、y和z向,与自定义风剖面、剪切流叠加计算.

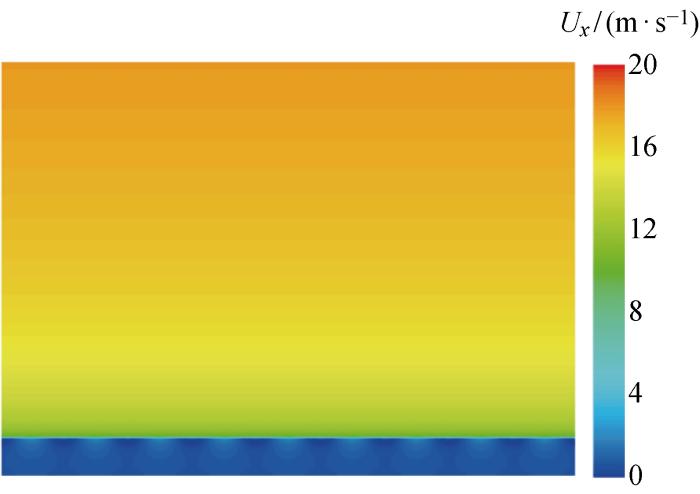
在计算域全域沿高度定义波峰以上、波谷以下及波浪发展范围内的风-浪-流解耦速度(式(10)),初始时刻计算域全域即实现了风-浪-流场解耦,解决现阶段数值造波方法存在的初始场形成前,风、浪、流要素已改变问题,同时提高计算效率和精度.图4给出初始化流场分布图.

图4

图4 风-浪-流水池初始化速度场云图

Fig.4 Initial velocity field cloud image of wind-wave-flow tank

图5给出了风-浪-流-海床耦合数值水池网格划分示意图.整体采用混合网格离散形式,以切割型六面体网格加密程度区分液面加密域、液面过渡域和其他区域.其中对液面加密域沿波浪传播方向、波高方向加密网格,液面过渡区相对于液面加密区两倍的网格尺寸进行加密.y⁺值为无量纲壁面距离,关乎近壁面湍流的发展状态,近壁面区域使用全y⁺壁面处理函数方法,近壁面第1层网格厚度为0.041 m,y⁺范围在150~250内,满足壁面函数法要求.

图5

图5 风-浪-流-海床三维数值粘性水池网格划分示意图

Fig.5 Diagram of wind-wave-stream-seabed three-dimensional numerical viscous pool grid

表1给出了不同水线加密工况下参数对比,其中L为波浪波长.由表可知:随着网格数量的增加,波高误差逐渐减小趋势,波高衰减情况改善.工况4和工况5的波高误差与规范结果相差较小,且两者之间也无明显差异,综合考虑计算精度与效率的平衡,本文选取网格工况4为数值模拟网格方案,时间步长按照T/(2.4r)取值.其中:T为波浪周期;r为一个波长的网格数量.时间步长为0.022 s.

表1 网格划分方案工况

Tab.1 Working condition of grid partitioning scheme

网格工况	波长方向网格间距	波高方向网格间距	网格数量	波高误差/%
1	L/20	H/5	1 335 795	-23.4
2	L/40	H/10	2 555 275	-15.4
3	L/80	H/15	9 707 365	-6.3
4	L/100	H/20	13 403 373	-1.04
5	L/120	H/40	69 950 595	-0.82

新窗口打开| 下载CSV

1.3 有效性验证

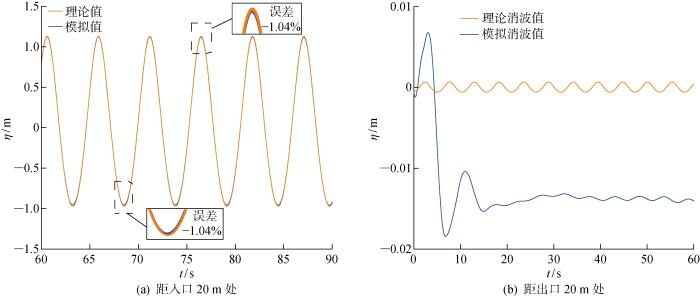
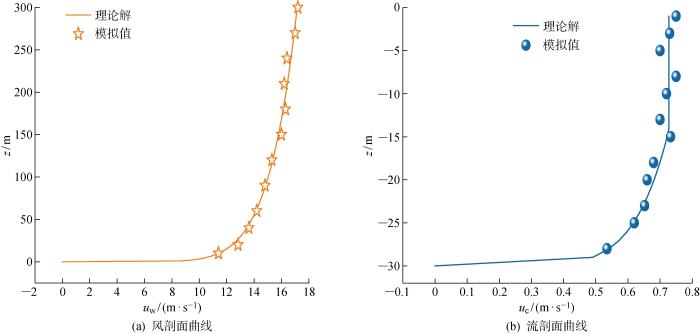
风-浪-流参数模拟精确度与试验结果有很大的关联性,为验证数值水池模拟试验结果,分别对波浪单独作用的波浪场及消波效果、对初始时刻风-浪-流耦合作用下的风场及海流场进行分析,通过距入口、出口20 m处监测的波面高程、纵向分布风速及流速的模拟值与理论值进行对比,来验证试验模拟的准确性,其中风-浪-流规范值参数如表2所示.

表2 风-浪-流参数

Tab.2 Wind-wave-current parameter

参数	取值	参数	取值
波浪模型	五阶Stokes波浪	剪切流模型	1/7指数率流剖面
L/m	44.8	v_c/(m·s^-1)	0.68
H/m	2.1	风剖面模型	指数率风剖面
D/m	30	u₁₀/(m·s^-1)	11.4
T/s	5.3	α	0.12

新窗口打开| 下载CSV

图6(a)为波浪单独作用时距入口20 m处波浪模拟值与理论值对比曲线,在模拟的60~90 s阶段,波浪的模拟值与理论值波形基本吻合,且无衰减的趋势;图6(b)为距出口20 m消波区波面高程时程曲线,由图可见相较于未消波和消波后的理论值,波浪在两个周期以后已基本消失,验证了阻尼消波的可行性.

图6

图6 波高模拟值与理论值对比时程曲线

Fig.6 Comparison of time-history of wave height simulation value with theoretical value

图7给出了风-浪-流耦合作用下初始时刻计算域距入口20 m处沿高度风速和流速模拟结果对比曲线.结果表明入口处风剖面和剪切流剖面与理论解吻合,初始条件下风场和海流场达到稳定.

图7

图7 距入口20 m处风速及流速剖面模拟值与理论值对比曲线

Fig.7 Comparison of simulated and theoretical values of wind speed and current speed at 20 m from inlet

2 耦合场时空演化规律

2.1 波浪场时空演化

图8给出了计算域中间(x=0 m)4种海床地貌下波浪场波形变化时程曲线.对比分析发现风-浪-流场与平坦地貌、海底斜坡和海槽的耦合作用使得波高大幅度减小、波长变长;平坦地貌、海底斜坡和海槽工况呈现衰减演化过程,海底平原工况呈现波浪破碎过程.平坦地貌、海底斜坡和海槽3种地貌下的衰减演化过程均可分为波面激增、衰减和稳定3个阶段,其中衰减阶段平坦地貌和海底斜坡工况波浪场处于持续衰减,而海槽地貌由于“浅-深-浅”的地形特征和色散定律,波浪场形成波群性衰减;海底平原工况先经历外破波和内破波两个阶段的波浪破碎,呈现波高突变和波形衰减的非线性变化,最后在爬波阶段受到触底回流的冲击,形成最后一次高达6 m的“直立”形波浪破碎现象.

图8

图8 不同海床地貌下波形高程-时程变化曲线

Fig.8 Waveform time-history curves in different seabed topographies

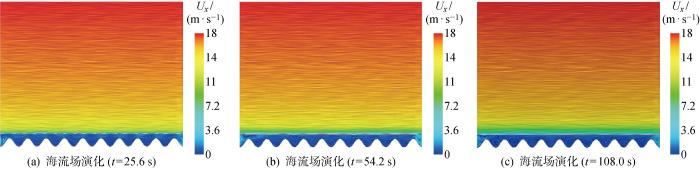
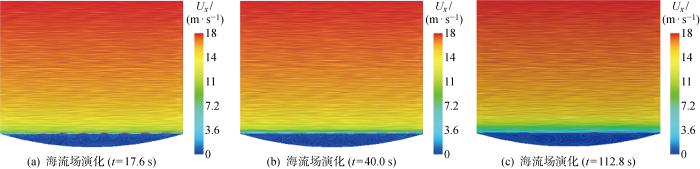
图9~12给出了演化阶段下各海床工况全域空间波形变化示意图.由图可知:平坦地貌、海底斜坡和海槽3个工况经历过激增阶段的波面陡立后,都呈现不同程度的衰减现象,其中海槽地形也由于色散定理和水深特征,波浪的前缘速度和后缘速度不同,波面的横向不对称性相比其他工况较明显;海底平原工况外破波阶段波浪破碎形态多为激破波与卷破波组合的破碎形式,内破波阶段形成出口端波浪折射现象和部分前沿陡立、后坡平坦的段波,与爬坡阶段的触底回流碰撞形成崩破波.

图9

图9 平坦地貌不同阶段三维空间波形演变云图

Fig.9 Three-dimensional spatial waveform variation diagram under flat geomorphic conditions

图10

图10 海底平原不同阶段三维空间波形变化图

Fig.10 Three-dimensional spatial waveform variation diagram under submarine plain working conditions

图11

图11 海底斜坡不同阶段三维空间波形变化图

Fig.11 Three-dimensional spatial waveform variation diagram under submarine slope conditions

图12

图12 海槽不同阶段三维空间波形变化图

Fig.12 Three-dimensional spatial waveform variation diagram under trough working conditions

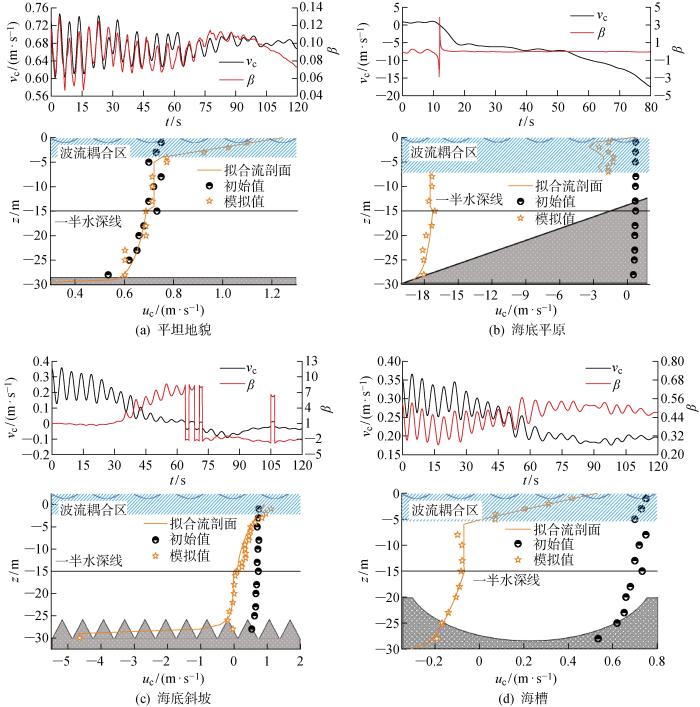
2.2 海流场时空演化

图13为各工况的剪切流模拟结果对比,其中每幅下图对应上图的最后时刻,β值为流剖面指数,初始为1/7.对比可见:与平坦地貌相反,海底平原、海底斜坡和海槽工况对流剖面要素均存在一定影响,其中平均流速皆呈现随时间逐渐减小的趋势;海底平原工况由于触底回流的原因,演化终期垂向流速基本为负值.分别采用指数型、多项式对一半水深以下、一半水深以上和波流耦合区3个区域进行拟合,并给出如下4个工况拟合后的垂向流速解析式.

图13

图13 不同海床地貌下剪切流模拟结果对比

Fig.13 Comparison of shear flow simulation results in different seabed geomorphologies

平坦地貌:

(11)U_x=

\{\begin{array}{l} 0.119 3 z + 1.237 2, & - \frac{H}{2} < z < η \\ \frac{10 791}{10 000} \times 0.667 9, & - 15 m < z \leq - \frac{H}{2} \\ 0.667 9 {(\frac{z + 30}{0.32 \times 30})}^{0.072 75}, & - 30 m < z \leq - 15 m \end{array}

海底平原:

(12)U_x=

\{\begin{array}{l} 0.032 4 z^{4} + 0.536 4 z^{3} + \\ 2.979 1 z^{2} + 6.111 z + 0.713 6, & - \frac{H}{2} < z < η \\ \frac{9 988}{10 000} \times (- 17.52), & - 15 m < z \leq - \frac{H}{2} \\ - 17.52 {(\frac{z + 30}{0.32 \times 30})}^{- 0.034}, & - 30 m < z \leq - 15 m \end{array}

海底斜坡:

(13)U_x=

\{\begin{array}{l} 0.003 1 z^{2} + 0.106 7 z + 1.018 9, & - 15 m < z < η \\ - 0.03 {(\frac{z + 30}{0.32 \times 30})}^{- 2.20}, & - 30 m < z \leq - 15 m \end{array}

海槽:

(14)U_x=

\{\begin{array}{l} 9.650 9 z - 5.107 5, & - \frac{H}{2} < z < η \\ - \frac{35}{100} \times 0.2, & - 15 m < z \leq - \frac{H}{2} \\ 0.2 {(\frac{z + 30}{0.32 \times 30})}^{0.47} - 0.308 2, & - 30 m < z \leq - 15 m \end{array}

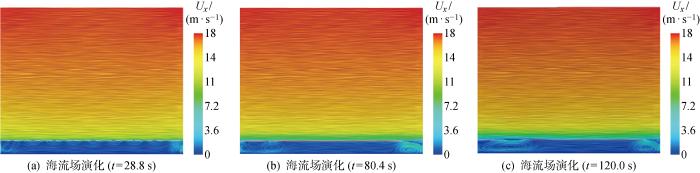
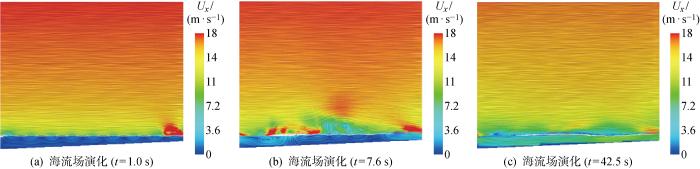
图14~17给出各工况下速度流线空间分布图.分析可得:不同于传统的风-浪-流耦合场波峰下部“V”形、波谷下部“U”形间隔涡区的研究结果,耦合场由于垂向压差,形成了不同尺度的周期性涡旋;平坦地貌工况地形对涡旋发展无阻碍,形成“多涡积聚”,海底斜坡工况“褶皱”地形的阻碍导致流场形成“多涡共存”的现象;而海底平原工况由于卷破波形成时部分空气卷入,加剧低空处风和波浪速度,波浪场加剧变化使得全域波形呈现“坡形”,风场与其碰撞形成图15(b)中风波耦合区的涡旋,爬坡阶段涡旋发展过程遇到触底回流,海流场涡旋体系被破坏;对于海槽工况,海流场发展空间较小,但经过长时间的演化,形成的小涡旋逐渐破坏初始“U+V”涡区形态.

图14

图14 平坦地貌工况流场时空演化图

Fig.14 Space-time evolution diagram of flow field under flat landform conditions

图15

图15 海底平原工况流场时空演化图

Fig.15 Space-time evolution diagram of flow field in submarine plain

图16

图16 海底斜坡工况流场时空演化图

Fig.16 Temporal and spatial evolution diagram of flow field under submarine slope conditions

图17

图17 海槽工况流场时空演化图

Fig.17 Temporal and spatial evolution diagram of flow field in trough conditions

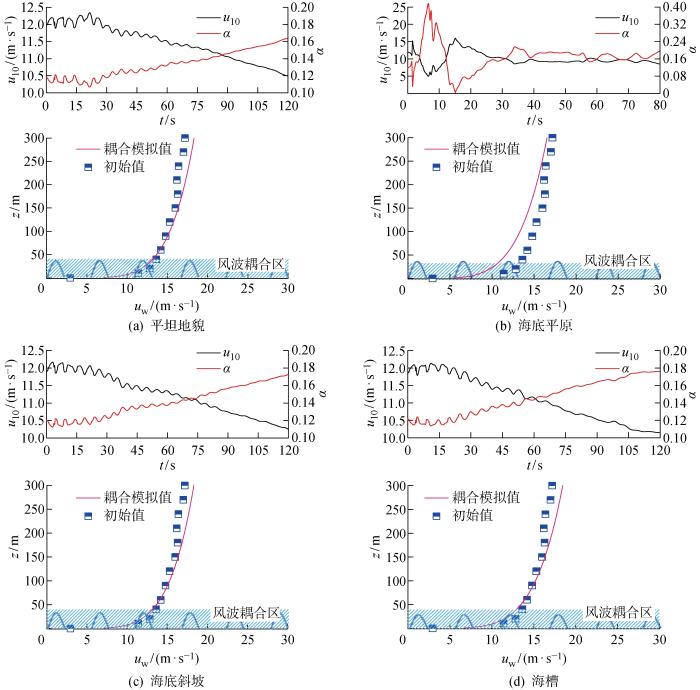
2.3 风场时空演化

图18为不同工况下风剖面拟合结果对比,其中每幅下图对应上图的最后时刻.对比发现4种海床地貌引起的波浪场变化均会造成风剖面指数的增大和基本风速的减小,且参考表1,发现海床床面高度与风剖面指数成正比关系,与A类地貌取值0.12^[26]相比,平坦地貌、海底平原、海底斜坡和海槽的演化终期风剖面指数分别为0.164、0.197、0.173和 0.176;海底平原工况由于外破波阶段波高全域性突变至7~8 m,海表面的粗糙度大幅度提高,此时风场也在波面抬升中损失大量能量,导致图18(b)中在t=7 s附近基本风速降到极小值5 m/s,风剖面指数提高到极大值0.4,在后面的演化阶段,风场恢复至稳定,但其基本风速的稳定值小于其他3个工况.

图18

图18 不同海床地貌下风剖面模拟结果对比

Fig.18 Comparison of simulation results of wind profile in different seabed topographies

3 耦合场非定常效应评价指标

建立综合评价体系来表达风-浪-流-海床耦合场的非定常变异性,以此来评判海洋环境的具体方法:对各海床地貌下风-浪-流非定常变化因素共选取6个无量纲化的环境因子,分别为波浪波高、波浪波长、平均流速、流剖面指数、基本风速与风剖面指数,作为影响风-浪-流耦合场非定常演化的环境因子.各环境因子先进行无量纲化处理,引用G表示模拟值G_m同原始值G_y之比:

(15)G=

\frac{G_{m}}{G_{y}}

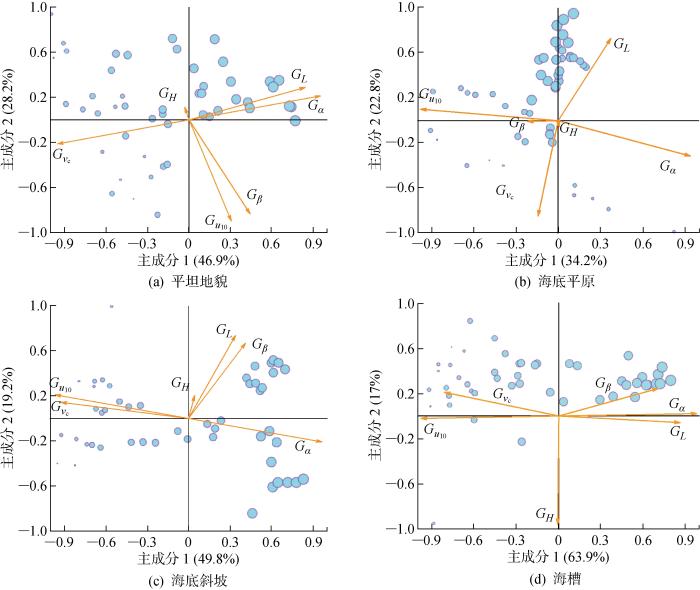
结合主成分分析方法,根据风-浪-流演化过程中每0.02 s模拟出的6个非定常环境因子作为样本,提取最大贡献主成分.图19分别为4个海床工况的非定常环境因子在主成分1×主成分2 上的投影.图中:圆点的大小与演化时间成正比;箭头终点的坐标值代表各非定常因子对主成分的贡献值.表3为不同海床地貌下主成分最大贡献数量及累计贡献率.其中平坦地貌、海底斜坡及海槽工况前3个主成分的累计贡献率分别达到91.7%、85.6%和94.6%;海底平原工况所需4个主成分,累计贡献率达到90.0%,已满足主成分分析法降维精度要求^[27].

图19

图19 非定常环境因子和样本数据对主成分贡献数值图

Fig.19 Unsteady environmental factors and sample data contribute to numerical diagram of principal components

表3 不同工况主成分贡献数量及累计贡献率

Tab.3 Number and cumulative contribution rate of principal components under different working conditions

海床地貌形式	主成分贡献数量	主成分累计贡献率/%
平坦地貌	3	91.7
海底平原	4	90.0
海底斜坡	3	85.6
海槽	3	94.6

新窗口打开| 下载CSV

据此可建立风-浪-流全生命周期非定常综合评价函数:

(16)F=

\{\begin{array}{l} 0.18 X_{1} + 0.293 X_{2} - 0.099 X_{3} - \\ 0.048 X_{4} - 0.314 X_{5} + 0.313 X_{6}, & 平 坦 地 貌 \\ 0.174 X_{1} + 0.246 X_{2} - 0.205 X_{3} + \\ 0.090 X_{4} - 0.227 X_{5} + 0.175 X_{6}, & 海 底 平 原 \\ 0.212 X_{1} + 0.205 X_{2} - 0.242 X_{3} + \\ 0.219 X_{4} - 0.243 X_{5} + 0.244 X_{6}, & 海 底 斜 坡 \\ - 0.208 X_{1} + 0.3 X_{2} - 0.308 X_{3} + \\ 0.173 X_{4} - 0.315 X_{5} + 0.315 X_{6}, & 海 槽 \end{array}

式中:X₁~X₆依次为波高、波长、平均流速、流剖面指数、基本风速与风剖面指数的非定常环境因子.基于此取演化终期的非定常环境因子数值,建立各海床地貌工况下风-浪-流耦合非定常评价指标参考值.得到平坦地貌、海底平原、海底斜坡和海槽的非定常评价指标分别为0.268、4.612、0.672和0.926.

4 结论

系统研究了典型海床地貌下风-浪-流耦合过程非定常演化规律及评价指标,尤其在多层风-浪-流耦合模型、风-浪-流场阶段性发展形态演化和非定常综合评价指标方面取得了原始创新,具体如下:

(1) 新型多层风-浪-流耦合模型能精确模拟出垂向风速、流速不均匀对风-浪-流耦合场造成的影响.以风-浪-流解耦模型运用于CFD初始条件中,有效提高计算效率和精度.

(2) 各海况的风-浪-流-海床演化过程:波浪场演变分为三阶段,其中平坦地貌、海底斜坡和海槽工况分为波面激增、衰减和稳定阶段;海底平原工况共分为外破波、内破波和爬坡阶段.海流场随演变过程在空间上呈多段式分布,一半水深以下的指数率函数、一半水深以上及波流耦合区的多次项函数.

(3) 海流速度场由于垂向压差形成涡旋,各工况根据海床地貌不同形成多涡积聚或多涡共存的现象;风-浪-流-海床耦合演化对风剖面指数产生放大作用,海床床面高度与风剖面系数成正比关系.

(4) 建立了基于主成分分析法的耦合场全生命周期非定常评价指标, 并提出演化终期各典型海床下非定常评价指标数值:平坦地貌、海底平原、海底斜坡和海槽分别为0.268、4.612、0.672和0.926. 非定常评价指标可精准预测浅海地区典型海床地貌下风、浪、流时空分布变异性特征, 可为我国海岸工程安全建设中海洋环境预测提供参考.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

在“十四五”时期协调推进海洋资源保护与开发推进海洋强国建设

[N]. 人民政协报, 2020-11-05(4).

Coordinate the protection and development of marine resources and promote the construction of marine power in the ‘14th Five-Year’period

[N]. People’s Political Consultative Conference, 2020-11-05(4).

[2]

中交第一航务工程勘察设计院有限公司.

港口与航道水文规范: JTS 145—2015

[S]. 北京: 人民交通出版社, 2015.

CCCC First Navigation Engineering Survey and

Design Institute Co., Ltd.. Code of harbor and channel hydrology: JTS 145—2015

[S]. Beijing: The People’s Communication Press, 2015.

[3]

Det Norske Verital AS.

Environmental conditions and environmental loads: DNV-RP-C205

[S]. Norway: DNV, 2010: 59-127.

DOI:10.6052/0459-1879-18-454 [本文引用: 1]

[4]

聂隆锋, 赵西增, 张志杭,

等.

基于VPM-THINC/QQ模型的波浪高保真模拟

[J]. 力学学报, 2019, 51(4): 1043-1053.

为实现波浪传播的高保真数值模拟,采用包含单元均值和点值(volume-average/point-value method,VPM)的有限体积法求解纳维-斯托克斯方程和具有二次曲面性质和高斯积分的双曲正切函数(THINC method with quadratic surface representation and Gaussian quadrature,THINC/QQ)方法来重构自由面,建立以开源求解库OpenFOAM底层函数库为基础的VPM-THINC/QQ模型. 在本模型中添加推板造波法实现波浪的产生功能,采用松弛法实现消波功能,构建高精度黏性流数值波浪水槽. 分别采用VPM-THINC/QQ模型和InterFoam求解器(OpenFOAM软件包中广泛使用的多相流求解器)开展规则波的数值模拟,重点探究网格大小和时间步长等因素对波浪传播过程的影响,定量地分析波高衰减程度;为验证本模型的适应性,对长短波进行模拟. 结果表明,在相同网格大小或时间步长条件下,VPM-THINC/QQ模型的预测结果与参考值吻合较好,波高衰减较少,且无相位差,在波浪传播过程的模拟中呈现出良好的保真性. 本文工作为波浪传播的模拟研究提供了一种高精度的黏性数值波浪水槽模型.

NIE

Longfeng

, ZHAO

Xizeng

, ZHANG

Zhihang

et al.

High-fidelity simulation of wave propagation based on VPM-THINC/QQ model

[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(4): 1043-1053.

DOI:10.6052/0459-1879-18-454 [本文引用: 1]

In order to achieve high-fidelity of numerical simulation of wave propagation, an improved finite volume method with volume-average and point-value (VPM) is used to solve the Navier-Stokes equation and the tangent of hyperbola for interface capturing with quadratic surface representation and Gaussian quadrature reconstructs the free surface. The VPM-THINC/QQ model based on OpenFOAM underlying function library is established. The piston wave-making method is added to the current model to realize the wave generation, and the relaxation method is used to realize the wave dissipation. A high-precision viscous numerical wave water tank is built. The numerical simulation of regular waves is carried out by using VPM-THINC/QQ model and interFoam solver (multiphase solver widely used in OpenFOAM software packages) respectively. The effects of grid size and time step on the wave propagation process are investigated mainly. The attenuation degree of wave height is quantitatively compared and analyzed. In order to verify the adaptability of the current model, simulation of long and short waves is carried out. The results show that under the same grid size or time step, the prediction results of the VPM-THINC/QQ model agree well with the theoretical solution compared with the interFoam solver. The wave height has little attenuation and there is no phase difference. It shows high-fidelity of the VPM-THINC/QQ model in the wave propagation process. A high-precision model of viscous numerical wave tank is provided for studying the wave propagation process in this work.

[5]

季顺迎, 田于逵,

基于多介质、多尺度离散元方法的冰载荷数值冰水池

[J]. 力学学报, 2021, 53(9): 2427-2453.

Shunying

, TIAN

Yukui

Numerical ice tank for ice loads based on multi-medium and multi-scale discrete element method

[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(9): 2427-2453.

[6]

柯世堂, 王硕, 张伟, 等.

风、浪、流多场耦合作用波浪传播演化机理对比分析

[J]. 哈尔滨工程大学学报, 2021, 42(9): 1312-1320.

Shitang

, WANG

Shuo

, ZHANG

Wei

et al.

Comparative analysis of the mechanism of wave propagation and evolution under the coupling effect of wind, waves, and currents

[J]. Journal of Harbin Engineering University, 2021, 42(9): 1312-1320.

[7]

张卓, 宋志尧, 孔俊.

波流共同作用下流速垂线分布及其影响因素分析

[J]. 水科学进展, 2010, 21(6): 801-807.

ZHANG

Zhuo

, SONG

Zhiyao

, KONG

Jun

Wave-current interaction effects on velocity profiles and influencing factor analysis

[J]. Advances in Water Science, 2010, 21(6): 801-807.

[8]

杨师宇, 吴静萍, 汪敏,

等.

基于去奇异边界元法的二维数值波浪水池计算参数影响分析

[J]. 武汉理工大学学报(交通科学与工程版), 2021, 45(5): 912-918.

YANG

Shiyu

, WU

Jingping

, WANG

Min

et al.

Influence analysis of calculation parameters in two-dimensional numerical wave tank based on dbiem

[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2021, 45(5): 912-918.

[9]

刘红兵, 陈国明, 吕涛,

等.

海洋工程数值风-浪-流水池模拟及分析

[J]. 中国海上油气, 2019, 31(6): 154-159.

LIU

Hongbing

, CHEN

Guoming

, LYU

Tao

et al.

Ocean engineering numerical simulation and analysis in the wind-wave-current pool

[J]. China Offshore Oil and Gas, 2019, 31(6): 154-159.

DOI:10.1016/j.wavemoti.2014.03.009 URL [本文引用: 1]

[10]

LIU

, LIN

, LIAO

Phase velocity effects of the wave interaction with exponentially sheared current

[J]. Wave Motion, 2014, 51(6): 967-985.

[11]

CHEN

, ZOU

Effects of following and opposing vertical current shear on nonlinear wave interactions

[J]. Applied Ocean Research, 2019, 89: 23-35.

DOI:10.1016/j.apor.2019.04.001 URL [本文引用: 1]

[12]

何广华, 荆芃霖, 王威,

等.

垂荡双箱间窄缝水动力共振特性

[J]. 哈尔滨工程大学学报, 2021, 42(11): 1588-1595.

Guanghua

, JING

Penglin

, WANG

Wei

et al.

Characteristics of hydrodynamic resonance in a narrow gap between two heaving boxes

[J]. Journal of Harbin Engineering University, 2021, 42(11): 1588-1595.

[13]

杨云涛, 朱仁传, 蒋银,

等.

三维无反射数值波浪水池及波浪与结构物相互作用的模拟

[J]. 上海交通大学学报, 2018, 52(3): 253-260.

YANG

Yuntao

, ZHU

Renchuan

, JIANG

Yin

et al.

Simulation of 3-D viscous non-reflection numerical wave tank and the interactions of waves and structures

[J]. Journal of Shanghai Jiao Tong University, 2018, 52(3): 253-260.

[14]

吴乘胜, 朱德祥, 顾民.

数值波浪水池及顶浪中船舶水动力计算

[J]. 船舶力学, 2008(2): 168-179.

Chengsheng

, ZHU

Dexiang

, GU

Min

Computation of hydrodynamic forces for a ship in regular heading waves by a viscous numerical wave tank

[J]. Journal of Ship Mechanics, 2008(2): 168-179.

DOI:10.1017/S0022112067002605 URL [本文引用: 1]

[15]

PEREGRINE

D H

Long waves on a beach

[J]. Journal of Fluid Mechanics, 1967, 27(4): 815-827.

Equations of motion are derived for long waves in water of varying depth. The equations are for small amplitude waves, but do include non-linear terms. They correspond to the Boussinesq equations for water of constant depth. Solutions have been calculated numerically for a solitary wave on a beach of uniform slope. These solutions include a reflected wave, which is also derived analytically by using the linearized long-wave equations.

[16]

BLENKINSOPP

, CHAPLIN

The effect of relative crest submergence on wave breaking over submerged slopes

[J]. Coastal Engineering, 2008, 55: 967-974.

DOI:10.1016/j.coastaleng.2008.03.004 URL [本文引用: 1]

[17]

李玉成, 于洋, 崔丽芳,

等.

平缓岸坡上波浪破碎的实验研究

[J]. 海洋通报, 2000(1): 10-18.

Yucheng

, YU

Yang

, CUI

Lifang

et al.

Experimental study of wave breaking on gentle slope

[J]. Marine Science Bulletin, 2000(1): 10-18.

DOI:10.1146/fluid.2013.46.issue-1 URL [本文引用: 1]

[18]

LAMB

K G

Internal wave breaking and dissipation mechanisms on the continental slope/shelf

[J]. Annual Review of Fluid Mechanics, 2014, 46: 231-254.

[19]

YAO

, HUANG

, MONISMITH

S G

et al.

Characteristics of monochromatic waves breaking over fringing reefs

[J]. Journal of Coastal Research, 2013, 29(1): 94-104.

DOI:10.2112/JCOASTRES-D-12-00021.1 URL [本文引用: 2]

[20]

郅长红, 陈科, 尤云祥.

弱非线性内孤立波在斜坡上的传播演化特性

[J]. 上海交通大学学报, 2021, 55(8): 916-923.

ZHI

Changhong

, CHEN

, YOU

Yunxiang

Propagation evolution char acteristics of weakly nonlinear internal solitary waves on slopes

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(8): 916-923.

[21]

孙志伟.

内孤立波在斜坡地形上传播的数值模拟及分析[D]. 大连: 大连理工大学, 2021.

SUN

Zhiwei

Numerical simulation and analysis of internal solitary wave propagation on a slope topography[D]. Dalian: Dalian University of Technology, 2021.

[22]

陈洁, 温宁.

南海地球物理图集[M]. 北京: 科学出版社, 2010: 1-8.

CHEN

Jie

, WEN

Ning

Geophysical atlas of the South China Sea[M]. Beijing: Science Press, 2010: 1-8.

[23]

杨涛涛, 吕福亮, 鲁银涛,

等.

南海西沙海域多种海底地貌特征及成因

[J]. 海相油气地质, 2021, 26(4): 307-318.

YANG

Taotao

, LÜ

Fuliang

, LU

Yintao

et al.

Characteristics and genesis of various seafloor topography in Xisha sea area, South China Sea

[J]. Marine Petroleum Geology, 2021, 26(4): 307-318.

[24]

KOCHEVSKY

A N

Possibilities of simulation of fluid flows using the modern CFD software tools

[J]. Physics, 2004, 1: 1-12.

[25]

李邦华, 郑向远, 李炜,

等.

波浪水槽中Stokes五阶波的数值生成

[J]. 武汉理工大学学报(交通科学与工程版), 2016, 40(2): 238-244.

Banghua

, ZHENG

Xiangyuan

, LI

Wei

et al.

Simulation of fifth-order Stokes waves in the numerical wave flume

[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2016, 40(2): 238-244.

[26]

中华人民共和国住房和城乡建设部.

建筑结构荷载规范: GB 50009—2012

[S]. 北京: 中国建筑工业出版社, 2012.

Ministry of Housing and Urban-Rural Development of the People’s Republic of China.

Load code for the design of building structures: GB 50009—2012

[S]. Beijing: China Architecture & Building Press, 2012.

[27]

李伟, 黄焱.

随机海洋环境下基于互相关函数和主成分分析的平台结构损伤辨识

[J]. 振动与冲击, 2021, 40(7): 179-187.

Wei

, HUANG

Yan

Damage identification of platform structure based on cross correlation function and PCA in random ocean environment

[J]. Journal of Vibration and Shock, 2021, 40(7): 179-187.