然而,MRI扫描时间较长,病人在扫描过程中易感到不适或发生移动导致图像伪影,影响病人的就医体验和扫描图像质量.为加快MRI的扫描速度,通常对k空间数据进行欠采样后再使用算法重建出图像,但欠采样易使图像质量下降,影响医生对患者病情的诊断.在算法模型中加入不同正则项可改善图像重建质量,但会导致重建速度较慢从而出诊断结果较慢,最终影响病人的就医满意度,限制了算法的推广与应用[3].因此,在保证MRI重建质量的同时,研究MRI的快速重建方法是非常实际且有意义的.
在PMRI技术中,Lustig等[7]提出一种针对任意k空间轨迹的并行成像重建方法,即迭代自一致性并行成像重建(Iterative Self-Consistent Parallel Imaging Reconstruction, SPIRiT)模型.该方法基于k空间数据自身的一致性,包括校正一致性和数据采集一致性,利用相邻k空间点之间的相关性恢复丢失的信息,已被广泛应用于临床实践中[8].SPIRiT是一种基于自一致性的广义PMRI重建框架,可以方便地与各种正则化方法结合,以实现更高性能的MRI重建.因此,许多研究者引入不同正则项对SPIRiT模型进行一系列的研究和改进[9⇓⇓⇓⇓⇓⇓⇓-17].其中,段继忠等[9]将联合稀疏性正则项引入SPIRiT模型,提出一种高效的重建方法.之后,Duan等[12]又在SPIRiT模型中引入联合全变分和联合L1范数正则项约束,提出另一种基于SPIRiT的快速重建方法.这两种方法都将复杂优化问题进行简化,然后利用算子分裂技术将其分解为易于计算或求解的子问题,最后使用快速迭代软阈值算法(Fast Iterative Shrinkage-Thresholding Algorithm, FISTA)[18]进行加速,缩短图像的重建时间.最近,Zhang等[15]将L1范数正则项加入SPIRiT模型中,提出一种基于快速投影迭代软阈值算法(projected FISTA, pFISTA)[19]的快速重建方法(pFISTA-SPIRiT).该方法允许在并行MR图像重建中使用不同的紧框架,是一个广义模型,已被用于人脑成像、肝脏动态增强成像和精准的脑肿瘤血管通透性成像等[20].
但pFISTA-SPIRiT方法对校正一致项与数据一致项都进行梯度计算,导致收敛速度较慢.将重建模型中的复杂优化问题进行简化可以有效提升算法的收敛速度[9,12].因此,本文基于pFISTA-SPIRiT模型,提出一种基于平移不变离散小波变换(Shift-Invariant Discrete Wavelets Transform, SIDWT)和SPIRiT的快速并行磁共振成像重建方法(fast SIDWT-SPIRiT, fSIDWT-SPIRiT).与pFISTA-SPIRiT利用图像域SPIRiT模型进行重建不同,该方法利用频域SPIRiT模型进行重建.使用SIDWT和SPIRiT模型,将校正一致项和数据一致项合并为一项后再使用pFISTA技术进行求解.实验结果表明,与其他两种方法相比,该方法能够有效提升算法的收敛速度,从而减少图像的重建时间,并且重建质量不变.
1 SPIRiT模型
SPIRiT是一种逐线圈、自动校准的并行MRI重建模型.设r为k空间数据点的位置,Rr为从k空间中选择需要的数据点的算子;xj为第j个线圈上的全部k空间数据,j=1,2,…,J,J为总线圈数;Rrxj为以第j个线圈位置r为中心从所有线圈提取的k空间邻域数据点;xi(r)为第i个线圈上位置r处的k空间数据,则xi(r)的重建如下:
式中:gji为SPIRiT卷积核,
式中:A为ACS的位置集合.式(1)是一组耦合线性方程,故可以将整个耦合方程组写成矩阵形式,则所有线圈的校正一致性如下:
式中:x为从所有线圈中获取的全部k空间数据;G为在适当位置包含gji的矩阵.
当然,除了考虑校正一致性,还应满足数据采集一致性.数据采集一致性如下:
式中:y为从所有线圈中获取的欠采样数据;D为从全k空间数据进行欠采样的矩阵.
2 fSIDWT-SPIRiT
在重建模型中加入正则项可以有效提升MRI的重建质量,因此在SPIRiT模型中引入L1范数正则项,则带L1范数正则项的SPIRiT并行MRI重建模型可以表示为以下最优化问题:
式中:Ψ为逐线圈小波变换,用于将图像稀疏化,是一个紧框架.本文选用SIDWT作为实验中的紧框架.F为逐线圈傅里叶变换,F-1为逐线圈傅里叶逆变换.
使用罚函数技术,可以得到式(5)的无约束版本:
式中:γ和λ分别为数据一致项和L1范数正则项的参数;I为对应维度的单位矩阵.Lustig等[7]指出保持已采样数据不变很重要,因此将x表示成x=
s.t. x=
式中:
对于式(7),首先利用pFISTA[19]技术求解没有约束条件x=
针对式(7)中无约束模型的求解,令α=ΨF-1x,并且有Ψ*Ψ=I,则
式中:α为图像在Ψ表示下的系数;Ψ*为Ψ的伴随.令f(α)=
式中:k为迭代次数;L为f(αk)梯度的Lipschitz常数.于是,易得式(9)的解为
式中:αk=Prange(Ψ)(
式中:β为输入矩阵;|β|为β的模.由于Ψ*Ψ=I故式(10)可重写为
因为
最后,利用FISTA[18]技术进行加速,则整个求解过程如下:
式中:θ为与FISTA加速相关的变量;z为FISTA加速中xk+1和xk的线性组合矩阵.由此,得到重建的多线圈图像的k空间数据xk+1,然后进行傅里叶逆变换,再使用平方和的平方根(Square Root of Sum of Squares, SOS)方法得到最终的重建图像
综上所述,得到基于SIDWT和SPIRiT模型的快速并行磁共振成像重建方法fSIDWT-SPIRiT,实现步骤如下.

算法一: fSIDWT-SPIRiT
1: Set x0=0, z0=0, θ0=0, k=0
2: Repeat
3: k=k+1
4: xk+1=FΨ*Tλ/L(ΨF-1{
5: θk+1=
6: zk+1=xk+1+
7: 直到达到最大迭代次数,否则返回步骤3
8:
9: Output

3 实验仿真及分析
3.1 实验设置
所有实验均在计算机上进行,计算机的配置为:Intel(R) Core(TM) i5-7200U CPU@2.50 GHz处理器、16 GB内存和Windows 10操作系统(64位),所有方法均使用MATLAB实现.
在实验中,将fSIDWT-SPIRiT的重建性能与pFISTA-SPIRiT和SIDWT-SPIRiT进行对比.后两种方法都基于SIDWT和SPIRiT模型,直接使用pFISTA技术进行求解得到,区别在于pFISTA-SPIRiT在图像域SPIRiT进行重建,而SIDWT-SPIRiT在k空间域SPIRiT进行重建.使用信噪比(Signal Noise Ratio, SNR)、结构相似性(Structural SIMilarity, SSIM)指标和高频误差范数(High-Frequency Error Norm, HFEN)3个评价指标来衡量图像的重建质量.3个评价指标的定义分别如下:
式中:VSNR为SNR值;VMSE为重建图像
式中:VSSIM为SSIM值;uX和
式中:VHFEN为HFEN值;filter(·)是一个拉普拉斯高斯滤波器,用于捕捉图像边缘,滤波核的大小为15×15像素,标准差为1.5像素.
VSNR和VSSIM的数值越高,VHFEN的数值越低,说明图像的重建质量越好.这3个评价指标均在感兴趣区域内进行计算,实验中手动调整所有方法的参数使得VSNR值达到最优.
为验证fSIDWT-SPIRiT的有效性,在不同人体器官数据集上对各种方法的重建性能进行比较,分别选取活体人类脑部切片图GE_human_brain[21]、train_brain_AXT1POST_200_6001959[22-23]、心脏切片图data_v1_k1[24]以及人类膝盖切片图train_knee_file1000005[22-23],并依次命名为数据集1,数据集2,数据集3和数据集4.其中,数据集1是尺寸为256×256像素的8通道脑部切片数据;数据集2是使用20通道线圈获取的脑部数据集的第1帧,然后使用线圈压缩技术将其压缩为8个虚拟线圈,尺寸为320像素×320像素;数据集3是使用28通道线圈获取的心脏数据集,然后使用线圈压缩技术将其压缩为12个虚拟线圈,尺寸为192像素×192像素;数据集4是在15通道线圈获取的膝盖数据集的第20个切片,然后使用线圈压缩技术将其压缩为8个虚拟线圈,尺寸为320像素×320像素.
实验中的所有数据集都使用具有不同加速因子R(不包括ACS)的二维泊松圆盘采样模式进行欠采样,并且所有方法都使用大小为24像素×24像素的校准区域和5像素×5像素的SPIRiT核.本文主要从重建质量和重建速度两个方面来对比各种方法的优劣.在重建质量方面,主要通过重建图和误差图从主观上比较各种方法的重建性能,并采用3个评价指标从客观上比较各种方法的重建性能;在重建速度方面,主要通过时间来比较各种方法的重建性能.
3.2 不同方法的重建质量比较
3.2.1 不同重建方法的视觉比较
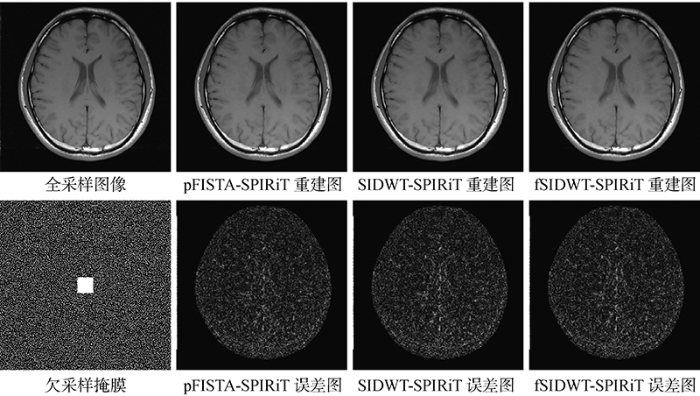
图1
图1
在5倍加速时不同方法对数据集1进行重建的视觉比较
Fig.1
Comparison of visual reconstruction for dataset 1 by different methods at 5 times acceleration
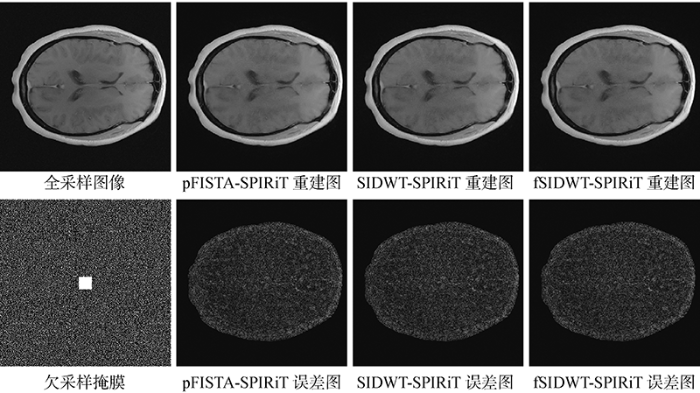
图2
图2
在5倍加速时不同方法对数据集2进行重建的视觉比较
Fig.2
Comparison of visual reconstruction for dataset 2 by different methods at 5 times acceleration
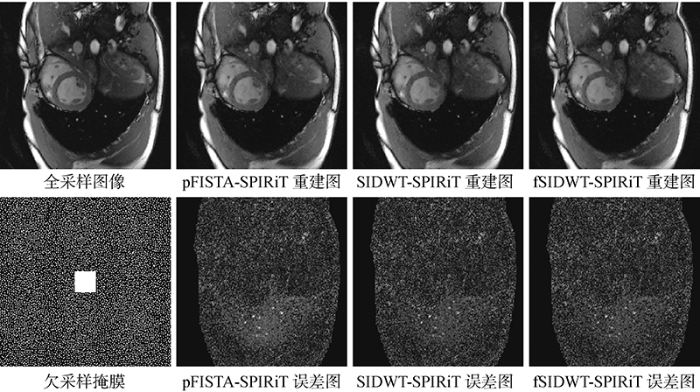
图3
图3
在5倍加速时不同方法对数据集3进行重建的视觉比较
Fig.3
Comparison of visual reconstruction for dataset 3 by different methods at 5 times acceleration
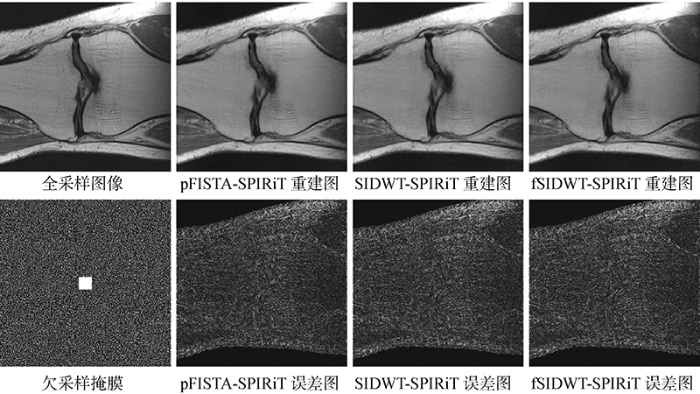
图4
图4
在5倍加速时不同方法对数据集4进行重建的视觉比较
Fig.4
Comparison of visual reconstruction for dataset 4 by different methods at 5 times acceleration
3.2.2 不同重建方法的评价指标比较
表1 在3~7倍加速时不同方法对数据集1进行重建的数值比较
Tab.1
| 算法 | 指标 | R=3 | R=4 | R=5 | R=6 | R=7 |
|---|---|---|---|---|---|---|
| pFISTA-SPIRiT | VSNR | 29.15 | 27.82 | 26.86 | 25.90 | 25.39 |
| VSSIM | 0.9879 | 0.9843 | 0.9811 | 0.9775 | 0.9755 | |
| VHFEN | 0.0574 | 0.0685 | 0.0788 | 0.0911 | 0.0980 | |
| SIDWT-SPIRiT | VSNR | 29.93 | 28.23 | 27.02 | 25.95 | 25.38 |
| VSSIM | 0.9902 | 0.9868 | 0.9840 | 0.9815 | 0.9800 | |
| VHFEN | 0.0544 | 0.0668 | 0.0791 | 0.0913 | 0.0986 | |
| fSIDWT-SPIRiT | VSNR | 29.98 | 28.29 | 27.10 | 26.00 | 25.43 |
| VSSIM | 0.9901 | 0.9870 | 0.9842 | 0.9818 | 0.9804 | |
| VHFEN | 0.0531 | 0.0658 | 0.0778 | 0.0908 | 0.0984 |
表2 在3~7倍加速时不同方法对数据集2进行重建的数值比较
Tab.2
| 算法 | 指标 | R=3 | R=4 | R=5 | R=6 | R=7 |
|---|---|---|---|---|---|---|
| pFISTA-SPIRiT | VSNR | 27.74 | 26.26 | 25.34 | 24.45 | 23.79 |
| VSSIM | 0.9799 | 0.9735 | 0.9683 | 0.9635 | 0.9590 | |
| VHFEN | 0.0721 | 0.0887 | 0.1035 | 0.1177 | 0.1321 | |
| SIDWT-SPIRiT | VSNR | 27.85 | 26.22 | 25.27 | 24.39 | 23.73 |
| VSSIM | 0.9879 | 0.9847 | 0.9826 | 0.9815 | 0.9799 | |
| VHFEN | 0.0722 | 0.0900 | 0.1051 | 0.1192 | 0.1332 | |
| fSIDWT-SPIRiT | VSNR | 27.87 | 26.26 | 25.32 | 24.44 | 23.77 |
| VSSIM | 0.9881 | 0.9850 | 0.9829 | 0.9817 | 0.9805 | |
| VHFEN | 0.0720 | 0.0893 | 0.1043 | 0.1184 | 0.1334 |
表3 在3~7倍加速时不同方法对数据集3进行重建的数值比较
Tab.3
| 算法 | 指标 | R=3 | R=4 | R=5 | R=6 | R=7 |
|---|---|---|---|---|---|---|
| pFISTA-SPIRiT | VSNR | 22.87 | 21.78 | 20.94 | 20.03 | 19.11 |
| VSSIM | 0.9521 | 0.9411 | 0.9309 | 0.9199 | 0.9082 | |
| VHFEN | 0.0644 | 0.0777 | 0.0901 | 0.1070 | 0.1253 | |
| SIDWT-SPIRiT | VSNR | 23.87 | 22.36 | 21.35 | 20.34 | 19.31 |
| VSSIM | 0.9517 | 0.9382 | 0.9288 | 0.9204 | 0.9073 | |
| VHFEN | 0.0617 | 0.0772 | 0.0907 | 0.1076 | 0.1260 | |
| fSIDWT-SPIRiT | VSNR | 23.83 | 22.34 | 21.33 | 20.34 | 19.31 |
| VSSIM | 0.9507 | 0.9381 | 0.9278 | 0.9196 | 0.9079 | |
| VHFEN | 0.0611 | 0.0767 | 0.0902 | 0.1064 | 0.1259 |
表4 在3~7倍加速时不同方法对数据集4进行重建的数值比较
Tab.4
| 算法 | 指标 | R=3 | R=4 | R=5 | R=6 | R=7 |
|---|---|---|---|---|---|---|
| pFISTA-SPIRiT | VSNR | 21.10 | 19.76 | 18.93 | 18.29 | 17.66 |
| VSSIM | 0.9414 | 0.9224 | 0.9100 | 0.8963 | 0.8851 | |
| VHFEN | 0.1951 | 0.2465 | 0.2801 | 0.3117 | 0.3480 | |
| SIDWT-SPIRiT | VSNR | 21.32 | 19.81 | 18.92 | 18.20 | 17.55 |
| VSSIM | 0.9615 | 0.9507 | 0.9434 | 0.9369 | 0.9314 | |
| VHFEN | 0.1988 | 0.2538 | 0.2878 | 0.3230 | 0.3591 | |
| fSIDWT-SPIRiT | VSNR | 21.22 | 19.77 | 18.89 | 18.19 | 17.55 |
| VSSIM | 0.9609 | 0.9502 | 0.9432 | 0.9366 | 0.9315 | |
| VHFEN | 0.2011 | 0.2531 | 0.2883 | 0.3219 | 0.3591 |
3.3 不同方法的重建速度比较
图5
图5
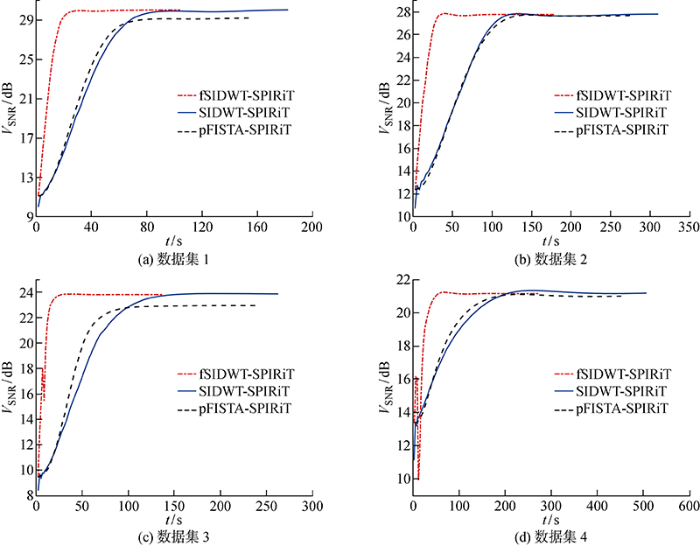
在3倍加速时3种方法对4个数据集的重建速度比较
Fig.5
Comparison of the reconstruction speed of the three methods for the 4 datasets at 3 times acceleration
图6
图6
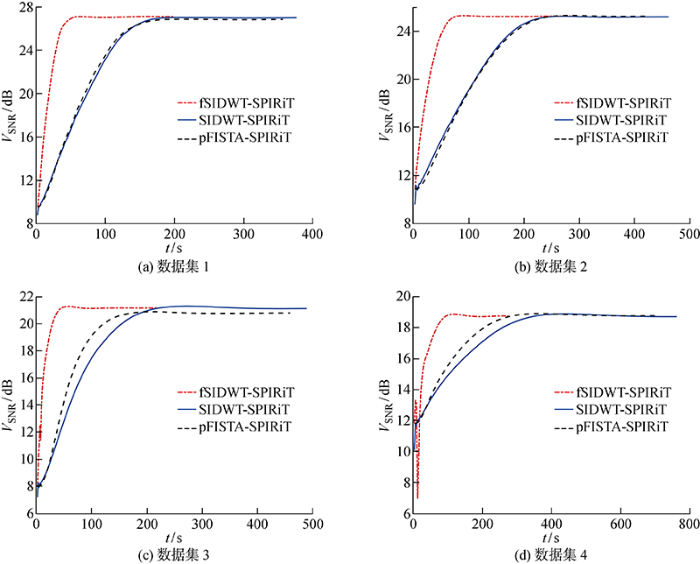
在5倍加速时3种方法对4个数据集的重建速度比较
Fig.6
Comparison of the reconstruction speed of the three methods for the 4 datasets at 5 times acceleration
从图5~6可以看出,对于4个不同的数据集,fSIDWT-SPIRiT与pFISTA-SPIRiT和SIDWT-SPIRiT两种方法相比,无论加速因子R=3还是R=5,均能获得比较接近的VSNR值.但fSIDWT-SPIRiT的收敛速度明显快于其他两种方法,表明所提方法可以实现更快速度的重建,并保证图像的重建质量,进一步验证方法的有效性.
从表5可以看出,从3倍加速增加到7倍加速,对于4个不同的数据集,与pFISTA-SPIRiT相比,fSIDWT-SPIRiT的重建速度分别提升3.2倍、3.7倍、3.8倍和3.4倍,平均提升3.5倍;与SIDWT-SPIRiT相比,fSIDWT-SPIRiT的重建速度分别提升3.5倍、3.4倍、4.9倍和4倍,平均提升3.9倍.由此可以说明,所提方法能够大大缩短图像重建时间,更进一步验证该方法的有效性.
表5 在3~7倍加速时不同方法对4个数据集进行重建的时间比较
Tab.5
| 数据集 | 算法 | R=3 | R=4 | R=5 | R=6 | R=7 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t | m | t | m | t | m | t | m | t | m | ||||||
| 数据集1 | pFISTA-SPIRiT | 89 | 3.3 | 116 | 3.2 | 194 | 3.3 | 240 | 3.2 | 268 | 3.2 | ||||
| SIDWT-SPIRiT | 91 | 3.4 | 121 | 3.4 | 203 | 3.4 | 259 | 3.5 | 303 | 3.6 | |||||
| fSIDWT-SPIRiT | 27 | 1.0 | 36 | 1.0 | 59 | 1.0 | 74 | 1.0 | 85 | 1.0 | |||||
| 数据集2 | pFISTA-SPIRiT | 148 | 4.4 | 216 | 3.8 | 281 | 3.3 | 347 | 3.4 | 426 | 3.6 | ||||
| SIDWT-SPIRiT | 128 | 3.8 | 198 | 3.5 | 274 | 3.3 | 313 | 3.1 | 390 | 3.3 | |||||
| fSIDWT-SPIRiT | 34 | 1.0 | 57 | 1.0 | 84 | 1.0 | 101 | 1.0 | 120 | 1.0 | |||||
| 数据集3 | pFISTA-SPIRiT | 133 | 4.0 | 180 | 4.1 | 206 | 3.7 | 247 | 3.6 | 319 | 3.4 | ||||
| SIDWT-SPIRiT | 150 | 4.5 | 232 | 5.3 | 293 | 5.3 | 316 | 4.6 | 446 | 4.8 | |||||
| fSIDWT-SPIRiT | 33 | 1.0 | 44 | 1.0 | 55 | 1.0 | 68 | 1.0 | 93 | 1.0 | |||||
| 数据集4 | pFISTA-SPIRiT | 237 | 3.9 | 294 | 3.5 | 358 | 3.3 | 431 | 3.3 | 506 | 3.2 | ||||
| SIDWT-SPIRiT | 259 | 4.2 | 343 | 4.0 | 431 | 4.0 | 515 | 3.9 | 625 | 3.9 | |||||
| fSIDWT-SPIRiT | 61 | 1.0 | 85 | 1.0 | 107 | 1.0 | 131 | 1.0 | 159 | 1.0 | |||||
3.4 方法的收敛性分析
探讨VSNR值、VHFEN值以及相对误差(Relative Error, RE)随迭代次数k的变化,分析fSIDWT-SPIRiT的收敛性.RE的值计算如下:
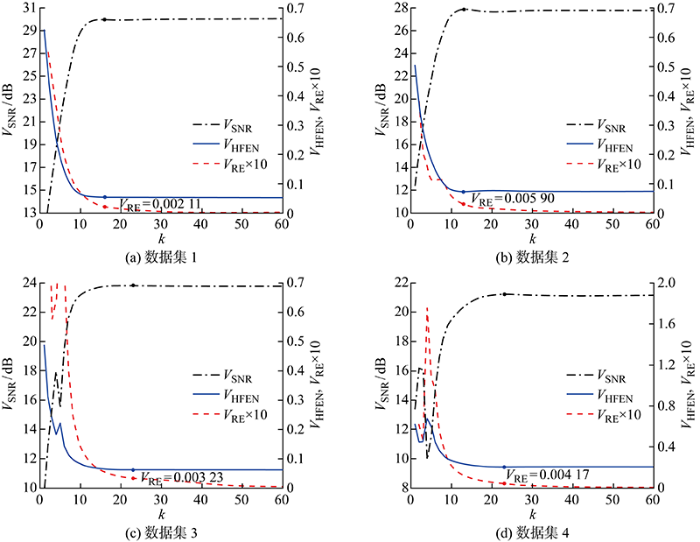
如图7所示,在3倍加速下,对于数据集1,在前10次迭代中VSNR值和VHFEN值变化很快,第10次迭代之后变化较为缓慢,当VRE<2×10-3即迭代次数大于16次时,VSNR值和VHFEN值基本不再变化.此时认为所提方法收敛,利用此特性提前终止算法可以减少计算量.对于其他3个数据集可以得出类似的结论.对于数据集2~4,当VRE分别小于5×10-3、3×10-3和4×10-3即迭代次数分别大于13次、23次和23次时,认为所提方法收敛,可以提前终止算法以减少计算量.
图7
图7
在3倍加速时对4个数据集进行重建的收敛性分析
Fig.7
Convergence analysis of the reconstruction for 4 datasets at 3 times acceleration
4 结语
基于SIDWT和SPIRiT模型,利用pFISTA技术进行求解,提出一种新的快速并行磁共振成像重建方法——fSIDWT-SPIRiT.在4个不同活体数据集上的仿真实验表明:与pFISTA-SPIRiT和SIDWT-SPIRiT两种方法相比,所提方法能获得与之相当的重建质量,而且收敛速度明显更快,平均提升3.5倍和3.9倍.因此,所提方法既保证图像的重建质量,还显著减少图像的重建时间.本文只选用紧框架SIDWT进行实验,后续研究中将考虑使用其他紧框架进一步提升图像的重建性能.
参考文献
Source localisation in concurrent EEG/fMRI: Applications at 7T
[J].
DOI:10.1016/j.neuroimage.2008.10.047
PMID:19049883
[本文引用: 1]

This paper investigates the application of source reconstruction methodologies to EEG data recorded in concurrent EEG/fMRI experiments at 7T. An EEG phantom containing a dipolar current source is described and used to investigate the accuracy of source localisation. Both dipole fitting and beamformer algorithms are shown to yield accurate locations for the dipole within the phantom. Source reconstruction methodologies are also shown to reduce significantly the level of interference in the recorded EEG, caused by the MR scanner. A comparison between beamformer and dipole fitting approaches is made and it is shown that, due to its adaptive weighting parameters, the beamformer provides better suppression of interference when compared to the dipole fit. In addition it is shown that, in the case of the beamformer, use of a high EEG channel density improves the level of interference reduction, and the ratio of measured signal to interference can be improved by a factor of approximately 1.6 if the number of EEG electrodes is increased from 32 to 64. The interference reduction properties of source localisation are shown theoretically, in simulation, and in phantom data. Finally, in-vivo experiments conducted at 7T show that effects in the gamma band can be recorded using simultaneous EEG/fMRI. These results are achieved by application of beamformer methodology to 64 channel EEG data.
非笛卡尔并行磁共振成像重建技术研究新进展
[J].
New research advances in non-Cartesian parallel MRI reconstruction
[J].
Recent advances in parallel imaging for MRI
[J].
Encoding and reconstruction in parallel MRI
[J].The advent of parallel MRI over recent years has prompted a variety of concepts and techniques for performing parallel imaging. A main distinguishing feature among these is the specific way of posing and solving the problem of image reconstruction from undersampled multiple-coil data. The clearest distinction in this respect is that between k-space and image-domain methods. The present paper reviews the basic reconstruction approaches, aiming to emphasize common principles along with actual differences. To this end the treatment starts with an elaboration of the encoding mechanisms and sampling strategies that define the reconstruction task. Based on these considerations a formal framework is developed that permits the various methods to be viewed as different solutions of one common problem. Besides the distinction between k-space and image-domain approaches, special attention is given to the implications of general vs lattice sampling patterns. The paper closes with remarks concerning noise propagation and control in parallel imaging and an outlook upon key issues to be addressed in the future.Copyright (c) 2006 John Wiley & Sons, Ltd.
Compressed sensing
[J].DOI:10.1109/TIT.2006.871582 URL [本文引用: 1]
Compressed sensing regularized calibrationless parallel magnetic resonance imaging via deep learning
[J].DOI:10.1016/j.bspc.2020.102399 URL [本文引用: 1]
SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-Space
[J].
DOI:10.1002/mrm.22428
PMID:20665790
[本文引用: 2]

A new approach to autocalibrating, coil-by-coil parallel imaging reconstruction, is presented. It is a generalized reconstruction framework based on self-consistency. The reconstruction problem is formulated as an optimization that yields the most consistent solution with the calibration and acquisition data. The approach is general and can accurately reconstruct images from arbitrary k-space sampling patterns. The formulation can flexibly incorporate additional image priors such as off-resonance correction and regularization terms that appear in compressed sensing. Several iterative strategies to solve the posed reconstruction problem in both image and k-space domain are presented. These are based on a projection over convex sets and conjugate gradient algorithms. Phantom and in vivo studies demonstrate efficient reconstructions from undersampled Cartesian and spiral trajectories. Reconstructions that include off-resonance correction and nonlinear l(1)-wavelet regularization are also demonstrated.
Practical parallel imaging compressed sensing MRI: Summary of two years of experience in accelerating body MRI of pediatric patients[C]//2011 IEEE International Symposium on Biomedical Imaging:From Nano to Macro
基于自一致性的磁共振并行成像高效重构算法
[J].
Efficient reconstruction algorithm for parallel magnetic resonance imaging based on self-consistency
[J].
RSPIRIT: Robust self-consistent parallel imaging reconstruction based on generalized Lasso[C]//2016 IEEE 13th International Symposium on Biomedical Imaging
Fast Implementation for compressive recovery of highly accelerated cardiac cine MRI using the balanced sparse model
[J].
DOI:10.1002/mrm.26224
PMID:27059406
[本文引用: 1]

Sparsity-promoting regularizers can enable stable recovery of highly undersampled magnetic resonance imaging (MRI), promising to improve the clinical utility of challenging applications. However, lengthy computation time limits the clinical use of these methods, especially for dynamic MRI with its large corpus of spatiotemporal data. Here, we present a holistic framework that utilizes the balanced sparse model for compressive sensing and parallel computing to reduce the computation time of cardiac MRI recovery methods.We propose a fast, iterative soft-thresholding method to solve the resulting ℓ1-regularized least squares problem. In addition, our approach utilizes a parallel computing environment that is fully integrated with the MRI acquisition software. The methodology is applied to two formulations of the multichannel MRI problem: image-based recovery and k-space-based recovery.Using measured MRI data, we show that, for a 224 × 144 image series with 48 frames, the proposed k-space-based approach achieves a mean reconstruction time of 2.35 min, a 24-fold improvement compared a reconstruction time of 55.5 min for the nonlinear conjugate gradient method, and the proposed image-based approach achieves a mean reconstruction time of 13.8 s.Our approach can be utilized to achieve fast reconstruction of large MRI datasets, thereby increasing the clinical utility of reconstruction techniques based on compressed sensing. Magn Reson Med 77:1505-1515, 2017. © 2016 International Society for Magnetic Resonance in Medicine.© 2016 International Society for Magnetic Resonance in Medicine.
Efficient operator splitting algorithm for joint sparsity-regularized SPIRiT-based parallel MR imaging reconstruction
[J].
DOI:S0730-725X(17)30236-9
PMID:29128678
[本文引用: 3]

Self-consistent parallel imaging (SPIRiT) is an auto-calibrating model for the reconstruction of parallel magnetic resonance imaging, which can be formulated as a regularized SPIRiT problem. The Projection Over Convex Sets (POCS) method was used to solve the formulated regularized SPIRiT problem. However, the quality of the reconstructed image still needs to be improved. Though methods such as NonLinear Conjugate Gradients (NLCG) can achieve higher spatial resolution, these methods always demand very complex computation and converge slowly. In this paper, we propose a new algorithm to solve the formulated Cartesian SPIRiT problem with the JTV and JL1 regularization terms. The proposed algorithm uses the operator splitting (OS) technique to decompose the problem into a gradient problem and a denoising problem with two regularization terms, which is solved by our proposed split Bregman based denoising algorithm, and adopts the Barzilai and Borwein method to update step size. Simulation experiments on two in vivo data sets demonstrate that the proposed algorithm is 1.3 times faster than ADMM for datasets with 8 channels. Especially, our proposal is 2 times faster than ADMM for the dataset with 32 channels.Copyright © 2017 Elsevier Inc. All rights reserved.
TV-RSPIRiT: Total variation regularized based robust self-consistent parallel imaging reconstruction[C]//2019 International Conference on Medical Imaging Physics and Engineering
Image reconstruction with low-rankness and self-consistency of k-space data in parallel MRI
[J].DOI:10.1016/j.media.2020.101687 URL [本文引用: 1]
A guaranteed convergence analysis for the projected fast iterative soft-thresholding algorithm in parallel MRI
[J].DOI:10.1016/j.media.2021.101987 URL [本文引用: 2]
基于K空间采样的MRI重建算法研究
[J].
Research on MRI reconstruction algorithm based on K-space sampling
[J].
Iterative self-consistent parallel magnetic resonance imaging reconstruction based on nonlocal low-rank regularization
[J].
DOI:10.1016/j.mri.2022.01.012
PMID:35114354
[本文引用: 1]

Iterative self-consistent parallel imaging reconstruction (SPIRiT) is an effective self-calibrated reconstruction model for parallel magnetic resonance imaging (PMRI). The joint L1 norm of wavelet or tight frame coefficients and joint total variation (TV) regularization terms are incorporated into the SPIRiT model to improve the reconstruction performance. The simultaneous two-directional low-rankness (STDLR) in k-space data is incorporated into SPIRiT to realize improved reconstruction. Recent methods have exploited the nonlocal self-similarity (NSS) of images by imposing nonlocal low-rankness of similar patches to achieve a superior performance. To fully utilize both the NSS in Magnetic resonance (MR) images and calibration consistency in the k-space domain, we propose a nonlocal low-rank (NLR)-SPIRiT model by incorporating NLR regularization into the SPIRiT model. We apply the weighted nuclear norm (WNN) as a surrogate of the rank and employ the Nash equilibrium (NE) formulation and alternating direction method of multipliers (ADMM) to efficiently solve the NLR-SPIRiT model. The experimental results demonstrate the superior performance of NLR-SPIRiT over the state-of-the-art methods via three objective metrics and visual comparison.Copyright © 2022 Elsevier Inc. All rights reserved.
A fast iterative shrinkage-thresholding algorithm for linear inverse problems
[J].DOI:10.1137/080716542 URL [本文引用: 3]
Projected iterative soft-thresholding algorithm for tight frames in compressed sensing magnetic resonance imaging
[J].
DOI:10.1109/TMI.2016.2550080
PMID:27071164
[本文引用: 3]

Compressed sensing (CS) has exhibited great potential for accelerating magnetic resonance imaging (MRI). In CS-MRI, we want to reconstruct a high-quality image from very few samples in a short time. In this paper, we propose a fast algorithm, called projected iterative soft-thresholding algorithm (pISTA), and its acceleration pFISTA for CS-MRI image reconstruction. The proposed algorithms exploit sparsity of the magnetic resonance (MR) images under the redundant representation of tight frames. We prove that pISTA and pFISTA converge to a minimizer of a convex function with a balanced tight frame sparsity formulation. The pFISTA introduces only one adjustable parameter, the step size, and we provide an explicit rule to set this parameter. Numerical experiment results demonstrate that pFISTA leads to faster convergence speeds than the state-of-art counterpart does, while achieving comparable reconstruction errors. Moreover, reconstruction errors incurred by pFISTA appear insensitive to the step size.
Spatiotemporal flexible sparse reconstruction for rapid dynamic contrast-enhanced MRI
[J].DOI:10.1109/TBME.2021.3091881 URL [本文引用: 1]
MR image reconstruction using block matching and adaptive kernel methods
[J].DOI:10.1371/journal.pone.0153736 URL [本文引用: 1]
Joint image reconstruction and sensitivity estimation in SENSE (JSENSE)
[J].Parallel magnetic resonance imaging (pMRI) using multichannel receiver coils has emerged as an effective tool to reduce imaging time in various applications. However, the issue of accurate estimation of coil sensitivities has not been fully addressed, which limits the level of speed enhancement achievable with the technology. The self-calibrating (SC) technique for sensitivity extraction has been well accepted, especially for dynamic imaging, and complements the common calibration technique that uses a separate scan. However, the existing method to extract the sensitivity information from the SC data is not accurate enough when the number of data is small, and thus erroneous sensitivities affect the reconstruction quality when they are directly applied to the reconstruction equation. This paper considers this problem of error propagation in the sequential procedure of sensitivity estimation followed by image reconstruction in existing methods, such as sensitivity encoding (SENSE) and simultaneous acquisition of spatial harmonics (SMASH), and reformulates the image reconstruction problem as a joint estimation of the coil sensitivities and the desired image, which is solved by an iterative optimization algorithm. The proposed method was tested on various data sets. The results from a set of in vivo data are shown to demonstrate the effectiveness of the proposed method, especially when a rather large net acceleration factor is used.
fastMRI: A publicly available raw k-space and DICOM dataset of knee images for accelerated MR image reconstruction using machine learning
[J].DOI:10.1148/ryai.2020190007 URL [本文引用: 2]