中央空调系统包含机组、水泵、末端多种设备,传统的控制方式为固定控制参数,而优化控制方式包含总体优化控制和具体设备优化控制.如Tang等[3]利用优化机组的启动时间和运行数量的方式将空调系统预冷时间缩短约0.5 h,降低空调系统晨间启动能耗.Zhao等[4]简化空调系统的冷却侧模型,利用在线优化方式提出一种水流量优化策略,降低3.45%的系统能耗.文献[5]则实时优化整个空调系统的送风温度、冷冻水供水温度和冷却水出水温度,通过TRNSYS模型验证发现相比传统控制方式,该方式可节约4.48%~10.85%的能耗.Chan等[6]集成了遗传算法(Genetic Algorithm, GA)以优化基于神经网络建立的冷水机组模型,与手动分配负载的方式相比,在55%~95%冷负载下节约14.55%左右的总能耗.
种群优化算法在各种实际问题中已得到具体应用.蔡晖等[7]利用粒子群算法优化多目标协调控制器的参数,有助于“双碳”背景下电力系统低碳稳定运行.杨博等[8]采用自适应蝠鲼觅食优化算法,既改善配电网的电压分布与有功功率的损耗,又兼顾经济性.薛晗等[9]基于文化萤火虫算法优化广义回归神经网络,提高了船舶交通流量的预测精度,不易陷入局部最优.在节能领域,种群优化算法也得到广泛应用.Afroz等[10]将粒子群算法与神经网络结合,有效降低7.8%的能源消耗.Mohanty等[11]基于GA优化电力市场价格的总体成本,有效减轻用电高峰期的用电负担.Chellamani等[12]构建基于缎蓝园丁鸟算法(Satin Bowerbird Optimizer, SBO)的家庭能源管理系统,有效地将峰均比降低10.28%,且不会影响消费者的舒适度.Tian等[13]提出一种基于SBO的混合预测系统来预测大规模风力发电并网中的风速,具有较好的预测精度和稳定性.Raghav等[14]首次将麻雀搜索算法(Sparrow Search Algorithm, SSA)应用于微电网能源管理问题,对电价弹性建模以准确评估消费者行为对市场价格变化的影响.
提出一种基于轮盘赌规则的改进SSA,并应用于具体的大型中央空调系统的空气调节子系统节能控制.改进的SSA相比于标准的SSA,利用自适应t分布增强算法的全局搜索能力;同时利用轮盘赌的规则使部分群体向最优群体学习,而不仅向最佳者靠近,强化算法跳出局部最优的能力.对 12个基准函数进行仿真实验,并将本文提出的算法应用到大型中央空调系统节能控制,验证了其可行性和有效性.
1 麻雀搜索算法
SSA是由Xue等[18]受麻雀觅食的群体行为启发于2020年提出的群体智能优化算法.麻雀群体主要分为以下3个部分:发现者约占群体的10%~20%,主要负责在解空间内随机搜索,为种群提供觅食方向和区域;跟随者约占群体的80%~90%,负责获取发现者发现的食物;发现者和跟随者均可以成为侦察预警者,占据总群体的10%~20%,负责监控危险,一旦危险来临,侦察预警者会立即离开当前位置.
1.1 初始化
假设初始化群体包含n只麻雀,若优化问题的解空间为D维,则第i只麻雀可表示为
式中:Xi,D为第i只麻雀第D维的值.
1.2 发现者
发现者旨在随机探索解空间,发现食物,其更新公式如下:
式中:
1.3 跟随者
麻雀群体中除了发现者,剩下的均作为跟随者,一部分跟随者会向发现者中找到食物的麻雀靠近,另一部分自身条件较差的跟随者会趋向死亡,具体更新方式如下:
式中:
1.4 侦察预警者
侦察预警者在发现危险来临时将离开当前位置,移动到群体最佳值所在位置的附近,通过下式更新:
式中:
2 改进SSA
2.1 基于t分布更新发现者
t分布随着其参数自由度r发生变化,当r较小时类似于柯西分布,具有较强的全局搜索能力;当r较大时类似于高斯分布,具有较强的局部搜索能力.基于t分布更新发现者如下:
式中::T(r=l)表示t分布,自由度r取当前迭代次数l.
基于t分布更新发现者可使发现者在迭代前期具有较强的全局搜索能力,相较于正态分布能提升标准SSA跳出局部最优、寻找全局最优的能力.
2.2 基于轮盘赌更新侦察预警行为
轮盘赌源于俄罗斯转盘,轮盘赌中的个体被选中概率与其适应度值成正比.轮盘赌选择方法使得适应度最好的个体被选择的概率最大,同时保留其他适应度相对较差的次最佳个体被选择的机会,能使种群向最优群体学习,而非仅向适应度最佳者学习,避免陷入局部最优.基于轮盘赌更新侦察预警者首先根据下式确定参加轮盘赌的最优麻雀群体Xtop,再改进式(5)使侦察预警者向最优群体学习.
式中:
基于轮盘赌更新侦察预警行为如下式所示:
式中:
2.3 改进的SSA
改进的SSA(Improved Sparrow Search Algorithm, ISSA)流程图如图1所示,相比于标准的SSA利用自适应t分布增强了算法的全局搜索能力,同时利用轮盘赌的规则使部分群体向最优群体学习,而不仅向最佳者靠近,取众家之所长,增加获得全局最优解的可能性.
图1
3 ISSA性能分析
为校验ISSA的性能,采用12个测试函数进行验证.在Intel(R) Core(TM) i5-7200U CPU@2.50 GHz 2.70 GHz、内存8.00 GB的Windows 10操作系统和Pycharm 2017下,使用版本为3.8.0的Python作为编译语言对ISSA进行性能验证,并与标准SSA、ISSA1(SSA结合基于t分布更新发现者)和ISSA2(SSA结合基于轮盘赌更新侦察预警行为)进行对比;再将ISSA与已有种群算法,如GA、差分进化算法(Differential Evolution, DE)和SBO进行对比.
3.1 函数测试及参数设置
表1列出12个测试函数的详细信息,包括变量维度和变量范围,变量维度均为30维;其中
表1 ISSA测试函数
Tab.1
| 测试函数 | 范围 | 最小值 |
|---|---|---|
| [-100, 100] | 0 | |
| [-10, 10] | 0 | |
| [-100, 100] | 0 | |
| [-100, 100] | 0 | |
| [-100, 100] | 0 | |
| [-30, 30] | 0 | |
| [-1, 1] | 0 | |
| [-5, 5] | 0 | |
| [-5.12, 5.12] | 0 | |
| [-600, 600] | 0 | |
| [-32, 32] | 0 | |
| [-50, 50] | 0 | |
| [-50, 50] | 0 |
3.2 ISSA的有效性验证
表2 ISSA测试函数优化结果对比
Tab.2
| 测试函数 | ISSA1 | ISSA2 | ISSA | |||||
|---|---|---|---|---|---|---|---|---|
| 平均值 | 标准差 | 平均值 | 标准差 | 平均值 | 标准差 | |||
| F1 | 4.81×10-14 | 1.52×10-13 | 1.09×10-16 | 2.93×10-16 | 1.72×10-16 | 8.11×10-16 | ||
| F2 | 5.78×10-6 | 1.34×10-5 | 5.97×10-8 | 1.60×10-7 | 2.86×10-7 | 9.22×10-7 | ||
| F3 | 1.25×10-11 | 4.12×10-11 | 3.19×10-12 | 8.58×10-12 | 9.38×10-16 | 5.1×10-15 | ||
| F4 | 6.55×10-8 | 1.64×10-7 | 1.96×10-8 | 6.41×10-8 | 5.76×10-9 | 1.85×10-8 | ||
| F5 | 1.06×10-7 | 1.79×10-7 | 1.04×10-9 | 1.10×10-9 | 6.47×10-10 | 5.67×10-10 | ||
| F6 | 4.20×10-6 | 6.38×10-6 | 4.83×10-7 | 4.32×10-7 | 7.47×10-7 | 8.02×10-7 | ||
| F7 | 4.24×10-17 | 2.09×10-16 | 6.63×10-19 | 2.68×10-18 | 6.85×10-18 | 3.19×10-17 | ||
| F8 | 3.52×10-10 | 1.31×10-9 | 8.19×10-13 | 2.41×10-12 | 5.55×10-13 | 1.68×10-12 | ||
| F9 | 3.01×10-14 | 1.05×10-13 | 4.91×10-14 | 1.25×10-13 | 2.75×10-11 | 9.29×10-11 | ||
| F10 | 3.74×10-16 | 1.09×10-15 | 1.47×10-14 | 5.49×10-14 | 3.70×10-18 | 1.34×10-18 | ||
| F11 | 1.68×10-6 | 3.16×10-6 | 4.72×10-10 | 1.91×10-9 | 4.53×10-19 | 2.38×10-9 | ||
| F12 | 2.06×10-8 | 3.77×10-8 | 7.35×10-11 | 8.93×10-11 | 2.71×10-11 | 9.78×10-11 | ||
由表2可见,ISSA和ISSA2的优化结果普遍好于ISSA1的结果,表明基于轮盘赌规则的改进方式提升了算法跳出局部最优的能力;而ISSA的优化结果略优于ISSA2的结果,故结合两种改进策略的ISSA优化效果最好.
3.3 ISSA与传统种群算法对比
针对表1中列出的各测试函数,各算法的均值与标准差如表3所示,各函数的最优指标加粗显示.从表3可以看出标准SSA本身就表现出较好的收敛性,针对测试函数F1~F6和F8,SSA本身的收敛精度在10-5~10-16量级,高出除ISSA外的其他对比算法1个数量级以上,ISSA的收敛精度又比SSA高出2~7个数量级,远优于DE、GA和SBO的优化效果;对于函数F7,ISSA的收敛精度差于DE,但也在10-15以上.对于多峰函数F10~F12,ISSA的收敛精度高出SSA算法4个数量级以上;而对于函数F9的寻优结果略差于SSA算法,但也在10-10以上,且仅相差1个数量级.从这12个测试函数总体上看,ISSA算法相比于SSA算法,测试函数的优化均值寻优精度提升2~4个数量级以上,远优于另外3个对比算法的优化结果.
表3 ISSA与其他种群算法的测试函数优化结果对比
Tab.3
| 测试 函数 | DE | GA | SBO | SSA | ISSA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 平均值 | 标准差 | 平均值 | 标准差 | 平均值 | 标准差 | 平均值 | 标准差 | 平均值 | 标准差 | |||||
| F1 | 3.88×10-5 | 1.08×10-5 | 7.09×10 | 1.34×102 | 1.44×10-3 | 3.46×10-4 | 1.86×10-12 | 8.75×10-12 | 1.72×10-16 | 8.11×10-16 | ||||
| F2 | 7.58×10-4 | 1.49×10-4 | 1.79×10 | 9.34×10-1 | 5.78×10-2 | 2.16×10-2 | 4.76×10-5 | 1.77×10-4 | 2.86×10-7 | 9.22×10-7 | ||||
| F3 | 2.55×10-3 | 5.98×10-4 | 8.05×103 | 9.54×103 | 1.97×10 | 5.77×10 | 5.94×10-9 | 3.04×10-8 | 9.38×10-16 | 5.10×10-15 | ||||
| F4 | 2.57 | 1.13 | 4.68×10 | 4.64 | 5.68 | 1.32 | 7.50×10-7 | 2.07×10-6 | 5.76×10-9 | 1.85×10-8 | ||||
| F5 | 3.92×10-5 | 1.21×10-5 | 3.07×10 | 5.09×10 | 1.69×10-3 | 6.45×10-4 | 2.31×10-6 | 5.52×10-6 | 6.47×10-10 | 5.67×10-10 | ||||
| F6 | 7.71×10 | 4.46×10 | 2.22×103 | 3.94×103 | 1.66×102 | 1.57×102 | 1.51×10-5 | 2.69×10-5 | 7.47×10-7 | 8.02×10-7 | ||||
| F7 | 4.57×10-23 | 2.07×10-22 | 9.41×10-7 | 4.91×10-6 | 4.52×10-11 | 3.29×10-11 | 4.95×10-16 | 2.13×10-15 | 6.85×10-18 | 3.19×10-17 | ||||
| F8 | 1.72×102 | 2.32×102 | 1.77×102 | 2.32×10 | 3.14 | 2.66 | 9.80×10-10 | 3.84×10-9 | 5.55×10-13 | 1.68×10-12 | ||||
| F9 | 6.73×10 | 1.14×10 | 6.59×10 | 5.93 | 2.59×10 | 8.05 | 8.22×10-12 | 3.02×10-11 | 2.75×10-11 | 9.29×10-11 | ||||
| F10 | 3.89×10-4 | 2.63×10-4 | 1.53 | 8.73×10-1 | 4.57×10-2 | 1.81×10-2 | 9.88×10-14 | 4.47×10-12 | 3.70×10-18 | 1.34×10-18 | ||||
| F11 | 1.58×10-3 | 2.16×10-3 | 2.26 | 1.07 | 1.70 | 1.59 | 1.97×10-6 | 8.11×10-6 | 4.53×10-19 | 2.38×10-9 | ||||
| F12 | 3.20×10-6 | 5.53×10-6 | 2.45 | 2.42 | 3.46 | 4.26 | 2.00×10-6 | 2.41×10-6 | 2.71×10-11 | 9.78×10-11 | ||||
将标准差作为评价算法收敛稳定性的指标,由表3可见,针对单峰函数F1~F6和F8,SSA本身的收敛精度在10-4~10-12量级,优于除ISSA外的另3个算法;而ISSA的收敛稳定性比SSA高出 2~7个数量级;对于函数F7,ISSA的收敛稳定性相对DE较差,但是优于GA和SBO,同时高出SSA两个数量级.ISSA展现了最佳的收敛稳定性,其收敛稳定性高出SSA算法3个数量级以上;对于函数F9的收敛稳定性略差于SSA算法,但是处于同一数量级.从这12个测试函数总体上看,ISSA算法相比于SSA算法,测试函数的收敛稳定性平均提升3个数量级以上,远优于另外3个对比算法的优化结果.
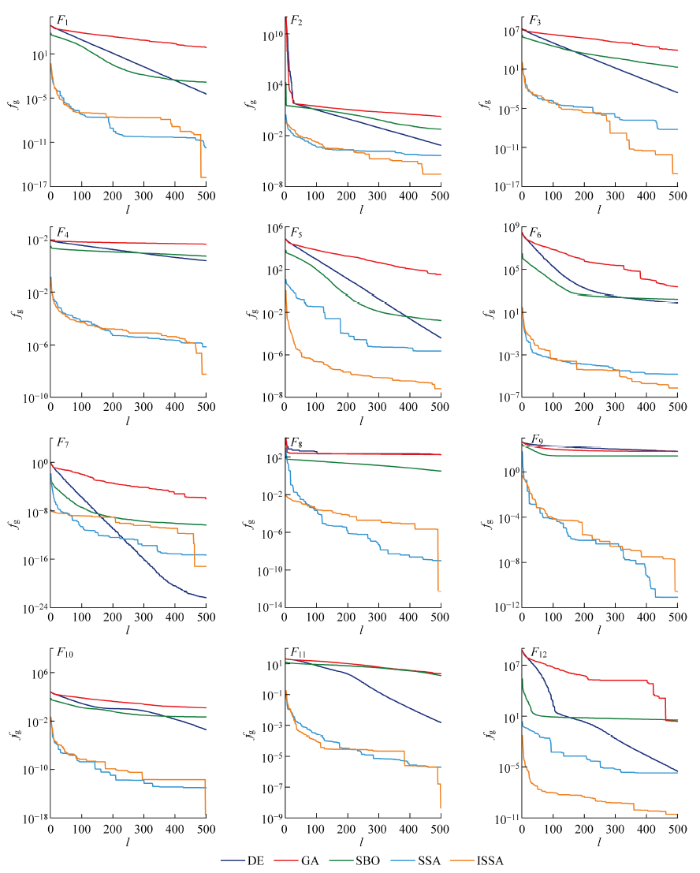
为展现ISSA的收敛速度,以图2展示5种优化算法针对12个测试函数的收敛曲线.总体上看,ISSA和SSA的收敛速度普遍高于其他算法.对于函数F1~F4、F6和F9~F11,ISSA与SSA在迭代前期保有接近的收敛速度;而在迭代后期ISSA仍保有较好的搜索能力,可以跳出局部最优.对于函数F5和F12,ISSA在迭代初期就展现出远优于其他对比算法的收敛速度,而在达到最大迭代次数时适应度仍具有继续减小的趋势.对于函数F7和F8,ISSA在迭代初期的收敛速度略差于SSA,但可以看到SSA很快陷入局部最优,由于引入基于轮盘赌的种群学习规则,ISSA在迭代后期仍能有效跳出局部最优,得到较好的适应度值.
图2
图2
ISSA与其他算法在12个测试函数下的迭代曲线
Fig.2
Iteration curves of ISSA and other algorithms under 12 test functions
综上所述,ISSA对12个测试函数在收敛结果上有一定程度的优化,且收敛稳定性和收敛速度也得到有效改善.同时,ISSA能有效避免陷入局部最优,即使在迭代后期,仍保持较好的跳出局部最优能力,由此可证明ISSA的可行性和优越性.
4 实际应用
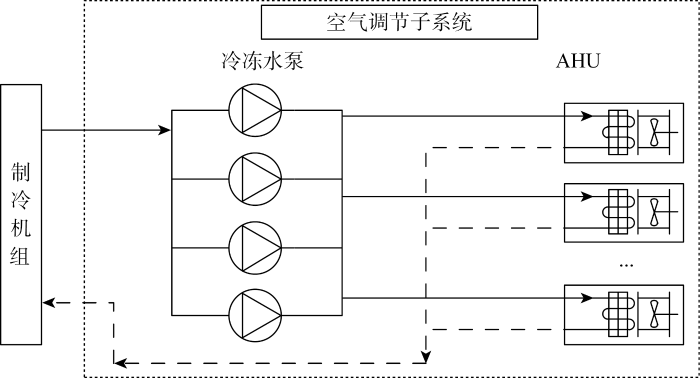
利用上海市某大型公共建筑集中空调系统的一个空气调节子系统中各空气处理单元(Air Handling Unit, AHU)的送风温度优化设定问题验证ISSA应用于实际工程中的可行性.此空调调节子系统的一套泵组及其对应末端如图3所示,其中包含4个型号相同的冷冻水泵和64个型号相同的变频空气处理单元.冷冻水泵负责为冷冻水从机组流向末端AHU提供动力;AHU由冷、热盘管和风机组成,冷、热盘管负责调节末端送风温度以改善室内环境,风机是其耗能部件,为送风提供动力.原系统以固定控制参数即固定送风温度19 ℃运行,在面对负荷变化时会出现过冷或供冷不足的情况, 既易造成能耗浪费,也会造成室内环境不舒适.
图3
图3
集中空调系统的空气调节子系统
Fig.3
Air conditioning subsystem of central air conditioning system
4.1 空气调节子系统能耗模型
空气调节子系统耗能部件主要包含风机和水泵,二者的能耗模型通过下式建立:
式中:Ppump, Pfan分别表示水泵功率和风机功率;βpump, βfan分别为水泵和风机的校正系数;av,bv (v=0,1,2,3)为设备模型拟合系数;Gwater,max, Gwater,min分别为冷冻水质量流量Gwater的上下限制;Gair,max,Gair,min分别为空气体积流量Gair的上下限制;相关系数以及约束由设备厂家给出.
水泵模型与风机模型的耦合关系通过换热器模型[19]建立:
式中:
由上式可建立风机能耗与送风温度之间的关系:
因为
所以
因为
所以
式中:
水泵能耗与送风温度之间的关系如下:
可得
因为
所以
故空气调节子系统总能耗可表示为
式中:
4.2 结果分析
以式(14)为目标函数进行优化,优化参数为64维的送风温度变量,目标函数为4台水泵和64台风机的总体能耗.假设式(13)中的传热系数随进出口温度变化很小,计算过程中视为常数.
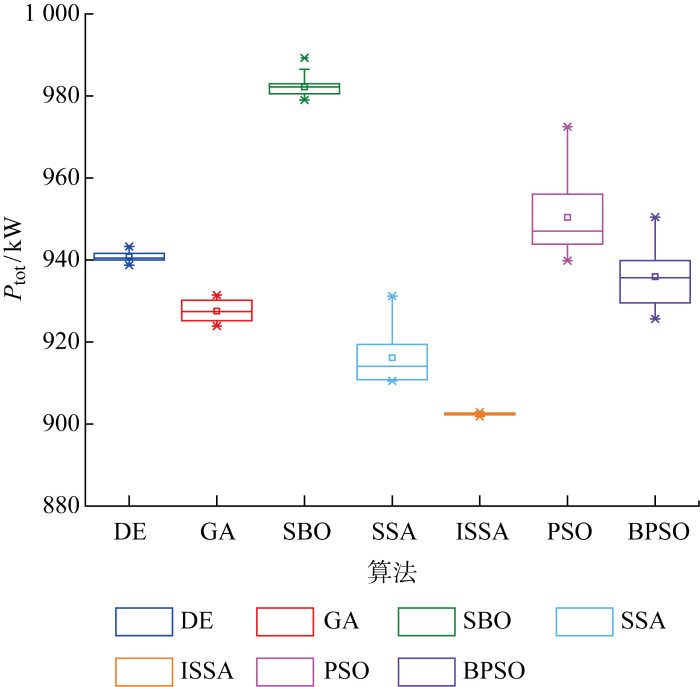
利用上述对比的5种算法和陈阳等[20]在类似研究中应用的天牛须-粒子群(Beetle Antennae Search-Particle Swarm Optimization, BPSO)算法进行模型优化,每种算法各计算30次,计算结果如图4所示.由图可见,ISSA的性能提升效果最好,相比于原策略降低系统能耗302.84 kW,节约能耗约25.13%,远优于SBO而略优于标准SSA.陈阳等[20]提出的BPSO算法优化结果和GA接近,但也低于ISSA.从图4可以看出,ISSA在针对实际问题时表现出优异的稳定性,标准差为0.26,优于SSA的6.09.总的来说,ISSA在此具体实际问题中较好的寻优结果和鲁棒性,验证了ISSA解决实际工程问题的可行性.
图4
图4
ISSA与其他算法对比优化结果
Fig.4
Comparison of optimization results between ISSA and other algorithms
5 结论
基于轮盘赌规则提出了一种改进的SSA——ISSA,能够稳定有效地应用于实际系统的节能优化控制,结论如下:
(1) ISSA寻优性能较SSA得到有效提升.在12个测试函数中,寻优精度和收敛稳定性大多提升2个数量级以上.
(2) ISSA的收敛速度远优于其他算法,较SSA略有提高,同时保有更好的全局寻优能力以跳出局部最优.引入轮盘赌的规则使部分群体向最优群体学习,而不仅向最佳者靠近,取众家之所长,增加获得全局最优解的可能性.
(3) ISSA针对实际空气调节子系统能耗优化问题表现出很好的节能潜力.相比于原有控制策略,降低系统能耗302.84 kW,节约能耗25.13%.
参考文献
Energy policy and standard for built environment in China
[J].DOI:10.1016/j.renene.2005.01.013 URL [本文引用: 1]
Towards sustainable-energy buildings
[J].DOI:10.1016/S0306-2619(03)00059-X URL [本文引用: 1]
Optimal control strategy of central air-conditioning systems of buildings at morning start period for enhanced energy efficiency and peak demand limiting
[J].DOI:10.1016/j.energy.2018.03.032 URL [本文引用: 1]
Study on simplified energy-efficient control methods of HVAC cooling water system from the global online optimization perspective
[J].
Distributed real-time optimal control of central air-conditioning systems
[J].
Application of artificial neural network and genetic algorithm to the optimization of load distribution for a multiple-type-chiller plant
[J].DOI:10.1007/s12273-017-0363-2 URL [本文引用: 1]
“双碳”背景下线间潮流控制器多目标协调控制策略
[J].
A coordination control strategy of interline power flow controller in carbon peaking and carbon neutrality
[J].
基于自适应蝠鲼觅食优化算法的分布式电源选址定容
[J].
Optimal sizing and placement of distributed generation based on adaptive manta ray foraging optimization
[J].
基于文化萤火虫算法-广义回归神经网络的船舶交通流量预测
[J].
Vessel traffic flow prediction based on CFA-GRNN algorithm
[J].
Predictive modelling and optimization of HVAC systems using neural network and particle swarm optimization algorithm
[J].
A genetic algorithm-based demand side management program for implementation of virtual power plant integrating distributed energy resources
[C]//
An optimized methodical energy management system for residential consumers considering price-driven demand response using satin bowerbird optimization
[J].
A novel wind speed forecasting system based on hybrid data preprocessing and multi-objective optimization
[J].DOI:10.1016/j.apenergy.2018.09.012 URL [本文引用: 1]
Analytic Hierarchy Process (AHP)-Swarm intelligence based flexible demand response management of grid-connected microgrid
[J].DOI:10.1016/j.apenergy.2021.118058 URL [本文引用: 1]
混沌麻雀搜索优化算法
[J].
Chaos sparrow search optimization algorithm
[J].
Environmental impact analysis and enhancement of factors affecting the photovoltaic (PV) energy utilization in mining industry by sparrow search optimization based gradient boosting decision tree approach
[J].DOI:10.1016/j.energy.2021.122561 URL [本文引用: 1]
A novel swarm intelligence optimization approach: Sparrow search algorithm
[J].