随着全球能源消耗量的日益增长,大气中二氧化碳含量逐年升高,导致全球极端气候现象频发[1 ] .为此,世界各国均提出了控制碳排放以及实现碳达峰、碳中和的目标,我国于2020年9月正式提出“双碳”目标,力争于2030年前实现碳达峰,2060年前实现碳中和.当前电力行业二氧化碳排放约占我国能源活动二氧化碳排放的40%,推进电力部门脱碳,加速终端能源的电气化是推动能源系统低碳转型和长期温室气体减排的主要手段[2 ] .因此,建设以可再生能源为主体的新型电力系统将成为实现“双碳”目标的重要途径[3 ] .
在以可再生能源为主体的新型电力系统中,风、光、水等一次能源供应与气象条件密切相关,可再生能源出力存在较大随机性与不确定性[4 -5 ] ,同时叠加负荷的不确定性,导致系统维持电力供需动态平衡的难度大幅增加,因此需要提升系统灵活性[6 ] 以确保系统安全稳定运行[7 ] .同时,可再生能源出力易受天气影响,容易出现负荷高且可再生能源出力低的情况,导致系统容量充裕性不足使系统面临停电风险[8 ⇓ -10 ] .传统基于持续负荷曲线和装机容量的电源规划模型已无法适应在高比例可再生能源情况下对系统的灵活性和容量充裕性要求.
针对高比例可再生能源电力系统的电源规划问题,现有研究在系统灵活性或容量充裕性问题上存在一定局限性.Bertsch等[11 ] 考虑多种灵活调节资源的规划,并分别对火电爬坡、机组启停、储能充放等灵活性约束建模,形成正负灵活性资源约束集,但仅考虑了负荷平衡约束而无其他容量充裕性约束.黄旭祥等[12 ] 建立了内嵌时序生产模拟的双层混合整数线性规划模型,协同规划火电、可再生能源与储能容量,同时包含火电等电源灵活性的精确建模,但未对系统容量充裕性进行明确约束.姜海洋等[13 ] 建立了协同规划源网荷储灵活性资源的线性规划模型,并内嵌全年8 760时段生产模拟,不仅包含多种灵活性约束还考虑可再生能源长时间尺度的波动性,但只是简单调节负荷曲线来确保系统容量充裕性.Kargarian等[14 ] 在电源规划时考虑了储能和快速爬坡机组的容量联合优化,并考虑调频性能约束,但同样未考虑系统容量充裕性约束.杨珺等[15 ] 在电源规划模型中引入了灵活性裕量约束,并内嵌生产运行模拟模型,同时直接引入最大失负荷概率约束,但原模型过于复杂难以求解,且简化后的模型并不能确保成本达到最优和足够的容量充裕性.鉴庆之等[16 ] 建立了包含规划层、运行层、灵活层的3层电源规划模型,针对机组启停和爬坡性能进行了详细建模,但过高估计了系统容量充裕性.何俊[17 ] 提出了一种基于置信容量的微电网风光储电源规划方法,根据系统可靠性需求,利用蒙特卡洛随机模拟确定系统总体置信容量水平,并以成本最小化为目标确定容量配置,保证了系统容量充裕性,但未考虑微电网中燃气机组灵活性约束.
针对电力系统灵活性问题,主要通过配置多种灵活调节资源提升系统灵活性,使系统能应对可再生能源和负荷的波动性和不确定性.灵活调节资源主要包括可调节的传统发电机组、储能系统[18 ] 、需求侧响应[19 ] 等,不同类型资源各有优劣,例如火电机组出力稳定、可靠性高,但碳中和背景下其出力受到碳排放额限制;储能可以削峰填谷,出力调节速度快,但投资成本高;需求侧响应资源投资成本低、响应较快,但响应价格较高且需要完善的市场机制配合.因此,在进行电源规划时应统筹考虑上述资源特性,以反映不同机组之间出力特性的互补关系.
针对电力系统容量充裕性问题,主要通过配置一定比例的装机容量裕度,使系统在机组突发故障停运或受一次能源影响降低出力时仍有充足的发电容量[20 ] .由于不同机组故障率以及一次能源禀赋不同,装机容量相同的机组对系统容量充裕性的贡献未必相同,特别是风力发电(简称风电)、光伏等新能源,传统电源规划模型中基于机组装机容量的系统充裕性约束已不适用于高比例可再生能源电力系统.为衡量不同停运率的火电机组所能承担的负荷大小,Garver[21 ] 提出了置信容量的概念,随后被推广应用于风电、光伏等可再生能源以及储能[22 ⇓ -24 ] .置信容量可以用来衡量系统容量充裕性,使得不同类型电源的容量充裕性可以在同一水平下进行相互比较[25 ] .然而,由于储能置信容量与系统装机结构等边界条件非线性相关,难以直接在规划模型中计算,目前尚无规划模型考虑储能置信容量.
为此,综合考虑系统灵活性和容量充裕性,建立包括传统火电、可再生能源、储能及需求侧响应等资源在内的多电源与储能规划模型,内嵌全年 8 760 时段生产运行模拟,并采用置信容量建立系统容量充裕性约束.针对储能置信容量与决策变量非线性耦合的问题,通过分析储能置信容量与系统其他因素的关系,设计一种迭代求解算法,最后基于某区域电网模型验证了规划模型的可行性与有效性.与传统电力系统规划模型相比,所提模型具有如下创新点:① 基于快速机组组合模型,统筹考虑包括传统火电、可再生能源、储能及需求侧响应等资源的运行模型,实现规划模型内嵌 8 760 时段产模拟,在小时级的精度上考虑可再生能源出力波动对系统供需平衡的影响,保障系统电源结构具有足够的灵活性;② 分析储能置信容量与装机结构等边界条件之间的关系,并使用置信容量衡量风电、光伏、储能等资源对系统容量充裕性的实际贡献,建立了考虑储能与需求响应资源的容量充裕性约束,确保最小化投资成本的同时系统有充足的置信容量,从而避免因可再生能源出力受限导致的实际可用发电容量不能满足负荷需求的问题;③针对规划结果与储能置信容量之间的非线性耦合关系设计一种基于迭代的解耦求解算法,使每次迭代的模型均为线性规划模型,可直接调用商业求解器快速求解,加快模型求解速度.
1 考虑需求响应资源和储能容量价值的新型电力系统规划方法
1.1 规划模型概述
规划模型综合考虑系统灵活性约束与容量充裕性约束,以系统总成本最小为目标,基于时序生产模拟规划多电源与储能的最优容量.在灵活性约束方面,模型重点考虑火电机组的最短启停时间、爬坡、出力上下限等约束.由于传统机组组合模型为混合整数线性规划问题,当系统规模较大时求解速度较慢甚至无法求解,因此通过采用适合大规模可再生能源系统规划建模的快速机组组合模型[26 ] ,在大幅缩短求解时间的同时保留规划模型所要求的精度.在容量充裕性约束方面,模型统筹考虑火电、风电、光伏、水力发电(简称水电)、储能、需求侧响应资源的置信容量,由于储能置信容量与系统可再生能源装机容量等因素非线性相关,所以提出一种适用于电源规划模型的储能置信容量动态迭代算法,将容量充裕性约束线性化,便于模型使用线性规划求解器求解.
1.2 考虑需求响应资源和储能容量价值的系统容量充裕性约束
1.2.1 间歇性可再生能源的置信容量
现有针对间歇性可再生能源的置信容量定义主要分为4类,分别是等效确定容量(EFC)、等效载荷容量(ELCC)、等效常规机组(ECPP)、保证出力(GC).EFC是指可再生能源可替代的完全可靠的常规发电机组容量,即保证系统可靠性指标不变的情况下,用可靠常规发电机组代替可再生能源发电机组;ELCC是指保证系统可靠性指标不变的情况下,系统新增可再生能源机组后系统可额外承载的负荷容量;ECPP与EFC类似,区别在于使用的常规机组具有一定强迫停运率;GC定义为在一定置信度下可再生能源的可用发电容量.上述4种置信容量中,EFC、ELCC、ECPP均需要通过大量计算才能获得,但GC定义的置信容量未考虑间歇性可再生能源出力与负荷的同时性问题,即可再生能源出力大小对系统容量充裕性的影响主要在尖峰时段内,因此选择历年系统负荷最大的1%时段(t 1% )内间歇性电源的平均出力与其装机容量之比作为其置信容量:
(1) C k r = ∑ t ∈ t 1 % α k r ( t ) 8760 × 0.05 , k ∈ Ω r , r ∈ R
式中:C k r k 表示机组序号;r 表示可再生能源类型;α k r Ωr 为可再生能源机组集合;R 为可再生能源技术集合,包括风电(w)、光伏(s)、水电(h).
1.2.2 储能系统的置信容量
储能本身不产生能量,在高比例可再生能源电力系统中,储能主要通过将低谷时段电量平移到尖峰时段提高系统容量充裕性,因此其对系统容量充裕性的贡献同时受限于装机容量和存储电量,可类比风电、光伏等电源,以置信容量衡量其对系统容量充裕性的贡献[23 -24 ] .目前关于储能置信容量的定义尚未达成共识,以文献[23 ]的定义为准,将“引入储能前后净负荷(即负荷减去储能净输出功率)曲线最高的100个时段平均值之差”作为储能置信容量.显然,储能的置信容量与多种因素有关,其中主要因素包括储能系统净负荷大小与波动情况即负荷减去可再生能源理论出力、最大持续放电时间、储能渗透率,其中系统净负荷又与波动情况、负荷、可再生能源装机容量、可再生能源容量因数序列有关,其函数关系为
(2) C e s = f ( α r , I r , D , E e s , P e s )
式中:C es 为储能置信容量比例系数,取值范围在[0,1]区间;Ir 为可再生能源装机容量;D 为系统负荷;E es 为储能电容量;P es 为储能功率.
由于αr 和D 为系统固有属性,与规划无关,以下逐项分析C es 与Ir ,E es ,P es 的关系.假设E es ,P es 充足,当净负荷波动越大时,储能可平移的峰谷电量越多,储能置信容量也越大,因此C es 和Ir 正相关.当净负荷波动和P es 一定时,E es 越大,储能可平移的峰谷电量越多,储能置信容量越大,因此C es 和E es /P es 正相关,即与储能最大持续放电时间正相关.当净负荷波动和E es /P es 一定时,P es 在从小变大的过程中,对系统的影响也从小到大,当储能对系统影响不可忽略时,其对系统容量充裕性的边际效益递减,C es 将随之减小.储能置信容量系数与各变量之间的关系如图1 所示.
图1
图1
储能置信容量系数与各变量之间的关系
Fig.1
Relationship between capacity credit of energy storage and relevant factors
1.2.3 考虑储能与需求响应资源的容量充裕性约束
在电源规划模型中,系统可靠性通常用电力不足期望值(LOLE)、期望缺供电量(EENS)等指标表示,其本质为在一定边界条件下求得系统可用容量不足以供应负荷的期望,因此对系统可靠性的约束可转化为对系统可用容量的约束,要求在一定置信率的情况下系统可用容量大于峰值负荷,即系统置信容量之和大于峰值负荷:
(3) ∑ k ∈ Ω f n ( 1 - θ k ) ( S f k + I f k ) + ∑ r ∈ R ∑ k ∈ Ω n r C k r ( S k r + I k r ) + ∑ k ∈ Ω n e s C k e s ( S k e s + I k e s ) + μ n S n d r ≥ D n ( 1 + β c c ) , ∀ n
式中: θ k S f k , S k r , S k e s I f k , I k r , I k e s S n d r D n β c c Ω f n , Ω n r , Ω n e s θk 通常作为其置信容量系数.可再生能源和储能的置信容量系数已在前文定义.对于需求侧响应资源,考虑实际响应时由于通信线路、用户参与度等因素,存在响应失败的可能,所以设置需求侧响应可用系数μn .
为保证系统装机容量满足N -1约束,即系统中任意一台机组故障后剩余机组仍能满足最大负荷需求,同时考虑系统负荷预测和实际运行的偏差以及机组检修等因素,置信容量裕度的取值应满足如下条件:
(4) β c c = m a x S m a x D m a x , β r
式中:S max 为系统中单台机组最大装机容量;βr 为备用容量比例;D max 为系统负荷最大值.
1.3 基于快速机组组合模型的系统灵活性约束
由于风电、光伏出力的随机性,需要在规划模型中考虑系统的灵活性,以小时级精度进行机组组合优化,使系统满足多种灵活性约束.传统机组组合模型为混合整数线性规划,在装机规模大、长时间尺度的系统优化中计算量极大,因此采用快速机组组合模型对火电机组灵活性约束建模,同时分别建立了可再生能源、储能及需求侧响应资源的运行模型.
1.3.1 快速机组组合模型约束集
火电机组的快速机组组合模型[3 ,26 -27 ] 如下:
(5) 0 ≤ S O k ( t ) , S U k ( t ) , S D k ( t ) ≤ S f k + I f k , ∀ k , t
(6) S O k ( t ) - S U k ( t ) = S O k ( t - 1 ) - S D k ( t ) , ∀ k , t
(7) A k _ ( t ) S O k ( t ) ≤ P f k ( t ) ≤ A k ¯ ( t ) S O k ( t ) , ∀ k , t
(8) P f k ( t ) - P f k ( t - 1 ) ≤ A k _ ( t ) S U k ( t ) - A k _ ( t ) S D k ( t ) + R U k ( S O k ( t ) - S U k ( t ) - S D k ( t + 1 ) ) , ∀ k , t
(9) P f k t - P f k t - 1 ≥ A k _ t S U k t - A k _ t S D k t - R D k S O k t - S U k t - S U k t - 1 , ∀ k , t
(10) P f k ( t ) ≤ A k ¯ ( t ) ( S O k ( t ) - S U k ( t ) - S D k ( t + 1 ) ) + A k _ ( t ) S U k ( t ) + A k _ ( t ) S D k ( t + 1 ) , ∀ k , t
(11) 0 ≤ S D k ( 1 ) ≤ S O k ( 0 ) , ∀ k
(12) 0 ≤ S D k ( t + 1 ) ≤ S O k ( t ) - ∑ τ = 0 t - 1 S U k ( t - τ ) , 1 ≤ t ≤ T U k - 1 , ∀ k
(13) 0 ≤ S D k ( t + 1 ) ≤ S O k ( t ) - ∑ t = 0 T U k - 2 S U k ( t - τ ) , T U k ≤ t ≤ T - 1 , ∀ k
(14) 0 ≤ S U k ( 1 ) ≤ S f k - S O k ( 0 ) , ∀ k
(15) 0 ≤ S U k ( t + 1 ) ≤ S k - S O k ( t ) - ∑ τ = 0 t - 1 S D k ( t - τ ) , 1 ≤ t ≤ T D k - 1 , ∀ k
(16) 0 ≤ S U k ( t + 1 ) ≤ S k - S O k ( t ) - ∑ τ = 0 T D k - 2 S k D ( t - τ ) , T D k ≤ t ≤ T - 1 , ∀ k
式中: S O k , S U k , S D k P f k A k _ , A k ¯ R U k , R D k T D k , T U k
1.3.2 可再生能源出力约束
(17) 0 ≤ P k r ( t ) ≤ α k r ( t ) ( S k r + I k r ) , ∀ k , t
1.3.3 需求侧响应资源出力约束
(18) 0 ≤ P n d r ( t ) ≤ R n m a x , ∀ n , t
式中:P n d r
1.3.4 储能运行模型约束集
(19) 0 ≤ P k e s , c (t) , P k e s , d (t) ≤ S k e s + I k e s , ∀ k , t
(20) 0 ≤ E k e s (t) ≤ T k e s ( S k e s + I k e s ) , ∀ k , t
(21) E k e s (t) - E k e s (t - 1) = η c k P k e s , c (t) - P k e s , d (t) η d k - γ s k E k e s (t - 1) , ∀ k , t
(22) E k e s ( 0 ) = E k e s ( T ) = λ T k e s ( S k e s + I k e s ) , ∀ k
(23) 0 ≤ P k e s , r t ≤ S k e s + I k e s - P k e s , c t - P k e s , d t , ∀ k , t
(24) P k e s , d (t) + P k e s , r (t) η d k ≤ E k e s (t) - γ s k E k e s (t - 1) , ∀ k , t
(25) P k e s (t) = P k e s , d (t) - P k e s , c (t) , ∀ k , t
式中: P k e s , c , P k e s , d T k e s η c k , η d k , γ s k P k e s , r
1.4 其他约束
(26) ∑ k ∈ Ω f n P f k ( t ) + ∑ r ∈ R ∑ k ∈ Ω n r P k r ( t ) + ∑ k ∈ Ω n e s P k e s ( t ) +
∑ l ∈ Ω n i n P l ( t ) - ∑ l ∈ Ω n o u t P l ( t ) =
D n ( t ) - P n d r ( t ) , ∀ n , t
(27) ∑ k ∈ Ω n f S O k ( t ) + ∑ r ∈ R ∑ k ∈ Ω n r α k r ( t ) ( S k r + I k r ) ×
( 1 - ε k r ) + ∑ k ∈ Ω n e s ( P k e s , r ( t ) + P k e s ( t ) ) +
∑ l ∈ Ω n i n P l ( t ) - ∑ l ∈ Ω n o u t P l ( t ) ≥
( D n ( t ) - P n d r ( t ) ) ( 1 + r d ) , ∀ n , t
(28) - S l - I l ≤ P l ( t ) ≤ S l + I l , ∀ l
(29) ∑ r ∈ R ∑ n ∈ N ∑ k ∈ Ω n r ∑ t P k r ( t ) ≥ ∑ n ∈ N ∑ t D n ( t ) ϕ r p s
式中: ε k r r d Ω n i n , Ω n o u t P l S l I l N [13 ] ,式(29)为可再生能源消纳量政策约束,要求可再生能源发电量必须占总发电量的比例至少为ϕ rps .
1.5 目标函数
(30) m i n ∑ n ∈ N ∑ k ∈ Ω f n [ ∑ t ( X k M , f P f k ( t ) + X k U , f S U k ( t ) ) + X k I , f I f k ] + ∑ n ∈ N ∑ r ∈ R ∑ k ∈ Ω n r X k I , r I k r + ∑ n ∈ N ∑ k ∈ Ω n r ( ∑ t X k M , e s P k e s ( t ) + X k I , e s I k e s ) + ∑ n ∈ N ∑ t X n M , d r P n d r ( t )
式中: X k M , f X k U , f X k I , f , X k I , r , X k I , e s X k M , e s X k M , d r
1.6 模型求解算法流程
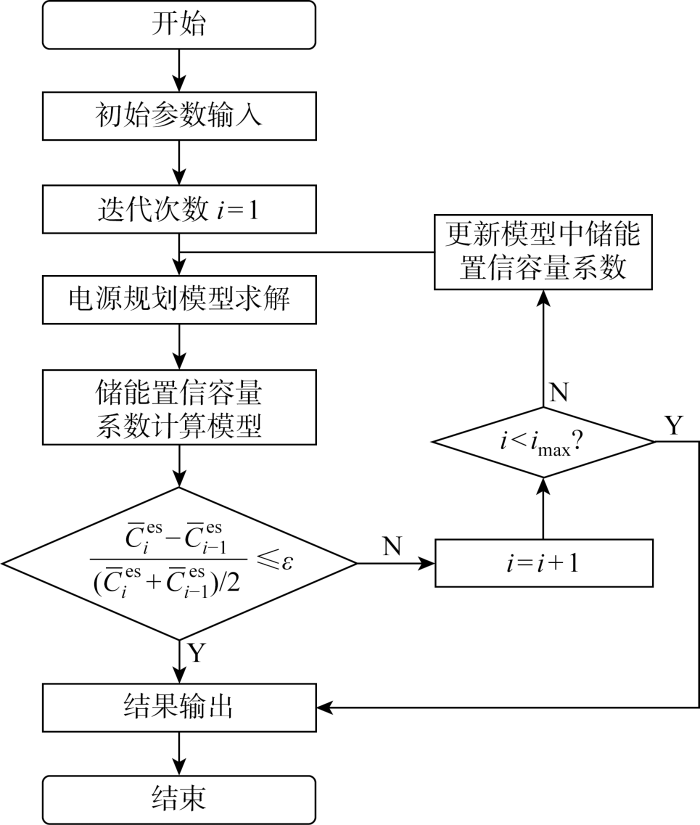
式(3)~(30)所构建的考虑需求侧响应与储能容量价值的新型电力系统规划模型为线性规划模型,可直接通过Gurobi等商业求解器求解.但模型中的储能置信容量系数为系统可再生能源装机比例、储能装机规模等参数的函数,需要迭代求解,具体流程如图2 所示.
图2
图2
模型求解流程图
Fig.2
Model solving process
首先需要指定储能置信容量系数的初值,由于置信容量系数只能在[0, 1]区间内,所以将初始置信容量系数C ¯ 0 e s ε 判断储能置信容量系数是否收敛,如果为否则用本次计算得到的置信容量系数作为下一次迭代的输入值重新迭代,如果为是则结束程序并输出结果.
由于不同储能设备置信容量系数不同,所以需先定义系统储能置信容量系数C ¯ e s
(31) C ¯ e s = ∑ n ∈ N ∑ k ∈ Ω n e s C k e s ( S k e s + I k e s ) ∑ n ∈ N ∑ k ∈ Ω n e s ( S k e s + I k e s )
2 算例分析
基于中国某区域电网的简化电网模型对所提模型进行求解和验证,该电网覆盖5个省份,共143台火电机组,分类别聚合燃煤、燃气机组以应用快速机组组合模型,规划期为2050年,按3%的负荷增长率预测峰值负荷为510 GW,RPS约束设置为80%,即要求80%的电量来自于可再生能源.由于缺少实际数据,本文未考虑输电线路约束及其扩建,而是考虑最大持续放电时间分别为2、4、6 h的电化学储能以及12 h最大持续放电时间的抽水蓄能,年化投资成本[3 ] 分别为351、486、621、1576 元/(kW·h).规划的电源类型包括煤电、气电、风电、光伏,需求侧响应激励价格设置为 1000~3500 元/MW.
2.1 储能的容量价值
在是否考虑储能装机的两种情况下进行电源规划,从系统装机结构、成本、机组利用时间、弃风弃光率的影响等方面,探讨储能的容量价值.
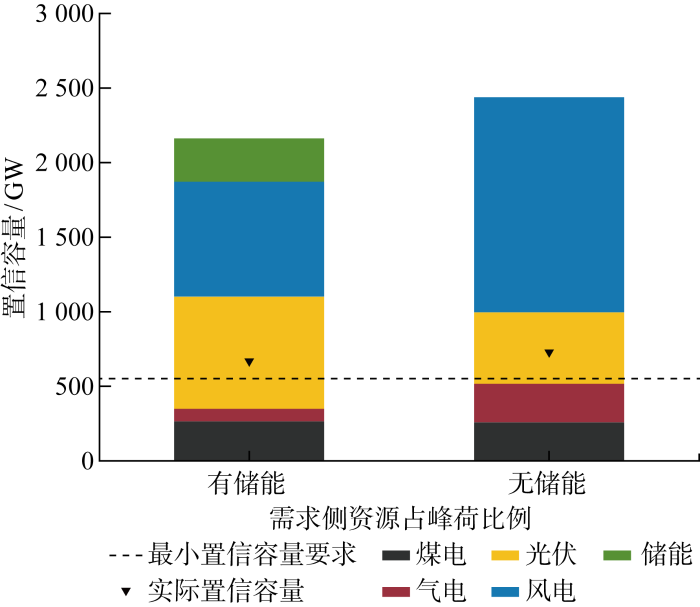
图3 展示了有无储能参与情况下的系统装机情况,两种情况下装机变化较大的是风电、光伏和气电.无储能情况下,负荷高峰时段可再生能源出力可能受到天气限制,因此需要多建气电机组为系统提供容量充裕性;光伏只有白天发电,对系统置信容量贡献有限,因此新建容量远小于风电.有储能参与的情况下,储能具有削峰填谷的作用,可以大幅减少风电和气电的装机,并增加光伏装机.从利用时间看,如表1 所示,储能可以大幅提高煤电和光伏的利用时间,但一定程度上取代了气电作为调峰机组,因此降低了气电的利用时间.同时,系统弃风弃光率从33.6%下降到9.8%,系统装机成本从 12487 亿元下降到 10199 亿元,下降幅度达18.3%,而系统置信容量仍在最小置信容量要求之上.可见,储能的容量价值分别在灵活性和系统容量充裕性上得到了体现,即增加了系统对可再生能源消纳能力,同时减少了气电等调峰机组的装机容量,降低了系统成本.
图3
图3
有无储能参与情况下的装机情况
Fig.3
System installed capacity with and without energy storage scenarios
2.2 不同需求侧响应资源容量的影响
探究系统引入不同需求侧响应容量对系统装机结构的影响,需求侧响应资源容量分别设置为峰值负荷的0%、5%、10%、15%和20%.
2.2.1 系统电源结构
不同需求侧资源容量场景下的系统装机容量如表2 所示,由于RPS设置为80%,即至少要求80%的电量来自于可再生能源,所以系统主要新增装机容量为风电和光伏机组.由于系统容量充裕性和灵活性限制,在没有需求侧响应资源的情况下,系统累计新建了137.8 GW的火电机组和131.1 GW的储能机组,占总新增装机的21.6%.在引入需求侧响应资源后,火电、储能、可再生能源机组装机容量均有所减少,其中火电机组减少幅度最大,而储能和可再生能源装机容量变化不大.需求侧响应资源占比从5%变化到20%的过程中,火电机组新增装机容量从137.8 GW下降到59.9 GW,平均需求侧响应资源每增加1%,火电机组装机容量下降3.9 GW.
从装机成本看,可再生能源和储能装机成本远高于火电,因此系统总装机成本相对变化不大,需求侧响应资源容量从0%增加到20%的过程中,系统装机成本分别为 10199、10138、10053、9943、9862 亿元,平均每1%的需求侧响应容量可以减少16.9亿元装机成本.
2.2.2 需求侧响应资源对火电的替代作用
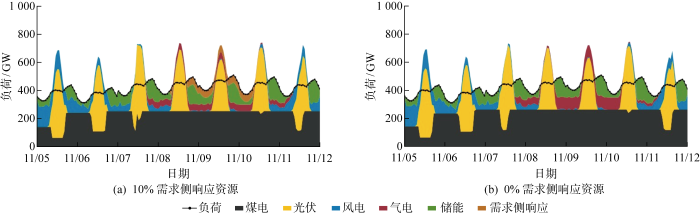
图4 为10%需求侧响应资源和0%需求侧响应资源情形下的电力周平衡图.在11月6日到11月8日期间,由于风力减小,风电机组出力受限,所以无法提供足够的发电容量,负荷主要靠煤电、气电和光伏供给,而光伏电源在傍晚时段出力迅速降低,负荷在此时达到一天中的峰值,主要靠储能白天存储光伏产生的额外电量,并在傍晚释放以平衡负荷.在11月7日,光伏出力受天气影响而降低,若无需求侧响应资源,系统只能多建火电机组以应对可再生能源出力不足的情况.由于可再生能源出力不足为小概率事件,所以此时额外建设的机组年利用时间较少,从而造成资源浪费.而引入了需求侧响应资源后,可由需求侧响应资源应对可再生能源出力不足的情况,优化了系统电源结构,同时由于此类事件出现频率较低,对用户正常用电影响较小.
图4
图4
电力周平衡图
Fig.4
Weekly power balance
2.2.3 系统置信容量
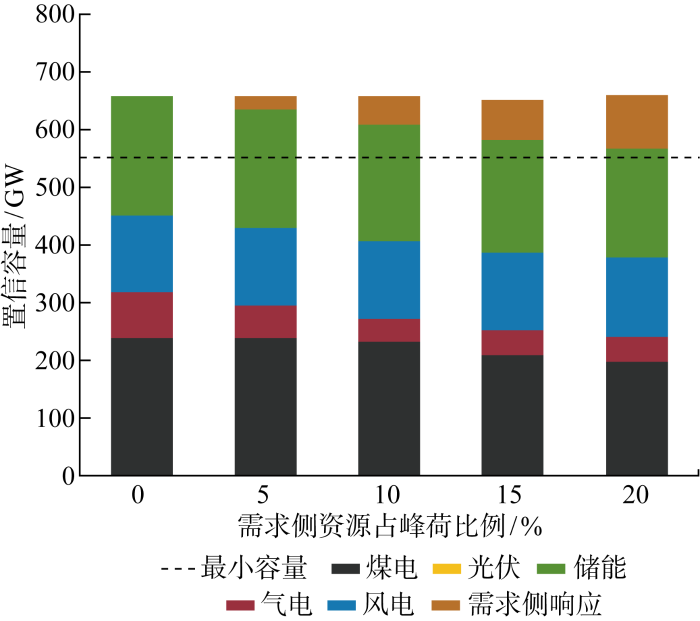
不同需求侧响应资源比例下的系统置信容量如图5 所示,由于RPS约束设置为80%,储能和风电的装机比较充裕,所以系统总体置信容量约在656 GW左右,高于最小置信容量要求.系统总体置信容量与需求侧响应资源接入系统资源比例基本无关,但需求侧响应资源可以代替一部分火电和储能提供的置信容量,因此其他能源提供的置信容量随需求侧响应资源增加而下降.同时,由于可再生能源出力受气象条件影响,无法随负荷大小调整,所以可再生能源置信容量占比较低,系统置信容量主要由火电和储能提供.
图5
图5
不同需求侧响应资源比例下的系统置信容量
Fig.5
System capacity credit at different demand response resource ratios
3 结语
综合考虑以可再生能源为主体的新型电力系统中容量充裕性和灵活性两方面约束,重点分析了储能置信容量与各因素之间的关系,基于快速机组组合和快速储能置信容量算法,建立了考虑需求响应资源和储能容量价值的新型电力系统规划模型,并设计了基于线性规划求解器的迭代求解算法流程,最后基于中国某区域电力系统对所提模型进行了验证.结果表明,以可再生能源为主体的新型电力系统中,主要影响系统成本的约束为系统灵活性约束,基于时序生产模拟的规划模型可精细刻画负荷、可再生能源出力之间的时序耦合以及火电机组爬坡、启停等约束.此外,需求侧响应资源可有效提供系统灵活性,相比新建火电和储能等机组成本更低,引入需求侧响应资源可有效降低系统成本.然而,由于主要讨论了储能和需求侧响应资源的引入对系统投资运行成本和容量充裕性的影响,未能详细分析储能系统对输电阻塞的缓解作用,将在未来研究中进一步讨论.
参考文献
View Option
[1]
MYHRE G BOUCHER O BRÉON F M , et al Declining uncertainty in transient climate response as CO2 forcing dominates future climate change
[J]. Nature Geoscience 2015 , 8 (3 ): 181 -185 .
DOI:10.1038/ngeo2371
[本文引用: 1]
[2]
康重庆 . 能源互联网促进实现“双碳”目标
[J]. 全球能源互联网 2021 , 4 (3 ): 205 -206 .
[本文引用: 1]
KANG Chongqing . Energy Internet promotes the achievement of carbon peak and neutrality targets
[J]. Journal of Global Energy Interconnection 2021 , 4 (3 ): 205 -206 .
[本文引用: 1]
[3]
CHEN X Y LIU Y X WANG Q , et al Pathway toward carbon-neutral electrical systems in China by mid-century with negative CO2 abatement costs informed by high-resolution modeling
[J]. Joule 2021 , 5 (10 ): 2715 -2741 .
DOI:10.1016/j.joule.2021.10.006
URL
[本文引用: 3]
[4]
舒印彪 , 张智刚 , 郭剑波 , 等 . 新能源消纳关键因素分析及解决措施研究
[J]. 中国电机工程学报 2017 , 37 (1 ): 1 -9 .
[本文引用: 1]
SHU Yinbiao ZHANG Zhigang GUO Jianbo , et al Study on key factors and solution of renewable energy accommodation
[J]. Proceedings of the CSEE 2017 , 37 (1 ): 1 -9 .
[本文引用: 1]
[5]
EL-KHATTAM W BHATTACHARYA K HEGAZY Y , et al Optimal investment planning for distributed generation in a competitive electricity market
[J]. IEEE Transactions on Power Systems 2004 , 19 (3 ): 1674 -1684 .
DOI:10.1109/TPWRS.2004.831699
URL
[本文引用: 1]
[6]
鲁宗相 , 李海波 , 乔颖 . 含高比例可再生能源电力系统灵活性规划及挑战
[J]. 电力系统自动化 2016 , 40 (13 ): 147 -158 .
[本文引用: 1]
LU Zongxiang LI Haibo QIAO Ying . Power system flexibility planning and challenges considering high proportion of renewable energy
[J]. Automation of Electric Power Systems 2016 , 40 (13 ): 147 -158 .
[本文引用: 1]
[7]
ZHANG N LU X MCELROY M B , et al Reducing curtailment of wind electricity in China by employing electric boilers for heat and pumped hydro for energy storage
[J]. Applied Energy 2016 , 184 : 987 -994 .
DOI:10.1016/j.apenergy.2015.10.147
URL
[本文引用: 1]
[9]
胡秦然 , 丁昊晖 , 陈心宜 , 等 . 美国加州2020年轮流停电事故分析及其对中国电网的启示
[J]. 电力系统自动化 2020 , 44 (24 ): 11 -18 .
[本文引用: 1]
HU Qinran DING Haohui CHEN Xinyi , et al Analysis on rotating power outage in California, USA in 2020 and its enlightenment to power grid of China
[J]. Automation of Electric Power Systems 2020 , 44 (24 ): 11 -18 .
[本文引用: 1]
[10]
王一 , 朱涛 , 张玉欣 , 等 . 适应中国电力现货市场发展的容量补偿机制初探
[J]. 电力系统自动化 2021 , 45 (6 ): 52 -61 .
[本文引用: 1]
WANG Yi ZHU Tao ZHANG Yuxin , et al Preliminary study on capacity compensation mechanism adapted to development of electricity spot market in China
[J]. Automation of Electric Power Systems 2021 , 45 (6 ): 52 -61 .
[本文引用: 1]
[11]
BERTSCH J GROWITSCH C LORENCZIK S , et al Flexibility in Europe’s power sector—An additional requirement or an automatic complement?
[J]. Energy Economics 2016 , 53 : 118 -131 .
DOI:10.1016/j.eneco.2014.10.022
URL
[本文引用: 1]
[12]
黄旭祥 , 韩学山 , 李家维 , 等 . 大电网储能与各类电源协同规划
[J]. 分布式能源 2019 , 4 (5 ): 67 -74 .
[本文引用: 1]
HUANG Xuxiang HAN Xueshan LI Jiawei , et al Coordinated planning of energy storage and various power sources in large power grid
[J]. Distributed Energy 2019 , 4 (5 ): 67 -74 .
[本文引用: 1]
[13]
姜海洋 , 杜尔顺 , 金晨 , 等 . 高比例清洁能源并网的跨国互联电力系统多时间尺度储能容量优化规划
[J]. 中国电机工程学报 2021 , 41 (6 ): 2101 -2115 .
[本文引用: 2]
JIANG Haiyang DU Ershun JIN Chen , et al Optimal planning of multi-time scale energy storage capacity of cross-national interconnected power system with high proportion of clean energy
[J]. Proceedings of the CSEE 2021 , 41 (6 ): 2101 -2115 .
[本文引用: 2]
[14]
KARGARIAN A HUG G MOHAMMADI J . A multi-time scale co-optimization method for sizing of energy storage and fast-ramping generation
[J]. IEEE Transactions on Sustainable Energy 2016 , 7 (4 ): 1351 -1361 .
DOI:10.1109/TSTE.2016.2541685
URL
[本文引用: 1]
[15]
杨珺 , 李凤婷 , 张高航 . 考虑灵活性需求的新能源高渗透系统规划方法
[J]. 电网技术 2022 , 46 (6 ): 2171 -2182 .
[本文引用: 1]
YANG Jun LI Fengting ZHANG Gaohang . Power system planning method with high new energy penetration considering flexibility requirements
[J]. Power System Technology 2022 , 46 (6 ): 2171 -2182 .
[本文引用: 1]
[16]
鉴庆之 , 刘晓明 , 杨金叶 , 等 . 考虑需求响应的电力系统灵活性资源优化配置
[J]. 现代电力 2021 , 38 (3 ): 286 -296 .
[本文引用: 1]
JIAN Qingzhi LIU Xiaoming YANG Jinye , et al Optimal allocation of power system flexible resources considering demand response
[J]. Modern Electric Power 2021 , 38 (3 ): 286 -296 .
[本文引用: 1]
[17]
何俊 . 基于等可信容量的含风光储微电网电源优化规划研究 [D]. 武汉 : 武汉大学 , 2014 .
[本文引用: 1]
HE Jun . Optimal power planning of micro grid containing wind PV battery power sources based on equivalent credible capacity theory [D]. Wuhan : Wuhan University , 2014 .
[本文引用: 1]
[18]
袁小明 , 程时杰 , 文劲宇 . 储能技术在解决大规模风电并网问题中的应用前景分析
[J]. 电力系统自动化 2013 , 37 (1 ): 14 -18 .
[本文引用: 1]
YUAN Xiaoming CHENG Shijie WEN Jinyu . Prospects analysis of energy storage application in grid integration of large-scale wind power
[J]. Automation of Electric Power Systems 2013 , 37 (1 ): 14 -18 .
[本文引用: 1]
[20]
BILLINTON R HUANG D G . Basic concepts in generating capacity adequacy evaluation
[C]// 2006 International Conference on Probabilistic Methods Applied to Power Systems Stockholm, Sweden : IEEE , 2006 : 1 -6 .
[本文引用: 1]
[21]
GARVER L L . Effective load carrying capability of generating units
[J]. IEEE Transactions on Power Apparatus and Systems 1966 , 85 (8 ): 910 -919 .
[本文引用: 1]
[22]
PUDARUTH G R LI F . Capacity credit evaluation: A literature review
[C]// 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies Nanjing, China : IEEE , 2008 : 2719 -2724 .
[本文引用: 1]
[24]
ZHOU Y T MANCARELLA P MUTALE J . Framework for capacity credit assessment of electrical energy storage and demand response
[J]. IET Generation, Transmission & Distribution 2016 , 10 (9 ): 2267 -2276 .
DOI:10.1049/gtd2.v10.9
URL
[本文引用: 2]
[25]
张宁 , 康重庆 , 肖晋宇 , 等 . 风电容量可信度研究综述与展望
[J]. 中国电机工程学报 2015 , 35 (1 ): 82 -94 .
[本文引用: 1]
ZHANG Ning KANG Chongqing XIAO Jinyu , et al Review and prospect of wind power capacity credit
[J]. Proceedings of the CSEE 2015 , 35 (1 ): 82 -94 .
[本文引用: 1]
[26]
HAN X N CHEN X Y MCELROY M B , et al Modeling formulation and validation for accelerated simulation and flexibility assessment on large scale power systems under higher renewable penetrations
[J]. Applied Energy 2019 , 237 : 145 -154 .
DOI:10.1016/j.apenergy.2018.12.047
URL
[本文引用: 2]
[27]
CHEN X Y LV J J MCELROY M B , et al Power system capacity expansion under higher penetration of renewables considering flexibility constraints and low carbon policies
[J]. IEEE Transactions on Power Systems 2018 , 33 (6 ): 6240 -6253 .
DOI:10.1109/TPWRS.2018.2827003
URL
[本文引用: 2]
Declining uncertainty in transient climate response as CO2 forcing dominates future climate change
1
2015
... 随着全球能源消耗量的日益增长,大气中二氧化碳含量逐年升高,导致全球极端气候现象频发[1 ] .为此,世界各国均提出了控制碳排放以及实现碳达峰、碳中和的目标,我国于2020年9月正式提出“双碳”目标,力争于2030年前实现碳达峰,2060年前实现碳中和.当前电力行业二氧化碳排放约占我国能源活动二氧化碳排放的40%,推进电力部门脱碳,加速终端能源的电气化是推动能源系统低碳转型和长期温室气体减排的主要手段[2 ] .因此,建设以可再生能源为主体的新型电力系统将成为实现“双碳”目标的重要途径[3 ] . ...
能源互联网促进实现“双碳”目标
1
2021
... 随着全球能源消耗量的日益增长,大气中二氧化碳含量逐年升高,导致全球极端气候现象频发[1 ] .为此,世界各国均提出了控制碳排放以及实现碳达峰、碳中和的目标,我国于2020年9月正式提出“双碳”目标,力争于2030年前实现碳达峰,2060年前实现碳中和.当前电力行业二氧化碳排放约占我国能源活动二氧化碳排放的40%,推进电力部门脱碳,加速终端能源的电气化是推动能源系统低碳转型和长期温室气体减排的主要手段[2 ] .因此,建设以可再生能源为主体的新型电力系统将成为实现“双碳”目标的重要途径[3 ] . ...
能源互联网促进实现“双碳”目标
1
2021
... 随着全球能源消耗量的日益增长,大气中二氧化碳含量逐年升高,导致全球极端气候现象频发[1 ] .为此,世界各国均提出了控制碳排放以及实现碳达峰、碳中和的目标,我国于2020年9月正式提出“双碳”目标,力争于2030年前实现碳达峰,2060年前实现碳中和.当前电力行业二氧化碳排放约占我国能源活动二氧化碳排放的40%,推进电力部门脱碳,加速终端能源的电气化是推动能源系统低碳转型和长期温室气体减排的主要手段[2 ] .因此,建设以可再生能源为主体的新型电力系统将成为实现“双碳”目标的重要途径[3 ] . ...
Pathway toward carbon-neutral electrical systems in China by mid-century with negative CO2 abatement costs informed by high-resolution modeling
3
2021
... 随着全球能源消耗量的日益增长,大气中二氧化碳含量逐年升高,导致全球极端气候现象频发[1 ] .为此,世界各国均提出了控制碳排放以及实现碳达峰、碳中和的目标,我国于2020年9月正式提出“双碳”目标,力争于2030年前实现碳达峰,2060年前实现碳中和.当前电力行业二氧化碳排放约占我国能源活动二氧化碳排放的40%,推进电力部门脱碳,加速终端能源的电气化是推动能源系统低碳转型和长期温室气体减排的主要手段[2 ] .因此,建设以可再生能源为主体的新型电力系统将成为实现“双碳”目标的重要途径[3 ] . ...
... 火电机组的快速机组组合模型[3 ,26 -27 ] 如下: ...
... 基于中国某区域电网的简化电网模型对所提模型进行求解和验证,该电网覆盖5个省份,共143台火电机组,分类别聚合燃煤、燃气机组以应用快速机组组合模型,规划期为2050年,按3%的负荷增长率预测峰值负荷为510 GW,RPS约束设置为80%,即要求80%的电量来自于可再生能源.由于缺少实际数据,本文未考虑输电线路约束及其扩建,而是考虑最大持续放电时间分别为2、4、6 h的电化学储能以及12 h最大持续放电时间的抽水蓄能,年化投资成本[3 ] 分别为351、486、621、1576 元/(kW·h).规划的电源类型包括煤电、气电、风电、光伏,需求侧响应激励价格设置为 1000~3500 元/MW. ...
新能源消纳关键因素分析及解决措施研究
1
2017
... 在以可再生能源为主体的新型电力系统中,风、光、水等一次能源供应与气象条件密切相关,可再生能源出力存在较大随机性与不确定性[4 -5 ] ,同时叠加负荷的不确定性,导致系统维持电力供需动态平衡的难度大幅增加,因此需要提升系统灵活性[6 ] 以确保系统安全稳定运行[7 ] .同时,可再生能源出力易受天气影响,容易出现负荷高且可再生能源出力低的情况,导致系统容量充裕性不足使系统面临停电风险[8 ⇓ -10 ] .传统基于持续负荷曲线和装机容量的电源规划模型已无法适应在高比例可再生能源情况下对系统的灵活性和容量充裕性要求. ...
新能源消纳关键因素分析及解决措施研究
1
2017
... 在以可再生能源为主体的新型电力系统中,风、光、水等一次能源供应与气象条件密切相关,可再生能源出力存在较大随机性与不确定性[4 -5 ] ,同时叠加负荷的不确定性,导致系统维持电力供需动态平衡的难度大幅增加,因此需要提升系统灵活性[6 ] 以确保系统安全稳定运行[7 ] .同时,可再生能源出力易受天气影响,容易出现负荷高且可再生能源出力低的情况,导致系统容量充裕性不足使系统面临停电风险[8 ⇓ -10 ] .传统基于持续负荷曲线和装机容量的电源规划模型已无法适应在高比例可再生能源情况下对系统的灵活性和容量充裕性要求. ...
Optimal investment planning for distributed generation in a competitive electricity market
1
2004
... 在以可再生能源为主体的新型电力系统中,风、光、水等一次能源供应与气象条件密切相关,可再生能源出力存在较大随机性与不确定性[4 -5 ] ,同时叠加负荷的不确定性,导致系统维持电力供需动态平衡的难度大幅增加,因此需要提升系统灵活性[6 ] 以确保系统安全稳定运行[7 ] .同时,可再生能源出力易受天气影响,容易出现负荷高且可再生能源出力低的情况,导致系统容量充裕性不足使系统面临停电风险[8 ⇓ -10 ] .传统基于持续负荷曲线和装机容量的电源规划模型已无法适应在高比例可再生能源情况下对系统的灵活性和容量充裕性要求. ...
含高比例可再生能源电力系统灵活性规划及挑战
1
2016
... 在以可再生能源为主体的新型电力系统中,风、光、水等一次能源供应与气象条件密切相关,可再生能源出力存在较大随机性与不确定性[4 -5 ] ,同时叠加负荷的不确定性,导致系统维持电力供需动态平衡的难度大幅增加,因此需要提升系统灵活性[6 ] 以确保系统安全稳定运行[7 ] .同时,可再生能源出力易受天气影响,容易出现负荷高且可再生能源出力低的情况,导致系统容量充裕性不足使系统面临停电风险[8 ⇓ -10 ] .传统基于持续负荷曲线和装机容量的电源规划模型已无法适应在高比例可再生能源情况下对系统的灵活性和容量充裕性要求. ...
含高比例可再生能源电力系统灵活性规划及挑战
1
2016
... 在以可再生能源为主体的新型电力系统中,风、光、水等一次能源供应与气象条件密切相关,可再生能源出力存在较大随机性与不确定性[4 -5 ] ,同时叠加负荷的不确定性,导致系统维持电力供需动态平衡的难度大幅增加,因此需要提升系统灵活性[6 ] 以确保系统安全稳定运行[7 ] .同时,可再生能源出力易受天气影响,容易出现负荷高且可再生能源出力低的情况,导致系统容量充裕性不足使系统面临停电风险[8 ⇓ -10 ] .传统基于持续负荷曲线和装机容量的电源规划模型已无法适应在高比例可再生能源情况下对系统的灵活性和容量充裕性要求. ...
Reducing curtailment of wind electricity in China by employing electric boilers for heat and pumped hydro for energy storage
1
2016
... 在以可再生能源为主体的新型电力系统中,风、光、水等一次能源供应与气象条件密切相关,可再生能源出力存在较大随机性与不确定性[4 -5 ] ,同时叠加负荷的不确定性,导致系统维持电力供需动态平衡的难度大幅增加,因此需要提升系统灵活性[6 ] 以确保系统安全稳定运行[7 ] .同时,可再生能源出力易受天气影响,容易出现负荷高且可再生能源出力低的情况,导致系统容量充裕性不足使系统面临停电风险[8 ⇓ -10 ] .传统基于持续负荷曲线和装机容量的电源规划模型已无法适应在高比例可再生能源情况下对系统的灵活性和容量充裕性要求. ...
The impact of variable renewable energy resources on power system reliability
1
2021
... 在以可再生能源为主体的新型电力系统中,风、光、水等一次能源供应与气象条件密切相关,可再生能源出力存在较大随机性与不确定性[4 -5 ] ,同时叠加负荷的不确定性,导致系统维持电力供需动态平衡的难度大幅增加,因此需要提升系统灵活性[6 ] 以确保系统安全稳定运行[7 ] .同时,可再生能源出力易受天气影响,容易出现负荷高且可再生能源出力低的情况,导致系统容量充裕性不足使系统面临停电风险[8 ⇓ -10 ] .传统基于持续负荷曲线和装机容量的电源规划模型已无法适应在高比例可再生能源情况下对系统的灵活性和容量充裕性要求. ...
美国加州2020年轮流停电事故分析及其对中国电网的启示
1
2020
... 在以可再生能源为主体的新型电力系统中,风、光、水等一次能源供应与气象条件密切相关,可再生能源出力存在较大随机性与不确定性[4 -5 ] ,同时叠加负荷的不确定性,导致系统维持电力供需动态平衡的难度大幅增加,因此需要提升系统灵活性[6 ] 以确保系统安全稳定运行[7 ] .同时,可再生能源出力易受天气影响,容易出现负荷高且可再生能源出力低的情况,导致系统容量充裕性不足使系统面临停电风险[8 ⇓ -10 ] .传统基于持续负荷曲线和装机容量的电源规划模型已无法适应在高比例可再生能源情况下对系统的灵活性和容量充裕性要求. ...
美国加州2020年轮流停电事故分析及其对中国电网的启示
1
2020
... 在以可再生能源为主体的新型电力系统中,风、光、水等一次能源供应与气象条件密切相关,可再生能源出力存在较大随机性与不确定性[4 -5 ] ,同时叠加负荷的不确定性,导致系统维持电力供需动态平衡的难度大幅增加,因此需要提升系统灵活性[6 ] 以确保系统安全稳定运行[7 ] .同时,可再生能源出力易受天气影响,容易出现负荷高且可再生能源出力低的情况,导致系统容量充裕性不足使系统面临停电风险[8 ⇓ -10 ] .传统基于持续负荷曲线和装机容量的电源规划模型已无法适应在高比例可再生能源情况下对系统的灵活性和容量充裕性要求. ...
适应中国电力现货市场发展的容量补偿机制初探
1
2021
... 在以可再生能源为主体的新型电力系统中,风、光、水等一次能源供应与气象条件密切相关,可再生能源出力存在较大随机性与不确定性[4 -5 ] ,同时叠加负荷的不确定性,导致系统维持电力供需动态平衡的难度大幅增加,因此需要提升系统灵活性[6 ] 以确保系统安全稳定运行[7 ] .同时,可再生能源出力易受天气影响,容易出现负荷高且可再生能源出力低的情况,导致系统容量充裕性不足使系统面临停电风险[8 ⇓ -10 ] .传统基于持续负荷曲线和装机容量的电源规划模型已无法适应在高比例可再生能源情况下对系统的灵活性和容量充裕性要求. ...
适应中国电力现货市场发展的容量补偿机制初探
1
2021
... 在以可再生能源为主体的新型电力系统中,风、光、水等一次能源供应与气象条件密切相关,可再生能源出力存在较大随机性与不确定性[4 -5 ] ,同时叠加负荷的不确定性,导致系统维持电力供需动态平衡的难度大幅增加,因此需要提升系统灵活性[6 ] 以确保系统安全稳定运行[7 ] .同时,可再生能源出力易受天气影响,容易出现负荷高且可再生能源出力低的情况,导致系统容量充裕性不足使系统面临停电风险[8 ⇓ -10 ] .传统基于持续负荷曲线和装机容量的电源规划模型已无法适应在高比例可再生能源情况下对系统的灵活性和容量充裕性要求. ...
Flexibility in Europe’s power sector—An additional requirement or an automatic complement?
1
2016
... 针对高比例可再生能源电力系统的电源规划问题,现有研究在系统灵活性或容量充裕性问题上存在一定局限性.Bertsch等[11 ] 考虑多种灵活调节资源的规划,并分别对火电爬坡、机组启停、储能充放等灵活性约束建模,形成正负灵活性资源约束集,但仅考虑了负荷平衡约束而无其他容量充裕性约束.黄旭祥等[12 ] 建立了内嵌时序生产模拟的双层混合整数线性规划模型,协同规划火电、可再生能源与储能容量,同时包含火电等电源灵活性的精确建模,但未对系统容量充裕性进行明确约束.姜海洋等[13 ] 建立了协同规划源网荷储灵活性资源的线性规划模型,并内嵌全年8 760时段生产模拟,不仅包含多种灵活性约束还考虑可再生能源长时间尺度的波动性,但只是简单调节负荷曲线来确保系统容量充裕性.Kargarian等[14 ] 在电源规划时考虑了储能和快速爬坡机组的容量联合优化,并考虑调频性能约束,但同样未考虑系统容量充裕性约束.杨珺等[15 ] 在电源规划模型中引入了灵活性裕量约束,并内嵌生产运行模拟模型,同时直接引入最大失负荷概率约束,但原模型过于复杂难以求解,且简化后的模型并不能确保成本达到最优和足够的容量充裕性.鉴庆之等[16 ] 建立了包含规划层、运行层、灵活层的3层电源规划模型,针对机组启停和爬坡性能进行了详细建模,但过高估计了系统容量充裕性.何俊[17 ] 提出了一种基于置信容量的微电网风光储电源规划方法,根据系统可靠性需求,利用蒙特卡洛随机模拟确定系统总体置信容量水平,并以成本最小化为目标确定容量配置,保证了系统容量充裕性,但未考虑微电网中燃气机组灵活性约束. ...
大电网储能与各类电源协同规划
1
2019
... 针对高比例可再生能源电力系统的电源规划问题,现有研究在系统灵活性或容量充裕性问题上存在一定局限性.Bertsch等[11 ] 考虑多种灵活调节资源的规划,并分别对火电爬坡、机组启停、储能充放等灵活性约束建模,形成正负灵活性资源约束集,但仅考虑了负荷平衡约束而无其他容量充裕性约束.黄旭祥等[12 ] 建立了内嵌时序生产模拟的双层混合整数线性规划模型,协同规划火电、可再生能源与储能容量,同时包含火电等电源灵活性的精确建模,但未对系统容量充裕性进行明确约束.姜海洋等[13 ] 建立了协同规划源网荷储灵活性资源的线性规划模型,并内嵌全年8 760时段生产模拟,不仅包含多种灵活性约束还考虑可再生能源长时间尺度的波动性,但只是简单调节负荷曲线来确保系统容量充裕性.Kargarian等[14 ] 在电源规划时考虑了储能和快速爬坡机组的容量联合优化,并考虑调频性能约束,但同样未考虑系统容量充裕性约束.杨珺等[15 ] 在电源规划模型中引入了灵活性裕量约束,并内嵌生产运行模拟模型,同时直接引入最大失负荷概率约束,但原模型过于复杂难以求解,且简化后的模型并不能确保成本达到最优和足够的容量充裕性.鉴庆之等[16 ] 建立了包含规划层、运行层、灵活层的3层电源规划模型,针对机组启停和爬坡性能进行了详细建模,但过高估计了系统容量充裕性.何俊[17 ] 提出了一种基于置信容量的微电网风光储电源规划方法,根据系统可靠性需求,利用蒙特卡洛随机模拟确定系统总体置信容量水平,并以成本最小化为目标确定容量配置,保证了系统容量充裕性,但未考虑微电网中燃气机组灵活性约束. ...
大电网储能与各类电源协同规划
1
2019
... 针对高比例可再生能源电力系统的电源规划问题,现有研究在系统灵活性或容量充裕性问题上存在一定局限性.Bertsch等[11 ] 考虑多种灵活调节资源的规划,并分别对火电爬坡、机组启停、储能充放等灵活性约束建模,形成正负灵活性资源约束集,但仅考虑了负荷平衡约束而无其他容量充裕性约束.黄旭祥等[12 ] 建立了内嵌时序生产模拟的双层混合整数线性规划模型,协同规划火电、可再生能源与储能容量,同时包含火电等电源灵活性的精确建模,但未对系统容量充裕性进行明确约束.姜海洋等[13 ] 建立了协同规划源网荷储灵活性资源的线性规划模型,并内嵌全年8 760时段生产模拟,不仅包含多种灵活性约束还考虑可再生能源长时间尺度的波动性,但只是简单调节负荷曲线来确保系统容量充裕性.Kargarian等[14 ] 在电源规划时考虑了储能和快速爬坡机组的容量联合优化,并考虑调频性能约束,但同样未考虑系统容量充裕性约束.杨珺等[15 ] 在电源规划模型中引入了灵活性裕量约束,并内嵌生产运行模拟模型,同时直接引入最大失负荷概率约束,但原模型过于复杂难以求解,且简化后的模型并不能确保成本达到最优和足够的容量充裕性.鉴庆之等[16 ] 建立了包含规划层、运行层、灵活层的3层电源规划模型,针对机组启停和爬坡性能进行了详细建模,但过高估计了系统容量充裕性.何俊[17 ] 提出了一种基于置信容量的微电网风光储电源规划方法,根据系统可靠性需求,利用蒙特卡洛随机模拟确定系统总体置信容量水平,并以成本最小化为目标确定容量配置,保证了系统容量充裕性,但未考虑微电网中燃气机组灵活性约束. ...
高比例清洁能源并网的跨国互联电力系统多时间尺度储能容量优化规划
2
2021
... 针对高比例可再生能源电力系统的电源规划问题,现有研究在系统灵活性或容量充裕性问题上存在一定局限性.Bertsch等[11 ] 考虑多种灵活调节资源的规划,并分别对火电爬坡、机组启停、储能充放等灵活性约束建模,形成正负灵活性资源约束集,但仅考虑了负荷平衡约束而无其他容量充裕性约束.黄旭祥等[12 ] 建立了内嵌时序生产模拟的双层混合整数线性规划模型,协同规划火电、可再生能源与储能容量,同时包含火电等电源灵活性的精确建模,但未对系统容量充裕性进行明确约束.姜海洋等[13 ] 建立了协同规划源网荷储灵活性资源的线性规划模型,并内嵌全年8 760时段生产模拟,不仅包含多种灵活性约束还考虑可再生能源长时间尺度的波动性,但只是简单调节负荷曲线来确保系统容量充裕性.Kargarian等[14 ] 在电源规划时考虑了储能和快速爬坡机组的容量联合优化,并考虑调频性能约束,但同样未考虑系统容量充裕性约束.杨珺等[15 ] 在电源规划模型中引入了灵活性裕量约束,并内嵌生产运行模拟模型,同时直接引入最大失负荷概率约束,但原模型过于复杂难以求解,且简化后的模型并不能确保成本达到最优和足够的容量充裕性.鉴庆之等[16 ] 建立了包含规划层、运行层、灵活层的3层电源规划模型,针对机组启停和爬坡性能进行了详细建模,但过高估计了系统容量充裕性.何俊[17 ] 提出了一种基于置信容量的微电网风光储电源规划方法,根据系统可靠性需求,利用蒙特卡洛随机模拟确定系统总体置信容量水平,并以成本最小化为目标确定容量配置,保证了系统容量充裕性,但未考虑微电网中燃气机组灵活性约束. ...
... 式中: ε k r r d Ω n i n , Ω n o u t P l S l I l N [13 ] ,式(29)为可再生能源消纳量政策约束,要求可再生能源发电量必须占总发电量的比例至少为ϕ rps . ...
高比例清洁能源并网的跨国互联电力系统多时间尺度储能容量优化规划
2
2021
... 针对高比例可再生能源电力系统的电源规划问题,现有研究在系统灵活性或容量充裕性问题上存在一定局限性.Bertsch等[11 ] 考虑多种灵活调节资源的规划,并分别对火电爬坡、机组启停、储能充放等灵活性约束建模,形成正负灵活性资源约束集,但仅考虑了负荷平衡约束而无其他容量充裕性约束.黄旭祥等[12 ] 建立了内嵌时序生产模拟的双层混合整数线性规划模型,协同规划火电、可再生能源与储能容量,同时包含火电等电源灵活性的精确建模,但未对系统容量充裕性进行明确约束.姜海洋等[13 ] 建立了协同规划源网荷储灵活性资源的线性规划模型,并内嵌全年8 760时段生产模拟,不仅包含多种灵活性约束还考虑可再生能源长时间尺度的波动性,但只是简单调节负荷曲线来确保系统容量充裕性.Kargarian等[14 ] 在电源规划时考虑了储能和快速爬坡机组的容量联合优化,并考虑调频性能约束,但同样未考虑系统容量充裕性约束.杨珺等[15 ] 在电源规划模型中引入了灵活性裕量约束,并内嵌生产运行模拟模型,同时直接引入最大失负荷概率约束,但原模型过于复杂难以求解,且简化后的模型并不能确保成本达到最优和足够的容量充裕性.鉴庆之等[16 ] 建立了包含规划层、运行层、灵活层的3层电源规划模型,针对机组启停和爬坡性能进行了详细建模,但过高估计了系统容量充裕性.何俊[17 ] 提出了一种基于置信容量的微电网风光储电源规划方法,根据系统可靠性需求,利用蒙特卡洛随机模拟确定系统总体置信容量水平,并以成本最小化为目标确定容量配置,保证了系统容量充裕性,但未考虑微电网中燃气机组灵活性约束. ...
... 式中: ε k r r d Ω n i n , Ω n o u t P l S l I l N [13 ] ,式(29)为可再生能源消纳量政策约束,要求可再生能源发电量必须占总发电量的比例至少为ϕ rps . ...
A multi-time scale co-optimization method for sizing of energy storage and fast-ramping generation
1
2016
... 针对高比例可再生能源电力系统的电源规划问题,现有研究在系统灵活性或容量充裕性问题上存在一定局限性.Bertsch等[11 ] 考虑多种灵活调节资源的规划,并分别对火电爬坡、机组启停、储能充放等灵活性约束建模,形成正负灵活性资源约束集,但仅考虑了负荷平衡约束而无其他容量充裕性约束.黄旭祥等[12 ] 建立了内嵌时序生产模拟的双层混合整数线性规划模型,协同规划火电、可再生能源与储能容量,同时包含火电等电源灵活性的精确建模,但未对系统容量充裕性进行明确约束.姜海洋等[13 ] 建立了协同规划源网荷储灵活性资源的线性规划模型,并内嵌全年8 760时段生产模拟,不仅包含多种灵活性约束还考虑可再生能源长时间尺度的波动性,但只是简单调节负荷曲线来确保系统容量充裕性.Kargarian等[14 ] 在电源规划时考虑了储能和快速爬坡机组的容量联合优化,并考虑调频性能约束,但同样未考虑系统容量充裕性约束.杨珺等[15 ] 在电源规划模型中引入了灵活性裕量约束,并内嵌生产运行模拟模型,同时直接引入最大失负荷概率约束,但原模型过于复杂难以求解,且简化后的模型并不能确保成本达到最优和足够的容量充裕性.鉴庆之等[16 ] 建立了包含规划层、运行层、灵活层的3层电源规划模型,针对机组启停和爬坡性能进行了详细建模,但过高估计了系统容量充裕性.何俊[17 ] 提出了一种基于置信容量的微电网风光储电源规划方法,根据系统可靠性需求,利用蒙特卡洛随机模拟确定系统总体置信容量水平,并以成本最小化为目标确定容量配置,保证了系统容量充裕性,但未考虑微电网中燃气机组灵活性约束. ...
考虑灵活性需求的新能源高渗透系统规划方法
1
2022
... 针对高比例可再生能源电力系统的电源规划问题,现有研究在系统灵活性或容量充裕性问题上存在一定局限性.Bertsch等[11 ] 考虑多种灵活调节资源的规划,并分别对火电爬坡、机组启停、储能充放等灵活性约束建模,形成正负灵活性资源约束集,但仅考虑了负荷平衡约束而无其他容量充裕性约束.黄旭祥等[12 ] 建立了内嵌时序生产模拟的双层混合整数线性规划模型,协同规划火电、可再生能源与储能容量,同时包含火电等电源灵活性的精确建模,但未对系统容量充裕性进行明确约束.姜海洋等[13 ] 建立了协同规划源网荷储灵活性资源的线性规划模型,并内嵌全年8 760时段生产模拟,不仅包含多种灵活性约束还考虑可再生能源长时间尺度的波动性,但只是简单调节负荷曲线来确保系统容量充裕性.Kargarian等[14 ] 在电源规划时考虑了储能和快速爬坡机组的容量联合优化,并考虑调频性能约束,但同样未考虑系统容量充裕性约束.杨珺等[15 ] 在电源规划模型中引入了灵活性裕量约束,并内嵌生产运行模拟模型,同时直接引入最大失负荷概率约束,但原模型过于复杂难以求解,且简化后的模型并不能确保成本达到最优和足够的容量充裕性.鉴庆之等[16 ] 建立了包含规划层、运行层、灵活层的3层电源规划模型,针对机组启停和爬坡性能进行了详细建模,但过高估计了系统容量充裕性.何俊[17 ] 提出了一种基于置信容量的微电网风光储电源规划方法,根据系统可靠性需求,利用蒙特卡洛随机模拟确定系统总体置信容量水平,并以成本最小化为目标确定容量配置,保证了系统容量充裕性,但未考虑微电网中燃气机组灵活性约束. ...
考虑灵活性需求的新能源高渗透系统规划方法
1
2022
... 针对高比例可再生能源电力系统的电源规划问题,现有研究在系统灵活性或容量充裕性问题上存在一定局限性.Bertsch等[11 ] 考虑多种灵活调节资源的规划,并分别对火电爬坡、机组启停、储能充放等灵活性约束建模,形成正负灵活性资源约束集,但仅考虑了负荷平衡约束而无其他容量充裕性约束.黄旭祥等[12 ] 建立了内嵌时序生产模拟的双层混合整数线性规划模型,协同规划火电、可再生能源与储能容量,同时包含火电等电源灵活性的精确建模,但未对系统容量充裕性进行明确约束.姜海洋等[13 ] 建立了协同规划源网荷储灵活性资源的线性规划模型,并内嵌全年8 760时段生产模拟,不仅包含多种灵活性约束还考虑可再生能源长时间尺度的波动性,但只是简单调节负荷曲线来确保系统容量充裕性.Kargarian等[14 ] 在电源规划时考虑了储能和快速爬坡机组的容量联合优化,并考虑调频性能约束,但同样未考虑系统容量充裕性约束.杨珺等[15 ] 在电源规划模型中引入了灵活性裕量约束,并内嵌生产运行模拟模型,同时直接引入最大失负荷概率约束,但原模型过于复杂难以求解,且简化后的模型并不能确保成本达到最优和足够的容量充裕性.鉴庆之等[16 ] 建立了包含规划层、运行层、灵活层的3层电源规划模型,针对机组启停和爬坡性能进行了详细建模,但过高估计了系统容量充裕性.何俊[17 ] 提出了一种基于置信容量的微电网风光储电源规划方法,根据系统可靠性需求,利用蒙特卡洛随机模拟确定系统总体置信容量水平,并以成本最小化为目标确定容量配置,保证了系统容量充裕性,但未考虑微电网中燃气机组灵活性约束. ...
考虑需求响应的电力系统灵活性资源优化配置
1
2021
... 针对高比例可再生能源电力系统的电源规划问题,现有研究在系统灵活性或容量充裕性问题上存在一定局限性.Bertsch等[11 ] 考虑多种灵活调节资源的规划,并分别对火电爬坡、机组启停、储能充放等灵活性约束建模,形成正负灵活性资源约束集,但仅考虑了负荷平衡约束而无其他容量充裕性约束.黄旭祥等[12 ] 建立了内嵌时序生产模拟的双层混合整数线性规划模型,协同规划火电、可再生能源与储能容量,同时包含火电等电源灵活性的精确建模,但未对系统容量充裕性进行明确约束.姜海洋等[13 ] 建立了协同规划源网荷储灵活性资源的线性规划模型,并内嵌全年8 760时段生产模拟,不仅包含多种灵活性约束还考虑可再生能源长时间尺度的波动性,但只是简单调节负荷曲线来确保系统容量充裕性.Kargarian等[14 ] 在电源规划时考虑了储能和快速爬坡机组的容量联合优化,并考虑调频性能约束,但同样未考虑系统容量充裕性约束.杨珺等[15 ] 在电源规划模型中引入了灵活性裕量约束,并内嵌生产运行模拟模型,同时直接引入最大失负荷概率约束,但原模型过于复杂难以求解,且简化后的模型并不能确保成本达到最优和足够的容量充裕性.鉴庆之等[16 ] 建立了包含规划层、运行层、灵活层的3层电源规划模型,针对机组启停和爬坡性能进行了详细建模,但过高估计了系统容量充裕性.何俊[17 ] 提出了一种基于置信容量的微电网风光储电源规划方法,根据系统可靠性需求,利用蒙特卡洛随机模拟确定系统总体置信容量水平,并以成本最小化为目标确定容量配置,保证了系统容量充裕性,但未考虑微电网中燃气机组灵活性约束. ...
考虑需求响应的电力系统灵活性资源优化配置
1
2021
... 针对高比例可再生能源电力系统的电源规划问题,现有研究在系统灵活性或容量充裕性问题上存在一定局限性.Bertsch等[11 ] 考虑多种灵活调节资源的规划,并分别对火电爬坡、机组启停、储能充放等灵活性约束建模,形成正负灵活性资源约束集,但仅考虑了负荷平衡约束而无其他容量充裕性约束.黄旭祥等[12 ] 建立了内嵌时序生产模拟的双层混合整数线性规划模型,协同规划火电、可再生能源与储能容量,同时包含火电等电源灵活性的精确建模,但未对系统容量充裕性进行明确约束.姜海洋等[13 ] 建立了协同规划源网荷储灵活性资源的线性规划模型,并内嵌全年8 760时段生产模拟,不仅包含多种灵活性约束还考虑可再生能源长时间尺度的波动性,但只是简单调节负荷曲线来确保系统容量充裕性.Kargarian等[14 ] 在电源规划时考虑了储能和快速爬坡机组的容量联合优化,并考虑调频性能约束,但同样未考虑系统容量充裕性约束.杨珺等[15 ] 在电源规划模型中引入了灵活性裕量约束,并内嵌生产运行模拟模型,同时直接引入最大失负荷概率约束,但原模型过于复杂难以求解,且简化后的模型并不能确保成本达到最优和足够的容量充裕性.鉴庆之等[16 ] 建立了包含规划层、运行层、灵活层的3层电源规划模型,针对机组启停和爬坡性能进行了详细建模,但过高估计了系统容量充裕性.何俊[17 ] 提出了一种基于置信容量的微电网风光储电源规划方法,根据系统可靠性需求,利用蒙特卡洛随机模拟确定系统总体置信容量水平,并以成本最小化为目标确定容量配置,保证了系统容量充裕性,但未考虑微电网中燃气机组灵活性约束. ...
1
2014
... 针对高比例可再生能源电力系统的电源规划问题,现有研究在系统灵活性或容量充裕性问题上存在一定局限性.Bertsch等[11 ] 考虑多种灵活调节资源的规划,并分别对火电爬坡、机组启停、储能充放等灵活性约束建模,形成正负灵活性资源约束集,但仅考虑了负荷平衡约束而无其他容量充裕性约束.黄旭祥等[12 ] 建立了内嵌时序生产模拟的双层混合整数线性规划模型,协同规划火电、可再生能源与储能容量,同时包含火电等电源灵活性的精确建模,但未对系统容量充裕性进行明确约束.姜海洋等[13 ] 建立了协同规划源网荷储灵活性资源的线性规划模型,并内嵌全年8 760时段生产模拟,不仅包含多种灵活性约束还考虑可再生能源长时间尺度的波动性,但只是简单调节负荷曲线来确保系统容量充裕性.Kargarian等[14 ] 在电源规划时考虑了储能和快速爬坡机组的容量联合优化,并考虑调频性能约束,但同样未考虑系统容量充裕性约束.杨珺等[15 ] 在电源规划模型中引入了灵活性裕量约束,并内嵌生产运行模拟模型,同时直接引入最大失负荷概率约束,但原模型过于复杂难以求解,且简化后的模型并不能确保成本达到最优和足够的容量充裕性.鉴庆之等[16 ] 建立了包含规划层、运行层、灵活层的3层电源规划模型,针对机组启停和爬坡性能进行了详细建模,但过高估计了系统容量充裕性.何俊[17 ] 提出了一种基于置信容量的微电网风光储电源规划方法,根据系统可靠性需求,利用蒙特卡洛随机模拟确定系统总体置信容量水平,并以成本最小化为目标确定容量配置,保证了系统容量充裕性,但未考虑微电网中燃气机组灵活性约束. ...
1
2014
... 针对高比例可再生能源电力系统的电源规划问题,现有研究在系统灵活性或容量充裕性问题上存在一定局限性.Bertsch等[11 ] 考虑多种灵活调节资源的规划,并分别对火电爬坡、机组启停、储能充放等灵活性约束建模,形成正负灵活性资源约束集,但仅考虑了负荷平衡约束而无其他容量充裕性约束.黄旭祥等[12 ] 建立了内嵌时序生产模拟的双层混合整数线性规划模型,协同规划火电、可再生能源与储能容量,同时包含火电等电源灵活性的精确建模,但未对系统容量充裕性进行明确约束.姜海洋等[13 ] 建立了协同规划源网荷储灵活性资源的线性规划模型,并内嵌全年8 760时段生产模拟,不仅包含多种灵活性约束还考虑可再生能源长时间尺度的波动性,但只是简单调节负荷曲线来确保系统容量充裕性.Kargarian等[14 ] 在电源规划时考虑了储能和快速爬坡机组的容量联合优化,并考虑调频性能约束,但同样未考虑系统容量充裕性约束.杨珺等[15 ] 在电源规划模型中引入了灵活性裕量约束,并内嵌生产运行模拟模型,同时直接引入最大失负荷概率约束,但原模型过于复杂难以求解,且简化后的模型并不能确保成本达到最优和足够的容量充裕性.鉴庆之等[16 ] 建立了包含规划层、运行层、灵活层的3层电源规划模型,针对机组启停和爬坡性能进行了详细建模,但过高估计了系统容量充裕性.何俊[17 ] 提出了一种基于置信容量的微电网风光储电源规划方法,根据系统可靠性需求,利用蒙特卡洛随机模拟确定系统总体置信容量水平,并以成本最小化为目标确定容量配置,保证了系统容量充裕性,但未考虑微电网中燃气机组灵活性约束. ...
储能技术在解决大规模风电并网问题中的应用前景分析
1
2013
... 针对电力系统灵活性问题,主要通过配置多种灵活调节资源提升系统灵活性,使系统能应对可再生能源和负荷的波动性和不确定性.灵活调节资源主要包括可调节的传统发电机组、储能系统[18 ] 、需求侧响应[19 ] 等,不同类型资源各有优劣,例如火电机组出力稳定、可靠性高,但碳中和背景下其出力受到碳排放额限制;储能可以削峰填谷,出力调节速度快,但投资成本高;需求侧响应资源投资成本低、响应较快,但响应价格较高且需要完善的市场机制配合.因此,在进行电源规划时应统筹考虑上述资源特性,以反映不同机组之间出力特性的互补关系. ...
储能技术在解决大规模风电并网问题中的应用前景分析
1
2013
... 针对电力系统灵活性问题,主要通过配置多种灵活调节资源提升系统灵活性,使系统能应对可再生能源和负荷的波动性和不确定性.灵活调节资源主要包括可调节的传统发电机组、储能系统[18 ] 、需求侧响应[19 ] 等,不同类型资源各有优劣,例如火电机组出力稳定、可靠性高,但碳中和背景下其出力受到碳排放额限制;储能可以削峰填谷,出力调节速度快,但投资成本高;需求侧响应资源投资成本低、响应较快,但响应价格较高且需要完善的市场机制配合.因此,在进行电源规划时应统筹考虑上述资源特性,以反映不同机组之间出力特性的互补关系. ...
Demand response for variable renewable energy integration: A proposed approach and its impacts
1
2020
... 针对电力系统灵活性问题,主要通过配置多种灵活调节资源提升系统灵活性,使系统能应对可再生能源和负荷的波动性和不确定性.灵活调节资源主要包括可调节的传统发电机组、储能系统[18 ] 、需求侧响应[19 ] 等,不同类型资源各有优劣,例如火电机组出力稳定、可靠性高,但碳中和背景下其出力受到碳排放额限制;储能可以削峰填谷,出力调节速度快,但投资成本高;需求侧响应资源投资成本低、响应较快,但响应价格较高且需要完善的市场机制配合.因此,在进行电源规划时应统筹考虑上述资源特性,以反映不同机组之间出力特性的互补关系. ...
Basic concepts in generating capacity adequacy evaluation
1
2006
... 针对电力系统容量充裕性问题,主要通过配置一定比例的装机容量裕度,使系统在机组突发故障停运或受一次能源影响降低出力时仍有充足的发电容量[20 ] .由于不同机组故障率以及一次能源禀赋不同,装机容量相同的机组对系统容量充裕性的贡献未必相同,特别是风力发电(简称风电)、光伏等新能源,传统电源规划模型中基于机组装机容量的系统充裕性约束已不适用于高比例可再生能源电力系统.为衡量不同停运率的火电机组所能承担的负荷大小,Garver[21 ] 提出了置信容量的概念,随后被推广应用于风电、光伏等可再生能源以及储能[22 ⇓ -24 ] .置信容量可以用来衡量系统容量充裕性,使得不同类型电源的容量充裕性可以在同一水平下进行相互比较[25 ] .然而,由于储能置信容量与系统装机结构等边界条件非线性相关,难以直接在规划模型中计算,目前尚无规划模型考虑储能置信容量. ...
Effective load carrying capability of generating units
1
1966
... 针对电力系统容量充裕性问题,主要通过配置一定比例的装机容量裕度,使系统在机组突发故障停运或受一次能源影响降低出力时仍有充足的发电容量[20 ] .由于不同机组故障率以及一次能源禀赋不同,装机容量相同的机组对系统容量充裕性的贡献未必相同,特别是风力发电(简称风电)、光伏等新能源,传统电源规划模型中基于机组装机容量的系统充裕性约束已不适用于高比例可再生能源电力系统.为衡量不同停运率的火电机组所能承担的负荷大小,Garver[21 ] 提出了置信容量的概念,随后被推广应用于风电、光伏等可再生能源以及储能[22 ⇓ -24 ] .置信容量可以用来衡量系统容量充裕性,使得不同类型电源的容量充裕性可以在同一水平下进行相互比较[25 ] .然而,由于储能置信容量与系统装机结构等边界条件非线性相关,难以直接在规划模型中计算,目前尚无规划模型考虑储能置信容量. ...
Capacity credit evaluation: A literature review
1
2008
... 针对电力系统容量充裕性问题,主要通过配置一定比例的装机容量裕度,使系统在机组突发故障停运或受一次能源影响降低出力时仍有充足的发电容量[20 ] .由于不同机组故障率以及一次能源禀赋不同,装机容量相同的机组对系统容量充裕性的贡献未必相同,特别是风力发电(简称风电)、光伏等新能源,传统电源规划模型中基于机组装机容量的系统充裕性约束已不适用于高比例可再生能源电力系统.为衡量不同停运率的火电机组所能承担的负荷大小,Garver[21 ] 提出了置信容量的概念,随后被推广应用于风电、光伏等可再生能源以及储能[22 ⇓ -24 ] .置信容量可以用来衡量系统容量充裕性,使得不同类型电源的容量充裕性可以在同一水平下进行相互比较[25 ] .然而,由于储能置信容量与系统装机结构等边界条件非线性相关,难以直接在规划模型中计算,目前尚无规划模型考虑储能置信容量. ...
A simple and fast algorithm for estimating the capacity credit of solar and storage
3
2020
... 针对电力系统容量充裕性问题,主要通过配置一定比例的装机容量裕度,使系统在机组突发故障停运或受一次能源影响降低出力时仍有充足的发电容量[20 ] .由于不同机组故障率以及一次能源禀赋不同,装机容量相同的机组对系统容量充裕性的贡献未必相同,特别是风力发电(简称风电)、光伏等新能源,传统电源规划模型中基于机组装机容量的系统充裕性约束已不适用于高比例可再生能源电力系统.为衡量不同停运率的火电机组所能承担的负荷大小,Garver[21 ] 提出了置信容量的概念,随后被推广应用于风电、光伏等可再生能源以及储能[22 ⇓ -24 ] .置信容量可以用来衡量系统容量充裕性,使得不同类型电源的容量充裕性可以在同一水平下进行相互比较[25 ] .然而,由于储能置信容量与系统装机结构等边界条件非线性相关,难以直接在规划模型中计算,目前尚无规划模型考虑储能置信容量. ...
... 储能本身不产生能量,在高比例可再生能源电力系统中,储能主要通过将低谷时段电量平移到尖峰时段提高系统容量充裕性,因此其对系统容量充裕性的贡献同时受限于装机容量和存储电量,可类比风电、光伏等电源,以置信容量衡量其对系统容量充裕性的贡献[23 -24 ] .目前关于储能置信容量的定义尚未达成共识,以文献[23 ]的定义为准,将“引入储能前后净负荷(即负荷减去储能净输出功率)曲线最高的100个时段平均值之差”作为储能置信容量.显然,储能的置信容量与多种因素有关,其中主要因素包括储能系统净负荷大小与波动情况即负荷减去可再生能源理论出力、最大持续放电时间、储能渗透率,其中系统净负荷又与波动情况、负荷、可再生能源装机容量、可再生能源容量因数序列有关,其函数关系为 ...
... .目前关于储能置信容量的定义尚未达成共识,以文献[23 ]的定义为准,将“引入储能前后净负荷(即负荷减去储能净输出功率)曲线最高的100个时段平均值之差”作为储能置信容量.显然,储能的置信容量与多种因素有关,其中主要因素包括储能系统净负荷大小与波动情况即负荷减去可再生能源理论出力、最大持续放电时间、储能渗透率,其中系统净负荷又与波动情况、负荷、可再生能源装机容量、可再生能源容量因数序列有关,其函数关系为 ...
Framework for capacity credit assessment of electrical energy storage and demand response
2
2016
... 针对电力系统容量充裕性问题,主要通过配置一定比例的装机容量裕度,使系统在机组突发故障停运或受一次能源影响降低出力时仍有充足的发电容量[20 ] .由于不同机组故障率以及一次能源禀赋不同,装机容量相同的机组对系统容量充裕性的贡献未必相同,特别是风力发电(简称风电)、光伏等新能源,传统电源规划模型中基于机组装机容量的系统充裕性约束已不适用于高比例可再生能源电力系统.为衡量不同停运率的火电机组所能承担的负荷大小,Garver[21 ] 提出了置信容量的概念,随后被推广应用于风电、光伏等可再生能源以及储能[22 ⇓ -24 ] .置信容量可以用来衡量系统容量充裕性,使得不同类型电源的容量充裕性可以在同一水平下进行相互比较[25 ] .然而,由于储能置信容量与系统装机结构等边界条件非线性相关,难以直接在规划模型中计算,目前尚无规划模型考虑储能置信容量. ...
... 储能本身不产生能量,在高比例可再生能源电力系统中,储能主要通过将低谷时段电量平移到尖峰时段提高系统容量充裕性,因此其对系统容量充裕性的贡献同时受限于装机容量和存储电量,可类比风电、光伏等电源,以置信容量衡量其对系统容量充裕性的贡献[23 -24 ] .目前关于储能置信容量的定义尚未达成共识,以文献[23 ]的定义为准,将“引入储能前后净负荷(即负荷减去储能净输出功率)曲线最高的100个时段平均值之差”作为储能置信容量.显然,储能的置信容量与多种因素有关,其中主要因素包括储能系统净负荷大小与波动情况即负荷减去可再生能源理论出力、最大持续放电时间、储能渗透率,其中系统净负荷又与波动情况、负荷、可再生能源装机容量、可再生能源容量因数序列有关,其函数关系为 ...
风电容量可信度研究综述与展望
1
2015
... 针对电力系统容量充裕性问题,主要通过配置一定比例的装机容量裕度,使系统在机组突发故障停运或受一次能源影响降低出力时仍有充足的发电容量[20 ] .由于不同机组故障率以及一次能源禀赋不同,装机容量相同的机组对系统容量充裕性的贡献未必相同,特别是风力发电(简称风电)、光伏等新能源,传统电源规划模型中基于机组装机容量的系统充裕性约束已不适用于高比例可再生能源电力系统.为衡量不同停运率的火电机组所能承担的负荷大小,Garver[21 ] 提出了置信容量的概念,随后被推广应用于风电、光伏等可再生能源以及储能[22 ⇓ -24 ] .置信容量可以用来衡量系统容量充裕性,使得不同类型电源的容量充裕性可以在同一水平下进行相互比较[25 ] .然而,由于储能置信容量与系统装机结构等边界条件非线性相关,难以直接在规划模型中计算,目前尚无规划模型考虑储能置信容量. ...
风电容量可信度研究综述与展望
1
2015
... 针对电力系统容量充裕性问题,主要通过配置一定比例的装机容量裕度,使系统在机组突发故障停运或受一次能源影响降低出力时仍有充足的发电容量[20 ] .由于不同机组故障率以及一次能源禀赋不同,装机容量相同的机组对系统容量充裕性的贡献未必相同,特别是风力发电(简称风电)、光伏等新能源,传统电源规划模型中基于机组装机容量的系统充裕性约束已不适用于高比例可再生能源电力系统.为衡量不同停运率的火电机组所能承担的负荷大小,Garver[21 ] 提出了置信容量的概念,随后被推广应用于风电、光伏等可再生能源以及储能[22 ⇓ -24 ] .置信容量可以用来衡量系统容量充裕性,使得不同类型电源的容量充裕性可以在同一水平下进行相互比较[25 ] .然而,由于储能置信容量与系统装机结构等边界条件非线性相关,难以直接在规划模型中计算,目前尚无规划模型考虑储能置信容量. ...
Modeling formulation and validation for accelerated simulation and flexibility assessment on large scale power systems under higher renewable penetrations
2
2019
... 规划模型综合考虑系统灵活性约束与容量充裕性约束,以系统总成本最小为目标,基于时序生产模拟规划多电源与储能的最优容量.在灵活性约束方面,模型重点考虑火电机组的最短启停时间、爬坡、出力上下限等约束.由于传统机组组合模型为混合整数线性规划问题,当系统规模较大时求解速度较慢甚至无法求解,因此通过采用适合大规模可再生能源系统规划建模的快速机组组合模型[26 ] ,在大幅缩短求解时间的同时保留规划模型所要求的精度.在容量充裕性约束方面,模型统筹考虑火电、风电、光伏、水力发电(简称水电)、储能、需求侧响应资源的置信容量,由于储能置信容量与系统可再生能源装机容量等因素非线性相关,所以提出一种适用于电源规划模型的储能置信容量动态迭代算法,将容量充裕性约束线性化,便于模型使用线性规划求解器求解. ...
... 火电机组的快速机组组合模型[3 ,26 -27 ] 如下: ...
Power system capacity expansion under higher penetration of renewables considering flexibility constraints and low carbon policies
2
2018
... 火电机组的快速机组组合模型[3 ,26 -27 ] 如下: ...
... 储能模型[27 ] 如下: ...