光伏发电系统动态离散等值模型研究

doi:10.16183/j.cnki.jsjtu.2021.505

光伏发电系统动态离散等值模型研究

刘可真, 陈雪鸥, 陈镭丹, 林铮, 沈赋^,

昆明理工大学电力工程学院,昆明 650500

Dynamic Discrete Equivalent Model of Photovoltaic Power Generation System

LIU Kezhen, CHEN Xueou, CHEN Leidan, LIN Zheng, SHEN Fu^,

School of Electric Power Engineering, Kunming University of Science and Technology, Kunming 650500, China

通讯作者: 沈赋,讲师;E-mail:shenfu@kust.edu.cn.

责任编辑: 孙伟

收稿日期: 2021-12-10 修回日期: 2022-03-6 接受日期: 2022-05-5

基金资助:

国家自然科学基金(52107097)
云南省应用基础研究计划(202101BE070001-061)
云南省应用基础研究计划(202201AU070111)
昆明理工大学高层次人才平台建设(KKZ7202004004)

Received: 2021-12-10 Revised: 2022-03-6 Accepted: 2022-05-5

作者简介 About authors

刘可真(1974-),教授,现主要从事以新能源为主体的新型电力系统多态势感知研究.

摘要

可再生能源在新型电力系统中的占比进一步加大,光伏机组并网容量有明显提升的趋势,而不同渗透率下的光伏发电系统动态行为对电网负荷特性产生显著影响,但光伏发电并网动态模型复杂、待辨识参数多,增大了模型实际运用难度.为此,基于光伏电站机理模型,建立光伏发电并网系统的动态离散等值模型,得到光伏发电并网系统的动态离散等值模型的模型参数;并采用IEEE 14节点系统研究不同渗透率下光伏发电并网系统的动态离散等值模型特性.仿真结果表明,光伏发电并网系统的动态离散等值模型能准确描述光伏发电系统的动态特性,且精度高、易于辨识.

关键词： 光伏发电; 动态等值; 不同渗透率; 参数辨识

Abstract

The proportion of renewable energy in the new power system is further increased, and the grid connected capacity of photovoltaic units has a trend of obvious improvement. The dynamic behavior of the photovoltaic (PV) power generation system at different permeabilities has a significant impact on the load characteristics of the power grid. However, the complex dynamic model of photovoltaic power generation grid connection and the large number of parameters to be identified increase the difficulty of practical application of the model. Therefore, a dynamic discrete equivalent model of the PV power generation model based on the physical model of the PV power generation model is established, and the parameters of the dynamic discrete equivalent model for the PV power generation model are obtained. The IEEE 14-bus system, which is subject to various PV permeabilities, is adopted to verify the superb dynamic characteristics of the proposed discrete equivalent model for the PV power generation in power system simulations. The pertinent simulation results show that the dynamic discrete equivalent model of the PV power generation system can accurately describe the dynamic characteristics of the PV power generation system with a high accuracy and an easy identification performance.

Keywords： photovoltaic (PV); dynamic equivalence; various permeabilities; parameter identification

PDF (6678KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘可真, 陈雪鸥, 陈镭丹, 林铮, 沈赋. 光伏发电系统动态离散等值模型研究[J]. 上海交通大学学报, 2023, 57(4): 412-421 doi:10.16183/j.cnki.jsjtu.2021.505

LIU Kezhen, CHEN Xueou, CHEN Leidan, LIN Zheng, SHEN Fu. Dynamic Discrete Equivalent Model of Photovoltaic Power Generation System[J]. Journal of Shanghai Jiaotong University, 2023, 57(4): 412-421 doi:10.16183/j.cnki.jsjtu.2021.505

随着高比例可再生能源接入电网,电力系统的负荷特性发生显著变化^[1⇓⇓-4].由于光伏系统具有不同于传统发电的独特特性,所以高光伏穿透水平会对系统的暂态稳定性产生显著影响^[5].当电网发生故障时,全网动态特性将发生改变,现有模型很难满足仿真需求,亟需研究光伏发电系统动态特性,建立符合实际工况的光伏发电系统动态离散等值模型^[6-7].

在光伏发电系统动态建模研究方面,文献[8]研究光伏发电系统各子系统的动态行为,揭示了光伏并网发电系统各组成部分之间的相互作用;文献[9]以核心器件逆变器为中心,建立了逆变器直流侧与光伏阵列、交流测与变压器之间整体的动态模型;文献[10]将逆变器等效为受控电流源和电压源,通过忽略光伏发电系统的控制作用,推导出逼近效果更好的光伏发电系统动态向量模型;文献[11]建立了含逆变控制的光伏发电系统3阶微分外特性模型,但由于需要确定模型初始条件,导致其模型参数分散性较大、暂态响应不足;文献[12]提出了三相单级光伏并网系统的动态模型,其外部特性拟合效果较好,但参数辨识难度较大,很难适用于大型光伏电站的电力系统仿真;文献[13]构建了面向广义负荷的光伏发电系统等效模型,能有效描述含光伏发电系统的配电网综合负荷特性,但含不同渗透率光伏发电系统的电网综合动态响应特性仍有待研究.

综上所述,光伏发电系统在动态响应建模方面已有明显突破,但多集中于光伏子系统部分的动态建模,对并网系统的故障特性研究没有形成准确、统一的等值描述.而随着光伏并网容量的持续增加,负荷特性急剧变化,现有模型很难满足仿真需求,研究光伏发电系统动态特性以及建立不同渗透率下符合实际工况的光伏发电系统动态离散等值模型十分必要.

基于光伏电站机理模型,本文建立了光伏发电并网系统的动态离散等值模型,并得到光伏发电并网系统的动态离散等值模型的模型参数.采用IEEE 14节点系统研究不同渗透率下光伏发电并网系统的动态离散等值模型特性,通过设置短路接地故障,利用最小二乘法辨识模型参数,验证光伏发电并网系统的动态离散等值模型的动态特性.

1 光伏发电系统并网动态模型

1.1 光伏发电系统并网对负荷建模的影响

电力系统负荷建模是电力系统运行、仿真的基础,电力系统潮流与稳定计算需要准确的负荷模型支持.相关学者对发电系统仿真建模进行了大量的机理研究,得出适用于不同精度需要的仿真模型,但在新型电力系统背景下,大量分布式光伏发电系统接入输电网,导致电网的不确定性提高,负荷波动性愈加明显.理想化的负荷模型结构与发、配电系统之间存在严重不平衡,造成实际运行与仿真运行结果差异较大,降低了电力系统建模可信度,无法匹配传统零膨胀泊松回归(ZIP)负荷模型.当电压以较快速度大范围变化时,采用纯静态负荷模型产生的误差无法满足仿真精度,因此,负荷建模需要考虑负荷的随机性、时变性、非线性及离散性的影响.

动态负荷模型用来描述有功、无功与电压、频率之间的微分关系,研究光伏发电系统动态特性要求光伏发电系统负荷模型不仅结构简单、准确,而且能够综合反映光伏发电系统模型的机电暂态特性^[14].本文考虑光伏发电系统微分方程,提出4阶动态非机理的光伏发电系统模型,以并网点电流实部和虚部与并网电压的关联关系描述光伏发电系统并网后的模型动态特性^[15].

1.2 光伏发电系统模型及控制系统

典型光伏发电系统是由光伏组件经过汇流箱并联形成的光伏阵列发电单元、DC/DC升压变换器、DC/AC三相逆变器及滤波器形成的集中式光伏电站,经单元隔离变压器通过多条集电线路并入功率汇集母线并接入电网^[16],光伏发电系统模型如图1所示.图中,PCC为光伏发电系统接入配电系统的并网点.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 光伏发电系统并网模型

Fig.1 Grid connected model of photovoltaic power generation system

研究光伏发电系统的机电暂态特性,主要考虑电网发生故障时,并网点母线电压发生不同程度的电压跌落后,光伏发电系统逆变器交流部分与并网点功率、电压之间的变化关系.因此,通过忽略光伏阵列模型及升压变换来研究光伏逆变器交流部分与并网母线之间的动态特性.

含光伏发电系统动态负荷的机电暂态特性过程极短,相对于电网暂态变化的毫秒级,光伏系统的时间尺度更长.因此,假设在极小的时间尺度下,光伏阵列的光照强度及温度变化不发生改变,逆变器的控制参数已知,调制参数为固定值,采用电压外环、电流内环的双环控制与脉冲宽度调制(PWM),此时光伏发电系统的外部特性取决于并网点的电压变换.

对于外部电网,光伏发电系统动态特性模型^[17]如下所示:

$\begin{matrix} \begin{array}{l} P = 3 (u_{g d} I_{d} + u_{g q} I_{q}) / 2 \\ Q = - 3 (u_{g q} I_{d} - u_{g d} I_{q}) / 2 \end{array}\} \end{matrix}$

(1)

令 $u_{g q}$ 为0,则:

$\begin{matrix} \begin{array}{l} P = 3 u_{g d} I_{d} / 2 \\ Q = 3 u_{g d} I_{q} / 2 \end{array}\} \end{matrix}$

(2)

式中: P、Q为光伏发电系统发出的有功功率和无功功率; $u_{g d} 、 u_{g q}$ 和 $I_{d} 、 I_{q}$ 分别为光伏发电系统并网点输出电压和电流的d-q轴分量.

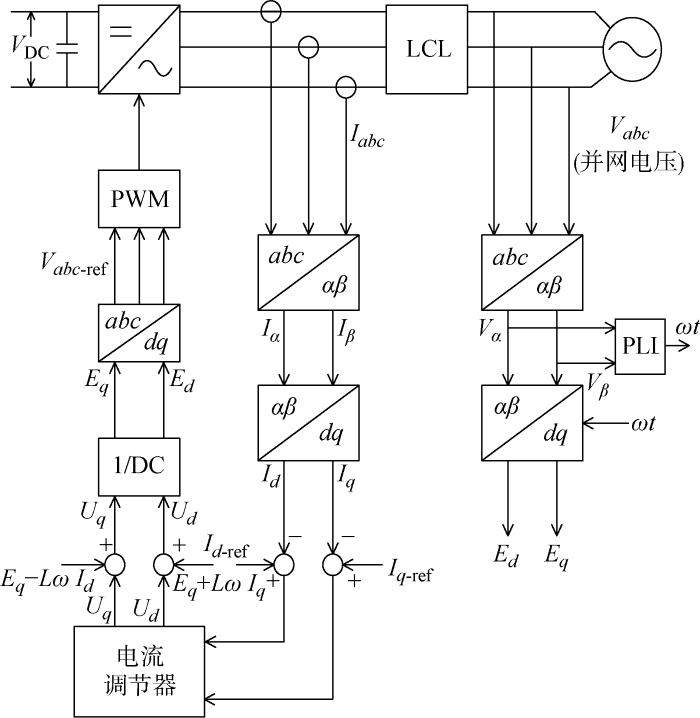
由式(1)、(2)可知,控制并网电流的d-q轴分量能控制光伏发电系统的有功功率及无功功率.采用d-q坐标矢量解耦控制^[18],经锁相环(PLL)得到脉宽调制信号.系统的并网控制拓扑结构如图2所示.其中,V_DC为直流侧参考电压;I_d_-ref、I_q_-ref为有功电流及无功电流参考值; $E_{d} 、 E_{q} 、 U_{d} 、 U_{q}$ 为并网母线及逆变交流侧abc三相电压的d-q轴分量;L为等值电感;ω为同步频率;V_abc_-ref为经d-q变换后的调制电压参考值;αβ为Clark变换过程;LCL为滤波器;t为时间.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 光伏发电系统并网控制拓扑结构

Fig.2 Grid connected control topology of photovoltaic power generation system

2 光伏发电系统动态离散等值模型

为准确、合理地描述光伏动态系统动态特性,建立光伏发电系统单相动态离散等值模型,如图3所示.其中,u_dc为光伏直流侧电压;i_pv为光伏输出电流;V_i为逆变器出口电压;R、L_g为逆变器到并网点的等值电阻及电抗;I_L为并网电流;u_g为并网电压.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 光伏发电系统单相动态离散等值模型

Fig.3 Single phase dynamic equivalent model of photovoltaic power generation system

根据基尔霍夫电压和电流定律,推导光伏发电系统的动态等值数学描述并进行派克变换,即可得到以d-q轴分量为状态变量的3阶动态微分方程^[19]:

$\begin{matrix} \begin{array}{l} \frac{d I_{d}}{d t} = \frac{1}{L} (u_{i d} - u_{g d} - I_{d} R) - ω I_{q} \\ \frac{d I_{q}}{d t} = \frac{1}{L} (u_{i q} - u_{g q} - I_{d} R) + ω I_{d} \\ \frac{d u_{d c}}{d t} = \frac{1}{C} (i_{p v} - 1.5 S_{d} I_{d} - 1.5 S_{q} I_{q}) \end{array}\} \end{matrix}$

(3)

式中: $u_{i d} 、 u_{i q}$ 分别为逆变器出口电压的d-q轴分量; $S_{q}$ 和 $S_{d}$ 为开关向量在同步坐标系下的d-q轴分量;C为光伏发电系统直流侧电容.

式(3)通过变形,可得到频域下的负荷模型:

$\begin{matrix} [\begin{array}{l} Δ I_{d} (s) \\ Δ I_{q} (s) \end{array}] = [\begin{array}{l} f_{1} (s) & f_{2} (s) \\ f_{3} (s) & f_{4} (s) \end{array}] [\begin{array}{l} Δ U_{g d} (s) \\ Δ U_{g q} (s) \end{array}] \end{matrix}$

(4)

式中:

$f_{1} (s) = \frac{B_{11} s^{3} + B_{12} s^{2} + B_{14} s}{A_{11} s^{4} + A_{12} s^{3} + A_{13} s^{2} + A_{14} s}$

$f_{2} (s) = \frac{B_{13} s^{2} + B_{15} s}{A_{11} s^{4} + A_{12} s^{3} + A_{13} s^{2} + A_{14} s}$

$f_{3} (s) = \frac{B_{22} s^{2} + B_{25} s}{A_{11} s^{4} + A_{12} s^{3} + A_{13} s^{2} + A_{14} s}$

$f_{4} (s) = \frac{B_{21} s^{3} + B_{23} s^{2} + B_{24} s}{A_{11} s^{4} + A_{12} s^{3} + A_{13} s^{2} + A_{14} s}$

其中: $A_{11} = 1$ , $A_{12} = \frac{2 R}{L}$ , $A_{13} = \frac{4 C R^{2} + 3 s_{d}^{2} R + 3 s_{q}^{2} L}{4 L^{2} C} - ω$ , $A_{14} = \frac{6 s_{d} s_{q} L ω + 3 s_{d}^{2} R + 3 s_{q}^{2} R}{4 L^{2} C}$ , $A_{15} = 0$ ,

$B_{11} = \frac{1}{L}$ , $B_{12} = - \frac{R}{L^{2}}$ , $B_{13} = - \frac{ω}{L}$ , $B_{21} = - \frac{1}{L}$ , $B_{22} = \frac{ω}{L^{2}}$ , $B_{23} = \frac{ω}{L^{2}}$ , $B_{24} = - \frac{3 s_{d}^{2}}{4 L^{2} C}$ , $B_{25} = \frac{1}{L^{2}}$

进一步得到相对于并网电压的电流实部与虚部对应的传递函数:

$\begin{array}{l} \frac{Δ I_{r} (s)}{Δ U_{g} (s)} = \frac{A_{r} s^{3} + C_{r} s^{2} + B_{r} s}{A_{11} s^{4} + A_{12} s^{3} + A_{13} s^{2} + A_{14} s} \\ \frac{Δ I_{j} (s)}{Δ U_{g} (s)} = \frac{A_{j} s^{3} + C_{j} s^{2} + B_{j} s}{A_{11} s^{4} + A_{12} s^{3} + A_{13} s^{2} + A_{14} s} \end{array}\}$

(5)

式中:

$A_{r} = \frac{s i n 2 θ_{0}}{2} (B_{21} - B_{11}) + s i n^{2} θ_{0} B_{11} + c o s^{2} θ_{0} B_{21}$

$A_{j} = \frac{s i n 2 θ_{0}}{2} (B_{21} - B_{11}) + s i n^{2} θ_{0} B_{21} + c o s^{2} θ_{0} B_{11}$

$B_{r} = \frac{s i n 2 θ_{0}}{2} (B_{13} + B_{22} + B_{23} - B_{12}) + s i n^{2} θ_{0} (B_{12} + B_{13}) + c o s^{2} θ_{0} (B_{22} + B_{23})$

$B_{j} = \frac{s i n 2 θ_{0}}{2} (B_{23} - B_{22} - B_{12} - B_{13}) + s i n^{2} θ_{0} (B_{22} + B_{23}) + c o s^{2} θ_{0} (B_{12} - B_{13})$

$C_{r} = \frac{s i n 2 θ_{0}}{2} (B_{15} + B_{25} + B_{24} - B_{14}) + s i n^{2} θ_{0} (B_{14} + B_{15}) + c o s^{2} θ_{0} (B_{24} + B_{25})$

$C_{j} = \frac{s i n 2 θ_{0}}{2} (B_{24} - B_{14} - B_{15} - B_{25}) + s i n^{2} θ_{0} (B_{24} + B_{25}) + c o s^{2} θ_{0} (B_{14} + B_{15})$

θ₀为并网功率因数角.

将上式进行坐标变换及双线性变换,可得到关于电流实部和虚部的差分方程:

$\begin{matrix} \begin{array}{l} Δ I_{r} (k + 4) = θ_{α 1} Δ I_{r} (k + 3) + \\ θ_{α 2} Δ I_{r} (k + 2) + θ_{α 3} Δ I_{r} (k + 1) + \\ θ_{α 4} Δ I_{r} (k) + θ_{α 5} Δ U (k + 4) + \\ θ_{α 6} Δ U (k + 3) + θ_{α 7} Δ U (k + 2) + \\ θ_{α 8} Δ U (k + 1) + θ_{α 9} Δ U (k) \\ Δ I_{j} (k + 4) = θ_{β 1} Δ I_{j} (k + 3) + \\ θ_{β 2} Δ I_{j} (k + 2) + θ_{β 3} Δ I_{j} (k + 1) + \\ θ_{β 4} Δ I_{j} (k) + θ_{β 5} Δ U (k + 4) + \\ θ_{β 6} Δ U (k + 3) + θ_{β 7} Δ U (k + 2) + \\ θ_{β 8} Δ U (k + 1) + θ_{β 9} Δ U (k) \end{array}\} \end{matrix}$

(6)

式中: $θ_{α i'}$ 和 $θ_{β i'} (i' = 1,2, \dots, 9)$ 为待辨识参数;k为采样时刻.参数推导结果见附录A.

3 光伏发电系统动态离散等值模型参数辨识方法

由于光伏发电系统动态离散等值模型受输入、输出数据的影响^[20],所以采用最小二乘法,利用已知的输入、输出数据进行模型参数辨识^[21].获取模型并网处的电压、有功功率及无功功率作为式(6)的已知条件,辨识模型中的θ_αi'和θ_βi'.选取并网点实部电流、虚部电流及母线电压的动态数据,以最小方差为目标修正参数估计值^[22],选取m组观测数据并分析对应的非线性模型方程:

$\begin{matrix} y_{i} = f (x_{i}, θ), i = 1,2, \dots, m \end{matrix}$

(7)

式中: $x_{i} = {[x_{i 1} x_{i 2} \dots x_{i m}]}^{T}; θ = [θ_{1} θ_{2} \dots θ_{n}]^{T}; y_{i} - f (x_{i}, θ) = ε, ε$ 为残差,且

$x_{1} = Δ I_{r} (k + 3)$ , $x_{2} = Δ I_{r} (k + 2)$ , $x_{3} = Δ I_{r} (k + 1)$ , $x_{4} = Δ I_{r} (k)$ , $x_{5} = Δ U (k + 4)$ , $x_{6} = Δ U (k + 3)$ ,

$x_{7} = Δ U (k + 2)$ , $x_{8} = Δ U (k + 1)$ , $x_{9} = Δ U (k)$ , $x_{10} = Δ I_{j} (k + 3)$ , $x_{11} = Δ I_{j} (k + 2)$ , $x_{12} = Δ I_{j} (k + 1)$ ,

$x_{13} = Δ I_{j} (k)$ , $x_{14} = Δ U (k + 4)$ , $x_{15} = Δ U (k + 3)$ , $x_{16} = Δ U (k + 2)$ , $x_{17} = Δ U (k + 1)$ , $x_{18} = Δ U (k)$ ,

$y_{1} = Δ I_{r} (k + 4)$ , $y_{2} = Δ I_{j} (k + 4)$

对应系统的方差如下:

$\begin{array}{l} J = \overset{m}{\sum_{i = 1}} ε_{i}^{2} = ε^{T} ε = \\ [y_{i} - f (x_{i} {, θ)]}^{T} [y_{i} - f (x_{i}, θ)] \end{array}$

(8)

存在一组 $\hat{θ}$ 使得:

$\begin{matrix} \hat{θ} = ({x^{T}}_{i} x_{i})^{- 1} {x^{T}}_{i} y'_{i} \end{matrix}$

(9)

为量化系统在动态离散等值模型与输配电并网系统实测值间的输出误差,采用系统均方根误差(RMSE)作为评估准则,即:

$E = \sqrt{\frac{\overset{N}{\sum_{k = 1}} (I_{r k} - {\hat{I}}_{r k})^{2}}{N}}$

(10)

$\hat{E} = \sqrt{\frac{\overset{N}{\sum_{k = 1}} (I_{j k} - {\hat{I}}_{j k})^{2}}{N}}$

(11)

式中:E和 $\hat{E}$ 分别为光伏并网发电系统并网实部电流及虚部电流的均方根误差;N为系统采用点数; $I_{r k} 、 I_{j k}$ 为第k个采样点的实部电流与虚部电流; ${\hat{I}}_{r k} 、 {\hat{I}}_{j k}$ 分别为等值动态离散模型下第k个采样点的实部电流与虚部电流.

4 仿真验算及分析

4.1 算例介绍

基于MATLAB/Simulink搭建如图4所示的含集中式光伏阵列输配电系统模型,以验证模型正确性及普适性.输电系统为IEEE 14节点系统模型,光伏发电系统为配电系统,经双绕组升压变压器T2接入,设定节点7为并网点,仿真具体设置如下:

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 光伏发电系统并入IEEE 14节点拓扑图

Fig.4 Photovoltaic power generation system integrated into IEEE 14-bus topology

(1) 输电系统参数.

IEEE 14节点中基准电压为23 kV,系统频率为50 Hz,系统阻抗采用串联型RL,参数分别为电感0.618 H、串联电阻0.4 Ω.

(2) 配电系统参数.

光伏阵列装机容量决定接入输电网的电压等级,选用单机容量为500 kW的光伏并网逆变器和LC型滤波器.其中,电感值为0.17 mH,电容值为 1.8 mF;双绕组升压变压器T2变比为35 kV/230 kV,容量为63 kW.各光伏阵列参数、并网逆变器控制器参数均相同,光伏阵列在理想情况(忽略电池环流、热斑等损耗)与标准测试环境(温度为25 ℃、光照强度为 1 000 W/m²)下进行不同光伏渗透率下的动态等值模型仿真,光伏阵列参数如表1所示.

表1 光伏阵列参数

Tab.1 Parameters of photovoltaic cell

参数	取值
开路电压V_oc/V	44.5
短路电流I_sc/A	8.20
最佳工作电压V_m/V	35.5
最佳工作电流I_m/A	7.51
串联数量/个	300
并联数量/个	200
组件转换效率/%	16.90

新窗口打开| 下载CSV

(3) 算例内容.

为研究所提模型在不同渗透率下的准确性,设置如下仿真:

步骤1 设置单相短路接地故障下,光伏渗透率为20%和40%;三相短路接地故障下,光伏渗透率为30%和60%,研究所提模型的普适性.

步骤2 在三相短路接地故障下,考虑步长对模型仿真的性能影响,分别设置光伏渗透率为30%和60%,步长为 0.001 s 和 0.002 s,研究步长对模型仿真的性能影响.

步骤3 在三相短路接地故障下,研究光伏渗透率在10%~80%时,不同电压跌落下模型的适用范围.

4.2 电网动态仿真分析

(1) 模型普适性验证.

算例设置如下:①步长为 0.001 s,采样频率为 1 000 Hz,当光伏渗透率为20%和40%时,发生单相短路接地故障(电压跌落为3%和5%);② 步长为 0.001 s,采样频率为 1 000 Hz,光伏渗透率为30%和60%时,发生三相短路接地故障(电压跌落为3%和5%).

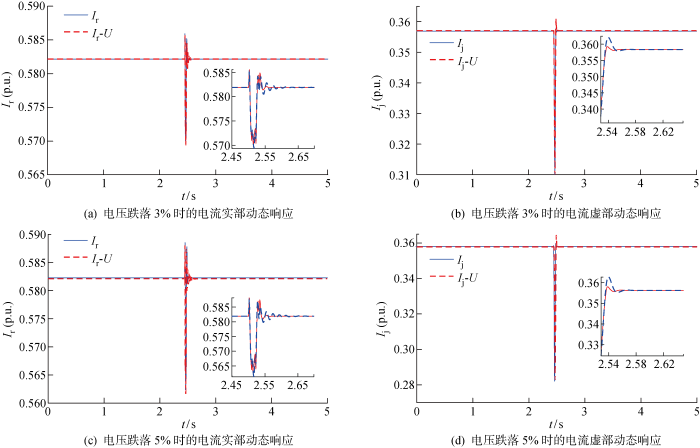
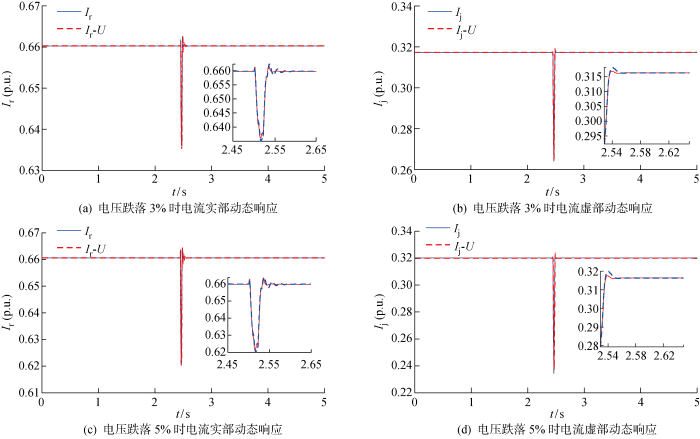
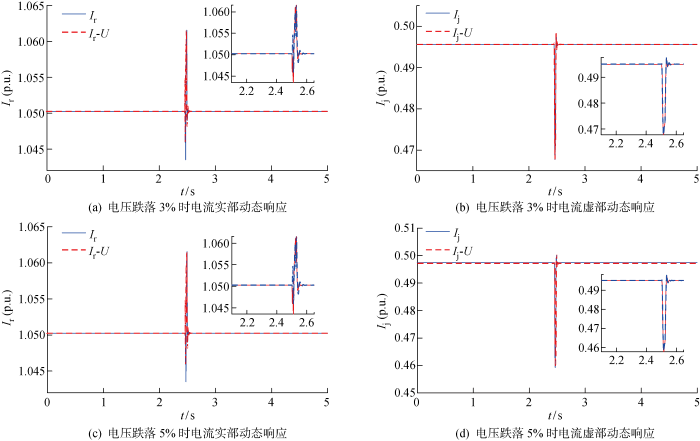
获取并网点实部电流(I_r)、虚部电流(I_j)及母线电压(U)的动态数据,经参数辨识分析模型暂态响应性能.三相短路接地故障动态响应结果如图5和图6所示;单相故障短路接地故障动态响应如图7和图8所示.其中,I_r、I_j为实测值,I_r-U、I_j-U为所提模型拟合值.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 渗透率30%三相短路接地故障动态响应描述

Fig.5 Dynamic response description of three-phase fault with a permeability of 30%

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 渗透率60%三相短路接地故障动态响应描述

Fig.6 Dynamic response description of three-phase fault with a permeability of 60%

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 渗透率20%单相故障动态响应描述

Fig.7 Dynamic response description of single-phase fault with a permeability of 20%

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 渗透率40%单相故障动态响应描述

Fig.8 Dynamic response description of single-phase fault with a permeability of 40%

经过分析图5~8可知:发生三相短路接地故障与单相短路接地故障时,模型拟合效果良好,充分验证该模型的普适性;对于两相接地故障,所提模型同样适用,但限于篇幅,暂不进行详细论述.此外,三相短路接地故障下求解模型参数所需时间为0.007~0.01 s,单相短路接地故障下求解模型参数所需时间为0.003~0.008 s.因此,故障类型的改变对模型复杂度的影响不大.

(2) 步长影响性能分析.

输配网发生最严重的三相短路接地故障,光伏渗透率为30%和60%,设置步长分别为0.001 s和0.002 s,计算三相短路接地故障时两种步长的拟合残差,结果如表2所示.可知:两种步长下的动态响应拟合残差十分接近,步长的改变对模型的准确性影响不大.

表2 不同渗透率条件下发生三相短路接地故障时电流参数拟合结果

Tab.2 Fitting results of current parameters in three-phase short-circuit grounding fault at different permeabilities

步长/s	渗透率/%	电压跌落/%	实部拟合残差	虚部拟合残差
0.001	30	3	1.099×10^-4	1.502×10^-4
0.001	30	5	2.044×10^-4	2.647×10^-4
0.001	60	3	1.056×10^-4	1.003×10^-4
0.001	60	5	2.089×10^-4	2.389×10^-4
0.002	30	3	1.517×10^-4	9.681×10^-5
0.002	30	5	2.292×10^-4	1.926×10^-4
0.002	60	3	8.541×10^-5	8.792×10^-5
0.002	60	5	1.535×10^-4	2.154×10^-4

新窗口打开| 下载CSV

由参数辨识结果可知:电流实部和虚部的参数辨识之和均接近于1.该规律可作为新的参数辨识求解思路以及参数是否辨识正确的依据.

(3) 模型适用范围研究.

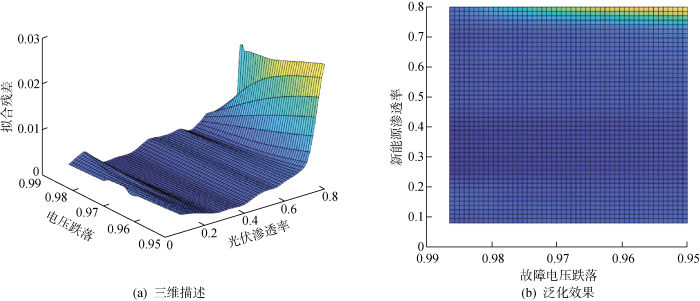
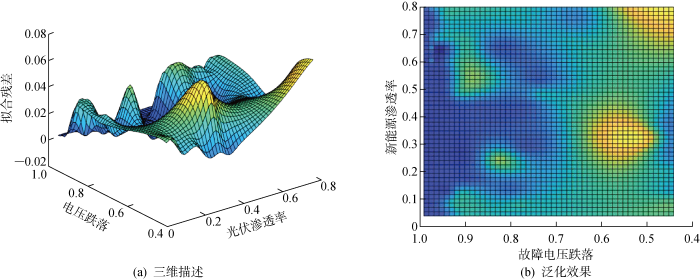
研究相同故障下不同电压的跌落深度,确定模型的有效适用范围.输配电网发生三相短路接地故障时,改变光伏电源的容量,设置条件为光伏渗透率从10%增加至80%(增加间隔为10%),电压跌落深度从5%增加至40%(增加间隔为10%),模型泛化效果如图9和图10所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同渗透率下电压跌落深度5%以内模型泛化能力

Fig.9 Generalization ability of the model with a voltage drop depth less than 5% at different permeabilities

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同渗透率下电压跌落深度40%以内模型泛化能力

Fig.10 Generalization ability of the model with a voltage drop depth less than 40% at different permeabilities

由图9和图10可知,10%~80%的光伏渗透率下,电压跌落5%范围内,所提模型电流暂态响应拟合效果良好;电压跌落在40%以内,模型虽存有一定误差,但仍有相对良好的拟合效果;电压跌落超过60%,模型不再适用于实际工况.由此可知:相较于渗透率,电压跌落的深度对模型泛化影响更加显著.

5 结论

基于光伏发电系统详细机理模型研究提出了一种计及不同渗透率下光伏发电系统动态离散等值模型,主要结论如下:

(1) 基于光伏电站机理模型,建立了光伏并网发电系统的动态4阶离散等值模型,获取动态离散等值模型的模型参数,并采用最小二乘法辨识模型参数,研究发现所提模型精度高、易于辨识.

(2) 从模型的普适性、步长对模型仿真的性能影响、模型的适用范围验证了所提模型的准确性.同时,经过辨识发现模型参数间存在一定规律,可将其作为参数是否辨识正确的依据.

(3) 相较于渗透率,电压跌落的深度对模型泛化影响更加显著.

未来,将研究风光混合配电系统整体动态负荷等值建模;同时,高电压降落情况下模型的修改、选择不同参数辨识策略是以后研究的重点.

附录见本刊网络版(xuebao.sjtu.edu.cn/article/2023/1006-2467-57-04-0412.shtml)

附录A

$θ_{α 1} = \frac{16 A_{13} h^{2} + 16 A_{12} h + 64 A_{11}}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A1)

$θ_{α 2} = \frac{24 A_{13} h^{2} + 96 A_{11}}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A2)

$θ_{α 3} = \frac{- 16 A_{13} h^{2} + 16 A_{12} h - A_{11}}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A3)

$θ_{α 4} = \frac{- 2 A_{14} h^{3} - 4 A_{13} h^{2} + 8 A_{12} h - 16 A_{11}}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A4)

$θ_{α 5} = \frac{2 B_{r} h^{3} + 4 C_{4} h^{2} + 8 A_{r} h}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A5)

$θ_{α 6} = \frac{- 16 A_{r} h}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A6)

$θ_{α 7} = \frac{- 12 C_{r} h^{2}}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A7)

$θ_{α 8} = \frac{- 4 B_{r} h^{3} + 24 A_{r} h}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A8)

$θ_{α 9} = \frac{2 B_{r} h^{3} - 4 C_{r} h^{2} - 8 A_{r} h}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A9)

$θ_{β 1} = \frac{16 A_{13} h^{2} + 16 A_{12} h + 64 A_{11}}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A10)

$θ_{β 2} = \frac{24 A_{13} h^{2} + 96 A_{11}}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A11)

$θ_{β 3} = \frac{- 16 A_{13} h^{2} + 16 A_{12} h - A_{11}}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A12)

$θ_{β 4} = \frac{- 2 A_{14} h^{3} - 4 A_{13} h^{2} + 8 A_{12} h - 16 A_{11}}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A13)

$θ_{β 5} = \frac{2 B_{j} h^{3} + 4 C_{j} h^{2} + 8 A_{j} h}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A14)

$θ_{β 6} = \frac{- 16 A_{j} h}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A15)

$θ_{β 7} = \frac{- 12 C_{j} h^{2}}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A16)

$θ_{β 8} = \frac{- 4 B_{j} h^{3} + 24 A_{j} h}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A17)

$θ_{β 9} = \frac{2 B_{j} h^{3} - 4 C_{j} h^{2} - 8 A_{j} h}{2 A_{14} h^{3} + 4 A_{13} h^{2} + 8 A_{12} h + 16 A_{11}}$

(A18)

式中:h为采样步长;z为Z变换因子.

表A1 三相短路接地故障下电流实部参数辨识结果

Tab.A1 Identification results of current real part parameters in three-phase fault

渗透率/%	电压跌落/%	θ_α₁	θ_α₂	θ_α₃	θ_α₄	θ_α₅	$\overset{5}{\sum_{i = 1}}$ θ_αi	θ_α₆	θ_α₇	θ_α₈	θ_α₉	$\overset{9}{\sum_{i = 6}}$ θ_αi
0	3	2.1553	-2.1487	1.4263	-0.5645	-0.2692	0.6001	0.6795	-0.6389	0.4571	-0.1850	0.3127
0	5	2.2664	-2.3475	1.5473	-0.5854	-0.2896	0.5912	0.7701	-0.7750	0.5368	-0.2060	0.3259
60	3	1.8282	-1.4017	0.8280	-0.3939	-0.1782	0.6824	0.5087	-0.3609	0.1878	-0.0519	0.2837
60	5	1.8644	-1.4669	0.8745	-0.4106	-0.1944	0.6670	0.5544	-0.4232	0.2256	-0.0639	0.2929

新窗口打开| 下载CSV

表A2 三相短路接地故障下电流虚部参数辨识结果

Tab.A2 Identification results of virtual part of current in three-phase fault

渗透率/%	电压跌落/%	θ_β₁	θ_β₂	θ_β₃	θ_β₄	θ_β₅	$\overset{5}{\sum_{i = 1}}$ θ_βi	θ_β₆	θ_β₇	θ_β₈	θ_β₉	$\overset{9}{\sum_{i = 6}}$ θ_βi
30	3	1.2533	-0.5739	0.6167	-0.4172	0.1268	1.0057	-0.0533	0.0618	0.0724	-0.0086	0.0723
30	5	1.3851	-0.8603	0.8250	-0.4791	0.1479	1.0186	-0.1631	0.2012	-0.0281	0.0354	0.0454
60	3	1.2803	-0.9183	1.0121	-0.5162	0.05237	0.91027	0.0469	0.3631	-0.1369	-0.0732	0.1999
60	5	1.3367	-0.9657	0.9922	-0.5025	0.0496	0.9103	-0.0009	0.4329	-0.2098	-0.0419	0.1803

新窗口打开| 下载CSV

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李林晏, 韩爽, 乔延辉, 等.

面向高比例新能源并网场景的风光-电动车协同调度方法

[J]. 上海交通大学学报, 2022, 56(5): 554-563.