无人机航拍城市建筑图像是获取建筑物的勘测和三维建模信息的重要手段,也是城市计算与智慧城市建设的重要组成部分.在雾霾天气下,航拍图像受到大气吸收和散射的影响,场景能见度和色彩饱和度下降,需要进行图像去雾.目前,主流图像去雾方法一般都采用物理模型[1 ] .文献[2 ]利用统计模型估计参数来恢复场景的可见性,文献[3 ]设计了模糊彩色图像的能见度恢复方法,以上方法通常使用高精度测距设备测出图像景深,在实际应用中具有局限性.文献[4 ]利用同一场景在不同天气下的退化图像作为先验信息计算场景深度,实用性同样受限,不易在不同条件下获取同一场景的多幅图像,图像景深的求解成为去雾的难点.另一个重要参数透射率描述了光线在空气中的传播能力,与场景深度密切相关.而在复原过程中,大气光估计值是否准确决定了去雾后图像的亮暗程度,影响透射率求解的准确性.因此,大气光值估计成为求解场景深度的一个思路.文献[5 ]从大量无雾图像的统计数据中总结得出了暗通道先验 (DCP) 理论,为估计大气光和透射率提供先验信息计算复原图像.文献[6 ]通过统计大量模糊图像发现,雾霾浓度与亮度和饱和度的差呈正比,称为颜色衰减先验(CAP),但在雾霾浓度较高的图像中效果不佳.同时,基于DCP、CAP等局部先验理论的方法,在求解透射率时过度依赖局部像素点,使得复原图能见度提升不显著、去雾效果不均匀.文献[7 ]认为大气光值并不是单一全局常量,而是与透射率一起被模型学习的变量,同时提出了基于DehazeNet的图像去雾算法,无需手动对模糊图像特征进行总结,减少了先验知识对复原图像质量的影响.文献[8 ]通过分析含雾图像在红、绿、蓝(RGB)颜色空间的像素分布,首次提出了雾霾线先验非局部先验理论,假设了像素簇内必有部分像素点位于场景深度较小、受雾霾影响较轻的区域.这一假设在绝大多数区域成立,但实际中存在部分像素数量较少的像素簇,簇内可能不存在无雾像素点,使得透射率估计值存在偏差.文献[9 ]采用了改进加权最小二乘模型求解最优透射率估计,改善了透射率估计精度,但模型缺乏纹理及结构区分项,优化后的透射率存在较多纹理.相对总变分(RTV)模型[10 ] 适合去除纹理,但边缘容易出现过度平滑,RTV模型本身仍需改进.
针对以上问题,本文提出了一种融合颜色衰减先验投影最小方差(MCAP)和引导相对总变分(GRTV)正则化的无人机图像去雾方法,所获得的复原图像更加清晰,平均梯度、对比度、雾霾感知密度估计(FADE)[11 ] 及模糊系数等指标均有提升.
1 雾霾图像降质模型
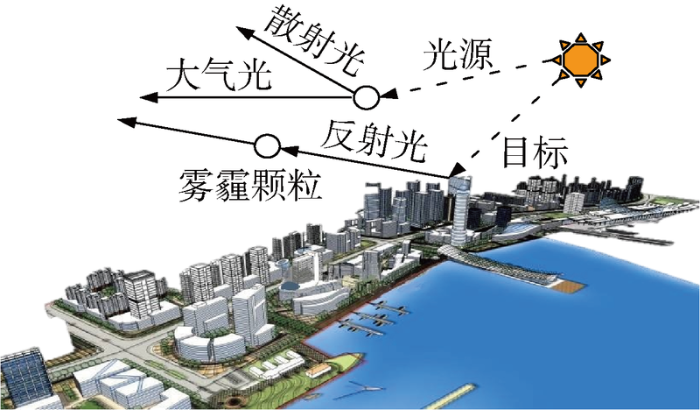
悬浮颗粒在雾霾天会散射和折射光线,从而导致图像模糊或离焦,降低图像质量.为了获得清晰的复原图像,现有主流去雾算法多通过分析图像模糊的原因建立光在雾天的传输过程模型,即反射光衰减模型和大气光模型[12 ] ,如图1 所示.由图1 可以看出,雾霾天无人机获取图像的光源可分为两大类:来自目标物体表面的反射光和场景外的大气光即空气中的光.该模型的数学表达式如下式所示:
(1) I ( x , y ) = I 0 ( x , y ) e - h d ( x , y ) + I s ( 1 - e - h d ( x , y ) )
式中: I(x,y)为像素点坐标为(x,y)的含雾降质图像像素值;d(x,y)为像素点坐标点(x,y)的场景深度; I 0 ( x , y ) e - h d ( x , y ) I 0 ( x , y ) e - h d ( x , y ) h 为大气散射系数; I s ( 1 - e - h d ( x , y ) ) I s κ 为微粒大小,η 为波长,其关系式如下:
(2) h ( η ) ∝ 1 η κ
图1
图1
雾霾颗粒对成像的影响过程
Fig.1
Influence of haze particles on imaging process
在大气光模型中,雾霾颗粒大小为1~10 μm,明显大于正常空气颗粒的10-4 μm.由式(2)可以看出,雾霾颗粒的尺寸决定了h ,此时不同波长可见光近似等量散射,因此所获取的无人机航拍图像呈灰白色,清晰度较低.此外,反射光衰减模型揭示了反射光的固有亮度随深度呈指数衰减.雾霾颗粒在光折射和散射时也会引入较多噪声,引起离焦模糊进而导致无人机航拍图像的质量进一步恶化.
2 MCAP的大气光图估计
传统DCP[5 ] 、CAP[6 ] 去雾方法,通常直接选取暗通道图像中最亮的0.1%像素点对应含雾图像中像素的亮度值作为大气光值,受近景部分中白色或高亮区域的影响,其估计的大气光值不够准确,存在较大局限性.无人机航拍图像中常含有大量天空区域,若采用单一值作为大气光值,当具有较大场景深度且出现光源直射现象时,由于天空区域出现部分失真,单一大气光值易取在失真区域,致使含有丰富信息的中近景区域难以被有效复原,航拍有用目标信息效果较差.所以,本文提出一种MCAP求取大气光图的方法,可以更加准确地获取大气光估计值.
2.1 CAP理论
根据CAP理论,无人机航拍图像中任意区域雾的浓度与该区域像素点的明度和饱和度之差呈正相关,根据这一规律可以得到含雾图像中不同区域景深的差异,其公式描述如下:
(3) d ( x , y ) ∝ c ( x , y ) ∝ v ( x , y ) - s ( x , y )
式中: c(x,y)为像素点坐标(x,y)处的雾气浓度;v(x,y)和s(x,y)分别为像素点坐标(x,y)处的明度和色彩饱和度.场景深度同亮度与饱和度之差的相关性如图2 所示.由图2 可知,场景深度越大,色彩明度与饱和度的差异越大.
图2
图2
CAP原理
Fig.2
Theory of CAP
2.2 MCAP求取大气光值
CAP理论中若直接选用图像中景深信息最大的点作为大气光值,则忽略了相邻像素间的联系,并且容易受到图像中噪声的影响,使大气光估计值产生偏差.首先,将含雾图像转换到色调、饱和度、明度(HSV)颜色空间,求解各个像素点的色彩明度和饱和度之差,即:
(4) I d i f ( x , y ) = v I ( x , y ) - s I ( x , y )
式中:v I i , j s I i , j I d i f ( x , y )
(5) d ( x , y ) ∝ c ( x , y ) ∝ I d i f ( x , y )
为了避免单一极大场景深度值对大气光估计带来的影响,对图像中每一点附近区域的颜色衰减率图像即场景深度进行比较,找出方差最小的区域则可以准确确定图像大气光所在区域,则有:
(6) M a ( x , y ) = m i n Ω ( x , y ) ∈ I d i f ( x , y ) δ Ω ( x , y )
式中:M a x , y r +1(r 为选取半径)列投影值之和,则有:
(7) R r ( x ) = 1 y m a x ∑ y = 1 y m a x [ I d i f ( x , y ) ]
(8) R r _ s ( x ) = ∑ k = x - r x + r R r ( k )
式中:y max 为图像最大列坐标值;R r x R r _ s ( x )
然后,找到R r_s 中所有极值的坐标点作为候选行坐标集合P r_p ,则有:
(9) P r _ p = f i n d p e a k R r _ s ( x )
式中:findpeak[·]为求取峰值的函数.同理,求取候选列坐标集合P c_p .以获得的行、列坐标为中心,确定大小为(2r +1)×(2r +1)候选区域,并利用式(6)得到图像大气光值所在区域,求解区域像素点中值,即为大气光估计值a sur ,公式如下:
(10) a s u r = m e d i a n M a ( x , y )
2.3 大气光图估计
根据大气光与像素位置相关的推论,通过实验发现图像复原效果与大气光估计值及像素所处景深位置密切相关.在大气光为单一全局常量条件下,当大气光估计值偏大时,远景区域复原效果较好,但近景区域亮度较低,细节难以辨认;当大气光估计值偏小时,远景区域出现“亮度饱和”,但近景区域亮度和清晰度较高.因此在求解大气光时,如果能够按照场景深度对图像中各个像素独立地求解大气光估计,使得大气光值不再是单一常量而是随场景深度变化,理论上能改善复原近景光照与远景能见度无法兼顾的问题,将满足这一条件的大气光定义为大气光图.由于场景深度变化为近似估计值,当图像内出现大量天空,且发生光源直射现象时,受成像设备影响,对远景高亮区域及天空区域的处理会出现部分失真,所以对大气光图的估计应在首先保证近景区域清晰的前提下,尽量避免天空区域的失真.大气光图的求解方法是采用含雾图像的暗通道图像作为景深信息图像I d ,利用景深相似度进行聚类分割得到子块图像I g d ( g 为子块图像索引).然后,求取各子块图像中亮度值前1%的像素点对应的含雾图像中的像素点,以这些像素点在RGB这3个通道的平均值作为当前深度子块的大气光估计图A g d A d ,则有:
(11) I d g = K M I d , g ∈ N *
(12) A d g = m e a n s o r t T o p 1 % I d g , g ∈ N *
(13) A d = A d 1 ⋃ A d 2 ⋃ …
式中:KM[·]为K -means聚类函数;mean[·]为取平均值函数;s o r t T o p 1 % ·
2.4 颜色衰减先验投影最小方差的大气光图估计
为了进一步提高大气光估计的鲁棒性,利用提出的颜色衰减先验最小方差投影法求得的全局大气光为基准大气光,以基于场景深度的区域大气光为位置相关大气光,将两种大气光估计进行融合,提出一种新的大气光值图求解方法.
定义基于最小方差投影法求得的全局大气光估计为基准大气光估计图A sur ,基于场景深度求得的区域大气光估计图为A d ,则定义大气光估计图的计算方式为
(14) A e = λ 1 A s u r + λ 2 G F ( I g r a , A d )
式中:λ 1 λ 2 λ 1 = 1 - λ 2 I gra 为引导图像,A d 为待滤波图像.由于引导滤波具有较好的保边平滑和融合引导图像特征的优势,以I gra 为引导图对A d 进行平滑处理,不仅能为大气光图引入区域间相关性,改善其区域间变化过大的问题,同时也能够使得平滑后的大气光图在局部区域内随图像内缓慢变化.引导滤波公式如下:
(15) I q i = α k I i n i + β k , ∀ i ∈ Ω k
(16) α k = 1 ω ∑ i ∈ Ω k I i n i I p i - μ k I - p k σ k 2 + ε 0
(17) β k = I - p k - α k μ k
式中:I in 为输入的引导图像;I q 为滤波后图像;I p 为待滤波图像; Ω k k 为滤波窗口索引;|ω |和σ k ε 0 i 为滤波窗口像素索引; μ k I - p k α k β k
3 基于GRTV正则化的透射率估计
针对透射率粗估计在部分位置存在偏差的问题,通过计算透射率可靠性函数,提出了基于最小通道的透射率修正方法.同时,针对透射率粗估计图像中存在大量无用纹理信息,设计了GRTV正则化方法来提升透射率估计精度,改善无人机航拍场景中浓雾及景深突变区域的复原图像质量.
3.1 雾霾线先验理论
文献[8 ]通过实验证明,清晰图像中色彩及亮度相似的像素点会被聚为同一簇,进一步发现同一簇内像素点一般散布在图像中不同景深区域.当这些像素点受雾霾影响时,降质后像素值大小仅与透射率t 相关,如下式所示:
(18) I l i n ( x , y ) = t l i n ( x , y ) J ( x , y ) + ( 1 - t l i n ( x , y ) ) a l i n = t l i n ( x , y ) ( J ( x , y ) - a l i n ) + a l i n
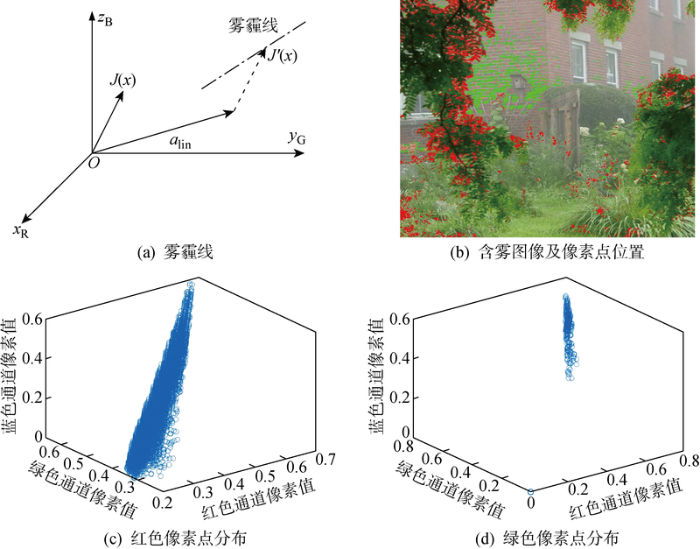
式中: J ( x , y ) I l i n ( x , y ) a l i n t l i n ( x , y ) a l i n t l i n ( x , y ) ( J ( x , y ) - a l i n ) I l i n ( x , y ) t l i n ( x , y ) t l i n ( x , y ) I l i n ( x , y ) 图3(a) 所示.因此,清晰图像中同一簇内像素点受雾霾影响时,在RGB空间Ox R y G z B 沿同一直线分布,将此直线定义为雾霾线.图3(b) 中红色与绿色标记位置为两束像素簇在图像中的分布,图3(c) 和3(d) 分别为这两簇像素点在RGB颜色空间的分布,可以看出像素点大致呈线型分布.
图3
图3
含雾图像像素点在RGB颜色空间的分布
Fig.3
Distribution of pixel points in RGB color space of hazy image
3.2 基于雾霾线理论的透射率估计方法
雾霾线先验理论提出了一种基于整幅图像像素分布的非局部特征,能够避免局部先验理论仅依赖局部像素来估计透射率的缺陷,为透射率估计引入全局相关性.透射率求解的关键是找出图像中存在的雾霾线.假设大气光已知,定义:
(19) I A ( x , y ) = I ( x , y ) - a l i n
式中: I A ( x , y ) 为 含 雾 图 像 坐 标 为 ( x , y )
(20) I A ( x , y ) = t l i n ( x , y ) ( J ( x , y ) - a l i n )
在笛卡尔坐标系下通过聚类求解雾霾线时坐标求解比较复杂,为了便于聚类计算,将I A ( x , y )
(21) I A ( x , y ) = ( γ ( l S p h ) , θ ( l S p h ) , φ ( l S p h ) )
式中: l S p h γ ( l S p h ) I A ( x , y ) θ ( l S p h ) φ ( l S p h ) I A ( x , y ) a l i n t l i n ( x , y ) I A ( x , y ) t l i n ( x , y ) t l i n ( x , y ) θ ( l S p h ) φ ( l S p h ) . 因此,若像素点l S p h 1 l S p h 2 θ ( l S p h 1 ) ≈ θ ( l S p h 2 ) φ ( l S p h 1 ) ≈ φ ( l S p h 2 ) ,
(22) { θ ( l S p h 1 ) ≈ θ ( l S p h 1 ) , φ ( l S p h 1 ) ≈ φ ( l S p h 1 ) } , ∀ t l i n ⇒ J ( x 1 , y 1 ) ≈ J ( x 2 , y 1 )
在球面坐标系下,若两个像素点具有相似的方位角φ (l Sph )和俯仰角θ (l Sph ),则其在空间上沿同一直线分布,两个像素点属于同一条雾霾线.因此,可以按θ (l Sph )及φ (l Sph )的相似性对像素进行聚类,求解像素点所属的簇类.实验中为了简化聚类过程,将球面坐标系按角度提前划分为 1000 个位置,采用构建临近查找树的方法来分别计算图中像素点与这些位置的相似性,将像素点归为不同簇类.为了便于描述,将向量I A ( x , y )
(23) γ ( x , y ) = t l i n ( x , y ) | | J ( x , y ) - a l i n | | = 1 e - h d ( x , y ) | | J ( x , y ) - a l i n | |
根据雾霾线理论,同一簇内的像素点一般散布在图像中不同景深位置上.在簇内像素点充足的条件下,总存在未受到雾霾影响或影响很小的像素点.假设像素x 为簇内不受雾霾影响的像素点,其对应的透射率t l i n x , y
(24) γ m a x = | | J ( x , y ) - a l i n | |
结合式(23)和(24)可知,对于簇内其他受雾霾影响的像素点,透射率可由该点辐射度γ (x , y )与簇内最大辐射度γ max 的比值近似表示,如下式所示:
(25) t l i n ( x , y ) = γ ( x , y ) / γ m a x
利用式(25)求解透射率时,假设像素簇内必有部分像素点位于场景深度较小,受雾霾影响较轻的区域.这一假设在绝大多数区域成立,但对于部分像素数量较少的像素簇,簇内可能不存在无雾像素点,使透射率估计值存在偏差.若簇内景深最小的像素点的辐射度为γ m ,根据式(23)推出γ m <γ max ,则由γ m 求得簇内其他像素点的透射率如下式所示:
(26) t ' l i n ( x , y ) = γ ( x , y ) / γ m t ' l i n ( x , y ) > t l i n ( x , y )
此时该簇内像素点的透射率估计普遍偏大,产生偏差,影响复原图像质量.为解决这一问题,提出一种基于最小通道的透射率修正方法.
为了有针对性地修正透射率,首先需要计算透射率粗估计的可靠性.根据雾霾线理论,影响透射率估计精度的主要因素是簇内像素点的数量及分布情况.当簇内像素点数量越多,簇内辐射度越大的像素点受雾霾影响的可能性越小,γ m 与γ max 越接近,透射率估计准确性越高.当簇内像素沿雾霾线分布间隔越大,即簇内像素点在图像中越分散,求得的雾霾线方向越准确,透射率精度越高.定义透射率可靠性计算方式如下式所示:
(27) Γ ( x , y ) = m i n { N ' / 150 , 1 } × m i n λ 3 γ ( x , y ) γ m a x + λ 4 γ m a x - γ m i n γ m a x , 1
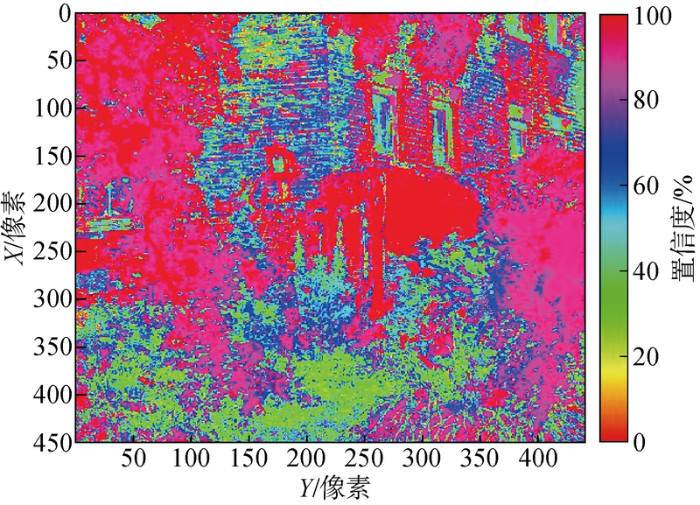
式中: Γ(x,y) 为透射率可靠性;N' 为簇内像素点数量; γ m i n λ 3 λ 4 N' /150,否则返回1,用来衡量该束像素簇是否可靠.然后分别计算该点的辐射值与簇内最大辐射值的比值,以及簇内最大最小辐射值之差与簇内最大辐射值的比值,将其加权求和后衡量该点的透射率可靠性.按照式(27)计算图3(b) 中的透射率可靠性,结果如图4 所示,其中:X 和Y 为X ,Y 轴方向.由图4 可知,由于透射率(见图3(b) )在近景地面存在部分影响透射率精度的噪点,所以这些位置上像素的透射率可靠性较低,且随着场景深度增大,透射率估计可靠性逐渐降低.
图4
图4
透射率可靠性图
Fig.4
Diagram of transmissibility reliability
3.3 RTV模型
RTV不依赖纹理先验知识和人工干预,仅利用函数的总变差区分纹理和结构信息,其公式[10 ] 为
(28) a r g S m i n ∑ p ( S p - I p ) 2 + τ D X ( p ) L X ( p ) + ψ + D Y ( p ) L Y ( p ) + ψ
式中: p 为某一局部区域; S p I p ( S p - I p ) 2 τ 为权重系数; D X D Y L X L Y ψ 为用来预防分母为0的调整系数.由于RTV模型本身的固定性,对于含雾降质图像而言,在多样的气象条件及拍摄方式影响下,无法适应去雾模型中大气透射率的粗略估计,所以必须改进.
3.4 GRTV模型
雾霾线理论求解透射率估计时,部分像素可能存在偏差且含有较多纹理,设计了一种GRTV模型进行透射率优化.按照透射率最优估计条件,优化后的透射率需要满足在可靠性较高的位置保真,而在可靠性较低的位置根据局部相关性结合临近像素点修正透射率,在纹理部分能够增大平滑能力,在结构部分能够保持强度,从而获得透射率的最优解.通过引入引导正则项与加权数据保真项,定义GRTV模型数学表达如下:
(29) m i n t b s t ∑ p { Γ ( p ) ( t b s t ( p ) - t ( p ) ) 2 + λ 5 ∑ p ρ X ∂ t b s t ( p ) ∂ X 2 + ρ Y ∂ t b s t ( p ) ∂ Y 2 + λ 6 ∑ p D X ( p ) L X ( p ) + ε + D Y ( p ) L Y ( p ) + ε }
式中: t 及t b s t ρ X ρ Y λ 5 λ 6 ρ X , ρ Y
(30) ρ X = 1 / ∂ I G ( p ) ∂ X 2 + ε
(31) ρ Y = 1 / ∂ I G ( p ) ∂ Y 2 + ε
式中:I G 为引导图像.在梯度变化剧烈区域ρ X , ρ Y
(32) ∑ p D X ( p ) L X ( p ) + ε = ∑ p ∑ q ∈ Ω ( p ) g p , q | ( ∂ X t b s t ) q | ∑ q ∈ Ω ( p ) g p , q ( ∂ X t b s t ) q + ε
式中${{({{\partial }_{X}}{{t}_{\text{bst}}})}_{q}}$为对t b s t g p , q p 中以q 为中心的标准高斯核函数.
为了求解式(29),需将相对总变分项构造为非线性项与二次项的组合.利用| ( ∂ X t b s t ) q | p 为中心的计算形式由于窗口内各点| ( ∂ X t b s t ) q | | ( ∂ X t b s t ) q | q 为中心的计算形式,变形后如下所示:
(33) ∑ p D X ( p ) L X ( p ) + ε = ∑ q ∑ p ∈ Ω ( q ) g p , q L X ( p ) + ε | ( ∂ X t b s t ) q | ≈ ∑ q ∑ p ∈ Ω ( q ) g p , q L X ( p ) + ε 1 | ( ∂ X t b s t ) q | + ε s r ( ∂ X t b s t ) q 2 = ∑ q u X , q w X , q ( ∂ X t b s t ) q 2
式中:ε sr 为调节系数.令uX , q wX , q
(34) u X , q = ∑ p ∈ Ω ( q ) g p , q L X ( p ) + ε = G σ * 1 | G σ * ∂ X t b s t | + ε q
(35) w X , q = 1 | ( ∂ X t b s t ) q | + ε s r
式中: G σ σ 的高斯滤波器;*为卷积运算符; ∂ X t b s t t b s t
同理,可得垂直方向相对总变分正则项及其参数u Y , q , w Y , q
(36) ∑ p D Y ( p ) L Y ( p ) + ε = ∑ q u Y , q w Y , q ( ∂ Y t b s t ) q 2
(37) u Y , q = ∑ p ∈ Ω ( q ) g p , q L Y ( p ) + ε = G σ * 1 | G σ * ∂ Y t b s t | + ε q
(38) w Y , q = 1 | ( ∂ Y t b s t ) q | + ε s r
根据式(30)~(31)、(33)~(38)将式(29)改写为矩阵形式:
(39) m i n ( ( v b s t - v I ) T Γ ( v b s t - v I ) + λ 5 ( v b s t T C T X P X C X v b s t + v b s t T C T Y P Y C Y v b s t ) + λ 6 ( v b s t T C T X U X W X C X v b s t + v b s t T C T Y U Y W Y C Y v b s t ) )
式中: v b s t v I t b s t Γ PX , P Y U X W X U Y W Y ρ X ρ Y u X , q w X , q u Y , q w Y , q C X C Y
(40) ( Γ I + λ 5 L 1 n + λ 6 L 2 n ) v b s t n + 1 = Γ v I
(41) L 1 n = C T X P X C X + C T Y P Y C Y
(42) L 2 n = C T X U X n W X n C X + C T Y U Y n W Y n C Y
(43) v b s t n + 1 = ( Γ I + λ 1 L 1 n + λ 2 L 2 n ) - 1 Γ v I n
式中: n 为迭代次数.根据式(43),以雾霾线理论得到的透射率估计t l i n ( x ) Γ 、含雾图像I 以及正则项系数λ 5 λ 6 v b s t
输入 透射率图像t ,透射率可靠性Γ ;含雾图像I ;正则项系数λ 5 ,λ 6
(1) function GTRV ( t , Γ , I , λ 5 , λ 6 )
(4) 根据式(30)~(31)、(33)~(38)计算正则项
(9) 将v bst 变形为M 行N 列即为优化后t bst
4 算法流程设计
按照前文所述的颜色衰减先验投影最小方差的大气光图估计求得大气光图A dak 以及结合基于引导相对总变差正则化的透射率估计优化后的透射率t fil ,雾天图像复原公式如下所示:
(44) J ( x , y ) = I ( x , y ) - A d a k m a x { t f i l ( x , y ) , t 0 } + A d a k
式中:t 0 为定义的透射率下阈值,取经验值为0.1.算法流程如图5 所示,算法步骤如下所示.
图5
图5
算法流程
Fig.5
Flow chart of algorithm
步骤2 采用最小方差投影法,对含雾图像的颜色衰减率分别向水平和垂直方向投影,以每一行或列像素的平均颜色衰减率为投影值,求满足与周围行、列像素投影和较大,且方差最小的行列位置.以该像素点为中心,半径为r 的矩形区域内像素点的均值为全局大气光估计值,实验中r 取值为40,将由此求得的全局大气光估计记作基准大气光.
步骤3 采用基于场景深度的区域大气光求解方法,以暗通道图为场景深度参考图像,使用聚类方法对含雾图像按深度进行分割,求解不同景深区域上的大气光估计值,记作区域大气光估计.
步骤4 按照大气光值图计算方法,对求得的基准大气光和区域大气光进行融合处理,使得融合后的大气光值图含有区域间相关性与景深位置信息.
步骤5 按照雾霾线理论,将图像中全部像素转换到以大气光为原点的球面坐标系中表示,而后按照像素点在球面坐标系中的方位角及俯仰角相似性,通过聚类的方式确定该像素归属的像素簇.根据每簇像素点构成的雾霾线,求解簇内最大、最小辐照度,计算透射率粗估计及透射率可靠性.
步骤6 以含雾图像、透射率粗估计、透射率可靠性为输入参数,按照式(30)~(42)及GRTV的求解过程,实验中正则项系数λ 5 和λ 6 分别为0.05和0.015,求解透射率最优估计t bst .
步骤7 将求解的大气光值图和优化后透射率代入雾天图像退化模型求解复原图像.
5 实验结果与分析
实验使用一组自行采集和下载的不同场景下无人机航拍建筑物图片(目前并无任何公开数据集),分别采用暗通道去雾[5 ] 算法、基于融合的变分图像去雾(FVID)[13 ] 算法、基于雾霾线的单图像去雾(Haze-Line)[8 ] 算法、基于深度学习的DehazeNet[7 ] 方法、基于改进梯度相似度核(IGSK)[14 ] 的去雾算法、基于多尺度窗口 (MSW)[15 ] 的自适应透射率图像去雾方法及本文算法进行处理.其中,图6 ~9 为选取4幅不同场景下关键帧的实验结果.同时,表1 中引入了平均梯度、灰度图像对比度、FADE[11 ] 、模糊系数[16 -17 ] 及运算时长等参数来客观评价去雾效果.其中,FADE为2015年提出的目前最权威的图像去雾评价指标[11 ] ,无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素.
图6
图6
E1图像去雾效果
Fig.6
Image dehazing effect of E1
图7
图7
E2图像去雾效果
Fig.7
Image dehazing effect of E2
图8
图8
E3图像去雾效果
Fig.8
Image dehazing effect of E3
图9
图9
E4图像去雾效果
Fig.9
Image dehazing effect of E4
5.1 主观评价
主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰.
实验组2(E2)为包含大量浓雾的河畔建筑航拍图像及其复原图像,如图7 所示.DCP复原了建筑的细节信息,但大量建筑区域色调偏暗,且在中景处仍含有薄雾,复原效果不佳.FVID的复原图像相比于DCP略有提升,但中远景区域仍有雾霾噪声.Haze-Line的复原图像整体色调产生偏差,图像色彩偏绿,色泽上明显失真.DehazeNet在图像复原上有所提升,但图像整体偏暗,对河畔远处区域复原效果不佳.IGSK复原后建筑的细节信息更加平滑,但天空区域有明显光圈,浓雾区域复原的建筑细节处理较差.MSW对薄雾的处理效果明显,但对较亮的浓雾区域处理效果差.与上述算法相比,本文方法的复原图像可以清楚看到建筑的纹理信息,对比度、亮度明显优于其他算法,河畔远处建筑也清晰可见.
实验组3(E3)为城市路口建筑物图像及其复原图像,包含近处绿化区域和远处建筑物,如图8 所示.DCP方法对近景区域和部分建筑区域进行了较好复原,但图像整体偏暗.FVID方法虽然复原质量有一定提高,但仍含有较多雾霾噪声未去除.Haze-Line方法受强光影响,远景建筑物区域色调偏绿,近景区域也出现了一定的失真.DehazeNet方法复原图像细节区域亮度偏低,局部区域仍含有雾霾噪声.IGSK起到一定的去雾作用,但对细节的复原不及其他算法.MSW对远处浓雾区域没有起到复原的效果,导致部分信息丢失.而本文方法有效提升了图像的色彩饱和度,亮度和对比度明显优于其他算法,且色彩也更加鲜艳.
实验组4(E4)为城市建筑航拍图像,包括远处的高楼大厦区域和近处的平房区域,如图9 所示.DCP能够较好复原近处平房建筑的细节,但整体色彩暗淡.FVID整体去雾效果较为均匀,但复原图像相比于DCP整体色调更暗,且对远处建筑处理也不理想.Haze-Line较好复原了远处浓雾区域的细节,但图像色调偏蓝偏绿,颜色明显失真.DehazeNet的复原图像有一层薄雾,细节处理不够明显.IGSK复原后整体上比较模糊,损失了很多细节信息.MSW整体复原效果有所提升,但是远处区域效果不佳.相比之下,本文方法较好复原出城市建筑细节,对远处高楼的处理优于其他算法,近处建筑均清晰可见,而且色彩更加鲜艳.
5.2 客观评价
在本文算法与同类文献主观效果对比占优的基础上,进一步考虑客观评价因素.采用平均梯度、灰度图像对比度、FADE及模糊系数等客观评价指标对复原图像质量进行评价,评价结果如图10 和表1 所示.
图10
图10
去雾图像参数评价
Fig.10
Evaluation of image parameters for dehazing images
结合图6 ~10 及表1 的实验结果分析可以看出,FVID算法得到的复原图像与原图像相比,客观评价指标有所提升,但灰度图像对比度较小,图像整体颜色产生偏差.且由于无人机航拍图片受天空影响过大,造成整体亮度估计过高,去雾后图像偏暗.DCP的复原图像的评价指标虽然都有所提升,但其灰度图像对比度仍然较低,导致整体图像色调偏暗.Haze-Line的复原图像在平均梯度等评价参数上表现良好,但结合实际去雾效果发现图像中有部分区域仍含有大量雾霾噪声,图像色彩有较多失真.DehazeNet的复原图像虽然在平均梯度指标上表现良好,但仍存在图像整体色调偏暗的问题,且由于其原有训练数据集为大量室内图像及人工合成雾霾图像,所以对自然浓雾及包含景深较大区域的复原效果较差.IGSK对含有噪声的含雾图像有较好的处理效果,但对没有噪声的图像效果并不理想,客观指标均不及其他方法且运算耗时长.MSW各指标良好,但远景浓雾区域的处理效果明显下降甚至会导致信息丢失.本文算法的复原图像与原图像相比各评价最优,图像内的有效细节信息最多,平均梯度及灰度图像对比度较高,参数FADE较低可说明图像的整体色调与原始场景相似度较高,结合实际复原图像可以发现对于城市中一些雾霾较重区域处理效果较好,得到图像色彩更加鲜艳.
6 结语
本文提出了一种融合MCAP和GRTV正则化的航拍建筑物图像去雾方法,通过MCAP大气光求解,确定全局大气光估计,解决了全局大气光取值易受场景中景物影响的问题.利用图像场景深度信息求解的区域大气光与全局大气光相融合,获得新的大气光.完成了基于雾霾线理论和GRTV正则化透射率估计与修正,消除了大量无用的纹理信息,提升了透射率估计精度.实验结果表明,通过与主流方法进行实验对比并采用主、客观评价指标进行分析,本文算法有效改善了无人机航拍场景中浓雾及景深突变区域的复原图像质量,多项客观评价指标均有较大幅度提升,对恶劣雾霾天气条件下,改善无人机航拍图像处理的复原质量具有积极意义.
参考文献
View Option
[1]
KIM J Y KIM L S HWANG S H . An advanced contrast enhancement using partially overlapped sub-block histogram equalization
[J]. IEEE Transactions on Circuits and Systems for Video Technology 2001 , 11 (4 ): 475 -484 .
DOI:10.1109/76.915354
URL
[本文引用: 1]
[2]
OAKLEY J P SATHERLEY B L . Improving image quality in poor visibility conditions using a physical model for contrast degradation
[J]. IEEE Transactions on Image Processing 1998 , 7 (2 ): 167 -179 .
DOI:10.1109/83.660994
PMID:18267391
[本文引用: 1]
In daylight viewing conditions, image contrast is often significantly degraded by atmospheric aerosols such as haze and fog. This paper introduces a method for reducing this degradation in situations in which the scene geometry is known. Contrast is lost because light is scattered toward the sensor by the aerosol particles and because the light reflected by the terrain is attenuated by the aerosol. This degradation is approximately characterized by a simple, physically based model with three parameters. The method involves two steps: first, an inverse problem is solved in order to recover the three model parameters; then, for each pixel, the relative contributions of scattered and reflected flux are estimated. The estimated scatter contribution is simply subtracted from the pixel value and the remainder is scaled to compensate for aerosol attenuation. This paper describes the image processing algorithm and presents an analysis of the signal-to-noise ratio (SNR) in the resulting enhanced image. This analysis shows that the SNR decreases exponentially with range. A temporal filter structure is proposed to solve this problem. Results are presented for two image sequences taken from an airborne camera in hazy conditions and one sequence in clear conditions. A satisfactory agreement between the model and the experimental data is shown for the haze conditions. A significant improvement in image quality is demonstrated when using the contrast enhancement algorithm in conjuction with a temporal filter.
[3]
TAN K OAKLEY J P . Enhancement of color images in poor visibility conditions
[C]// Proceedings 2000 International Conference on Image Processing Vancouver, BC, Canada : IEEE , 2000 : 788 -791 .
[本文引用: 1]
[4]
NARASIMHAN S G NAYAR S K . Contrast restoration of weather degraded images
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence 2003 , 25 (6 ): 713 -724 .
DOI:10.1109/TPAMI.2003.1201821
URL
[本文引用: 1]
[5]
HE K M SUN J TANG X O . Single image haze removal using dark channel prior
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence 2011 , 33 (12 ): 2341 -2353 .
DOI:10.1109/TPAMI.2010.168
PMID:20820075
[本文引用: 7]
In this paper, we propose a simple but effective image prior-dark channel prior to remove haze from a single input image. The dark channel prior is a kind of statistics of outdoor haze-free images. It is based on a key observation-most local patches in outdoor haze-free images contain some pixels whose intensity is very low in at least one color channel. Using this prior with the haze imaging model, we can directly estimate the thickness of the haze and recover a high-quality haze-free image. Results on a variety of hazy images demonstrate the power of the proposed prior. Moreover, a high-quality depth map can also be obtained as a byproduct of haze removal.
[6]
ZHU Q S MAI J M SHAO L . A fast single image haze removal algorithm using color attenuation prior
[J]. IEEE Transactions on Image Processing 2015 , 24 (11 ): 3522 -3533 .
DOI:10.1109/TIP.2015.2446191
PMID:26099141
[本文引用: 2]
Single image haze removal has been a challenging problem due to its ill-posed nature. In this paper, we propose a simple but powerful color attenuation prior for haze removal from a single input hazy image. By creating a linear model for modeling the scene depth of the hazy image under this novel prior and learning the parameters of the model with a supervised learning method, the depth information can be well recovered. With the depth map of the hazy image, we can easily estimate the transmission and restore the scene radiance via the atmospheric scattering model, and thus effectively remove the haze from a single image. Experimental results show that the proposed approach outperforms state-of-the-art haze removal algorithms in terms of both efficiency and the dehazing effect.
[7]
CAI B L XU X M JIA K , et al DehazeNet: An end-to-end system for single image haze removal
[J]. IEEE Transactions on Image Processing 2016 , 25 (11 ): 5187 -5198 .
DOI:10.1109/TIP.2016.2598681
PMID:28873058
[本文引用: 6]
Single image haze removal is a challenging ill-posed problem. Existing methods use various constraints/priors to get plausible dehazing solutions. The key to achieve haze removal is to estimate a medium transmission map for an input hazy image. In this paper, we propose a trainable end-to-end system called DehazeNet, for medium transmission estimation. DehazeNet takes a hazy image as input, and outputs its medium transmission map that is subsequently used to recover a haze-free image via atmospheric scattering model. DehazeNet adopts convolutional neural network-based deep architecture, whose layers are specially designed to embody the established assumptions/priors in image dehazing. Specifically, the layers of Maxout units are used for feature extraction, which can generate almost all haze-relevant features. We also propose a novel nonlinear activation function in DehazeNet, called bilateral rectified linear unit, which is able to improve the quality of recovered haze-free image. We establish connections between the components of the proposed DehazeNet and those used in existing methods. Experiments on benchmark images show that DehazeNet achieves superior performance over existing methods, yet keeps efficient and easy to use.
[8]
BERMAN D TREIBITZ T AVIDAN S . Non-local image dehazing
[C]// 2016 IEEE Conference on Computer Vision and Pattern Recognition Las Vegas, NV, USA : IEEE , 2016 : 1674 -1682 .
[本文引用: 7]
[9]
BERMAN D TREIBITZ T AVIDAN S . Single image dehazing using haze-lines
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence 2020 , 42 (3 ): 720 -734 .
DOI:10.1109/TPAMI.2018.2882478
PMID:30475710
[本文引用: 1]
Haze often limits visibility and reduces contrast in outdoor images. The degradation varies spatially since it depends on the objects' distances from the camera. This dependency is expressed in the transmission coefficients, which control the attenuation. Restoring the scene radiance from a single image is a highly ill-posed problem, and thus requires using an image prior. Contrary to methods that use patch-based image priors, we propose an algorithm based on a non-local prior. The algorithm relies on the assumption that colors of a haze-free image are well approximated by a few hundred distinct colors, which form tight clusters in RGB space. Our key observation is that pixels in a given cluster are often non-local, i.e., spread over the entire image plane and located at different distances from the camera. In the presence of haze these varying distances translate to different transmission coefficients. Therefore, each color cluster in the clear image becomes a line in RGB space, that we term a haze-line. Using these haze-lines, our algorithm recovers the atmospheric light, the distance map and the haze-free image. The algorithm has linear complexity, requires no training, and performs well on a wide variety of images compared to other state-of-the-art methods.
[10]
XU L YAN Q XIA Y , et al Structure extraction from texture via relative total variation
[J]. ACM Transactions on Graphics 2012 , 31 (6 ): 1 -10 .
[本文引用: 2]
[11]
CHOI L K YOU J BOVIK A C . Referenceless prediction of perceptual fog density and perceptual image defogging
[J]. IEEE Transactions on Image Processing 2015 , 24 (11 ): 3888 -3901 .
DOI:10.1109/TIP.2015.2456502
PMID:26186784
[本文引用: 3]
We propose a referenceless perceptual fog density prediction model based on natural scene statistics (NSS) and fog aware statistical features. The proposed model, called Fog Aware Density Evaluator (FADE), predicts the visibility of a foggy scene from a single image without reference to a corresponding fog-free image, without dependence on salient objects in a scene, without side geographical camera information, without estimating a depth-dependent transmission map, and without training on human-rated judgments. FADE only makes use of measurable deviations from statistical regularities observed in natural foggy and fog-free images. Fog aware statistical features that define the perceptual fog density index derive from a space domain NSS model and the observed characteristics of foggy images. FADE not only predicts perceptual fog density for the entire image, but also provides a local fog density index for each patch. The predicted fog density using FADE correlates well with human judgments of fog density taken in a subjective study on a large foggy image database. As applications, FADE not only accurately assesses the performance of defogging algorithms designed to enhance the visibility of foggy images, but also is well suited for image defogging. A new FADE-based referenceless perceptual image defogging, dubbed DEnsity of Fog Assessment-based DEfogger (DEFADE) achieves better results for darker, denser foggy images as well as on standard foggy images than the state of the art defogging methods. A software release of FADE and DEFADE is available online for public use: http://live.ece.utexas.edu/research/fog/index.html.
[12]
HUANG H SONG J GUO L , et al Haze removal method based on a variation function and colour attenuation prior for UAV remote-sensing images
[J]. Journal of Modern Optics 2019 , 66 (12 ): 1282 -1295 .
DOI:10.1080/09500340.2019.1615141
URL
[本文引用: 1]
[13]
GALDRAN A VAZQUEZ-CORRAL J PARDO D , et al Fusion-based variational image dehazing
[J]. IEEE Signal Processing Letters 2017 , 24 (2 ): 151 -155 .
[本文引用: 5]
[14]
汪贵平 , 宋京 , 杜晶晶 , 等 . 基于改进梯度相似度核的交通图像去雾算法
[J]. 中国公路学报 2018 , 31 (6 ): 264 -271 .
[本文引用: 5]
雾霾天气下,交通图像采集设备获取的降质图像含有较多噪声,图像边缘不突出,整体偏暗且对比度不高,灰白不清。针对传统交通图像滤波和去雾算法存在着滤波效果和边缘保持能力不能兼顾,容易出现噪声斑块,导致去雾后图像质量较低的问题,在传统梯度双边滤波基础上,设计了一种新的梯度相似度核,提出了基于改进梯度相似度核的雾霾天气下交通图像去雾算法。新算法首先将采集的含雾图像转换到Lab颜色空间,提升色域宽度,再利用改进梯度相似度核和空间相似度核分别计算图像中每一像素点与滤波框内临近像素点的梯度相似度和空间相似度权值,根据权值对图像进行滤波处理,然后将其转换到RGB颜色空间。最后根据大气光散射模型和暗通道先验原理,对滤波后的交通图像进行去雾处理,得到复原图像。试验结果表明:与传统双边滤波和梯度双边滤波算法相比,使用新算法处理后的复原图像峰值信噪比、归一化灰度差平均提升了13.25%、9.41%和21.76%、22.7%。新算法在保证了滤波效果,避免“噪声斑块”的同时,能够尽可能保持图像边缘细节信息,提升了雾霾天气下交通图像的去雾质量,对加强交通监控,保障交通安全有十分重要的应用价值和现实意义。
WANG Guiping SONG Jing DU Jingjing , et al Haze defogging algorithm for traffic images based on improved gradient similarity kernel
[J]. China Journal of Highway and Transport 2018 , 31 (6 ): 264 -271 .
[本文引用: 5]
In fog and haze weather, the degraded images collected by traffic image acquisition equipment contain more noise and the edge of the image is not prominent. Images are dark and the contrast is low, and the images are pale and gray. For traditional traffic image filtering and image defogging algorithms, the filtering effect and edge preserving ability cannot be taken into account, which is prone to cause noise patches, resulting in low image quality after defogging. Based on traditional gradient bilateral filtering, a new gradient similarity kernel is designed, and a haze defogging algorithm for traffic images based on the improved gradient similarity kernel is proposed. Firstly, collected images containing noise are transformed into the Lab color space to enhance the color gamut width. Next, by using the improved similarity kernel and the space similarity, the weights of gradient similarity and spatial similarity are calculated, which are between each pixel of the image and the neighboring pixels in the filter box, respectively. The images are filtered according to the weights, and the filtered images are transformed into the RGB color space. Finally, according to the atmospheric scattering model and the dark channel prior principle, the filtered traffic images are subjected to defogging processing, and restored images can be obtained. The experimental results show that compared with the traditional bilateral filter and gradient bilateral filter, after processing with the proposed algorithm, the peak signal-to-noise ratio and normalized gray difference of the restored image are improved by 13.25% and 9.41%, and 21.76% and 22.7%, respectively. While ensuring the filtering effect and avoiding the "noise patch", as many of the edge details of the image as possible can be retained. This can improve the quality of fog traffic images, and has important application value and practical significance for enhancing traffic monitoring and ensuring traffic safety.
[15]
黄鹤 , 李昕芮 , 宋京 , 等 . 多尺度窗口的自适应透射率修复交通图像去雾方法
[J]. 中国光学 2019 , 12 (6 ): 1311 -1320 .
[本文引用: 5]
HUANG He LI Xinrui SONG Jing , et al A traffic image dehaze method based on adaptive transmittance estimation with multi-scale window
[J]. Chinese Optics 2019 , 12 (6 ): 1311 -1320 .
DOI:10.3788/co.
URL
[本文引用: 5]
[16]
董亚运 , 毕笃彦 , 何林远 , 等 . 基于非局部先验的单幅图像去雾算法
[J]. 光学学报 2017 , 37 (11 ): 83 -93 .
[本文引用: 1]
DONG Yayun BI Duyan HE Linyuan , et al Single image dehazing algorithm based on non-local prior
[J]. Acta Optica Sinica 2017 , 37 (11 ): 83 -93 .
[本文引用: 1]
[17]
黄鹤 , 胡凯益 , 宋京 , 等 . 雾霾线求解透射率的二次优化方法
[J]. 西安交通大学学报 2021 , 55 (8 ): 130 -138 .
[本文引用: 1]
HUANG He HU Kaiyi SONG Jing , et al A twice optimization method for solving transmittance with haze-lines
[J]. Journal of Xi’an Jiaotong University 2021 , 55 (8 ): 130 -138 .
[本文引用: 1]
An advanced contrast enhancement using partially overlapped sub-block histogram equalization
1
2001
... 无人机航拍城市建筑图像是获取建筑物的勘测和三维建模信息的重要手段,也是城市计算与智慧城市建设的重要组成部分.在雾霾天气下,航拍图像受到大气吸收和散射的影响,场景能见度和色彩饱和度下降,需要进行图像去雾.目前,主流图像去雾方法一般都采用物理模型[1 ] .文献[2 ]利用统计模型估计参数来恢复场景的可见性,文献[3 ]设计了模糊彩色图像的能见度恢复方法,以上方法通常使用高精度测距设备测出图像景深,在实际应用中具有局限性.文献[4 ]利用同一场景在不同天气下的退化图像作为先验信息计算场景深度,实用性同样受限,不易在不同条件下获取同一场景的多幅图像,图像景深的求解成为去雾的难点.另一个重要参数透射率描述了光线在空气中的传播能力,与场景深度密切相关.而在复原过程中,大气光估计值是否准确决定了去雾后图像的亮暗程度,影响透射率求解的准确性.因此,大气光值估计成为求解场景深度的一个思路.文献[5 ]从大量无雾图像的统计数据中总结得出了暗通道先验 (DCP) 理论,为估计大气光和透射率提供先验信息计算复原图像.文献[6 ]通过统计大量模糊图像发现,雾霾浓度与亮度和饱和度的差呈正比,称为颜色衰减先验(CAP),但在雾霾浓度较高的图像中效果不佳.同时,基于DCP、CAP等局部先验理论的方法,在求解透射率时过度依赖局部像素点,使得复原图能见度提升不显著、去雾效果不均匀.文献[7 ]认为大气光值并不是单一全局常量,而是与透射率一起被模型学习的变量,同时提出了基于DehazeNet的图像去雾算法,无需手动对模糊图像特征进行总结,减少了先验知识对复原图像质量的影响.文献[8 ]通过分析含雾图像在红、绿、蓝(RGB)颜色空间的像素分布,首次提出了雾霾线先验非局部先验理论,假设了像素簇内必有部分像素点位于场景深度较小、受雾霾影响较轻的区域.这一假设在绝大多数区域成立,但实际中存在部分像素数量较少的像素簇,簇内可能不存在无雾像素点,使得透射率估计值存在偏差.文献[9 ]采用了改进加权最小二乘模型求解最优透射率估计,改善了透射率估计精度,但模型缺乏纹理及结构区分项,优化后的透射率存在较多纹理.相对总变分(RTV)模型[10 ] 适合去除纹理,但边缘容易出现过度平滑,RTV模型本身仍需改进. ...
Improving image quality in poor visibility conditions using a physical model for contrast degradation
1
1998
... 无人机航拍城市建筑图像是获取建筑物的勘测和三维建模信息的重要手段,也是城市计算与智慧城市建设的重要组成部分.在雾霾天气下,航拍图像受到大气吸收和散射的影响,场景能见度和色彩饱和度下降,需要进行图像去雾.目前,主流图像去雾方法一般都采用物理模型[1 ] .文献[2 ]利用统计模型估计参数来恢复场景的可见性,文献[3 ]设计了模糊彩色图像的能见度恢复方法,以上方法通常使用高精度测距设备测出图像景深,在实际应用中具有局限性.文献[4 ]利用同一场景在不同天气下的退化图像作为先验信息计算场景深度,实用性同样受限,不易在不同条件下获取同一场景的多幅图像,图像景深的求解成为去雾的难点.另一个重要参数透射率描述了光线在空气中的传播能力,与场景深度密切相关.而在复原过程中,大气光估计值是否准确决定了去雾后图像的亮暗程度,影响透射率求解的准确性.因此,大气光值估计成为求解场景深度的一个思路.文献[5 ]从大量无雾图像的统计数据中总结得出了暗通道先验 (DCP) 理论,为估计大气光和透射率提供先验信息计算复原图像.文献[6 ]通过统计大量模糊图像发现,雾霾浓度与亮度和饱和度的差呈正比,称为颜色衰减先验(CAP),但在雾霾浓度较高的图像中效果不佳.同时,基于DCP、CAP等局部先验理论的方法,在求解透射率时过度依赖局部像素点,使得复原图能见度提升不显著、去雾效果不均匀.文献[7 ]认为大气光值并不是单一全局常量,而是与透射率一起被模型学习的变量,同时提出了基于DehazeNet的图像去雾算法,无需手动对模糊图像特征进行总结,减少了先验知识对复原图像质量的影响.文献[8 ]通过分析含雾图像在红、绿、蓝(RGB)颜色空间的像素分布,首次提出了雾霾线先验非局部先验理论,假设了像素簇内必有部分像素点位于场景深度较小、受雾霾影响较轻的区域.这一假设在绝大多数区域成立,但实际中存在部分像素数量较少的像素簇,簇内可能不存在无雾像素点,使得透射率估计值存在偏差.文献[9 ]采用了改进加权最小二乘模型求解最优透射率估计,改善了透射率估计精度,但模型缺乏纹理及结构区分项,优化后的透射率存在较多纹理.相对总变分(RTV)模型[10 ] 适合去除纹理,但边缘容易出现过度平滑,RTV模型本身仍需改进. ...
Enhancement of color images in poor visibility conditions
1
2000
... 无人机航拍城市建筑图像是获取建筑物的勘测和三维建模信息的重要手段,也是城市计算与智慧城市建设的重要组成部分.在雾霾天气下,航拍图像受到大气吸收和散射的影响,场景能见度和色彩饱和度下降,需要进行图像去雾.目前,主流图像去雾方法一般都采用物理模型[1 ] .文献[2 ]利用统计模型估计参数来恢复场景的可见性,文献[3 ]设计了模糊彩色图像的能见度恢复方法,以上方法通常使用高精度测距设备测出图像景深,在实际应用中具有局限性.文献[4 ]利用同一场景在不同天气下的退化图像作为先验信息计算场景深度,实用性同样受限,不易在不同条件下获取同一场景的多幅图像,图像景深的求解成为去雾的难点.另一个重要参数透射率描述了光线在空气中的传播能力,与场景深度密切相关.而在复原过程中,大气光估计值是否准确决定了去雾后图像的亮暗程度,影响透射率求解的准确性.因此,大气光值估计成为求解场景深度的一个思路.文献[5 ]从大量无雾图像的统计数据中总结得出了暗通道先验 (DCP) 理论,为估计大气光和透射率提供先验信息计算复原图像.文献[6 ]通过统计大量模糊图像发现,雾霾浓度与亮度和饱和度的差呈正比,称为颜色衰减先验(CAP),但在雾霾浓度较高的图像中效果不佳.同时,基于DCP、CAP等局部先验理论的方法,在求解透射率时过度依赖局部像素点,使得复原图能见度提升不显著、去雾效果不均匀.文献[7 ]认为大气光值并不是单一全局常量,而是与透射率一起被模型学习的变量,同时提出了基于DehazeNet的图像去雾算法,无需手动对模糊图像特征进行总结,减少了先验知识对复原图像质量的影响.文献[8 ]通过分析含雾图像在红、绿、蓝(RGB)颜色空间的像素分布,首次提出了雾霾线先验非局部先验理论,假设了像素簇内必有部分像素点位于场景深度较小、受雾霾影响较轻的区域.这一假设在绝大多数区域成立,但实际中存在部分像素数量较少的像素簇,簇内可能不存在无雾像素点,使得透射率估计值存在偏差.文献[9 ]采用了改进加权最小二乘模型求解最优透射率估计,改善了透射率估计精度,但模型缺乏纹理及结构区分项,优化后的透射率存在较多纹理.相对总变分(RTV)模型[10 ] 适合去除纹理,但边缘容易出现过度平滑,RTV模型本身仍需改进. ...
Contrast restoration of weather degraded images
1
2003
... 无人机航拍城市建筑图像是获取建筑物的勘测和三维建模信息的重要手段,也是城市计算与智慧城市建设的重要组成部分.在雾霾天气下,航拍图像受到大气吸收和散射的影响,场景能见度和色彩饱和度下降,需要进行图像去雾.目前,主流图像去雾方法一般都采用物理模型[1 ] .文献[2 ]利用统计模型估计参数来恢复场景的可见性,文献[3 ]设计了模糊彩色图像的能见度恢复方法,以上方法通常使用高精度测距设备测出图像景深,在实际应用中具有局限性.文献[4 ]利用同一场景在不同天气下的退化图像作为先验信息计算场景深度,实用性同样受限,不易在不同条件下获取同一场景的多幅图像,图像景深的求解成为去雾的难点.另一个重要参数透射率描述了光线在空气中的传播能力,与场景深度密切相关.而在复原过程中,大气光估计值是否准确决定了去雾后图像的亮暗程度,影响透射率求解的准确性.因此,大气光值估计成为求解场景深度的一个思路.文献[5 ]从大量无雾图像的统计数据中总结得出了暗通道先验 (DCP) 理论,为估计大气光和透射率提供先验信息计算复原图像.文献[6 ]通过统计大量模糊图像发现,雾霾浓度与亮度和饱和度的差呈正比,称为颜色衰减先验(CAP),但在雾霾浓度较高的图像中效果不佳.同时,基于DCP、CAP等局部先验理论的方法,在求解透射率时过度依赖局部像素点,使得复原图能见度提升不显著、去雾效果不均匀.文献[7 ]认为大气光值并不是单一全局常量,而是与透射率一起被模型学习的变量,同时提出了基于DehazeNet的图像去雾算法,无需手动对模糊图像特征进行总结,减少了先验知识对复原图像质量的影响.文献[8 ]通过分析含雾图像在红、绿、蓝(RGB)颜色空间的像素分布,首次提出了雾霾线先验非局部先验理论,假设了像素簇内必有部分像素点位于场景深度较小、受雾霾影响较轻的区域.这一假设在绝大多数区域成立,但实际中存在部分像素数量较少的像素簇,簇内可能不存在无雾像素点,使得透射率估计值存在偏差.文献[9 ]采用了改进加权最小二乘模型求解最优透射率估计,改善了透射率估计精度,但模型缺乏纹理及结构区分项,优化后的透射率存在较多纹理.相对总变分(RTV)模型[10 ] 适合去除纹理,但边缘容易出现过度平滑,RTV模型本身仍需改进. ...
Single image haze removal using dark channel prior
7
2011
... 无人机航拍城市建筑图像是获取建筑物的勘测和三维建模信息的重要手段,也是城市计算与智慧城市建设的重要组成部分.在雾霾天气下,航拍图像受到大气吸收和散射的影响,场景能见度和色彩饱和度下降,需要进行图像去雾.目前,主流图像去雾方法一般都采用物理模型[1 ] .文献[2 ]利用统计模型估计参数来恢复场景的可见性,文献[3 ]设计了模糊彩色图像的能见度恢复方法,以上方法通常使用高精度测距设备测出图像景深,在实际应用中具有局限性.文献[4 ]利用同一场景在不同天气下的退化图像作为先验信息计算场景深度,实用性同样受限,不易在不同条件下获取同一场景的多幅图像,图像景深的求解成为去雾的难点.另一个重要参数透射率描述了光线在空气中的传播能力,与场景深度密切相关.而在复原过程中,大气光估计值是否准确决定了去雾后图像的亮暗程度,影响透射率求解的准确性.因此,大气光值估计成为求解场景深度的一个思路.文献[5 ]从大量无雾图像的统计数据中总结得出了暗通道先验 (DCP) 理论,为估计大气光和透射率提供先验信息计算复原图像.文献[6 ]通过统计大量模糊图像发现,雾霾浓度与亮度和饱和度的差呈正比,称为颜色衰减先验(CAP),但在雾霾浓度较高的图像中效果不佳.同时,基于DCP、CAP等局部先验理论的方法,在求解透射率时过度依赖局部像素点,使得复原图能见度提升不显著、去雾效果不均匀.文献[7 ]认为大气光值并不是单一全局常量,而是与透射率一起被模型学习的变量,同时提出了基于DehazeNet的图像去雾算法,无需手动对模糊图像特征进行总结,减少了先验知识对复原图像质量的影响.文献[8 ]通过分析含雾图像在红、绿、蓝(RGB)颜色空间的像素分布,首次提出了雾霾线先验非局部先验理论,假设了像素簇内必有部分像素点位于场景深度较小、受雾霾影响较轻的区域.这一假设在绝大多数区域成立,但实际中存在部分像素数量较少的像素簇,簇内可能不存在无雾像素点,使得透射率估计值存在偏差.文献[9 ]采用了改进加权最小二乘模型求解最优透射率估计,改善了透射率估计精度,但模型缺乏纹理及结构区分项,优化后的透射率存在较多纹理.相对总变分(RTV)模型[10 ] 适合去除纹理,但边缘容易出现过度平滑,RTV模型本身仍需改进. ...
... 传统DCP[5 ] 、CAP[6 ] 去雾方法,通常直接选取暗通道图像中最亮的0.1%像素点对应含雾图像中像素的亮度值作为大气光值,受近景部分中白色或高亮区域的影响,其估计的大气光值不够准确,存在较大局限性.无人机航拍图像中常含有大量天空区域,若采用单一值作为大气光值,当具有较大场景深度且出现光源直射现象时,由于天空区域出现部分失真,单一大气光值易取在失真区域,致使含有丰富信息的中近景区域难以被有效复原,航拍有用目标信息效果较差.所以,本文提出一种MCAP求取大气光图的方法,可以更加准确地获取大气光估计值. ...
... 实验使用一组自行采集和下载的不同场景下无人机航拍建筑物图片(目前并无任何公开数据集),分别采用暗通道去雾[5 ] 算法、基于融合的变分图像去雾(FVID)[13 ] 算法、基于雾霾线的单图像去雾(Haze-Line)[8 ] 算法、基于深度学习的DehazeNet[7 ] 方法、基于改进梯度相似度核(IGSK)[14 ] 的去雾算法、基于多尺度窗口 (MSW)[15 ] 的自适应透射率图像去雾方法及本文算法进行处理.其中,图6 ~9 为选取4幅不同场景下关键帧的实验结果.同时,表1 中引入了平均梯度、灰度图像对比度、FADE[11 ] 、模糊系数[16 -17 ] 及运算时长等参数来客观评价去雾效果.其中,FADE为2015年提出的目前最权威的图像去雾评价指标[11 ] ,无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素. ...
... Evaluation of image parameters for dehazing images
Tab.1 实验组 去雾算法 平均梯度 灰度图像对比度 FADE 模糊系数 运算时长/s E1 原始图像 3.4132 38.0438 3.3746 — — DCP[5 ] 4.6308 41.5066 1.6240 1.2875 10.83 FVID[13 ] 5.0402 44.8432 1.5107 1.3973 1.22 Haze-Line[8 ] 7.1235 66.1660 0.9111 1.9979 5.34 DehazeNet[7 ] 5.0708 55.1841 1.5434 1.3558 1.27 IGSK[14 ] 2.9055 43.6854 1.8265 0.4058 16.89 MSW[15 ] 5.4143 53.9913 1.4022 1.4407 2.54 本文方法 8.1420 72.9530 0.7171 2.3017 6.21 E2 原始图像 2.7286 49.5167 2.3164 — — DCP[5 ] 3.6947 56.4930 1.0717 1.3913 10.81 FVID[13 ] 4.4220 53.6060 1.2449 1.6863 0.81 Haze-Line[8 ] 4.9044 58.5268 0.5796 1.8093 4.07 DehazeNet[7 ] 4.1678 67.0087 0.7425 1.5658 1.27 IGSK[14 ] 2.0462 49.3389 2.9110 0.6316 16.40 MSW[15 ] 4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72
5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
5 ]
3.6947 56.4930 1.0717 1.3913 10.81 FVID[13 ] 4.4220 53.6060 1.2449 1.6863 0.81 Haze-Line[8 ] 4.9044 58.5268 0.5796 1.8093 4.07 DehazeNet[7 ] 4.1678 67.0087 0.7425 1.5658 1.27 IGSK[14 ] 2.0462 49.3389 2.9110 0.6316 16.40 MSW[15 ] 4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
5 ]
6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
5 ]
5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
A fast single image haze removal algorithm using color attenuation prior
2
2015
... 无人机航拍城市建筑图像是获取建筑物的勘测和三维建模信息的重要手段,也是城市计算与智慧城市建设的重要组成部分.在雾霾天气下,航拍图像受到大气吸收和散射的影响,场景能见度和色彩饱和度下降,需要进行图像去雾.目前,主流图像去雾方法一般都采用物理模型[1 ] .文献[2 ]利用统计模型估计参数来恢复场景的可见性,文献[3 ]设计了模糊彩色图像的能见度恢复方法,以上方法通常使用高精度测距设备测出图像景深,在实际应用中具有局限性.文献[4 ]利用同一场景在不同天气下的退化图像作为先验信息计算场景深度,实用性同样受限,不易在不同条件下获取同一场景的多幅图像,图像景深的求解成为去雾的难点.另一个重要参数透射率描述了光线在空气中的传播能力,与场景深度密切相关.而在复原过程中,大气光估计值是否准确决定了去雾后图像的亮暗程度,影响透射率求解的准确性.因此,大气光值估计成为求解场景深度的一个思路.文献[5 ]从大量无雾图像的统计数据中总结得出了暗通道先验 (DCP) 理论,为估计大气光和透射率提供先验信息计算复原图像.文献[6 ]通过统计大量模糊图像发现,雾霾浓度与亮度和饱和度的差呈正比,称为颜色衰减先验(CAP),但在雾霾浓度较高的图像中效果不佳.同时,基于DCP、CAP等局部先验理论的方法,在求解透射率时过度依赖局部像素点,使得复原图能见度提升不显著、去雾效果不均匀.文献[7 ]认为大气光值并不是单一全局常量,而是与透射率一起被模型学习的变量,同时提出了基于DehazeNet的图像去雾算法,无需手动对模糊图像特征进行总结,减少了先验知识对复原图像质量的影响.文献[8 ]通过分析含雾图像在红、绿、蓝(RGB)颜色空间的像素分布,首次提出了雾霾线先验非局部先验理论,假设了像素簇内必有部分像素点位于场景深度较小、受雾霾影响较轻的区域.这一假设在绝大多数区域成立,但实际中存在部分像素数量较少的像素簇,簇内可能不存在无雾像素点,使得透射率估计值存在偏差.文献[9 ]采用了改进加权最小二乘模型求解最优透射率估计,改善了透射率估计精度,但模型缺乏纹理及结构区分项,优化后的透射率存在较多纹理.相对总变分(RTV)模型[10 ] 适合去除纹理,但边缘容易出现过度平滑,RTV模型本身仍需改进. ...
... 传统DCP[5 ] 、CAP[6 ] 去雾方法,通常直接选取暗通道图像中最亮的0.1%像素点对应含雾图像中像素的亮度值作为大气光值,受近景部分中白色或高亮区域的影响,其估计的大气光值不够准确,存在较大局限性.无人机航拍图像中常含有大量天空区域,若采用单一值作为大气光值,当具有较大场景深度且出现光源直射现象时,由于天空区域出现部分失真,单一大气光值易取在失真区域,致使含有丰富信息的中近景区域难以被有效复原,航拍有用目标信息效果较差.所以,本文提出一种MCAP求取大气光图的方法,可以更加准确地获取大气光估计值. ...
DehazeNet: An end-to-end system for single image haze removal
6
2016
... 无人机航拍城市建筑图像是获取建筑物的勘测和三维建模信息的重要手段,也是城市计算与智慧城市建设的重要组成部分.在雾霾天气下,航拍图像受到大气吸收和散射的影响,场景能见度和色彩饱和度下降,需要进行图像去雾.目前,主流图像去雾方法一般都采用物理模型[1 ] .文献[2 ]利用统计模型估计参数来恢复场景的可见性,文献[3 ]设计了模糊彩色图像的能见度恢复方法,以上方法通常使用高精度测距设备测出图像景深,在实际应用中具有局限性.文献[4 ]利用同一场景在不同天气下的退化图像作为先验信息计算场景深度,实用性同样受限,不易在不同条件下获取同一场景的多幅图像,图像景深的求解成为去雾的难点.另一个重要参数透射率描述了光线在空气中的传播能力,与场景深度密切相关.而在复原过程中,大气光估计值是否准确决定了去雾后图像的亮暗程度,影响透射率求解的准确性.因此,大气光值估计成为求解场景深度的一个思路.文献[5 ]从大量无雾图像的统计数据中总结得出了暗通道先验 (DCP) 理论,为估计大气光和透射率提供先验信息计算复原图像.文献[6 ]通过统计大量模糊图像发现,雾霾浓度与亮度和饱和度的差呈正比,称为颜色衰减先验(CAP),但在雾霾浓度较高的图像中效果不佳.同时,基于DCP、CAP等局部先验理论的方法,在求解透射率时过度依赖局部像素点,使得复原图能见度提升不显著、去雾效果不均匀.文献[7 ]认为大气光值并不是单一全局常量,而是与透射率一起被模型学习的变量,同时提出了基于DehazeNet的图像去雾算法,无需手动对模糊图像特征进行总结,减少了先验知识对复原图像质量的影响.文献[8 ]通过分析含雾图像在红、绿、蓝(RGB)颜色空间的像素分布,首次提出了雾霾线先验非局部先验理论,假设了像素簇内必有部分像素点位于场景深度较小、受雾霾影响较轻的区域.这一假设在绝大多数区域成立,但实际中存在部分像素数量较少的像素簇,簇内可能不存在无雾像素点,使得透射率估计值存在偏差.文献[9 ]采用了改进加权最小二乘模型求解最优透射率估计,改善了透射率估计精度,但模型缺乏纹理及结构区分项,优化后的透射率存在较多纹理.相对总变分(RTV)模型[10 ] 适合去除纹理,但边缘容易出现过度平滑,RTV模型本身仍需改进. ...
... 实验使用一组自行采集和下载的不同场景下无人机航拍建筑物图片(目前并无任何公开数据集),分别采用暗通道去雾[5 ] 算法、基于融合的变分图像去雾(FVID)[13 ] 算法、基于雾霾线的单图像去雾(Haze-Line)[8 ] 算法、基于深度学习的DehazeNet[7 ] 方法、基于改进梯度相似度核(IGSK)[14 ] 的去雾算法、基于多尺度窗口 (MSW)[15 ] 的自适应透射率图像去雾方法及本文算法进行处理.其中,图6 ~9 为选取4幅不同场景下关键帧的实验结果.同时,表1 中引入了平均梯度、灰度图像对比度、FADE[11 ] 、模糊系数[16 -17 ] 及运算时长等参数来客观评价去雾效果.其中,FADE为2015年提出的目前最权威的图像去雾评价指标[11 ] ,无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素. ...
... Evaluation of image parameters for dehazing images
Tab.1 实验组 去雾算法 平均梯度 灰度图像对比度 FADE 模糊系数 运算时长/s E1 原始图像 3.4132 38.0438 3.3746 — — DCP[5 ] 4.6308 41.5066 1.6240 1.2875 10.83 FVID[13 ] 5.0402 44.8432 1.5107 1.3973 1.22 Haze-Line[8 ] 7.1235 66.1660 0.9111 1.9979 5.34 DehazeNet[7 ] 5.0708 55.1841 1.5434 1.3558 1.27 IGSK[14 ] 2.9055 43.6854 1.8265 0.4058 16.89 MSW[15 ] 5.4143 53.9913 1.4022 1.4407 2.54 本文方法 8.1420 72.9530 0.7171 2.3017 6.21 E2 原始图像 2.7286 49.5167 2.3164 — — DCP[5 ] 3.6947 56.4930 1.0717 1.3913 10.81 FVID[13 ] 4.4220 53.6060 1.2449 1.6863 0.81 Haze-Line[8 ] 4.9044 58.5268 0.5796 1.8093 4.07 DehazeNet[7 ] 4.1678 67.0087 0.7425 1.5658 1.27 IGSK[14 ] 2.0462 49.3389 2.9110 0.6316 16.40 MSW[15 ] 4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72
5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
7 ]
4.1678 67.0087 0.7425 1.5658 1.27 IGSK[14 ] 2.0462 49.3389 2.9110 0.6316 16.40 MSW[15 ] 4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
7 ]
6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
7 ]
5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
Non-local image dehazing
7
2016
... 无人机航拍城市建筑图像是获取建筑物的勘测和三维建模信息的重要手段,也是城市计算与智慧城市建设的重要组成部分.在雾霾天气下,航拍图像受到大气吸收和散射的影响,场景能见度和色彩饱和度下降,需要进行图像去雾.目前,主流图像去雾方法一般都采用物理模型[1 ] .文献[2 ]利用统计模型估计参数来恢复场景的可见性,文献[3 ]设计了模糊彩色图像的能见度恢复方法,以上方法通常使用高精度测距设备测出图像景深,在实际应用中具有局限性.文献[4 ]利用同一场景在不同天气下的退化图像作为先验信息计算场景深度,实用性同样受限,不易在不同条件下获取同一场景的多幅图像,图像景深的求解成为去雾的难点.另一个重要参数透射率描述了光线在空气中的传播能力,与场景深度密切相关.而在复原过程中,大气光估计值是否准确决定了去雾后图像的亮暗程度,影响透射率求解的准确性.因此,大气光值估计成为求解场景深度的一个思路.文献[5 ]从大量无雾图像的统计数据中总结得出了暗通道先验 (DCP) 理论,为估计大气光和透射率提供先验信息计算复原图像.文献[6 ]通过统计大量模糊图像发现,雾霾浓度与亮度和饱和度的差呈正比,称为颜色衰减先验(CAP),但在雾霾浓度较高的图像中效果不佳.同时,基于DCP、CAP等局部先验理论的方法,在求解透射率时过度依赖局部像素点,使得复原图能见度提升不显著、去雾效果不均匀.文献[7 ]认为大气光值并不是单一全局常量,而是与透射率一起被模型学习的变量,同时提出了基于DehazeNet的图像去雾算法,无需手动对模糊图像特征进行总结,减少了先验知识对复原图像质量的影响.文献[8 ]通过分析含雾图像在红、绿、蓝(RGB)颜色空间的像素分布,首次提出了雾霾线先验非局部先验理论,假设了像素簇内必有部分像素点位于场景深度较小、受雾霾影响较轻的区域.这一假设在绝大多数区域成立,但实际中存在部分像素数量较少的像素簇,簇内可能不存在无雾像素点,使得透射率估计值存在偏差.文献[9 ]采用了改进加权最小二乘模型求解最优透射率估计,改善了透射率估计精度,但模型缺乏纹理及结构区分项,优化后的透射率存在较多纹理.相对总变分(RTV)模型[10 ] 适合去除纹理,但边缘容易出现过度平滑,RTV模型本身仍需改进. ...
... 文献[8 ]通过实验证明,清晰图像中色彩及亮度相似的像素点会被聚为同一簇,进一步发现同一簇内像素点一般散布在图像中不同景深区域.当这些像素点受雾霾影响时,降质后像素值大小仅与透射率t 相关,如下式所示: ...
... 实验使用一组自行采集和下载的不同场景下无人机航拍建筑物图片(目前并无任何公开数据集),分别采用暗通道去雾[5 ] 算法、基于融合的变分图像去雾(FVID)[13 ] 算法、基于雾霾线的单图像去雾(Haze-Line)[8 ] 算法、基于深度学习的DehazeNet[7 ] 方法、基于改进梯度相似度核(IGSK)[14 ] 的去雾算法、基于多尺度窗口 (MSW)[15 ] 的自适应透射率图像去雾方法及本文算法进行处理.其中,图6 ~9 为选取4幅不同场景下关键帧的实验结果.同时,表1 中引入了平均梯度、灰度图像对比度、FADE[11 ] 、模糊系数[16 -17 ] 及运算时长等参数来客观评价去雾效果.其中,FADE为2015年提出的目前最权威的图像去雾评价指标[11 ] ,无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素. ...
... Evaluation of image parameters for dehazing images
Tab.1 实验组 去雾算法 平均梯度 灰度图像对比度 FADE 模糊系数 运算时长/s E1 原始图像 3.4132 38.0438 3.3746 — — DCP[5 ] 4.6308 41.5066 1.6240 1.2875 10.83 FVID[13 ] 5.0402 44.8432 1.5107 1.3973 1.22 Haze-Line[8 ] 7.1235 66.1660 0.9111 1.9979 5.34 DehazeNet[7 ] 5.0708 55.1841 1.5434 1.3558 1.27 IGSK[14 ] 2.9055 43.6854 1.8265 0.4058 16.89 MSW[15 ] 5.4143 53.9913 1.4022 1.4407 2.54 本文方法 8.1420 72.9530 0.7171 2.3017 6.21 E2 原始图像 2.7286 49.5167 2.3164 — — DCP[5 ] 3.6947 56.4930 1.0717 1.3913 10.81 FVID[13 ] 4.4220 53.6060 1.2449 1.6863 0.81 Haze-Line[8 ] 4.9044 58.5268 0.5796 1.8093 4.07 DehazeNet[7 ] 4.1678 67.0087 0.7425 1.5658 1.27 IGSK[14 ] 2.0462 49.3389 2.9110 0.6316 16.40 MSW[15 ] 4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72
5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
8 ]
4.9044 58.5268 0.5796 1.8093 4.07 DehazeNet[7 ] 4.1678 67.0087 0.7425 1.5658 1.27 IGSK[14 ] 2.0462 49.3389 2.9110 0.6316 16.40 MSW[15 ] 4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
8 ]
8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
8 ]
9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
Single image dehazing using haze-lines
1
2020
... 无人机航拍城市建筑图像是获取建筑物的勘测和三维建模信息的重要手段,也是城市计算与智慧城市建设的重要组成部分.在雾霾天气下,航拍图像受到大气吸收和散射的影响,场景能见度和色彩饱和度下降,需要进行图像去雾.目前,主流图像去雾方法一般都采用物理模型[1 ] .文献[2 ]利用统计模型估计参数来恢复场景的可见性,文献[3 ]设计了模糊彩色图像的能见度恢复方法,以上方法通常使用高精度测距设备测出图像景深,在实际应用中具有局限性.文献[4 ]利用同一场景在不同天气下的退化图像作为先验信息计算场景深度,实用性同样受限,不易在不同条件下获取同一场景的多幅图像,图像景深的求解成为去雾的难点.另一个重要参数透射率描述了光线在空气中的传播能力,与场景深度密切相关.而在复原过程中,大气光估计值是否准确决定了去雾后图像的亮暗程度,影响透射率求解的准确性.因此,大气光值估计成为求解场景深度的一个思路.文献[5 ]从大量无雾图像的统计数据中总结得出了暗通道先验 (DCP) 理论,为估计大气光和透射率提供先验信息计算复原图像.文献[6 ]通过统计大量模糊图像发现,雾霾浓度与亮度和饱和度的差呈正比,称为颜色衰减先验(CAP),但在雾霾浓度较高的图像中效果不佳.同时,基于DCP、CAP等局部先验理论的方法,在求解透射率时过度依赖局部像素点,使得复原图能见度提升不显著、去雾效果不均匀.文献[7 ]认为大气光值并不是单一全局常量,而是与透射率一起被模型学习的变量,同时提出了基于DehazeNet的图像去雾算法,无需手动对模糊图像特征进行总结,减少了先验知识对复原图像质量的影响.文献[8 ]通过分析含雾图像在红、绿、蓝(RGB)颜色空间的像素分布,首次提出了雾霾线先验非局部先验理论,假设了像素簇内必有部分像素点位于场景深度较小、受雾霾影响较轻的区域.这一假设在绝大多数区域成立,但实际中存在部分像素数量较少的像素簇,簇内可能不存在无雾像素点,使得透射率估计值存在偏差.文献[9 ]采用了改进加权最小二乘模型求解最优透射率估计,改善了透射率估计精度,但模型缺乏纹理及结构区分项,优化后的透射率存在较多纹理.相对总变分(RTV)模型[10 ] 适合去除纹理,但边缘容易出现过度平滑,RTV模型本身仍需改进. ...
Structure extraction from texture via relative total variation
2
2012
... 无人机航拍城市建筑图像是获取建筑物的勘测和三维建模信息的重要手段,也是城市计算与智慧城市建设的重要组成部分.在雾霾天气下,航拍图像受到大气吸收和散射的影响,场景能见度和色彩饱和度下降,需要进行图像去雾.目前,主流图像去雾方法一般都采用物理模型[1 ] .文献[2 ]利用统计模型估计参数来恢复场景的可见性,文献[3 ]设计了模糊彩色图像的能见度恢复方法,以上方法通常使用高精度测距设备测出图像景深,在实际应用中具有局限性.文献[4 ]利用同一场景在不同天气下的退化图像作为先验信息计算场景深度,实用性同样受限,不易在不同条件下获取同一场景的多幅图像,图像景深的求解成为去雾的难点.另一个重要参数透射率描述了光线在空气中的传播能力,与场景深度密切相关.而在复原过程中,大气光估计值是否准确决定了去雾后图像的亮暗程度,影响透射率求解的准确性.因此,大气光值估计成为求解场景深度的一个思路.文献[5 ]从大量无雾图像的统计数据中总结得出了暗通道先验 (DCP) 理论,为估计大气光和透射率提供先验信息计算复原图像.文献[6 ]通过统计大量模糊图像发现,雾霾浓度与亮度和饱和度的差呈正比,称为颜色衰减先验(CAP),但在雾霾浓度较高的图像中效果不佳.同时,基于DCP、CAP等局部先验理论的方法,在求解透射率时过度依赖局部像素点,使得复原图能见度提升不显著、去雾效果不均匀.文献[7 ]认为大气光值并不是单一全局常量,而是与透射率一起被模型学习的变量,同时提出了基于DehazeNet的图像去雾算法,无需手动对模糊图像特征进行总结,减少了先验知识对复原图像质量的影响.文献[8 ]通过分析含雾图像在红、绿、蓝(RGB)颜色空间的像素分布,首次提出了雾霾线先验非局部先验理论,假设了像素簇内必有部分像素点位于场景深度较小、受雾霾影响较轻的区域.这一假设在绝大多数区域成立,但实际中存在部分像素数量较少的像素簇,簇内可能不存在无雾像素点,使得透射率估计值存在偏差.文献[9 ]采用了改进加权最小二乘模型求解最优透射率估计,改善了透射率估计精度,但模型缺乏纹理及结构区分项,优化后的透射率存在较多纹理.相对总变分(RTV)模型[10 ] 适合去除纹理,但边缘容易出现过度平滑,RTV模型本身仍需改进. ...
... RTV不依赖纹理先验知识和人工干预,仅利用函数的总变差区分纹理和结构信息,其公式[10 ] 为 ...
Referenceless prediction of perceptual fog density and perceptual image defogging
3
2015
... 针对以上问题,本文提出了一种融合颜色衰减先验投影最小方差(MCAP)和引导相对总变分(GRTV)正则化的无人机图像去雾方法,所获得的复原图像更加清晰,平均梯度、对比度、雾霾感知密度估计(FADE)[11 ] 及模糊系数等指标均有提升. ...
... 实验使用一组自行采集和下载的不同场景下无人机航拍建筑物图片(目前并无任何公开数据集),分别采用暗通道去雾[5 ] 算法、基于融合的变分图像去雾(FVID)[13 ] 算法、基于雾霾线的单图像去雾(Haze-Line)[8 ] 算法、基于深度学习的DehazeNet[7 ] 方法、基于改进梯度相似度核(IGSK)[14 ] 的去雾算法、基于多尺度窗口 (MSW)[15 ] 的自适应透射率图像去雾方法及本文算法进行处理.其中,图6 ~9 为选取4幅不同场景下关键帧的实验结果.同时,表1 中引入了平均梯度、灰度图像对比度、FADE[11 ] 、模糊系数[16 -17 ] 及运算时长等参数来客观评价去雾效果.其中,FADE为2015年提出的目前最权威的图像去雾评价指标[11 ] ,无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素. ...
... [11 ],无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素. ...
Haze removal method based on a variation function and colour attenuation prior for UAV remote-sensing images
1
2019
... 悬浮颗粒在雾霾天会散射和折射光线,从而导致图像模糊或离焦,降低图像质量.为了获得清晰的复原图像,现有主流去雾算法多通过分析图像模糊的原因建立光在雾天的传输过程模型,即反射光衰减模型和大气光模型[12 ] ,如图1 所示.由图1 可以看出,雾霾天无人机获取图像的光源可分为两大类:来自目标物体表面的反射光和场景外的大气光即空气中的光.该模型的数学表达式如下式所示: ...
Fusion-based variational image dehazing
5
2017
... 实验使用一组自行采集和下载的不同场景下无人机航拍建筑物图片(目前并无任何公开数据集),分别采用暗通道去雾[5 ] 算法、基于融合的变分图像去雾(FVID)[13 ] 算法、基于雾霾线的单图像去雾(Haze-Line)[8 ] 算法、基于深度学习的DehazeNet[7 ] 方法、基于改进梯度相似度核(IGSK)[14 ] 的去雾算法、基于多尺度窗口 (MSW)[15 ] 的自适应透射率图像去雾方法及本文算法进行处理.其中,图6 ~9 为选取4幅不同场景下关键帧的实验结果.同时,表1 中引入了平均梯度、灰度图像对比度、FADE[11 ] 、模糊系数[16 -17 ] 及运算时长等参数来客观评价去雾效果.其中,FADE为2015年提出的目前最权威的图像去雾评价指标[11 ] ,无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素. ...
... Evaluation of image parameters for dehazing images
Tab.1 实验组 去雾算法 平均梯度 灰度图像对比度 FADE 模糊系数 运算时长/s E1 原始图像 3.4132 38.0438 3.3746 — — DCP[5 ] 4.6308 41.5066 1.6240 1.2875 10.83 FVID[13 ] 5.0402 44.8432 1.5107 1.3973 1.22 Haze-Line[8 ] 7.1235 66.1660 0.9111 1.9979 5.34 DehazeNet[7 ] 5.0708 55.1841 1.5434 1.3558 1.27 IGSK[14 ] 2.9055 43.6854 1.8265 0.4058 16.89 MSW[15 ] 5.4143 53.9913 1.4022 1.4407 2.54 本文方法 8.1420 72.9530 0.7171 2.3017 6.21 E2 原始图像 2.7286 49.5167 2.3164 — — DCP[5 ] 3.6947 56.4930 1.0717 1.3913 10.81 FVID[13 ] 4.4220 53.6060 1.2449 1.6863 0.81 Haze-Line[8 ] 4.9044 58.5268 0.5796 1.8093 4.07 DehazeNet[7 ] 4.1678 67.0087 0.7425 1.5658 1.27 IGSK[14 ] 2.0462 49.3389 2.9110 0.6316 16.40 MSW[15 ] 4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72
5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
13 ]
4.4220 53.6060 1.2449 1.6863 0.81 Haze-Line[8 ] 4.9044 58.5268 0.5796 1.8093 4.07 DehazeNet[7 ] 4.1678 67.0087 0.7425 1.5658 1.27 IGSK[14 ] 2.0462 49.3389 2.9110 0.6316 16.40 MSW[15 ] 4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
13 ]
6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
13 ]
5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
基于改进梯度相似度核的交通图像去雾算法
5
2018
... 实验使用一组自行采集和下载的不同场景下无人机航拍建筑物图片(目前并无任何公开数据集),分别采用暗通道去雾[5 ] 算法、基于融合的变分图像去雾(FVID)[13 ] 算法、基于雾霾线的单图像去雾(Haze-Line)[8 ] 算法、基于深度学习的DehazeNet[7 ] 方法、基于改进梯度相似度核(IGSK)[14 ] 的去雾算法、基于多尺度窗口 (MSW)[15 ] 的自适应透射率图像去雾方法及本文算法进行处理.其中,图6 ~9 为选取4幅不同场景下关键帧的实验结果.同时,表1 中引入了平均梯度、灰度图像对比度、FADE[11 ] 、模糊系数[16 -17 ] 及运算时长等参数来客观评价去雾效果.其中,FADE为2015年提出的目前最权威的图像去雾评价指标[11 ] ,无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素. ...
... Evaluation of image parameters for dehazing images
Tab.1 实验组 去雾算法 平均梯度 灰度图像对比度 FADE 模糊系数 运算时长/s E1 原始图像 3.4132 38.0438 3.3746 — — DCP[5 ] 4.6308 41.5066 1.6240 1.2875 10.83 FVID[13 ] 5.0402 44.8432 1.5107 1.3973 1.22 Haze-Line[8 ] 7.1235 66.1660 0.9111 1.9979 5.34 DehazeNet[7 ] 5.0708 55.1841 1.5434 1.3558 1.27 IGSK[14 ] 2.9055 43.6854 1.8265 0.4058 16.89 MSW[15 ] 5.4143 53.9913 1.4022 1.4407 2.54 本文方法 8.1420 72.9530 0.7171 2.3017 6.21 E2 原始图像 2.7286 49.5167 2.3164 — — DCP[5 ] 3.6947 56.4930 1.0717 1.3913 10.81 FVID[13 ] 4.4220 53.6060 1.2449 1.6863 0.81 Haze-Line[8 ] 4.9044 58.5268 0.5796 1.8093 4.07 DehazeNet[7 ] 4.1678 67.0087 0.7425 1.5658 1.27 IGSK[14 ] 2.0462 49.3389 2.9110 0.6316 16.40 MSW[15 ] 4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72
5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
14 ]
2.0462 49.3389 2.9110 0.6316 16.40 MSW[15 ] 4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
14 ]
3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
14 ]
1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
基于改进梯度相似度核的交通图像去雾算法
5
2018
... 实验使用一组自行采集和下载的不同场景下无人机航拍建筑物图片(目前并无任何公开数据集),分别采用暗通道去雾[5 ] 算法、基于融合的变分图像去雾(FVID)[13 ] 算法、基于雾霾线的单图像去雾(Haze-Line)[8 ] 算法、基于深度学习的DehazeNet[7 ] 方法、基于改进梯度相似度核(IGSK)[14 ] 的去雾算法、基于多尺度窗口 (MSW)[15 ] 的自适应透射率图像去雾方法及本文算法进行处理.其中,图6 ~9 为选取4幅不同场景下关键帧的实验结果.同时,表1 中引入了平均梯度、灰度图像对比度、FADE[11 ] 、模糊系数[16 -17 ] 及运算时长等参数来客观评价去雾效果.其中,FADE为2015年提出的目前最权威的图像去雾评价指标[11 ] ,无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素. ...
... Evaluation of image parameters for dehazing images
Tab.1 实验组 去雾算法 平均梯度 灰度图像对比度 FADE 模糊系数 运算时长/s E1 原始图像 3.4132 38.0438 3.3746 — — DCP[5 ] 4.6308 41.5066 1.6240 1.2875 10.83 FVID[13 ] 5.0402 44.8432 1.5107 1.3973 1.22 Haze-Line[8 ] 7.1235 66.1660 0.9111 1.9979 5.34 DehazeNet[7 ] 5.0708 55.1841 1.5434 1.3558 1.27 IGSK[14 ] 2.9055 43.6854 1.8265 0.4058 16.89 MSW[15 ] 5.4143 53.9913 1.4022 1.4407 2.54 本文方法 8.1420 72.9530 0.7171 2.3017 6.21 E2 原始图像 2.7286 49.5167 2.3164 — — DCP[5 ] 3.6947 56.4930 1.0717 1.3913 10.81 FVID[13 ] 4.4220 53.6060 1.2449 1.6863 0.81 Haze-Line[8 ] 4.9044 58.5268 0.5796 1.8093 4.07 DehazeNet[7 ] 4.1678 67.0087 0.7425 1.5658 1.27 IGSK[14 ] 2.0462 49.3389 2.9110 0.6316 16.40 MSW[15 ] 4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72
5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
14 ]
2.0462 49.3389 2.9110 0.6316 16.40 MSW[15 ] 4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
14 ]
3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
14 ]
1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
多尺度窗口的自适应透射率修复交通图像去雾方法
5
2019
... 实验使用一组自行采集和下载的不同场景下无人机航拍建筑物图片(目前并无任何公开数据集),分别采用暗通道去雾[5 ] 算法、基于融合的变分图像去雾(FVID)[13 ] 算法、基于雾霾线的单图像去雾(Haze-Line)[8 ] 算法、基于深度学习的DehazeNet[7 ] 方法、基于改进梯度相似度核(IGSK)[14 ] 的去雾算法、基于多尺度窗口 (MSW)[15 ] 的自适应透射率图像去雾方法及本文算法进行处理.其中,图6 ~9 为选取4幅不同场景下关键帧的实验结果.同时,表1 中引入了平均梯度、灰度图像对比度、FADE[11 ] 、模糊系数[16 -17 ] 及运算时长等参数来客观评价去雾效果.其中,FADE为2015年提出的目前最权威的图像去雾评价指标[11 ] ,无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素. ...
... Evaluation of image parameters for dehazing images
Tab.1 实验组 去雾算法 平均梯度 灰度图像对比度 FADE 模糊系数 运算时长/s E1 原始图像 3.4132 38.0438 3.3746 — — DCP[5 ] 4.6308 41.5066 1.6240 1.2875 10.83 FVID[13 ] 5.0402 44.8432 1.5107 1.3973 1.22 Haze-Line[8 ] 7.1235 66.1660 0.9111 1.9979 5.34 DehazeNet[7 ] 5.0708 55.1841 1.5434 1.3558 1.27 IGSK[14 ] 2.9055 43.6854 1.8265 0.4058 16.89 MSW[15 ] 5.4143 53.9913 1.4022 1.4407 2.54 本文方法 8.1420 72.9530 0.7171 2.3017 6.21 E2 原始图像 2.7286 49.5167 2.3164 — — DCP[5 ] 3.6947 56.4930 1.0717 1.3913 10.81 FVID[13 ] 4.4220 53.6060 1.2449 1.6863 0.81 Haze-Line[8 ] 4.9044 58.5268 0.5796 1.8093 4.07 DehazeNet[7 ] 4.1678 67.0087 0.7425 1.5658 1.27 IGSK[14 ] 2.0462 49.3389 2.9110 0.6316 16.40 MSW[15 ] 4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72
5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
15 ]
4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
15 ]
7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
15 ]
6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
多尺度窗口的自适应透射率修复交通图像去雾方法
5
2019
... 实验使用一组自行采集和下载的不同场景下无人机航拍建筑物图片(目前并无任何公开数据集),分别采用暗通道去雾[5 ] 算法、基于融合的变分图像去雾(FVID)[13 ] 算法、基于雾霾线的单图像去雾(Haze-Line)[8 ] 算法、基于深度学习的DehazeNet[7 ] 方法、基于改进梯度相似度核(IGSK)[14 ] 的去雾算法、基于多尺度窗口 (MSW)[15 ] 的自适应透射率图像去雾方法及本文算法进行处理.其中,图6 ~9 为选取4幅不同场景下关键帧的实验结果.同时,表1 中引入了平均梯度、灰度图像对比度、FADE[11 ] 、模糊系数[16 -17 ] 及运算时长等参数来客观评价去雾效果.其中,FADE为2015年提出的目前最权威的图像去雾评价指标[11 ] ,无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素. ...
... Evaluation of image parameters for dehazing images
Tab.1 实验组 去雾算法 平均梯度 灰度图像对比度 FADE 模糊系数 运算时长/s E1 原始图像 3.4132 38.0438 3.3746 — — DCP[5 ] 4.6308 41.5066 1.6240 1.2875 10.83 FVID[13 ] 5.0402 44.8432 1.5107 1.3973 1.22 Haze-Line[8 ] 7.1235 66.1660 0.9111 1.9979 5.34 DehazeNet[7 ] 5.0708 55.1841 1.5434 1.3558 1.27 IGSK[14 ] 2.9055 43.6854 1.8265 0.4058 16.89 MSW[15 ] 5.4143 53.9913 1.4022 1.4407 2.54 本文方法 8.1420 72.9530 0.7171 2.3017 6.21 E2 原始图像 2.7286 49.5167 2.3164 — — DCP[5 ] 3.6947 56.4930 1.0717 1.3913 10.81 FVID[13 ] 4.4220 53.6060 1.2449 1.6863 0.81 Haze-Line[8 ] 4.9044 58.5268 0.5796 1.8093 4.07 DehazeNet[7 ] 4.1678 67.0087 0.7425 1.5658 1.27 IGSK[14 ] 2.0462 49.3389 2.9110 0.6316 16.40 MSW[15 ] 4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72
5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
15 ]
4.4642 71.8793 0.7974 1.6494 1.56 本文方法 6.8819 72.3219 0.3560 2.5359 5.00 E3 原始图像 4.0277 34.3381 1.4294 — — DCP[5 ] 6.2019 37.0552 0.5512 1.5606 10.78 FVID[13 ] 6.5895 36.3347 0.5775 1.7264 0.81 Haze-Line[8 ] 8.5561 34.4546 0.2612 2.1607 4.68 DehazeNet[7 ] 6.4785 44.1485 0.4464 1.6495 1.25 IGSK[14 ] 3.0247 33.7982 1.8486 0.6427 16.47 MSW[15 ] 7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
15 ]
7.3224 50.1062 0.4932 1.8492 1.54 本文方法 11.6165 57.2106 0.1953 2.9986 5.01 E4 原始图像 3.6964 28.8263 2.2842 — — DCP[5 ] 5.1626 35.8074 1.1885 1.6117 10.89 FVID[13 ] 5.7754 19.5894 1.2384 1.7113 0.81 Haze-Line[8 ] 9.7989 57.8329 0.4250 2.5171 4.34 DehazeNet[7 ] 5.3420 38.9765 1.3434 1.6479 1.31 IGSK[14 ] 1.8620 28.6709 3.4998 0.2421 16.58 MSW[15 ] 6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
... [
15 ]
6.2033 48.6046 1.0322 1.7546 1.53 本文方法 9.6690 59.4137 0.2788 2.5483 4.72 5.1 主观评价 主观效果是评价去雾的首要考虑因素.针对航拍图像处理的需求,设定去雾的主观评价准则首先保证近景地面目标建筑细节复原清晰,其次保证中远景图质量,最后尽量保证天空清晰.实验组1(E1)为城市建筑航拍图及其复原图像,如图6 所示,较大的天空区域及城市远处较浓的雾霾区域为丰富的建筑细节复原带来了较大困难.采用DCP虽然较好复原出近景区域的建筑物,但是远景和天空区域仍残留一定浓度的雾霾,且图像整体色调偏暗.FVID对近景建筑物区域有一定程度提升,但对远景和天空区域的复原较差.Haze-Line对远景区域有明显效果,但有一定程度失真,远处建筑发暗甚至偏黑,图像整体亮度和饱和度较低;基于深度学习的DehazeNet虽然在图像色调上与原图相似度较好,但整幅图像上存在一定薄雾,没有滤除干净.IGSK有一定的去雾效果,但是建筑细节不够突出,视觉上略显模糊.MSW对近景区域建筑有较好的修复效果,但中远景效果不佳,色彩有一定失真.而本文方法得到的复原图像饱和度有较大程度提升,对所航拍的近、中、远景建筑物细节处理更加细致清晰. ...
基于非局部先验的单幅图像去雾算法
1
2017
... 实验使用一组自行采集和下载的不同场景下无人机航拍建筑物图片(目前并无任何公开数据集),分别采用暗通道去雾[5 ] 算法、基于融合的变分图像去雾(FVID)[13 ] 算法、基于雾霾线的单图像去雾(Haze-Line)[8 ] 算法、基于深度学习的DehazeNet[7 ] 方法、基于改进梯度相似度核(IGSK)[14 ] 的去雾算法、基于多尺度窗口 (MSW)[15 ] 的自适应透射率图像去雾方法及本文算法进行处理.其中,图6 ~9 为选取4幅不同场景下关键帧的实验结果.同时,表1 中引入了平均梯度、灰度图像对比度、FADE[11 ] 、模糊系数[16 -17 ] 及运算时长等参数来客观评价去雾效果.其中,FADE为2015年提出的目前最权威的图像去雾评价指标[11 ] ,无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素. ...
基于非局部先验的单幅图像去雾算法
1
2017
... 实验使用一组自行采集和下载的不同场景下无人机航拍建筑物图片(目前并无任何公开数据集),分别采用暗通道去雾[5 ] 算法、基于融合的变分图像去雾(FVID)[13 ] 算法、基于雾霾线的单图像去雾(Haze-Line)[8 ] 算法、基于深度学习的DehazeNet[7 ] 方法、基于改进梯度相似度核(IGSK)[14 ] 的去雾算法、基于多尺度窗口 (MSW)[15 ] 的自适应透射率图像去雾方法及本文算法进行处理.其中,图6 ~9 为选取4幅不同场景下关键帧的实验结果.同时,表1 中引入了平均梯度、灰度图像对比度、FADE[11 ] 、模糊系数[16 -17 ] 及运算时长等参数来客观评价去雾效果.其中,FADE为2015年提出的目前最权威的图像去雾评价指标[11 ] ,无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素. ...
雾霾线求解透射率的二次优化方法
1
2021
... 实验使用一组自行采集和下载的不同场景下无人机航拍建筑物图片(目前并无任何公开数据集),分别采用暗通道去雾[5 ] 算法、基于融合的变分图像去雾(FVID)[13 ] 算法、基于雾霾线的单图像去雾(Haze-Line)[8 ] 算法、基于深度学习的DehazeNet[7 ] 方法、基于改进梯度相似度核(IGSK)[14 ] 的去雾算法、基于多尺度窗口 (MSW)[15 ] 的自适应透射率图像去雾方法及本文算法进行处理.其中,图6 ~9 为选取4幅不同场景下关键帧的实验结果.同时,表1 中引入了平均梯度、灰度图像对比度、FADE[11 ] 、模糊系数[16 -17 ] 及运算时长等参数来客观评价去雾效果.其中,FADE为2015年提出的目前最权威的图像去雾评价指标[11 ] ,无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素. ...
雾霾线求解透射率的二次优化方法
1
2021
... 实验使用一组自行采集和下载的不同场景下无人机航拍建筑物图片(目前并无任何公开数据集),分别采用暗通道去雾[5 ] 算法、基于融合的变分图像去雾(FVID)[13 ] 算法、基于雾霾线的单图像去雾(Haze-Line)[8 ] 算法、基于深度学习的DehazeNet[7 ] 方法、基于改进梯度相似度核(IGSK)[14 ] 的去雾算法、基于多尺度窗口 (MSW)[15 ] 的自适应透射率图像去雾方法及本文算法进行处理.其中,图6 ~9 为选取4幅不同场景下关键帧的实验结果.同时,表1 中引入了平均梯度、灰度图像对比度、FADE[11 ] 、模糊系数[16 -17 ] 及运算时长等参数来客观评价去雾效果.其中,FADE为2015年提出的目前最权威的图像去雾评价指标[11 ] ,无需参考额外的清晰图像,不依赖局部特征等信息,而是通过统计雾霾图像及其对应的清晰图像差异,对其特征进行学习建立的一种雾霾浓度评价模型,能准确评价复原图像中的雾霾浓度.为了对比各算法运算过程的耗时,在计算运算时长时统一将含雾图像尺寸大小调整为540像素×400像素. ...