k-out-of-n系统机会维护与库存控制多层级优化策略

doi:10.16183/j.cnki.jsjtu.2022.030

k-out-of-n系统机会维护与库存控制多层级优化策略

曹蕾, 安向昕, 夏唐斌^,, 郑美妹, 奚立峰

上海交通大学机械与动力工程学院,上海 200240

Multi-Level Optimization Policy of Opportunistic Maintenance and Inventory Control of k-out-of-n System

CAO Lei, AN Xiangxin, XIA Tangbin^,, ZHENG Meimei, XI Lifeng

School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 夏唐斌,副教授,博士生导师,电话(Tel.):021-34208589;E-mail:xtbxtb@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2022-02-14 接受日期: 2022-05-24

基金资助:

国家自然科学基金(51875359)
上海市“科技创新行动计划”自然科学基金(20ZR1428600)
上海商用飞机系统工程科创中心联合研究基金(FASE-2021-M7)
教育部-中国移动联合基金建设项目(MCM20180703)
上海交通大学深蓝计划基金(SL2021MS008)
中船-交大海洋装备前瞻创新基金(22B010432)

Received: 2022-02-14 Accepted: 2022-05-24

作者简介 About authors

曹蕾(1999-),硕士生,从事制造系统的可靠性建模与维护决策研究.

摘要

面向服务型制造的复杂系统维护外包决策需求,针对k-out-of-n:G系统中冗余设备干涉、停机惩罚高昂和备件库存限制的挑战,提出了机会维护与库存控制多层级优化策略(OMICP).在设备层,构建各独立设备衰退模型,通过最小化维护成本率,贯序输出各设备预防维护周期;在系统层,以各设备维护时点为契机,综合考虑库存水平、关停数量和冗余干涉,制定动态组合机会维护策略;在联合层,基于机会维护决策反馈,建模分析备件订购利润结余,制定实时更新库存控制策略.通过服务商承担外包维护下的多层级交互决策,整合复杂系统维护与库存控制耦合关系,优化维护外包服务总成本.算例分析证明,所提OMICP具有复杂决策可行性和成本优化有效性.

关键词： 维护外包; k-out-of-n:G系统; 机会维护; 库存控制; 多层级优化

Abstract

For the maintenance outsourcing requirements of complex systems in service-oriented manufacturing, a multi-level optimization policy of opportunistic maintenance and inventory control (OMICP) is proposed by considering the challenges of redundant machine interference, high shutdown penalty, and spare parts inventory limit of k-out-of-n: G system. At the machine layer, the degeneration model of each machine is built. Then, preventive maintenance cycles of each machine are outputted in sequence by minimizing the maintenance cost rate. At the system level, these maintenance time points are taken as opportunities. In addition, a dynamic combination opportunistic maintenance policy is established by comprehensively considering inventory level, shutdown quantity, and redundancy interference. At the joint level, based on the opportunistic maintenance decision feedback, the inventory control policy is updated in real time by modeling and analyzing the profit balance of spare parts ordering. Through this multi-level interactive decision-making under outsourcing maintenance, the coupling relationship between complex system maintenance and inventory control is integrated to optimize the total cost of maintenance outsourcing services. The case study has shown that OMICP has the feasibility of complex decision-making and the effectiveness of cost optimization.

Keywords： maintenance outsourcing; k-out-of-n: G system; opportunistic maintenance; inventory control; multi-level optimization

PDF (2485KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

曹蕾, 安向昕, 夏唐斌, 郑美妹, 奚立峰. k-out-of-n系统机会维护与库存控制多层级优化策略[J]. 上海交通大学学报, 2023, 57(3): 285-296 doi:10.16183/j.cnki.jsjtu.2022.030

CAO Lei, AN Xiangxin, XIA Tangbin, ZHENG Meimei, XI Lifeng. Multi-Level Optimization Policy of Opportunistic Maintenance and Inventory Control of k-out-of-n System[J]. Journal of Shanghai Jiaotong University, 2023, 57(3): 285-296 doi:10.16183/j.cnki.jsjtu.2022.030

随着服务型制造的行业应用日益广泛,原始设备生产商(Original Equipment Manufacturer, OEM)越发重视维护外包服务,以保证竞争优势和增加业务收益^[1];而作为客户的生产企业也可通过租赁产线并将维护业务外包给OEM,降低系统运维成本和设备采购投入^[2⇓-4].近年来,具有复杂结构的电力系统、通信系统等的维护外包需求逐年上升^[5-6],此类安全性要求高、运维决策复杂的系统面临故障惩罚成本高昂的共性挑战.因此其结构多被设计为k-out-of-n:G系统,冗余组件的设置允许系统在某些组件发生故障或实施维护的情况下仍能保持工作.此外,由于此类系统具有组成设备多样、运维技术难度高、备件库存影响大的特点,往往需要通过专业的OEM运维服务外包来满足动态维护需求,并合理规划相应备件库存的水平.

面向日益复杂化、动态化的多机系统运维需求,预防维护(Preventive Maintenance,PM)领域的策略研究不断发展^[7⇓-9],目前学者们大多聚焦在单机、多机、串联以及串并联结构.在单机系统维护建模的基础上,许多学者针对多机复杂系统的运维决策开展了研究.田雪雁等^[10]利用马尔可夫决策过程,研究双机系统不完美维护策略,建立生产系统利润模型进行预防性维护决策.宁小涵等^[11]针对串行生产线系统,提出了一种时间窗与引力窗相结合的机会维护决策方法,有效解决生产等待和持续时间的不确定性问题.Xia等^[12]以制造系统的串并联结构为研究重点,提出一种面向容量均衡问题的租赁利润优化策略,动态优化实时维护决策.值得注意的是,由于k-out-of-n系统的结构特性不同于传统串并联系统,其维护建模需考虑冗余设备的影响,目前相应维护决策研究相对较少.刘学娟等^[13]提出了基于延迟时间理论的k-out-of-n系统检测区间模型.王莹等^[14]研究了k-out-of-n系统长期单位成本最小的最佳预防维护周期与最小维护界限.上述针对k-out-of-n系统的研究主要面向预防维护周期规划,而未考虑库存水平对预防维护的影响,缺乏系统机会维护和动态库存调度的融合决策.

考虑到k-out-of-n系统高停机惩罚特性将导致备件库存极大影响维护总成本,忽略备件库存进行维护决策往往导致次优决策;过度增加库存则会导致备件持有成本的巨大浪费.为解决上述问题,将备件库存控制决策纳入k-out-of-n系统维护建模进行联合优化决策有重要理论和应用价值.分析两者之间存在的强耦合关系:一方面维护行为将消耗库存,直接影响库存持有与订购成本;另一方面备件不足会妨碍维护计划的开展,并影响生产活动.因此维护与库存决策相互干涉,为联合优化建模带来技术挑战.Wang等^[15] 基于维纳过程和伽马过程对k-out-of-n系统进行退化建模,利用马尔可夫决策过程与动态规划联合优化检查周期与订购策略.Bjarnason等^[16]基于定期检查原则,采用(S, s)库存控制策略,寻求k-out-of-n系统最优维护检查间隔与库存控制策略.综上所述,目前的库存优化策略多基于传统订货策略,亟需进一步制定可随维护计划更新的动态库存控制策略.

本文面向k-out-of-n:G系统维护建模需求,弥补机会维护与传统订货策略无法动态更新的不足,构建维护利润结余(Maintenance Profit Saving, MPS)与库存利润结余(Inventory Profit Saving, IPS)模型,提出机会维护与库存控制多层级优化策略(Opportunistic Maintenance and Inventory Control Policy, OMICP).统筹考虑k-out-of-n:G系统中系统冗余设备干涉、系统停机惩罚高昂、维护能力有限、备件库存有限对联合决策的影响,通过在维护利润结余模型中纳入库存水平因素并在库存利润结余模型中纳入拟维护需求,解决了服务型制造背景下k-out-of-n:G系统预防维护与库存控制强耦合关系的技术难点,应用多层级优化与动态更新的思想,动态输出机会维护与备件订购方案,实现维护外包服务总成本有效降低的目的.

1 问题描述

针对k-out-of-n:G系统具有n个独立设备,至少需其中k个设备正常运行可保证整个系统工作的特点,对k-out-of-n:G系统的建模假设如下.

(1) 在租赁期开始时设备均为全新,维护行为会使得设备折旧加快,造成固定资产的损失.

(2) n个设备退化过程相互独立,并在预防性和纠正性维护期间不会退化,只有当机器继续运行时才会继续退化和产生故障.

(3) 若在维护周期内出现了设备故障,则进行纠正性维护,由于纠正性维护针对非计划性故障,所以维护时长与成本均大于计划性的预防性维护.

(4) 在订购周期内若需纠正性维护则需紧急订购,将产生高于常规订购成本的紧急订购成本.

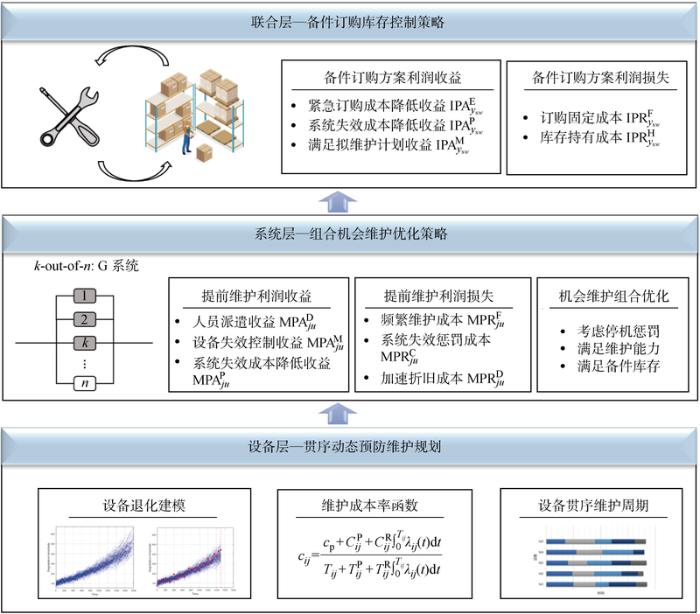
基于上述假设,统筹考虑其冗余设备干涉和备件库存限制的建模难点,提出了涵盖设备层、系统层和联合层的多层级OMICP.OMICP框架如图1所示,多层级维护与库存交互决策构建如下.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 OMICP框架图

Fig.1 Illustration of OMICP

(1) 设备层-贯序动态预防维护规划:面向服务型制造维护外包服务,基于k-out-of-n系统中各独立租赁设备衰退趋势,考虑环境工况并结合备件成本进行建模,构建设备衰退函数与维护成本率模型,贯序获取各设备最佳预防维护周期,作为系统层机会维护优化的输入.

(2) 系统层-组合机会维护优化策略:实时获取各设备最佳预防维护时间间隔,以各台设备的贯序维护时点为机会维护契机,计算非修设备的MPS作为最大化利润参考,进一步考虑系统停机惩罚、维护能力和备件水平的约束,对MPS获取的维护组合进行优化更新,生成实时系统层维护周期机会维护方案.

(3) 联合层-备件订购库存控制策略:根据系统层维护周期机会维护方案,实时生成后续预防维护与纠正性维护计划,在IPS建模中综合考虑机会维护计划、当前设备状况与备件库存水平,通过最大化备件订购方案的IPS,生成当前联合层周期的备件订购方案, 从而周期递进地实现动态机会维护与库存控制联合优化.

2 设备层贯序动态预防维护规划

k-out-of-n: G系统中各设备功能相近,而由于设备役龄、工况环境等因素的影响,n个部件的退化过程相互独立,需要对每台设备的健康衰退进行单独建模.在仅考虑更换型维护的情况下,维护后役龄时长更新为t=0.考虑环境工况的因素,引入基于调整因子ε_j(ε_j>1)(j=1, 2, …, n)的修复模型,用以表征新部件由于工况因素退化加速的情况.采用Weibull 函数表征设备的初始故障率(t=0).因此设备M_j(j=1, 2, …, n)在第i维护周期内的衰退函数为

(1)λ_ij(t)=

\{\begin{array}{l} \frac{β_{j}}{η_{j}} {(\frac{t}{η_{j}})}^{β_{j} - 1}, & i = 1 \\ ε_{j} λ_{(i - 1) j} (t), & i > 1 \end{array}

式中:β_j和η_j分别为威布尔分布的形状参数和比例参数,且β_j>1.

从成本角度出发,在设备层建立考虑备件成本的维护成本率模型,动态输出各独立设备动态预防维护方案.设备M_j在第i个维护周期中的维护成本率可以表示为

(2)

\begin{array}{l} c_{i j} = \frac{c_{p} + C^{P}_{i j} + C^{R}_{i j} \int_{0}^{T_{i j}} λ_{i j} (t) d t}{T_{i j} + T^{P}_{i j} + T^{R}_{i j} \int_{0}^{T_{i j}} λ_{i j} (t) d t} \\ i = 1, 2, \dots, j = 1, 2, \dots, n \end{array}

式中:c_p为单件备件成本; ${C^{P}}_{i j}$ 为预防维护作业成本; ${T^{P}}_{i j}$ 为预防维护作业时长; ${C^{R}}_{i j}$ 为纠正性维护作业成本; ${T^{R}}_{i j}$ 为纠正性维护作业时长;T_ij为待求的最佳维护周期.因此,式(2)中分子表示第i个维护周期维护行为总成本,分母为第i个维护周期总时长,本问题为凸规划问题,令dc_ij/dT_ij=0,可以获得各设备的贯序动态维护周期 $T_{i j}^{*}$ .

3 系统层组合机会维护优化策略

独立设备贯序动态维护计划仅考虑每台设备单位时间维护成本最优,多次派遣维护团队将产生多余固定成本,使得单设备独立维护计划总体次优.本研究提出一种机会维护策略对设备层预知维护方案进行优化,以系统中各台设备贯序维护时点为契机,当其中一台设备M_j最先到达其预防维护时点t_ij时,将其定义为系统层的机会维护时点t_u=min t_ij,并将触发设备M_j定义为M_m.通过分析整个系统中各台非修设备若提前预防维护对维护利润的影响,计算租赁设备维护利润收益(Maintenance Profit Addition, MPA)和利润损失(Maintenance Profit Reduction, MPR),从而获得各台租赁设备的MPS.以此作为决策依据,结合设备特性、库存水平和维护能力进行机会维护优化,决策最佳维护组合GP_u.

3.1 考虑库存水平的提前维护利润收益

若将其他非修设备的预防维护作业提前至机会维护时点t_u可以产生利润收益,MPA分为人员派遣收益MP $A_{j u}^{D}$ 、设备失效控制收益MP $A_{j u}^{M}$ 和系统失效成本降低收益MP $A_{j u}^{P}$ .

若每台设备都分别独立维修,那么每一次都需要派遣维修人员,将会产生较高的人员派遣固定成本,提前成组维护可以节省一次单独人员单独派遣的固定成本,即

(3)

M P {A^{D}}_{j u} = {C^{D}}_{i j}

式中: ${C^{D}}_{i j}$ 为第i个维护周期派遣维护设备M_j的单次人员派遣成本.

另一方面,提前更换部件缩短了非修设备的原始间隔时间,使得设备M_j的维护周期从 $T_{i j}^{*}$ 降低为 $T_{i j}^{*}$ -(t_ij-t_u),因此累计失效概率也随之降低,从而减少了纠正性维护成本,即

(4)

M P {A^{M}}_{j u} = (\int_{0}^{T_{i j}^{*}} λ_{i j} (t) d t - \int_{0}^{T_{i j}^{*} - (t_{i j} - t_{u})} λ_{i j} (t) d t) ({C^{R}}_{i j} - {C^{P}}_{i j})

提前维护还可以降低由于维护周期内突发故障可能造成的系统失效惩罚成本以及紧急订购成本.MP $A_{j u}^{P}$ 需分两种情况进行讨论,若t_u时刻正常运行的设备数量u_M_u_-≤k,则

(5)

M P {A^{P}}_{j u} = (\int_{0}^{T_{i j}^{*}} λ_{i j} (t) d t - \int_{0}^{T_{i j}^{*} - (t_{i j} - t_{u})} λ_{i j} (t) d t) \times [(1 - s g n (v_{s u})) (c_{d} L + K_{p e m}) + c_{d} {T^{R}}_{i j}]

若u_M_u_->k,则由于冗余设备的存在不会产生系统失效成本,即

(6)

M P {A^{P}}_{j u} = (\int_{0}^{T_{i j}^{*}} λ_{i j} (t) d t - \int_{0}^{T_{i j}^{*} - (t_{i j} - t_{u})} λ_{i j} (t) d t) \times K_{p e m} (1 - s g n (v_{s u}))

式中:c_d为单位时间不能满足系统最低运行设备数量要求的惩罚成本;v_s_u为第u个系统层维护周期进行预防维护前的备件库存水平;K_pem为紧急订购备件的固定成本,包含人员、物流等成本;L为备件订购提前期.

3.2 考虑关停数量的提前维护利润损失

相应地,提前预防维护也会产生租赁利润损失,包括频繁维护成本MP $R_{j u}^{F}$ 、系统失效惩罚成本MP $R_{j u}^{C}$ 、加速折旧成本MP $R_{j u}^{D}$ .首先,提前预防维护缩短了预防维护间隔时间,因此在维护合同总周期内需要进行更多预防维护作业,从而产生更多预防维护与备件购买成本,则有

(7)

M P {R^{F}}_{j u} = \frac{t_{i j} - t_{u}}{T_{i j}^{*} - (t_{i j} - t_{u})} ({C^{P}}_{i j} + c_{p})

同时,提前预防维护意味着在同一时段内有更多设备关停,若机会维护设备总数大于系统最大允许关停设备数量,则会造成在预防维护期间产生系统失效惩罚,则有

(8)

M P {R^{C}}_{j u} = c_{d} m a x {0, k - u_{M u} -} {T^{P}}_{i j}

另外,参考资产评估的要素,频繁维护会造成设备加速折旧,造成固定资产的损失.定义维护合同总周期为T_L,折旧系数为δ_j,合同始末的价值折损为 ${V^{S}}_{j}$ - ${V^{E}}_{j}$ ,则有

(9)

M P {R^{D}}_{j} = δ_{j} \frac{t_{i j} - t_{u}}{T_{L}} ({V^{S}}_{j} - {V^{E}}_{j})

3.3 冗余设备干涉的机会维护利润择优

通过整合MPA和MPR得到租赁设备组合MPS,则第u个系统层维护周期各设备的MPS为

(10)

{M P S}_{j u} = M P {A^{D}}_{j u} + M P {A^{M}}_{j u} + M P {A^{P}}_{j u} - M P {R^{F}}_{j u} - M P {R^{C}}_{j u} - M P {R^{D}}_{j u}

式中:j=1, 2, …, n,且j≠m.

若MPS_ju>0,说明M_j的预防维护提前至t_u时点可降低成本.识别提前预防维护的设备

(11)

Ω (j, t_{u}) = \{\begin{array}{l} 1, & M P S_{j u} > 0 \\ 0, & M P S_{j u} \leq 0 \end{array}

即Ω(j, t_u)=1则表示提前维护,Ω(j, t_u)=0则表示不提前维护.则可定义提前预防维护的设备数量x_s_u为

(12)

x_{s u} = \overset{a}{\sum_{k = 1}} Ω (j, t_{u})

上述提前预防维护决策仅从最大化利润结余的角度出发,而决策维护组合GP_u需要进一步考虑系统冗余设备干涉的特性以及维护能力和备件水平的约束,对MPS_ju得出的组合进行进一步优化.设定e为维护能力,第u个周期系统层的组合机会维护策略优化的具体步骤如下.

(1) 判断维护组合GP_u是否满足系统最低正常运行设备数量约束,若满足,则进入第2步;若不满足,更新MPS'_ju=MPS_ju-P_ju, P_ju为不满足系统要求的惩罚成本.若GP_u中设备均满足MPS'_ju>0则进入第2步,若不满足,则将GP_u中对应MPS'_ju较小的x_s_u-n+k台待修设备更新为Ω(j,t_u)=0并进入第2步.

(2) 判断维护组合GP_u是否满足维护能力与备件库存约束,若满足则进入第3步,若不满足则选择MPS_ju较大的min {e, v_s_u}台设备保持Ω(j, t_u)=1,将其余GP_u中待修设备更新为Ω(j, t_u)=0并进入第3步.

(3) 获得最终维护组合GP_u,从而开展第u个系统层维护周期的维护.

4 联合层备件订购库存控制策略

在联合层进一步分析库存备件在维护消耗后的订购策略.备件库存水平与维护决策密切相关,较低的订购频率会造成更大的紧急订购概率,造成更长的故障停机时间,而较为频繁的订购会产生更多的订购固定成本与库存持有成本.维护行为将降低库存水平产生订购机会时点,于此时进行库存检查并决策订购计划是最优订购频率.已有研究^[17]表明,当维护间隔与库存检查间隔相等时可以获得最低的停机成本率、库存成本率与缺货成本率.由于机会维护计划与库存控制策略之间存在耦合关系,需要进一步考虑机会维护计划、当前设备状况与备件库存水平,形成以IPS为导向的动态备件订购方案.

4.1 备件订购方案约束确定

在机会维护计划执行后进行库存检查,进入联合层第w周期,定义待决策的备件订购数量为y_s_w.一方面,订购后的库存水平应至少保证下个维护周期后能满足最低运行设备数量要求;另一方面,由于下个维护时点至少有一台触发设备需要维护,需保证v_s(_u₊₁₎≥1.定义第w个联合层周期库存检查所得备件库存为v_w,与v_s_u满足关系v_w=v_s_u-x_s_u,因此备件订购数量下约束为

(13)

y_{s w} \geq n - u_{M u +} - (n - k)

(14)

y_{s w} \geq m a x {0, 1 - v_{w}}

式中:u_M_u₊为在维护时点t_u进行机会维护后设备正常运行数量.两式可合并为

(15)

y_{s w} \geq m a x {0, 1 - v_{w}, k - u_{M u +}}

另外,定义最大备件库存容量等于设备总数n,y_s_w的上约束需要满足关系

(16)

y_{s w} \leq n - v_{w}

4.2 备件订购方案利润评估

订购的备件数量将直接影响维护外包服务成本.备件的采购提前期相对较长,在备件库存水平较低的情况下可能会出现突发故障时无备件可用的情况,紧急备件订购将产生更多的备件订购成本与停机时间;而若订购数量较多则会产生较高的库存持有成本.因此,一方面考虑备件订购带来的利润收益,包含紧急订购成本降低收益IP $A_{y_{s w}}^{E}$ 、系统失效成本降低收益IP $A_{y_{s w}}^{P}$ 以及满足拟维护计划收益IP $A_{y_{s w}}^{M}$ ;另一方面,考虑备件订购带来的利润损失,包含订购固定成本IP $R_{y_{s w}}^{F}$ 和库存持有成本IP $R_{y_{s w}}^{H}$ .

在下一机会维护维护时点到来之前,若出现突发故障但无备件可用时则需要紧急订购,因此及时订购备件可避免紧急订购成本,带来一定收益,即

(17)

{IPA}_{y_{s w}}^{E} = min \{max \{\sum_{j = 1}^{n} \int_{0}^{t_{u + 1} - t_{u}} λ_{i j} (t) dt - v_{w}, 0\}, y_{s w}\} \times K_{p e m}

式中: $\overset{n}{\sum_{j = 1}} \int_{0}^{t_{u + 1} - t_{u}}$ λ_ij(t)dt-v_w为在不订购情况下第 u+1个系统层维护周期内无法进行预防性维护的设备数量.

在紧急备件订购提前期内,若超过n-k台设备需要维护,将产生系统失效惩罚成本,即

(18)

{IPA}^{P}_{y_{s w}} = c_{d} L m i n \{m a x \{\overset{n}{\sum_{j = 1}} \int_{0}^{t_{u + 1} - t_{u}} λ_{i j} (t) d t - v_{w} - (n - k), 0\}, y_{s w}\}

另外,库存水平下限需要考虑第u+1个系统层维护周期的维护计划.在不考虑备件库存的情况下获得维护组合GP_u₊₁来衡量备件库存满足拟维护组合带来的维护利润结余增加.定义从大到小的维护利润结余为MPS_[_j_](_u₊₁₎, j=1, 2, …, x_s(_u₊₁₎,则IP ${A^{M}}_{y_{s w}}$ 可以表示为

(19)

{IPA}^{M}_{y_{s w}} = \overset{min \{x_{s (u + 1)}, y_{s w} + v_{w}, n\}}{\sum_{j = v_{w} + 1}} M P S_{[j] (u + 1)}

备件订购带来的利润损失包含IP $R_{y_{s w}}^{F}$ 和IP $R_{y_{s w}}^{H}$ .定义单次订购固定成本为K_p,若进行订购则I_p_w=1,否则I_p_w=0,则

(20)

{IPR}^{F}_{y_{s w}} = K_{p} I_{p w}

备件库存持有成本与持有数量以及持有时间成正比,库存持有数量的增量定义为订购数量与维护周期内纠正性维护次数之差,则有

(21)

{IPR}^{H}_{y_{s w}} = m a x \{y_{s w} - \overset{n}{\sum_{j = 1}} \int_{0}^{t_{u + 1} - t_{u}} λ_{i j} (t) d t, 0\} \times t_{u}_{+ 1} - t_{u} - L) c_{h}

式中:c_h为单位时间单位数量库存的持有成本.

4.3 备件动态订购策略

通过比较库存利润收益与利润损失,获得在订购部件数量为y_s_w下库存备件订购利润结余为

(22)

I P S_{y_{s w}} = I P {A^{E}}_{y_{s w}} + I P {A^{P}}_{y_{s w}} + I P {A^{M}}_{y_{s w}} - I P {R^{F}}_{y_{s w}} - I P {R^{H}}_{y_{s w}}

因此,第w个联合层决策周期的备件订购数量决策流程如下.

(1) 确定维护后各设备的运行状态,确定组合维护后预计正常运行设备数量u_M_u₊.

(2) 利用式(15)和(16)确定订购数量的上下限.

(3) 令y_s_w=max{0, 1-v_w, k-u_M_u₊},利用式(22)计算IP $S_{y_{s w}}$ .

(4) 更新y_s_w=y_s_w+1,重新计算IP $S_{y_{s w}}$ .

(5) 若y_s_w>n-v_w,停止计算.

(6) 最大IP $S_{y_{s w}}$ 对应的y_s_w即为订购数量y_w.

5 机会维护与库存控制多层级决策流程

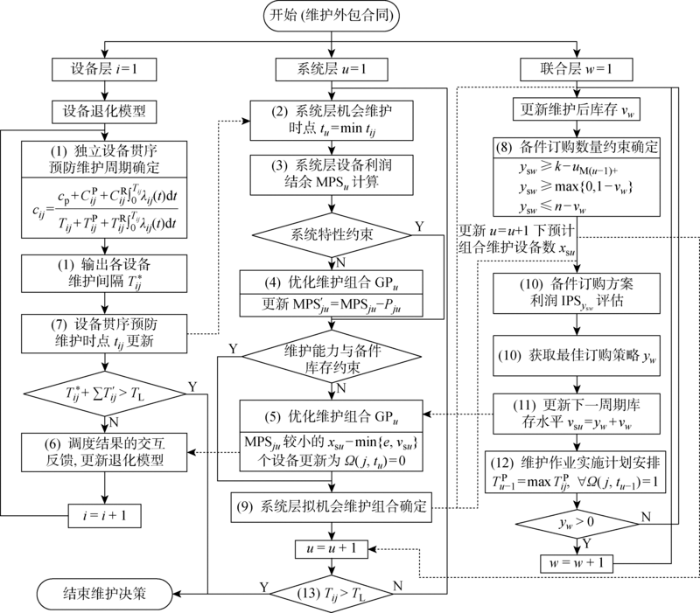
动态更新的机会维护与库存控制的多层级决策基于两者之间耦合关系:一方面,机会维护策略需要考虑当前库存水平约束,同时需要量化维护后消耗库存造成的影响;另一方面,库存控制需要考虑维护后的剩余库存水平和后续的机会维护计划.由此,多层级交互的OMICP求解框架如图2所示,图中虚线表示各层之间的信息交互.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 OMICP求解框架图

Fig.2 Framework diagram of OMICP solution

(1) 独立设备贯序预防维护周期确定.根据维护成本率c_ij实时获取各租赁设备维护周期 $T_{i j}^{*}$ .

(2) 系统层机会维护时点确定.根据各租赁设备的维护周期 $T_{i j}^{*}$ 对应获得各设备M_j的机会维护时点t_ij,从而确定最先到达维护时点的触发设备M_m以及系统层机会维护时点为

(23)

t_{u} = m i n t_{i j}, j = 1, 2, \dots, n

(3) 系统层设备利润结余计算.根据租赁设备维护利润结余计算公式计算MPS_u,将MPS_u>0的设备与触发设备M_m构成维护组合GP_u,对其赋值Ω(j, t_u)=1.

(4) 考虑系统特性的组合机会维护策略优化.考虑系统特性,定义系统失效惩罚成本P_ju,若原维护组合不满足最低运行设备要求,更新MPS'_ju=MPS_ju-P_ju.若GP_u中任一设备不满足MPS'_ju>0,则将GP_u中对应MPS'_ju值最小的设备更新为Ω(j, t_u)=0.

(5) 考虑维护能力与备件库存的组合机会维护策略优化.若不满足约束则选择MPS_ju较小的x_s_u-min{e, v_s_u}台待修设备更新为Ω(j, t_u)=0.

(6) 调度结果的交互反馈.将机会维护调度结果,即系统层实际的维护周期T'_ij反馈至设备层的维护成本率c_ij,并贯序输出设备第i+1周期最佳维护周期 $T_{(i + 1) j}^{*}$ .其中,T'_ij的计算方式为

(24)

T'_{i j} = T_{i j}^{*} - (t_{i j} - t_{u}), \forall Ω (j, t_{u}) = 1

(7) 设备贯序预防维护时点更新.赋值u=u+1,根据第u-1周期的机会维护计划更新各设备的预防维护时点为

(25)

t_{(i + 1) j} = \{\begin{array}{l} t_{i j}, & Ω (j, t_{u - 1}) = 0 \\ t_{u - 1} + max T^{P}_{i j} + T_{(i + 1) j}^{*}, & Ω (j, t_{u - 1}) = 1 \end{array}

(8) 备件订购数量约束确定.根据维护组合GP_u_-1、预计维护后库存v_w以及机会维护后设备正常运行数量u_M(_u_-1)+,确定y_s_w的上下限约束.

(9) 系统层拟机会维护组合确定.进行步骤(2)~(5)获得MPS_u与不考虑库存约束下的GP_u,确定t_u时点组合机会维护设备数x_s_u.

(10) 备件订购方案利润评估.基于备件订购数量约束计算IP $S_{y_{s w}}$ ,比较IP $S_{y_{s w}}$ 确定最佳订购方案y_w.

(11) 更新下一周期库存水平.基于最佳订购方案,更新v_s_u=y_w+v_w.

(12) 维护作业实施计划安排.将所有满足 Ω(j, t_u_-1)=1的设备进行预防维护,维护时长为维护组合GP_u_-1中维护时间最长的设备维护时长

(26)

{T^{P}}_{u - 1}

=max

{T^{P}}_{i j}

, ∀Ω(j, t _u_-1)=1

(13) 维护合同期与决策结束终止条件判断.判断维护机会时点t_u是否超出维护合同期T_L, 若超

出则结束决策;若未超出,返回步骤(2).

6 算例分析

为验证本文所提机会维护与库存控制联合优化策略,以某3-out-of-5: G发电系统为例进行分析.

6.1 算例参数设置

设备的可靠性参数和维护外包参数如表1所示,库存控制参数如表2所示,以上参数均由某发电设备生产服务厂商提供.

表1 各台设备的可靠性与维护外包参数

Tab.1 Maintenance and outsourcing parameters of each machine

j	β_j	η_j	ε_j	${T^{P}}_{i j}$ /h	${T^{R}}_{i j}$ /h	${C^{P}}_{i j}$ /美元	${C^{R}}_{i j}$ /美元	${V^{S}}_{j}$ /美元	${V^{E}}_{j}$ /美元	δ_j	${C^{D}}_{i j}$ /美元	c_d/美元
1	3.1	7 000	1.035	20	66	6 500	18 000	700 000	630 000	0.11	2 400	3 000
2	2.8	6 800	1.042	25	74	7 000	20 000	760 000	660 000	0.15	2 800	3 000
3	3.1	7 200	1.054	20	58	6 400	18 800	700 000	650 000	0.12	2 200	3 000
4	2.9	7 500	1.041	18	68	6 000	16 800	730 000	650 000	0.16	2 800	3 000
5	2.8	6 600	1.036	15	55	6 800	22 900	750 000	670 000	0.12	2 500	3 000

新窗口打开| 下载CSV

表2 库存控制参数

Tab.2 Parameters of inventory control

c_p/美元	K_p/美元	K_pem/美元	c_h/美元	L/h
5 000	4 000	7 000	5	96

新窗口打开| 下载CSV

6.2 算例结果分析与对比

为评估OMICP效果,综合考量维护与库存相关成本之和作为维护外包服务的总成本.设定维护相关成本包含人员派遣固定成本C_D、纠正性维护成本C_R、预防维护成本C_P和系统失效惩罚C_B;库存相关成本包含订购固定成本C_F、备件购买成本C_U、库存持有成本C_H和紧急订购额外成本C_E 即无备件可用时可能造成的系统失效成本以及紧急订购相比普通订购增加的订购固定成本.随机选取OMICP第8个系统层维护周期的维护决策作为展示,如表3所示.M₂在第8周期有最小预防维护时点 13 662 h,因此M₂为触发设备,则系统层面的机会维护时点t₈=13 662 h.对其余非修设备计算维护利润结余MPS_j₈,由于MPS₁₈=3 724.15 美元和MPS₃₈=3 056.07 美元为正值,得到Ω(j, t₈)=1 (j=1, 2, 3),Ω(j, t₈)=0 (j=4, 5).

表3 第8个系统层维护周期机会维护决策结果

Tab.3 Opportunistic maintenance decision of 8th system-layer cycle

j	t_ij/h	t₈/h	$T_{i j}^{*}$ /h	T'_ij/h	MPA_j₈/美元	MPR_j₈/美元	MPS_j₈/美元	Ω(j, t₈)
1	14 051	13 662	4 675	4 286	5 923.41	1 168.55	3 724.15	1
2	13 662	13 662	4 471	4 471	—	—	—	1
3	13 860	13 662	4 669	4 471	3 610.42	554.35	3 056.07	1
4	17 429	13 662	4 997	1 230	6 488.41	35 697.68	-29 209.28	0
5	16 304	13 662	3 872	1 230	6 945.97	26 402.82	-19 456.84	0

新窗口打开| 下载CSV

由于维护能力e=3台,库存水平v_s8=4件,满足当前维护计划.但是目前的维护计划不符合电力系统最低发电能力要求,将造成系统失效惩罚.因此需要根据系统特性优化GP₈,如表4所示.由于MPS'₁₈与MPS'₃₈为负,选择两者中数值较小的一台设备取消预防维护,因此最终第8个系统层维护周期的机会维护组合为设备M₂与M₁.

表4 第8维护周期的优化后机会维护决策结果

Tab.4 Optimized maintenance decision of 8th system-layer cycle

j	Ω(j, t₈)	P_j₈/美元	MPS'_j₈/美元	Ω(j, t₈)'	$T_{8}^{P}$ /h
1	1	60 000.00	-56 275.85	1	25
2	1	—	—	1	25
3	1	60 000.00	-56 943.93	0	25
4	0	—	—	0	25
5	0	—	—	0	25

新窗口打开| 下载CSV

维护后进入联合层的第4周期,更新库存水平v₄=2 件,同时进行备件订购决策.确定备件订购上下限分别为3和0件,计算不同订购方案y_s4下订购利润如表5所示.比较利润结余IP $S_{y_{s 4}}$ ,最大的IP $S_{y_{s 4}}$ 对应 y_s4即为订购数量,因此y₄=0.

表5 第4个联合层周期的库存控制计划

Tab.5 Inventory control decision for 4th joint-layer cycle

y_s4/件	IP $R_{y_{s 4}}^{F}$ /美元	IP $R_{y_{s 4}}^{H}$ /美元	IP $S_{y_{s 4}}$ /美元
0	0	0	0
1	4 000	510	-4 510
2	4 000	1 020	-5 020
3	4 000	1 530	-5 530

新窗口打开| 下载CSV

每个系统维护周期的利润结余和维护组合如表6所示.其中,“PM”为OMICP的触发设备,“1”表示机会维护设备.

表6 整个维护周期内的机会维护与库存控制计划输出

Tab.6 Opportunistic maintenance and inventory control decision of all cycles

u	t_u/h	v_s_u/件	Ω(j,t_u)					y_w/件
u	t_u/h	v_s_u/件	j=1	j=2	j=3	j=4	j=5	y_w/件
1	4 230	2	0	0	0	1	PM	4
2	4 604	4	0	PM	1	0	0	0
3	4 779	2	PM	0	0	0	0	6
4	8 425	4	0	0	0	1	PM	0
5	9 166	2	0	PM	1	0	0	0
6	9 356	2	PM	0	0	0	0	6
7	12 414	6	0	0	0	1	PM	0
8	13 662	4	1	PM	0	0	0	0
9	13 860	2	0	0	PM	0	0	0
10	16 304	1	0	0	0	0	PM	1
11	17 429	1	0	0	0	PM	0	3
12	18 093	3	0	PM	1	0	0	0
13	18 310	1	PM	0	0	0	0	1
14	20 143	1	0	0	0	0	PM	1
15	22 375	1	0	0	0	PM	0	6
16	22 460	6	0	PM	0	0	0	0
17	22 632	4	1	0	PM	0	0	—

新窗口打开| 下载CSV

为了验证OMICP的联合优化效果,将其与单独采用维护优化策略(OM)或单独采用库存优化策略(IC)对比,并且与已有针对k-out-of-n:G系统维护与文献[15-16]的库存联合优化(Joint Opt)方法进行对比.在订购策略方面,采用常用的(S, s)订购策略,即当库存水平小于s时决策订购,订购量为S与当前库存水平的差值.在维护策略方面,分别选用独立按期预防维护策略(IPM)与定期维护策略(SMP),IPM根据各台租赁设备的预防维护周期独立进行维护,不考虑设备间的结构和经济依赖性.SMP则是基于优化所得的固定周期定期对租赁设备进行维护.策略成本对比结果如表7所示.

表7 不同策略下的维护外包服务总成本对比

Tab.7 Comparison of total cost of different policies

成本/美元	SMP+(S, s) S=3 s=2	OM		IC		Joint Opt		OMICP
成本/美元	SMP+(S, s) S=3 s=2	OM+(S,s) S=2 s=1	OM+(S,s) S=3 s=2	IPM+IC	SMP+IC	2014 RESS 文献[16]	2021 EJOR 文献[15]	OMICP
C_D	80 365	56 920	51 420	79 130	73 430	78 555	79 421	56 480
C_P	163 500	176 700	172 780	159 540	130 800	163 500	163 500	172 780
C_R	128 865	116 220	90 340	132 740	176 050	116 315	123 591	85 780
C_B	63 000	15 000	12 000	5 400	147 000	35 400	37 350	12 000
C_F	100 000	62 400	60 000	38 400	20 400	96 000	10 280	38 400
C_U	166 500	171 000	169 000	170 000	151 500	149 350	157 800	156 000
C_H	157 501	170 932	236 470	214 069	86 292	80 500	149 125	132 673
C_E	21 000	42 000	22 400	17 500	24 500	41 090	6 860	23 800
维护相关成本	355 365	364 840	326 540	376 810	527 280	393 770	403 862	327 040
库存相关成本	445 001	446 332	487 870	439 969	282 692	366 940	324 065	350 873
总成本	880 731	811 172	814 410	816 779	809 972	760 710	727 927	677 913

新窗口打开| 下载CSV

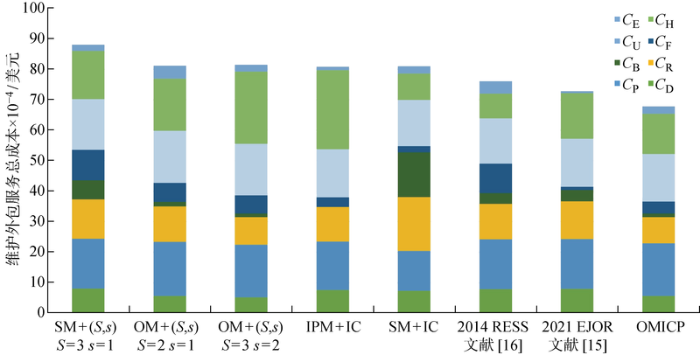
OMICP在维护合同期内产生的总租赁成本为 677 913 美元,相比于SMP与(S, s)订购策略组合成本降低达到23.03%,相比于单独采用某一优化策略的成本降低达到15%~17%,相比于已有联合优化文献[15-16]策略的成本降低分别达到10.9%与6.8%,验证了OMICP在维护外包总成本优化方面的优势.如图3所示,从具体成本类别可知,本文所提出的机会维护策略在降低C_D、C_R与C_B方面有显著的成本优势,实现更有效的预防维护;提出的库存控制策略在降低C_F和C_E方面有显著的优势,可以在较少的订购次数即较低的订购固定成本情况下实现较低的紧急订购成本.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 不同策略下的维护外包服务总成本对比图

Fig.3 Comparison of total cost of maintenance outsourcing services of different policies

另一方面,算例结果也直观展示了维护与库存之间的影响关系,同时证明了本文所提OMICP对其耦合关系的考虑实现了维护与库存两者的联合优化.库存检查频率依赖于预防维护时点,因此库存相关成本的优化效果取决于预防维护策略的优劣:在IPM+IC组合策略中, IPM造成频繁库存检查与订购决策,使得库存相关成本的优化效果有限,而OMICP中机会维护策略的优势使得库存策略发挥显著效果;另一方面,预防维护策略效果也取决于库存控制策略的优劣,不同库存控制策略下维护相关成本差异显著,过低的库存水平使得机会维护的需求无法被满足,造成维护周期内更多的纠正性维护成本,而在OMICP下,得益于库存控制策略的优势实现了合理库存水平下较低的维护相关成本,动态机会维护策略的优势得到充分发挥.

此外,OMICP所得库存相关成本相比文献[16]方法优化所得有小部分下降,而虽然相比文献[15]方法优化所得库存相关成本有部分上升,但是OMICP更好地保障了维护行为开展,得以显著降低维护相关总成本,尤其所提策略对于降低C_R和C_B有明显优势.证明了本文通过考虑动态可变维护周期与订购策略,相比已有文献中优化固定检查间隔以及优化库存平均水平数等静态优化方式有一定的优势.

6.3 模型敏感性分析

对策略的关键参数进行敏感性分析,并与其他方法进行对比.所考虑的参数分为两种:与维护活动相关的参数和库存控制活动相关的参数,分别为停机惩罚成本c_d与订购固定成本K_p.

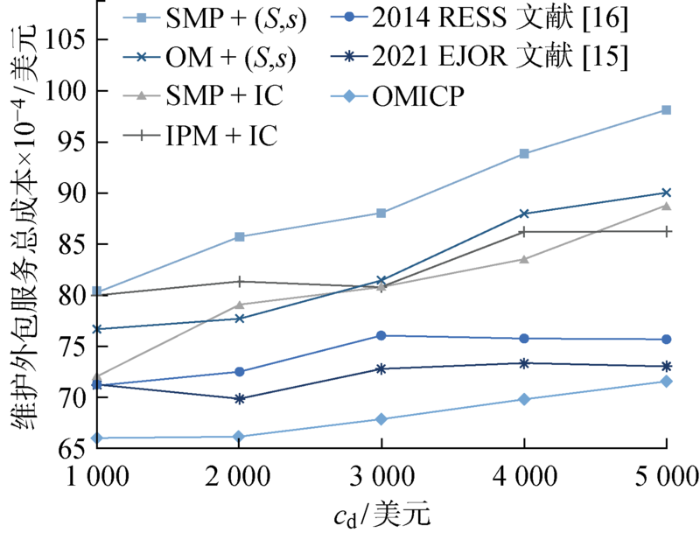
为研究c_d对维护外包服务总成本的影响,选取c_d=1 000~5 000 美元,增量为 1 000 美元,其余参数不变,所得数值结果展示于图4.显然,对于所有方法c_d的增加会导致总成本的增加.值得注意的是,OMICP相比其他算法在不同的c_d下依然有明显成本优势,并且相比于非联合优化策略,对c_d的变化更不敏感,证明了OMICP对维护外包总成本的鲁棒性.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同策略下c_d对总成本的影响

Fig.4 Impact of c_d on total cost of different policies

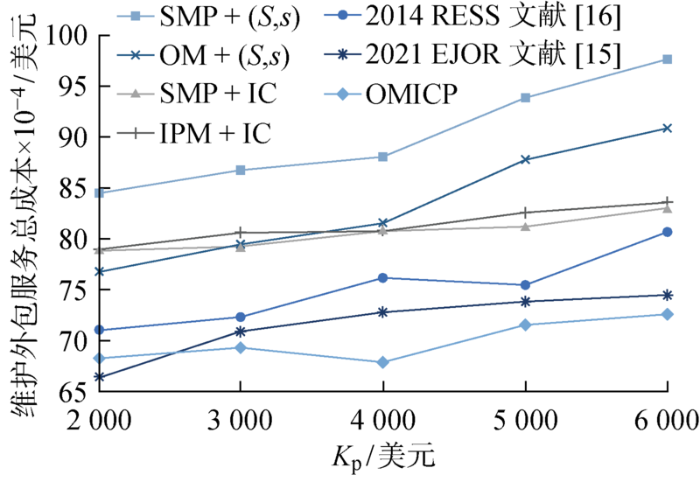
另外,针对K_p对总成本的影响,选取K_p=2 000~6 000 美元,增量为 1 000 美元,所得数值结果展示于图5.同样,本文所提策略在不同K_p下均有较好表现,并且可以发现IPM+IC、SMP+IC以及本文所提OMICP,相比传统(S, s)订购策略与文献[15]和[16] 所提策略而言对K_p的敏感度较低.而文献[15]在K_p较小情况下有更好的表现,但在K_p增大后成本迅速增长,表明其在动态调整订购频率方面有一定缺陷.综上,可以证明本文所提策略相比其他策略对库存相关成本与总成本具有更好的鲁棒性.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同策略下K_p对总成本的影响

Fig.5 Impact of K_p on total cost of different policies

7 结语

本文基于维护外包背景下服务方对于k-out-of-n:G系统的维护需求,考虑系统冗余设备干涉的建模难点,进一步纳入维护过程中备件有限的实际生产情形,针对复杂系统维护与库存控制的耦合关系,提出一种机会维护与库存控制多层级优化策略,实现维护外包服务成本降低.在进行机会维护决策时,以设备贯序预防维护时点为机会维护契机,通过考虑库存水平、冗余设备、维护能力因素优化更新设备MPS生成的机会维护组合;在进行库存控制决策时,将组合维护计划、设备健康状况与当前备件库存情况纳入决策考量,通过最大化IPS生成最佳订购方案.通过策略对比,证明了OMICP对成本优化的有效性与对复杂决策的可行性,并通过模型敏感性分析验证模型具有较好的鲁棒性.所提出的策略具有动态优化的特性,更符合实际工业场景的应用条件,未来将根据不同维护服务方的实际需求对模型参数进行动态采集和提取,进一步应用于更为复杂的电力系统、通信系统等冗余系统的智能运维决策.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

JACKSON

, PASCUAL

Joint pricing and maintenance strategies in availability-based product-service systems under different overhaul conditions

[J]. Reliability Engineering & System Safety, 2021, 216: 107817.