海洋电磁发射机二级母线冲击电压产生机理及抑制

doi:10.16183/j.cnki.jsjtu.2022.403

海洋电磁发射机二级母线冲击电压产生机理及抑制

陶海军^,¹^,², 杜长顺³, 张金生¹, 郑征¹^,²

1.河南理工大学电气工程与自动化学院,河南焦作 454003

2.河南省煤矿装备智能检测与控制重点实验室,河南焦作 454003

3.河南许继电力电子有限公司,河南许昌 461000

Generating Mechanism and Suppression of Impulse Voltage on Secondary Bus of Marine Electromagnetic Transmitter

TAO Haijun^,¹^,², DU Changshun³, ZHANG Jinsheng¹, ZHENG Zheng¹^,²

1. School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454003, Henan, China

2. Henan Key Laboratory of Intelligent Detection and Control of Coal Mine Equipment, Henan Polytechnic University, Jiaozuo 454003, Henan, China

3. Henan Xuji Power Electronics Co., Ltd., Xuchang 461000, Henan, China

责任编辑: 王一凡

收稿日期: 2022-10-14 修回日期: 2022-12-21 接受日期: 2023-02-21

基金资助:

国家重大科研装备研制项目(ZDYZ2012)
河南省科技攻关项目(222102220014)
河南省高校基本科研业务费专项资金(NSFRF210409)

Received: 2022-10-14 Revised: 2022-12-21 Accepted: 2023-02-21

作者简介 About authors

陶海军(1980-),副教授,从事大功率开关电源及其控制的研究;E-mail:taohj99@hpu.edu.cn.

摘要

电磁探测法是海洋油气资源勘探的主要方法,而海洋电磁发射机是海洋电磁探测系统的关键设备.目前海洋电磁发射机水下拖体长时间工作时,会出现开关器件损坏现象.首先分析了采用单向可控源电路的发射桥换流过程,发现发射偶极寄生电感回馈能量使二级母线产生冲击电压,增大了开关管的电压应力.然后分析了双向可控源电路的工作模式,提出一种双变量解耦控制策略,在变压器前后两级建立的模型基础上,将原来的耦合非线性系统全局线性化为两个单输入单输出系统,以此获得滑模控制器的函数关系.仿真与实验结果表明,所设计的可控源电路可以明显减小母线电容的冲击电压和开关管的电压应力,提高系统的动态性能和效率.

关键词： 电磁发射机; 双向可控源电路; 冲击电压; 解耦控制

Abstract

Electromagnetic detection is the main method of marine oil and gas resources exploration, and marine electromagnetic transmitter is the key equipment of marine electromagnetic detection system. At present, when the underwater towed body of the marine electromagnetic transmitter operates for a long time, the switch devices will be damaged. First, the commutation process of the transmitting bridge with unidirectional controlled-source circuit is analyzed. It is found that the feedback energy of the transmitting dipole parasitic inductor makes the secondary bus generate impulse voltage, which increases the voltage stress of the switch devices. Then, the operating mode of bidirectional controllable source circuit is analyzed, and a dual variable decoupling control strategy is proposed. Based on the model established at the front and back of the transformer, the original coupling nonlinear system is globally linearized into two single input single output systems, so as to obtain the functional relationship of the sliding mode controller. The simulation and experimental results show that the designed controllable source circuit can significantly reduce the impulse voltage of bus capacitor and the voltage stress of switch device, and improve the dynamic performance and efficiency of the system.

Keywords： electromagnetic transmitter; bidirectional controlled-source circuit; impulse voltage; decoupling control

PDF (10479KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

陶海军, 杜长顺, 张金生, 郑征. 海洋电磁发射机二级母线冲击电压产生机理及抑制[J]. 上海交通大学学报, 2023, 57(12): 1597-1608 doi:10.16183/j.cnki.jsjtu.2022.403

TAO Haijun, DU Changshun, ZHANG Jinsheng, ZHENG Zheng. Generating Mechanism and Suppression of Impulse Voltage on Secondary Bus of Marine Electromagnetic Transmitter[J]. Journal of Shanghai Jiaotong University, 2023, 57(12): 1597-1608 doi:10.16183/j.cnki.jsjtu.2022.403

地球物理地质勘探方法中,海洋电磁勘探法以各类气液资源、岩矿石的极化率和导电性等性质的差异作为基本依据,并观测其电磁场来实现对目标体的有效探测^[1].如油气结构特征是具有较高的电阻率,周围充满盐水的海底底层则具有很好的导电性^[2].在20世纪时,石油和天然气行业每年使用钻井等传统方法花费数亿美元来寻找海上碳氢化合物,如今,电磁探测系统被视为研究海上地质的标准工具包的一部分^[3].目前国内的海洋电磁发射机对 1 000 m 以内的油气资源有较好的勘探效果,但面向深部资源,电磁发射机的功率、频率及方法技术精度探测等方面仍存在诸多要解决的技术难题^[4].

海洋可控源电磁发射机是海洋电磁探测系统的核心设备^[5-6].然而,目前我国大型海域地球物理勘探装备几乎全部依赖于进口^[7],严重影响了我国深部资源电磁探测新技术的发展进程,因此拥有我国自主知识产权的海底地球物理探测设备并掌握其核心技术至关重要.德国Metronix公司的TXM-22发射机采用不控整流技术,输出功率大.通过调节发电机的励磁电流来完成对输出电压的调节,发电机的制造较为复杂,体积与质量较大.美国Zonge公司研制的GGT-30发射机采用相控整流技术来设计可控源电路^[8],通过控制触发角来控制输出电压的大小,当触发角较大时,会导致功率因数较低.此外,加拿大Phoenix公司利用脉冲宽度调制(Pulse Width Modulation,PWM)变换设计了TXU-30发射机^[9].

对于陆地电磁发射机,文献[10]中介绍了电磁发射机偶极电感对发射电流的边沿陡度的影响,文献[11]中提出采用吸收电路,减小关断时间,但未提及偶极电感储能对母线电压的影响.当海洋电磁发射机拖体长时间在水下工作时,会导致开关管出现损坏,根据文献[12] 中介绍可知,发射偶极子存在500 μH的寄生电感,如果忽略这个电感的影响,当发射桥换流时,产生的感应电压会损害设备,通过电容槽吸收电感上反馈的能量,这种方法需要增加母线电容,电路体积增大,由于水下拖体体积受限,尤其对于大功率电磁发射机是不可行的.

双有源全桥(Dual-active full Bridge,DAB)DC-DC变换器结构对称, 可以实现能量双向流动,且具有较高的功率密度、电气隔离等特点,被广泛应用.其控制方式包括单移相(Single-phase-shift, SPS)控制、双重移相(Dual-phase-shift,DPS)控制、扩展移相(Extended-phase-shift,EPS)控制、三重移相(Triple-phase-shift,TPS)控制,在不同的控制方法上,基本是以电感电流应力、回流功率、软开关范围为优化目标^[13⇓-15],进行控制算法的设计.DAB变换器本质上是一种多输入多输出(Multi-input Multi-output,MIMO)系统,在输出特性上内部变量相互耦合才能完整表述.近年来,基于微分几何的非线性控制方法为MIMO系统解耦提供了一种解决思路.其通过系统的电感电流与母线电压作为反馈控制量,给定值和反馈值进行比较得到误差信号,以误差和误差的积分值构建切换函数,进而设计系统的滑模控制律,获得滑模控制器的函数关系.该输出反馈滑模控制策略除了能够对电流应力与母线电压控制,还可以提高系统的抗扰能力.

相对于传统单向可控源电路采用电容槽抑制的方法,本文提出的双向可控源电路只需要把变压器副边的整流二极管换成全控型电力电子器件,开关管的数量不变,对整个电路的体积基本没有影响,然后结合变换器实现软开关的条件,设计了一种双变量解耦控制策略.通过分析、建立其数学模型,将原来的耦合非线性系统全局线性化为两个单输入单输出系统,实验结果表明,解耦控制策略实现了控制变量之间完全解耦,电感电流峰值与母线电压都得到了进一步优化,使控制系统具有了良好的鲁棒性和动态性能.

1 海洋电磁发射机拓扑结构与换流过程分析

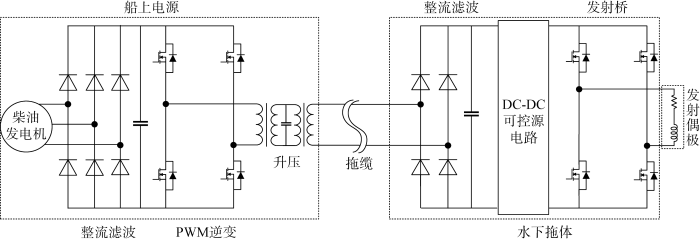
海洋电磁发射机系统主要由船上电源、拖缆、水下拖体和发射偶极4部分组成^[16],如图1所示,船上电源由柴油发电机、整流滤波电路、升压变压器、PC监控装置组成,为水下拖体提供电能.拖缆为光电复合缆,传输电能和信号.水下拖体由可控源电路、发射电路、发射偶极、传输系统的控制单元、载波通信模块组成,可控源电路负责输出可控的直流电压,经发射桥生成时域或频域经发射偶极向海底激发电磁波.目前可控源电路主要包括PWM变换和相控整流式可控源电路两种方式^[17],但这两种变换方式由于高频变压器副边采用二极管整流,发射偶极储存的能量无法回馈,导致二级母线电压产生冲击,下面通过分析发射桥换流过程来分析冲击电压产生的原因.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 海洋电磁发射机电路结构示意图

Fig.1 Schematic diagram of circuit structure of marine electromagnetic transmitter

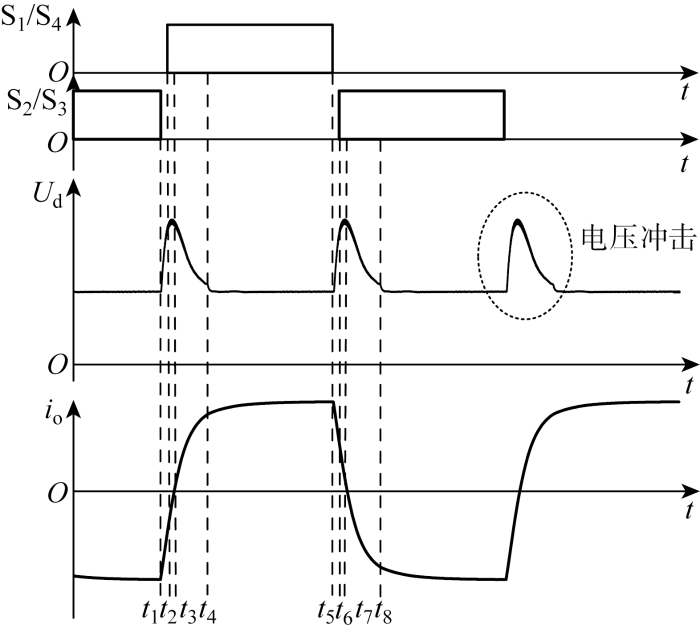
图2给出了发射桥电路的主要工作波形.图中:t为时间,为了防止上下桥臂直通,留有一定的死区时间t₁—t₂,t₃时刻电流降至0,t₄时刻系统达到稳态;U_d为发射桥母线电压; i_o为发射桥等效电流;开关管S₁/S₄和开关管S₂/S₃交替导通.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 母线电压与发射电流波形

Fig.2 Voltage of busbar and waveforms of transmit current

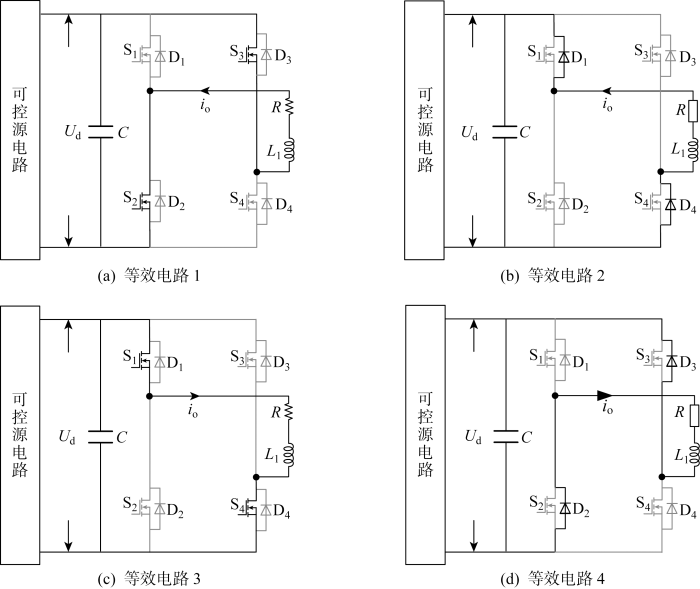
在一个开关周期内,发射桥电路有8种工作模态,不同工作模态下发射桥的等效电路如图3所示.图中:R为发射桥等效负载;L₁为负载电感;C为发射桥滤波电容;D₁~D₄分别为对应开关管的寄生二极管.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 不同工作模态下发射桥的等效电路

Fig.3 Equivalent circuits of launching bridge in different operating modes

模态1 t₁时刻之前.

开关管S₂和S₃导通,电路等效状态如图3(a)所示,负载电流i_o流通的路径是开关管S₃、R、L₁、开关管S₂、电源U_o,负载电感处于饱和状态,负载电压U_o=U_d,负载电流i_o=U_d/R.

模态2 t₁—t₂.

开关管S₂和S₃关断,由于负载电感的作用,负载电流i_o通过二极管D₁、R、L₁、二极管D₄续流,如图3(b)所示.

模态3 t₂—t₃.

二极管D₁和D₄导通,电感继续释放能量,负载电流i_o减小,到t₃时刻负载电流降为0,母线电压U_C达到峰值.死区时间应小于t₃—t₁,否则负载电流不连续.

模态4 t₃—t₄.

开关管S₁和S₄导通,负载电流i_o反向增加,如图3(c)所示.到t₄时刻负载电流达到稳态值,母线电压U_C降到稳态电压U_d.发射桥开始下半周期的工作,工作情况类似于上半周期.

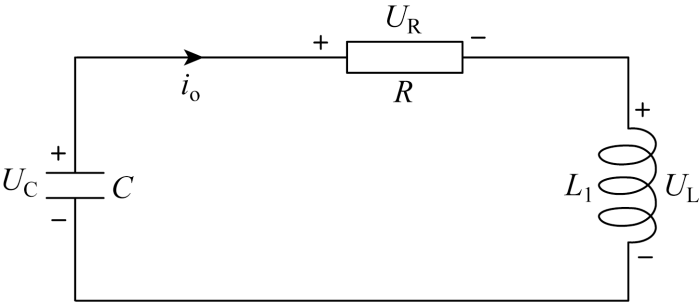
储存在电感上的能量谐振到母线电容C,忽略二极管导通的管压降,此时发射桥电路的简化电路如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 发射桥等效电路

Fig.4 Equivalent circuit of transmit bridge

根据图4参考方向,由基尔霍夫电压定律(Kirchhoff Voltage Laws,KVL),求得电路方程为

(1)U_C=U_R+U_L

式中:U_C为母线电压;U_R和U_L分别为负载R和L₁电压.

由电压电流关系可得

(2)U_L=L₁

\frac{d i_{o}}{d t}

(3)i_o=C

\frac{d u_{C}}{d t}

式中:u_C为母线电压关于t的函数.

将式(2)和(3)代入式(1)可得

(4)L₁C

\frac{d^{2} u_{C}}{d t^{2}}

+RC

\frac{d u_{C}}{d t}

-U_C=0

得出特征方程为

(5)L₁Cs²+RCs-1=0

式中:s为拉普拉斯算子.

由于(RC)²+4L₁C>0,系统工作在欠阻尼状态,母线电压U_C为

(6)U_C=

\frac{U_{o} ω_{0}}{ω}

e^-^δtsin(ωt+β)+

\frac{I_{0}}{ω C}

e^-^δtsin(ωt)

δ=

\frac{R}{2 L_{1}}

, ω²=

\frac{1}{L_{1} C}

{(\frac{R}{2 L_{1}})}^{2}

ω₀=

\sqrt{δ^{2} + ω^{2}}

, β=arctan

\frac{ω}{δ}

式中:I_o为发射桥内电流.

综上所述,发射桥换流过程中,负载电感储存的能量向母线电容回馈,由于传统可控源电路仅只能单向电能传输,导致二级母线产生冲击电压,增大了开关器件电压应力,甚至会烧毁开关管和整流二极管.电磁发射机拖体需要在水下长时间工作,故系统的可靠性对设备的稳定运行至关重要.DAB是双向DC-DC变换器的拓扑结构之一,不仅可以实现电气隔离,还具有较大的功率传输范围、较快的动态响应、宽电压输出范围^[18]等优点,故本文采用双有源变换器DAB作为海洋电磁发射机的DC-DC可控源电路.

2 双向可控源电路

2.1 双向可控源电路工作模式分析

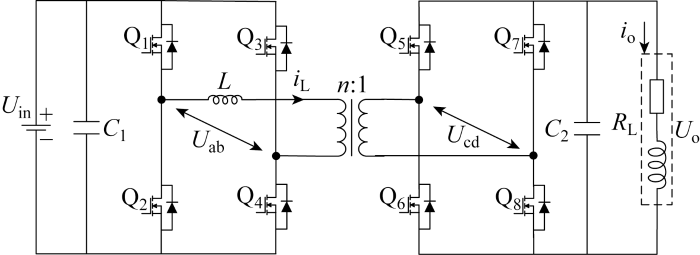
双向可控源电路拓扑如图5所示,主要由两个H桥和高频隔离变压器组成.图中:U_in为可控源电路的输入电压;C₁、C₂分别为DAB可控源的输入侧支撑电容、输出侧滤波电容;L为辅助电感;i_L为DAB可控源的电感电流;U_ab和U_cd分别为变压器两侧交流电压;R_L为等效负载;Q₁~Q₈为开关管;变压器的变比为n∶1.定义电压传输比K=U_in/nU_o,根据K的取值,DAB可控源电路可分为以下不同的工作状态:

(1) K>1,降压状态.

(2) K<1,升压状态.

(3) K=1,匹配状态.

本文主要针对K>1的情况,分析DAB的工作过程.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 双有源桥DC-DC可控源电路

Fig.5 DC-DC controlled-source circuit of dual active bridge

根据EPS控制下的移相比关系,可将DAB可控源电路划分为4种工作模式:0≤D₁≤D₂≤1,1≤D₂≤1+D₁≤2,0≤D₂≤D₁≤1,1≤1+D₁≤D₂≤2.其中:D₁为内移相比,即开关管Q₁与Q₃之间的移相比(Q₁超前Q₃);D₂为外移相比,即开关管Q₁与Q₃之间的移相比(Q₁超前Q₅).

扩展移相控制方式下的最大传输功率P_N为

(7)P_N=

\frac{n U_{a b} U_{c d}}{8 f L}

式中:f为双有源桥的开关频率.

4种模式下传输功率P的标幺值P_i(i=1, 2, 3, 4)分别为

(8)

\begin{array}{l} P_{1} = P / P_{N} = 2 (- D_{1}^{2} + 2 D_{1} D_{2} - D_{1} - \\ 2 D_{2}^{2} + 2 D_{2}) \\ P_{2} = 2 (- 2 D_{2} + 2 - D_{1}^{2} + 2 D_{1} D_{2} - D_{1}) \\ P_{3} = 2 (2 D_{2} + D_{1}^{2} - 2 D_{1} D_{2} - D_{1}) \\ P_{4} = 2 (D_{1}^{2} - 2 D_{1} D_{2} + 3 D_{1} + 2 D_{2}^{2} - 6 D_{2} + 4) \end{array}\}

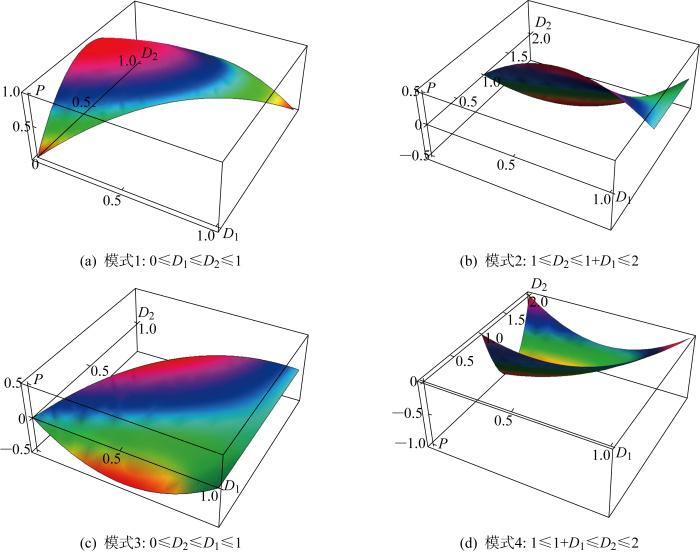
根据式(8)可得传输功率与移相角的关系曲线,如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 DAB输出功率和移相角的关系曲线

Fig.6 DAB output power versus phase shift angle

4种工作模式的传输功率标幺值的上下限如表1所示.第1种模式传输功率范围为[0,1],第2与第3种模式传输功率范围为[-0.5, 0.5],第4种模式传输功率范围为[-1, 0].

表1 不同工作模式的功率区间

Tab.1 Power range in different operating modes

工作模式	功率下限	功率上限
模式1	0	1
模式2	-0.5	0.5
模式3	-0.5	0.5
模式4	-1	0

新窗口打开| 下载CSV

2.2 双向可控源电路软开关的实现

海洋电磁发射机水下拖体内部空间相对狭小,且对外封闭,散热困难,提高功率密度极其重要.通过零电压开通(Zero Voltage Switch,ZVS)技术可以极大降低开关管的开关损耗,提升系统效率.由于电感电流的波形是半周期对称的,即i_L(t₀)=-i_L(t₀+T_s/2),T_s为一个开关周期,再结合同一个桥臂的两个开关管有一个实现ZVS,另一个必实现ZVS.所以,所有开关管ZVS的条件如表2所示.

表2 不同工作模式下开关管ZVS条件

Tab.2 Conditions of ZVS in different operating modes

工作模式	开关管	约束条件	开关管	约束条件
模式1	Q₁、Q₂ Q₃、Q₄	i_L(t₀)≤0 i_L(t₄)≥0	Q₅、Q₈ Q₆、Q₇	i_L(t₂)≥0 i_L(t₅)≤0
模式2	Q₁、Q₂ Q₃、Q₄	i_L(t₀)≤0 i_L(t₅)≥0	Q₅、Q₈ Q₆、Q₇	i_L(t₄)≥0 i_L(t₆)≤0
模式3	Q₁、Q₂ Q₃、Q₄	i_L(t₀)≤0 i_L(t₅)≥0	Q₅、Q₈ Q₆、Q₇	i_L(t₁)≥0 i_L(t₄)≤0
模式4	Q₁、Q₂ Q₃、Q₄	i_L(t₀)≤0 i_L(t₄)≥0	Q₅、Q₈ Q₆、Q₇	i_L(t₅)≥0 i_L(t₂)≤0

新窗口打开| 下载CSV

3 双向可控源电路的状态反馈线性化

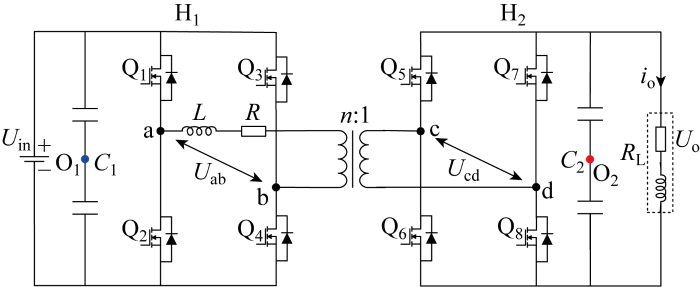
为了使控制系统更加准确,考虑高频变压器的阻抗建立双向可控源电路数学模型,重新绘制出双向可控源电路如图7所示,原边H₁电容和副边H₂电容中点用O₁和O₂表示.其等效电路如图8所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 双向可控源电路

Fig.7 Bidirectional controlled-source circuit

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 EPS控制下双向可控源等效电路

Fig.8 Equivalent circuit of bidirectional controlled-source under EPS control

3.1 双向可控源电路的数学模型

令可控源电路原边全桥H₁与副边全桥H₂两侧的直流并联电容中点O_i(i=1, 2)为直流电压零点(见图7),即

(9)

\begin{array}{l} V_{a O_{1}} (t) = \{\begin{array}{l} \frac{U_{i n}}{2}, & t \in [0, T_{h s}] \\ - \frac{U_{i n}}{2}, & t \in (T_{h s}, T_{s}] \end{array} \\ V_{b O_{1}} (t) = \\ \{\begin{array}{l} \frac{U_{i n}}{2}, & t \in [D_{1} T_{h s}, D_{1} T_{h s} + T_{h s}] \\ - \frac{U_{i n}}{2}, & t \in (D_{1} T_{h s} + T_{h s}, T_{s}] \end{array} \\ V_{c O_{2}} (t) = \\ \{\begin{array}{l} \frac{U_{o}}{2}, & t \in [D_{2} T_{h s}, D_{2} T_{h s} + T_{h s}] \\ - \frac{U_{o}}{2}, & t \in (D_{2} T_{h s} + T_{h s}, T_{s}] \end{array} \\ V_{d O_{2}} (t) = \\ \{\begin{array}{l} \frac{U_{o}}{2}, & t \in [D_{2} T_{h s}, D_{2} T_{h s} + T_{h s}] \\ - \frac{U_{o}}{2}, & t \in (D_{2} T_{h s} + T_{h s}, T_{s}] \end{array} \end{array}\}

式中:T_hs为半个开关周期;U_o为双向可控源电路的输出电压; $V_{a O_{1}}$ 、 $V_{b O_{1}}$ 、 $V_{c O_{2}}$ 和 $V_{d O_{2}}$ 分别为全桥a、b、c和d点到直流并联电电容中点O₁和O₂电压.

将式(9)中占空比为50%的交流方波电压信号展开为有限和的形式为

(10)

\begin{array}{l} U_{a O_{1}} (t) = U_{i n} \overset{+ \infty}{\sum_{k = 1, 3, 5, \dots}} \frac{2 s i n (k ω t)}{k π} \\ U_{b O_{1}} (t) = U_{i n} \overset{+ \infty}{\sum_{k = 1, 3, 5, \dots}} \frac{2 s i n (k ω t - α_{1} - π)}{k π} \\ U_{c O_{2}} (t) = U_{o} \overset{+ \infty}{\sum_{k = 1, 3, 5, \dots}} \frac{2 s i n (k ω t - α_{2})}{k π} \\ U_{d O_{2}} (t) = U_{o} \overset{+ \infty}{\sum_{k = 1, 3, 5, \dots}} \frac{2 s i n (k ω t - α_{2} - π)}{k π} \end{array}\}

式中:ω=2πf;α₁=kD₁π/2;α₂=kD₂π/2.

从图9中可得高频变压器原副边两侧交流电压为

(11)

\begin{array}{l} U_{a b} (t) = \\ U_{i n} \overset{+ \infty}{\sum_{k = 1, 3, 5, \dots}} \frac{2 [s i n (k ω t) + s i n (k ω t - α_{1})]}{k π} = \\ U_{o} S_{1} (t) \\ U_{c d} (t) = \\ U_{o} \overset{+ \infty}{\sum_{k = 1, 3, 5, \dots}} \frac{4 s i n (k ω t - α_{2})}{k π} = U_{o} S_{2} (t) \end{array}\}

式中:S₁(t)、S₂(t)为开关函数.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同控制方式下的母线冲击电压波形

Fig.9 Waveforms of bus impulse voltage in different control modes

基于KVL列写双向可控源电路的原副边电压,可得出图8中等效电路的动态方程为

(12)

\frac{d i_{L} (t)}{d t}

\frac{R}{L}

i_L(t)+

\frac{1}{L}

U_inS₁(t)-

\frac{1}{L}

nU_oS₂(t)

根据输出电容列写基尔霍夫电流定律(Kirchhoff Current Law,KCL):

(13)

\frac{d u_{o}}{d t}

\frac{1}{R_{L} C_{2}}

U_o+

\frac{1}{C_{2}}

ni_L(t)S₂(t)

式中:u_o为U_o关于t的函数.

根据式(12)与(13)得到一对离散的非线性动态系统.引入开关函数,对式(12)和(13)重写,可得其数学模型为

(14)

\begin{array}{l} \frac{d i_{L} (t)}{d t} = - \frac{R}{L} i_{L} (t) + \frac{1}{L} U_{i n} S_{1} (t) - \\ \frac{1}{L} n U_{o} S_{2} (t) \\ \frac{d u_{o}}{d t} = - \frac{1}{R_{L} C_{2}} U_{o} + \frac{1}{C_{2}} n i_{L} (t) S_{2} (t) \end{array}\}

3.2 精确反馈线性化模型

式(14)是基于大信号建立的数学模型,且未忽略系统任何高次项.同时也表明,该变换器是一个2输入2输出的非线性控制系统.选取状态变量为x,控制输入变量为u,输出变量为y.各变量具体含义为

x=[x₁x₂]^T=[i_L(t) U_o(t)]^T

u=[u₁u₂]^T=[S₁(t) S₂(t)]^T

y=[y₁y₂]^T=[h₁(x) h₂(x)]^T=

[x₁-x₂-]^T

其中: $i_{L}^{r e f}$ 为变压器原边的电感电流参考值; $U_{o}^{r e f}$ 为输出电压参考值.

可以看出,系统维数为2,式(14)对应的仿射非线性2输入2输出系统模型为

(15)

\begin{array}{l} \overset{\cdot}{x} = f (x) + g_{1} (x) u_{1} + g_{2} (x) u_{2} \\ y = h (x) \end{array}\}

f(x)=

[\begin{array}{l} - \frac{R}{L} x_{1} \\ - \frac{1}{R_{L} C_{2}} x_{2} \end{array}]

, g₁(x)=

[\begin{array}{l} \frac{1}{L} U_{1} (t) \\ 0 \end{array}]

g₂(x)=

[\begin{array}{l} - \frac{1}{L} n x_{2} \\ \frac{1}{C_{2}} n x_{1} \end{array}]

由以上数学模型可知,系统的输出控制变量y对状态量x是非线性的,但对控制量u是线性可达的.因此,可将系统模型整理为一个标准2输入、2输出的状态仿射非线性模型.

系统可满足精确反馈线性化的充要条件是:在x(0)=x₀的邻域内,总关系度r与系统状态变量的维数n_o相等,其中x₀为系统的初始状态.

若系统在x₀的邻域内,对于k<r_i-1有李导数L_g_j $L_{f}^{k_{i}}$ h_i(x)=0 (i=1, 2, …, m;j=1, 2, …, m),构建m阶B(x)矩阵

(16)B(x)=

[\begin{array}{l} L_{g_{1}} L_{f}^{r_{1} - 1} h_{1} (x) & \dots & L_{g_{m}} L_{f}^{r_{1} - 1} h_{1} (x) \\ L_{g_{1}} L_{f}^{r_{2} - 1} h_{2} (x) & \dots & L_{g_{m}} L_{f}^{r_{2} - 1} h_{2} (x) \\ ︙ & ⋱ & ︙ \\ L_{g_{1}} L_{f}^{r_{m} - 1} h_{m} (x) & \dots & L_{g_{m}} L_{f}^{r_{m} - 1} h_{m} (x) \end{array}]

是非奇异的,则r={r₁, r₂, …, r_m}为系统的关系度集合,且其中每个子关系度r_i与输出y_i(t)=h_i(x)是对应的.

根据李导数的定义:

L_{g_{1}} L_{f}^{0}

h₁(x)=[1 0]

[\begin{array}{l} \frac{U_{i n} (t)}{L} \\ 0 \end{array}]

\frac{U_{i n} (t)}{L}

L_{g_{2}} L_{f}^{0}

h₁(x)=[1 0]

[\begin{array}{l} - \frac{n x_{2}}{L} \\ \frac{n x_{1}}{C_{2}} \end{array}]

\frac{n x_{2}}{L}

L_{g_{1}} L_{f}^{0}

h₂(x)=[0 1]

[\begin{array}{l} \frac{U_{i n} (t)}{L} \\ 0 \end{array}]

L_{g_{2}} L_{f}^{0}

h₂(x)=[0 1]

[\begin{array}{l} - \frac{n x_{2}}{L} \\ \frac{n x_{1}}{C_{2}} \end{array}]

\frac{n x_{1}}{C_{2}}

则:

(17)B(x)=

[\begin{array}{l} L_{g_{1}} L_{f}^{0} h_{1} (x) & L_{g_{2}} L_{f}^{0} h_{1} (x) \\ L_{g_{1}} L_{f}^{0} h_{2} (x) & L_{g_{2}} L_{f}^{0} h_{2} (x) \end{array}]

[\begin{array}{l} \frac{U_{i n} (t)}{L} & - \frac{n x_{2}}{L} \\ 0 & - \frac{n x_{1}}{C_{2}} \end{array}]

由式(17)可知,系统各子关系度r₁=r₂=1,总关系度r=2,与系统状态变量的维数n_o相等.因此,在x₀的邻域内,存在合适的坐标变换与状态反馈可实现系统的精确反馈线性化.

3.3 非线性系统的线性化

由上述分析可知,系统可化为Brunovsky标准型线性系统.选取以下形式进行坐标变换.

(18)

\begin{array}{l} z_{1} = h_{1} (x) \\ z_{2} = h_{2} (x) \end{array}\}

由式(15)可知:

(19)

\overset{\cdot}{z}

=a(x)+B(x)u

a(x)=

\frac{\partial h (x)}{\partial x}

f(x)=

[\begin{array}{l} - \frac{R}{L} x_{1} \\ - \frac{1}{R_{L} C_{2}} x_{2} \end{array}]

引入新的控制变量v=[v₁v₂],令z与v满足线性关系,即 $\overset{\cdot}{z}$ =v.因此:

u=B^-1(x)[v-a(x)]=

[\begin{array}{l} \frac{v_{1} L}{U_{i n} (t)} + \frac{R x_{1}}{U_{i n} U_{i n} (t)} + \frac{C_{2} v_{2}}{U_{i n} (t)} + \frac{x_{2}}{R_{L} U_{i n} (t)} \\ \frac{C_{2} v_{2}}{n x_{2}} + \frac{1}{n R_{L}} \end{array}]

3.4 滑模控制器的设计

由于实际工况下存在较多不确定的因素,所以系统模型难免存在一定偏差.为提升系统稳定性与响应速度,降低建模时带来的不利影响,选择积分滑模控制器对系统进行控制.

选择滑模面:

(20)S=

[\begin{array}{l} s_{1} \\ s_{2} \end{array}]

[\begin{array}{l} k_{11} e_{1} + k_{12} \int e_{1} \\ k_{21} e_{2} + k_{22} \int e_{2} \end{array}]

e₁=

i_{L}^{r e f}

-i_L, e₂=

U_{o}^{r e f}

-U_o

式中:k_ij(i=1, 2;j=1, 2)为积分滑模面系数.

(21)

{\overset{\cdot}{s}}_{i}

=-ξsgn(s_i)-βs_i

式中:β为指数趋近项系数;ξ为滑模增益;sgn(s_i)为符号函数,

(22)sgn(s_i)=

\{\begin{array}{l} 1, & s_{i} > 0 \\ 0, & s_{i} = 0 \\ - 1, & s_{i} < 0 \end{array}

在本文研究中,将sgn函数替换为双曲正切(tanh)函数,以获得无抖振的平滑控制信号,如下所示:

(23)

{\overset{\cdot}{s}}_{1}

=k₁₁

{\overset{\cdot}{e}}_{1}

+k₁₂e₁=-ξtanh s₁-βs₁

所以v₁= $\frac{1}{k_{11}}$ (k₁₂e₁+ξtanh s₁+βs₁), 同理可得v₂= $\frac{1}{k_{21}}$ (k₂₂e₂+ξtanh s₂+βs₂).

综上可得,系统精确反馈线性化后的多环积分滑模控制率为

(24)

\begin{array}{l} u_{1} = \frac{L}{U_{i n} (t)} \frac{1}{k_{11}} (k_{12} e_{1} + ξ t a n h s_{1} + β s_{1}) + \\ \frac{R x_{1}}{U_{i n} (t)} + \frac{C_{2}}{U_{i n} (t)} \frac{1}{k_{21}} \times \\ (k_{22} e_{2} + ξ t a n h s_{2} + β s_{2}) + \frac{x_{2}}{R_{L} U_{i n} (t)} \\ u_{2} = \frac{C_{2}}{n x_{2}} \frac{1}{k_{21}} (k_{22} e_{2} + ξ t a n h s_{2} + β s_{2}) + \frac{1}{n R_{L}} \end{array}\}

3.5 双向可控源电路的变压器电流重构

由式(12)可知:

(25)U_ab(t)-U_cd(t)-Ri_L(t)-L

\frac{d i_{L} (t)}{d t}

忽略高频变压器电感的阻抗(R=0)时,可得双向可控源电路电感电流表达式:

(26)$\begin{aligned} i_{\mathrm{L}}(t)= & \left\{2 U _ { \mathrm { in } } ^ { \text { ref } } \sum _ { k = 1, 3, 5, \ldots } ^ { + \infty } \left[\frac{2 \sin \left(k \omega t-\frac{\pi}{2}\right)}{k \pi}-\right.\right. \\ & \left.\frac{2 \sin \left(k \omega t-\alpha_{1}-\pi-\frac{\pi}{2}\right)}{k \pi}\right]- \\ & 2 U_{0}^{\text {ref }} \sum_{k=1,3,5, \ldots}^{+\infty}\left[\frac{2 \sin \left(k \omega t-\alpha_{2}-\frac{\pi}{2}\right)}{k \pi}-\right. \\ & \left.\left.\frac{2 \sin \left(k \omega t-\alpha_{2}-\pi-\frac{\pi}{2}\right)}{k \pi}\right]\right\} /\left(k^{2} \pi \omega L\right) \end{aligned}$

4 仿真结果及分析

搭建基于双向可控源的海洋电磁发射机电路仿真模型,参数如表3所示.

表3 可控源电路仿真参数

Tab.3 Simulation parameters of controlled-source circuit

参数	取值	参数	取值
U_in/V	500	L/μH	10
U_o/V	100	f/kHz	20
n	4.7	发射桥频率/Hz	50
C₂/μF	2 200	R_L/Ω	0.3
C₁/μF	30	L₁/mH	0.5

新窗口打开| 下载CSV

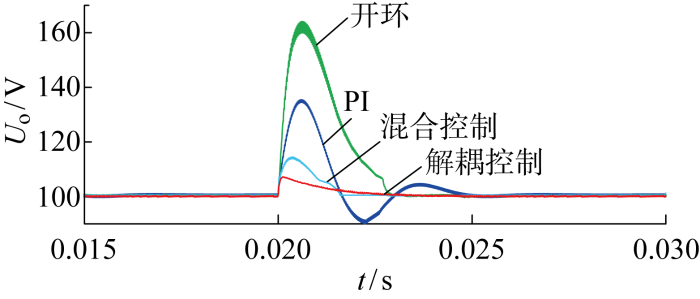
图9给出了开环控制方式、比例积分(PI)控制方式、混合控制方式^[19]以及解耦控制方式下母线冲击电压的波形.在相同参数情况下,母线额定电压为100 V情况下,混合控制方式下冲击电压为14.4 V,双变量解耦控制下,电压冲击为8 V,因此,双变量解耦控制,电压冲击峰值相比混合控制缩减为额定电压的6.4%.

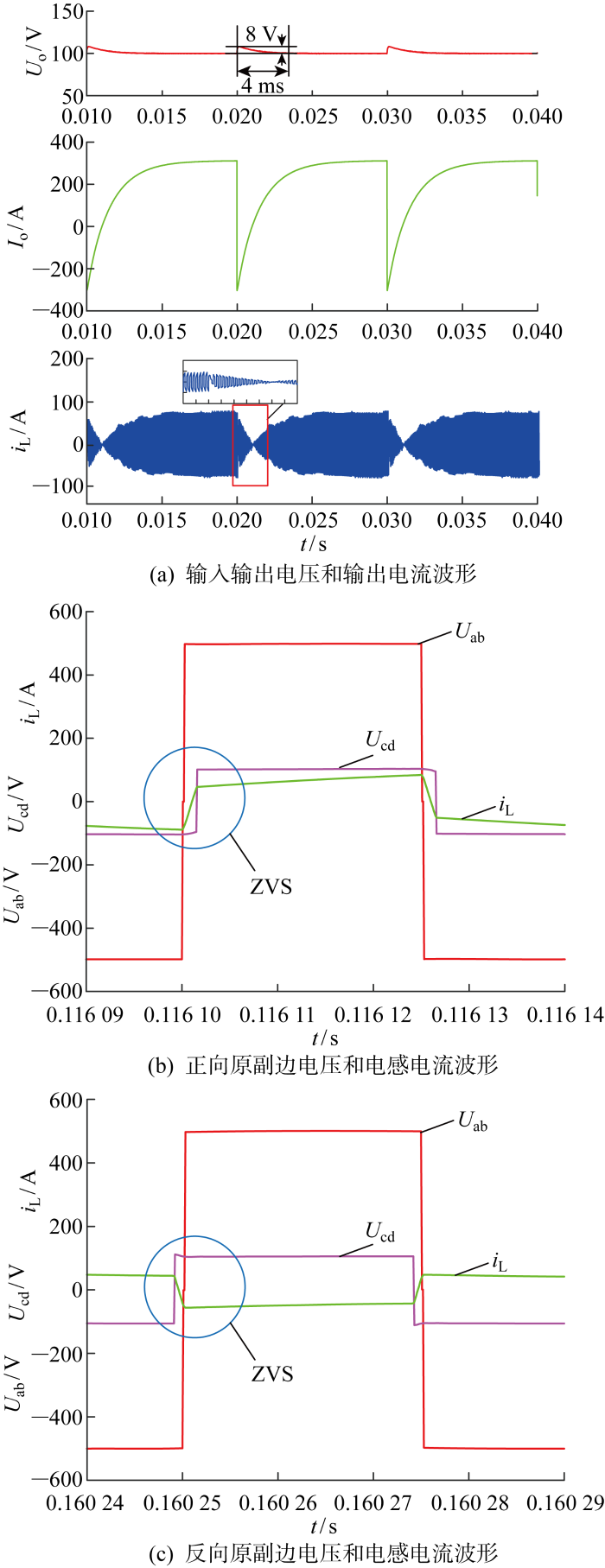
可控源电路工作波形如图10所示.在正常工作时,如图10(a)所示,响应时间随着电压的降落,时间会有所延长,因感性负载电流下降速率与电压负相关,但变压器原边侧电感电流在能量反向时,并没有出现较大振荡.变压器原副边电压以及电感电流波形如图10(b)和图10(c)所示,图10(b)正向传输,图10(c)反向传输.根据图10(b)和图10(c)的主要波形图,结合开关管ZVS限制条件可得变换器在功率切换前后均能实现变换器全部器件的ZVS,验证了控制策略的有效性.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 可控源电路工作波形

Fig.10 Operating waveforms of controlled-source circuit

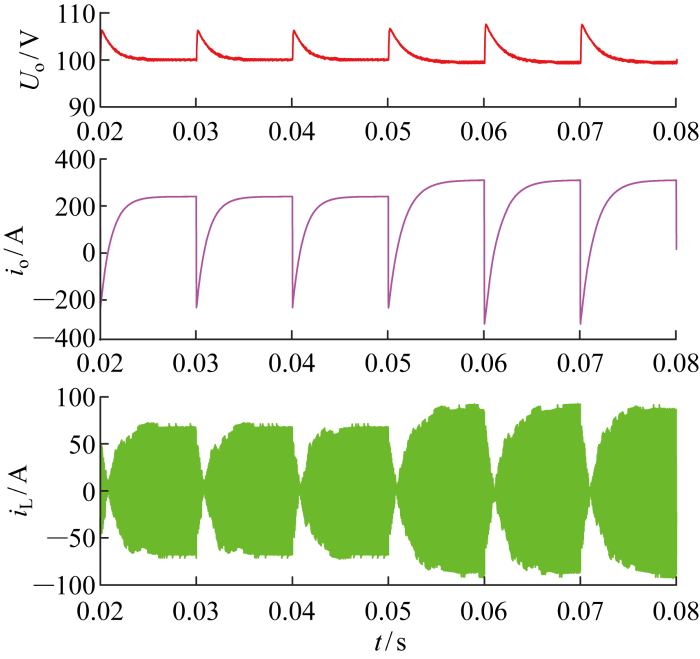
由于海底地质的不同,负载的磁导率会发生变换,所以分别仿真了负载电阻变化与电感变化的情况.图11给出了输出电压为100 V时,负载电阻由0.4 Ω变为0.3 Ω时,输出电压与设定值相比有所跌落,但仍在正常的调节范围内.随着负载电阻减小,输出功率与电感电流峰值增大,输出电压减小.根据电阻与电感的并联特性,输出电流的上升时间得到拉长.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 电阻变化时波形

Fig.11 Waveforms in resistance change

图12给出了输出电压为100 V时负载电感由0.5 mH变为0.14 mH时,输出电压与设定值相比无稳态误差.随着负载电感的减小,稳态的输出功率不变,暂态的反向功率得到减小.因此输出电压峰值与输出电流的上升时间得到减小.在两种负载变化或换相情况下,电感电流在换相时刻都无出现振荡与抖动.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 电感变化时波形

Fig.12 Waveforms in inductance change

5 实验验证

为验证上述提出的控制策略的可行性和有效性,在所搭建的实验平台上进行实验.图13给出了实验平台图片.图中有3块主电路板,每块均为一个H桥模块,组成双向可控源电路与发射桥,下方是采样模块,其基本设计参数如表4所示.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 实验平台实物图

Fig.13 Experimental platform

表4 实验样机主要参数

Tab.4 Design index of DC-DC converter

参数	取值	参数	取值
U_in/V	15	L/H	1×10^-5
U_o/V	15	n	1
C₁/μF	2 200	C₂/μF	2 200
f/kHz	20	发射桥频率/Hz	50
R_L/Ω	0.33	L₁/μH	500

新窗口打开| 下载CSV

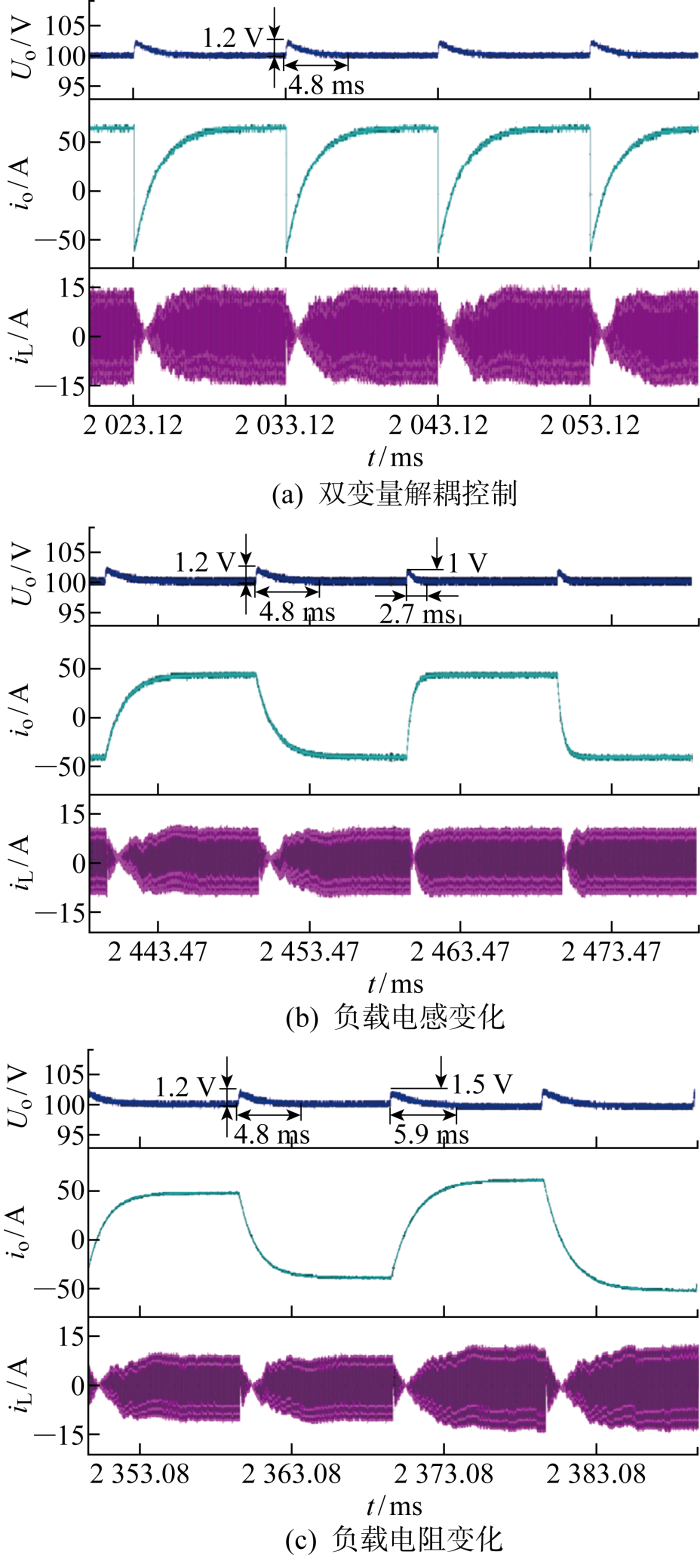
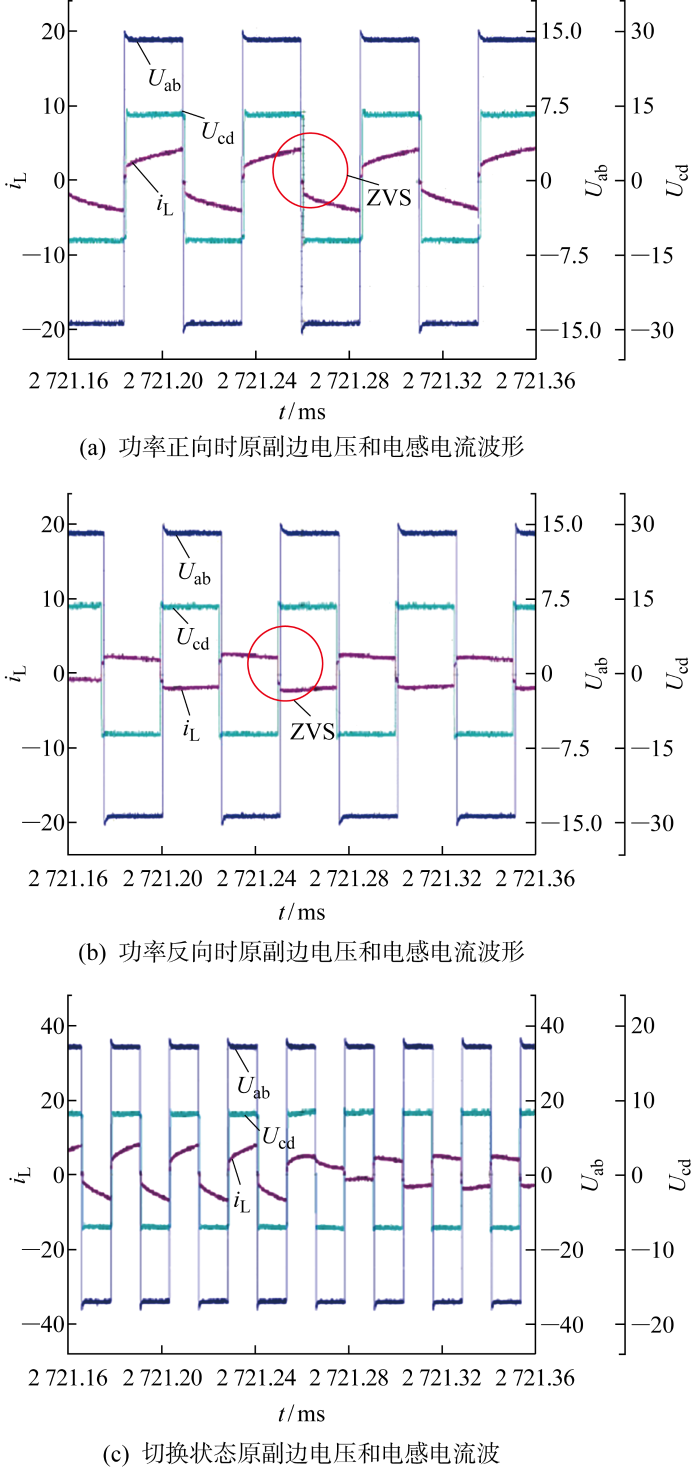
双变量解耦时输出电压和电流波形如图14所示.图14(a)给出了输出电压、输出电流与原边电感的波形,由于发射桥的换相,输出电流跌落后恢复到正常值有一定时间,与发射电流上升与下降一致.图14(b)为输出电压为100 V、负载电感由0.5 mH变为0.25 mH时,输出电压与设定值相比无稳态误差.随着负载电感的减小,稳态的输出功率不变,暂态的反向功率得到减小.因此输出电压峰值与输出电流的上升时间得到减小.在两种负载变化或换相情况下,电感电流在换相时刻都无出现振荡与抖动.图14(c)给出了输出电压为100 V时,负载电阻由0.4 Ω变为0.3 Ω时的实验波形.随着负载电阻减小,输出功率与电感电流峰值得到增大,输出电压减小.根据电阻与电感的并联特性,输出电流的上升时间得到拉长.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 双变量解耦时输出电压和电流波形

Fig.14 Output voltage and current waveforms in two-variables decoupling

双变量解耦时实验波形如图15所示.图15(a)给出了发射桥在换相前能量正向传输时,变压器原副边电压与电感电流实验波形,图15(b)给出了发射桥在换相后能量反向传输时,变压器原副边电压与电感电流实验波形,图15(c)给出了发射桥在换相前后能量传输时,变压器原副边电压与电感电流实验波形,同时都满足软开关的特性.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 双变量解耦时实验波形

Fig.15 Experimental waveforms in two-variables decoupling

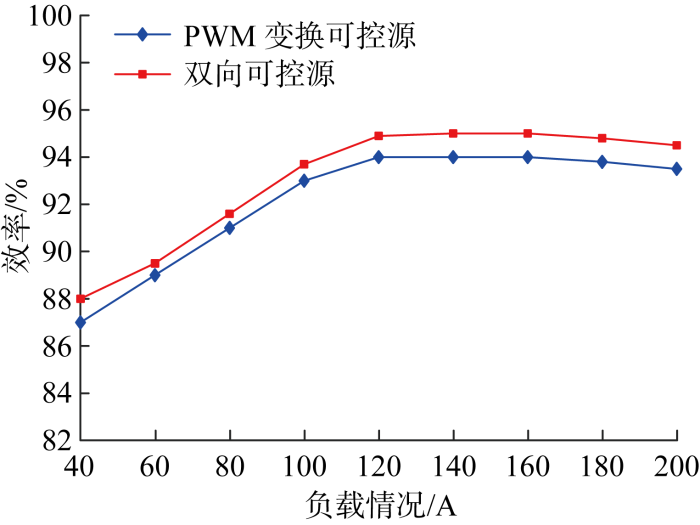
PWM变换方式下的系统整体的最大效率为94%,而双向可控源系统最大效率可达95%,由于发射电流不一致,所以系统仅对比了相同的状态,如图16所示.双向可控源电路效率的提升主要是整个负载范围内实现软开关以及所设计的控制策略对电流应力有优化作用.双向可控源电路发射电流约为PWM变换方式下的1.5倍,增强了输出信号的强度,提高了输出功率,为深海探测研究提供了一定的理论研究基础.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 可控源电路测试效率

Fig.16 Measurement efficiency of the proposed controlled-source circuit

6 结语

通过对发射桥换流过程分析可知,偶极电感能量回馈导致母线产生冲击电压,增大了开关管的电压应力,导致开关管长时间工作时出现损坏现象,提出双向可控源电路.针对双向可控源电路控制变量无法实现完全解耦、功率受限的问题,提出了基于状态反馈精确线性化的滑模控制方法.对通用型负载的双向可控源电路利用动态相量法与基波近似法建立变压器前后两级的平均相量模型,并通过分析系统闭环误差动态方程,得出了反馈控制律参数取值范围,为参数选择提供了理论依据.仿真和实验结果表明,该控制方法可以在实验的全过程内实现软开关,极大地提高了发射机可控源电路的效率和动态性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

底青云, 朱日祥, 薛国强, 等.

我国深地资源电磁探测新技术研究进展

[J]. 地球物理学报, 2019, 62(6): 2128-2138.

DOI:10.6038/cjg2019M0633 [本文引用: 1]

诸多研究表明我国深部资源潜力巨大，但目前的开发开采深度普遍停留在500 m以浅，开展"攻深探盲"是构建国家资源安全体系的有效途径.应用最先进的科学技术手段，提取深部地质信息，已成为我国当前地球物理科学研究的发展方向.作为地球物理学的重要分支，电磁法是矿产资源探查的主体手段之一.在分析我国现阶段航空、地面及海洋电磁探测技术进展的基础上，本文重点说明了极低频电磁法（简称WEM法），多通道瞬变电磁法（简称MTEM）和电性源短偏移瞬变电磁法（简称SOTEM）等电磁探测新技术.WEM法建立一套包括岩石层、大气层和电离层在内的全空间电磁传播理论，通过新研制的观测系统，获取地下10 km的地电信息；MTEM方法是地下埋深4 km目标体精细勘查的有效手段；SOTEM实现地下1.5 km深度范围内目标体的精细探测.通过多种电磁探测技术组合，可实现地下10 km深度范围内多尺度探测，达到"望远镜+放大镜+显微镜"探测效果.同时，本文指出进一步研发与新方法配套的装备、资料处理技术和大数据人工智能识别等将是我国电磁法未来的发展方向.

Qingyun

, ZHU

Rixiang

, XUE

Guoqiang

, et al.

New development of the electromagnetic (EM) methods for deep exploration

[J]. Chinese Journal of Geophysics, 2019, 62(6): 2128-2138.