基于用户意愿的电动汽车备用容量多目标优化

doi:10.16183/j.cnki.jsjtu.2022.131

基于用户意愿的电动汽车备用容量多目标优化

邵萍¹, 杨之乐^,², 李慷³, 朱晓东¹

1.郑州大学电气与信息工程学院, 郑州 450001

2.中国科学院深圳先进技术研究院,广东深圳 518000

3.利兹大学电子与电气工程学院,英国利兹 LS2 9JT

Multi-Objective Optimization of Electric Vehicle Spare Capacity Based on User Wishes

SHAO Ping¹, YANG Zhile^,², LI Kang³, ZHU Xiaodong¹

1. School of Electrical and Information Engineering, Zhengzhou University, Zhengzhou 450001, China

2. Shenzhen Institute of Advanced Technology of the Chinese Academy of Sciences, Shenzhen 518000, Guangdong, China

3. School of Electronics and Electrical Engineering, University of Leeds, Leeds LS2 9JT, U.K.

通讯作者: 杨之乐,博士,副研究员;E-mail:zl.yang@siat.ac.cn.

责任编辑: 王历历

收稿日期: 2022-04-27 修回日期: 2022-07-18 接受日期: 2022-07-22

基金资助:

国家自然基金委面上项目(52077213)
国家自然科学基金青年科学基金项目(62003332)

Received: 2022-04-27 Revised: 2022-07-18 Accepted: 2022-07-22

作者简介 About authors

邵萍(1997-),硕士生,研究方向为EV入网及其优化调度.

摘要

电动汽车(EV)保有量可观且具有储能的特性,使其参与电力系统运行调控提供备用服务成为可能.针对此建立基于EV用户意愿,以集电商经济收益、微电网功率波动和用户满意度为目标的多目标优化调度模型.考虑到负荷预测误差的影响,对模型进行日前阶段和日内实时修正阶段的多时间尺度优化调度分析.求解方法采用主流的多目标智能优化算法NSGA-III 算法,同时将NSGA-II 和MOEA/D算法作为对比算法,通过对比实验选出最优调度方案并分析EV提供备用容量的场景.仿真结果证明所提模型的有效性.

关键词： 备用容量; 用户意愿; 多目标; 多时间尺度; 负荷需求不确定性

Abstract

Due to the considerable number and the characteristics of energy storage, it is possible for electric vehicles (EVs) to participate in the operation and regulation of power system to provide reserve service. In view of this, a multi-objective optimal scheduling model is established based on the wishes of electric vehicle users, with the objectives of the economic benefits of electricity collectors, microgrid power fluctuations and user satisfaction. Considering the uncertainty of load demand, the optimal scheduling analysis of multi-time scale scenes with the day-ahead time scale and the intra-day real-time correction time scale is conducted. The mainstream multi-objective intelligent optimization algorithm NSGA-III algorithm is adopted in the solution method, and the NSGA-II and MOEA/D algorithms are used for comparison. The optimal dispatching scheme is selected through comparative experiments and scenarios where EVs provide spare capacity are analyzed. The simulation results verify the feasibility and effectiveness of the proposed model.

Keywords： spare capacity; user wishes; multi-objective; multi-time scale; load demand uncertainty

PDF (5565KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

邵萍, 杨之乐, 李慷, 朱晓东. 基于用户意愿的电动汽车备用容量多目标优化[J]. 上海交通大学学报, 2023, 57(11): 1501-1511 doi:10.16183/j.cnki.jsjtu.2022.131

SHAO Ping, YANG Zhile, LI Kang, ZHU Xiaodong. Multi-Objective Optimization of Electric Vehicle Spare Capacity Based on User Wishes[J]. Journal of Shanghai Jiaotong University, 2023, 57(11): 1501-1511 doi:10.16183/j.cnki.jsjtu.2022.131

随着全球能源危机和环境污染问题^[1]日益严峻,2020年9月,国家主席习近平提出我国力争“2030年碳达峰、2060年碳中和”的目标^[2].为了促进能源电力的高质量发展,构建以新能源为主体的新型电力系统已成为未来能源电力的发展趋势,而高比例波动性新能源接入对电力系统的灵活运行构成新挑战^[3].与此同时,电动汽车(EV)因节能、零排放^[4]的优点得到不同国家的大力支持,其保有量不断增加.EV^[5]的快速化和规模化发展为提高电力系统的灵活性、缓解能源^[6]危机和改善环境污染问题提供了新的解决方案.但是大量EV无序充放电可能会进一步加重电网的峰谷差^[7],造成电网峰值负荷激增,影响电网的经济稳定运行,甚至可能造成配电系统崩溃^[8].EV的电池可以快速响应信号,然而大多数私人EV都处于怠速状态,一天中大部分时间没有驾驶,这成为EV调控调度的现实条件以及有利因素.由于EV兼具可调控负荷和储能的特性^[9],不仅可以作为常规负载从电网中汲取电能,还可以利用汽车入网(V2G)技术^[10]接入电网作为储能为电网提供备用服务^[11].如果基于用户的需求和意愿对EV的充电和放电行为加以合理调节和控制,可以有效达到减小电网负荷波动、削峰填谷^[12]以及将EV作为一种备用电源向电网供电,提供备用和辅助服务^[13-14]的目的.

目前,对EV参与电网提供辅助备用服务的优化调度问题已有一定研究.文献[15]中基于EV的运行约束研究其聚合模型,并提出EV参与电网调度满足旋转备用需求的方案,从而提升系统的稳定性和经济性.文献[16]中提出一种基于双重激励机制(DIM)的EV充/放电日前调度策略以提高EV的备用服务能力.文献[17]中提出计及多因素的系统及各分区的备用需求容量设置方法,并构建区域联合优化出清数学模型.文献[18]中针对用户侧用电需求不确定性及调频备用需求,建立EV参与调频辅助服务的备用优化与实时调度模型,有效提高聚合商参与辅助服务的鲁棒性和经济性.文献[19]中提出一种多市场优化模型,用于最小化EV充电的净运营成本,以确定EV聚合的最优运营策略和每辆EV的充电功率.文献[20]中考虑影响系统备用需求的随机性因素,并构建以备用服务的经济性、可靠性及碳排放的多目标竞价模型.文献[21]中将EV用户成本及经济调度成本作为目标函数,并将EV有序充放电作为经济调度时的备用容量.然而以上研究模型大多以经济性为导向,单纯追求微电网运行的经济性而未考虑用户的参与意愿以及负荷预测的误差,难以适用于实际情况.

针对上述问题,在现有研究背景下,综合考虑集电商的经济性、微电网功率波动和用户满意度,建立基于用户意愿的EV备用容量多目标优化模型.同时考虑日前预测负荷误差的影响,在日前和日内多种时间尺度上进行多目标优化调度分析.最后对一个微电网案例进行仿真分析,采用NSGA-III 算法对模型进行优化,同时将NSGA-II 和MOEA/D算法作为对比算法,通过3种算法的对比选出综合最优的调度方案,实验结果证明了所提基于用户意愿的EV备用容量的多目标优化模型的有效性和合理性.

1 调度架构及可信备用容量的获取

1.1 调度架构

在电力系统日前调度计划中,发电侧调度计划完成后会同时发布分时电价引导需求侧负荷的分布导向,因此在日内短期计划中发电侧的调度计划不会更改.而负荷预测具有不准确性,较长时间的调度计划难以保证在较短时间尺度^[22]上顺利进行,为此提出基于日前调度计划和日内修正计划的EV备用容量的优化调度模型,如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 日前日内调度计划

Fig.1 Day-ahead and intra-day scheduling plans

在日前调度阶段:集电商汇集负荷预测信息和具有参与V2G意愿的EV用户信息,以集电商经济性、微电网功率波动和用户满意度为目标做出日前阶段每小时的EV调度计划.日前调度以一天为周期,每24 h调度一次,调度时段为1 h,从每天中午12:00到次日中午12:00,因此市场负荷需求以及EV车主申报信息需要在12:00之前获取.

在日内调度阶段,当日内实时负荷需求信息和日前预测信息出现偏差时,日前微电网制定的调度计划已经不能满足市场的负荷需求,需要启动日内短期滚动调度计划.此时集电商根据实际负荷信息和日前调度的EV每小时备用容量信息制定日内15 min时段的调度计划.其调度目标仍为集电商经济性、微电网功率波动和用户满意度,除此之外将日前调度结果中的备用容量作为日内调度计划中的容量约束.日内调度每隔15 min进行一次,调度时段为当前时刻至调度周期的剩余时段.其中日内调度需结合日前调度结果做容量约束,制定当天剩余时段的短期调度计划并对日前调度计划修正.

1.2 可信备用容量的获取

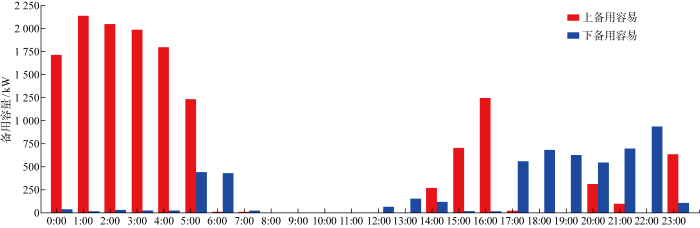
EV兼具可调控负荷和储能的特性, 可迅速切换充、放电状态提供瞬时响应,是需求侧重要的潜在备用措施.EV功率理论上具有双向可调的特性,其备用能力按调节方向可分为上备用能力和下备用能力两类.目前EV充电负荷建模的方法主要根据美国公布的私家车出行数据假设用户的初始充电状态(SOC)遵循一定的正态分布,再使用蒙特卡罗方法绘制EV的出行和到达时间、行驶里程和初始SOC样本,以计算每日充电负荷曲线^[23-24].还可使用基于马尔可夫随机过程的出行链理论来描述用户出行行为的时空随机性^[25].然而EV车主的出行信息受出行的便利性、用户的偏好性和经济性等多种因素影响,美国家庭出行数据并不一定适合现有的实际场景.为了刻画EV用户每个时段的可信备用容量,基于文献[26]的研究,首先采用问卷调查的形式对EV车主的出行信息和参与V2G的意愿进行知识提取,构建反映用户意愿不确定性统计分布的多代理模型.然后分析采集到的EV出行数据,采用蒙特卡洛法抽样形成与多代理个体对应的EV状态参数.最后构建用户意愿影响因素与EV状态信息对应关系,分析用户参与车网互动意愿.抽取一定规模的EV信息,与多代理个体心理阈值比较,可进行愿意或不愿意参与调控的EV用户分类.通过此方法判定的EV用户被认为已经达到其参与调度的心理阈值,其次日信息不会改变.以某小区的微电网系统为例,根据用户决策模型得到的200辆EV的上下可信备用容量如图2所示.其中可信备用容量是基于EV用户充电需求被满足的前提下得到的每小时可被调度上下可信备用容量.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 EV可信备用容量的时间分布

Fig.2 Time distribution of EV trusted reserve capacity

2 多时间尺度调度模型

2.1 日前调度

2.1.1 目标函数

(1)F₁=max(C_R-C_U+C_G)

式中:F₁为集电商的经济收益,主要由三部分构成,分别为EV参与V2G提供备用服务的收益C_R、集电商与电网交互的购电成本C_U和集电商与用户之间的零售收益C_G.其中备用服务的收益C_R表示为

(2)$\begin{array}{c}C_{\mathrm{R}}=\sum_{t=1}^{T} \sum_{i=1}^{M}\left[-V_{\mathrm{b}}\left(u P_{\text {ue }, i, t} \Delta t+v P_{\mathrm{de}, i, t} \Delta t\right)+\right. \\\left.P_{\mathrm{u}, i, t} V_{\mathrm{u}, t} \Delta t+P_{\mathrm{d}, i, t} V_{\mathrm{d}, t} \Delta t+u P_{\text {ue }, i, t} V_{\mathrm{ue}, t} \Delta t\right]\end{array}$

式中:t为调度时段;T表示调度周期,为24 h; i为被调度的车辆;M=200代表集电商所负责区域的总EV数量;V_b为EV充放电之间状态切换的损耗价格;u、v为一对关于EV上下备用电量的决策因子,表示实际场景中EV充电和放电不可同时进行;P_ue,_i_,_t、P_de,_i_,_t为每辆EV每小时实际参与调用时通过向电网放电提供的上、下备用容量;Δt为调度时间段1 h;P_u,_i_,_t、P_d,_i_,_t分别为每辆EV每小时的上下可信备用容量;V_u,_t、V_d,_t分别为EV参与备用服务的上下可信备用容量价格;V_ue,_t为EV为参与电网互动提供备用服务后每小时放电的价格.

集电商向电网交付的购电成本C_U是其所负责区域内EV的充电费用:

(3)C_U=

\overset{T}{\sum_{t = 1}} \overset{M}{\sum_{i = 1}}

vP_de,_i_,_tV_batΔt

式中:V_bat为集电商长期与电网交易所定的平均价格.

集电商与EV用户之间的零售收益C_G是所负责区域内参与V2G提供备用服务的EV日内24 h内实际充电的费用:

(4)C_G=

\overset{T}{\sum_{t = 1}} \overset{M}{\sum_{i = 1}}

vP_de,_i_,_tV_de,_tΔt

式中:V_de,_t为EV用户为参与电网互动提供备用服务市场后每小时充电的价格.

微电网功率波动的情况以需求侧的等效负荷均方差表示:

(5)$\begin{aligned}F_{2}= & \min \sum_{t=1}^{T}\left\{P_{1, t}-\sum_{i=1}^{M}\left(u P_{\mathrm{ue}, i, t}-v P_{\mathrm{de}, i, t}\right)-\right. \\& \left.\frac{1}{T} \sum_{t=1}^{T}\left[P_{1, t}-\sum_{i=1}^{M}\left(u P_{\mathrm{ue}, i, t}-v P_{\mathrm{de}, i, t}\right)\right]\right\}^{2}\end{aligned}$

式中:P_l,_t为日前的负荷需求预测值.F₂越小对电网的经济性和安全性越有利.

EV用户对优化调度结果的满意度(F₃)表示为其调度中每个参与V2G的时段提供的上下备用容量能与实际申报时最大程度相近,即

(6)F₃=max

\overset{T}{\sum_{t = 1}} \overset{M}{\sum_{i = 1}} (\frac{u P_{u e, i, t}}{G P_{u, i, t}} + \frac{v P_{d e, i, t}}{H P_{d, i, t}})

式中:G、H分别为拥有提供上、下备用能力的车辆.只有EV用户在长时间内对调度结果保持一定的满意度,EV参与V2G向电网提供备用容量才有意义.

2.1.2 约束条件

主要从集电商的角度出发,考虑集电商的经济效益,同时兼顾电网的负荷波动和EV用户对调度结果的满意度,因而约束条件主要偏向于集电商和用户层.

(1) 充放电状态约束.

EV在实际应用场景中,上下备用电量不能同时被调用.因此引入决策因子u、v,满足如下条件:

(7)u+v≤1, u, v∈{0, 1}

(2) 系统功率平衡约束.

电力系统调度的基本要求是系统的发电功率和负载功率保持平衡,当发电量小于负载需求电量时就需要调用上备用容量,反之当发电量大于负载的需求量时需调用下备用容量.因此,对于系统总体的功率平衡约束可表示为

(8)P_g,_t+

\overset{T}{\sum_{t = 1}} \overset{M}{\sum_{i = 1}}

(uP_ue,_i_,_t-vP_de,_i_,_t)=P_l,_t

式中:P_g,_t表示微电网每个时段t的发电功率.

(3) 备用容量约束.

EV备用容量的获取以用户意愿为前提,在调度过程中不可忽略用户意愿,EV备用容量实际参与调用时上下备用容量不应超过其上下可信备用容量,即

(9)0≤P_ue,_i_,_t≤P_u,_i_,_t

(10)0≤P_de,_i_,_t≤P_d,_i_,_t

2.2 日内调度模型

日内短时间尺度的调度计划是基于日前调度的结果将EV每个时段的可信备用容量限制在日前调度结果中的备用容量之间.以15 min为尺度进行滚动优化,当需求侧预测负荷与实际场景中负荷需求量不一致时启动日内调度计划.

2.2.1 目标函数

日内调度模型仍以集电商经济收益最大化、EV用户参与V2G的满意度最大化和微电网的功率波动最小为目标进行多目标优化调度.

(11)$\begin{aligned}F_{1}= & \sum_{t=z}^{4 T} \sum_{i=1}^{M} \max \left[-V_{\mathrm{b}}\left(u P_{\mathrm{ue}, i, t} \Delta t+v P_{\mathrm{de}, i, t} \Delta t\right)+\right. \\& P_{\mathrm{u}, i, t} V_{\mathrm{u}, t} \Delta t+P_{\mathrm{d}, i, t} V_{\mathrm{d}, t} \Delta t+v P_{\mathrm{de}, i, t} V_{\mathrm{de}, t} \Delta t- \\& \left.v P_{\mathrm{de}, i, t} V_{\mathrm{bat}} \Delta t+u P_{\mathrm{ue}, i, t} V_{\mathrm{ue}, t} \Delta t\right]\end{aligned}$

式中:z为日内需求侧负荷与预测负荷不匹配的第1个时段.与日前调度目标不同,Δt代表的时段为0.25 h.

(12)$\begin{array}{c}F_{2}=\min \sum_{t=z}^{4 T}\left\{P_{1, t}-\sum_{i=1}^{M}\left(u P_{\mathrm{ue}, i, t}-v P_{\mathrm{de}, i, t}\right)-\right. \\\left.\frac{1}{4 T-z} \sum_{t=z}^{4 T}\left[P_{1, t}-\sum_{i=1}^{M}\left(u P_{\mathrm{ue}, i, t}-v P_{\mathrm{de}, i, t}\right)\right]\right\}^{2}\end{array}$

(13)F₃=max

\overset{4 T}{\sum_{t = z}} \overset{M}{\sum_{i = 1}} (\frac{u P_{u e, i, t}}{G P_{u, i, t}} + \frac{v P_{d e, i, t}}{H P_{d, i, t}})

F₂和F₃与日前调度模型保持一致.日前和日内调度模型中,差异之处主要体现在调度时段和起始时间的差异.另外,日前调度和日内调度在已知信息上需求侧负荷也不一样,日前调度的需求侧负荷为预测负荷而日内调度负荷为真实的负荷信息,日内调度是在日前调度的基础上在更精细时间颗粒度下的优化和微调.

2.2.2 约束条件

日内调度模型除了满足日前调度模型中所提约束条件外,还需满足日前修正条件.

日前修正约束:将日前调度的每辆EV每个小时的上下备用容量作为日内滚动调度每15 min的上界.保证日内滚动调度在不影响发电侧整体调度计划的同时满足应对预测误差的影响,为电力系统提供备用服务.

(14)0≤P_ue,_i_,_t≤P_gue,_i_,_t

(15)0≤P_de,_i_,_t≤P_gde,_i_,_t

式中:P_gue,_i_,_t、P_gde,_i_,_t分别为日前调度的每辆电动汽在每个小时内所提供的上下备用容量.

3 算例分析

3.1 参数说明

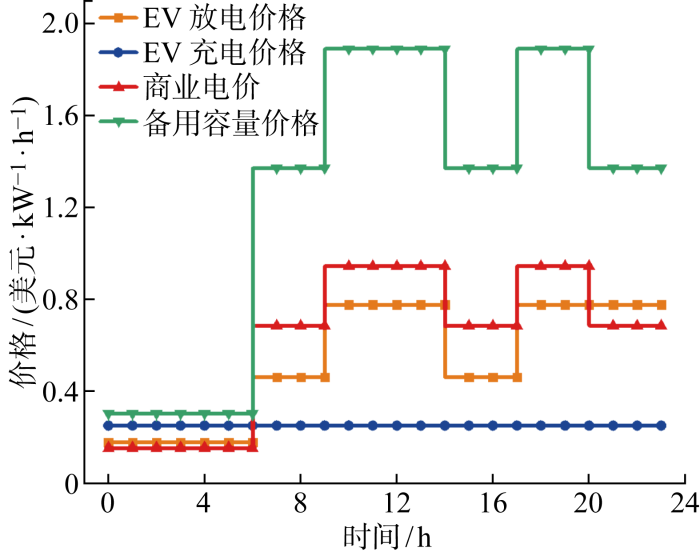
以深圳市某小区的微电网系统为例对200辆EV参与V2G提供备用容量的模型进行分析和讨论.针对以上EV备用容量多目标优化模型中高维多目标的特点,选择多目标优化算法中较为主流的NSGA-III 算法对模型进行求解,同时将MOEA/D、NSGA-II 作为对比算法.通过3种算法求解该模型的实验结果,对比选出最适合求解该模型的算法并采取该算法所优化的帕累托前沿中综合最优的EV备用容量多目标优化调度方案.该区域每小时的预测负荷数据是综合深圳市的平均负荷需求得到的,该微电网系统中分时电价如图3所示.V_bat设为商业电价的0.6倍,V_b设为 0.043 75 美元/(kW·h)^[27],微电网每小时的负荷预测和发电功率如表1所示. NSGA-III 和NSGA-II 算法的参数选择如下:种群个体数为 130, 交叉率为 0.8, 变异率为 0.1,交叉参数为2,变异参数为5. 设定最大迭代次数为800.MOEA/D算法的参数为种群个体数300, 邻居个数20,交叉率0.8, 变异率0.1,交叉参数2,变异参数5,最大迭代次数800.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 分时电价

Fig.3 Time-of-use electricity price

表1 模型参数值

Tab.1 Values of the model parameter

时间	负荷/kW	发电功率/kW	时间	负荷/kW	发电功率/kW
0:00	7000	6500	12:00	14000	14000
1:00	7500	6000	13:00	13000	13000
2:00	8500	6600	14:00	12000	12000
3:00	9500	7700	15:00	10500	10300
4:00	10000	8300	16:00	10000	9500
5:00	11000	9500	17:00	11000	10000
6:00	11500	10500	18:00	12000	12000
7:00	12000	12000	19:00	14000	14000
8:00	13000	13000	20:00	13000	13000
9:00	14000	14000	21:00	11000	10800
10:00	14500	14500	22:00	9000	9000
11:00	15000	15000	23:00	8000	8000

新窗口打开| 下载CSV

3.2 结果分析

3.2.1 多目标优化算法

将主流多目标优化算法NSGA-III 作为主要的模型求解算法.NSGA-III 算法是针对NSGA-II 算法在处理高维多目标问题时由于优化计算代价大,难以挑选帕累托解的情况而开发的,基本流程与NSGA-II 相似,但选择个体时结合了基于参考点的方法,能够有效降低计算代价,适用于求解高维多目标问题.NSGA-III 算法步骤描述如下:

(1) 初始化操作.初始化参考点W=[W₁W₂ … W_p], p= $[\begin{array}{l} m + Q - 1 \\ Q \end{array}]$ ,其中m为目标空间的维度即目标个数,为3;Q为每个目标所要划分的份数,设为14.生成上备用容量和下备用容量的初始化种群X=[x₁x₂ … x_N],并计算每个个体的目标值F_j={F₁, F₂, …, F_m}, N为种群数目.初始化理想点Z^*={ $Z_{1}^{*}$ , $Z_{2}^{*}$ , …, $Z_{m}^{*}$ }, $Z_{m}^{*}$ 为第m个目标的最小值.

(2) 对初始化后的上下备用容量种群进行充放电状态约束、系统功率平衡约束、EV充放电功率约束和备用容量约束等约束处理.

(3) 种群进化.父代种群X通过锦标赛选择策略、模拟二项式交叉和多项式变异产生子代种群Y,合并父代种群和子代种群,则混合种群规模为2N.同时,对进化后的种群进行(2)中的约束处理.

(4) 更新理想点 Z^*={ $Z_{1}^{*}$ , $Z_{2}^{*}$ , …, $Z_{m}^{*}$ }.

(5) 环境选择.对混合种群进行快速非支配排序操作,并利用小生境选择策略对个体进行选择,得到个体数为N的新种群.如果非支配临界层F_j中的个体全部选择超出种群数目N,则标准化目标空间、根据参考点Z^*计算参考线、进行个体与参考线关联操作并根据参考线关联的个体数从临界非支配层中F_j选择剩余个体进入新一代种群中.

(6) 判断是否达到迭代次数,如果达到迭代次数则结束日前调度,否则执行步骤(3).

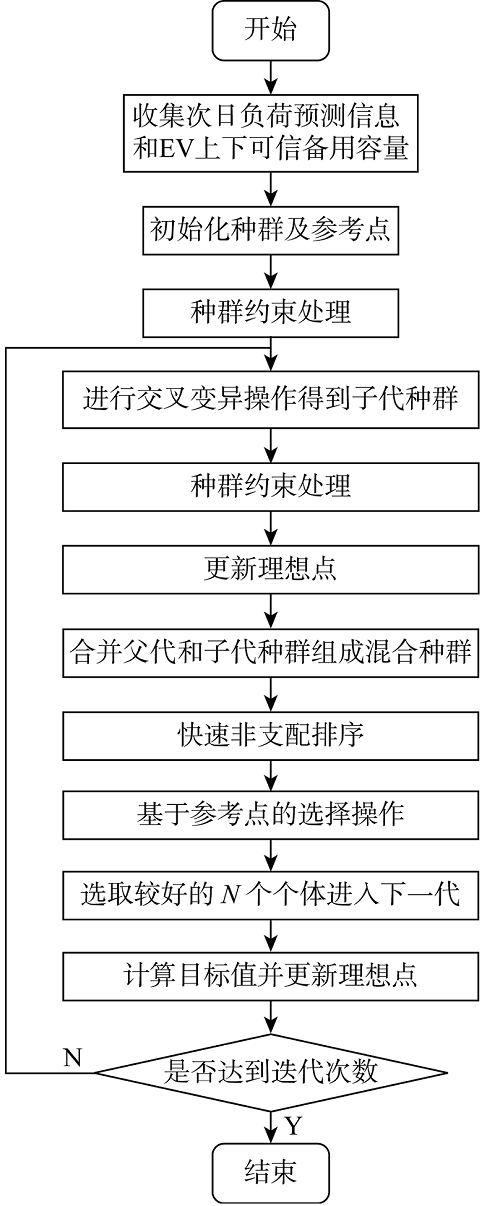
使用NSGA-III 算法求解EV备用容量的多目标优化模型的总体流程图如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 日前的调度流程图

Fig.4 Flow chart for day-ahead scheduling schemes

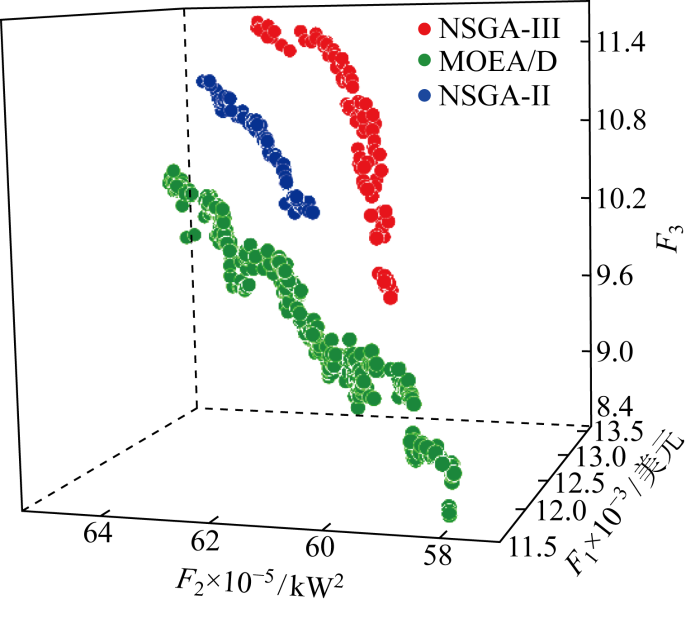
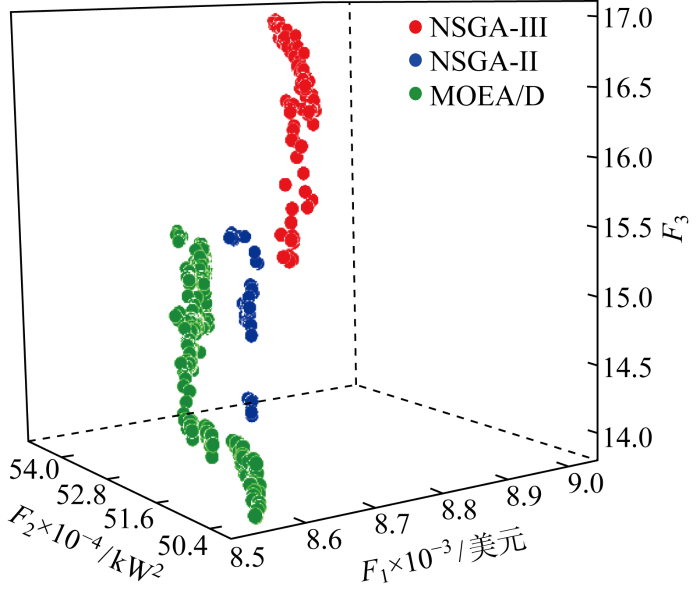
为了验证所提EV备用容量的多目标优化模型的有效性,采取主流的NSGA-III 算法对模型进行求解,同时将MOEA/D、NSGA-II 算法作为对比算法.对日前时间尺度和日内时间尺度模型做优化调度,分析日前和日内EV备用容量和各个目标之间的关系,同时选择合适的算法以求调度方案在3个目标之间综合表现最优.其中日前3种算法的调度结果如图5所示,从图中可以看出NSGA-III 算法的帕累托前沿在右上角,而MOEA/D和NSGA-II 的帕累托前沿总体偏左下方.这意味着NSGA-III 在集电商经济性和用户满意度方面有绝对优势.与MOEA/D相比,NSGA-II 在集电商经济性方面表现较优,每日经济收益集中于13000美元,而MOEA/D经济收益分布在11800~12600美元.相反,MOEA/D算法在减小微电网功率波动方面明显比NSGA-II 更有优势,在用户满意度方面二者表现相差不大.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 日前调度结果对比

Fig.5 Comparison of day-ahead scheduling results

当日前预测负荷与日内实际负荷需求不匹配时,启动日内短期滚动调度方案.在日前调度中EV的上下备用容量均留有一定裕量以应对随时发生的负荷需求变化,文中以17:00负荷需求激增的变化场景为例,模拟当日前调度不满足实际情况下的日内短期滚动调度情况.同时对MOEA/D、NSGA-II 和NSGA-III 3种算法求解日内调度模型的实验结果进行对比,结果如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 日内调度算法对比

Fig.6 Comparison of algorithms for intra-day scheduling

对比日内调度中3种算法的帕累托前沿可知, NSGA-III 算法在经济收益上比其他两种算法表现更好,集电商经济效益稳定在8800 美元/d.NSGA-II 算法次之,而MOEA/D算法表现效果最差,这与日前调度的表现一致.在平滑微电网的功率波动方面MOEA/D比NSGA-III 和NSGA-II 算法更有优势.在用户满意度方面MOEA/D算法和NSGA-II 算法表现相近,NSGA-III 算法表现最优.总而言之,NSGA-III 在3个目标上综合表现最优.

选择MOEA/D、NSGA-II 和NSGA-III 算法对上述应用场景进行优化后得到的解为帕累托前沿,而在实际应用系统中只能采用一种调度方案,因此需要从帕累托前沿中选择一个相对而言综合最优的解.考虑到在EV备用容量的多目标优化模型中所有目标对于评价体系的作用相同,不存在某一个目标函数影响更大的情况,因此3个目标函数权重均相同,通过正向化和归一化后加权和选出在3个目标上综合表现最优的解.表2中的数据为经过加权和方法在日前调度和日内调度的时间尺度上选出的3种算法的综合最优解.从3种算法的最优解方面来看,对比日前日内调度的数据,NSGA-III 在经济收益和用户满意度方面的表现明显优于其他两种算法,且在平滑微电网的功率波动方面日前优化更有优势.该数据进一步证实NSGA-III 算法对于求解EV备用容量多目标优化模型的优越性.

表2 3种算法的最优目标值

Tab.2 Optimal target values of three algorithms

模式	算法	F₁/美元	F₂/kW²	F₃
日前调度	NSGA-III	13362.74	6352108.49	11.53
	NSGA-II	13158.60	6419170.18	11.06
	MOEA/D	12756.56	6448278.59	10.44
日内调度	NSGA-III	8947.78	432816.70	16.59
	NSGA-II	8771.79	430594.38	15.38
	MOEA/D	8695.90	427959.96	15.15

新窗口打开| 下载CSV

3.2.2 日前日内时间尺度的优化调度

将日前NSGA-III 算法优化调度的最优结果和日内的最优结果在集电商经济性、微电网的功率波动情况和用户满意度这3个目标上的表现做对比,分析日前和日内调度的情况.从表2可以看出,NSGA-III 算法的折衷解在日前调度中F₁的最优值为 13 362.74 美元,而日内调度剩余时段的经济收益为 8 947.78 美元;加之前5 h的经济收益为 7 086 美元,累计日内为 16 033 美元,日内调度相比日前调度在集电商的经济性上提高20%.而在用户满意度方面,日前调度的NSGA-III 算法的F₃折衷解为11.53,日内调度为16.59,用户满意度提高44%.

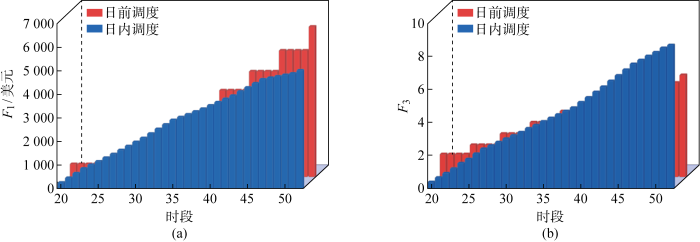
图7展示了在负荷预测产生误差的情况下,日前调度和日内调度在之后8 h的目标值变化情况.日内调度以15 min为周期进行调度,即每15 min为1个时段.从图中可以看出日内调度的结果变化相对于日前调度结果变化更加平缓,一直在稳步提高.这说明日内调度时段在应对实际负荷与预测负荷相比负荷激增或者负荷骤降的情况下更有优势,即日内调度的灵敏度更高,这也说明了多时间尺度的必要性.图7(a)为集电商的经济性变化情况,图中显示在20~40这个时段日内调度的集电商收益更高,这是由于需求侧负荷激增所以EV需要在允许调度范围内最大程度上调用更多的上备用容量以满足需求差额,而集电商作为中间商则可以从中获取更多经济效益.而在40~50这个时段其集电商收益反而不及日前调度的经济收益,这主要是因为在20~40时段增加调用EV的备用容量对剩余时段产生影响.图7(b)为用户满意度变化情况,从图中可以明显看出日内调度的方案对于EV用户来说更容易接受.日内调度是基于用户意愿对可信备用容量的多目标优化,其优化是在日前调度基础上针对负荷需求差额变化的微调.对于EV用户来说微调意味着为了应对突增的负荷需求需要调用更多的上备用容量,也即收益更多用户满意度更大.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 日前日内调度方案的目标对比

Fig.7 Comparison of day-ahead and intra-day scheduling schemes in terms of various objectives

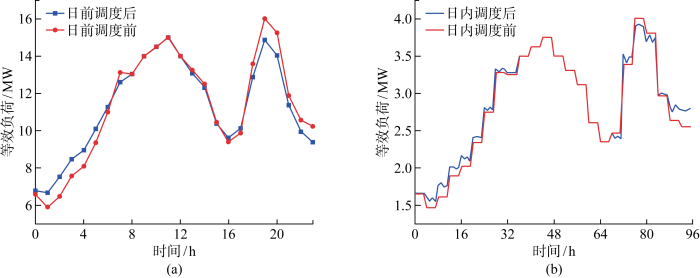
图8为日前日内调度在第2个目标微电网的功率波动情况,图8(a)为日前调度前后的等效负荷, 即需求侧常规负荷与EV上下备用容量的等效负荷.在问题设计中,认为微电网的功率波动一定程度上代表削峰填谷的效果,峰谷差越小,微电网的功率波动即F₂取值越小.将图8模型优化前后的负荷曲线作对比观察削峰填谷的效果.由图可见,原始负荷曲线的峰时是11:00和19:00, 谷时是16:00.EV的可信上备用容量主要集中在 0:00—5:00和 15:00—16:00,可信下备用容量主要是 5:00—6:00 和 17:00—22:00.原始负荷曲线的第2个峰值时刻在EV的可信备用容量覆盖区域内,经过优化后其峰值从 16 020.19 kW降到 14 880.32 kW.同理,在图8(b)日内调度的曲线上,可以看到优化后的等效负荷相对于日前优化等效负荷峰时的值从 4 005 kW降低到 3 925 kW,在可信备用容量允许范围内有效地达到了削峰目的.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 日前日内调度方案的等效负荷

Fig.8 Day-ahead and intra-day scheduling schemes of in terms of equivalent load

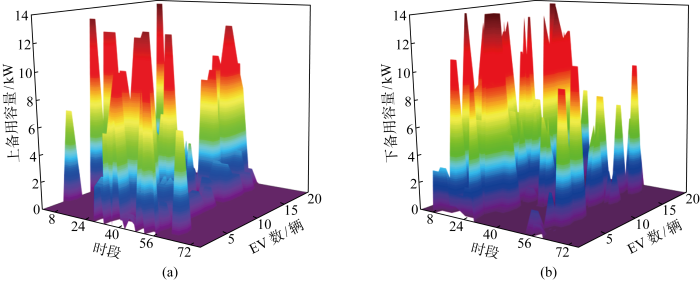
EV日前调度结果的热力图如图9所示,以20辆EV为例,由图可知EV的上备用容量调用集中在1:00—6: 00和15:00—18:00,该段时间为EV使用的非高峰阶段,EV用户可在不影响日常生活的同时赚取一定经济收益.下备用容量的调用集中在6:00—8:00以及18:00—24:00,即上班之前和下班之后,可以有效地利用富余时间进行充电.5:00—7:00 为充电电价的低谷时段.在不影响EV用户日常生活的前提下通过调度时段将备用容量参与电网出售为电网提供备用服务即可满足电网的备用需求,用户和集电商还可获取一定经济收益.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 日前调度中EV备用容量优化结果

Fig.9 Optimization results of spare capacity on EVs in day-ahead scheduling

EV日内调度结果如图10所示,选取同样的20辆EV为例.由图可知,在4~20时段EV调用的上备用容量可以达到10~13 kW,而该时段对应着日前的18:00—22:00,相比日前该时段的调用有所增加.与此同时,在32~52时段上备用容量调用较多,这对应于1:00—6:00.下备用容量主要集中在8~28时段和52~56时段,对应 19:00—24:00 和 6:00—7:00.总体来说和日前调度的结果保持一致,在17:00 预测负荷发生偏差时及时调整上备用容量的调用以应对日前调度中不能满足的情况.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 日内调度中EV备用容量优化结果

Fig.10 Optimization results of spare capacity on EVs in intra-day scheduling

4 结语

建立基于用户意愿的EV备用容量多目标优化调度模型.考虑集电商调度EV的综合经济成本、用户对调度结果满意度以及微电网的功率波动情况;同时考虑到预测误差的影响,对模型进行日前和日内两个时间尺度上的调度分析;并通过NSGA-III、NSGA-II 和MOEA/D等3种多目标智能优化算法对模型进行求解分析.对比3种算法发现:NSGA-III 算法在日前时间尺度和日内时间尺度上的优化调度均达到集电商的经济性、微电网的功率波动和用户满意度3个目标上的综合最优.实验结果证明所构建模型的有效性和合理性.

然而,本文EV的可信备用容量基于问卷调查生成的用户意愿多代理模型进而产生各个时段的上下备用容量,不能保证用户的实际行为和代理模型决策的完全一致.未来将考虑通过商业化运行来规避调度偏差产生的风险并分摊相应成本.另外,在日内时间尺度的滚动调度中,实验场景仅考虑实际负荷需求与预测负荷相比突增的情况,没有考虑负荷需求突然降低的情况.未来将进一步研究不同场景下EV参与V2G提供备用服务的情况.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

何西, 涂春鸣, 王丽丽,

等.

考虑用户行车习惯的电动汽车充电双层控制策略

[J]. 电力系统自动化, 2018, 42(3): 64-69.