浅海质点振速场强度的深度分布特性
张海刚, 谢金怀, 刘佳琪, 龚李佳, 李智
上海交通大学学报
2024, 58 ( 7):
995-1005.
DOI:10.16183/j.cnki.jsjtu.2023.073
质点振速场强度的深度分布特性对水声探测与估计具有重要影响.基于简正波非相干模态和变换到角度积分的近似条件,推导出质点振速的非相干简正波的角度积分形式,避免了本征值和本征函数的复杂计算,并揭示了质点振速强度在声源深度及对称深度具有显著变化特性的物理机理.数值结果表明:非相干质点振速的角度积分解析式可实现快速计算,并可较好地表征出质点振速强度的深度分布特性;同时,由于简正波模态幅度函数的叠加效应,垂直质点振速与水平质点振速的深度分布存在显著差异性;随后,以质点振速强度差为研究对象,分析了水平距离、声源频率、声速剖面及海水深度等参数对质点振速场强度的深度分布特性的影响.相关结论可为基于矢量场的被动目标深度估计提供理论依据.
View image in article
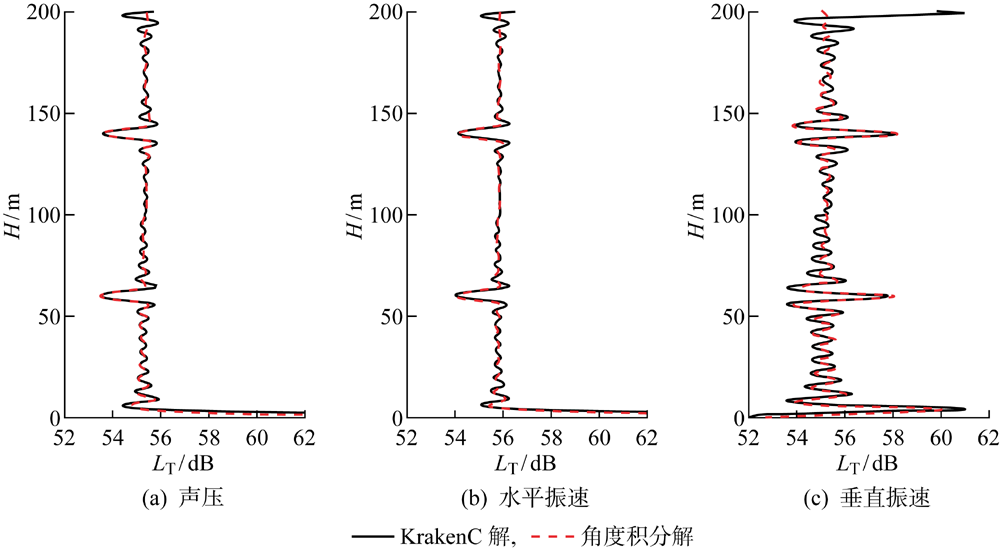
图1
等声速波导环境的深度分布
正文中引用本图/表的段落
为了验证等声速波导环境下质点振速的角度积分形式用于表征质点振速场强度的深度分布特性的有效性,以及该解析式的计算效率,以KrakenC声场计算软件[25]计算结果作为标准解,仿真计算声矢量场传播损失LT=-10lg(F/Fref)随深度的分布.仿真海水深度为200 m,水中声速 1 500 m/s,海底声速 1 800 m/s的波导环境,计算声源深度为 60 m,频率为200 Hz,在距离声源2 km处的深度分布曲线如图1所示.
可以看到,利用声矢量各分量的角度积分解析式计算的深度分布结果与KrakenC声场计算软件计算结果基本吻合,且利用声场计算软件计算本征值和本征函数,进一步计算质点振速强度的深度分布特性需耗时 3 314.854 ms,而利用上文推导解析式进行相关计算仅需 11.756 ms,计算效率显著提高.由此,验证了非相干质点振速角度积分解析式用于表征深度分布特性的有效性及高效性.同时,图1中所示声压与水平质点振速强度的深度分布规律基
在海水深度为200 m,水中声速 1 500 m/s,海底声速 1 800 m/s的等声速波导环境下,声源深度60 m,频率200 Hz的质点振速强度差计算结果如图2所示.在声源深度和声源对称深度的强度差起伏高达5 dB,而图1(b)中的水平质点振速强度起伏为2 dB,且强度差的深度分布缓和了垂直质点振速在其他深度的振荡性.另一方面,利用非相干质点振速强度差进行质点振速场强度的深度分布特性研究,仅仅需要水平质点振速和垂直质点振速信号的非相干传播损失差值,避免了信号声源强度起伏所带来的误差.因此,可利用非相干质点振速强度差描述浅海质点振速场强度的深度分布特性,进一步分析水平距离、声源参数、声速剖面和海水深度等环境对质点振速深度分布特性的影响.
本文的其它图/表
|
