上海交通大学学报

上海交通大学学报, 2025, 59(9): 1315-1326 doi: 10.16183/j.cnki.jsjtu.2023.486

新型电力系统与综合能源

代理模型辅助的复杂地形风电场微观选址多目标优化设计

刘佳惠, 王聪,, 张宏立, 马萍, 李新凯, 董颖超

新疆大学 电气工程学院, 乌鲁木齐 830017

Multi-Objective Optimization Design of Micro-Site Selection of Complex Terrain Wind Farms Assisted by Proxy Model

LIU Jiahui, WANG Cong,, ZHANG Hongli, MA Ping, LI Xinkai, DONG Yingchao

School of Electrical Engineering, Xinjiang University, Urumqi 830017, China

通讯作者: 王 聪,副教授,博士生导师;E-mail:wangc@xju.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-09-21   修回日期: 2023-11-23   接受日期: 2023-12-4  

基金资助: 国家重点研发计划项目(2021YFB1507000)
新疆维吾尔自治区自然科学杰出青年基金(2022D01E33)

Received: 2023-09-21   Revised: 2023-11-23   Accepted: 2023-12-4  

作者简介 About authors

刘佳惠(1998—),硕士生,从事风电场微观选址及智能优化算法研究.

摘要

为解决复杂地形下风电场微观选址优化难度大、耗时长的问题,提出一种基于代理模型辅助的复杂地形风电场微观选址多目标优化方法.首先,考虑复杂地形起伏大的地理特征,计算崎岖度指数,将地面平整度进行数值量化,并对崎岖度过大的点进行约束处理;其次,建立三维多风向下尾流叠加计算发电量的数学模型,构建三维地形集电线路拓扑优化代理模型,检验代理模型的预测精度,表明可替代集电线路拓扑优化的大量计算,有效提高计算效率,然后采用多目标离散状态转移算法,获得复杂地形微观选址多目标优化设计的Pareto前沿;最后,以中国新疆某实际复杂地形风电场为例,实现复杂地形风电场多目标微观选址,并将该算法与单目标优化结果进行比较.仿真结果表明,在考虑复杂地形因素特点的情况下,代理模型辅助的多目标离散状态转移算法能在优化年发电量的前提下减少总电缆铺设长度,降低工程建设投资,为工程实际提供更多布局方案.

关键词： 风电场; 微观选址; 复杂地形; 多目标优化算法; 崎岖度指数; 代理模型

Abstract

To tackle the challenges of high difficulty and time-consuming micro-site optimization of wind farms in complex terrains, a multi-objective optimization method for micro-site selection is proposed, assisted by proxy model. First, considering the geographical features of complex terrains with significent undulations, the ruggedness index is calculated and the ground flatness is numerically quantified, constraining the points with excessive ruggedness. Then, a mathematical model for three-dimensional windy downward wake superposition calculation of power generation is established, a three-dimensional terrain collector line topology optimization agent model is constructed, and the prediction accuracy of the proxy model is verified, demonstrating the ability to replace numerous calculations in collector line topology optimization and effectively improving the computing efficiency. Finally, taking a real complex terrain wind farm in Xinjiang Uygur Autonomous Region, China as an example, multi-objective micro-site selection of complex terrain wind farm is realized, and the results are compared with those obtained through the single-objective optimization. The simulation results show that the multi-objective discrete state transfer algorithm assisted by the proxy model can reduce the total cable laying length, decrease the construction costs, and provide more feasible layout schemes while optimizing the annual power generation.

Keywords： wind farms; microscopic situation; complex terrain; multi-objective optimization algorithm; terrain ruggedness index (TRI); proxy model

PDF (5456KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

刘佳惠, 王聪, 张宏立, 马萍, 李新凯, 董颖超. 代理模型辅助的复杂地形风电场微观选址多目标优化设计[J]. 上海交通大学学报, 2025, 59(9): 1315-1326 doi:10.16183/j.cnki.jsjtu.2023.486

LIU Jiahui, WANG Cong, ZHANG Hongli, MA Ping, LI Xinkai, DONG Yingchao. Multi-Objective Optimization Design of Micro-Site Selection of Complex Terrain Wind Farms Assisted by Proxy Model[J]. Journal of Shanghai Jiaotong University, 2025, 59(9): 1315-1326 doi:10.16183/j.cnki.jsjtu.2023.486

风能作为清洁能源近年来得到了广泛关注,由于中国“碳达峰、碳中和”目标的提出及陆上风电场的设备制造技术、风力机安装技术不断提高,风电场的建设需求逐渐增加.风电场的前期规划设计对能源的利用率会产生较大影响,其中微观选址是风电场设计的核心环节,通过对微观选址的设计以减少风力机间的尾流折损来达到更好的发电效果.风电场微观选址是指在风电场规划区域内,结合风电场气象与地理数据并考虑风力机间的相互尾流影响,设计一种使风力机在各种约束条件下能源利用率最优的布局方式[1].

风电场微观选址设计分为专家经验布局和智能优化算法布局,专家经验布局常使用规则的排布方式,难以考虑多种因素对风电场的风力机布局影响以及获得最优的风电场微观选址方案[2].随着人工智能的发展,智能优化算法被应用于微观选址问题.针对平坦地形的微观选址中萤火虫算法[3]、风力机尾流排斥优化算法[4]及珊瑚礁算法[5]等相继被提出.

随着新能源的大力并网,平坦地形不足以满足陆上风电场的建设需求,针对复杂地形的微观选址成为一个研究热点.Feng等[6-7]提出采用随机搜索算法求解风电场布局优化问题,并提出一种适应复杂地形工程的尾流模型和风电场布局的优化框架,Hu等[8]提出一种仅考虑风力功率密度和地形加速效应的改进遗传算法.以上方法在风电场设计中取得较好的效果,但针对复杂地形的风电场设计仍存在以下问题:① 在优化过程中未考虑复杂地形地面平整度对风力机安置的约束;② 复杂地形风电场集电系统拓扑优化需较长的计算时间;③ 以年发电量最大为目标产生的风力机排布方式对风电场年能源产量有较大提高,但仅以此优化目标产生的排布方式会使风力机尽可能分散分布,加大风力机间的连接距离,增加电缆的铺设长度[9-10],而实际工程上未将年发电量优化环节与集电系统拓扑优化间的影响作为参考因素.

为解决复杂地形风电场设计中风力机安置对地面平整度的限制,以及在前期风电场规划时未将微观选址环节与集电系统拓扑优化联合考虑的问题,本文提出一种针对复杂地形风电场微观选址的新方法.主要完成以下工作:① 引入崎岖度指数(terrain ruggedness index, TRI)约束处理以排除某些地形过于崎岖的场地,解决地面平整度对风力机安置的影响;② 采用基于径向基函数(radial basis function, RBF)的代理模型技术,构建三维地形集电系统拓扑优化的辅助计算模型,解决优化过程计算时长较大的问题;③ 基于构建的代理模型进行辅助计算,将年发电量与集电线路总长度同时作为优化目标,采用多目标离散状态转移算法(discrete multi-objective state transition algorithm, DMOSTA)对多风向下复杂地形风电场风力机布局进行优化,获得其Pareto前沿,选择出符合要求的最优方案.

1 集电线路拓扑优化代理模型

1.1 集电线路拓扑优化

1.1.1 三维复杂地形中两点距离计算

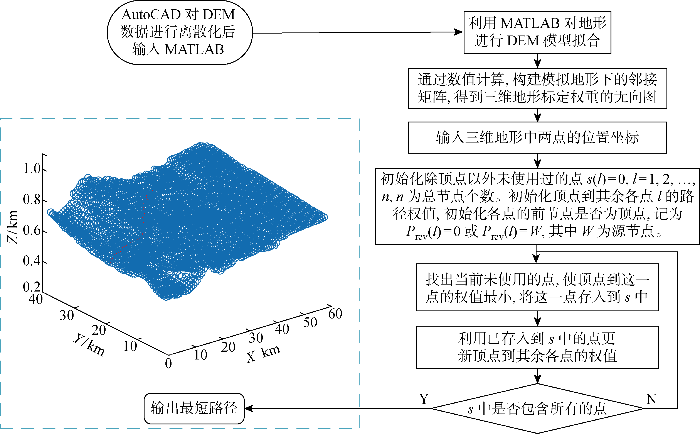
复杂地形下风电场集电线路因地处山地地形,设计主要采用电缆直埋的方式.在复杂地形中两台风力机的实际距离需与地形数据相结合,因此在该阶段采用单源最短路径(Dijkstra)算法对其进行计算.为提高算法的运算速度,通过AutoCAD对地形的数字高程模型(digital elevation model, DEM)数据进行离散化处理,利用MATLAB平台对地形的三维坐标散点进行DEM模型拟合实现Dijkstra算法.

在MATLAB平台的地形图中任取两点,根据地形图的坐标位置,利用最短路径算法,得到其最短距离,算法流程及结果如图1所示.图中:X、Y、Z分别为风电场的长度、宽度、地形高度.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   复杂地形中两点的最短路径计算

Fig.1   Calculation of the shortest path between two points in complex terrain


1.1.2 复杂地形集电线路最小生成树算法实现

本研究利用最小生成树(minimum spanning tree, MST)算法中的Prime算法.将风电场中的风力机坐标位置看作最小生成树中点的集合,每一台风力机间需要连接的线路作为边,将上节三维复杂地形中两点距离的计算数值作为最小生成树边的权值.若具有M个风电机组的风电场,则在一条回路中,可建立M(M-1)/2条带权路径,运用Prime算法得到M-1条路径构成的网络,该网络若总权值最低且连通风电场中的每台风力机即为达到最优.算法优化目标为风电场集电线路的连接长度最短:

L=min $\sum _{t=1}^{M-1}$lt

式中:lt为第t台风力机与其最近位置风力机之间的距离.

1.2 RBF代理模型的集电线路优化

1.2.1 代理模型训练

工程设计中常采用最小生成树算法得到集电线路拓扑优化结果,该方法对拓扑优化结果的计算需多个Dijkstra算法叠加运算来得到最小生成树的权值,以牺牲运算时间为代价得到足够的求解精度,本文采用该种方法生成少量样本以训练代理模型来得到集电线路拓扑优化结果,在保证求解精度的前提下有效减少运算时长.代理模型方法可根据已知的一定数目样本点,通过神经网络训练,得到合适的数学模型给出近似结果,大大减少风电场集电线路的计算时间.RBF神经网络有很强的逼近能力、分类能力和学习速度,其工作原理是通过选择各隐含层神经元的传输函数,把网络来逼近未知函数,对于复杂的非线性函数关系具有较强的拟合能力.而复杂地形风电场的集电线路优化过程为复杂的非线性函数映射问题,因此选择采用RBF代理模型技术,建立地形与风力机选点位置及网络回路构成之间的函数关系.

在多目标优化算法寻优过程中,根据总迭代个体数值按比例区间判断是否达到代理模型训练要求,并在迭代过程中将最小生成树算法精确计算的个体样本数据进行保存记录.由于地形变化难以线性拟合,所以在优化过程中建立两个模型训练点及检测点.若迭代算法整体种群总数量为N,设置检验精度为E,其样本点训练比例区间取值如表1所示,训练点及检测点的判断过程如下.

表1   模型训练的样本点取值

Tab.1  Sample point value of model training

总样本比例区间训练样本数量
0.7N0.85Stot
0.7N~0.8NSave
0.8N~0.85N0.85Stot
0.85N~0.95NSave
0.95N~NSave

新窗口打开| 下载CSV


步骤1 确定完全迭代的总个体数量,记为N,并设置检验精度E,其表达式如下:

$\left.\begin{array}{l}{e}_{ssi}\le 0.05\\ {D}_{NR}\le 0.03\end{array}\right\}$

式中:essi为相对误差;DNR为归一化均方根偏差.

步骤2 初始种群经算子变换迭代产生相应个体,在适应度值计算时,判断算法此时所产生的个体数量,当算法迭代产生的个体数量小于70%N时,使用最小生成树算法计算,并将每个个体的精确计算结果保存.

步骤3 当算法迭代产生的个体数量为总个体数量N的70%~80%时,基于所保存的个体样本即0.7N个精确计算样本训练代理模型,其模型表达式如下:

hj=exp$\left(-\frac{{‖x-{c}_{j}‖}^{2}}{2{b}_{j}^{2}}\right)$, j=1, 2, …, m
yi=$\sum _{j=1}^{m}$wjihj, i=1, 2, …, n

式中:x为输入参数向量,即风力机选点位置坐标;m是隐含层的节点个数;cj为隐含层节点j的中心向量;bj是一个正的标量,表示高斯基函数的宽度;hj为隐含层的激活函数;n是输出节点个数;wji是隐含层节点j输出节点i的输出层权值;yi为输出节点i的神经网络输出,即集电线路拓扑优化结果.然后计算代理模型的预测误差,并比对初始设置的检验精度E,若精度符合则在0.7N ~0.8N个体计算中采用代理模型预测值.

步骤4 当迭代过程产生个体数量为总个体数量N的80%~85%时,再次使用最小生成树算法计算,并将每个个体的精确计算结果保存.

步骤5 当算法迭代产生的个体数量为总个体数量N的85%~95%时,基于前面所保存的精确计算的个体样本,训练代理模型后计算代理模型的预测误差,并比对初始设置的检验精度E,若误差符合则在0.85N~0.95N个体计算中采用代理模型预测值.

步骤6 当算法迭代产生的个体数量为总样本数量N的95%~100%时,再次使用最小生成树算法计算.

通过算法精确计算保存的总样本数量读取为Stot,利用其中0.85Stot个样本点对模型进行训练,此时,样本保存的数量为Save.建立地形与风力机选点位置及网络回路构成之间函数关系的RBF模型,利用0.15Stot个样本点进行模型精度检验,若预测精度符合则在后续多目标算法优化中采用代理模型替代集电线路拓扑优化计算.

1.2.2 代理模型精度检验

采用代理模型辅助计算是将此计算过程抽象为一个拥有输入变量和输出变量的系统,需要判断采用代理模型的合理性,因此本文在代理模型建立后对其进行精度检验.

在算法精确计算保存的总样本中选取比例为15%的样本数量作为模型精度分析的检测点,比较代理模型预测值和集电线路拓扑优化算法精确计算值之间的误差.使用essi和DNR评估误差大小及预测精度:

essi=$\left|\frac{{\hat{a}}_{q}-{a}_{q}}{{a}_{q}}\right|$
DNR=$\frac{1}{\stackrel{-}{a}}\sqrt{\frac{1}{0.15{S}_{tot}}\sum _{q=1}^{0.15{S}_{tot}}({\hat{a}}_{q}-{a}_{q}{)}^{2}}$

式中:${\hat{a}}_{q}$为使用代理模型预测的近似集电线路拓扑优化结果值;aq为集电线路算法优化计算的精确值;下标q为检测点的序号;$\stackrel{-}{a}$为aq的算数平均值.

2 风电场微观选址多目标优化设计

2.1 复杂地形下崎岖度指数计算

由于风力机安装在复杂地形处需排除某些不利的场地,例如平均风速过低、湍流强度过高或地形过于崎岖的区域,本文为限制风力机安装在复杂地形风电场中崎岖度过大的点位,将TRI指数作为约束进行选址优化处理.该指数最早由Riley等[11]提出,其数值可以根据划分的网格高程数据进行计算.给定沿横轴和纵轴方向的栅格尺寸为Δx和Δy,则栅格(xi, yj)处的TRI指数可根据其高程和周围8个栅格的高程值计算为

$\begin{aligned} \alpha_{\mathrm{TRI}}\left(x_{i},\right. & \left.y_{j}\right)=\frac{1}{8}\left[\frac{\left(z\left(x_{i}, y_{j}\right)-z\left(x_{i+1}, y_{j}\right)\right)^{2}}{\Delta x^{2}}+\right. \\ & \frac{\left(z\left(x_{i}, y_{j}\right)-z\left(x_{i-1}, y_{j}\right)\right)^{2}}{\Delta x^{2}}+ \\ & \frac{\left(z\left(x_{i}, y_{j}\right)-z\left(x_{i}, y_{j+1}\right)\right)^{2}}{\Delta y^{2}}+ \\ & \frac{\left(z\left(x_{i}, y_{j}\right)-z\left(x_{i}, y_{j-1}\right)\right)^{2}}{\Delta y^{2}}+ \\ & \frac{\left(z\left(x_{i}, y_{j}\right)-z\left(x_{i+1}, y_{j+1}\right)\right)^{2}}{\Delta x^{2}+\Delta y^{2}}+ \\ & \frac{\left(z\left(x_{i}, y_{j}\right)-z\left(x_{i+1}, y_{j-1}\right)\right)^{2}}{\Delta x^{2}+\Delta y^{2}}+ \\ & \frac{\left(z\left(x_{i}, y_{j}\right)-z\left(x_{i-1}, y_{j+1}\right)\right)^{2}}{\Delta x^{2}+\Delta y^{2}}+ \\ & \left.\frac{\left(z\left(x_{i}, y_{j}\right)-z\left(x_{i-1}, y_{j-1}\right)\right)^{2}}{\Delta x^{2}+\Delta y^{2}}\right]^{\frac{1}{2}} \end{aligned}$

式中:z(xi, yj)为栅格点(xi, yj)处的地形高度.

2.2 多目标离散状态转移算法

目前应用于风电场微观选址的方法大多为基于群智能优化的算法,而状态转移算法是一种基于状态转移的新型随机优化算法,借助状态空间的概念,离散状态转移算法(discrete state transition algorithm, DSTA)生成候选解的统一形式[12]定义为

$\left.\begin{array}{l}{x}_{k+1}={A}_{k}{x}_{k}+{B}_{k}{u}_{k}\\ {y}_{k+1}=f\left({x}_{k+1}\right)\end{array}\right\}$

式中:xk∈Rn表示当前状态;Ak和Bk为状态转移矩阵;uk∈Rn为控制变量;f(·)为评价函数.

多目标离散状态转移算法设计了交换、平移、对称和替换算子4种典型离散状态变换算子[13].该算法已经在车间调度问题[14]、员工指派问题[15]等典型离散优化问题得到验证.

(1) 交换变换算子.

xk+1=${A}_{k}^{swap}$maxk

式中:${A}_{k}^{swap}$为交换变换矩阵;ma为交换因子,控制交换元素的个数.

(2) 移动变换算子.

xk+1=${A}_{k}^{shift}$mbxk

式中:${A}_{k}^{shift}$为移动变换矩阵;mb为移动因子,控制移动元素的个数.

(3) 对称变换算子.

xk+1=${A}_{k}^{sym}$mcxk

式中:${A}_{k}^{sym}$为对称变换矩阵;mc为对称因子,控制翻转变换元素的个数.

(4) 替代变换算子.

xk+1=${A}_{k}^{sub}$mdxk

式中:${A}_{k}^{sub}$为替代变换矩阵;md为替代因子,控制候选解中替代变换元素的个数.

为得到风电场微观选址问题的Pareto前沿,其Pareto解集的候选解由4种上述定义的状态变换算子生成,然后引入更新高效非支配排序策略及拥挤距离多样性维护策略[16-18].

2.3 复杂地形风电场微观选址流程

对于复杂地形风电场微观选址多目标优化问题描述如下:

$\left.\begin{array}{l}max {A}_{EP}\\ min L\\ 0\le {x}_{i}\le {l}_{1}, 0\le {y}_{i}\le {l}_{2}\\ 　i=1, 2, \dots, {N}_{wt}\\ ({x}_{i}-{x}_{j}{)}^{2}+({y}_{i}-{y}_{j}{)}^{2}\ge 64{R}_{r}^{2}\\ 　i=1, 2, \dots, {N}_{wt}, \\ 　j=1, 2, \dots, {N}_{wt}, i\ne j\\ {\alpha }_{TRI}^{max}-{\alpha }_{TRI}({x}_{i}, {y}_{i})\ge 0\\ 　i=1, 2, \dots, {N}_{wt}\end{array}\right\}$

式中:AEP为风电场的年发电量;L为集电线路网络路径总长度,由式(1)得出;(xi, yi)和(xj, yj)为风力机的坐标;l1为风电场的长;l2为风电场的宽;Nwt为风力机的数量;Rr为风力机半径;αTRI(xi, yi)为风力机坐标点(xi, yi)的崎岖度指数;${\alpha }_{TRI}^{max}$为设定的崎岖度指数最大值.

复杂地形风电场微观选址流程步骤如下.

步骤1 根据地形高程与坐标数据计算每个栅格点的TRI指数,使用二进制编码方式对位置坐标进行编码,将TRI过大的点剔除后生成初始排布.

对于离散状态转移算法,初始解的优质性对优化结果的表现具有一定的影响,本文通过初始解的约束,在随机生成初始布局后,剔除崎岖度较差的点后将崎岖度较小的点进行填补,优化初始布局点的构成.对于栅格点位置,采用式(7)求出TRI值,其约束如式(13)所示.

步骤2 初始化种群,使用上述定义的状态变换算子生成候选解.

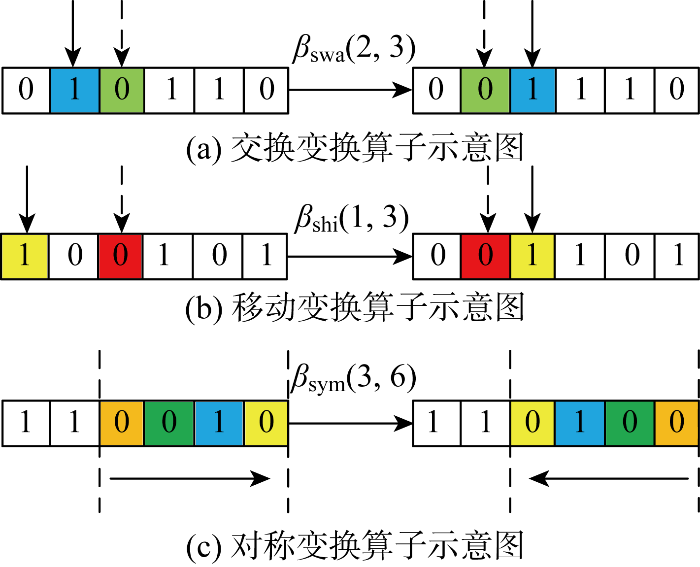
针对风电场微观选址优化问题,将风电场整体区域依据风力机间最小距离作为网格长度进行划分,对候选解风力机位置坐标采用作为二进制排布的编码方式,将设置风力机的坐标点编码为1,未设置风力机的坐标点编码为0,通过离散状态转移算法的3种算子,将风力机移动到新的位置,形成新的风力机排布方案,各种算子的示意图如图2所示.图中:βswa(2, 3)表示交换2与3位置内变量;βshi(1, 3)表示移动1至3位置内变量;βsym(3, 6)表示对称3至6位置内变量.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   离散状态转移算法算子示意图

Fig.2   Schematic diagram of DSTA operator


步骤3 结合地形数据,考虑复杂地形下风力机间的尾流效应,计算3种算子变换下产生的风电场排布方案中的年发电量数值及集电线路网络路径总长度,并保存目标函数的计算值及其对应的排布方案.

在实际风电场中,下游风力机可能会处于上游多个风力机的尾流区域,因此Nwt台风力机产生的叠加尾流对下游风力机的风速损失可以表示为

vλ,0=$\sum _{\eta =1}^{{N}_{wt}}\left(1-\frac{{v}_{\eta,\lambda }}{{v}_{r}}\right)$

式中:vλ,0为第λ台下游风力机受Nwt台上游风力机影响的总风速损失值;vη,λ为给定风力机η的尾流区域内风速,由引入地形高度计算的Jensen尾流模型[19-20]得到;vr是入流风速.

发电功率一般通过概率密度离散法计算[21],本文将风向划分为16个方向,计算Nwt台风力机的年发电量功率为

g(θ,v0)=$\frac{k\left(\theta \right)}{c\left(\theta \right)}{\left(\frac{{v}_{0}}{c\left(\theta \right)}\right)}^{k\left(\theta \right)-1}$×exp$\left[-{\left(\frac{{v}_{0}}{c\left(\theta \right)}\right)}^{k\left(\theta \right)}\right]$
AEP=8 760$\sum _{t=1}^{{N}_{wt}}\sum _{f=1}^{16}$w(θf,t)×${\int }_{{u}_{cut-in}}^{{u}_{cut-out}} $g(θf,t, v0)p(u)du

式中:g(θ,v0)为风向扇区θ的威布尔分布函数;v0为风向扇区θ内的自由风速;c(θ)、k(θ)为风向扇区θ内的威布尔参数;g(θf,t, v0)为f风向下第t台风力机的威布尔分布函数;w(θf,t)为f风向下第t台风力机的风向频率;ucut-in为风力机切入风速;ucut-out为风力机切出风速;p(u)为风力机功率曲线拟合函数.

集电线路网络路径总长度L由式(1)得出.在迭代过程中对年发电量目标的计算进行历史采样保留及相应适应度值记录,目标函数计算时将每种采样与历史采样进行比对,若相同则直接调用其记录的适应度数值.对集电线路网络路径总长度目标的计算则进行采样数量判断,若达到RBF代理模型的计算区间则在该种群样本空间内选取样本点,对模型进行训练拟合及精度检验,若符合精度则在后续迭代计算中采用该代理模型预测值.

步骤4 根据高效非支配排序策略及拥挤距离多样性维护策略更新Pareto最优解集.

步骤5 判断停止条件,符合条件,算法结束;否则,跳到步骤6.

步骤6 在已知最优风力机排布方案上更新风力机位置.

步骤7 对更新位置的风力机进行崎岖度约束修正,返回步骤3.

在风力机位置坐标变换下有一定概率产生包含崎岖度指数较高的候选解,在迭代的过程中,对被选中的坐标点进行判断,若包含崎岖度指数较高的点,则对产生的候选解进行修正,按照崎岖度指数大小进行排布,剔除崎岖度指数大的位置,再将崎岖度指数小的备选点填充进来.

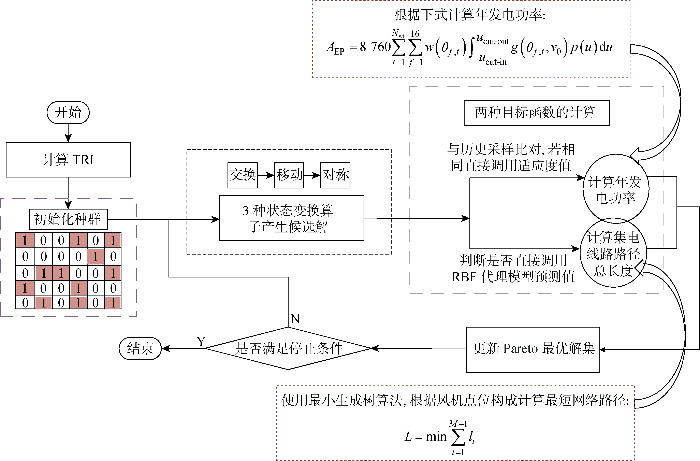
根据上述步骤,基于改进离散状态转移算法风电场微观选址的流程图如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   风电场微观选址DMOSTA流程图

Fig.3   Flow chart of DMOSTA for micro-siting of wind farms


3 计算实例

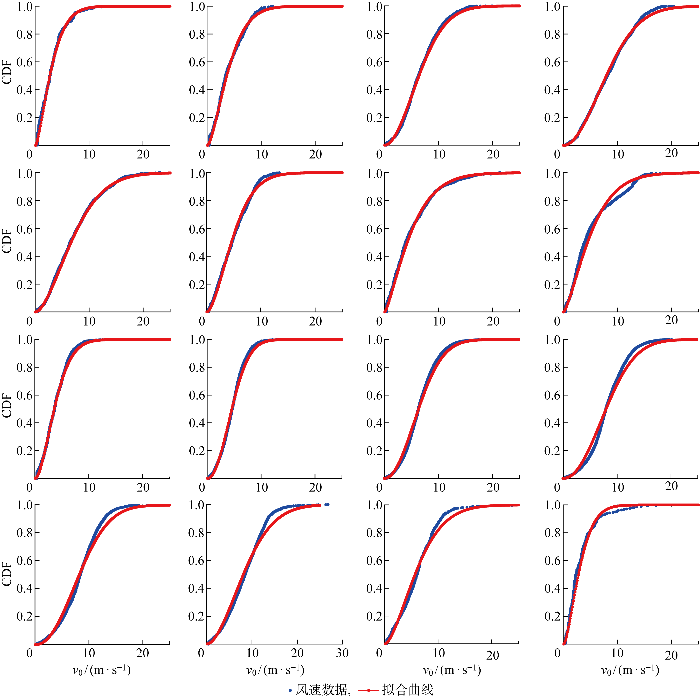
3.1 风电场描述及分析

本文以中国新疆某复杂地形风电场微观选址为例,在该风电场范围内布置20台5 MW的风力机,并以升压站设定在区域中心为前提进行集电系统优化.风电场的地形图如图4所示.风电场东西长约57 km,南北宽约37 km,场址区域西北至东南走向地势较高,而东北部和西南部地势略低,北部区域地形有一定起伏,海拔介于815~1 050 m 之间,场区地貌主要为戈壁滩.该风电场的风向玫瑰图如图5所示.图中:vw为风速;0%~25%为风向频率;风向分为16个扇区.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   风电场地形图

Fig.4   Site map of wind farm


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   风向玫瑰图

Fig.5   Rose diagram of wind direction


该风电场16个风向扇区的双参数威布尔分布拟合结果如图6所示.图中:CDF表示累积分布函数,是一个无量纲的量.其风向的威布尔拟合参数数值如表2所示.风力机选型为WTG1型风力发电机组,表3为采用的风力机参数,根据工程建设规定及该机型半径数值可得到风力机间最小距离为764 m,并将该数值作为网格长度大小对风电场进行划分,划分后的风电场区域共有 3 800 个可供选址的网格.选用机型满足国家电网公司风电场接入电网技术规定,具有低电压穿越能力和高电压穿越能力.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   风速威布尔拟合

Fig.6   Weibull fitting for wind speed


表2   16风向下威布尔参数拟合

Tab.2  Weibull parameter fitting for 16 wind directions

θ/(°)k(θ)c(θ)θ/(°)k(θ)c(θ)
348.75~11.251.408 03.443 4168.75~191.251.680 84.373 5
11.25~33.751.487 74.565 9191.25~213.752.068 95.402 1
33.75~56.251.889 47.708 3213.75~236.252.075 97.570 5
56.25~78.751.938 79.582 5236.25~258.752.148 19.534 0
78.75~101.251.650 78.176 7258.75~281.252.156 29.634 1
101.25~123.751.633 65.648 9281.25~303.751.783 79.853 7
123.75~146.251.296 15.513 1303.75~326.251.571 97.066 4
146.25~168.751.360 95.789 3326.25~348.751.497 23.481 6

新窗口打开| 下载CSV


表3   风力机参数

Tab.3  Parameters of wind turbine

参数取值
轮毂高度/m110
叶轮直径/m191
切入风速/(m·s-1)2.5
切出风速/(m·s-1)20
额定风速/(m·s-1)8.9

新窗口打开| 下载CSV


3.2 参数设置

通过该风电场实例比较DMOSTA与DSTA的计算结果.在该实例中,针对DSTA,取采样值Se为10,最大迭代次数Mxit为50.对于DMOSTA,取采样值S'e为5,最大迭代次数Gner为20,选中解的数量T为5,种群数量N为75.两种算法的参数设置如表4所示.根据地形起伏程度及风力机安置效果,经过多次实验将TRI指数约束设置为0.01,并将风电场边界网格点的TRI指数设置为1,以避免风力机安置在风电场边界位置,根据式(7)计算得到崎岖度过大的点位,如图7所示.

表4   DMOSTA和DSTA的参数设置

Tab.4  Parameter settings of DMOSTA and DSTA

DSTADMOSTA
Se=10S'e=5
Mxit=50Gner=20
ma=1 000T=5
mb=1N=75
mc=1ma=1 000
mb=1
mc=1

新窗口打开| 下载CSV


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   风电场崎岖度较大点位

Fig.7   High-ruggedness locations in wind farm


3.3 结果分析

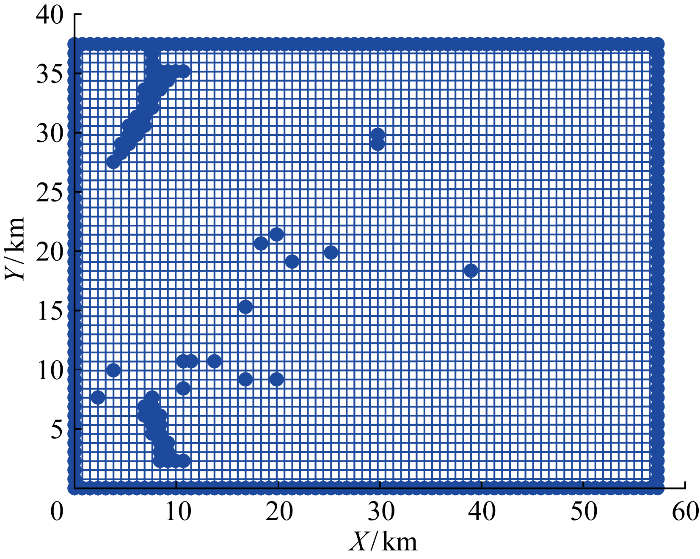
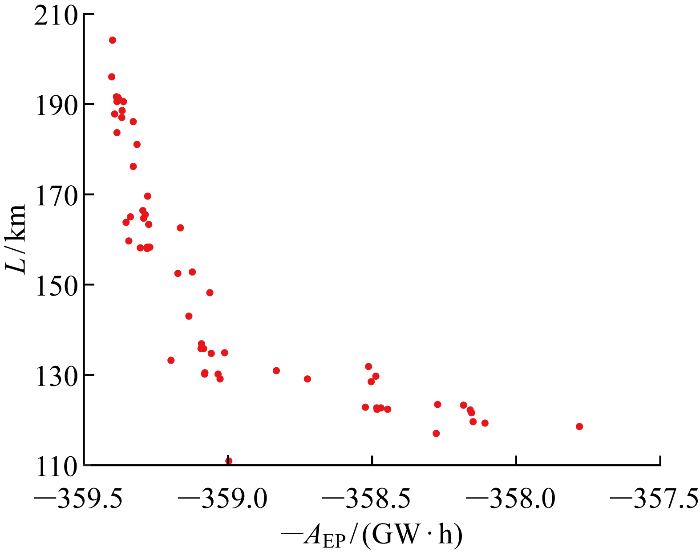
基于不同参数设置以及迭代次数的试验,在该57 km×37 km的风电场内进行风力机的自由布置,通过机位布置实现年发电量最大化的同时在设定区域内进行集电系统优化.相关性分析结果显示,在复杂地形风电场微观选址设计中,年发电量最大化和集电系统路径最小化呈现相反的优化方向,以年发电量最大为目标的微观选址使风力机尽可能地分散分布以减少尾流效应,其扩散式分布对后续集电系统拓扑优化环节将产生较大影响,增加电缆的铺设长度,因此不能同时获得最大年发电量和最小电缆铺设长度.Pareto最优化方法可以处理多个相悖目标变量之间的优化问题.利用DMOSTA计算出Pareto最优解集,如图8所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   风电场微观选址的Pareto前沿

Fig.8   Pareto frontier diagram of micro-siting of wind farms


Pareto前沿由一系列“最优解点”构成,不存在目标变量均优于“最优解点”的点.其原理是当一个向量的目标函数中没有一个值大于且至少有一个值小于另一个向量的目标函数值,则称该向量支配另一个向量.在图6所示的风资源状况下,通过代理模型辅助计算的DMOSTA可得到10个备选方案,其选择方式是将最优解集以其中一个目标函数值进行降序排序,并划分为10个区间,在每个区间内选择1个备选方案,备选方案各子目标的函数值如表5所示.

表5   备选方案各子目标函数值

Tab.5  Sub-objective function values of alternative solutions

方案AEP/(MW·h)L/m
01359 385.69183 673.16
02359 403.80196 050.94
03359 295.61166 408.48
04358 277.44117 050.69
05359 174.25152 501.29
06358 482.79122 395.84
07359 093.88135 843.85
08358 503.18128 507.61
09359 279.34158 308.29
10359 316.02181 074.42

新窗口打开| 下载CSV


首先对各目标函数值进行归一化处理.年发电量归一化公式为

f1=1-$\frac{{f}_{max}-{f}_{0}}{{f}_{max}-{f}_{min}}$

式中:fmax为对应列表中最大值;fmin为对应列表中最小值;f0为对应列表中任意值.

集电线路总长度归一化公式为

f2=$\frac{{f}_{max}-{f}_{0}}{{f}_{max}-{f}_{min}}$

经过处理后,目标函数值均被处理为0~1之间的评价值,且尾流折减越多、电缆投资越大、拓扑网络风险越高,其评价值越小,归一化后的评价值如表6所示.表中:F为综合评价值.

表6   归一化后的备选方案各子目标函数值

Tab.6  Normalized sub-objective function values of alternative solutions

方案f1f2F
010.980.160.816
021.000.000.800
030.900.380.796
040.001.000.200
050.800.550.750
060.180.930.330
070.720.760.728
080.200.860.332
090.890.480.808
100.920.190.774

新窗口打开| 下载CSV


将归一化后的各子目标评价值与设定的权重系数相乘后求和,得到F:

F=f1W1+f2W2

式中:根据专家经验分析及投资占比评估,评价值的权重系数W1、W2分别为0.8、0.2.

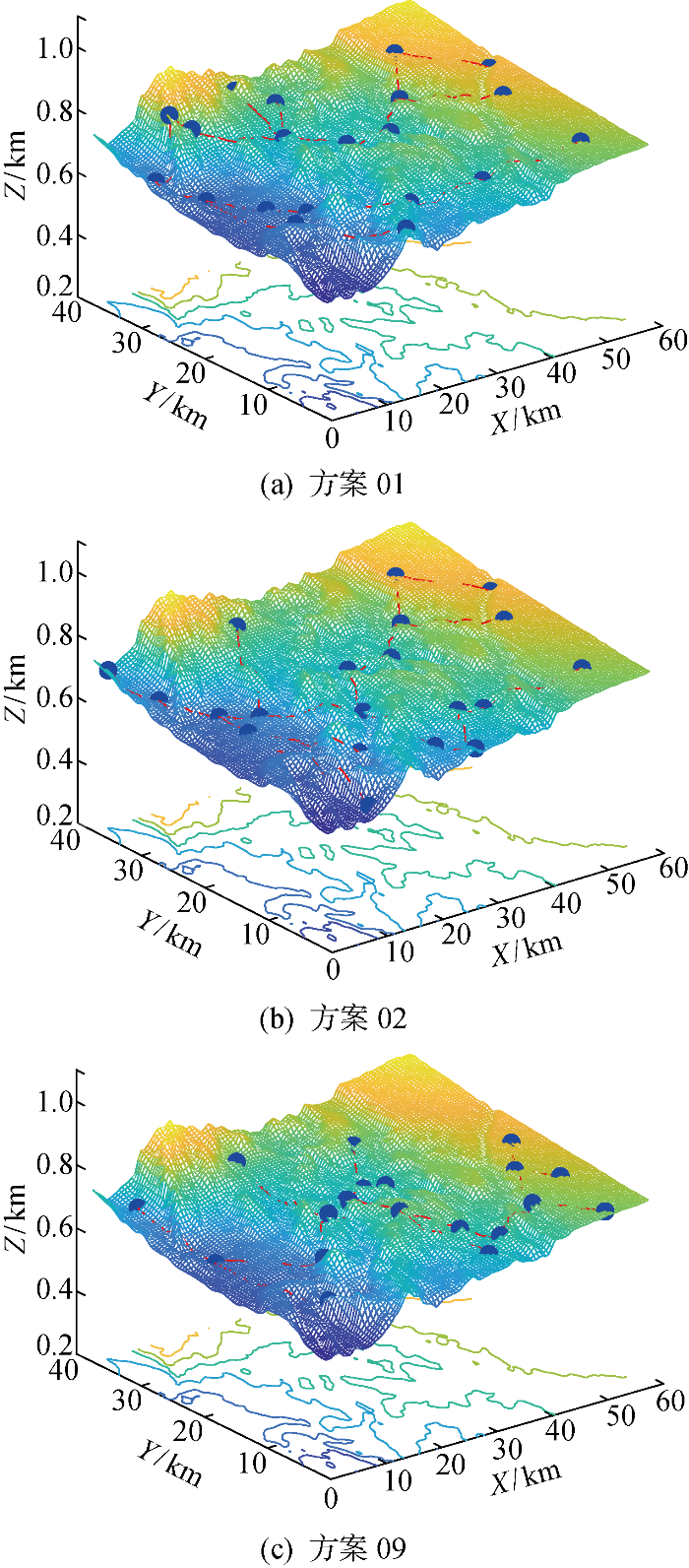
由表6可得,方案01、方案02及方案09的综合评价值为0.816、0.800、0.808,在10种布局方案中相对最高,其中方案01与方案02的风力机排布及电缆铺设相近.图9为DMOSTA布局结果,其中图9(a)和9(b)分别为DMOSTA方案01、方案02中风力机的位置排布以及电缆铺设.方案09的布局结果显示其尾流折减相对较大,发电量较小,风力机明显较为集中布置,但其电缆总长度最短,其风力机位置和集电拓扑结构如图9(c)所示.3种方案中,方案01在该权重系数选取下综合评分最高,说明其较符合该综合评价的评价标准.子目标函数评价值的权重系数可随电缆投资占比、风力发电的上网电价等因素重新设定,备选方案的评价值及评价指标也会产生变化,通过该算法得到的最优方案也会随之更新.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   DMOSTA布局结果

Fig.9   DMOSTA layout results


为验证DMOSTA获得解的最优性,在同一地形条件和目标函数背景下,将该算法与DSTA结果进行比较.为通过一定次数的迭代试验来分析验证DSTA的收敛性与稳定性,选择迭代次数为50,其适应度值变化如图10所示,DSTA在迭代前期已达到相对稳定的优化结果,其风力机布局结果如图11所示.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   DSTA适应度值变化

Fig.10   Changes in fitness value of DSTA


图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   DSTA布局结果

Fig.11   DSTA layout results


4种排布方式的年发电量如表7所示,DSTA优化结果的年发电量比DMOSTA方案09高出47.49 MW·h,但比DMOSTA方案01及方案02分别降低了58.86和76.97 MW·h,DMOSTA在年发电量优化结果上与DSTA单目标优化结果之间的相差很小,说明优化设计结果的稳定性较好.

表7   风力机布局方案对比

Tab.7  Comparison of fan layout solutions

风力机排布方法AEP/(MW·h)L/m
DMOSTA方案01359 385.69183 673.16
DMOSTA方案02359 403.80196 050.94
DMOSTA方案09359 279.34158 308.29
DSTA359 326.83215 762.18

新窗口打开| 下载CSV


为对比验证DMOSTA在集电线路总长度结果上的优越性,根据DSTA得到的风力机布局位置,采用最小生成树算法进行集电线路铺设路径长度计算,其计算结果见表7.由该表可知,在相似发电量的情况下,优化方案01可以使集电线路铺设总长度降低14.87%.DMOSTA在优化年发电量的同时实现集电线路拓扑结构优化,为工程实际提供更多不同考虑因素下的选址方案.

4 结论

针对复杂地形风电场微观选址,引入TRI约束处理以排除某些地形过于崎岖的场地,从而满足实际工程应用中风力机安装对某些场地变量的约束,以及在多目标优化实现中加入代理模型有效解决迭代过程中复杂计算耗时长的问题.基于DMOSTA的优化策略具有实际工程应用价值,该算法可实现多风向下风电场风力机布局优化,且优化结果较好,并基于权重系数的选取可提供更多符合工程要求的微观选址方案.

(1) 本文为限制风力机安装在复杂地形风电场中崎岖度过大的点位,将TRI指数作为约束进行选址优化处理,将地面平整度进行数值量化,解决地面平整度对风力机安置的影响,从而满足实际工程应用中风力机安装对某些场地变量的要求.

(2) 针对复杂地形风电场微观选址多目标优化计算量大、耗时长问题,构建三维地形集电系统拓扑优化代理模型进行辅助计算,检验代理模型的预测精度,替代集电系统拓扑优化的复杂计算过程.本文采用的代理模型方法可有效减少计算时长,提升计算效率.

(3) 仿真显示,基于DMOSTA解决此类问题的优化设计结果稳定性较好,且在优化年发电量的同时,实现集电系统拓扑结构优化,为工程实际提供更多考虑不同因素的选址方案.

实例证明该方法在复杂地形风电场微观选址方面具有一定的工程应用性,但是对复杂地形风电场的建设需考虑因素较多,其优化方案也会随之受到影响,其综合评价值权重系数的选取仍待进一步探究.

参考文献

ANTONINI E G A, ROMERO D A, AMON C H.

Optimal design of wind farms in complex terrains using computational fluid dynamics and adjoint methods

[J]. Applied Energy, 2020, 261: 114426.

[本文引用: 1]

YANG K, KWAK G, CHO K, et al.

Wind farm layout optimization for wake effect uniformity

[J]. Energy, 2019, 183: 983-995.

DOI:10.1016/j.energy.2019.07.019      [本文引用: 1]

The basic objective of wind farm layout optimization is to maximize the energy produced by wind farms. However, when wind turbines are arranged in a limited space like an onshore wind farm, specific wind turbines may have greater wake exposure than other wind turbines. This phenomenon can be conspicuous in a mixed layout that consists of turbines with different capacities and hub heights. In this study, we developed and tested a new objective function to increase wind farm energy output while making the wake loss of each wind turbine uniform. The purpose of this function is to adjust the wake effects of all of the wind turbines on a wind farm to similar levels, thereby promoting the operational stability of all of the wind turbines. Layout optimization was performed using a simulated annealing algorithm, which is a heuristic method, with actual wind conditions for an existing wind farm in operation. Then, the results obtained using the proposed method were compared with those yielded by layout optimization for energy maximization. The layout generated using the proposed objective function had lower energy output than that obtained by energy maximization. However, this difference was small and the proposed method prevented wake effect concentration on specific turbines by making the wake effect levels uniform. (C) 2019 Elsevier Ltd.

刘永前, 邵振州, 颜灵伟, 等.

基于改进二进制萤火虫算法的风电场微观选址优化研究

[J]. 可再生能源, 2019, 37(1): 112-118.

[本文引用: 1]

LIU Yongqian, SHAO Zhenzhou, YAN Lingwei, et al.

Optimization research of wind farm micro-sitting based on improved binary firefly algorithm

[J]. Renewable Energy Resources, 2019, 37(1): 112-118.

[本文引用: 1]

王洁, 许昌, 韩星星, 等.

基于风力机尾流排斥的平坦地形风电场微观选址优化

[J]. 电力系统自动化, 2020, 44(15): 62-69.

[本文引用: 1]

WANG Jie, XU Chang, HAN Xingxing, et al.

Micro-siting optimization of wind farm in flat terrain based on wind turbine wake repellency

[J]. Automation of Electric Power Systems, 2020, 44(15): 62-69.

[本文引用: 1]

PÉREZ-ARACIL J, CASILLAS-PÉREZ D, JIMÉNEZ-FERNÁNDEZ S, et al.

A versatile multi-method ensemble for wind farm layout optimization

[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2022, 225: 104991.

[本文引用: 1]

FENG J, SHEN W Z.

Solving the wind farm layout optimization problem using random search algorithm

[J]. Renewable Energy, 2015, 78: 182-192.

[本文引用: 1]

FENG J, SHEN W, LI Y.

An optimization framework for wind farm design in complex terrain

[J]. Applied Sciences, 2018, 8(11): 2053.

[本文引用: 1]

HU W, YANG Q, CHEN H P, et al.

A novel approach for wind farm micro-siting in complex terrain based on an improved genetic algorithm

[J]. Energy, 2022, 251: 123970.

[本文引用: 1]

唐程辉, 张凡, 张宁, 等.

基于风电场总功率条件分布的电力系统经济调度二次规划方法

[J]. 电工技术学报, 2019, 34(10): 2069-2078.

[本文引用: 1]

TANG Chenghui, ZHANG Fan, ZHANG Ning, et al.

Quadratic programming for power system economic dispatch based on the conditional probability distribution of wind farms sum power

[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2069-2078.

[本文引用: 1]

盛四清, 范林涛, 李兴, 等.

基于帕累托最优的配电网多目标规划

[J]. 电力系统自动化, 2014, 38(15): 51-57.

[本文引用: 1]

SHENG Siqing, FAN Lintao, LI Xing, et al.

Multi-objective planning of distribution network based on Pareto optimality

[J]. Automation of Electric Power Systems, 2014, 38(15): 51-57.

[本文引用: 1]

RILEY S J, DEGLORIA S D, ELLIOT R.

Index that quantifies topographic heterogeneity

[J]. Intermountain Journal of Sciences, 1999, 5(1-4): 23-27.

[本文引用: 1]

董颖超, 张宏立, 王聪.

带有策略自适应的状态转移算法

[J]. 控制与决策, 2022, 37(3): 574-582.

[本文引用: 1]

DONG Yingchao, ZHANG Hongli, WANG Cong.

State transition algorithm with strategy adaptation

[J]. Control and Decision, 2022, 37(3): 574-582.

[本文引用: 1]

周晓君, 阳春华, 桂卫华.

状态转移算法原理与应用

[J]. 自动化学报, 2020, 46(11): 2260-2274.

[本文引用: 1]

ZHOU Xiaojun, YANG Chunhua, GUI Weihua.

The principle of state transition algorithm and its applications

[J]. Acta Automatica Sinica, 2020, 46(11): 2260-2274.

[本文引用: 1]

余佳英, 张宏立, 董颖超.

基于离散状态转移算法的无等待流水车间调度研究

[J]. 系统仿真学报, 2023, 35(5): 1034-1045.

DOI:10.16182/j.issn1004731x.joss.22-0048      [本文引用: 1]

针对制造行业中广泛存在的无等待流水车间调度问题，提出一种改进的离散状态转移算法进行求解。基于流水车间调度问题的特性，设计工件的编码方式，采用基于工件加工时间标准差为优先级的NEH(Nawaz-Enscore-Ham)方法构造初始解，设计基于插入和交换的多邻域组合搜索策略以提高初始解的质量；提出一种基于群状态的离散状态转移算法，并利用带二次状态转移操作的三种离散操作算子扩大算法的搜索范围；为进一步提高离散状态转移算法的求解性能，设计了基于莱维飞行的破坏重构局部搜索方法，对全局搜索发现的优质解进行细致搜索。仿真实验表明，改进的离散状态转移算法能够有效求解无等待流水车间调度问题。

YU Jiaying, ZHANG Hongli, DONG Yingchao, et al.

Research on no-wait flow shop scheduling based on discrete state transition algorithm

[J]. Journal of System Simulation, 2023, 35(5): 1034-1045.

DOI:10.16182/j.issn1004731x.joss.22-0048      [本文引用: 1]

In view of the no-wait flow shop problem (NWFSP) widely existing in the manufacturing industry, an improved discrete state transition algorithm (IDSTA) is proposed to solve the problem. The coding mode of the workpiece is designed based on the characteristics of the flow shop scheduling problem (FSSP). The initial solution is constructed by the Nawaz-Enscore-Ham (NEH) method with the standard deviation of the processing time of the workpiece as the priority, and a multi-neighborhood combinatorial search strategy based on insertion and exchange is designed to improve the quality of the initial solution. A discrete state transition algorithm (DSTA) based on group state is proposed, and the search range of the algorithm is expanded by using three discrete operators with quadratic state transition operations. In order to further improve the solution performance of DSTA, a local search method based on Levy flight for damage reconstruction is designed, and the high-quality solution detected by global search is searched carefully. The simulation experiments show that IDSTA can effectively solve the NWFSP.

董天雪, 阳春华, 周晓君, 等.

一种求解企业员工指派问题的离散状态转移算法

[J]. 控制理论与应用, 2016, 33(10): 1378-1388.

[本文引用: 1]

DONG Tianxue, YANG Chunhua, ZHOU Xiaojun, et al.

A novel discrete state transition algorithm for staff assignment problem

[J]. Control Theory & Applications, 2016, 33(10): 1378-1388.

[本文引用: 1]

LI W, HAN J, LI Y, et al.

Optimal sensor placement method for wastewater treatment plants based on discrete multi-objective state transition algorithm

[J]. Journal of Environmental Management, 2022, 307: 114491.

[本文引用: 1]

HAO J, YANG X, WANG C, et al.

An improved NSGA-II algorithm based on adaptive weighting and searching strategy

[J]. Applied Sciences, 2022, 12(22): 11573.

HAN J, YANG C, LIM C C, et al.

Power scheduling optimization under single-valued neutrosophic uncertainty

[J]. Neurocomputing, 2020, 382: 12-20.

[本文引用: 1]

WEN Y, SONG M, WANG J.

Wind farm layout optimization with uncertain wind condition

[J]. Energy Conversion and Management, 2022, 256: 115347.

[本文引用: 1]

REDDY S R.

Wind farm layout optimization (Wind FLO): An advanced framework for fast wind farm analysis and optimization

[J]. Applied energy, 2020, 269: 115090.

[本文引用: 1]

王凯, 许昌, 韩星星, 等.

基于边界适应和风电场间影响的海上风电场微观选址优化研究

[J]. 可再生能源, 2022, 40(4): 481-486.

[本文引用: 1]

WANG Kai, XU Chang, HAN Xingxing, et al.

Micro-siting optimization of offshore wind farms based on boundary adaptation and inter-wind farm impacts

[J]. Renewable Energy Resources, 2022, 40(4): 481-486.

[本文引用: 1]

/

〈 〉