上海交通大学学报

上海交通大学学报, 2025, 59(8): 1192-1202 doi: 10.16183/j.cnki.jsjtu.2024.272

机械与动力工程

Fe-Mn合金及其螺旋弹簧的阻尼特性

涂田刚1,2, 杨蔚涛2, 杨旗,2, 徐斌1,2

1.中国机械科学研究总院, 北京 100044

2.上海材料研究所有限公司 上海市工程材料应用与评价重点实验室, 上海 200437

Damping Characteristics of Fe-Mn Alloy and Its Helical Spring

TU Tiangang1,2, YANG Weitao2, YANG Qi,2, XU Bin1,2

1. China Academy of Machinery Science and Technology, Beijing 100044, China

2. Shanghai Key Laboratory of Engineering Materials Application and Evaluation, Shanghai Research Institute of Materials Co., Ltd., Shanghai 200437, China

通讯作者: 杨 旗,正高级工程师,博士生副导师,电话(Tel.):021-65557050;E-mail:m1866733474@163.com.

责任编辑: 王一凡

收稿日期: 2024-07-8   修回日期: 2024-09-9   接受日期: 2024-10-14  

基金资助: 上海市中央引导地方科技发展资金(三期)(YDZX20233100002004)

Received: 2024-07-8   Revised: 2024-09-9   Accepted: 2024-10-14  

作者简介 About authors

涂田刚(1989—),博士生,从事阻尼材料及其应用技术研究.

摘要

为改变传统螺旋弹簧的无阻尼现状,采用Fe-Mn合金研制了一种具有良好阻尼特性的螺旋弹簧.首先,研究了用于制作螺旋弹簧的Fe-Mn合金材料的最佳工艺参数;然后,制备了Fe-Mn合金螺旋弹簧,并采用优化的工艺参数对其进行处理,以实现高阻尼特性;最后,通过螺旋弹簧的功能原理和解析模型,进一步分析了Fe-Mn合金螺旋弹簧的阻尼性能.结果表明,在相同外部激励条件下,与65Mn螺旋弹簧相比,Fe-Mn合金螺旋弹簧表现出显著的耗能效果.在特定的加载位移下,其损耗因子随位移的增加呈非线性指数增长,而等效刚度随位移的增加呈线性下降,表现出明显的软化特性.特别地,当Fe-Mn合金螺旋弹簧的等效应变幅小于0.3%时,可以利用其扭转应变能预测耗能特性,为弹簧设计提供理论依据.该研究为减振与隔振产品的开发和应用提供了新的思路.

关键词： Fe-Mn合金; 阻尼性能; Fe-Mn合金螺旋弹簧; 耗能特性

Abstract

In order to change the undamped state of traditional helical spring, a helical spring with improved damping characteristics is developed by using Fe-Mn alloy. First, the optimal process parameters for Fe-Mn alloy material in manufacturing helical springs is investigated. Then, Fe-Mn alloy helical springs are fabricated and treated with optimized parameters to achieve high damping properties. Finally, the damping properties of Fe-Mn alloy helical spring are studied through the functional principle and analytical model of the helical spring. The results show that the Fe-Mn alloy helical spring exhibits a significant energy dissipation effect compared with the 65Mn helical spring under identical external excitation conditions. Within a specific loading displacement range, the loss factor of Fe-Mn alloy helical spring increases exponentially with the increase of displacement, while its equivalent stiffness decreases linearly, exhibiting pronounced softening characteristics. Specifically, when the equivalent strain amplitude of Fe-Mn alloy helical spring is less than 0.3%, its energy dissipation can be predicted using its torsional strain energy, providing a theoretical basis for spring design. This study provides a new direction for the development and application of vibration isolation products.

Keywords： Fe-Mn alloy; damping property; Fe-Mn alloy helical spring; energy dissipation characteristics

PDF (11755KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

涂田刚, 杨蔚涛, 杨旗, 徐斌. Fe-Mn合金及其螺旋弹簧的阻尼特性[J]. 上海交通大学学报, 2025, 59(8): 1192-1202 doi:10.16183/j.cnki.jsjtu.2024.272

TU Tiangang, YANG Weitao, YANG Qi, XU Bin. Damping Characteristics of Fe-Mn Alloy and Its Helical Spring[J]. Journal of Shanghai Jiaotong University, 2025, 59(8): 1192-1202 doi:10.16183/j.cnki.jsjtu.2024.272

螺旋弹簧是减振降噪领域应用最广泛的元件之一[1].传统的螺旋弹簧一般采用弹簧钢材料,如60Si2Mn、65Mn、60Si2CrV等,其微观组织主要由α’回火马氏体组成,具有优异的弹性性能.然而,它们的阻尼性能非常有限,通常需要额外的阻尼装置进行补偿.汪志昊等[2]研制了一种将电涡流阻尼与螺旋弹簧相结合的电涡流调谐质量阻尼器,用于抑制大跨度桥梁的振动.尹学军等[3]引进并研制了一种将黏滞阻尼与螺旋弹簧相结合的阻尼弹簧隔振器,用于核电汽轮发电机组的振动控制.蔡龙奇等[4]提出了一种将筒式黏滞阻尼器与螺旋弹簧相结合的阻尼弹簧减振支座,用于大悬挑结构的抗风减振.由此可知,在减隔振控制领域,隔振产品需要具备一定刚度和阻尼性能来抑制结构共振的幅值.由于附加阻尼装置的使用,不仅增加了产品的体积和成本,而且在一些安装空间有限、环境温度恶劣的场景中也难以满足应用需求.所以,本文探索开发一种同时提供刚度和阻尼的螺旋弹簧,具有重要的应用价值和科学意义.

阻尼合金是一种利用材料自身的内耗机制将外界振动能量转化为热能进行耗散的新型金属功能材料[5].基于阻尼合金的耗能特征,采用其制备弹簧作为减隔振单元逐渐成为研究的热点.王怡鑫等[6]采用锰铜阻尼合金制成的矩形截面螺旋弹簧设计了一种六自由度弹簧隔振系统,通过仿真分析与试验测试验证了其隔振效果,有效地隔离了反作用轮微振动对卫星成像质量的影响.朱锐等[7]采用锰铜阻尼合金制成的碟形弹簧设计了一种锰铜阻尼合金碟簧缓冲器,通过仿真分析与试验测试验证了其隔振效果.结果表明,锰铜阻尼合金碟簧缓冲器相对原弹簧缓冲器具有更好的隔振效果.Wang等[8]采用形状记忆合金(SMA)制成的环形弹簧设计了一种SMA环形弹簧的自复位装置,通过试验验证了该自复位装置能有效降低梁柱节点的损伤.结果表明,SMA环形弹簧的自复位装置具有稳定的旗形滞回耗能特性.辛泰阿等[9]采用Fe-Mn阻尼合金丝材绕制了一种Fe-Mn金属橡胶,分析了不同热处理状态对Fe-Mn金属橡胶力学性能的影响,并与304不锈钢金属橡胶进行了对比研究.结果表明,固溶热处理可以牺牲部分阻尼性能来提高其力学性能;Fe-Mn金属橡胶具有金属丝干摩擦耗能和材料微观耗能的双重效应,其阻尼性能更优于304不锈钢金属橡胶.这些研究表明,阻尼合金弹簧在实际工程中具有显著的耗能效果和广泛的应用前景.

Mn-Cu基阻尼合金因其优异的阻尼性能在某领域得到了应用,但其存在一些不足之处,如强度低、塑性差、成本高,Mn-Cu的抗拉强度和屈服强度比Fe-Mn低约一半,价格是Fe-Mn的4倍,这限制了其广泛应用.此外,形状记忆合金,如Mn-Cu基合金、Mg基合金、Ni-Ti合金等,虽然具有良好的可恢复性和耗能特性,但其需要特定的激励条件(如温度变化)才能发挥作用,这也在一定程度上制约了其应用范围.相较之下,Fe-Mn阻尼合金逐渐受到关注,主要因Fe-Mn合金不仅力学性能和阻尼性能优越,而且成本较低、加工性能良好,成为制备阻尼弹簧的理想材料.这使得Fe-Mn合金在满足市场对新型阻尼材料需求方面具有更大的潜力.

国内外学者针对化学成分、热处理温度、变形方式等因素对Fe-Mn合金阻尼性能的影响进行了广泛研究.对于化学成分,Lee等[10]研究了Mn含量对Fe-Mn合金阻尼性能的影响.结果表明,阻尼性能随Mn含量的增加而增加,在Mn的质量分数约为17%时达到最大值,然后随Mn含量的进一步增加而降低.与其他Fe-Mn合金相比,Fe-17Mn合金具有较高的γ单相的阻尼能力、γ/ε界面导致的阻尼能力和ε马氏体的体积分数,而ε马氏体被认为是最为重要的阻尼源.滕劲等[11]研究了C含量对合金阻尼性能的影响,研究表明,C元素的加入显著恶化了Fe-17Mn合金的阻尼性能.一方面C元素提高了合金的层错能,减少了合金中的层错数量,进而减少了合金阻尼源界面;另一方面,C原子作为间隙原子,易偏聚于层错区形成能力更低的铃木气团,钉扎阻碍阻尼源界面的移动,进一步降低了合金的阻尼性能.对于热处理温度,王世宏等[12]对Fe-19Mn合金在950~1 100 ℃固溶处理下的阻尼性能进行了研究.结果表明,随着温度的升高,合金中ε马氏体板条的尺寸逐渐增大,层错密度降低,ε马氏体与γ奥氏体界面的相对长度减小,从而导致阻尼性能的下降.对于冷变形,Huang等[13]研究了不同的应变幅和温度对Fe-19Mn合金冷拔固溶处理后阻尼性能的影响.研究发现,较小的冷变形可以增加合金中层错几率,从而提高阻尼性能;然而,较大的冷变形会导致ε马氏体与层错的相互交割,使不全位错的运动(脱钉)变得更加困难,从而降低了阻尼性能.此外,冷拉拔过程会导致Fe-Mn合金的位错密度增加,位错相互作用会阻碍晶格滑移,从而提高其强度.

Fe-Mn合金综合性能制备、弹簧卷绕特殊工艺及解析模型推导尚未有报道,制备的弹簧拓展了阻尼合金弹簧的产品类型.研究表明,当Fe-Mn合金中Mn的质量分数为17%时,其阻尼性能表现较好,因此本文选择了Mn的质量分数为17.77%的合金,并将C的质量分数控制在0.003%,得到具体牌号为Fe-17.77Mn-0.003C的合金.鉴于该合金的阻尼及力学性能尚无相关研究,探讨其加工工艺参数至关重要.本文旨在确定获得综合力学和阻尼性能最佳的Fe-Mn合金螺旋弹簧材料的制备工艺,并以此制造Fe-Mn合金螺旋弹簧,为其在实际应用中的阻尼性能研究奠定基础.

1 Fe-Mn合金的制备与测试

Fe-17.77Mn-0.003C合金的主要制备工艺如下.首先,采用真空感应炉熔炼制备钢锭.钢锭经1 150 ℃下进行热锻,终锻温度控制为880 ℃,如图1所示.随后,将锻态合金热轧至5 mm厚.热轧合金的加热温度分别为500、700、900、1 100 ℃,每级保温10 h,采用水冷WC方式冷却.最后,在室温下对热处理合金进行静态单向拉伸预变形,最大变形量为10%.该工艺旨在通过控制合金的加工过程优化其组织和性能.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   Fe-Mn合金锻造

Fig.1   Fe-Mn alloy forging


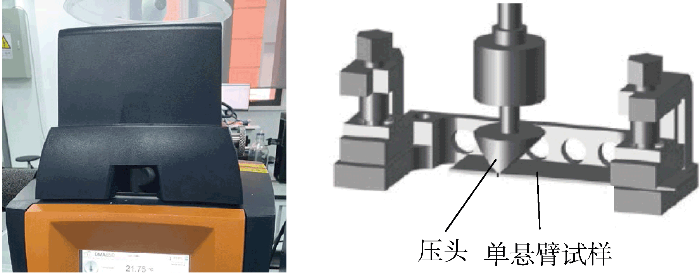
在振幅扫描实验条件下,室温( 20 ℃),采用单悬臂梁法,频率1 Hz、且应变幅值范围1×10-4~1×10-3,对尺寸为17.5 mm×7.9 mm×0.7 mm的材料进行阻尼性能测试.测试使用TA-Q850动态力学分析仪(dynamic mechanical analysis, DMA),如图2所示.通过测量损耗因子tan δ来表征材料的阻尼性能,其中δ为应力与应变的相位差角.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   TA-Q850动态力学分析仪

Fig.2   TA-Q850 dynamic mechanical analyzer


采用Instron5982型万能试验机对材料进行力学性能测试.拉伸试验按照GB/T 228.1—2010标准[14]进行.试验条件为:室温,具体拉伸速率为:在2%工程应变前,拉伸速率为0.5 mm/min,超过2%工程应变后,拉伸速率增加至3.75 mm/min,直至材料破坏.试样的工作截面尺寸为60 mm×10 mm,采用标距为40 mm的引伸计测量应变.

2 Fe-Mn合金材料的性能研究

2.1 热处理温度对Fe-Mn合金阻尼性能的影响

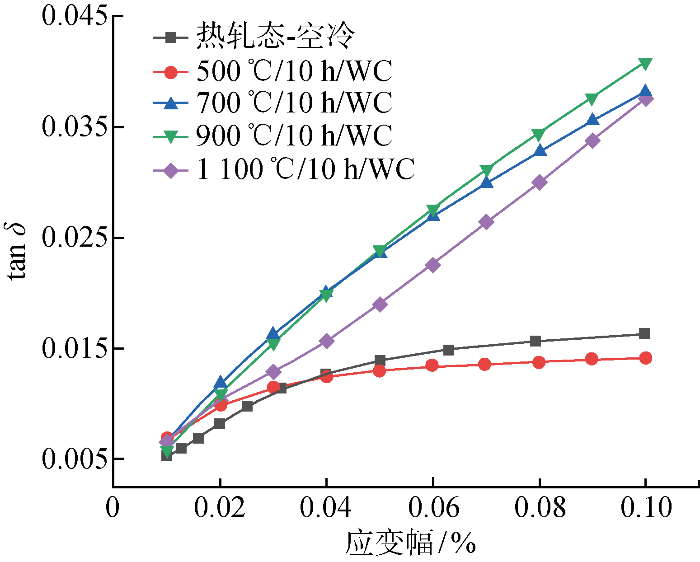
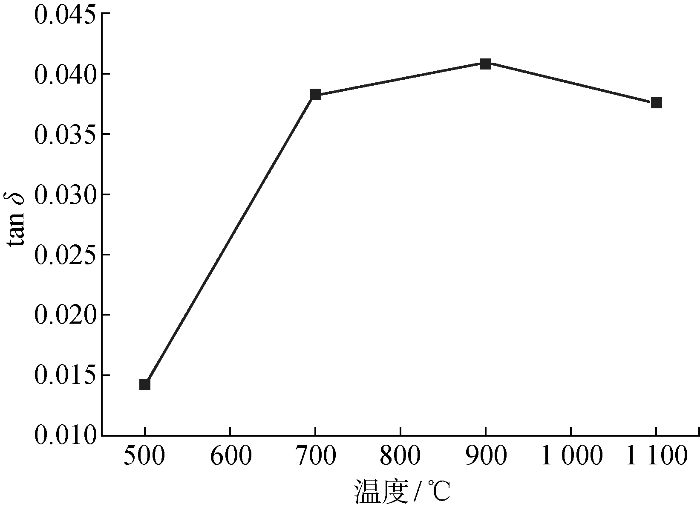
图3为Fe-Mn合金在500、700、900、1 100 ℃不同热处理温度下的阻尼性能的变化曲线.图4为1×10-3应变幅下损耗因子与热处理温度的关系.从图中可看出,当合金处于热轧态(as-hot-rolled)时,1×10-3应变幅下的损耗因子tan δ为0.016.这一现象归因于热轧变形在900 ℃以上,而Fe-Mn的奥氏体化温度低于900 ℃(As奥氏体转变开始点约为200 ℃,Af奥氏体转变结束点约为245 ℃),其在变形过程中发生完全奥氏体化,产生大量位错.冷却后,奥氏体化产生了不全位错的产生和滑移,降低了合金的阻尼性能.经500 ℃热处理后,1×10-3应变幅下的 tan δ 为0.014.相较于热轧试样略有下降,这可能是由于热处理温度较低,奥氏体化后组织未发生明显回复.在700~1 100 ℃温度范围内,合金的损耗因子随应变幅近似线性增加,随热处理温度的升高而呈现先升高后降低的趋势,在900 ℃时达到最大0.041.与900 ℃热处理试样相比,1 100 ℃试样的损耗因子有所降低,这可能是由于ε马氏体板条尺寸的增加,板条内的层错密度和ε马氏体/γ奥氏体界面长度相对减少,从而降低了损耗因子.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   不同热处理温度下损耗因子与应变幅曲线

Fig.3   Loss factor and strain amplitude curves at different heat treatment temperatures


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   1×10-3应变幅下损耗因子与热处理温度的关系

Fig.4   Relationship between loss factor and heat treatment temperature at 1×10-3 strain amplitude


2.2 预变形对Fe-Mn合金阻尼性能的影响

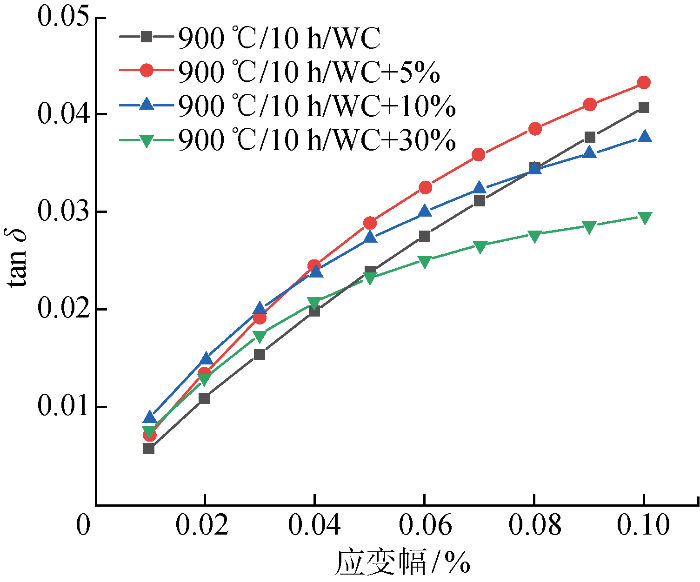
图5为不同预变形量(0%、5%、10%、30%)下应变幅度对Fe-Mn合金阻尼性能的影响.图6给出了Fe-Mn合金在应变幅为1×10-3时,损耗因子tan δ随预变形量的变化规律.合金仅热处理未预变形时,损耗因子为0.041;经过5%预变形后,损耗因子增到0.054,相比未预变形试样,较小的预变形增加了合金的层错几率,从而提高了合金的损耗因子.然而,当预变形量增至到10%和30%时,损耗因子分别下降到0.038和0.030,表明阻尼性能出现了明显的降低.较大的冷变形引起合金中ε马氏体与层错的相互交割,增加了不全位错(阻尼源)滑移的难度,从而降低了合金的损耗因子[13].

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   不同预变形下损耗因子与应变幅曲线

Fig.5   Loss factor and strain amplitude at different pre-deformations


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   0.1%应变幅下损耗因子与预变形量的关系

Fig.6   Relationship between loss factor and pre-deformation at 0.1% strain amplitude


根据上述实验分析可以得出,热处理温度为900 ℃,预变形量为5%对提高Fe-Mn合金的阻尼性能有显著效果.然而,对于制造Fe-Mn螺旋弹簧,除了阻尼性能外,还有其他重要的因素需要考虑,尤其是材料的力学性能和延伸率.适当的预变形可以调控晶粒尺寸和相变,从而影响材料的强度、硬度、延伸率等力学性能.这些特性对螺旋弹簧在使用过程中的稳定性和寿命有着重大的影响.因此,有必要研究预变形对Fe-Mn合金材料微观组织和力学性能的影响,以期获得综合力学性能和阻尼性能最佳的螺旋弹簧材料.

2.3 预变形后Fe-Mn合金的微观组织分析

图7显示了Fe-Mn合金在900 ℃/10 h/WC和900 ℃/10 h/WC+5%不同工艺处理后的界面分布.图中:红色实线代表ε马氏体变体界面;绿色实线代表ε马氏体孪晶界面.900 ℃/10 h/WC试样中的ε马氏体变体界面占大角晶界的比例为37.4%,ε马氏体孪晶界占大角晶界的比例为33.3%.在900 ℃/10 h/WC+5%试样中,ε马氏体变体界面占大角晶界的比例为39.7%,ε马氏体孪晶界占大角晶界的比例为32.7%.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   不同工艺处理后Fe-Mn合金界面分布

Fig.7   Fe-Mn alloy interface distribution after different process treatments


两种试样相比,900 ℃/10 h/WC试样和900 ℃/10 h/WC+5%试样中ε马氏体孪晶界占比均较高.基于微观组织的综合分析,900 ℃/10 h/WC+5%工艺制备的Fe-Mn合金基体中含有大量的阻尼源,包括奥氏体与ε马氏体两相之间的界面、奥氏体与ε马氏体层错之间的界面、ε马氏体变体之间的界面以及ε马氏体孪晶之间的界面,赋予了合金良好的阻尼性能[10].由于Fe-Mn合金阻尼能力与ε马氏体含量、层错密度、界面滑移以及奥氏体与ε马氏体界面等相关,难以量化精确表达.所以,本文仅从宏观角度比较预变形对Fe-Mn合金阻尼性能的影响.

2.4 预变形后的Fe-Mn合金的力学性能分析

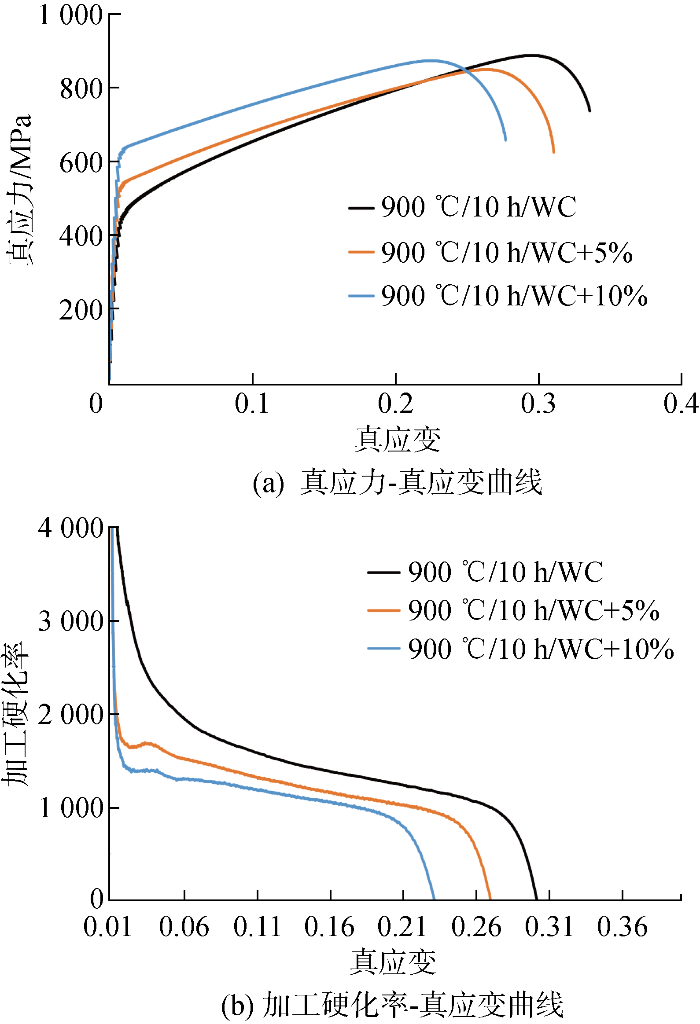
图8为Fe-Mn合金预变形后的应力-应变曲线.图8(a)为真应力-真应变曲线.结果表明,热处理后未经过预变形的试样具有较高的断后伸长率和较低的屈服强度.随着预变形量的增加,合金的断后伸长率逐渐降低,而屈服强度则逐渐增加.预变形使得合金的屈服强度显著增加,相较未预变形试样,5%预变形试样的屈服强度增加114 MPa,10%预变形试样的增加量高达208 MPa.相比之下,预变形对于Fe-Mn合金的抗拉强度的影响较小,5%预变形试样抗拉强度减少4 MPa,10%预变形试样抗拉强度增加42 MPa,均大幅小于屈服强度增加量.同时,预变形使断后伸长率有所降低,5%预变形试样的断后伸长率减少3.5%,10%预变形试样减少了8%.图8(b)为加工硬化率-真应变曲线.结果显示,热处理后未预变形试样具有较高的加工硬化率,然而,随预变形量的增加,合金的加工硬化率逐渐降低.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   Fe-Mn合金预变形后应力-应变曲线

Fig.8   Stress-strain curves of Fe-Mn alloy after pre-deformation


因此,为了使Fe-Mn合金材料同时具有良好的力学和阻尼性能及较高的延伸率,适合制造Fe-Mn螺旋弹簧,优选的合金制备优选900 ℃/10 h/WC+5%处理.实验结果表明,该工艺下的Fe-Mn合金在4×10-4应变幅下表现出良好的性能特征:损耗因子为3%,表现出高阻尼性能;屈服强度达到464 MPa,表明合金具有足够的抗变形能力;抗拉强度为656 MPa,表明合金在外力作用下的稳定性;断后伸长率达到36.5%,表明合金具有良好的延展性和韧性.与GB/T 1222—2016标准[15]中的70Mn弹簧钢(抗拉强度785 MPa,屈服强度450 MPa,断后伸长率8%,无阻尼特性)相比,Fe-Mn合金具有相近的力学性能,但断后伸长率提高了4.6倍,且具有良好的阻尼效果,适合作为耗能型螺旋弹簧的制造材料.

3 Fe-Mn合金螺旋弹簧的制备及测试分析

图9为Fe-Mn合金阻尼螺旋弹簧的制备过程及试样.Fe-Mn合金螺旋弹簧制备工艺如下.① Fe-Mn合金丝材制备:使用热轧方式制备Fe-Mn合金丝材,热轧温度控制在800~1 150 ℃范围内.通过拉伸试验机对2 m长丝材进行工程应变5%的预变形处理,以提高Fe-Mn合金丝材的力学和阻尼性能.② 使用辊压机或其他冷加工设备将磨光后的丝材冷加工成所需形状和尺寸的螺旋弹簧,确保每个弹簧的几何尺寸和机械性能符合设计要求.③ 热处理:对冷卷加工后的螺旋弹簧进行热处理.热处理温度一般为900~1 000 ℃,根据Fe-Mn合金的工艺要求,选择适当的保温时间和冷却方式,以调整弹簧的微观组织,提高其强度和耐久性.④ 冷卷热处理后的强压处理.由弹簧材料许用应力控制其强压变形产生的极限应力,采用循环强压处理提高材料的力学和阻尼性能.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   Fe-Mn合金螺旋弹簧的制备过程和试样

Fig.9   Preparation process and sample of Fe-Mn alloy helical spring


图10为Fe-Mn和65Mn螺旋弹簧锤击法试验图.对相同尺寸规格的弹簧(丝径12 mm、中径80 mm、自由高度110 mm、有效圈数5圈,支撑圈数1圈)进行试验.对每个弹簧施加10 kg的负载质量.采用数据采集和信号处理(DASP)多功能仪测试了由Fe-Mn和65Mn合金螺旋弹簧与质量块组成的弹簧质量阻尼系统的振动响应,并采用自振衰减法分析了其耗能能力.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   Fe-Mn和65Mn合金螺旋弹簧锤击试验

Fig.10   Fe-Mn and 65Mn alloy helical springs hammering test


根据GB/T15168—2013《振动与冲击隔离器静、动态性能测试方法》[16]和结构动力学理论[17],螺旋弹簧的动态损耗因子ηs可按对数衰减计算.其表达式如下:

ηs=$\frac{1}{N\mathrm{\pi }}$ln$\left(\frac{{x}_{i}}{{x}_{i+N}}\right)$

式中:xi、xi+N分别为第i个和第i+N个波峰的位移幅值,N为自振衰减波形的数量.

采用椭圆法对Fe-Mn合金螺旋弹簧和65Mn螺旋弹簧进行了静态压缩加卸载循环测试,如图11所示.试验条件为:加载变形速率15 mm/min,加载位移幅值25 mm,自由复位卸载,至少5次加卸载循环.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   Fe-Mn和65Mn合金螺旋弹簧静态加卸载测试图

Fig.11   Static loading and unloading test of Fe-Mn and 65Mn alloy helical springs


图12为耗能螺旋弹簧单个周期的能量耗散曲线.在该曲线中,OA加载曲线和卸载曲线所围成的闭环面积表示了一个加卸载循环过程中的损耗能量ΔW,可以通过积分来计算[18].

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   耗能螺旋弹簧单个周期的力-位移曲线

Fig.12   Force-displacement of energy dissipation helical spring in a single cycle


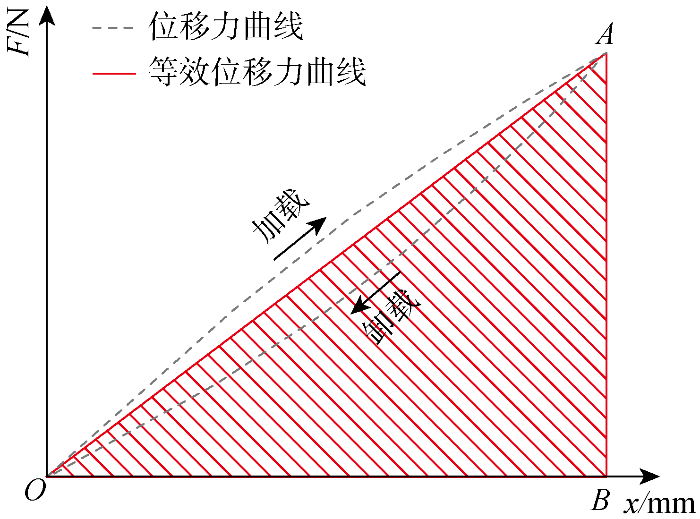
OA加载曲线下方的区域代表弹簧在一个周期内储存的最大变形能W,而OA等效刚度曲线绕x轴的三角形面积则由图中红色阴影区域表示,该区域代表在一个周期内储存的最大弹性势能U.滞回曲线直观地表示了阻尼合金材料在循环加卸载下的能量损耗情况.损耗因子是用来量化这类能量损耗的指标.静态损耗因子η的公式清楚地表明了材料在振动周期中损失与存储的能量之间的比例关系:

η=$\frac{\mathrm{\Delta }W}{\mathrm{\pi }U}$=$\frac{\mathrm{\Delta }W}{\mathrm{\pi }(W-\mathrm{\Delta }W/2)}$

当螺旋弹簧受到轴向载荷时,根据弹簧材料截面的受力解析模型[19-20]和Wahl[21]的机械弹簧理论,弹簧沿加载方向的轴向力F可由扭矩和弯矩的矢量和求得.弹簧材料的弹性应变能Vε可由弹簧丝截面的切应变和法向应变求得,分别为弹簧材料的扭转切应变能和弯曲正应变能.

为简化计算,Fe-Mn螺旋弹簧的升角α很小,α<9°.当承受轴向载荷时,其弯曲变形相对较小,可以忽略不计.因此,弹簧材料的弹性应变能可以等效为材料的扭矩应变能.假设弹簧横截面上远离圆心的任意一点的扭转切应力为τρ,弹簧材料截面应变为平均等效应变ε,考虑弹簧的曲度系数kw的影响,可以得到弹簧的弹性应变能Vε和平均等效应变ε:

$\begin{aligned}V_{\varepsilon}= & \int_{V} \frac{\left(\tau_{\rho}\right)^{2}}{2 G} \mathrm{~d} V=\int_{V} \frac{128 F^{2} D^{2} \rho^{2}}{G \pi^{2} d^{8}} \mathrm{~d} V= \frac{4 F^{2} D^{3} n}{G d^{4}}\end{aligned}$
$\varepsilon=\sqrt{\frac{k_{\mathrm{w}}^{2} G d^{2}}{2 E_{\pi}^{2} D^{4} n^{2}}} x$

式中:V、d、D、E、G、ρ、n和x分别表示弹簧的有效体积、丝径、中径、弹性模量、切变模量、密度、有效圈数和变形量.

4 Fe-Mn合金螺旋弹簧的阻尼性能研究

4.1 Fe-Mn与65Mn合金螺旋弹簧阻尼性能的比较

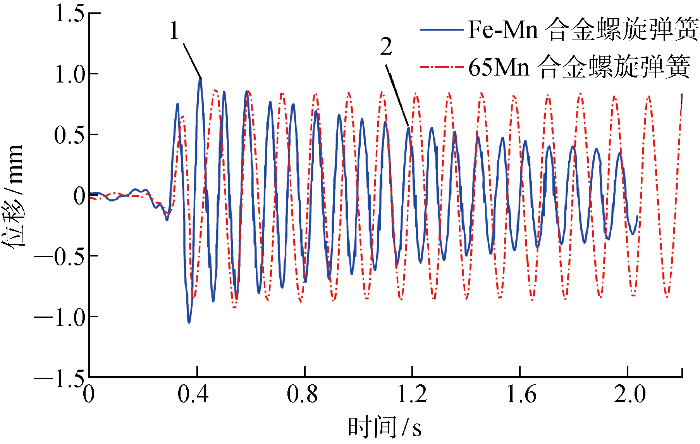
图13为 Fe-Mn和65Mn合金螺旋弹簧的位移时程曲线.弹簧质量减振系统中Fe-Mn合金螺旋弹簧和65Mn弹簧的自由振动位移时程曲线存在明显差异.波峰1到波峰2包含10个自振衰减波,其中两个峰值对应的位移幅值分别为 0.996 2 mm 和 0.562 8 mm.根据实测数据,Fe-Mn合金螺旋弹簧的动态损耗因子ηs=0.018 2,而65Mn螺旋弹簧的ηs=0.002.结果表明,Fe-Mn合金螺旋弹簧的动态损耗因子略高于65Mn螺旋弹簧.进一步分析可知,Fe-Mn合金螺旋弹簧的动态损耗因子ηs实际上受到负载和自身的弹性应变的影响.系统中配置单个弹簧与质量块,系统不稳定且负载质量有限,使得Fe-Mn合金螺旋弹簧产生的弹性应变幅值过小,导致阻尼性能无法充分发挥.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   Fe-Mn和65Mn合金螺旋弹簧的位移时程曲线

Fig.13   Displacement-time history curves of Fe-Mn and 65Mn alloy helical springs


图14为Fe-Mn和65Mn合金螺旋弹簧的加载-卸载循环力-位移特性曲线.Fe-Mn螺旋弹簧的加载和卸载曲线不重合,形成了一个闭合的迟滞环,等效刚度约为52 N/mm,损耗因子η=0.101 7.相比之下,65Mn螺旋弹簧的加载和卸载特性曲线重合,线性刚度约为72 N/mm,η=0.001,几乎没有耗能特性.在0~25 mm的循环压缩变形下,Fe-Mn合金螺旋弹簧的滞回曲线高度重合,卸载曲线可以回到原点,表明其在弹性范围内具有耗能作用.这一特性对于在压缩载荷中需要高耐久性和能量耗散能力的应用非常重要.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14   Fe-Mn和65Mn合金螺旋弹簧的力-位移特性曲线

Fig.14   Force-displacement characteristic of Fe-Mn and 65Mn alloy helical springs


4.2 Fe-Mn合金螺旋弹簧耗能特性分析

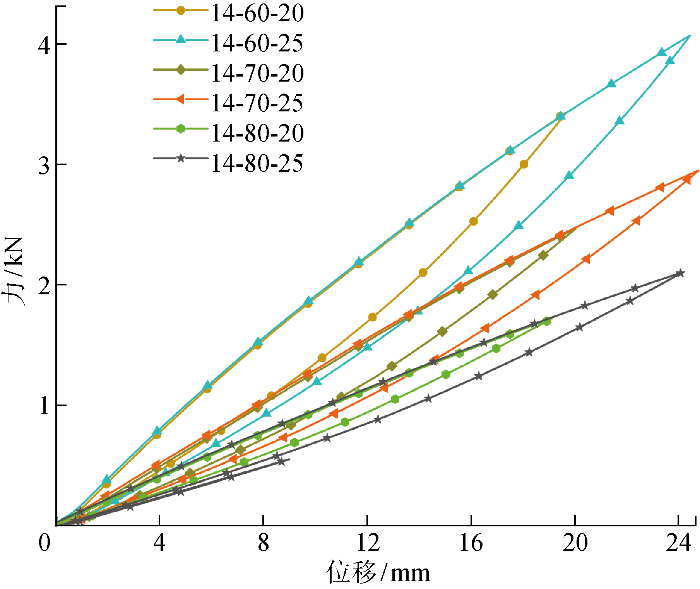
为了进一步研究Fe-Mn合金螺旋弹簧的压缩变形与耗能效果之间的关系,对不同规格(丝径 14 mm,中径60、70、80 mm,自由高度160 mm,有效圈数5圈,支撑圈数1圈)的Fe-Mn合金螺旋弹簧进行静态加载-卸载循环试验.

不同中径Fe-Mn合金螺旋弹簧的循环加卸-载特性曲线,如图15所示.图中线型标注以14-60-20为例,数字分别代表弹簧的丝径为14 mm,中径为60 mm,加载位移幅值为20 mm. Fe-Mn合金螺旋弹簧的耗能能力随着位移幅值的增加而增强.对于相同丝径和中径的螺旋弹簧,其加载曲线在不同位移幅下呈现良好的重合性,加载刚度呈现非线性下降.对比图14和图15,在相同位移条件下,Fe-Mn弹簧的耗能能力随丝径增加而增大,而随中径的增大而减小.这表明Fe-Mn弹簧的耗能特性受到材料阻尼特性和弹簧几何参数的共同影响.可以通过增强材料阻尼特性、增大弹簧的丝径或减小中径来提高Fe-Mn弹簧的阻尼性能.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15   不同中径Fe-Mn合金螺旋弹簧的循环特性曲线

Fig.15   Cyclic characteristics of Fe-Mn alloy helical spring with different middle diameters


图16为14-60-Fe-Mn合金螺旋弹簧的循环加卸载特性曲线.在一定的位移幅度下,Fe-Mn弹簧的滞回曲线面积随着位移幅的增加显著增大.当位移幅从5 mm增加到30 mm时,Fe-Mn弹簧的耗散能量从52.8 N·mm增加到 17.320 3 kN·mm,展现出其显著的耗能能力.这一现象的产生是因为在压缩变形过程中,Fe-Mn合金弹簧材料的应变幅随着位移的增大而增大,从而增强了材料的“内耗”能力.这与理论预期一致,即在一定的应变幅度范围内,Fe-Mn合金材料的耗能能力(损耗因子)与其应变幅呈正相关.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16   14-60-Fe-Mn合金螺旋弹簧循环加卸载特性曲线

Fig.16   Cyclic loading and unloading characteristics of 14-60-Fe-Mn alloy helical spring


通过对14-60-Fe-Mn合金螺旋弹簧试验特性曲线进行位移积分和最小二乘法数据拟合,得到了如图17所示的Fe-Mn合金螺旋弹簧能量曲线.在位移幅为20 mm时,Fe-Mn弹簧的弹性应变能为 30.044 13 kN·mm,而试验卸载段的弹簧储能为 30.641 68 kN·mm,相对误差为1.95%.同时,当Fe-Mn弹簧的位移幅从5 mm增加到20 mm时,其理论等效平均应变幅从0.07%增加到0.3%.此时,弹簧的理论应变能曲线与试验卸载段的弹簧储能曲线近似重合.结果表明,在0.3%应变幅下,Fe-Mn螺旋弹簧的弹性应变能可以通过其材料的扭转应变能等效来理论预测,而不需进行具体的弹簧试验,这有助于进一步指导Fe-Mn螺旋弹簧的设计.但当Fe-Mn螺旋弹簧的加载应变幅超过0.3%时,其理论计算的应变能低于试验卸载段的能量,且随着变形量的增加,两者之间的误差逐渐增大.表明在较大应变幅时,Fe-Mn弹簧的弯曲应变能不能被忽略.

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17   14-60-Fe-Mn合金螺旋弹簧能量曲线

Fig.17   Energy curves of 14-60-Fe-Mn alloy helical spring


根据螺旋弹簧的解析模型和能量守恒,螺旋弹簧的外力做功W近似等于弹簧材料的弹性应变能.对于具有能量耗散特性的Fe-Mn螺旋弹簧,外力所做的功应等于弹簧的弹性应变能Vε与耗散能ΔW之和:

$W=V_{\varepsilon}+\Delta W=\frac{4 F^{2} D^{3} n}{k_{\mathrm{w}} G d^{4}}+\Delta W$

测得Fe-Mn材料的弹性模量为205.5 GPa,泊松比为0.244,切变模量为82.6 GPa.通过拟合14-60-Fe-Mn弹簧的几何参数及其能量曲线,得到了加载力与位移之间的二次非线性关系:

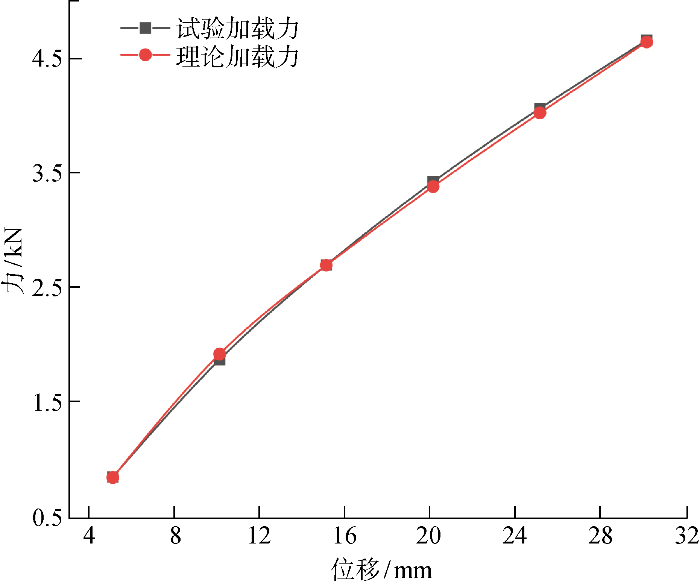
$\begin{aligned}F= & \sqrt{\frac{k_{\mathrm{w}} G d^{4}}{4 n D^{3}}} \times \sqrt{11.67 x^{2}+420.03 x-1663.87}\end{aligned}$

将14-60-Fe-Mn弹簧的试验加载力位移曲线与用式(6)计算的力位移曲线进行比较,如图18所示.结果表明,在5~30 mm弹簧变形范围内,两者的误差范围为0.07%~2.63%,吻合较好.该理论解析模型能较好地反映14-60-Fe-Mn弹簧力学性能,并能利用理论计算简化及节省试验过程,提高工程应用效率.

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18   14-60-Fe-Mn合金螺旋弹簧加载力与位移的关系曲线

Fig.18   Relationship between loading force and displacement of 14-60-Fe-Mn alloy helical spring


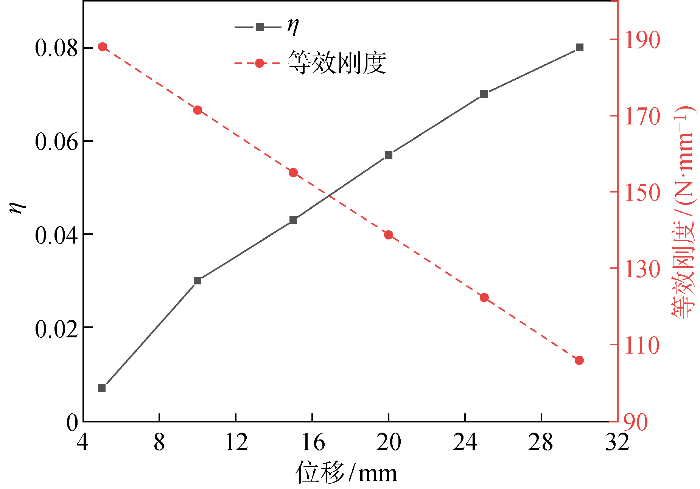
图19为14-60-Fe-Mn合金螺旋弹簧的等效刚度和损耗因子随位移变化的关系曲线,通过对Fe-Mn合金弹簧的耗能特性进行分析,可知Fe-Mn弹簧的损耗因子随着位移的增加呈现非线性增长趋势.采用最小二乘法对数据进行拟合,得到Fe-Mn弹簧的损耗因子与位移的指数关系符合

η=1 754·exp(x/12.3)-2 914.7

拟合系数R2=0.997.表明模型具有良好的拟合效果,能量的耗散率沿着压缩变形方向遵循指数衰减规律.此外,Fe-Mn合金螺旋弹簧的等效刚度随着位移的增加呈现线性减小,这与弹簧材料在变形过程中耗能增加的一般特征一致.

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19   14-60-Fe-Mn合金螺旋弹簧等效刚度和损耗因子与位移的关系曲线

Fig.19   Relationship of equivalent stiffness and loss factor with displacement of 14-60-Fe-Mn alloy helical spring


5 结论

(1) 综合考虑合金的阻尼性能和力学性能,得到了Fe-Mn合金螺旋弹簧材料的最佳处理工艺参数.

(2) 阻尼性能测试表明,在相同激励条件下,Fe-Mn合金螺旋弹簧的静态循环试验损耗因子为 0.101 7,相较于65Mn螺旋弹簧的 0.001 0,显示出明显的优越性能;在锤击试验中,Fe-Mn弹簧的位移时程曲线衰减较快,也表现了显著的耗能效果.

(3) 基于螺旋弹簧的功能原理和解析模型,研究了Fe-Mn合金螺旋弹簧的耗能特性.结果表明,在一定的加载位移幅下,Fe-Mn合金的耗能能力随着位移幅的增加而显著增强.对于等效应变幅小于0.3%的情况,可以通过弹簧材料的扭转应变能对其耗能特性进行理论预测.

(4) 利用最小二乘法对数据进行拟合,得到Fe-Mn合金螺旋弹簧的损耗因子与位移的关系式:

η=1 754×exp(x/12.3)-2 914.7, R2=0.997

结果表明,损耗因子随着变形量的增加呈指数增长,而等效刚度随位移的增加而线下降低,表现出明显的软化特性.

(5) Fe-Mn弹簧的耗能特性与材料的阻尼特性和几何参数有关.通过改善弹簧材料阻尼性能、增大弹簧的丝径或减小中径,可以有效提升Fe-Mn弹簧的阻尼性能.

参考文献

张英会, 刘辉航, 王德成. 弹簧手册(精)[M]. 第3版. 北京: 机械工业出版社, 2017.

[本文引用: 1]

ZHANG Yinghui, LIU Huihang, WANG Decheng. Spring manual[M]. 3rd ed. Beijing: Machinery Industry Press, 2017.

[本文引用: 1]

汪志昊, 华旭刚, 陈政清, 等.

基于微型永电磁式涡流阻尼TMD的人行桥模型减振试验研究

[J]. 振动与冲击, 2014, 33(20): 129-132.

[本文引用: 1]

WANG Zhihao, HUA Xugang, CHEN Zhengqing, et al.

Experimental study on vibration control of a model footbridge by a tiny eddy-current tuned mass damper magnets

[J]. Journal of Vibration and Shock, 2014, 33(20): 129-132.

[本文引用: 1]

尹学军, 彭雪平, 王伟强.

某1 000 MW等级核电半速机组弹簧基础的设计与振动实测

[J]. 武汉大学学报, 2013 (Sup. 1): 236-240.

[本文引用: 1]

YIN Xuejun, PENG Xueping, WANG Weiqiang.

Design and vibration measurement for 1 000 MW half speed nuclear power spring supported T/G foundation at an NPP

[J]. Journal of Wuhan University, 2013 (Sup. 1): 236-240.

[本文引用: 1]

蔡龙奇, 李毅, 何伟, 等.

阻尼合金的研究发展现状

[J]. 金属功能材料, 2021, 28(2): 15-28.

[本文引用: 1]

CAI Longqi, LI Yi, HE Wei, et al.

Research and progress in damping alloys

[J]. Metallic Functional Materials, 2021, 28(2): 15-28.

[本文引用: 1]

叶卫林. Fe-Mn基阻尼合金的马氏体相变与阻尼性能[D]. 哈尔滨: 哈尔滨工程大学, 2018.

[本文引用: 1]

YE Weilin. Martensitic transformation and damping characteristic of Fe-Mn based damping alloys[D]. Harbin: Harbin Engineering University, 2018.

[本文引用: 1]

王怡鑫, 徐洋, 盛晓伟, 等.

基于锰铜高阻尼合金弹簧的反作用轮隔振器性能研究

[J]. 振动与冲击, 2023, 42(14): 314-320.

[本文引用: 1]

WANG Yixin, XU Yang, SHENG Xiaowei, et al.

Performance of reaction wheel vibration isolator with isolator a spring made of manganese-copper high damping alloy

[J]. Jorunal of Vibration and Shock, 2023, 42(14): 314-320.

[本文引用: 1]

朱锐, 毛保全, 赵俊严, 等.

机枪遥控武器站锰铜基阻尼合金缓冲器非线性有限元分析及试验

[J]. 北京理工大学学报, 2022, 42(9): 935-946.

[本文引用: 1]

ZHU Rui, MAO Baoquan, ZHAO Junyan, et al.

The nonlinear finite element analysis and txperiment of Mn-Cu damping alloy buffer for remote control weapon station

[J]. Journal of Beijing University of Technology, 2022, 42 (9): 935-946.

[本文引用: 1]

WANG W, FANG C, FENG W, et al.

SMA-based low-damage solution for self-centering steel and composite beam-to-column connections

[J]. Journal of Structural Engineering, 2020, 146(6): 04020092.

[本文引用: 1]

辛泰阿, 苏明杨, 李诗成, 等.

固溶热处理对Fe-Mn金属橡胶力学性能的影响

[J]. 现代制造工程, 2022, 504(9): 82-90.

[本文引用: 1]

XIN Taia, SU Mingyang, LI Shicheng, et al.

Effect of solution heat treatment on the mechanical proformance of Fe-Mn metal rubber

[J]. Modern Manufacturing Engineering, 2022, 504 (9): 82-90.

[本文引用: 1]

LEE Y K, JUN J H, CHOI C S.

Dammping capacity in Fe-Mn binary alloys

[J]. ISIJ International, 1997, 37(10): 1023-1030.

[本文引用: 2]

滕劲, 李宁, 宋顺远, 等.

C对Fe-Mn阻尼合金组织及性能的影响

[C]// 2011中国功能材料技术与产业论坛. 重庆,中国:2011.

[本文引用: 1]

TENG Jin, LI Ning, SONG Shunyuan, et al.

Effect of C on microstructure and damping capacity of Fe-Mn alloys

[C]// Proceedings of 2011 China Functional Materials Technology and Industry Forum. Chongqing, China: Scientific Research Publishing, 2011.

[本文引用: 1]

王世宏, 李健, 柴锋, 等.

固溶温度对Fe-19Mn合金的γ→ε相变和阻尼性能的影响

[J]. 金属学报, 2020, 56(9): 1217-1226.

DOI:10.11900/0412.1961.2020.00005      [本文引用: 1]

采用动态机械分析仪(DMA)对Fe-19Mn合金经950~1100 ℃固溶处理后的的阻尼性能进行了测试，利用OM和TEM观察了显微组织的演变，利用XRD进行了物相分析和不同类型层错几率的计算。结果表明：经固溶处理的Fe-19Mn合金的阻尼性能随振幅的增加呈近似线性增加，且振幅小于临界振幅A' (A'≈30 μm)时的阻尼性能变化符合G-L位错模型，振幅高于A'时的阻尼性能变化与微塑性变形有关。随着固溶温度的升高，Fe-19Mn合金的阻尼性能降低，其中经950 ℃固溶处理后的阻尼性能最好。在不同的振幅范围内，其阻尼性能呈现不同的变化特征：当振幅小于等于170 μm时，阻尼性能呈指数形式降低，并且与ε-马氏体中的形变层错几率的变化趋势相似，此时Fe-19Mn合金的阻尼性能主要受ε-马氏体中的形变层错边界的影响；当振幅大于170 μm时，阻尼性能呈线性降低，并且与γ/ε相界面相对长度的变化趋势相似，此时Fe-19Mn合金的阻尼性能随固溶温度的变化主要受γ/ε相界面的影响。由γ-奥氏体中的层错观察可知，γ-奥氏体中的层错边界对Fe-19Mn合金的阻尼性能随振幅的变化无明显贡献。

WANG Shihong, LI Jian, CHAI Feng, et al.

Influence of solution temperature on γ→ε transformation and damping capacity of Fe-19Mn alloy

[J]. Acta Metallurgica Sinica, 2020, 56(9): 1217-1226.

DOI:10.11900/0412.1961.2020.00005      [本文引用: 1]

Due to the high damping capacity and excellent mechanical properties, Fe-Mn alloy is considered to be a promising high damping alloy, and suitable for constructional and vehicle metal parts application, which can enhance the fatigue property of structures and metal parts, and also improve the working and living environment. It's generally accepted at present that damping capacity of Fe-Mn alloy is influenced by the stacking fault boundaries in γ-austenite and ε-martensite, γ/ε phase boundaries and ε/ε variant boundaries; another view is that boundaries of the above damping sources are made up of partial dislocations, so the damping capacity of Fe-Mn alloy is caused by the motion of partial dislocations, and interpreted by G-L dislocation pinning model and stacking fault probabilities calculation. But there is no distinction between the probabilities of different type stacking faults. Both deformation stacking fault and growth stacking fault can be formed in γ-austenite and ε-martensite, and the change of process parameters has different influence on them, which will lead to different changes of deformation and growth stacking fault probabilities. So it's necessary to analyze whether boundaries of different stacking fault types will have different effects on damping capacity of Fe-Mn alloy. Based on that, a hot-rolled Fe-19Mn alloy is prepared and then solution treated between 950~1100 ℃. Damping capacity is measured by dynamic mechanical analyzer (DMA). The microstructure evolution is observed by OM and TEM, and XRD is used to analyze phase constitution and to measure stacking fault probabilities. The results reveal that Fe-19Mn alloy shows amplitude-dependent damping capacity which almost linearly increases with amplitude, and frequency-independent damping capacity. From G-L plot, the variation of damping capacity below the critical amplitude A' (A'≈30 μm) is interpreted by G-L model, while it's associated with micro-plastic deformation when above A'. As the increase of solution treatment temperature, the damping capacity of Fe-19Mn decreases, and possesses the best performance at 950 ℃; furthermore, it shows different characteristics in different amplitude ranges: when the amplitude is lower than 170 μm, damping capacity decreases in exponential form, which changes similarily with deformation stacking fault probability in ε-martensite, so it can be considered the boundaries of deformation stacking fault as the main damping source; when the amplitude is higher than 170 μm, damping capacity decreases linearly, which changes similarily with the relative length of γ/ε phase boundary, so it can be considered γ/ε phase boundary as the main damping source. Based on TEM observation of stacking faults in γ-austenite, it can be inferred that stacking fault boundaries in γ-austenite have no obvious contribution to the change of damping capacity of Fe-19Mn with amplitude.

HUANG S K, ZHOU D C, LIU J H, et al.

Effects of strain amplitude and temperature on the damping capacity of an Fe-19Mn alloy with different microstructures

[J]. Materials Characterization, 2010, 61(11): 1227-1231.

[本文引用: 2]

全国钢标准化技术委员会(SAC/TC 183). 金属材料拉伸试验第1部分——室温试验方法: GB/T 228.1—2021[S]. 北京: 中国标准出版社, 2021.

[本文引用: 1]

National Steel Standardization Technical Committee (SAC/TC183). Tensile test of metal materials Part 1—Room temperature test method: GB/T 228.1—2021[S]. Beijing: China Standard Press, 2021.

[本文引用: 1]

全国钢铁标准化技术委员会(SAC/TC 183). 弹簧钢: GB/T 1222—2016[S]. 北京: 中国标准出版社, 2016.

[本文引用: 1]

National Iron and Steel Standardization Technical Committee (SAC/TC183). Steel Standardization Technical Committee (SAC/TC183). Spring steel: GB/T 1222—2016[S]. Beijing: China Standard Press, 2016.

[本文引用: 1]

全国机械振动, 冲击与状态监测标准化技术委员会(SAC/TC 53). 振动与冲击隔离器静、动态性能测试方法: GB/T 15168—2013[S]. 北京: 中国标准出版社, 2013.

[本文引用: 1]

National Technical Committee for Standardization of Mechanical Vibration, Shock and Condition Monitoring (SAC/TC 53). Vibration and shock isolator static and dynamic performance test method: GB/T 15168—2013[S]. Beijing: China Standard Press, 2013.

[本文引用: 1]

张亚辉. 结构动力学基础[M]. 大连: 大连理工大学出版社, 2007.

[本文引用: 1]

ZHANG Yahui. Basis of structural dynamics[M]. Dalian: Dalian University of Technology Press, 2007.

[本文引用: 1]

HU J, DU Q, GAO J, et al.

Compressive mechanical behavior of multiple wire metal rubber

[J]. Materials & Design, 2018, 140: 231-240.

[本文引用: 1]

姜晗, 于超, 康国政.

富氢环境下镍钛形状记忆合金弹簧变形行为的实验和理论研究

[J]. 力学学报, 2023, 56(2): 422-432.

[本文引用: 1]

JIANG Han, YU Chao, KANG Guozheng.

Experimental and theoretical study of the deformation behavior for NiTi shape memory alloy spring under hydrogen-rich environment

[J]. Theoretical and Applied Mechanics, 2023, 56(2): 422-432.

[本文引用: 1]

ENEMARK S, SANTOS I F, SAVI M A.

Modelling, characterisation and uncertainties of stabilised pseudoelastic shape memory alloy helical springs

[J]. Journal of Intelligent Material Systems and Structures, 2016, 27(20): 2721-2743.

[本文引用: 1]

WAHL A. Springs[M]. New York, USA: McGraw-Hill, 1963.

[本文引用: 1]

/

〈 〉